Pathway hunting by random survival forests

Abstract

Motivation: Pathway or gene set analysis has been widely applied to genomic data. Many current pathway testing methods use univariate test statistics calculated from individual genomic markers, which ignores the correlations and interactions between candidate markers. Random forests-based pathway analysis is a promising approach for incorporating complex correlation and interaction patterns, but one limitation of previous approaches is that pathways have been considered separately, thus pathway cross-talk information was not considered.

Results: In this article, we develop a new pathway hunting algorithm for survival outcomes using random survival forests, which prioritize important pathways by accounting for gene correlation and genomic interactions. We show that the proposed method performs favourably compared with five popular pathway testing methods using both synthetic and real data. We find that the proposed methodology provides an efficient and powerful pathway modelling framework for high-dimensional genomic data.

Availability: The R code for the analysis used in this article is available upon request.

Contact: xi.steven.chen@gmail.com

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

High-throughput genomic technologies, such as gene expression microarrays, single nucleotide polymorphism arrays and next-generation sequencing have revolutionized biological and medical research by making it possible to measure thousands to millions of biomarkers across the genome simultaneously. However, detecting meaningful signals and making appropriate inferences from these massive datasets remains challenging because of the high dimensionality and complex correlation and interactions that are at play.

To reduce dimensionality, and to increase statistical test power, pathway (or gene set) analysis has become increasingly popular. Instead of applying statistical tests to one gene at a time, pathway analysis takes advantages of previous biological knowledge and examines the gene expression patterns of a group of related genes (e.g. grouped by biological functions) for their associations with disease outcomes. Since the well-known gene set enrichment analysis (GSEA) method (Mootha et al., 2003; Subramanian et al., 2005) was published, a number of pathway analysis approaches have been developed, including parametric analysis of gene set enrichment (Kim and Volsky, 2005), averaged t-statistic gene set scores (Tian et al., 2005), the maxmean statistic for improved GSEA (Efron and Tibshirani, 2007), the random-sets method (Newton et al., 2007), mixed-effects models (Wang et al., 2008, 2009) and principal components (Chen et al., 2008; Tomfohr et al., 2005). Web-based pathway tools, such as DAVID (Huang et al., 2009), GeneTrail (Backes et al., 2007) and the online GSEA interface at the Broad Institute, are also widely used.

Although pathway analyses are designed to test effects from multiple genes in place of single genes, typically they rely on test statistics based on simple summary statistics (e.g. the mean) of individual genes that ignore correlation between genes, and more importantly, gene–gene interactions. Recent genomic studies have demonstrated the importance of gene–gene interactions and gene networks for complex diseases (Cordell, 2009; Horvath et al., 2006; Moore and Williams, 2009; Schadt et al., 2008) that are not being addressed with these methods.

One recent pathway analysis method for modelling gene–gene relationships makes use of random forests (RF) (Breiman, 2001) by constructing RF for genes in each pathway and ranking pathways based on prediction accuracy. This method automatically incorporates two-way or high-order genes interactions effects with marginal association patterns (Pang et al., 2006, 2010).

However, a limitation of these RF pathway approaches is that they ignore genes outside of the targeted pathway. Complex diseases often result from multiple pathway disturbances and interactions. A well known example is the Ras pathway, which activates multiple signalling pathways to drive uncontrolled proliferation in cancer (McCormick, 1999). Therefore, a single pathway may not fully explain phenotype variations in complex diseases. Goeman and Buhlmann (2007) discussed the need to include genes outside the gene sets for pathway testing, and they indicated these should be dependent on biological hypothesis. The ideal solution is to combine all available candidate pathway gene expression data together for RF modelling. However, finding a reliable gene importance measure for ultra-high-dimensional genomic data and resolving the computational issues in RF are challenging.

In this article, we propose a new pathway hunting algorithm for survival outcomes using random survival forests (RSF) (Ishwaran et al., 2008) that prioritize important pathways by accounting for transcriptome-wise gene correlations and interactions. In Section 2, we describe the RSF framework, a minimal depth measure of variable importance, our pathway hunting algorithm and a testing procedure for pathway analysis. In Section 3.1, we show that our method performs favourably compared with five popular pathway testing methods using a simulation study. We illustrate the pathway hunting approach in Sections 3.2 and 3.3 using two microarray survival datasets involving colon cancer and ovarian cancer. Section 4 presents a summary discussion.

2 METHODS

2.1 Random survival forests

RF (Breiman, 2001) is a non-parametric ensemble tree learning method that has become increasingly popular for genetic and gene expression data analyses (Diaz-Uriarte and de Andres, 2006; Lunetta et al., 2004; Pang et al., 2006). An RF ensemble comprises randomly grown recursively partitioned binary trees. Each tree is grown from an independent bootstrap sample. Trees are generally grown deeply, and during the tree growing process, each node is split using a randomly selected subset of variables. These features enable RF to reduce both bias and variance.

RSF is a new extension of RF to right-censored survival data settings (Ishwaran et al., 2008). RSF possesses similar properties to RF. It is a data adaptive procedure able to model non-linear effects and complex interactions among features. These properties make it an attractive tool for the analysis of complex survival data. RSF has been successfully applied to cancer staging and integrative genomic modelling (Chen et al., 2010; Ishwaran et al., 2009; Weichselbaum et al., 2008).

In this article, RSF models were constructed using the following four steps:

1. A total of ntree independent bootstrap samples are drawn. Each bootstrap sample excludes on average 36.8% of the original data, called out-of-bag (OOB) data. For each bootstrap sample, a single random survival tree is grown.

2. When growing the tree, at each tree node, mtry variables are randomly selected. A maximum of nsplit split-points are chosen randomly for each of the mtry variables. The node is split by finding the variable that maximizes the log-rank test across its nsplit randomly selected split points (in our examples, we used nsplit equal to 10).

3. Each survival tree is grown to full size under the constraint that the minimum number of unique event times in a node is no smaller than the integer nodesize.

4. The forest ensemble is the tree-averaged cumulative hazard function. The predicted value mortality is defined as the forest cumulative hazard function summed over the event times.

All RSF models in this article were calculated using the R-package randomSurvivalForest. Default settings for the software were used except for nsplit, which was set to 10 (as stated earlier in the text).

2.2 Minimal depth

A useful feature of RF is that it provides a rapidly computable internal measure of variable importance (VIMP) that can be used for ranking features. To calculate VIMP for a variable, the given variable is randomly permuted in the OOB data, and the permuted OOB data are dropped down the tree. OOB prediction error is then calculated. The difference between this estimate and the OOB error without permutation (i.e. from the original tree), averaged over all trees, is the VIMP of the variable. The larger the VIMP of a variable, the more predictive the variable (Breiman, 2001). VIMP has been widely used to rank predictors in microarray expression and genetic association data analysis.

Recently, Ishwaran et al. (2010) described a new high-dimensional variable selection method based on a tree concept referred to as minimal depth which measures the importance of a variable in terms of its splitting behaviour relative to the root node. This avoids directly working with prediction error and is non-randomized, which makes it possible to provide a theoretical basis for selecting variables (something that is not available with VIMP). The minimal depth of a variable v is the depth at which the variable first splits within a tree, relative to the root node. The smaller the minimal depth, the more predictive the variable.

Denote the minimal depth for a variable v by D_v. In high-dimensional sparse settings under the assumption that v is noisy (i.e. is unrelated to the outcome), it was shown (Ishwaran et al., 2010) that for 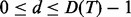, where 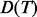is the depth of the tree ,

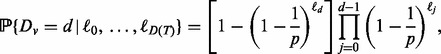(1)

where 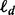equals the number of non-terminal nodes at depth d and p equals the number of features.

Minimal depth selection selects a variable v if its tree-averaged minimal depth is less than or equal to the mean of D_v under the distribution (1). Although Equation (1) is conditional on the tree-node values 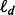, which are unknown, in practice, is estimated using forest averaged values. This makes minimal depth selection easily and rapidly computable in practice. The performance of minimal depth variable selection was systematically compared with VIMP in Ishwaran et al. (2011). The results repeatedly demonstrated superiority to VIMP. Thus, we use minimal depth to measure importance of a gene in this article.

2.3 Pathway hunting

Although minimal depth is reliable in moderately high-dimensional settings, it is still difficult to obtain accurate measurements in ultra-high-dimensional scenarios (Ishwaran et al., 2010). To overcome this dimensionality problem, we propose a minimal depth pathway hunting approach adapted from the variable hunting method of Ishwaran et al. (2010). The algorithm consists of the following steps:

1. Split the data into training and test sets (we used 80 and 20%, respectively).

2. Select P genes randomly from all available genes p. The default setting is P = p/5 when P < 1000, otherwise P = 1000.

3. Fit a survival forest, 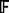, to the training data using P genes.

4. Determine the minimal depth for each of the P genes.

5. Calculate the test set prediction error of 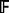using the test data.

6. Repeat step 1–5 B times.

7. Determine the average minimal depth for each of the p genes from the B RF.

8. Compute the pathway minimal depth by averaging the minimal depth of all genes within the given pathway. The smaller the averaged pathway minimal depth measure, the more important the pathway.

The algorithm breaks the ultra-high-dimensional feature space into more manageable subspaces to better estimate the minimal depth for each gene. The number of replicates B generally needs to be large enough to fully span all genes. In this article, we set B = 200 for all analyses. A pathway-ranked list of genes can be obtained using the ordered pathway level minimal depth values.

2.4 Pathway significant testing

For significance testing of pathways, permutation tests that permute sample labels are often used. However, this approach is too computationally extensive with RSF, as it requires that the entire pathway hunting steps be repeated for each permutation sample. Instead, we shall adopt the random-set enrichment scoring framework (Newton et al., 2007) to analyse pathway minimal depth. Specifically, for a given pathway with m genes, we calculate its entire set of gene minimal depth values 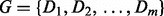. We define the enrichment score for the pathway to be 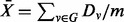. We test the null hypothesis that 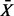is not different from the mean of a random set of m distinct genes drawn randomly from a total of p genes representing the genome background. When p is large, the distribution of minimal depth is approximately Gaussian. Applying the δ method, we obtain

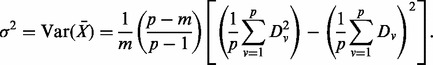The null hypothesis can be tested by comparing the standardized pathway minimal depth enrichment score to a standard normal distribution. Small values of Z indicate a pathway enriched with predictive genes.

3 RESULT

3.1 Simulation studies

We use simulation studies to assess the effectiveness of the RSF pathway hunting method for identifying pathways with gene–gene interactions. We compare our method with several well-known pathway analysis methods. We focus on a pathway cross-talk simulation, as it poses a difficult scenario for standard pathway approaches.

We set n = 250 for the sample size and P = 500 for the number of genes. For each observation, expression values for the p genes 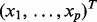were generated from a multivariate normal distribution with mean zero and autoregressive correlation structure 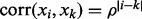for two genes i and k. The 500 genes were divided into 50 pathways with 10 genes each. The survival time of each sample was generated based on six randomly selected causal genes 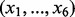from an exponential distribution with mean

(2)

where the coefficient was set at β = 8. Censoring times were drawn independently from an exponential distribution with mean 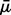, the average of μ over the samples.

To simulate pathways associated with the survival outcomes, we designed two scenarios. In the first scenario, there was one disease associated pathway and three of the six causal genes (x₁,x₂,x₃) were randomly selected from the 10 genes in Pathway 1, and genes (x₄,x₅,x₆) were randomly selected from the remaining 490 genes. Under this simulation set-up, Pathway 1 was the only disease associated pathway. Note, genes x₄,x₅,x₆ were disease associated genes, but not located within the causal pathway (i.e. Pathway 1).

In the second scenario, there were two causal pathways that included disease associated genes. Genes (x₁,x₂,x₃) were again randomly selected from Pathway 1, whereas genes (x₄,x₅,x₆) were randomly selected from another single pathway, which was drawn randomly from the remaining 49 pathways. Both pathways were considered as disease associated pathways in this case. In each of two cases aforementioned, the correlation parameter ρ was 0.5, 0.7 and 0.9. We repeated each of the six simulation scenarios 100 times independently.

We compared the performance of our RSF pathway hunting approach to five other pathway testing methods. These included (i) the random-set method (Newton et al., 2007) implemented in the R-package allez; (ii) Fisher’s exact test, where the threshold for classifying significant genes was set at a nominal P-value of 0.05 obtained from univariate Cox regression modelling of a gene; (iii) GSEA (Subramanian et al., 2005) implemented using the javaGSEA program available from the Broad Institute at http://www.broadinstitute.org/gsea/downloads.jsp; (iv) the maxmean test (Efron and Tibshirani, 2007) implemented in the R-package GSA; and (v) the RSF pathway approach Pwayrfsurvival of Pang et al. (2010) based on single pathways.

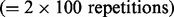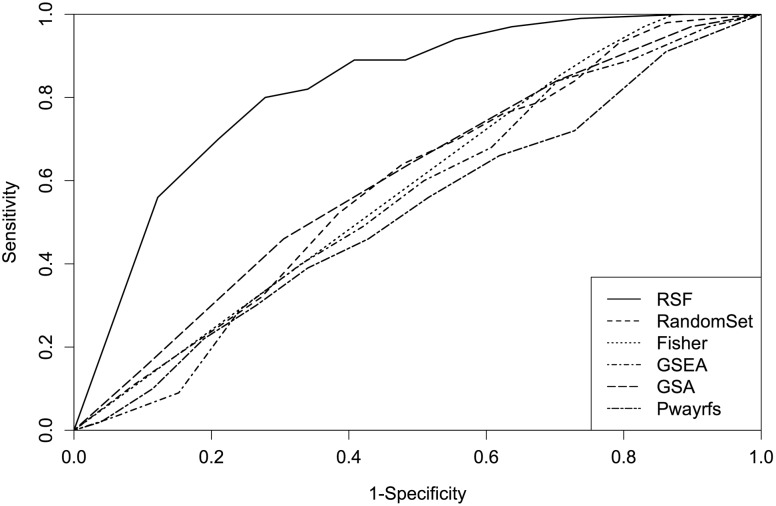
In the first scenario, there was one disease associated pathway in each simulation dataset (or repetition); therefore, there were 100 pathways associated with the survival outcome and 49 × 100 = 4900 control pathways. In the second scenario, there were two disease associated pathways in each simulation dataset; therefore, there were 200 survival outcome associated pathways and 4800 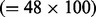control pathways. In each scenario, the P-values obtained for these 5000 pathways were then used to compute the receiver operator characteristics (ROC) curves. These show the trade-off between sensitivity and specificity as the threshold for declaring a significant pathway varies. To compare the overall discriminative abilities of the methods over all possible cut-offs, we calculated the area under the ROC curve (AUC). Table 1 records the AUC under all six simulation scenarios. We find that our RSF method (denoted simply as RSF) significantly outperforms all other methods. Figure 1 displays the ROC curves of all six methods for scenario 2 of Table 1. RSF sensitivity is better across all levels of specificities.

Table 1.

Simulation study results comparing RSF, random-set, Fisher’s exact test, GSEA and Pwayrfsurvival (abbreviated as Pwayrfs)

Scenario	No. of casual pathway	ρ	AUC
			RSF	Random-set	Fisher	GSEA	GSA	Pwayrfs
1	1	0.5	0.805	0.595	0.585	0.512	0.580	0.502
2	1	0.7	0.838	0.590	0.584	0.550	0.607	0.524
3	1	0.9	0.917	0.562	0.575	0.597	0.552	0.555
4	2	0.5	0.809	0.586	0.585	0.540	0.531	0.507
5	2	0.7	0.886	0.587	0.595	0.528	0.570	0.536
6	2	0.9	0.959	0.615	0.586	0.544	0.598	0.522

Note: No. of casual pathway, the number of pathway used for generating survival outcomes; ρ: Correlation parameter.

Fig. 1.

Comparison of performances of RSF, random-set, Fisher’s exact test, GSEA, GSA and Pwayrfsurvival using simulated expression data. This figure shows the ROC curves for simulation scenario 2 of Table 1

We also performed another simulation study based on a real gene expression dataset, GSE17538 (with 250 patients), pulled from the NCBI GEO database. Three BioCarta and KEGG pathways with sizes 10, 21 and 43 were selected as the causal pathways for comparison. These were chosen as all had similar pairwise gene correlations (∼0.17; see the Supplementary Material). Then 37 pathways were randomly chosen as background pathways. The number of genes for all 40 pathways was 987. We designed the following three simulations. Genes (x₁,x₂,x₃) were randomly selected from 10 genes in Pathway 1, and genes (x₄,x₅,x₆) were randomly selected from the remaining 977 genes. These represent the x-variables in the simulation. Then survival times and censoring status for the x-variables were generated as in Equation (2) with β = 15. A similar procedure was applied to Pathways 2 and 3, with the number of causal genes set to 12 and 26, where half of them were from the causal pathway and the rest were from other genes. Each simulation was repeated 100 times. The AUC values from the simulation results are shown in Table 2. Once again, the RSF pathway hunting method has the best performance.

Table 2.

Simulation study results comparing RSF, random-set, Fisher’s exact test, GSEA and Pwayrfsurvival using real microarray data

Pathway	AUC
	RSF	Random-set	Fisher	GSEA	GSA	Pwayrfs
1	0.868	0.608	0.537	0.554	0.653	0.628
2	0.856	0.527	0.534	0.581	0.511	0.624
3	0.861	0.560	0.501	0.505	0.510	0.606

3.2 Colon cancer data

For our next example, we applied the RSF pathway hunting method to a colon cancer gene expression data (Smith et al., 2010). The data were from 223 colorectal adenocarcinoma patients from the Vanderbilt Medical Center and Moffitt Cancer Center. All patients had disease-free survival outcomes. The gene expression data comprise 54 675 probes based on Affymetrix HGU133 plus 2.0 expression chip. The data are available from the NCBI GEO database (accession no. GSE17538). A collection of 403 pathways, including 186 KEGG pathways (www.genome.jp/kegg) and 217 BioCarta pathways (www.biocarta.com), were used for the analysis.

For each pathway, we calculated a nominal P-value based on our pathway hunting method, as well as an adjusted P-value controlled using the false discovery rate (FDR) (Benjamini and Hochberg, 1995). Table 3 lists the top pathways controlled at a 0.2 FDR threshold. For comparison, the data were also analysed using the previous five methods (see Supplementary Material). It is interesting that several of the listed pathways, including extracellular matrix (ECM) receptor interaction, focal adhesion and the transforming growth factor-beta (TGF-β) signalling, were also ranked as top pathways by the comparison methods. For GSEA and GSA, the smallest adjusted P-values were 0.311 and 0.423, respectively. The top pathways identified by random-set were those related to central nervous system degenerative disorders, such as Parkinson and Alzheimer’s disease.

Table 3.

Top pathways for colon cancer data identified by RSF using a 0.2 FDR cut-off

Pathway term	Size	P-value	FDR
PPAR signalling pathway	68	6.82E-11	2.75E-08
Adipocytokine signalling pathway	66	2.08E-06	0.00042
Leptin pathway	11	6.91E-06	0.00092
ECM receptor interaction	83	8.78E-05	0.00884
mTOR signalling pathway	23	0.00046	0.037
TGF-β signalling pathway	83	0.001	0.068
Focal adhesion	196	0.002	0.101
P53hypoxia pathway	22	0.004	0.179
Tryptophan metabolism	39	0.005	0.179
P53 pathway	16	0.005	0.179
VEGF pathway	29	0.005	0.179

The P53 pathway, vascular endothelial growth factor (VEGF) pathway and TGF-β signalling pathway listed in Table 3 are well-known to be involved in cancer development and metastasis. The most significant pathway identified by RSF is the peroxisome-proliferator-activated receptor (PPAR) signalling pathway. PPARs are ligand-activated transcription factors that belong to the nuclear-hormone-receptor family, and the PPARs family is composed of three isotypes, including PPARα, PPARβ/δ and PPARγ. The association between activation of PPARγ and the growth and differentiation of colon cancer has been shown in different experimental models (Gupta et al., 2004; Sarraf et al., 1998; Yang and Frucht, 2001). The PPAR signalling pathway is closely linked with other top pathways in carcinogenesis. For example, the adipocytokine signalling pathway and the leptin pathway are key mediators in adipose tissue for inflammation and immune response. It has been shown that the increased incidence of colon cancer with a high-fat diet could be caused by activation of PPARγ by fatty acids (Wasan et al., 1997). The level of PPARα and PPARγ can be controlled by adiponectin and leptin, which are two adipocytokines (Qian et al., 1998; Yamauchi et al., 2003). Suppression of the TGF-β signalling pathway is regulated by PPARγ (Lee et al., 2008). It has been suggested that p53 mediates the PPARγ ligand-induced apoptosis (Nagamine et al., 2003). There is evidence suggesting that PPARβ/δ and PPARγ mediate VEGF induction in colorectal tumour (Rohrl et al., 2011).

This analysis suggests that the PPAR signalling pathway is not only associated with survival in colon cancer patients, but that it may also play a hub-role in connecting with other important pathways. PPARγ agonists, such as thiazolidinediones, have been discovered to have anticancer effects for multiple cancer types (Michalik et al., 2004; Ondrey, 2009).

3.3 Ovarian cancer data

As another example, we applied RSF pathway hunting to an ovarian cancer gene expression dataset (Bonome et al., 2008). The analysis was based on tumour tissues obtained from 185 stage III and IV ovarian cancer patients using Affymetrix HGU133A expression chip with 22 823 probes (GEO accession no. GSE26712). We used the same 403 KEGG and BioCarta pathways as in the colon cancer data analysis. Table 4 lists pathways meeting an FDR threshold of 0.1 from our RSF method. For the inositol phosphate metabolism and phosphatidylinositol signalling system pathways, PIK3CA had been identified as an oncogene in ovarian cancer, and clinical trial data support that inositol hexaphosphate (IP6) plus inositol can enhance the anticancer effect of chemotherapy and slow tumour metastasis (Shayesteh et al., 1999; Vucenik and Shamsuddin, 2003). Extrinsic (cytoplasmic) and intrinsic (mitochondrial) pathways are apoptosis signal transduction pathways in cancer cells and are targets of variety of anticancer chemotherapies (Fulda and Debatin, 2006). In contrast, GSA and Fisher’s exact test did not find any significant pathways associated with survival outcomes (see the Supplementary Material).

Table 4.

Top pathways for ovarian cancer data identified by RSF using a 0.1 FDR cut-off

Pathway term	Size	P-value	FDR
ECM receptor interaction	81	1.29E-09	5.20E-07
Focal adhesion	190	5.74E-06	0.00088
Inositol phosphate metabolism	49	6.55E-06	0.00088
Phosphatidylinositol signalling system	70	2.48E-05	0.002
Endocytosis	163	2.70E-05	0.002
Intrinsic pathway	23	2.54E-03	0.014
Regulation of actin cytoskeleton	195	2.56E-03	0.026
Fc gamma R-mediated phagocytosis	88	5.34E-03	0.026
Adipocytokine signalling pathway	63	8.88E-03	0.039
Acute myeloid leukaemia	57	0.001	0.057
Par1 pathway	36	0.002	0.063
Leukocyte transendotheial migration	106	0.003	0.089
Extrinsic pathway	13	0.003	0.095
AMI pathway	20	0.003	0.098

The most interesting findings were the top two pathways: ECM receptor interaction and focal adhesion, which were also among our top pathways from the colon cancer analysis. Focal adhesions are macromolecules that mediate the regulatory effects of ECM, which connects cells within most tissues. Signalling between cells and ECM is essential for cell migration, proliferation and survival. Cross-talk between tumour cells and the microenvironment of the local host is critical for development of tumours (Liotta and Kohn, 2001). Knowledge and control of the microenvironment become more important for understanding the mechanism of carcinogenesis and developing effective chemotherapy (Albini and Sporn, 2007).

The importance of the ECM pathway agrees well with another recent study. To increase power for detecting pathway-level perturbations, Krupp et al. (2011) conducted a large-scale gene expression meta-study that combined 649 tumour samples from >1400 experiments and 58 tumour types. Even though there were only 39 ovarian cancer samples and no colon cancer samples in this combined dataset, ECM receptor interaction and PPAR signalling pathway were significantly enriched and conserved across tumour types.

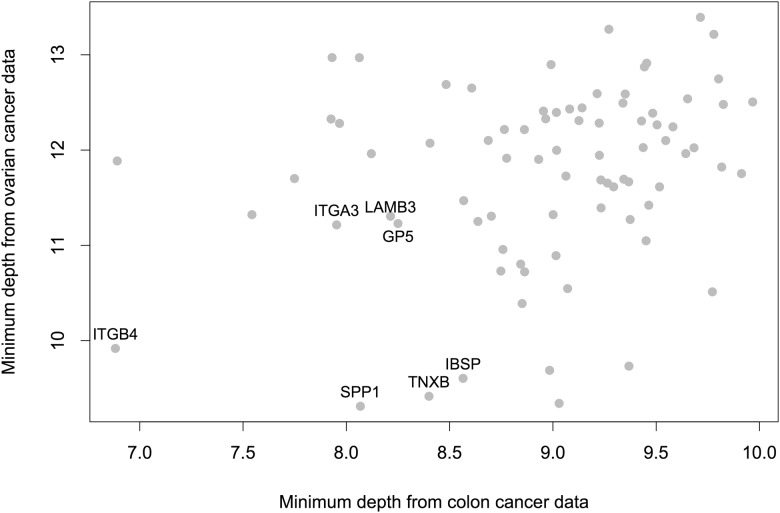
The important genes within each pathway can be screened using minimal depth. For the ECM receptor interaction pathway, the minimal depth of all genes within the pathway from both colon cancer and ovarian cancer is plotted in Figure 2. The overlapping genes from the first quartile of each data are labelled with their gene symbols. These genes can be further evaluated and used as biomarkers for metastasis risk prediction in multiple cancer types.

Fig. 2.

Minimal depth plot for genes in ECM receptor interaction pathway using both colon cancer and ovarian cancer data. Top overlapping genes are labelled by their gene symbols

4 DISCUSSION

Complex diseases are generally the consequences of interactions from multiple genes and pathways. Although pathway enrichment and association testing approaches have been developed, because of computational and statistical modelling challenges, the information from gene–gene interactions are either ignored or restricted to within an individual pathway.

In this article, we presented a novel RSF pathway hunting method for identifying and ranking the importance of pathways for their association with survival outcome. The proposed method is based on a new measure of variable importance, termed minimal depth, which has been shown to be an efficient and effective method for variable selection in high dimensions (Ishwaran et al., 2010, 2011). Our RSF pathway hunting approach is capable of capturing both marginal gene effects and gene–gene interactions at the genome level, and it approximates the complexity of the transcriptome by taking advantage of a priori biological knowledge.

In our simulation studies, we specifically designed scenarios where censored survival outcomes were associated with gene interactions and pathway cross-talk. The RSF approach outperformed standard well-known procedures. In our real data analyses involving colon and ovarian cancer, RSF identified key pathways. These findings indicate that the RSF pathway hunting algorithm can identify essential cancer signalling pathways with a relatively small sample size.

In summary, we have described a new method to model complex gene–gene interactions and multiple interactions between pathways, integrated within a traditional pathway analysis framework. It can be further extended to model different phenotypes, such as categorical or continuous outcomes. This new approach helps to expand the scope of current pathway analysis to understand the complexities underlying diseases.

Funding: X.C. was funded in part by grant R01CA158472 from the National Cancer Institute. H.I. was funded in part by DMS grant 1148991 from the National Science Foundation and grant R01CA163739 from the National Cancer Institute.

Conflict of Interest: none declared.