Nonlinear Modeling of Dynamic Interactions within Neuronal Ensembles using Principal Dynamic Modes

Abstract

A methodology for nonlinear modeling of multi-input multi-output (MIMO) neuronal systems is presented that utilizes the concept of Principal Dynamic Modes (PDM). The efficacy of this new methodology is demonstrated in the study of the dynamic interactions between neuronal ensembles in the Pre-Frontal Cortex (PFC) of a behaving non-human primate (NHP) performing a Delayed Match-to-Sample task. Recorded spike trains from Layer-2 and Layer-5 neurons were viewed as the “inputs” and “outputs”, respectively, of a putative MIMO system/model that quantifies the dynamic transformation of multi-unit neuronal activity between Layer-2 and Layer-5 of the PFC. Model prediction performance was evaluated by means of computed Receiver Operating Characteristic (ROC) curves. The PDM-based approach seeks to reduce the complexity of MIMO models of neuronal ensembles in order to enable the practicable modeling of large-scale neural systems incorporating hundreds or thousands of neurons, which is emerging as a preeminent issue in the study of neural function. The “scaling-up” issue has attained critical importance as multi-electrode recordings are increasingly used to probe neural systems and advance our understanding of integrated neural function. The initial results indicate that the PDM-based modeling methodology may greatly reduce the complexity of the MIMO model without significant degradation of performance. Furthermore, the PDM-based approach offers the prospect of improved biological/physiological interpretation of the obtained MIMO models.

1 Introduction

The study of neuronal ensemble activity and the quantitative understanding of neural function remain challenging goals that rely on effective mathematical/computational methodologies to advance scientific knowledge and enable the design of advanced neuroprostheses (Schwartz 1990; Abeles 1991; Anderson 1991; Berger et al. 1994, 2001, 2005, 2010; Deadwyler & Hampson 1995, 2006; Churchland & Sejnowski 1999; Anderson & Eliasmith 2004; Marmarelis 2004). The early use of “integrate-and-fire” models was useful in the exploratory phase but it soon reached its limits of utility because of its intrinsic limitations in representing the actual neuronal dynamics with adequate fidelity (Koch & Segev 1989; Eeckman 1992; Anderson 1996). These limitations are also evident in the use of “generalized linear models” which can only describe a restricted set of neuronal characteristics (Dobson 2002). On the other hand, detailed compartmental approaches in the mold of the Hodgkin-Huxley model or its variants, such as the Fitzhugh-Nagumo, Morris-Lecar and Hindmarsh-Rose models (Hodgkin & Huxley 1952; Fitzhugh 1955, 1969; Nagumo et al. 1962; Morris & Lecar 1981; Hindmarsh & Rose1984; Koch & Segev 1989; Johnston & Wu 1997; Abbott 1999; Koch 1999; Hille 2001; Izhikevich 2007) were proven rather cumbersome to be practically useful in the context of large-scale neuronal ensembles. In addition, these elaborate models describe only the generation of action potentials and leave out the important neuronal processes of synaptic transmission, somatodendritic integration and axonal propagation. The introduction of perceptron-type artificial neural networks (Rosenblatt 1962; Koch & Segev 1989; Widrow & Lehr 1990; Eeckman 1992; Dobson 2002) or Hopfield-type recurrent neural networks (Hopfield 1982; Hertz et al. 1991) generated initial excitement which, however, dissipated upon realizing that these formulations were not necessarily meaningful representations of the dynamics of actual neural systems. Thus, there exists a need for modeling methodologies that can balance the dual requirements of fidelity to actual neural function and feasibility within a practical context. This paper is a contribution in the great effort to develop a general and rigorous methodology that can yield parsimonious models of neuronal ensembles in a practical experimental and computational context that can represent the actual neural function with adequate fidelity in a manner amenable to biological/physiological interpretation. We take the view that such Multi-Input/Multi-Output (MIMO) models must be based on experimental time-series data and be able to predict the output of multi-unit neuronal systems to arbitrary inputs of multi-unit neuronal activity (Song et al. 2007, 2009; Zanos et al. 2008, 2009; Berger et al. 2010, 2011).

Recent years have seen rapid progress on many fronts of computational neuroscience. The latter must be viewed as distinct from connectionist approaches of artificial intelligence and machine learning (e.g. artificial neural networks), because it seeks functional/computational descriptions (dynamic models) of biologically realistic neurons and neural systems. These models must capture the essential functional characteristics of the neural systems that are observed at multiple spatio-temporal scales in order to allow formulation of scientific hypotheses that can be tested though properly designed experiments. This task is complicated by the experimental difficulty of collecting neuronal activity data from multiple neurons simultaneously – a limitation that is gradually overcome with the advent of reliable multi-electrode arrays and spike-sorting algorithms. Thus, we are currently at the stage of scientific developments in this area where the main limiting factor has become the availability of effective data analysis and modeling methods, instead of the data collection task. Thoughtful treatments of this subject, although lacking the benefit of multi-unit recordings, have been published (e.g. Amit 1989; Koch & Segev 1989; Schwartz 1990; Abeles 1991; Eeckman 1992; Anderson 1996; Churchland & Sejnowski 1999; Arbib 2003) These studies did not have the full benefit of actual multi-unit recordings and were confined, by necessity, to the detailed modeling study of single neurons and only theoretical or conjectural explorations of the broader problem of neuronal ensemble modeling (e.g. Abeles’ “synfire chain” theory). Within the vast literature on the structure and function of the central nervous system, the work that explicitly addresses the issue of quantitative/predictive modeling of the dynamic interrelationships among neuronal ensembles based on actual data includes statistical, Bayesian and information theoretic methods (Barbieri et al. 2001; Borst & Theunissen 1999; Brockwell et al. 2004; Brown et al. 2004; Knill & Pouget 2004; Lewicki 2008; MacKay 1995; Rieke et al. 1997; Theunissen et al. 1996; Victor & Brown 2003). Considerable progress has also been achieved in the case of sensory systems, where early nonlinear modeling studies of the visual system (Marmarelis & Naka 1972, 1973, 1974; Marmarelis & Marmarelis 1978; Citron et al. 1981, 1983, 1988; Emerson et al. 1987,1992) and of the auditory system (Eggermont et al. 1983, 1993) led to sophisticated studies of spatio-temporal receptive fields (Cottaris & DeValois 1998; Dan et al. 1998; David & Gallant 2005; Pack et al. 2006; Wu et al. 2006) and spectro-temporal receptive fields (Lewis & van Dijk 2004; Atencio & Schreiner 2008, 2010). An important note ought to be made regarding the considerable literature on Artificial Neural Networks which, although shares some of the issues of biological neural networks and has found useful computational applications, does not represent in our opinion a faithful or credible representation of the actual networks of neuronal ensembles. We also note some recent interesting work on structural large-scale modeling of brain regions (Izhikevich 2007; Izhikevich and Edelman 2008; Lytton 2008) that is based in part on actual data.

Our research group has had a strong interest in the study of neuronal interconnections in the hippocampus. Over the last 25 years, we have conducted a series of experimental and modeling studies that have sought to elucidate our understanding of the dynamic (nonlinear) interrelationships among the various regions of the hippocampus (Berger et al. 1988, 1994, 2010; Deadwyler & Hampson 2004, 2006; Hampson et al. 2003, 2004, 2011; Marmarelis & Berger 2005; Song et al. 2007, 2009; Dimoka et al. 2008; Zanos et al. 2008, 2009; Marmarelis et al. 2009). The causal relationship between the activity of neuronal ensembles in the CA3 and CA1 regions has been quantified by MIMO models estimated from experimental data recorded via multi-electrode arrays in the hippocampus of rodents performing specific behavioral tasks (Song et al. 2007, 2009; Zanos et al. 2008, 2009). These models have been validated through their predictive capability and the efficacy of model-based multi-unit stimulation patterns to induce specific behavioral responses (Berger et al. 2011, 2012; Hampson et al. 2012; Marmarelis et al. 2011).

Notwithstanding the success of our previous efforts, the challenge of practicable “scaling up” of this approach to large populations of neurons remains a formidable task. When the number of input-output neurons rises into the hundreds or thousands, the complexity of the current MIMO model begins to test our computational limits. For this reason, considerable efforts have been dedicated to exploring rigorous ways to compact the MIMO models without compromising performance. The work presented herein is part of this effort and concerns the use of the concept of Principal Dynamic Modes (PDM) that has been recently introduced by our group and applied successfully to various other physiological systems (Marmarelis 2004). In the PDM modeling approach, we seek to determine a set of basis functions (the PDMs) that represent an efficient “coordinate system” for the canonical representation of the general nonlinear (Volterra-like) model of a given system. The PDMs are obtained from the input-output data following a rigorous methodology that is outlined below. To complete the nonlinear MIMO model, we must also estimate the associated nonlinear functions (ANF) representing the nonlinear transformation of the PDM outputs, as well as the cross-terms of the MIMO model that represent the interactions among the various inputs as they impact each output. Thus, the PDM modeling approach separates the representation of system dynamics (PDMs) from its nonlinearities (ANFs) and inter-modulation characteristics (cross-terms).

An additional benefit of the PDM-based modeling approach is that it offers the potential means for biological/physiological interpretation of the obtained MIMO model. This is enabled by examining the form of the obtained PDMs (which describe the dynamic characteristics of the system) and the obtained ANFs (which describe the interneuronal connectivity). For instance, it was found that the frequency-domain representations of the PDMs exhibit resonant peaks at the well-known neural rhythms (delta, theta, alpha, beta, gamma) that have been associated in numerous previous studies with specific sensory, motor and cognitive functions. Since a significant ANF indicates an active connection between the respective Layer 2 (input) and Layer 5 (output) neurons of the pre-frontal cortex (Opris et al. 2011), the specific form of the respective PDM suggests the transfer of specific type of neural information between the corresponding input and output (e.g. a PDM with a theta-band resonant peak channels information related to memory functions and sensorimotor integration). Phase-locked rhythmic activity has been observed in distant brain regions, suggesting a critical role of neural rhythms in achieving cortical synchronization and corroborating the temporal coding hypothesis in neural information processing. The latter is the fundamental conceptual and scientific context within which MIMO modeling can be interpreted in terms of neuronal function – thus making the PDMs a useful interpretational tool for understanding and dissecting neural function. Based on published experimental observations of neuronal spiking activity, local-field potentials (LFPs), electroencephalography (EEGs) and magnetoencephalography (MEGs) during behavioral tasks, there is growing acceptance of the view that cognitive functions (e.g. sensorimotor integration, memory, attention, decision making and perception) rely on neural rhythms to coordinate the timing of neuronal firing (Jacobs et al. 2007). Specific neural rhythms have been associated with specific sensorimotor and/or cognitive functions. The interpretation of PDM-based MIMO models in terms of neural rhythms is elaborated further in the Discussion section.

This paper presents the PDM-based MIMO modeling methodology in the case of neural systems with point-process inputs and outputs (spike trains) and demonstrates its efficacy using data of neuronal ensemble activity collected from a small number of neurons (4 inputs and 4 outputs) in the pre-frontal cortex (PFC) of two non-human primates. The results hold promise in terms of model compaction that, if confirmed in additional studies, can achieve the ultimate goal of large-scale neural modeling and biological/physiological interpretability.

2 Methodology

We seek to obtain parsimonious representations of nonlinear MIMO (Volterra-like) canonical models that are able to describe the dynamic nonlinear transformations of arbitrary spatio-temporal input-output data (i.e. spike-trains from multiple neurons of neuronal ensembles). We propose to achieve this by use of the concept of PDMs. The proposed methodology starts with a previously developed method (Marmarelis 1993; Marmarelis & Orme 1993; Marmarelis 1997) for efficient estimation of Volterra kernels using Laguerre expansions for Volterra models of the relationship between each observed output and its inputs (Marmarelis 2004).

To determine the PDMs of the input-output relationship of interest from the respective estimated self-kernels, we follow a three-step procedure: (1) we perform eigen-decomposition on all second-order self-kernels and retain only the “significant” eigen-vectors that correspond to absolute eigen-values larger than 10% of the maximum absolute eigen-value (this threshold value was determined empirically by observing the decline of absolute eigen-values in the results); (2) we construct a rectangular matrix composed of all the first-order kernels and all the selected significant eigen-vectors of the second-order self-kernels weighted by the corresponding eigen-values for all inputs and outputs; and (3) we perform singular value decomposition (SVD) of this rectangular matrix (using the standardized Matlab SVD algorithm) and select the significant singular vectors by applying the previously described selection criterion to the respective singular values. The selected singular vectors are the PDMs of the MIMO model connecting each output to its respective inputs and represent an efficient kernel expansion basis for all input-output dynamic relationships in the subject system. Since we are interested in a MIMO model that is valid during various phases of a behavioral task (e.g. the Sample Presentation and the Match Presentation phases of the Delayed-Match-to-Sample task of this study), we must obtain the “global” PDMs of the MIMO model by “fusing” the respective PDMs for the various phases. This is done by applying SVD to a rectangular matrix composed of the relevant PDMs and selecting the most significant singular vectors according to the previously described threshold criterion applied to the respective singular values. The selected “global” PDMs contain the essential dynamic components of the functional characteristics of the MIMO system and serve as a “functional coordinate system” for compact model representation and, at the same time, facilitate the biological/functional interpretation of the obtained model. Fusion of PDMs may also occur across different tasks and different animals.

In order to complete the estimation of the PDM-based MIMO model, we must also determine the associated nonlinear functions (ANFs) which represent the amplitude nonlinearities of the system, as well as the cross-terms of the MIMO model that represent the interactions among the various inputs as they impact each output. The ANF of each (global) PDM is evaluated by computation of the ratio of the histogram of the specific PDM output values that correspond to a spike at the respective output divided by the histogram of all PDM output values (i.e. the ANF may be viewed as the conditional probability of having an output spike given a specific value of the respective PDM output). The computed ratios are smoothed with a three-point moving average to redress abrupt changes in the ANF form due to the inadvertent roughness of the histograms caused by the relative sparsity of the experimental data.

The cross-terms of the MIMO model are determined on the basis of a statistical significance test of the correlation coefficient between the respective output and each product of all possible pairs of PDM outputs. This statistical significance test employs the w-distribution of the correlation coefficient under the null hypothesis that there is no correlation between a given pair product of PDM outputs and the respective output (Marmarelis & Marmarelis 1978). A cross-term is included in the MIMO model when this null hypothesis is rejected on the basis of the available data. The coefficients of the selected significant cross-terms are then estimated via least-squares regression on the output spike-train, where the sum of the ANF outputs are also taken into account as another regression variable (for calibration purposes). The efficacy of this approach has been tested and validated with simulated examples where “ground truth” is available.

The predictive performance of the PDM-based MIMO model is evaluated through the computation of Receiver Operating Characteristic (ROC) curves which are the most commonly used evaluation tools in studies where true-positive predictions must be balanced against false-positive predictions (e.g. telemetry/detection systems, diagnostic/clinical procedures and modeling of systems with point-process outputs – such as the spike-trains generated by neural systems). In this procedure, the numbers of true-positive and false-positive predictions (normalized by the total number of bins with or without an output spike respectively) are plotted against each other for each putative threshold value of the threshold-trigger operator TT, which incorporates an exponential refractory component. The two parameters (initial amplitude and time-constant) of this refractory component of the TT operator are determined by maximizing the area under the ROC curve, which is often used as an index of performance. We take the view that it is more relevant to consider only the values of the ROC curve for low probability of false-positive predictions (e.g. up to 25 false-positives in this study), so that the model-predicted spike-trains are not inundated by false-positives.

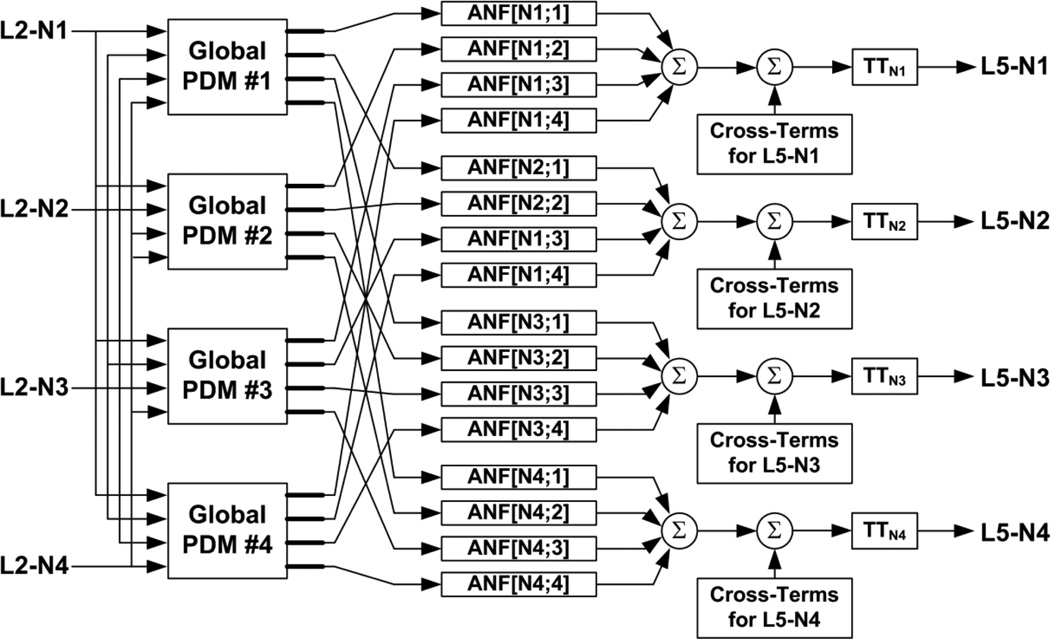
Figure 1 shows a schematic (block-diagram) of one module of the PDM-based MIMO model that corresponds to one output neuron. The full MIMO model is composed of four such modules – one for each of the four output neurons with four input neurons. The designation of the PDMs as “global” alludes to the fact that these PDMs result from “fusion” of PDMs derived for all output neurons and the two phases of the DMS task (Sample Presentation and Match Presentation). The four PFC-L2 input neurons (and the four PFC-L5 output neurons) are designated for abbreviation purposes as: N1 or UL (upper-left unit), N2 or UR (upper-right unit), N3 or LL (lower-left unit) and N4 or LR (lower-right unit).

Fig. 1.

Block diagram of the PDM-based MIMO model employing 4 global PDMs with 4 PFC-L2 input neurons for a single PFC-L5 output neuron Ni (i=1,2,3,4) (N1: upper-left unit, N2: upper-right unit, N3: lower-left unit, N4: lower-right unit). In the notation ANF[i, j, k), i=output #, j=input #, k=PDM #. The threshold-trigger (TT) operator includes an exponential refractory component (see text).

The detailed experimental methods used for the collection of the actual data are described in (Opris et al. 2011; Hampson et al. 2011b). The data were collected in the labs of Dr. Deadwyler and Dr. Hampson at Wake-Forest University from Layers 2 (L2) and 5 (L5) of the pre-frontal cortex (PFC) in non-human primates (NHP) that were trained to acknowledge a displayed (and immediately removed) computer-generated icon. The NHPs of this study were adult male rhesus macaque, Macaca mulata. After a random delay, the NHP is presented with several computer-generated icons, containing among them the previously acknowledged icon. The NHP is trained to re-select (match) this image by moving a cursor on the screen -- i.e. a Delayed-Match-to-Sample (DMS) task. When the correct icon is selected, the animal is rewarded. During this task, the neuronal activity is recorded at PFC L2 neurons viewed as the “inputs” and PFC L5 neurons viewed as the “outputs” of a putative MIMO system that represents this transformation of neuronal activity during the various phases of the DMS task. The presented computer-generated icons are randomly changed from trial to trial.

We analyzed the collected data in two phases of the DMS task: (1) the “Match Presentation” phase between the onset of the match-presentation and the NHP behavioral response to the match stimulus, and (2) the “Sample Presentation” phase between the onset of the sample-presentation and the NHP behavioral response. The spikes of the collected data were identified as occurring between the temporal markers for the respective phase and binned with 2 msec binwidth (Opris et al. 2011; Hampson et al. 2011). A mean-firing-rate between 0.25 and 25 spikes per second was used as an inclusion criterion. We estimated the 1^st and 2^nd order Volterra kernels using Laguerre expansions with 5 Laguerre basis functions of the appropriate Laguerre parameter alpha determined through a search procedure (Marmarelis 2004).

3 Results

We seek to estimate the PDM-based MIMO model of the nonlinear dynamic transformation of spike-train data from four PFC-L2 (input) neurons to four PFC-L5 (output) neurons in NHPs performing the DMS task. A block-diagram of this MIMO model is shown in Figure 1. The designation of the PDMs as “global” alludes to the fact that they result from “fusion” of the sets of PDMs derived for all output neurons and the two phases of the DMS task: Sample Presentation (SP) and Match Presentation (MP). The four PFC-L2 input neurons and the four PFC-L5 output neurons are designated for abbreviation purposes as: N1 or UL (upper-left unit), N2 or UR (upper-right unit), N3 or LL (lower-left unit), N4 or LR (lower-right unit). The spike-train of each input neuron convolves with each of the four global PDMs to generate the PDM outputs (graded signals) that are subsequently being transformed by the respective ANFs in a static nonlinear fashion to generate their respective contributions to the likelihood of firing of each output neuron. The ANF outputs for all input-PDM-ANF cascades that affect the same output neuron, are summed and added to the cross-terms affecting this output to yield a graded “internal” signal that is subjected to a “threshold-trigger” (TT) operator in order to generate the model prediction of the output spike-train. The TT includes an exponential refractory component with two parameters (initial refractory amplitude and relaxation time-constant) which are found to be 0.4 and 10, respectively, following the procedure described in Methods. It should be noted that the unknown quantities of this PDM-based MIMO model are the ANFs and the coefficients of the cross-terms, since the global PDMs are fixed for a given behavioral task. The parameters of the TT operators may also be viewed as unknown quantities of the model but they can also be viewed in conjunction with the ROC curves as “model evaluation parameters” and not “structural parameters” of the model.

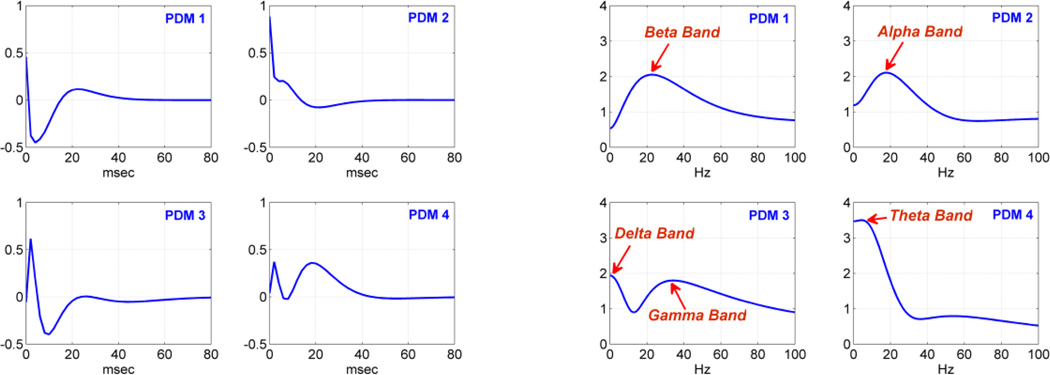
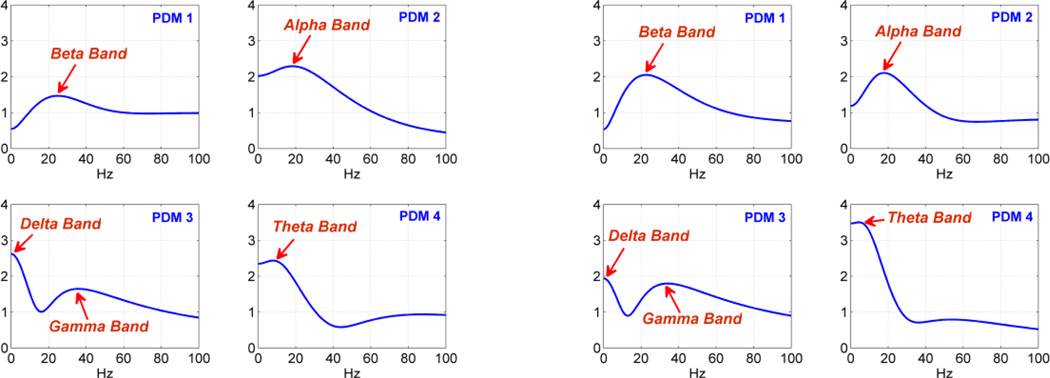
Following the previously described procedure for the selection of the global PDMs of the MIMO model for the SP and the MP phases of the DMS task with correct behavioral outcome, we obtain the 4 global PDMs for NHP 1504 shown in Figure 2, using the data from 40 successful trials of the DMS task (Session 0726). These global PDMs are viewed as an efficient basis of orthonormal functions for representing all kernels of the MIMO model for NHP 1504 during the SP and MP phases of the DMS task with correct outcome. We note that each PDM may generally incorporate several biological mechanisms that must be delineated through subsequent scientific analysis (experimental or computational). These biological mechanisms pertain to the integrated neuronal dynamics of the transfer and processing of information from Layer 2 to Layer 5 of the PFC. The specific functional characteristics of these mechanisms are depicted on the waveform of the global PDMs and discussed further below.

Fig. 2.

The four global PDMs of the MIMO model in the time domain (left) and in the frequency domain (right) that are obtained from the data of NHP1504 during the Sample Presentation and Match Presentation phases of 40 successful DMS trials of Session 0726 (see text). The annotated resonant peaks in the frequency-domain representation of these global PDMs correspond to well-known frequency-bands of neuronal ensemble activity (α, β, γ, δ, θ) that have been associated in previous studies with specific cognitive functions.

We see in the frequency-domain representations in the right panel of Figure 2 that the 1^st PDM (top left) exhibits a resonant peak ~25 Hz in the beta-band (15–30 Hz) that has been associated in previous studies of the PFC in NHPs, using elecroencephalograms (EEGs) and local field potentials (LFPs), with sensorimotor integration and preparation for motor action. The 2^nd PDM (top right) exhibits a resonant peak ~15 Hz in the high end of the alpha-band (10–15 Hz) associated in previous EEG studies of the PFC with internalized attention and memory load, as well as processing of internal mental content. The 3^rd PDM (bottom left) exhibits a resonant peak ~35 Hz in the low end of the gamma-band (30–80) associated in previous studies with various cognitive tasks (including sensory and working memory) and motor tasks. The 3^rd PDM also has high values in the delta-band (<4 Hz) that has been associated in previous studies with short-term plasticity, anticipation of reaction, hormonal secretion, general neuropsycological performance and deep sleep. The 4^th PDM (bottom right) exhibits a theta-band resonant peak ~7 Hz that has been associated in previous studies with memory tasks, such as memory formation, delineation of memory-encoding from memory-retrieval, and cortical synchronization. More on the biological/functional interpretation of the PDMs is given in the Discussion section.

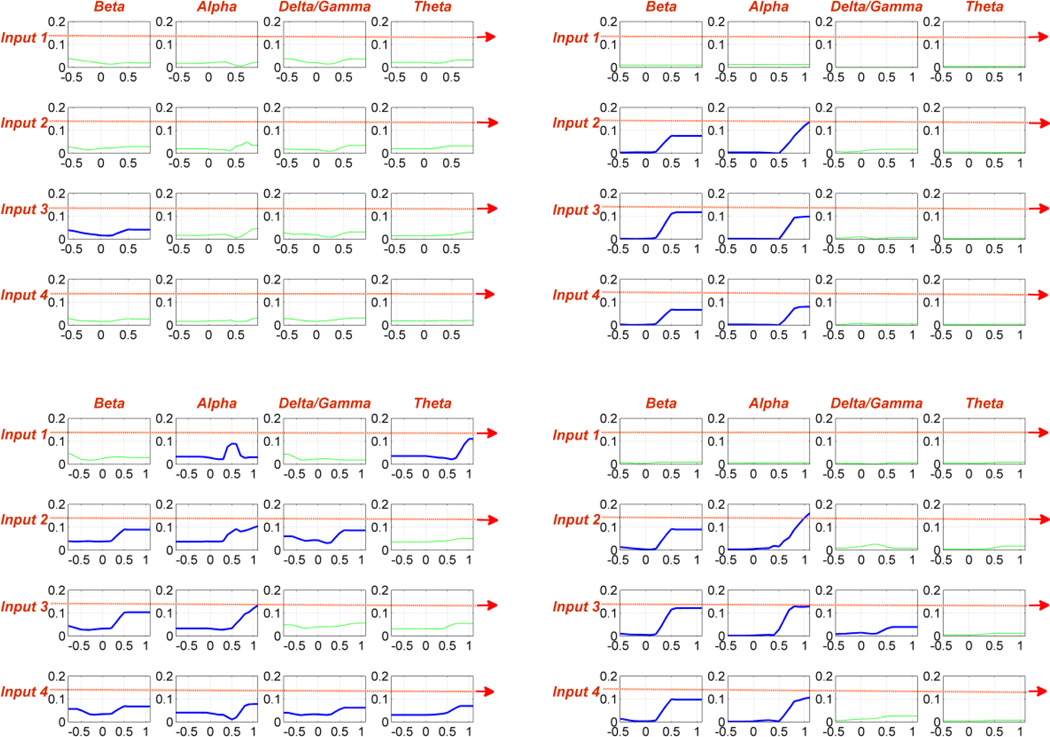
To complete the construction of the MIMO model of this system, we must also estimate the ANFs, associated with the individual input-PDM “channels” for each output, as well as the significant cross-terms for each output neuron. Each ANF represents a static nonlinear transformation of the respective PDM output and defines the relative contribution of each input-PDM “channel” to the likelihood of firing at the respective output. Note that the ANF abscissa is the amplitude of the respective PDM output and the ordinate is the relative contribution of the respective input-PDM “channel” to the probability of firing at the respective output neuron. The latter has arbitrary units and combines with the outputs of the other ANFs and the cross-terms to define the internal variable that generates the prediction of the output spike-train upon application of the TT operator.

For each output neuron, the maximum number of required ANFs is equal to the product of the number of its inputs times the number of global PDMs (i.e. 4×4=16 ANFs in this case). Generally, some of these ANFs will make insignificant contributions to the likelihood of firing at the respective output neuron – suggesting the practical possibility of “pruning” using a statistical significance test based on the null hypothesis of uncorrelated Poisson outputs (of the same firing rate as the experimentally observed output) for the given inputs. Application of this statistical significance test yields the significant set of ANFs shown in Figure 3 with blue line, while the insignificant (pruned) ANFs are shown in green line. The latter are not included in the model and, therefore, do not contribute to the predicted firing probability of the respective output neuron. We observe that only 25 out of a total of 64 ANFs (39%) are found to be significant in this case, demonstrating considerable reduction of MIMO model complexity without degradation of model predictive performance. The latter point was examined and confirmed through the computation of ROC curves based on the actual data that are shown in Figure 4. We note that the ANFs provide quantitative guidance about which input-PDM channels are affecting the firing of each output neuron and to what degree. For instance, it is shown in Figure 3 that the connection between the first input neuron and the first output neuron is functionally insignificant and the first input neuron has a significant connection only with the third output in the beta-band PDM channel (blue line in top-left panel of Figure 3). The strongest connections are between the other three input neurons (UR, LL and LR) and the 2^nd (UR) and 4^th (LR) output neurons in the first two PDM channels that correspond to the beta and alpha bands respectively (see top-right panel of Figure 3). This affords a level of functional detail and insight in terms of the information processing characteristics of this neural network that has been heretofore unavailable – i.e. the ANFs quantify the strength of connectivity between input-output neurons via specific PDM channels which exhibit the functional characteristics depicted in Figure 2 (e.g. resonant peaks in frequency bands associated in previous work with specific cognitive tasks). This important point is further discussed in Section 4.

Fig. 3.

The 64 ANFs for the four output neurons in Layer-5 of the PFC of NHP 1504. The ANFs for each output are plotted as 4×4 sets of panels where the 4 inputs correspond to 4 rows and the 4 PDMs to 4 columns. The ANFs that make insignificant contributions to output firing (39 out of 64) are pruned by the algorithm described in the text and shown in green line.

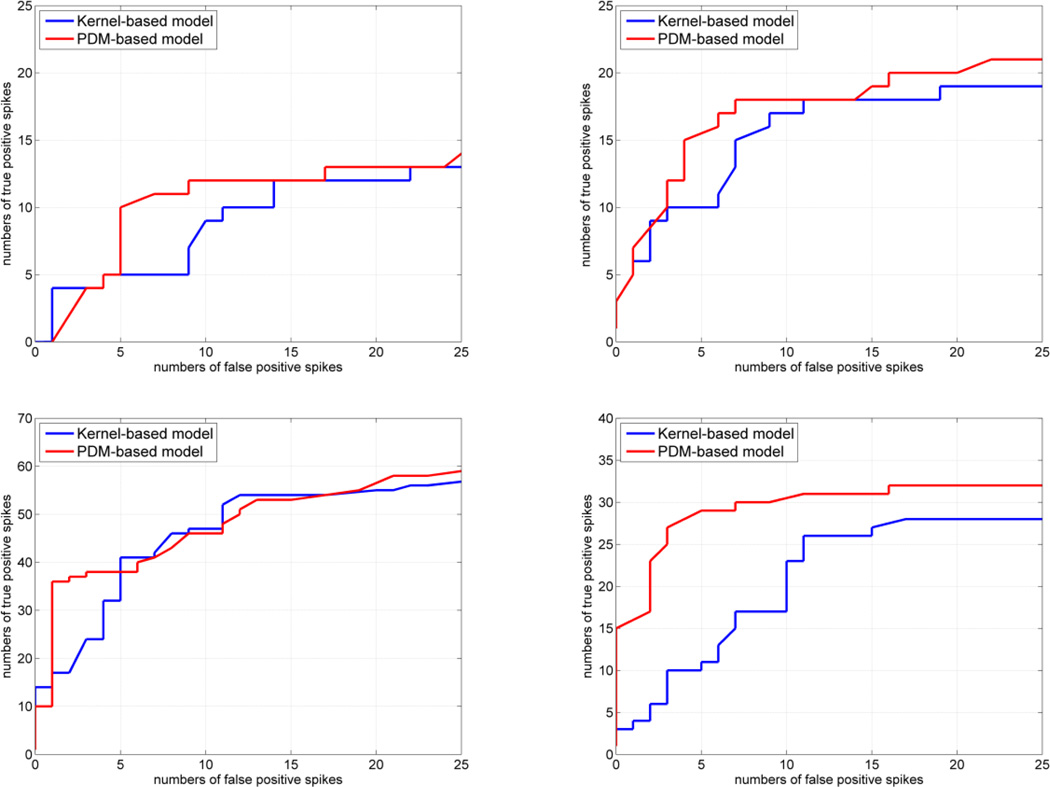
Fig. 4.

The ROC curves obtained for the PDM-based MIMO model with the pruned ANFs of Figure 3 (red line) and for the kernel-based MIMO model (blue line) for each of the four output neurons. Overall, the two types of MIMO models exhibit comparable performance (with a slight advantage for the PDM model), although the complexity of the PDM-based model is significantly reduced. The axes show the numbers of the true-positives (ordinate) and false-positives (abscissa) to facilitate interpretation.

Final completion of the PDM-based MIMO model requires the inclusion of the significant cross-terms, using the approach outlined in the previous section. These cross-terms represent the interactions of the various inputs as they impact the activity of the respective common output. The significant cross-terms were generally found to be a small proportion of all pair-product combinations (less than 10%) and seem to have only occasional impact on the MIMO model prediction performance. This impact is primarily in terms of reducing the number of false-positives. For instance, the number of significant cross-terms in this example is 2, 8, 9, and 7 for the four output neurons UL, UR, LL, LR respectively. These 26 significant cross-terms represent only 5.4 % of the total 480 possible pair-products (120 per output neuron).

The overall predictive performance of the PDM-based and kernel-based MIMO models is evaluated by means of the respective ROC curves (depicting the relation of true-positive with false-positive predictions for various thresholds) that are shown in Figure 4. The ROC curves are comparable for the two types of models, with a slight advantage exhibited by the PDM-based model (red line), mainly when the cross-terms have some impact on the model prediction by reducing the number of false-positives. Note that the kernel-based MIMO model lacks cross-interaction terms but, nonetheless, has more free parameters (greater model complexity). This supports the proposition that the PDM modeling approach may indeed offer a more parsimonious alternative for practical MIMO modeling of neuronal ensembles. We observe in Figure 4 that the probability of true-positive prediction is rather low in all cases. Since there are about 200 actual spikes in each output-neuron record, this probability ranges from about 5% (output neuron #1) to about 25% (output neuron #3) when the detection threshold is chosen so that the number of false-positives is not allowed to exceed the number of true-positives. For those thresholds, the kernel-based prediction yields about half the number of true-positives. This demonstrates the superior predictive capability of the PDM-based (average ~ 15%) relative to the kernel-based model (average ~ 10%), which becomes even more impressive when placed in the context of linear predictions based on cross-correlograms (Opris et al. 2011; Hampson et al. 2011). This point is discussed further in the following section.

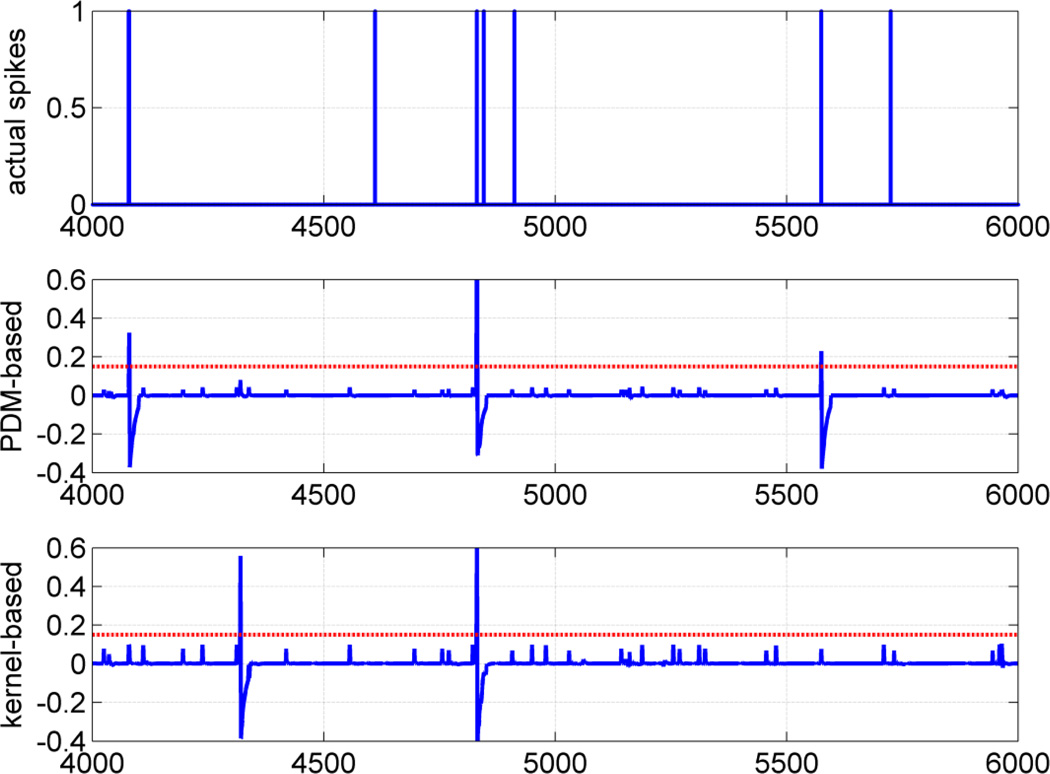
Another illustration of the predictive capability of the PDM-based model in comparison with its kernel-based counterpart is shown in Figure 5, where a 2 sec data segment of output data (L5 neuron #4) is shown along with the two model predictions. For the indicated thresholds, we have 3 true-positives and no false-positives for the PDM-based model versus 1 true-positive and 1 false-positive for the kernel-based model. It is also evident in these model-prediction plots that the subthreshold values that potentially give rise to false-positives (small values of blue line) are generally lower for the PDM-based model.

Fig. 5.

Illustrative example of the PDM-based model prediction (middle trace) of the spike-train output of an actual Layer-5 neuron over a 2 sec data-segment (top trace) and comparison with its kernel-based counterpart (bottom trace). For the indicated thresholds (red dashed line), the PDM-based model makes 3 true-positive predictions without any false-positives, while the kernel-based model makes 1 true-positive and 1 false-positive prediction.

In order to examine the consistency in the form of the global PDMs for different NHPs, we repeated the estimation procedure for data from NHP 1418 (34 successful DMS trials of Session 0727) under similar experimental conditions. The resulting global PDMs for NHP 1418 are shown in Figure 6 (frequency- domain representation only) along with their counterparts for NHP 1504. The two sets of global PDMs exhibit remarkable similarities in terms of resonant peaks. However, the obtained ANFs for the two NHPs are different (not shown in the interest of space), because the precise location of the recording electrode is somewhat different for different experimental preparations. This is viewed as an indication that the basic biological mechanisms (quantified by the PDMs) are similar in the two NHPs but the corresponding “functional connectivities” of the PFC neuronal ensembles that are probed in each case (and quantified by the ANFs) are distinct. This issue is further discussed in the following section.

Fig. 6.

The four global PDMs in the frequency domain for the MIMO model of NHP 1418 (left) and NHP 1504 (right) exhibiting similar characteristics in terms of resonant peaks.

4 Discussion

4.1 MIMO Model Compactness

A key issue in MIMO modeling is the feasibility of scaling up to numerous inputs/outputs, which depends on the ability to achieve model compactness. The PDM-based approach offers a significant advantage in this regard, relative to the kernel-based MIMO modeling approach. Since the total number of ANFs for each output is the product of the number of PDMs (P) times the number of inputs (I), the complexity of the MIMO model will increase linearly (i.e. proportionally) with increasing number of inputs (for each output), provided that the number of cross-terms also grows linearly with the number of inputs. The latter has been shown to be the case in the NHP pre-frontal cortex data, where the number of cross-terms was found to be bound by 2PI. If 3 parameters are allotted for the description of each ANF, then the total number of free parameters in the PDM-based MIMO model (prior to pruning) is bound by 5PI. On the other hand, the number of free parameters in the kernel-based 2^nd order MIMO model (i.e. the number of required Laguerre expansion coefficients) is: I(L+2)(L+1)/2+I(I−1)L²/2, when cross-kernels are included (where L denotes the number of Laguerre basis functions) [Marmarelis 2004; Zanos et al. 2008]. Thus, the relative complexity ratio of kernel-based to PDM-based MIMO models (as measured by the number of required free parameters) is: R = [(L+1)(L+2)+(I−1)L²)/(10P), prior to any pruning of insignificant terms (ANFs or kernels, respectively). Since P<=L, this ratio is always favorable to the PDM-based approach and increases proportionally to the number of inputs. For example, we had L=5, P=4 and I=4 in the previously presented results, yielding a relative complexity ratio of R= 2.92. When the number of inputs increases to 64, then the relative complexity ratio R rises to 40.42 and the number of model parameters prior to pruning is 51,744 for the kernel-based model and 1,280 for the PDM-based model. Obviously, this vast difference in model compactness has important practical implications for large-scale models. We also note that the PDM-based MIMO model is not limited to any finite order of nonlinearity, since the ANFs represent the full nonlinearities of the system.

A comment ought to be made regarding the relative predictive capability of these models. It was found in this study (see, for instance, the ROC curves in Figure 4) that probability of true-positive prediction by the PDM-based model ranges between 5% and 25% (i.e. an average of about 15%), while these numbers are about half for the kernel-based model. Although this predictive capability appears modest when judged by these numbers, we believe that it is rather remarkable when viewed in the context of the complexity of this task and the expected large number of “interference spikes” in the output record (i.e. spikes that are not due to the monitored input neurons). This view is corroborated by the findings of previous studies of the same system using predictions based on cross-correlograms (Opris et al. 2011; Hampson et al. 2011) where significantly fewer output spikes were accounted for (i.e. less true-positives) than the kernel-based model.

4.2 Biological Interpretation of the PDMs

An important benefit of the advocated PDM-based modeling approach is the potential for physiological/biological interpretation of the obtained PDMs that can elucidate the functional characteristics of these neuronal networks and advance our scientific understanding of the biological mechanisms that subserve the function of these neural systems. The interpretation of PDM-based MIMO models in terms of neural rhythms attains great importance because phase-locked rhythmic activity has been observed in distant brain regions, suggesting a critical role of neural rhythms in achieving cortical synchronization (e.g. Singer 1993, 1999; Fries 2005). Furthermore, there is growing acceptance of the view that cognitive functions rely on neural rhythms to coordinate the timing of neuronal firing. This supports the temporal coding hypothesis in neural information processing, which is the fundamental justification for the utility of predictive MIMO modeling in the central nervous system. Thus, the PDMs can be a useful tool for understanding and dissecting neural function using experimental observations of neuronal spike-trains, local-field potentials (LFPs) and electroencephalograms (EEGs). It should be emphasized that the presented comments below are conjectural and careful studies, including pharmacological manipulations, ought to be conducted in the future in order to substantiate (or refute) these conjectures.

Specifically, it is shown in Figure 2 that the 1^st PDM exhibits a resonant peak ~25 Hz in the beta-band (15–30 Hz) that has been associated in previous studies, using elecroencephalograms (EEGs) and local field potentials (LFPs), with sensorimotor integration (Murthy and Fetz, 1992, 1996; Sanes and Donoghue, 1993; Courtemanche et al. 2003) and preparation for motor action (Baker et al. 1999; Donoghue et al. 1998; Zhang et al. 2008). Note that the LFPs are not simply a result of neuronal spiking, but they are involved with the synchronization of spike timing in the sensorimotor and frontal cortex (Lebedev and Nelson 1995; Baker et al. 1999). Beta-band LFP oscillations have been also observed in the cerebellum and the striatum in connection with action-selection tasks (Courtemanche et al., 2002).

The 2^nd PDM in Figure 2 exhibits a resonant peak ~14 Hz in the high end of the alpha-band (10–14 Hz) associated in previous EEG studies of the PFC with internalized attention and memory load (Klimesch et al. 1998; Aftanas & Golocheikine, 2001; Jensen et al. 2002), as well as processing of internal mental content (Stein & Sarnthein 2000). This resonant peak is at a slightly higher frequency than the alpha resonance observed and reported in previous EEG studies (closer to 12 Hz), but this should be expected because the EEG signal is recorded after it traverses the brain tissues and the skull -- thus spreading its waveform somewhat during propagation due to dispersion (about 10–15% downshift). This is not the case for the signals recorded directly at the PFC.

The 3^rd PDM in Figure 2 exhibits a resonant peak ~35 Hz in the low end of the gamma-band (31–80 Hz) associated in previous studies with various cognitive tasks, including sensory and working memory functions (Singer 1993, 1999; Fries 2005; Fries et al. 2001, 2007; Rizzuto et al. 2003; Jensen et al. 2007) and motor tasks (Sanes & Donoghue 1993; Fetz et al. 2000; Lebedev & Nelson 1995). Gamma rhythms are generated in the cortex by either transient excitation of fast-spiking interneurons via metabotropic glutamate receptors or neuromodulatory excitation of interneurons and principal cells via cholinergic receptors (Roopun et al. 2008). Somatic inhibition mediated by GABA_A receptors and activation of interneurons by AMPA receptors are deemed essential for the generation of gamma rhythms. The 3^rd PDM also has high values in the delta-band (<4 Hz) that has been associated in previous studies with short-term plasticity (Kiss et al. 2011) and anticipation of reaction (Gabor et al. 2010). The only possible trace of the delta band on the time-domain waveform of this PDM is the late (and shallow) negative trough ~ 50 ms, which gives rise to the low-frequency component in the frequency-domain representation of this PDM. We note the critical role of the delta rhythm in hormonal secretion through hypothalamic action (Hobson and Pace-Schott 2002; Brandenberger 2003) and general neuropsycological performance (Anderson & Horn 2003). Based on the obtained ANFs in Figure 3, the main PFC connection utilizing this PDM is between the UR Layer-2 neuron (2^nd row) and the LL Layer-5 neuron (lower left panel). Thus, although this PDM seems to have the potential for playing many intricate roles in terms of neural information processing, its presence is rather subtle in the MIMO model (based on the ANFs obtained from the data).

Finally, the 4^th PDM in Figure 2 exhibits a resonant peak ~7 Hz in the theta-band (5–9 Hz) that has been associated in numerous previous studies with memory tasks, such as memory formation (Fox et al. 1986; Buzsaki 2002, 2005; Eckstrom et al. 2005; Jacobs et al. 2006, 2007; Kahana 2006) and the delineation of memory-encoding from memory-retrieval processes (Hasselmo et al. 2002; Vertes 2005), as well as behavior (Hyman et al. 2005) and cortical synchronization (Jones & Wilson 2005; Siapas et al. 2005). Based on the obtained ANFs in Figure 3, the main PFC connection utilizing this PDM is between the UL Layer-2 neuron and the LL Layer-5 neuron. As discussed above for the 3^rd PDM, this PDM also seems to have a subtle presence in the MIMO models (based on the obtained ANFs), in spite of its potential importance in terms of neural information processing.

The obtained ANFs in Figure 3 indicate that the strongest connections are between the UR, LL and LR input (Layer 2) and output (Layer 5) neurons over the two PDMs that exhibit resonant peaks in the beta and alpha bands – suggesting that this is the primary activity in the probed PFC region during the aforementioned MP phase of the DMS behavioral task (i.e. sensorimotor integration, preparation for motor action, internalized attention and memory load, processing of internal mental content).

The significance of the observed resonant peaks in the global PDMs arises from the possibility that the gain of the respective input-PDM channel of information transmission to the output neuron is modulated by the activity in the respective frequency-band. The extent to which each input-PDM channel impacts the activity in an output neuron is quantified by the respective ANF. Thus, a significant ANF at an input-PDM-output channel of neural information transmission between Layer 2 and Layer 5 of the PFC indicates that the signal at the Layer 2 neuron is strengthened within the resonant frequency-band of the respective PDM. For example, the strong ANF of the 4^th PDM (4^th column) for the UL input (1^st row) of the LL output (lower left panel) shown in Figure 3 indicates that the activity of the UL input neuron influences strongly the activity of the LL output neuron when it happens to have significant power in the theta band (i.e. information associated with memory functions and cortical synchronization).

4.3 Neural Rhythms and PDM Resonances

The estimated global PDMs exhibit resonant peaks at celebrated neural rhythms in the delta (1–4 Hz), theta (5–9 Hz), alpha (10–14 Hz), beta (15–30 Hz) and gamma (31–80 Hz) bands. This implies that a periodic spike-train of frequency consistent with one of those rhythms will be transferred more efficiently to the respective output through those input-PDM “channels” that exhibit a resonant peak at the corresponding band. For example, if a cognitive process is related to a theta oscillation, then this process will employ (and be facilitated by) the input-PDM channels that exhibit a resonant peak in the theta band. This effect is expected to become more pronounced when it is cascaded through various neuronal layers. Although this is conjectural at this point in time, we postulate that these resonant peaks in the PDMs are due to either neuronal intermodulation at the respective frequencies or closed-loop operation of local/regional neural circuitry. It is worth noting in this regard that the spectral characteristics of the activity of Layer 2 neurons are not very distinctive in the analyzed PFC data (i.e. broadband spectrum), while the spectra of the activity of Layer 5 neurons exhibit distinctive peaks in the frequency bands associated with the respective significant ANFs.

4.4 Functional Interpretation of the ANFs

As discussed above, the significant ANFs define the “functional connectivity” or “circuitry” in this part of the PFC for the respective behavioral tasks. They also ascribe specific functional characteristics to these neural connections (in the time and frequency domains) by virtue of the properties of the associated PDMs, which become “active” only when the respective ANF has significant values. Although it is not presently possible to provide full and detailed neurophysiological meaning to the obtained sets of ANFs, it is evident that they enable an organization and representation of neural information flow (akin to neural encoding) heretofore unavailable. The implications of this novel insight provided by the ANFs and PDMs are potentially vast in terms of assisting (ultimately) clinical diagnosis of specific neurological impairments and allowing deliberate and targeted intervention via properly designed multi-unit neurostimulation patterns. The latter portrays the prospect of a new generation of functional neurosurgery techniques (Gale et al. 2011; Rigosa et al. 2011).

4.5 Neural Coding and Decomposition of Spike-Trains

The PDM/ANF concepts and the configuration of the PDM-based model allows the functional “decomposition” of the spike-trains observed at an output neuron into components that correspond to the various input-PDM-ANF channels (e.g. distinct theta and beta oscillation components that reach the output neuron via PDM-ANF channels that have such PDM resonant peaks and significant ANFs). This decomposition points directly to a plausible spectro-temporal neural coding scheme of the information that flows through the neuronal ensembles in the form of spatiotemporal spike-trains. The plausibility of this coding scheme is supported by the aforementioned observation of the spectral characteristics of Layer 5 neurons matching the respective significant PDM-ANF resonant peaks.

4.6 Relation with the GLM and lateral/recurrent connections

The PDM-based model incorporates the case of the Generalized Linear Model (GLM) as a special case, because the GLM structure is similar to a single PDM-ANF cascade branch of the PDM-based model (i.e. the PDM is the linear component/filter of the GLM and the ANF is its "link" function). It is important to note that lateral output connections may exist in cortical models (i.e. connections between Layer-5 neurons in this case) and should be explored in future studies via PDM-based models with such explicit output lateral connections, which may lead to simplification of the model (e.g. a smaller number of required PDMs) or improved predictive performance. However, it should be noted that the possible effects of lateral output connections are also included implicitly in the equivalent feedforward configuration of the PDM-based model, since each output can be expressed in terms of all inputs (basic Volterra formulation). Therefore, if the j-th output depends on the k-th output through a lateral connection, this effect can be expressed in terms of all the common inputs since the k-th output (and any output) can be expressed in terms of its inputs. Nonetheless, the practical issue of "efficiency of model representation" remains and may be well-served by the inclusion of explicit lateral output connections in the model formulation. This modeling issue can be likened to the relation between auto-regressive and moving-average models in the linear case. Similar arguments hold in the case of recurrent connections. Thus, the Volterra-equivalent PDM-based models are valid in all those cases and incorporate in principle the effects of lateral or recurrent connections. Nevertheless, the resulting model parsimony may be improved if such lateral/recurrent connections are explicitly included in the model configuration.

5 Conclusions

A methodology for modeling the nonlinear interrelationships between neuronal ensembles with Volterra-equivalent canonical models was presented that may have predictive capability for arbitrary input patterns and achieves representational efficiency (i.e. model compactness). This methodology is based on the concept of Principal Dynamic Modes (PDMs) and their associated nonlinear functions (ANFs) that has been recently applied successfully to various physiological systems (Marmarelis 2004). The obtained PDM-based multi-input/multi-output (MIMO) models are dynamic and nonlinear, but their complexity increases linearly with increasing number of inputs (for each output), while the complexity of their Volterra-type counterparts increases faster (e.g. quadratically for a second-order MIMO model). This fact has critical practical implications in the scaling-up of MIMO models of neuronal ensembles to accommodate hundreds (or even thousands) of input-output neurons in the future. In addition, the PDM-based approach yields MIMO models of the relationship between neuronal ensembles that are potentially interpretable in terms of the respective functional characteristics of the neuronal interconnections and the underlying biological mechanisms.

Initial results of the application of this methodology to data collected from PFC cortical neurons of Layer 2 (inputs) and Layer 5 (outputs) in two behaving non-human primates corroborated the basic premise of the advocated approach by demonstrating significant reduction in the complexity of the PDM-based MIMO model without any degradation in predictive performance. If this result becomes confirmed by additional studies involving larger numbers of input-output neurons, then we will have at our disposal a practical methodology that can yield PDM-based MIMO models of general applicability with the ability to incorporate large numbers of input-output neurons within ordinary computational means. Furthermore, it was discovered that the obtained PDM-based MIMO model reveals specific functional characteristics of the neuronal interconnections related to the celebrated neural rhythms (delta, theta, alpha, beta and gamma) with implications for their functional characterization and utility. This, in turn, points to a plausible neural coding scheme that decomposes the spike-trains generated by a neuron of interest in terms of band-specific and connection-specific information.