A flaw in the typical evaluation scheme for pair-input computational predictions

To the Editor: Computational prediction methods that operate on pairs of objects by considering features of each (hereafter referred to as “pair-input methods”) have been crucial in many areas of biology and chemistry over the past decade. Among the most prominent examples are protein-protein interaction (PPI)^1-2, protein-drug interaction^3-4, protein-RNA interaction⁵ and drug indication⁶ prediction methods. A sampling of more than fifty published studies involving pair-input methods is provided in Supplementary Table 1. In this study we demonstrate that the paired nature of inputs has significant, though not yet widely perceived, implications for the validation of pair-input methods.

Given the paired nature of inputs for pair-input methods, one can envision evaluating their predictive performance on different classes of test pairs. As an example, proteochemometrics modeling³, a well-known computational methodology for predicting protein-drug interactions, takes a feature vector for a chemical and a feature vector for a protein receptor in order to predict the binding between the chemical and protein receptor³. In this case, a test pair may share either the chemical or protein component with some pairs in a training set; it may also share neither. We found that pair-input methods tend to perform much better for test pairs that share components with a training set than for those that do not. As a result, it is necessary to distinguish test pairs based on their component-level overlap when evaluating performance. A test set that is used to estimate predictive performance may be dominated by pairs that share components with a training set, yet such pairs may form only a minority of cases on the population level. In this case, a predictive performance estimated on the test set may be impressive, yet it should fail to generalize to the population level. Indeed, this component-level overlap issue for the validation of pair-input methods was early recognized by some researchers (e.g., by Vert, Yamanishi and others; see Supplementary Table 1). However, it has been overlooked by most researchers across biology and chemistry, and as a result cross-validations for pair-input methods usually did not distinguish test pairs based on the component-level overlap criterion.

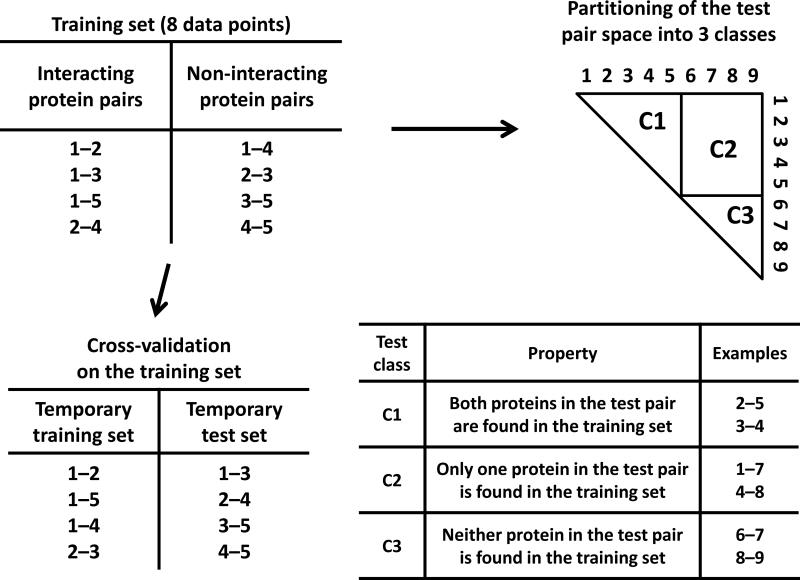
To illustrate the component-level overlap issue, we consider PPI prediction methods with the toy example of Fig. 1, in which the protein space is composed of 9 proteins and a training set consists of 4 positive and 4 negative protein pairs. This training set is used to train a PPI prediction method, which is in turn applied to the full set of 28 test pairs (Fig. 1). How well would the trained method perform on the 28 test pairs? To this end, one usually performs a cross-validation on the training set. For example, a temporary training set is prepared by randomly picking some pairs (Fig. 1) while the rest serve as a temporary test set from which predictive accuracy can be measured. This cross-validated predictive performance is then implicitly assumed to hold for the full space of 28 test pairs.

Figure 1.

Illustrating shortcomings of a typical cross-validation with a toy example of predicting protein-protein interactions. Here, the protein space contains 9 proteins and a training set consists of 4 interacting and 4 non-interacting protein pairs. The training set is used to train a PPI prediction method, which is then applied to the 28 (i.e., 9×8/2 - 8) test pairs shown in the triangle. The paired nature of inputs leads to a natural partitioning of the 28 test pairs into 3 distinct classes: C1, test pairs sharing both proteins with the training set; C2, test pairs sharing only one protein with the training set; and C3, test pairs sharing neither protein with the training set. To estimate how well the trained method would perform for the 28 test pairs, one would perform a cross-validation on the training set, typically by randomly dividing the 8 training pairs into a temporary training set and a temporary test set as shown, without regard to the partitioning of test pairs into distinct classes. Predictive performances achieved for such randomly generated temporary test sets are then assumed to generalize to the target population (i.e., the 28 test pairs in this toy example). As this form of cross-validation overlooks the partitioning of test pairs into distinct classes, predictive performances estimated by it fail to generalize to the population level.

The paired nature of inputs leads to a natural partitioning of the 28 test pairs into 3 distinct classes (C1 – C3), as shown in Fig. 1: C1, test pairs sharing both proteins with the training set; C2, test pairs sharing only one protein with the training set; and C3, test pairs sharing neither protein with the training set. To demonstrate that the predictive performance of pair-input methods differs significantly for distinct test classes, we performed computational experiments using large-scale yeast and human PPI data that mirror the toy example of Fig. 1 (Supplementary Methods). Supplementary Table 2 shows that, for seven PPI prediction methods (M1 – M7, chosen to be a representative set of algorithms, Supplementary Methods), the predictive performances for the three test classes differ significantly. The differences are not only statistically significant (Supplementary Table 3) but also numerically large in many cases. M1 – M4 are support vector machine (SVM)-based methods, M5 is based on the random forest algorithm, and M6 and M7 are heuristic methods. Thus, regardless of core predictive algorithms, significant differences for the three distinct test classes are consistently observed. These differences arise partly from the learning of differential representation of components among positive and negative training examples (Supplementary Discussion).

In a typical cross-validation for pair-input methods, available data are randomly divided into a training set and a test set, without regard to the partitioning of test pairs into distinct classes. How representative would such randomly generated test sets be of full populations? To answer this question, we performed the typical cross-validation using the yeast and human PPI data of Supplementary Table 2. Not surprisingly, the C1 class accounted for more than 99% of each of the test sets generated for the typical cross-validations, and accordingly the cross-validated predictive performances closely match those for the C1 class (Supplementary Table 2). In contrast, within the full population (i.e., the set of possible human protein pairs), the C1 class represents only a minority of cases: 21,946 protein-coding human genes⁷ implies 240,802,485 possible human protein pairs. According to HIPPIE⁸, a meta-database integrating 10 public PPI databases, the space of C1 type human protein pairs (i.e. those pairs formed by proteins that are represented among highly confident PPIs) accounts for only 19.2% of these cases, compared with 49.2% and 31.6%, respectively, for the C2 and C3 classes. Hence, the C1 class is far less frequent at the population level than for typical cross-validation test sets, and performance estimates obtained by a typical cross-validation should not be expected to generalize to the full population level. Given that these yeast and human PPI data sets have also been broadly analyzed by others, this conclusion is very likely to hold generally, at least for pair-input PPI prediction methods.

In summary, computational predictions—whether pair-input or not^9-10—that are tested by cross-validation on non-representative subsets should not be expected to generalize to the full test populations. A unique aspect of pair-input methods, as compared with methods operating on single objects, is that one additionally needs to take into account the paired nature of inputs. We have demonstrated that 1) the paired nature of inputs leads to a natural partitioning of test pairs into distinct classes, and 2) pair-input methods achieve significantly different predictive performances for distinct test classes. We note that if one is only interested in the population of C1 test pairs, then typical cross-validations employing randomly generated test sets may be just fine, although this limitation should then be noted. For general-purpose pair-input methods, however, it is imperative to distinguish distinct classes of test pairs, and we propose that predictive performances should be reported separately for each distinct test class. In the case of PPI prediction methods, three independent predictive performances should be reported as in Supplementary Table 2. In the case of protein-drug interaction prediction methods, one should report four independent predictive performances, as either the protein or drug component of a test pair might each be found in training data.