Clarifying differences in natural history between models of screening: The case of colorectal cancer

Abstract

Background

Microsimulation models are important decision support tools for screening. However, their complexity creates a barrier, making it difficult to understand models and, as a result, limiting realization of their full potential. Therefore, it is important to develop documentation that clarifies assumptions. We demonstrate this problem and explore a solution for the natural history, using three independently developed colorectal cancer screening models.

Methods

We begin by projecting the cost-effectiveness of colonoscopy screening for the three microsimulation models. Next, we provide a conventional presentation of each of them, including information that would usually be published with a decision analysis. Finally, for the three models, we provide the simulated reduction in clinical cancer incidence following a one-time complete removal of adenomas and preclinical cancers. We denote this measure as maximum clinical incidence reduction (MCLIR).

Results

There are considerable between-model differences in projected effectiveness. Conventional documentation describes model structure and associated parameter values. Given only this information, it is very difficult to compare models, largely because differences in structure make parameter values incomparable. In contrast, the MCLIR clearly shows the differences in assumptions on the key issue of the natural history: the dwell time of progressive preclinical disease, explaining between-model differences in projected effectiveness.

Conclusions

The simulated “maximum clinical incidence reduction” adds to the insight in dwell time, the critical characteristic of the natural history of disease, and how it differs between models. Inclusion of the MCLIR as a standard description would clarify the implications of assumptions for models applied to screening questions.

Introduction

Microsimulation modeling is a widely used tool for decision analyses examining the benefits of cancer screening. Although clinical trials show the effectiveness of interventions for a limited number of screening strategies, for a limited follow up period, and for a specific population, models enable the extrapolation of information gained from clinical trials to alternative screening strategies and in a broader population. Several recent studies used models to evaluate the effectiveness and cost-effectiveness of screening for colorectal cancer (CRC) (1–5) as well as for other cancers (6–9).

Models are complex, and it takes a major effort from stakeholders, such as clinicians and policy makers, to understand the implications of underlying assumptions and why different models produce different answers. Even individuals with an understanding of model structure and parameter values can find it difficult to grasp the full implications of these assumptions. Developing clear and simple model documentation that demonstrates the impact of assumptions is therefore critical.

In this article, we explore additional ways of documenting the natural history assumptions of screening models. The natural history module is typically used in combination with a screening module to determine the effect of screening on disease outcomes. For the natural disease, we focus on the dwell time of the progressive preclinical phase, when disease is biologically present but does not yet yield clinical symptoms (10). Dwell time represents the time frame in which the disease could be caught by screening, and therefore is a key factor for the potential impact of screening.

To allow model comparisons, a great deal of effort has been put toward improving the description of model structure and model inputs. While all input of the model should always be reported (e.g., in an online appendix), (6) assumptions on dwell time and their implications remain difficult to assess even with this documentation. Another level of documentation has been proposed (11, 12), focusing on specific model predictions. We used this approach to describe the impact of model assumptions on the dwell time of preclinical disease on screening effectiveness. Specifically, we explored one possible prediction measure, the maximum clinical incidence reduction (MCLIR) for each model. This measure represents the reduction in incidence of clinically diagnosed disease following a one-time complete removal of preclinical disease. As an example, we applied this method to 3 independently developed CRC screening models.

The measure we propose in this article, the MCLIR, is a summary measure. For more detailed results, especially for subgroups of individuals with and without adenomas or cancer at the time of the hypothetical one-time complete disease removal, we refer to the analyses presented in a companion article published in this issue of Medical Decision Making (13).

Methods

We demonstrate the limitations associated with model description using the 3 CRC models. Each of these models was developed as part of the National Cancer Institute's (NCI's) Cancer Intervention and Surveillance Modeling Network (CISNET). To enhance the transparency of the models, we created structured model descriptions, referred to as `model profiles'. These profiles are posted online (http://cisnet.cancer.gov/profiles/). In spite of the detail provided in model profiles, differences in natural history models only became apparent to us, collaborating modelers, after carrying out specific model predictions. We use these models to demonstrate how our proposed measure of MCLIR adds value to the description of the model structure.

The three models are Microsimulation Screening Analysis (MISCAN), from the Erasmus University Medical Centre, Department of Public Health; Colorectal Cancer Simulated Population model for Incidence and Natural history (CRC-SPIN), from Group Health Research Institute, Seattle; and Simulation Model of Colorectal Cancer (SimCRC), from the University of Minnesota and Massachusetts General Hospital. Although independently developed, the three microsimulation models have much in common. Each model describes the natural history of CRC in individuals using a structure that builds upon the adenoma-carcinoma sequence (14). Individuals are simulated one by one from a young age to death. At age 20 years, individuals have no adenomas. From there onwards, individuals are at risk of developing new adenomas in the colorectum; the risk depends on age. Multiple adenomas may form within an individual, and within individuals adenomas develop independently of each other. In the absence of screening, adenomas grow in size and may eventually transform into preclinical invasive CRC. These preclinical cancers may later become clinically detected through presentation of symptoms. Once a cancer becomes clinically detected, a stage-specific survival function determines whether and when the simulated individual dies of CRC. Simulated individuals are also at risk of dying from other causes. As a consequence, even an individual diagnosed with incurable CRC may die from another cause before dying from the CRC.

The MISCAN and SimCRC models do not explicitly define the starting size of an adenoma. Because models were calibrated to adenoma prevalence data (described below), this implies that simulated adenomas are initiated when they are macroscopically detectable. The CRC-SPIN model initiates adenomas at 1 mm, explicitly assuming that this is the earliest point of preclinical detection.

The 3 models were calibrated to the same CRC incidence and adenoma prevalence data. CRC incidence was calibrated based on Surveillance, Epidemiology and End-Results (SEER) CRC incidence rates in 1975–1979 because this represents CRC incidence in the US when there was little or no CRC screening (15). Adenoma prevalence data were based on autopsy data that reported adenoma information by age and sex (16).

In the Results section, we first provide the projected effectiveness and cost-effectiveness of colonoscopy screening for the 3 models, showing how they differ. Next, we provide a conventional description of each model, including information that would usually be published with a decision analysis. Finally, for each model, we provide the background incidence (no intervention) by age and the simulated MCLIR.

The population and the comparator situation

For all 3 models the simulated population represents the general US population that is 25 years and older. By calibrating the models without intervention to SEER CRC incidence rates in 1975 to 1979, we assumed this would be the incidence level if there were no screening for CRC. None of the models explicitly simulated incidental detection of symptomless disease; it was included in the observed 1975 to 1979 CRC incidence to which the models were calibrated for the incidence without screening.

The Effectiveness and Cost Effectiveness of Screening

We examined the effectiveness and cost-effectiveness of screening as predicted by each model for colonoscopy screening every 10 years beginning at age 50 and ending at age 80 years (17, 18). Under this screening scenario, polypectomy was followed by colonoscopy surveillance. We assumed that the sensitivity of colonoscopy was 75%, for small adenomas (<5 mm), 85%, for medium adenomas (6–9 mm) and 95% for large adenomas (10+ mm) and cancers. We also assumed that colonoscopies are complete (reach the cecum) in 95% of the procedures, and the reach in the remaining 5% is distributed evenly over the colorectum. When an adenoma is detected, it is completely removed, after which it stops to develop. When preclinical cancer is detected, the models simulate a stage-specific survival that (stochastically) replicates survival as observed in SEER (SEER 1997–2001 (15)). All models use the same stage-specific survival distributions for screen- and clinically-detected cancers. Finally, all models assumed 1 fatal complication per 10,000 screening or surveillance colonoscopies in which at least one adenoma or cancer is detected and removed.

We use life years gained to measure effectiveness, and the projected number of colonoscopies as our cost, with cost-effectiveness measured by the number of colonoscopies per 1000 life years gained. We also estimate the projected incidence and mortality reductions relative to no screening.

Conventional model descriptions

We provide descriptions of each natural history model, drawn from their CISNET profiles and published articles, at a level of detail that would normally be accepted in a published article.

Maximum Clinical Incidence Reduction

The prediction measure MCLIR is defined as the simulated incidence reduction in the remaining years until, for example, age 80 years, after complete removal of prevalent detectable preclinical disease, relative to the background (no intervention) disease incidence, and is reported as a percentage. To estimate the MCLIR in CRC, we simulated 2 cohorts. The first had no intervention and was used to provide background incidence. The second simulated cohort had preclinical disease (adenomas and preclinical cancers) completely removed (100% sensitivity, 100% cure) at a given age.

For the example presented here, we placed the complete removal of disease at age 65 years, in the middle of the 50- to 80-year age ranged often recommended for average-risk individuals. The resulting MCLIR provides a direct measure of the impact of the natural history of disease after age 65 years, because we have eliminated variations due to test sensitivity, repeated screening, and surveillance. Models projected CRC incidence after the intervention, which included only clinically diagnosed cases since there was no further screening (and the detected preclinical cancers at age 65 were not included). When calculating CRC incidence, individuals were removed from the risk set (censored) once they transitioned to clinically diagnosed CRC or died from other causes.

Several simulation issues need clarification because they affect the MCLIR. First it must be clear where detectability starts (in the case presented: at the onset of small adenomas as defined in our example models). Next, the composition of the population addressed must be determined (e.g., the distribution of gender and categories of risk factors). Finally, it must be clear whether and how the model accounts for incidental detection of asymptomatic (preclinical) disease (e.g., by imagining procedures for other diseases).

Dwell time is often modeled in an implicit way, for example, by specifying the proportions of individuals who transition in and out of disease states based on probabilities that vary by age and other factors. But even when time to progression is a direct model input, implied differences in dwell time across models can be difficult to determine because of structural differences. The MCLIR, however, relies only on model outputs. The definition of the simulation run is relatively simple (no missed cases and complete cure of cancers and pre-cancerous lesions in prevalent at the time of the one-time, perfect intervention) and the output considered is driven by dwell time (“what percent of the clinical cancers at each age had a dwell time shorter than x years?”). It shows the potential of screening if its effectiveness were strictly limited by the lengths of the pre-clinical phase: even the perfect test could not detect the disease earlier, because detectable disease was not yet in existence.

Moving the age of adenoma removal from age 65 years to another age will affect the MCLIR depending on how dwell time parameters vary by age. In the event of such dependency, and if detailed documentation is required, presenting the MCLIR for different ages would provide additional information. However, there is a limitation in the amount of useful information that can be displayed. For a standard manuscript, we would propose the “mid-screening-age-only” approach presented here.

We calculated the MCLIR for 1-year periods, for 5-year periods and for the period from the intervention up to age 80 years (in this case a 15-year period). To calculate the MCLIR for an x-year period, we cumulated the incidence reduction percentages for each year in that period and divided the result by the number of years. For the reduction between 5 and 10 years after disease removal at age 65 we use the following notation: MCLIR₆₅^5–10. We propose this notation as a standard way to report the MCLIR.

Results

Effectiveness and cost-effectiveness results

Simulation of colonoscopy screening every 10 years from age 50 years to age 80 years shows differences in projected effectiveness, with CRC-SPIN and SimCRC projecting greater effectiveness than MISCAN (Table 1). The incidence reduction varied between the models from 52% to 91% and mortality reduction from 65% to 92%, with the SimCRC and CRC-SPIN models predicting the largest reductions. The life years gained (from 207 to 327 per 1000 individuals) and the number of colonoscopies per life year gained (from 19 to 13) varied accordingly: fewer life years gained and more colonoscopies per life year gained in MISCAN. In general, the results of CRC-SPIN and SimCRC are close to each other.

Table 1.

Model Outcomes for Colonoscopy Screening Every 10 Years from Age 50 to 80 Years, with Surveillance in Adenoma Patients

	MISCAN	CRC-SPIN	SimCRC
Incidence* reduction	52%	91%	82%
Mortality* reduction	65%	92%	84%
Life years gained†	207	260	327
Screening colonoscopies†	2288	2580	2574
Surveillance colonoscopies†	1715	1341	1609
Total colonoscopies†	4002	3921	4184
CRC incidence cases prevented†	30	56	54
CRC mortality cases prevented†	19	25	30
Colonoscopies per incidence case prevented	135	70	77
Colonoscopies per life year gained	19	15	13

^*25+ years of age

^†per 1000 25-year-old individuals lifetime

Conventional natural history model descriptions

The following natural history descriptions were retrieved from recent articles (5, 19,20). Model parameters are described in Tables 2, 3, and 4. For additional detailed information concerning the respective models, all three modeling groups refer to the CISNET model profiler (http://cisnet.cancer.gov/profiles/).

Table 2.

Conventional Model Description: Basic Structure of the Microsimulation Screening Analysis (MISCAN)-Colon Natural History Model

Model parameter	Value
Distribution of risk for adenomas over the general population	Gamma distributed, mean 1, variance 2
Probability that a new adenoma is progressive	Dependent on age at onset:
	0–45 years: linearly increasing from 0 to 3%
	45–65 years: linearly increasing from 3% to 17%
	65–100 years: linearly decreasing from 17% to 13%
Mean duration of development of progressive adenomas to clinical cancer	20 years (without competing other cause mortality)
Mean duration of preclinical cancer	3.6 years
Mean duration of adenoma	16.4 years
Percent of non-progressive adenomas that do not develop beyond 6–9mm	50%
Percent of non-progressive adenoma that become 10mm or larger	50%
Percent of cancers that develops from 6–9mm adenoma and from 10+mm adenoma	30% of cancer develops from 6–9 mm, 70% from 10+mm

Table 3.

Conventional Model Description: Basic Structure of the CRC-SPIN Natural History Model (19).

Adenoma Risk: Non-homogeneous Poisson process

Log-risk for the ith individual = ${\alpha }_{0i}+{\alpha }_{1}se{x}_i+{\sum }_{k=1}^4\delta (A_k<ag{e}_i\left(t\right)\le A_{k+1})\left\{ag{e}_i\left(t\right){\alpha }_{2k}+{\sum }_{j=2}^k{A}_j({\alpha }_{2,j-1}-{\alpha }_{2j})\right\}$

Baseline log-risk, α0i, is Normally distributed, mean Λ, standard deviation σ  δ(·) is an indicator function with δ(x)=1 when x is true and δ(x)=0 otherwise  agei(t) is the ith individual's age at time t  A1=20, A2=50, A3=60, A4=70, A5=∞ (effectively 100 years old)

Calibrated parameters: Λ, σ, α1, α21, α22, α23, and α24

Adenoma Growth: Janoshek Growth Curve

dij (t) = d∞ − (d∞ − d0)exp(−λijt)

dij(t) is the maximum diameter of the jth adenoma in the ith individual at time t after initiation.  d0=1mm, minimal detectable adenoma size  d∞=50mm, maximum adenoma size  time to reach 10mm: − ln((d∞ −10)/(d∞ − d0))/λ .

Time to Reach 10mm: Type 2 extreme value distribution

Adenomas in the colon: distribution parameterised by β1c and β2c

Adenomas in the rectum: distribution parameterised by β1r and β2r

Calibrated parameters: β1c, β2c, β1r, and β2r

Transition to Preclinical Cancer: Normal cumulative distribution

Probability of transition, male colon  ϕ({ln(γ1cmsize + γ2cm(a − 50)}/γ3)

Probability of transition, male rectum  ϕ({ln(γ1rmsize + γ2rm(a − 50)}/γ3)

Probability of transition, female colon  ϕ({ln(γ1cfsize + γ2cf(a − 50)}/γ3)

Probability of transition, female rectum  ϕ({ln(γ1rfsize + γ2rf(a − 50)}/γ3)

Where ϕ(·) is the standard Normal cumulative distribution function, size is adenoma size in mm, and a is age at adenoma initiation.

Calibrated parameters: γ1cm, γ2cm, γ1rm, γ2rm, γ1cf, γ2cf, γ1rf, γ2rf, and γ3

Sojourn Time: Lognormal distribution

Preclinical colon cancer, lognormal with mean μc, standard deviation τcμc

Preclinical rectal cancer, lognormal with mean μr, standard deviation τrμr

Calibrated parameters: μc, τc, μr, and τr

Table 4.

Conventional Model Description: Basic Structure of the SimCRC Natural History Model.

Adenoma risk index: Drawn for each individual from a normal distribution truncated to non-negative values with a mean of 1 and a variance ranging from 0.020 to 0.021.

Adenoma growth index: Drawn for each adenoma from a normal distribution truncated to non-negative values with a mean of 1 and a variance ranging from 0.392 to 0.438.

Adenoma growth: Location- and sex-specific annual probability that adenoma of a given size category transitions to the next size category, ranging from 0.038 to 0.603 (adenoma <6 mm) and 0.009 to 0.368 (adenoma 6–9 mm).

Transition to preclinical CRC: Sex- and location-specific probability that a 10+mm adenoma transitions to a stage I preclinical CRC. Modelled as a logistic function of age with intercept ranging from −5.812 to −4.479, coefficient on age ranging from 0.008 to 0.058, and coefficient on the square of age ranging from −4.5 × 10−5 to −7.0 × 10−6.

Progression of preclinical (i.e., undiagnosed) CRC: Location-, sex-, and stage-specific annual probability that a preclinical CRC progresses to the next stage, ranging from 0.241 to 0.388 (stage I), 0.275 to 0.654 (stage II), and 0.509 to 0.769 (stage III).

Progression of preclinical (i.e., undiagnosed) CRC: Location-, sex-, and stage-specific annual probability that a preclinical CRC progresses to the next stage, ranging from 0.241 to 0.388 (stage I), 0.275 to 0.654 (stage II), and 0.509 to 0.769 (stage III).

The MISCAN model

The MISCAN-Colon natural history parameters are presented in Table 2. A person-specific risk index is generated for each individual in the simulated population.

Subsequently, adenomas are generated in the population according to this person-specific risk index and an age-specific incidence rate of adenomas. This results in no adenomas for most persons and 1 or more adenomas for others. Adenomas can progress in size from small (1–5 mm) to medium (6–9 mm) to large (10+ mm). Most adenomas will never develop into cancer (non-progressive adenomas), but some (progressive adenomas) may eventually become malignant, transforming from medium or large size to a preclinical stage I cancer. The cancer may then progress from stage I to stage IV. In every stage there is a probability of the cancer being diagnosed because of symptoms.

The CRC-SPIN model

The CRC-SPIN natural history is described in Table 3. The risk of an observable adenoma (≥1mm) is modeled using a nonhomogeneous Poisson model that allows adenoma risk to depend on gender and to increase with age. The log-risk of adenoma occurrence varies across individuals and has a Normal distribution. Each adenoma is stochastically assigned a time to reach 10mm, based on a type II extreme value distribution. Adenoma size is modeled continuously in time using a Janoschek growth curve model (21,22), with growth rates determined by a transformation of the time to 10mm. CRC-SPIN allows direct transition to CRC from adenomas of any size. The probability that an adenoma transitions to preclinical cancer increases with size and the age of adenoma initiation. The time from preclinical cancer to clinical cancer is modeled using a lognormal distribution. Adenoma growth, the probability of transition to preclinical cancer, and dwell time all depend on adenoma location (colon or rectum). Once a cancer becomes clinically detectable, it is stochastically assigned a size and stage at clinical detection. The CRC-SPIN model was developed to examine CRC screening and therefore projects CRC incidence and mortality through age 85.

The SimCRC model

The SimCRC natural history is described in Table 4. Over time, each person is at risk for forming 1 or more adenomas. Each adenoma may grow in size from small (≤5 mm) to medium (6 to 9 mm) to large (≥10 mm). Medium-size and large adenomas may progress to preclinical colorectal cancer, although most will not in an individual's lifetime. Preclinical cancers may progress in stage (I to IV) and may be detected by the presence of symptoms, becoming a clinical case.

The SimCRC model allows for heterogeneity in growth and progression rates across multiple adenomas within an individual. Although all adenomas have the potential to develop into colorectal cancer, most will not do so in an individual's lifetime. The likelihood of adenoma growth and progression to colorectal cancer is allowed to vary by location in the colorectal tract (that is, proximal colon v. distal colon v. rectum).

Dwell time in the 3 models

The dwell time from adenoma onset to clinical cancer in each model is influenced by all the input parameters listed in the respective Tables 2 to 4, with the exception of the parameters on (fractions of) nonprogressive adenomas in MISCAN (items b, f, and g in Table 2).

Maximum Clinical Incidence Reduction (MCLIR)

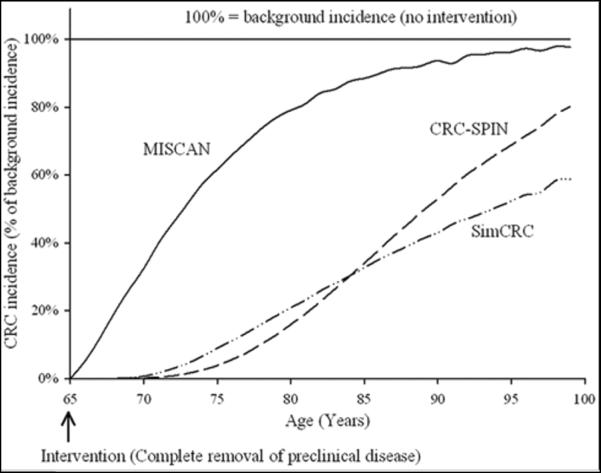
Table 5b presents the MCLIR after disease removal at 65 years for each model in the successive 5-year periods from 65 onwards. SimCRC and CRC-SPIN models projected large MCLIR₆₅^0–15 values until age 80 (90% and 88% respectively). The MISCAN model projected a MCLIR₆₅^0–15 of 51%. The differences show that the assumptions of the first two models imply a longer preclinical phase, because more adenomas and polyps are caught in the preclinical stage at age 65 years and are prevented from progressing to clinical cancer. Figure 1 shows these results as the percentage of the background incidence (100% - MCLIR) by year. This figure demonstrates that the MISCAN model projected that 62% of cancers in individuals 75 years old developed within 10 years (namely after age 65), whereas the CRC-SPIN and SimCRC models projected that only 4% and 9% of cancers in individuals 75 years developed within 10 years, respectively. These differences show why CRC-SPIN and SimCRC models project greater effectiveness and more favorable cost-effectiveness of screening than MISCAN.

Table 5.

Simulated Outcomes of 3 Models Representing the 25 and Older US General Population: a) The Background CRC Incidence by Age Group per 100,000 Person Years and b) the Maximum Clinical Incidence Reduction (MCLIR₆₅) after Complete Removal of Preclinical Cancer and Adenomas at Age 65 for 5-Year Periods and until Age 80, by Age Group and by Period Since Complete Removal.

Age	50–54	55–59	60–64	65–69	70–74	75–79	80–84	65–79
(a)	Background incidence
MISCAN	51	88	139	208	286	370	440	279
CRC-SPIN	52	85	127	180	247	327	424	243
SimCRC	61	96	142	202	277	357	424	271

(b)	MCLIR65
Time since complete removal (years)	0–5	5–10	10–15	15–20	0–15
MISCAN, %	84	55	30%	17%	51%
CRC-SPIN, %	100	99	92%	77%	90%
SimCRC, %	100	97	86%	74%	88%

Figure 1.

CRC incidence after complete removal of adenomas and preclinical cancers prevalent at age 65, as a percentage of the background incidence (100% – MCLIR₆₅ *); calculations for one cohort of individuals with three models representing the US general population: MISCAN, CRC-SPIN and SimCRC.

*MCLIR = Maximum Clinical Incidence Reduction

As shown in Table 5a, the differences in MCLIR between the CRC-SPIN and SimCRC on the one hand and MISCAN on the other cannot be explained by differences in background incidences, since these rates are very similar. This combination of similar incidence and different dwell time models is not surprising: a given incidence curve can be reproduced by very different dwell times by adjusting the (unobservable) age of onset of adenomas that make it to clinical cancers. Given the similarity in age trend of the background incidence, the differences in MCLIR are determined entirely by dwell time assumptions.

Discussion

A complete description of the structure and inputs of a model is necessary, but limited in the insights that are provided for natural history models. In correspondence with the idea of developing standard outputs to describe models, we propose to include the projected MCLIR as a prediction measure in the description of screening models. By comparing the MCLIRs between models, similarities or differences in natural history, and more specifically, the models' implicitly assumed length of the preclinical disease phase, become apparent. The MCLIR should be relatively easy to calculate with any screening model. Because it is based on model output instead of input, it is uniformly applicable regardless of the type of model. We propose this approach as a general way to describe models that are used to estimate the effectiveness or cost-effectiveness of screening strategies.

Closely related output measures to express the impact of dwell time are lead time (restricted to disease that would progress to clinical cancer without intervention) and dwell time itself (from disease onset to clinical cancer). In MISCAN, CRC-SPIN and SimCRC dwell time on average was 8, 25 and 21 years respectively (13). Given that dwell time is the main driver of the MCLIR, it clearly gives the same type of information but arranged differently. The MCLIR is presented by time since complete removal of disease (e.g., age 65 years). The difference between the metrics is their relation to clinical incidence by age, given that at each ages, the incident cases represent a difficult-to-grasp mix of shorter and longer dwell times. This relation is not straightforward for the dwell time distribution, whereas it is part of the metric of the MCLIR. Dwell time is closer to the inputs of the model; the MCLIR is closer to effects of screening that could be observed. Even though lead time, like the MCLIR, is bound to an age of intervention, it lacks straightforward relation to the cancer incidence by age. In addition, the lead time distribution (as opposed to average lead time) is difficult if not impossible to output for many models that do not produce paried life histories with and without intervention (e.g., models build with the TreeAge program).

We chose to present the MCLIR for age 65 years because this is in the middle of the age range (50–80 years) when individuals are often recommended to get CRC screening. As pointed out in the Methods section, it may be useful to present the MCLIR for different ages (e.g. the MCLIR₅₅, MCLIR₆₅ and MCLIR₇₅), if dwell time assumptions differ by age. Similarly, if dwell time depends on disease characteristic (such as location of disease, e.g., colon cancer v. rectal cancer) or other patient characteristics than age (such as gender or race), then it would be valuable to present the MCLIR for each of these groups.

Are model differences a limitation, or even a failure, of modeling? We think the differences between our CRC screening models reflect genuine uncertainty because all 3 models provide good fit to observed data such as CRC incidence and adenoma prevalence rates (13). The demonstrated differences indicated areas where additional data are needed to inform models, and where, in the absence of data, strong assumptions must be made. Only when more relevant data have become available, will it become clear which model is more accurate. Very recently, the incidence and mortality endpoint results of a large randomized controlled once only sigmoidoscopy study have become available (23). This study's 11-years follow up contains strong information on dwell time in combination with endoscopy sensitivity, at least for the distal colon. We expect that after the three model groups have calibrated their models to these new data, the MCLIRs will differ substantially less. Remaining uncertainty will concern the proximal part of the colon that is not reached by sigmoidoscopy. In the meantime, the way to handle uncertainties is to perform sensitivity analyses to investigate the robustness of the results for the uncertainties.

In this article we presented CRC screening models. Our approach, however, is relevant for any screening model, including those for nonneoplastic disease. The reason is that screening by definition presumes a detectable preclinical phase before disease becomes symptomatic. The duration of this phase always is an important determinant of the potential of screening. Although the concept is generalizable, specific issues may need attention when the MCLIR is applied to other diseases. One issue is that, unlike for CRC, the possibility of `incidental' detection of asymptomatic disease (e.g., breast or lung cancer on a computed tomography examination for unrelated indication) may be important. As pointed out in the Methods section, the absence or presence of incidental detection when simulating the MCLIR, should be specified since the MCLIR assumes no further screening. The best comparison of MCLIRs between models will be made when they handle incidental detection in a similar way.

In the models presented, the simulation of natural history begins at the onset of detectable disease (i.e., the onset of small adenomas). In some models, the simulation of natural history may begin before the disease is in a detectable state. Given that nondetectable disease is not relevant for the effectiveness of screening, we included detectability in the definition of the MCLIR. If the onset of detectable disease is not defined in a model, the MCLIR will automatically simulate the removal of any and all preclinical disease. In that case, however, it becomes more important to also present the clinical incidence reduction (CLIR) after removal that is incomplete due to assumed realistic lack of sensitivity (see next paragraph).

The MCLIR addresses the modeling of the limitation imposed by the natural history (the limitation of screening effectiveness). To describe the limitation imposed by (lack of) test sensitivity would be a logical next step. Interestingly, one could use the same method used for the MCLIR, by presenting the clinical CLIR after screening with the base case sensitivity. Due to the high sensitivity the CLIR after colonoscopy was only slightly lower than the MCLIR for our models (results not shown). The difference between the MCLIR and the CLIR after removal of disease detected with a fecal occult blood test (FOBT) of course will be much larger. Also, dwell time of detectable preclinical disease and sensitivity of the test under evaluation are to some extent interchangeable when calibrating models to data on screening effectiveness. A model with long dwell time combined with low sensitivity can project similar effectiveness to a model with short dwell time and high sensitivity. Typically, these models will show different MCLIRs but similar CLIRs after detection with estimated sensitivity.

Suggestions for using projections to describe models date back to the 1990's (11). We build on those suggestions by proposing a standardized metric for comparing models. Projections cannot replace input description. The latter is necessary for reproducibility. However, projections do have value. Where needed, they can show the implications of implicit assumptions in a concise manner. Projections, combined with a restricted input description, are suitable to be included in the main text of a journal, whereas complete lists of input parameters can be placed in a supplemnentary (online) document.

In conclusion, adding the simulated maximum clinical incidence reduction (MCLIR) after complete removal of precursor disease is a simple way to clarify the impact of natural history in (CRC) screening models. It would be worthwhile to include such a measure in all screening modeling papers. We have described how to calculate the MCLIR and proposed standard notation for reporting it.