The Representation of Biological Classes in the Human Brain

Abstract

Evidence of category specificity from neuroimaging in the human visual system is generally limited to a few relatively coarse categorical distinctions—e.g., faces versus bodies, or animals versus artifacts—leaving unknown the neural underpinnings of fine-grained category structure within these large domains. Here we use fMRI to explore brain activity for a set of categories within the animate domain, including six animal species—two each from three very different biological classes: primates, birds, and insects. Patterns of activity throughout ventral object vision cortex reflected the biological classes of the stimuli. Specifically, the abstract representational space—measured as dissimilarity matrices defined between species-specific multivariate patterns of brain activity—correlated strongly with behavioral judgments of biological similarity of the same stimuli. This biological class structure was uncorrelated with structure measured in retinotopic visual cortex, which correlated instead with a dissimilarity matrix defined by a model of V1 cortex for the same stimuli. Additionally, analysis of the shape of the similarity space in ventral regions provides evidence for a continuum in the abstract representational space—with primates at one end and insects at the other. Further investigation into the cortical topography of activity that contributes to this category structure reveals the partial engagement of brain systems active normally for inanimate objects in addition to animate regions.

Introduction

Neuroimaging studies of object vision in humans reveal a set of functional landmarks associated with a stable but relatively coarse set of categorical distinctions (for review, see Martin, 2007; Kanwisher, 2010; Mahon and Caramazza, 2011). For example, a system centered in the lateral fusiform is active for living things including faces (Kanwisher et al., 1997; Haxby et al., 2000), bodies (Peelen and Downing, 2005), and animals (Chao et al., 1999), while a complementary system in the medial ventral stream is active for nonliving things, including scenes (Epstein et al., 1999) and tools (Chao et al., 1999). While such landmarks provide insight into how the brain's resources are divided among broad categories, far less is known about finer distinctions—for instance, how we tell one animal species from another. For finer grained distinctions, further experimentation is unlikely to yield a similar set of regional landmarks, e.g., a region specific for squirrels and another for raccoons.

Finer grained category structure is evident, however, by measuring category-specific signals embedded in distributed patterns of brain activity (Haxby, 2010). Multivariate pattern classifiers can decode a large number of natural categories including discriminating between members of subordinate object classes (Haxby et al., 2001; Cox and Savoy, 2003; Reddy and Kanwisher, 2007; Eger et al., 2008). However, classification accuracy alone provides limited information about representational structure. To better understand the structure of representations, it is additionally helpful to investigate the similarity spaces defined by multivariate patterns (Edelman et al., 1998; Hanson et al., 2004; O'Toole et al., 2007; Connolly et al., 2012). This latter approach—coined recently as representational similarity analysis (RSA) (Kriegeskorte et al., 2008)—measures how categories are organized in abstract representational space, providing greater insight into underlying encoded dimensions. Kiani et al. (2007) used RSA to measure neural population responses in monkey inferotemporal cortex using multiple single-unit recordings revealing a rich, hierarchical category structure for a large number of categories—including a major distinction between animate and inanimate objects, a distinction within the animate domain between faces and bodies, and a finer grained hierarchical structure among animal bodies that appears to reflect information about biological relationships among species. A follow-up RSA study using functional magnetic resonance imaging (fMRI) in humans (Kriegeskorte et al., 2008) revealed a high degree of agreement between representational spaces in monkeys and humans for broad distinctions, but did not address the fine-grained structure for animate categories evident in monkeys.

Here, we use RSA to investigate fine-grained category structure for a set of animal classes—documenting for the first time using human neuroimaging a hierarchical category structure that mirrors biological class structure. Analysis of the topographies of responses reveals a continuum that appears to reflect the degree of animacy in the ventral visual cortex. The “least animate” objects in our study—the bugs—evoke cortical activity similar to that evoked by artifacts, whereas the most human-like—the primates—evoke activity similar to that evoked by animate stimuli in previous studies, thus suggesting that the animate–inanimate distinction in human cortex may also reflect a graded dimension among animate categories.

Materials and Methods

We recorded brain activity associated with viewing color photographs of six species: ladybird beetles, luna moths, common yellowthroat warblers, mallard ducks, ring-tailed lemurs, and squirrel monkeys. These species were chosen to represent a simple natural hierarchy comprising three superordinate classes—insects, birds, and primates—as well as a higher-level grouping of invertebrates and warm-blooded vertebrates. We refer to these classes as bugs, birds, and mammals corresponding to the so-called “life form” rank identified in cross-cultural studies as having folk-biological significance (Berlin, 1992). Each individual species was chosen because it was judged to have salient visual features common to that species but distinct from the others.

Participants.

Participants were 12 right-handed adults with normal or corrected vision from the Dartmouth College community (age range 20–35 years; mean age 25 years; 7 males). Before participation, subjects were screened for MRI scanning and provided informed consent in accordance with the Institutional Review Board of Dartmouth College. Subjects were paid an hourly rate for their participation.

Stimuli.

The stimuli for the fMRI experiment comprised 32 images for each species, plus left–right flipped complements, for a total of 64 unique images per species and a grand total of 384 images. The original high-resolution digital images were collected from the internet. Image background of all stimuli was erased and made transparent. Images were scaled to fit into a 400 × 400 pixel frame. Stimuli were presented to subjects in the MRI scanner using a rear-projection screen positioned at the rear of the scanner and viewed with a mirror mounted to the head coil. Viewed images subtended ∼10° of visual angle.

Procedure.

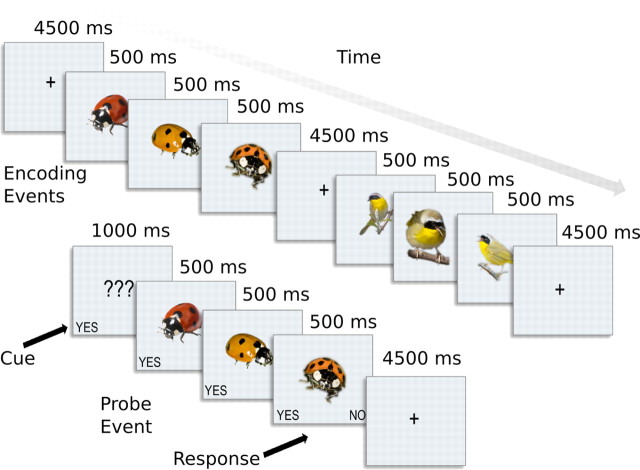
The stimuli were presented to subjects using a slow event-related design while they were engaged in a simple recognition memory task (Fig. 1). An encoding event consisted of three different images of the same species each presented consecutively for 500 ms without gaps. Events were followed by a 4500 ms interstimulus interval. A trial consisted of six encoding events—one for each category—followed by a probe event that was either identical to an event from that trial or was new. Each trial included a blank encoding event—6 s of fixation— interspersed pseudo-randomly among the encoding events so that a set of encoding events never began or ended with a blank event. Event order was pseudo-randomized to approximate a first-order counterbalancing of species—each species followed every other the same number of times (Aguirre, 2007). The subject's task was to indicate whether the probe was old or new via button press. A scanning run comprised six trials, and there were 10 runs per session for a total of 60 encoding events per species.

Figure 1.

Slow event-related fMRI design. During fMRI scanning, subjects engaged in a simple recognition memory task to ensure attention was paid to each stimulus. During encoding events images were presented in sequences of three exemplars of the same class. A set of six encoding events—one for each stimulus class—was followed by a probe event, which prompted subjects to answer yes or no depending on whether the probe was identical to one of the encoding events.

Image acquisition.

Brain images were acquired using a 3 T Philips Achieva Intera scanner with an eight-channel head coil. The functional imaging used gradient-echo echoplanar imaging with SENSE reduction factor of 2. The MR parameters were TE/TR = 35/2000 ms, flip angle = 90°, resolution = 3 × 3 mm, matrix size of 80 × 80, and FOV = 240 × 240 mm. There were 42 transverse slices with full-brain coverage, and the slice thickness was 3 mm with no gap. Slices were acquired in an interleaved order. Each of the 10 functional runs included 164 dynamic scans and 4 dummy scans for a total time of 336 s per run. At the end of each scanning session a single, high-resolution T1-weighted (TE/TR = 4.53/9848 ms) anatomical scan was acquired with a 3D-turbo field echo sequence. The voxel resolution was 0.938 × 0.938 × 1.0 mm with a bounding box matrix of (256 × 256 × 160) (FOV = 240 × 240 × 160 mm).

Image preprocessing.

Before all other analyses, time series data were preprocessed according to a standard set of steps. The goal was to diminish the effects of noise from various sources to better estimate the blood oxygen level-dependent signal. First, images were corrected for differences in slice acquisition time due to the interleaved slice order within the TR. Second, to correct for subject movement, individual volumes were spatially registered to the last volume of the last functional run—the volume closest in time to the high-resolution anatomical scan. Third, the data were despiked to remove any high values not attributable to physiological processes, thus correcting for normal scanner noise. Fourth, each run was detrended using Legendre polynomials to remove linear, quadratic, and cubic trends. Motion parameters—estimated during the motion-correction step—were also regressed out of the time series data at this step. Fifth, time series data were z-normalized within each run. Finally, volumes were spatially smoothed using a 4 mm FWHM Gaussian kernel. Time series preprocessing was done using AFNI software (Cox, 1996).

Neural similarity.

The first step in calculating neural similarity was to estimate the average voxelwise hemodynamic responses across the entire experiment for our six stimulus categories using deconvolution using AFNI software (3dDeconvolve). Each stimulus event was modeled by a set of eight tent functions expanding from the onset of the event out to 16 s with 2 s intervals. In addition to modeling events for the six stimulus classes, we also modeled yes-and-no probe events as regressors-of-no-interest. The resulting hemodynamic response functions were robust throughout the ventral pathway and tended to have peaks at 6 s poststimulus onset. These peak responses—the β values for the fourth tent functions—were used as the patterns from which we derived dissimilarity matrices (DMs). We calculated neural DMs within each mask for each subject by calculating the correlation distance (i.e., 1 − their Pearson correlation) between all pairs of species-specific β patterns—resulting in a 6 × 6 symmetrical DM. We chose correlation distance as a metric for deriving neural similarity, because prior work has shown that it is a good choice for RSA, outperforming other metrics such as Euclidean distance (Kriegeskorte et al., 2008). Derivation and analyses of similarity structures were performed primarily using Python programming tools for neuroimaging and mathematical computing, especially PyMVPA (http://www.pymvpa.org) (Hanke et al., 2009), NumPy (http://numpy.scipy.org), and SciPy (http://www.scipy.org).

Pattern classification.

We tested the discriminability of patterns for the six animal species using linear support vector machines (SVMs) (Vapnik, 2000) (LIBSVM, http://www.csie.ntu.edu.tw/∼cjlin/libsvm/) implemented within the PyMVPA (Hanke et al., 2009) framework using the default soft margin option that automatically scales the C parameter according to the norm of the data. The preprocessed time series data were coded so that only time points corresponding to peak hemodynamic responses for events (6 s after stimulus onset) were labeled by species category. All other time points were discarded. Within each run, time points were averaged within category—resulting in a single pattern per category per run—then z-scored within each run at each voxel. Note that it was not possible to use the β-weights used in calculating neural similarity for classification because those were estimated once for the entire time series, whereas classification required one independent estimate per run. Classification training and testing were done using a leave-one-run-out cross-validation strategy.

Behavioral similarity judgments.

Eight of the 12 fMRI participants returned to the laboratory after the original scanning sessions to participate in two behavioral similarity judgment tasks administered in a single 45 min session. The first task was a triad judgment task, in which subjects were instructed to “choose the odd-one-out” given a set of three animals. The stimuli were digital images that included a representative image from each of the six species used in the imaging experiment (targets) and images of nine additional species (barracuda, beetle, chimpanzee, fox, kingbird, lizard, brown moth, shark, and snake)—the additional animals served to elicit a greater number of responses from subjects and provided a more general context for judgments. We tested a subset of possible triads excluding triads that contained less than two targets—a total of 371 judgments. In a second task, subjects rated pairwise similarity of two animals at a time on a scale from 0 to 100—excluding all pairings without at least one target—a total of 90 judgments. For both tasks, subjects were told to make their decisions based on the “type of animal depicted by each image.”

The pairwise task and the triad task yielded consistent results across tasks and subjects. The data were combined to create a single behavioral DM as follows. The pairwise judgments for each subject were represented as a 6 × 15 (6 targets plus 9 additional animals) matrix corresponding to one judgment per animal pair, and the triad data were represented as a 6 × 15 matrix corresponding to the number of times a pair was chosen as belonging together, while a third item was chosen as the odd-one-out. These two matrices were concatenated horizontally, and a single DM was computed as the correlation distance between all pairs of rows. Resulting DMs were averaged across subjects to produce a single standard behavioral similarity structure (see Fig. 2A).

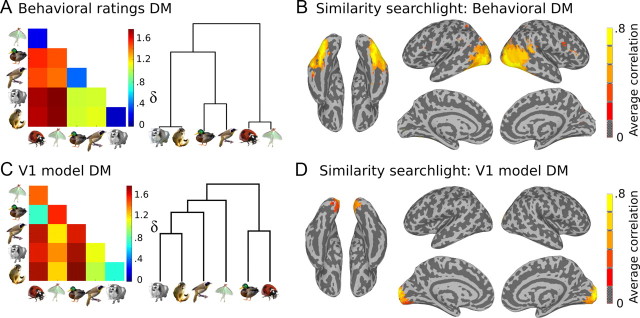
Figure 2.

Similarity searchlight analyses. A, DM based on behavioral ratings and corresponding dendrogram. B, Whole-brain searchlight results for correlation with behavioral DM. Neural DMs evaluated within searchlight spheres (radius = 9 mm) correlated significantly with the behavioral DM throughout the LOC region, but not in early visual regions of the occipital pole. C, DM based on V1 model of stimuli and corresponding dendrogram. D, Searchlight results for correlation with V1 model. Neural DMs for searchlight spheres correlated with the V1 model in the medial occipital pole. Searchlight maps show the average Pearson product-moment correlation with the target DMs (A, C) across subjects in MNI standard space. Maps are thresholded at t₍₁₁₎ = 4.41, p < 0.001, one-sample t test for z > 0, for z-values converted from permutation-based p values.

V1 model similarity structure.

To account for low-level visual properties such as retinotopic shape biases and spatial frequency information across our stimulus categories, we tested an alternative target similarity structure based on a model of V1 cortical neurons (Serre et al., 2007). Using software provided on the web site for the Center for Biological & Computational Learning at MIT (http://cbcl.mit.edu/software-datasets/), we modeled each of our stimulus images with a set of spatial filters that mimics the receptive fields of V1 complex cortical cells—specifically as C1 units in the second layer of the HMAX model (Serre et al., 2007). We averaged the C1 unit response vectors for each stimulus image within each animal species and used correlation distance to calculate the V1 model DM (see Fig. 2C).

Results

Similarity searchlights

Using the behavioral and V1 model DMs as target similarity structures, we used the searchlight mapping technique (Kriegeskorte et al., 2006) to map the correlation between neural similarity and target similarity throughout the brain for each subject. Neural DMs were calculated for each searchlight sphere (radius = 9 mm) using the correlation distance method described in Materials and Methods, Neural similarity. The correlation between these DMs and the target DMs were recorded at each searchlight center. The maps from group analysis shown in Figure 2, B and D, reveal a clear dissociation between regions that correlated highly with the behavioral and V1 model DMs. High correspondence with behavioral similarity was observed throughout the lateral occipital complex (LOC) region but was absent in early visual (EV) areas, whereas the retinotopic regions of the medial occipital lobe correlated significantly with the V1 model. Statistical significance of the correlation values was determined using a Monte Carlo method by generating a set of 1000 chance correlations by permuting the labels on the neural DM at each sphere. The resulting p value maps were then converted to z-scores (by calculating the inverse of the cumulative normal distribution) for group analysis (one-sample t test).

Classification searchlight

To map the discriminability between our six-stimulus classes throughout the brain, we ran searchlights that recorded the accuracy of a six-way SVM pattern classifier (see Materials and Methods, Pattern classification). Pattern classification was robust throughout EV areas and the LOC region (Fig. 3A), and was significant to a lesser degree in other parts of the brain including dorsal parietal and lateral frontal cortices. The area with the highest classification accuracy across subjects was in the occipital pole. Unlike the similarity searchlights, the classification searchlight did not differentiate between early and later stages of visual processing as classification was robust in both regions. Comparing the two analyses highlights the differences between classification analysis and similarity analysis. While two regions may have equivalently high performance on a classification measure, they nevertheless may have very different organization in terms of informational content. Searchlight analyses (both classification and similarity searchlights) were performed in subject native space, and the results were transformed into standard space for group analysis.

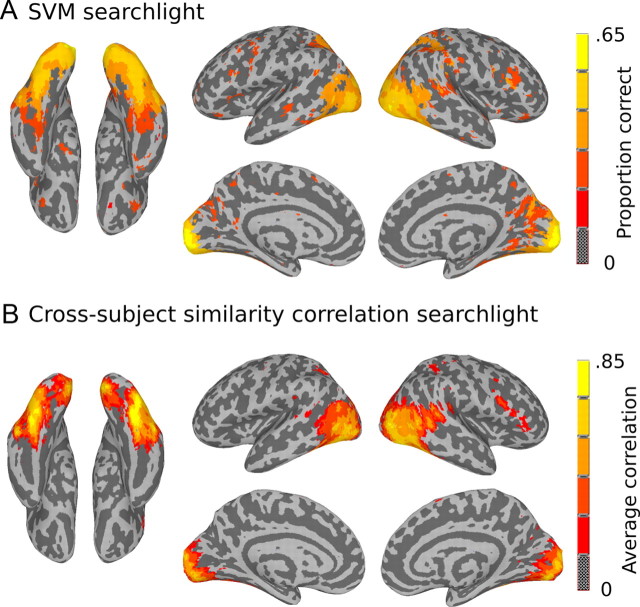
Figure 3.

A, Searchlight results for six-way SVM classification. Classification performance was high throughout visual cortex and in other parts of the brain. The highest classification accuracy was observed in the occipital pole: mean proportion correct = 0.64 (x = 9, y = −93, z = 3). The map is thresholded at t₍₁₁₎ = 5.9, p < 0.0001, for values greater than chance (0.1̄6). B, Searchlight results for correlation between DMs calculated within searchlight spheres for different subjects. Mapped values reflect the average correlation across subjects for each searchlight sphere in MNI space. High across-subject correlations were observed throughout EV cortex and the LOC region. The highest cross-subject correlations were observed in right fusiform gyrus: mean = 0.85 (x = 39, y = −63, z = −15).

Across-subject similarity correlation searchlight

We next explored the reproducibility of similarity structures across subjects by using an across-subject similarity correlation searchlight. The purpose of this analysis was to reveal the locations of common representational structure across subjects that were independent of the target similarity structures—thus leaving open the possibility of discovering common structure that is unique to neural representation and not predicted by the target models. For this analysis, an individual subject's data were first transformed into standard MNI space—using the symmetric nonlinear MNI152 brain template at 3 mm isotropic resolution (resampled from Fonov et al., 2009). For each searchlight sphere, we calculated the neural DM for all 12 subjects and recorded the average correlation between DMs across subjects. Figure 3B shows the map of across-subject similarity correlations. The map reveals shared structure throughout EV cortex and the LOC region, and extended to small patches of cortex in bilateral intraparietal sulcus and right inferior frontal gyrus. Similar to the SVM searchlight results, however, this analysis is unable to dissociate regions based on different types of representational organization.

Region of interest analyses of representational structure: LOC and EV

The searchlight analyses above reveal the location of interesting structure in our data, including a marked dissociation between semantic structure and low-level visual structure between early and later sections of the visual pathway. However, several questions remain—especially for understanding representational structure throughout the LOC. For example: How will the similarity space defined over larger patterns throughout LOC compare with behavioral similarity? Is neural similarity in LOC identical to behavioral judgments, or is there a systematic difference between LOC similarity and behavioral similarity? What prominent dimensions define the representational space in LOC?

To answer these questions it is necessary to investigate structure in distributed patterns across regions larger than the field of view of single searchlight spheres. It is a challenge, however, to identify separate regions of interest (ROIs) for EV and LOC without introducing arbitrary anatomical delineations or running into circularity without the help of appropriate functional localizers. For example, it would be circular to use the EV and LOC regions identified in Figure 2 for the purpose of comparing neural similarity with the behavioral and V1 models because those regions were identified using those models. Similarly, it would be difficult to justify the use of hand-drawn anatomical masks that included only those areas (although this latter technique is often pursued to satisfactory effect, despite reliance on imprecise anatomical landmarks). To overcome these difficulties, we developed a method for identifying shared representational structure across subjects that does not rely on external assumptions about representational structure, and does not require arbitrary segregation of anatomical regions. The technique combines three well known data analysis techniques, two of which have already been used in combination above, namely, searchlight analysis and representational similarity analysis, and the third is cluster analysis. First, we compute all dissimilarity matrices defined per searchlight from all subjects, and then we cluster those dissimilarity matrices to identify clusters of shared representational structure. After clustering, searchlight centers are mapped back into an individual subject's brain space to identify regions that produced shared structure across subjects. Once identified, those voxels were used to define ROIs to further explore representational structure throughout each region.

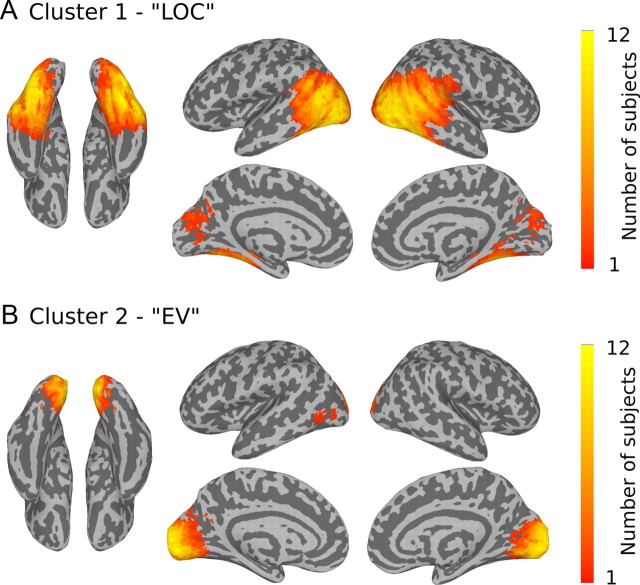
Due to computational limitations (in terms of computer memory) of clustering all searchlight similarities from all 12 subjects in a single analysis, some data reduction is a necessary first step. For this purpose, we used the data from the across-subject similarity correlation searchlight (Fig. 3B) to produce a mask that included all of the searchlight centers that had high average correlation across pairs of subjects using an arbitrary threshold of r > 0.3, and a spatial clustering criterion of 500 contiguous voxels. This mask was then dilated to include all of the voxels that contributed to the between-subject correlations recorded at the searchlight centers. The dilated mask was edited to include only voxels that were in the cerebrum mask. This single large mask, which included a contiguous set of voxels spanning nearly all of the EV cortex and the LOC region, was resampled to individual subject's spaces. (We note that limiting the scope of our ROI analyses to voxels within this mask precludes further investigation into possible shared representational structure for visual object categories outside of visual cortex. However, our primary focus is understanding the representation of object categories in visual cortex, especially within LOC. Exploration of shared representational structure outside of visual cortex is beyond our current scope.) Because the number of searchlight similarities from within the masks from all subjects was still prohibitively large, we further reduced the number of voxels by including only those voxels within each subject's gray-matter mask and whose spatial coordinates were divisible by two in the x-, y-, and z-dimensions, thus sampling a sparse evenly distributed subset of the voxels in the mask. (Note that although the searchlight centers included only those in this sparse mask, the corresponding dissimilarity matrices were calculated using data from all the voxels in a subject's volume using a 3 voxel radius around each searchlight center.) This second data reduction step resulted in a tractable number of observations for clustering, with each subject contributing 616 DMs on average (minimum = 534, maximum = 697). We clustered these DMs (total 7386) using agglomerative hierarchical clustering using a single linkage algorithm (Sibson, 1973) based on a distance matrix for all DMs (computed using correlation distance). Using a threshold of 10% of the maximum distance between nodes in the clustered hierarchy, the solution revealed two main clusters. The largest cluster, “Cluster 1,” included 1549 observations, and the second largest, “Cluster 2,” included 513. The third largest cluster only had 39 DMs, and beyond that there were no clusters with >10. We will limit our analysis to the two largest clusters. Without exception, voxels from Cluster 1 mapped into every subject within the LOC region and voxels from Cluster 2 mapped into every subject within medial occipital lobe, although the number of contributing voxels and precise locations varied across subjects. The average number of voxels contributing to Cluster 1 from each subject was 129 (minimum = 31, maximum = 212, SD = 61), and the average number contributing to Cluster 2 from each subject was 43 (minimum = 5, maximum = 85, SD = 22). To complete the ROI masks in each subject, we expanded the searchlight centers that contributed to Clusters 1 and 2 to include the entire corresponding searchlight spheres, but restricted to include only voxels that were also in the subject's gray-matter mask. Finally, any voxels that were overlapping from the expanded masks for Clusters 1 and 2 were excluded from both. Henceforth, we will refer to the ROIs for Cluster 1 and Cluster 2 as LOC and EV, respectively. Figure 4 shows the overlap across subjects for LOC and EV masks (shown in standard space).

Figure 4.

Definitions of ROIs, LOC, and EV, by maximizing across-subject reproducibility. DMs defined by searchlight spheres from all subjects were clustered to identify two major groups of similarity structures. The searchlight centers were then coded by cluster and mapped back into individual brains. A, The largest cluster was formed by DMs from voxels throughout LOC. B, The second largest cluster was formed by DMs from voxels in EV. Searchlight DMs in both clusters included voxels from every subject. The maps show the overlap of voxels from different subjects in MNI space for Clusters 1 and 2.

The DMs for LOC and EV are presented in Figure 5. For visualization of the similarity structures, we used hierarchical clustering to produce the dendrograms in Figure 5. The dendrogram for LOC shows the familiar hierarchical category structure that also characterizes behavioral judgments. The correlations between LOC DMs and the behavioral DM and between EV and the V1 model DMs were quite high (Fig. 5).

Figure 5.

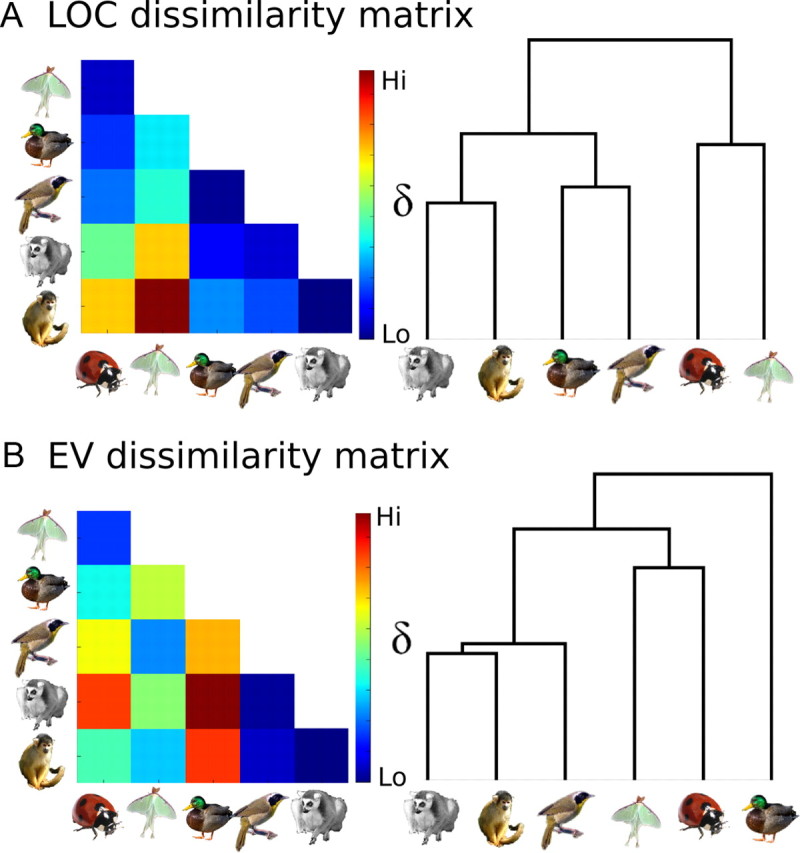
A, B, Average neural DMs and corresponding dendrograms for LOC (A) and EV (B). The mean between-subject correlations for neural DMs were r = 0.94 for LOC and r = 0.71 for EV. The correlation between the average LOC DM (A) and the behavioral DM (Fig. 2A) was r = 0.76, and between the EV DM (B) and the V1 model DM (Fig. 2C) was r = 0.78. The correlation between the average EV and LOC DMs was r = 0.09.

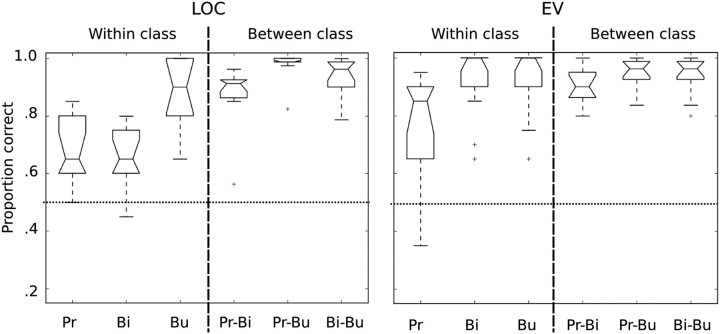
It is important to confirm that the patterns investigated using similarity analysis also support reliable classification between all pairs of stimuli. That is because if two patterns are indistinguishable from each other, giving them unique labels in a similarity analysis can spuriously boost correlations between DMs. Figure 6 summarizes results for pairwise SVM classification for all stimulus pairings. These results show robust classification between all pairs of stimuli in LOC and in EV. In LOC, the highest classification accuracy was observed for bugs versus primates discriminations, and was generally higher for between-class discriminations than for within-class discriminations. In EV, there was no apparent difference for accuracies for within-class versus between-class discrimination, with the exception of within primates. These analyses demonstrate that two regions that support equivalently robust classification can nevertheless have very different representational organization in terms of similarity structure. Note that the purpose of these analyses was not to claim that classification accuracy is higher in LOC and EV than in other parts of the brain—that has already been demonstrated by the searchlight analysis reported above (Fig. 3A).

Figure 6.

Accuracies for pairwise SVM classification within LOC (left) and EV (right). Classification accuracies were significantly above chance for all pairs of stimuli within and between superordinate classes in LOC; however, overall accuracies were higher for between-class pairs than within-class pairs. The best discrimination was observed between primates and bugs. Classification accuracies in EV were all well above chance for all stimulus pairings. Pr, primates; Bi, birds; Bu, bugs. Boxplots show the upper and lower quartiles of the distribution of values across subjects (top and bottom extents of the boxes), the median (center line), the range within 150% of the inner quartile (whiskers), and outliers (crosshairs).

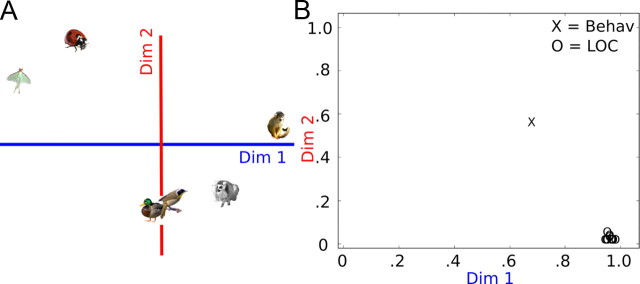
An additional finding, consistent with the classification results and evident when inspecting the dissimilarity matrices (Fig. 5), is that the dissimilarity values in LOC are greatest between the primates and the bugs, and the values between birds and the other two superordinate classes are intermediate. These relationships are made clear through visualization using multidimensional scaling (MDS) (Takane et al., 1977). In Figure 7, we plot the results for an individual differences MDS solution computed for all 12 individual LOC DMs plus the behavioral DM. This analysis allows for an assessment of the variation across subjects in terms of the structure of representation, and it allows for a direct comparison between the structure of the behavioral DM and neural DMs that is more informative than simple correlation measures. Figure 7A shows the best fit MDS solution for all 13 input DMs. Dimension 1 in the solution defines a continuum in representational space with primates at one end and bugs at the other with the birds in between, and Dimension 2 defines a continuum with birds at one extreme and the bugs at the other. The weights for individual input DMs (Fig. 7B) show the importance of each dimension for each input matrix. The weights plot shows that Dimension 1 is more important than Dimension 2 for all input DMs; however, while Dimension 2 is of intermediate importance for the behavioral DM, it is unimportant for the LOC DMs.

Figure 7.

MDS of DMs from LOC and behavioral ratings. A, 2D MDS solution that reflects the best fit Euclidean distances for all 13 input matrices (12 subjects plus the behavioral DM) computed using individual differences scaling (Takane et al., 1977). B, Individual differences are reflected in the weights assigned to each dimension for each input matrix. The weights reflect the importance of each dimension to each DM. The LOC DMs all have high weights on Dimension 1 and low weights on Dimension 2. Four subjects had weights equal to zero on Dimension 2, which means that the MDS solutions for those subjects are equivalent to a projection of the stimulus points onto the x-axis in A, and scaled along the x-axis by the weight on Dimension 1. Thus, for those subjects a single-dimensional solution with primates at one end and bugs at the other accounted for the most variance in LOC. Dim, Dimension.

Mapping category structure to cortical topographies

Similarity analysis reveals a high level of reproducibility across subjects in abstract representational spaces defined by neural DMs—especially with respect to the primate-to-bugs dimension observed in LOC. How does this abstract representational space map onto cortical topographies? The final set of analyses are aimed at better understanding how patterns of activity across the cortical anatomy give rise to the category structure observed in the previous analyses.

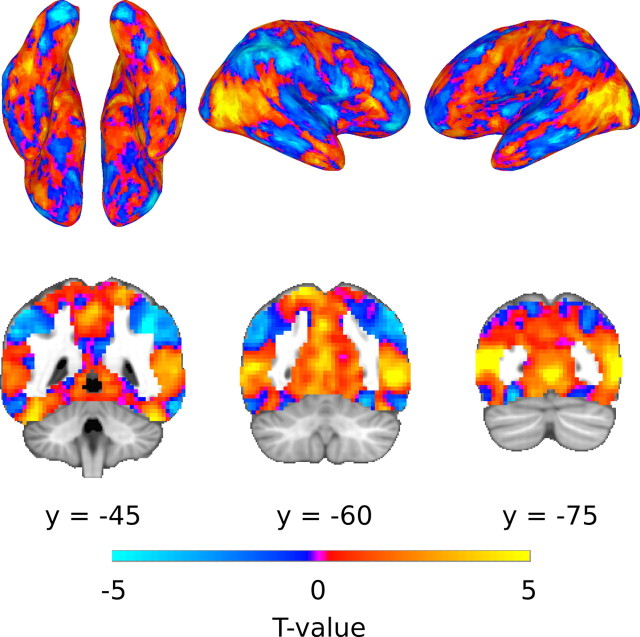
Figure 8 shows the group results of the projection of Dimension 1 from Figure 7 onto the fitted β coefficients for the six categories for each subject, calculated as the dot-product of the dimension weights (1 × 6 vector) and β-weights (6 × n voxel matrix). The distribution of activity shows a consistent set of bilateral structures that are positively correlated with Dimension 1, including lateral fusiform cortex, posterior superior temporal sulcus (STS), and the medial and lateral portions of occipital cortex. Positive correlation with Dimension 1 means that there is greater activity in these areas for categories on the positive end of the dimension (i.e., primates) and less activity for categories on the negative end of the dimension (i.e., bugs). A complementary set of structures that is negatively correlated with Dimension 1 includes medial and posterior fusiform and lingual gyri, the inferior temporal lobe, and inferior parietal lobule. Interestingly, this pattern is similar to previous findings that have compared activity for animate versus inanimate objects, like faces and animals versus tools and other artifacts (Chao et al., 1999, 2002; Chao and Martin, 2000; Haxby et al., 2001; Beauchamp et al., 2002; Mahon et al., 2007).

Figure 8.

Projection of Dimension 1 (Fig. 7) onto the β-weights for the six categories. Positive values correspond to a positive correlation between β-weights and the values along Dimension 1, i.e., the highest positive values indicate voxels where activity was greatest for monkeys and lowest for luna moths, while strong negative values indicate greater activity for luna moths and less for monkeys. The colors indicate t values from a group analysis for projected values different from zero. Values of |t₍₁₁₎| > 3.11 have p < 0.01; however, the full range of values are shown to highlight the consistent bilateral distribution of activity correlated with Dimension 1.

Correspondence between our findings and findings that compare animate versus inanimate objects is surprising because all of our categories are animate categories. However, our results may be consistent with previous studies if the continuum we observe in our data is part of a larger continuum that encompasses a wider range of stimuli that ranges from the most animate objects (humans) to the properly inanimate (e.g., tools). To fully test this hypothesis, it is necessary to sample a wider range of objects, which will require further experimentation outside the scope of the present study. However, it is possible to directly compare our result with previously reported results using a common set of coordinates. For this purpose, we compare our data to those reported in Mahon et al. (2009) using their technique to compute a medial-to-lateral index. Mahon et al. (2009) used this index to analyze the topography for living versus nonliving stimuli in the brains of sighted subjects viewing images and congenitally blind subjects hearing words. Here we use the living–nonliving index for image viewing from Mahon et al. (2009) for direct comparison with our data. Following Mahon et al. (2009), the medial-to-lateral index is computed as the average t value for the group analysis for a given contrast in each y-by-z slab at each x-coordinate within a bilateral ventral temporal mask for medial-to-lateral indices in the range of 25 ≤ |x| ≤ 40 (Fig. 9). Here, instead of contrasts between conditions, we use the values of the principal MDS projection, which reflects the continuum from bugs to birds to primates. Consistent with the topographies shown in Figure 8, the medial-to-lateral index for the MDS projection was positively correlated with the living–nonliving index (Fig. 9). Because primates and bugs represent the two poles of the continuum represented by Dimension 1, we expected to obtain similar results when comparing the contrasts of primates and bugs. Figure 9C shows the results for this contrast, which are nearly identical to those for the projection of Dimension 1. This pattern of results can be explained if we assume that our categories fall along a continuum in representational space identical to Dimension 1 in the MDS solution in Figure 7 with the assumption that nonliving objects fall on the far left end of this continuum. In agreement with this hypothesis, the medial-to-lateral index reported by Mahon et al. (2009) shows greater negative values at the most medial coordinates, which is expected if actual inanimate objects (like those used by Mahon et al., 2009) produced more activity than did bugs in the medial “inanimate” regions. In addition to the range of medial coordinates used to compare data across studies, we also provide data in Figure 9 for lateral coordinates out to |x| = 60, showing an inverted U shape consistent with findings that show greater activity for inanimate stimuli in lateral regions of the inferior temporal lobe (Chao et al., 1999; Beauchamp et al., 2003).

Figure 9.

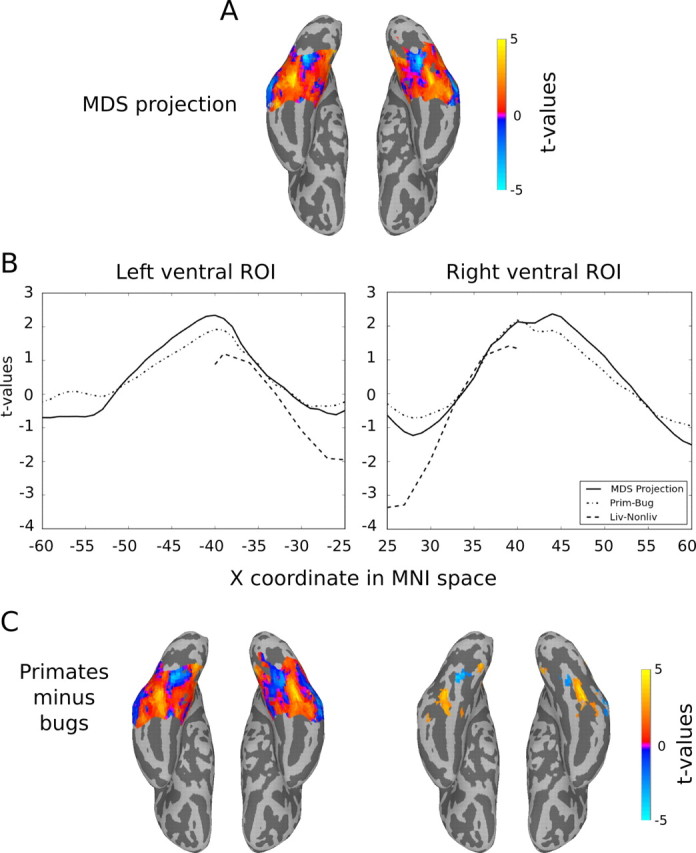
Comparison of the projection of the bugs-to-primates dimension (Fig. 7) to the living–nonliving contrast from Mahon et al. (2009). Using a method described by Mahon et al. (2009), we calculated the medial-to-lateral index for the projected Dimension 1 from the MDS analysis (Fig. 8). A, The colored regions show the extent of the mask used in the analysis, and the colors reflect the unthresholded t values for the group result. The mask we used covers a greater extent of the ventral surface in the medial-to-lateral dimension than that reported by Mahon et al. (2009). While these extra data points played no role in the comparison with the living–nonliving contrast, they illustrate the extent of consistent activity across the ventral surface. B, The medial-to-lateral index for our results and for living–nonliving. The values reported for the living–nonliving contrast were kindly provided to us by Brad Mahon and are also plotted in Mahon et al. (2009; their Fig. 5B, p. 402). The linear fits between our data and the living–nonliving contrast were highly significant with R² of 0.83 and 0.82 for the left and right ROIs, respectively. C, For comparison, we present the results of the contrast of primates and bugs within the left and right ventral ROIs. The unthresholded contrast on the left shows a nearly identical pattern to that of the Dimension 1 projection, which is also reflected by the medial-to-lateral index calculated for the primates–bugs contrast (B). On the right, we plot all voxels that pass a statistical threshold (t₍₁₁₎ > 2.2, p < 0.05) for the contrast. Blue voxels reveal bilateral medial regions in which the activity for bugs was greater than that for primates; warm-colored voxels reveal bilateral regions in the lateral fusiform in which activity was greater for primates.

Given the prominence of Dimension 1 in the representational space of LOC across our subjects, it is natural to ask whether this singular dimension accounted for all of the measurable variance across our categories. To rule out this possibility, we removed variance accounted for by Dimension 1 and recomputed several classification analyses. If Dimension 1 accounted for all of the reproducible variation across our stimulus categories, then classification accuracies should be at chance after collapsing the data onto a hyperplane perpendicular to that dimension. We removed the variance accounted for by Dimension 1 by computing a least-squares solution fitting that dimension to the data and keeping the residuals. This was done individually on each run of each subject's data using the individually weighted MDS model for each subject. Fitting a separate model for each run was necessary because of the leave-one-run-out cross-validation strategy used in classification.

The results of pairwise classification in LOC (Fig. 10A) show that despite the prominence of Dimension 1 in LOC, classification accuracies were still robustly above chance for all pairs of stimuli even after removing variance accounted for by the MDS model. Within-class discriminations (monkeys vs lemurs, warblers vs mallards, and luna moths vs ladybugs) were unaffected by removing this dimension, suggesting that these fine-grained distinctions are not coded along this dimension. In contrast, between-class discriminations dropped from classification accuracies of >90% to <75%, indicating that this dimension captures much of the variance for these distinctions. Similar to LOC, within-class discrimination in EV was not affected. While there was some reduction in accuracies for between-class discriminations in EV, the effect was less than that observed in LOC, remaining >80% on average.

Figure 10.

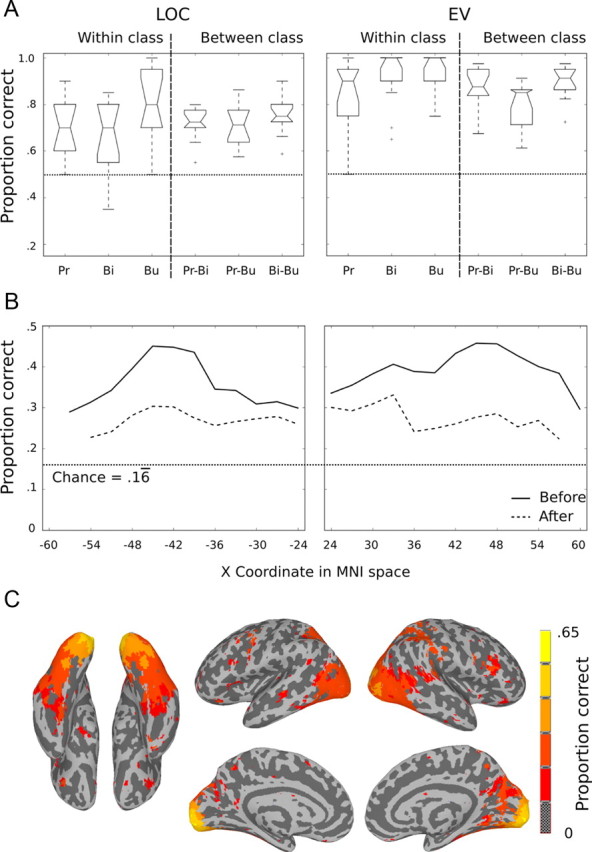
The effect of removing variance accounted for by Dimension 1 on classification accuracy. A, Pairwise classification accuracies for LOC and EV after removing variance accounted for by Dimension 1. Compare to Figure 6. B, Six-way SVM classification as a function of medial-to-lateral coordinates before and after removing variance accounted for by Dimension 1. C, Six-way SVM searchlight after removing Dimension 1 variance. Colored voxels show areas of classification accuracy that were significantly above chance using the same threshold as in Figure 3A (t₍₁₁₎ > 5.9, p < 0.0001). Pr, Primates; Bi, birds; Bu, bugs.

Next, we assessed the extent to which representation of Dimension 1 was limited to lateral portions of the ventral LOC region. We know from our previous analysis (Fig. 9) that Dimension 1 is most strongly represented in the lateral parts of the fusiform |x| = ∼45. If the lateral fusiform is driven completely by Dimension 1, then after removing Dimension 1 variance, classification accuracy should drop to chance. To rule out this possibility, we ran classification analyses for ROIs defined by 3 mm medial-to-lateral slabs within the ventral temporal ROI used in the analyses reported in Figure 9. The results shown in Figure 10B illustrate that before removal of Dimension 1, classification accuracies were highest in lateral fusiform (as expected), and significantly above chance throughout the medial-to-lateral extent. After removing Dimension 1, classification accuracies were reduced across the entire medial-to-lateral extent indicating that this dimension contributed to classification performance across the entire region. Crucially, even after removing Dimension 1, classification accuracies remained significantly above chance across the entire extent with the exception of the most lateral parts corresponding to voxels in inferior temporal lobe.

To provide a complete picture of the effect of removing variance accounted for by Dimension 1, we report the results of a full-brain SVM searchlight after removing Dimension 1 (Fig. 10C). In line with our previous findings, classification accuracies in the LOC region were diminished (compare Fig. 3A), but remained significantly above chance. Notably, classification accuracies in the occipital pole remained high compared with the LOC region.

Together, these analyses demonstrate that classification accuracy in LOC remains robust after removal of Dimension 1 variance, indicating that while Dimension 1 is a major component of the representation in LOC, it is only one dimension of a high-dimensional representational space (Haxby et al., 2011). The exact number of informative dimensions, the psychological dimensions they encode, and their distribution across cortex remain unspecified. A full accounting of the high-dimensional representational space is beyond the scope of this article.

Discussion

Using behavioral judgments as a target, we found semantic structure to be reflected strongly throughout the LOC. This finding was strengthened by the complementary distribution of representational structure corresponding to low-level visual features reflected in medial occipital cortex. Although the set of animal classes was small, this study is the first human neuroimaging study to document category structure within the domain of animate objects that reflects biological relations among species. The results are consistent with findings in monkey inferotemporal cortex that showed a similarity structure with separate clusters for quadrupeds, human bodies, fish, reptiles, butterflies, and other insects (Kiani et al., 2007), thus providing converging evidence that representation of animal classes is supported by neuronal population codes in primate object vision cortex. These results also extend a recent trend of uncovering finer grain semantic category structure within LOC using multivariate decoding techniques (Kriegeskorte et al., 2008; Naselaris et al., 2009; Haxby et al., 2011), and in addition demonstrate how RSA is an essential component of the multivariate pattern analysis toolkit, providing insights into structure that are left merely implicit in most pattern classification analyses—for more discussion on this point refer to Connolly et al. (2012).

A set of unexpected discoveries suggests that animal categories are represented along a continuum within LOC, and the structures that mediate this continuum are directly related to—if not identical to—the structures that underlie the animate–inanimate distinction. This hypothesis deserves closer attention, and we begin by reviewing the evidence that prompts it.

The first unexpected observation was that interesting representational structure for animals within LOC was not limited to activity within the known animate regions, e.g., within lateral fusiform and STS, and in contrast semantic structure was reflected throughout LOC across purported animate and inanimate regions. The second observation was that the structure of similarity spaces in LOC did not conform exactly to our expectations about semantic structure, and instead revealed a representational structure unique to LOC. The characteristic similarity structure produced by LOC activity was remarkably reproducible across subjects, with an average correlation between dissimilarity matrices across subjects of r = 0.94. Thus, similarity spaces in LOC were virtually identical across subjects, and individual LOC similarities were more like other subjects' LOC similarities than the semantic space defined by behavioral judgments, despite the fact that both behavioral and neural similarities shared a common hierarchy of animal classes. MDS revealed that the major commonality in LOC similarities—and something that set LOC similarity apart from semantic similarity—was the organization of stimuli with respect to a single dimension in representational space. This prominent dimension is characterized as a continuum with primates at one end, bugs at the other, and birds in between (Fig. 7). We found that the topographical distribution of activity underlying the single-dimensional organization implicates a set of brain structures that has been shown in other studies to mediate the dissociation of animate and inanimate stimuli. Greater activity for primates than for bugs was observed in lateral fusiform and STS, while greater activity for bugs than for primates was observed in medial fusiform and lingual gyrus, middle/inferior temporal gyrus, and inferior parietal lobule. This pattern of activity has been reported by various studies that have directly compared animate and inanimate stimuli (Chao et al., 1999, 2002; Chao and Martin, 2000; Haxby et al., 2001; Beauchamp et al., 2002, 2003; Mahon et al., 2007), with bugs taking the place of inanimate objects (like tools) and primates taking the place of animate objects (like animals or people). In the absence of actual inanimate stimuli to compare our results against, we borrowed data from a study that contrasted activity for viewing pictures of living and nonliving objects (Mahon et al., 2009). The direct comparison of our results using the medial-to-lateral index demonstrated a direct relationship between our observed continuum and differential activity associated with living and nonliving objects.

How can we explain these findings? One possibility is that the animal categories we have tested fall along a continuum in representational space that is predictable by the degree of animacy exhibited by each category. This suggestion follows from the observation that activity for primates resembles that for animate objects and activity for bugs resembles that for inanimate objects. We further assert that primates are subjectively “more animate” than are bugs. We can safely assume that experimental participants when prompted to make such decisions will agree that monkeys are more likely than bugs, for example, to have a mind, to initiate actions, and to be aware of their surroundings. Accordingly, our legal systems confer special rights to primates but not to bugs: killing a bug is inconsequential, whereas gratuitous killing of a monkey may result in criminal penalties. It is natural to expect gradations in similarity to the animate prototype—human beings—across the range of animate entities that includes, at least, all other animals. The fact that there are gradations of animacy (alternatively: gradations in similarity to humans) across the range of organisms in the animal kingdom is not surprising. What is new here is that the hierarchy of animacy appears to be reflected in the patterns of neural activity across cortical regions that have previously been described as dedicated for processing objects within discrete domains. Our new hypothesis predicts that testing a wider range of stimuli including humans and, for instance, tools will result in the same continuum reported here but flanked on the animate side by human stimuli and on the inanimate side by tools.

The animate–inanimate distinction is a fundamental psychological distinction that appears early in cognitive development (Rakison and Poulin-Dubois, 2001), deteriorates late in dementia (Hodges et al., 1995), and is a major determinant of morpho-syntactic structure throughout the languages of the world (Dahl, 2008). Because our findings suggest that degree of animacy is reflected by differential activity across the same systems that underlie the animate–inanimate distinction in cortex, it is a clear possibility that those subsystems in part encode the ubiquitous ontological dimension of animacy itself. This proposal agrees with the social brain hypothesis (Dunbar and Shultz, 2007), which proposes that the large human neocortex evolved as a result of evolutionary advantages conferred by social collaboration, with the perception of and communication with other minds as a primary function. Similarly, the domain-specific theory of category specificity in the brain (Caramazza and Shelton, 1998) proposes a dedicated subsystem for representing conspecifics as the basis of the animate-specific regions of cortex. In addition to the animate subsystems, however, the domain-specific theory also proposes that the subsystem underlying inanimate representations arose out of evolutionary pressures for representing affordances in manipulability, thus facilitating the advancement of tool use among our ancestors. It remains to be seen how marginally animate objects, like bugs, can fit within the same domain as manipulable objects, like tools, as there are no obvious affordances for manipulability associated with bugs.

Important caveats are necessary to avoid misrepresentation of this discussion of our findings. Foremost, we are not proposing a single-dimensional psychological model for representation in LOC. In fact, our results show that this single dimension does not account for fine-grained distinctions—for within-class discriminations. While the dimension we have identified accounts for a considerable amount of variance in our data, removing that variance nevertheless resulted in category-specific patterns that supported robust classification performance across all pairs of animal categories. Thus, the dimension of animacy is most certainly just a single dimension within a high-dimensional representational space. In recent related work, we explore evidence for a common high-dimensional model of object representation in ventral temporal cortex (Haxby et al., 2011) that proposes >30 such dimensions. Second, the proposal that animacy is the psychological dimension encoded by the dimension in question is an open hypothesis that will require further investigations to adequately address. The proposal is compelling, especially given the high reproducibility of the dimension across our subjects and the strong demonstrated relationship between the dimension and the cortical systems that underlie the animate–inanimate distinction. However, further experimentation is needed to know whether the graded representation of animacy is in fact the primary dimension that defines the macro-structure of representation for animate categories.