Scaling-law for the energy dependence of anatomic power spectrum in dedicated breast CT

Abstract

Purpose: To determine the x-ray photon energy dependence of the anatomic power spectrum of the breast when imaged with dedicated breast computed tomography (CT).

Methods: A theoretical framework for scaling the empirically determined anatomic power spectrum at one x-ray photon energy to that at any given x-ray photon energy when imaged with dedicated breast CT was developed. Theory predicted that when the anatomic power spectrum is fitted with a power curve of the form k f^−β, where k and β are fit coefficients and f is spatial frequency, the exponent β would be independent of x-ray photon energy (E), and the amplitude k scales with the square of the difference in energy-dependent linear attenuation coefficients of fibroglandular and adipose tissues. Twenty mastectomy specimens based numerical phantoms that were previously imaged with a benchtop flat-panel cone-beam CT system were converted to 3D distribution of glandular weight fraction (f_g) and were used to verify the theoretical findings. The 3D power spectrum was computed in terms of f_g and after converting to linear attenuation coefficients at monoenergetic x-ray photon energies of 20–80 keV in 5 keV intervals. The 1D power spectra along the axes were extracted and fitted with a power curve of the form k f^−β. The energy dependence of k and β were analyzed.

Results: For the 20 mastectomy specimen based numerical phantoms used in the study, the exponent β was found to be in the range of 2.34–2.42, depending on the axis of measurement. Numerical simulations agreed with the theoretical predictions that for a power-law anatomic spectrum of the form k f^−β, β was independent of E and k(E) = k₁[μ_g(E) − μ_a(E)]², where k₁ is a constant, and μ_g(E) and μ_a(E) represent the energy-dependent linear attenuation coefficients of fibroglandular and adipose tissues, respectively.

Conclusions: Numerical simulations confirmed the theoretical predictions that in dedicated breast CT, the spatial frequency dependence of the anatomic power spectrum will be independent of x-ray photon energy, and the amplitude of the anatomic power spectrum scales by the square of difference in linear attenuation coefficients of fibroglandular and adipose tissues.

INTRODUCTION

Dedicated breast computed tomography (CT) can overcome the tissue superposition problem that may mimic the presence of a lesion or mask a lesion in mammography. Bochud et al.¹ showed that certain imaging tasks are affected by background anatomy. Specific to mammography, Burgess et al.² and Chakraborty and Kundel³ independently showed that detection of lesions is impaired by anatomic noise. It has been previously shown that the anatomic power spectrum of the breast, often referred to as anatomic noise, is dominant at low spatial frequencies and follows a power-law of the form K f^−β in mammography.² In mammography, several studies^{2, 4, 5} have shown that the value of the exponent β is approximately 3.

The motivation for this study was based on the following observations. Metheany⁶ and Chen⁷ using a clinical prototype dedicated breast CT system operating at 80 kVp determined the value of the exponent β for power-law anatomic noise as approximately 1.8. In a recent exploratory study with a clinical prototype dedicated breast CT system operating at 49 kVp,⁸ we determined the value of the exponent as approximately 1.6. It is unknown if the observed difference in β values between the aforementioned studies reflected the subject population in those studies, or if it was at least partly influenced by the mean energy of the x-ray spectrum used for acquisition. Hence, we conducted this investigation from the theoretical perspective as to whether the mean x-ray photon energy influences the estimate of β.

Additional motivation for this study pertains to our continuing efforts to optimize dedicated breast CT. In addition to experimental studies using phantoms with homogenous background,⁹ there are ongoing efforts to optimize dedicated breast CT using analytical modeling^{10, 11} and human observer studies.^{12, 13} The extension of cascaded linear systems analysis to reconstructed image domain provides a framework for task-specific analytical optimization.¹⁴ For optimization studies using analytical modeling or numerical observers, it is important to include the anatomic background. Specifically, given an imaging task, T(f), the International Commission on Radiation Units (ICRU) recommended figure of merit,¹⁵ the detectability index, d^′, can be computed for the case of an ideal observer as

$$d^{\prime 2}=\int \frac{T^2\left(f\right){\mathrm{MTF}}^2\left(f\right)}{W_A\left(f\right)+W_S\left(f\right)}df$$ (1)

where, f is the spatial frequency, MTF(f) is the system modulation transfer function, W_S(f) represents the system noise power spectrum inclusive of any additive noise source such as detector electronic noise, and W_A(f) is the anatomic noise spectrum. Methods to analytically estimate MTF(f) and W_S(f) in projection views,^{11, 16, 17, 18} and in reconstructed image domain^{14, 19} have been described. For studies investigating the optimal x-ray photon energy for a given imaging task, one important aspect that needs to be addressed is the energy dependence of the anatomic power spectrum, W_A(f). Specifically, we needed to determine appropriate energy dependent scaling of the power-law fit coefficients, K and β. Hence, a theoretical framework was developed to address this need and was validated with numerical simulations.

METHODS AND MATERIALS

Theory

If one considers a breast void of any abnormalities, either benign or malignant such as microcalcifications, soft tissue lesions, cysts, etc., then for any given location (x, y, z) within the interior of the breast, i.e., excluding the skin, the tissue distribution can be considered as a mixture of adipose and fibroglandular tissue. At a given location (x, y, z), if m_g(x, y, z) and m_a(x, y, z) represent the mass of fibroglandular and adipose tissue, respectively, then the fibroglandular tissue weight distribution is defined as

$$\begin{array}{c}\hfill f_g(x,y,z)=m_g(x,y,z)/\left[m_a(x,y,z)+m_g(x,y,z)\right].\end{array}$$ (2)

In this study, x − y plane is the transverse or radial plane that corresponds to the coronal plane during in vivo breast CT, x − z and y − z planes are the longitudinal planes that correspond to sagittal and axial planes, respectively, during in vivo breast CT. Thus, the peripheral skin layer is not considered in our study, consistent with methods used for estimating the power spectrum of the anatomic background in dedicated breast CT.^{6, 7, 8} The linear attenuation coefficient distribution, μ(x, y, z, E) at energy E can be stated as

$$\begin{array}{ccc}\hfill \mu (x,y,z,E)& =& f_g(x,y,z){\mu }_g\left(E\right)\hfill \\ & & +\left[1-f_g(x,y,z)\right]{\mu }_a\left(E\right),\hfill \end{array}$$ (3)

where μ_g(E) and μ_a(E) represent the linear attenuation coefficient of fibroglandular and adipose tissue, respectively. For the case μ_g(E) = μ_a(E), Eq. 3 results in a uniform background. For the energy range of relevance (10–80 keV) and using elemental composition and density data from Hammerstein et al.,²⁰ the energy-dependent linear attenuation coefficients of adipose and fibroglandular tissue were obtained from NIST database²¹ and is shown in Fig. 1. From Fig. 1, we observe that μ_g(E) ≠ μ_a(E) for the energy range considered in this study. Hence, all subsequent analysis corresponds to the case μ_g(E) ≠ μ_a(E). Equation 3 can be rewritten as

$$\begin{array}{c}\hfill \mu (x,y,z,E)={\mu }_a\left(E\right)+f_g(x,y,z)\left[{\mu }_g\left(E\right)-{\mu }_a\left(E\right)\right].\end{array}$$ (4)

Fourier transforming Eq. 4 and applying the linear property of Fourier transform yields

$$\begin{array}{ccc}\hfill \mathbb{F}\left[\mu (x,y,z,E)\right]& =& {\mu }_a\left(E\right)\delta (u,v,w)+\left[{\mu }_g\left(E\right)-{\mu }_a\left(E\right)\right]\hfill \\ & & \times \left[F_g(u,v,w)\right],\hfill \end{array}$$ (5)

where (u, v, w) are the spatial frequency coordinates, F represents the Fourier transform, and F_g(u, v, w) is the Fourier transform of f_g(x, y, z), and the delta-term arises from the constant term in Eq. 4. The delta-term is defined as

$$\delta (u,v,w)=\left\{\begin{array}{c}1\mathrm{at}(0,0,0)\hfill \\ 0\mathrm{elsewhere}\hfill \end{array}\right..$$ (6)

The squared magnitude of Eq. 5 yields

$$\begin{array}{ccc}\hfill {\left|\mathbb{F}\left[\mu (x,y,z,E)\right]\right|}^2& =& |{\mu }_a\left(E\right)\delta (u,v,w)\hfill \\ & & +\left[{\mu }_g\left(E\right)-{\mu }_a\left(E\right)\right]\left[F_g(u,v,w)\right]{|}^2.\hfill \end{array}$$ (7)

It is known that the anatomic power spectrum of the breast obtained by ensemble average follows a power-law process.²² Further, such power spectrum computation does not include the zero-spatial frequency. Also, we do not have prior knowledge as to whether the amplitude k and the exponent β are energy-dependent. Hence, assuming that k and β may vary with energy,

$$\frac{1}{N}\sum _{i=1}^N|\mathbb{F}\left[{\mu }^i(x,y,z,E)\right]{|}^2=\frac{k\left(E\right)}{{\left(\sqrt{u^2+v^2+w^2}\right)}^{\beta \left(E\right)}}.$$ (8)

From Eqs. 7, 8 and ignoring the zero-spatial frequency term, it follows

$$\begin{array}{ccc}& & \frac{1}{N}\sum _{i=1}^N|\left[{\mu }_g\left(E\right)-{\mu }_a\left(E\right)\right]\left[F_g^i(u,v,w)\right]{|}^2\hfill \\ & & =\frac{k\left(E\right)}{{\left(\sqrt{u^2+v^2+w^2}\right)}^{\beta \left(E\right)}}.\hfill \end{array}$$ (9)

As μ_g(E) and μ_a(E) are dependent only on energy and not on spatial frequency coordinates (u, v, w), Eq. 9 implies that $\frac{1}{N}{\sum }_{i=1}^N|F_g^i(u,v,w){|}^2$ should also follow a power-law process with the same exponent β. Thus,

$$\frac{1}{N}\sum _{i=1}^N|F_g^i(u,v,w){|}^2=\frac{k_1\left(E\right)}{{\left(\sqrt{u^2+v^2+w^2}\right)}^{\beta \left(E\right)}}.$$ (10)

Since, $F_g^i(u,v,w)$ is independent of energy, it follows that β(E) and k₁(E) are also independent of energy, i.e., β(E) = β and k₁(E) = k₁. The implication is that the spatial frequency dependence of the anatomic power spectrum is independent of the energy at which the breasts are imaged. Hence, Eq. 10 can be restated as

$$\frac{1}{N}\sum _{i=1}^N|F_g^i(u,v,w){|}^2=\frac{k_1}{{\left(\sqrt{u^2+v^2+w^2}\right)}^{\beta }}.$$ (11)

Also, μ_g(E) and μ_a(E) are independent of location and hence, spatial frequency. Hence, Eq. 9 can be stated as

$$\begin{array}{ccc}& & {\left[{\mu }_g\left(E\right)-{\mu }_a\left(E\right)\right]}^2\frac{1}{N}\sum _{i=1}^N|F_g^i(u,v,w){|}^2\hfill \\ & & =\frac{k\left(E\right)}{{\left(\sqrt{u^2+v^2+w^2}\right)}^{\beta }}.\hfill \end{array}$$ (12)

Substituting Eq. 11 in Eq. 12 yields

$$\begin{array}{ccc}& & {\left[{\mu }_g\left(E\right)-{\mu }_a\left(E\right)\right]}^2\frac{k_1}{{\left(\sqrt{u^2+v^2+w^2}\right)}^{\beta }}\hfill \\ & & =\frac{k\left(E\right)}{{\left(\sqrt{u^2+v^2+w^2}\right)}^{\beta }}.\hfill \end{array}$$ (13)

The implication of Eq. 13 is that the amplitude of the power spectrum is energy-dependent and scales by the square of the difference in energy-dependent linear attenuation coefficients of fibroglandular and adipose tissue

$$k\left(E\right)=k_1{\left[{\mu }_g\left(E\right)-{\mu }_a\left(E\right)\right]}^2.$$ (14)

In summary, theory predicts that in dedicated breast CT, the spatial frequency dependence of the anatomic power spectrum will be independent of x-ray photon energy, and the amplitude of the anatomic power spectrum scales by the square of difference in linear attenuation coefficients of fibroglandular and adipose tissues.

Figure 1.

Linear attenuation coefficient of adipose and fibroglandular breast tissue plotted as a function of x-ray photon energy. Over the energy range of 10–80 keV, the linear attenuation coefficient of fibroglandular tissue is always larger than that of the adipose tissue.

Numerical simulations

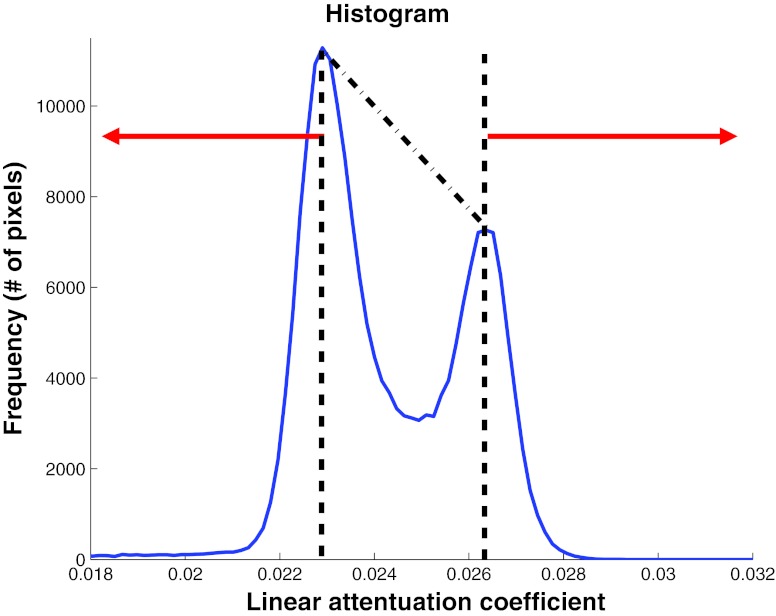
Numerical simulations were conducted to verify if the exponent β of the anatomic power spectrum is independent of energy and if the amplitude of the power spectrum k(E) scales by [μ_g(E) − μ_a(E)]² when the energy E is varied. Under an institutional review board (IRB)-approved protocol and with informed patient consent, fresh mastectomy specimens were obtained immediately following surgery and prior to tissue gross pathology. A total of 20 surgical mastectomy specimens were included in this analysis. Using a previously described benchtop prototype system,²³ each specimen was imaged by placing it in a holder modeling the uncompressed, pendant breast position used in dedicated breast CT. Every attempt was made to consistently position the lateral and medial breast at the same locations in the holder, and the nipple toward the bottom of the holder. Typical acquisition parameters were 300 projections over a single 360° circular half cone-beam geometry with an x-ray technique of 40 kVp and 0.5 mAs per projection. Figure 2a shows the geometry used for image acquisition with the benchtop system and this geometry differs from that used in clinical prototype breast CT systems [Fig. 2b]. The projection set was then reconstructed using the filtered backprojection (FBP) algorithm²⁴ to an isotropic voxel size of 0.2 mm. Postreconstruction processing steps include noise reduction using a nonlinear, 3D anisotropic diffusion filter²⁵ and correction for cupping artifacts²⁶ prior to segmentation. Image segmentation was then performed by calculating the peak histogram values for adipose and fibroglandular tissue (Fig. 3). Voxels to the left of the adipose tissue peak were assigned to be composed of 100% adipose tissue, whereas voxels to the right of the fibroglandular peak were assigned to be 100% fibroglandular. Voxels of value between the two peaks were linearly scaled to be composed of a mixture of adipose and fibroglandular tissue. The full description of the process used to generate these numerical phantoms in terms of f_g is given in a prior work.²⁷

Figure 2.

Geometry of (a) the benchtop system used for imaging mastectomy specimens, and (b) a clinical prototype dedicated breast CT system.

Figure 3.

Method used to convert the linear attenuation coefficient from the mastectomy specimen reconstruction to fibroglandular weight fraction. All voxels with linear attenuation coefficient less than the adipose peak were assigned 100% adipose tissue and those above the fibroglandular peak were assigned 100% fibroglandular tissue. Voxels with linear attenuation coefficient values between the two peaks were linearly scaled to be composed of a mixture of adipose and fibroglandular tissue.

Power spectral analysis was conducted in terms of f_g, and after converting to linear attenuation coefficients at monoenergetic x-ray photon energies of 20–80 keV in 5 keV intervals. A single (128)³ volume centered within each reconstructed mastectomy specimen was extracted and a 3D Hann window was applied. The 3D power spectrum (IDL 8.0.0, Exelis Visual Information Solutions, Inc., Boulder, CO) was computed as

$$\begin{array}{ccc}\hfill W_X(u,v,w)& =& \frac{1}{N}\sum _{i=1}^N\left|\mathbb{F}\right\{\left[X_i(x,y,z)-\overline{X(x,y,z)}\right]\hfill \\ & & \times {H(x,y,z)\left\}\right|}^2\frac{\Delta x\Delta y\Delta z}{N_x{N}_y{N}_z}.\hfill \end{array}$$ (15)

In Eq. 15, X_i(x, y, z) represents either f_g(x, y, z) or μ(x, y, z, E) of the ith volume, $\overline{X(x,y,z)}$ is the average from N volumes either in f_g(x, y, z) or μ(x, y, z, E), H(x, y, z) is the 3D Hann window,²⁸F represents the Fourier transform, Δx = Δy = Δz = 0.2 mm are the voxel dimensions, and N_x = N_y = N_z = 128 are the number of voxels within the volume in the three orthogonal directions used in the analysis. The 1D anatomic power spectra, W_X(f), where X = f_g or μ(E) and the spatial frequency f = u, v or w, were extracted along the corresponding axes. For a power curve of the form k f^−β, the fit coefficients k and β were obtained by linear fitting log(f) vs log[W_X(f)] over the spatial frequency range [0.06, 0.81] and was used to analyze the energy dependence of k and β. Prior work²⁹ on characterization of noise power spectrum with the benchtop CT system using a uniform background showed that the peak amplitude occurred at a spatial frequency of ∼0.8 cycles/mm. Hence, the choice of spatial frequencies for estimating the power-law fit coefficients of the anatomic power spectrum is appropriate.

RESULTS

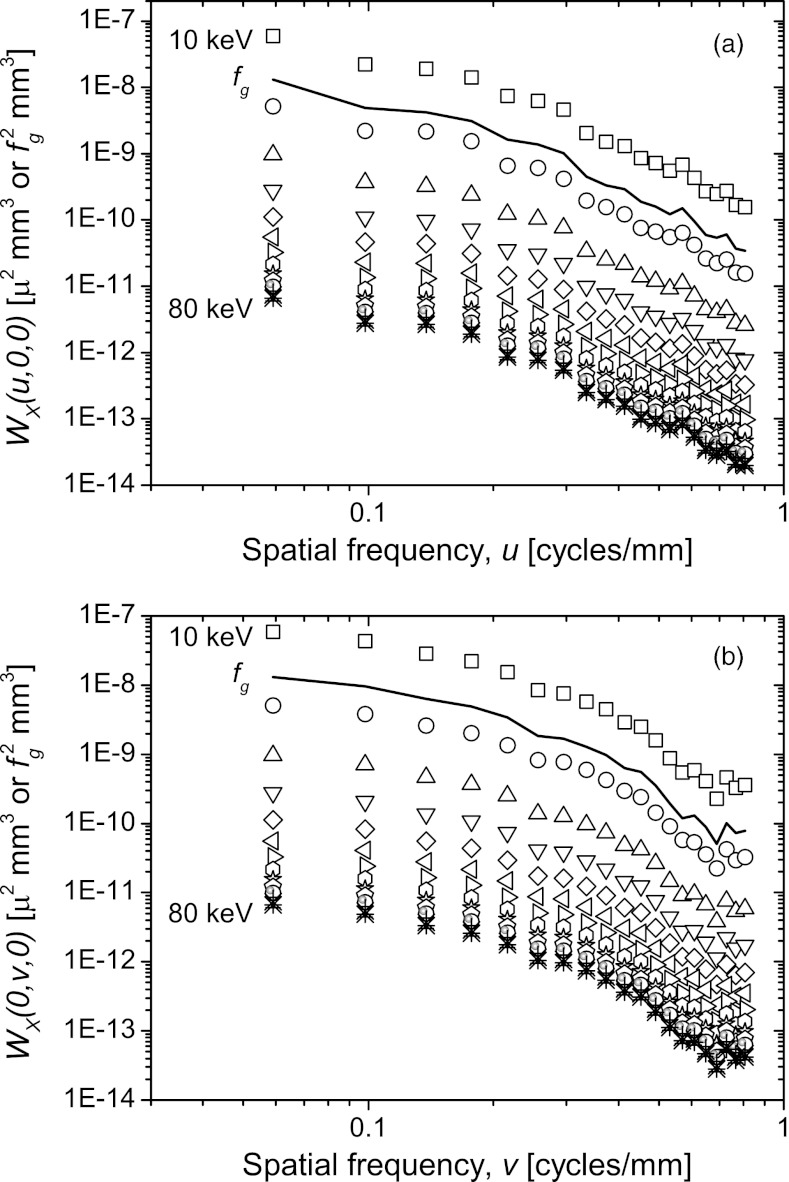
Figure 4 shows the 2D anatomic power spectrum at 30 keV along the three orthogonal planes. Figures 4b, 4c showed the presence of higher amplitude along the w-axis, in spite of application of the Hann window. Hence, we considered only the power-law fit coefficients k and β determined along the u and v axes for further analysis.

Figure 4.

Two-dimensional anatomic power spectrum at 30 keV along the three orthogonal planes.

Figure 5 shows the 1D anatomic power spectrum at each of the x-ray photon energy considered over the spatial frequency range [0.06, 0.81]. The power spectrum of the glandular weight distribution (f_g) is also shown. The spatial frequency dependence of the anatomic power spectra at all energies and that of f_g are similar.

Figure 5.

The 1D anatomic power spectra (log-log scale) along the u and v axes in the spatial frequency range from 0.06 to 0.8 cycles/mm. The power spectrum of the glandular weight distribution (f_g) is also shown as solid line. The symbols represent the power spectrum computed at each of the x-ray photon energies. The spatial frequency dependence of the anatomic power spectra at all energies and that of f_g are similar.

Figure 6 shows the plot of β as a function of x-ray photon energy. The error bars represent the standard error in the estimate of β. The solid line represents the estimate of β from the power spectrum of glandular weight distribution (f_g) and the dashed lines the ±1 standard error in its estimate. Figure 6 confirms the theoretical prediction that the spatial frequency dependence of the anatomic power spectra is independent of the x-ray photon energy at which the breasts are imaged. Values for β along the u and v axes were 2.42 and 2.34, respectively, which is higher than that reported in prior studies with dedicated breast CT.^{6, 8}

Figure 6.

The power-law exponent β along the u and v axes are plotted as a function of x-ray photon energy. The error bars represent the ±1 standard error in the estimate of β. The solid line represents the estimate of β from the power spectrum of glandular weight distribution (f_g) and the dashed lines the ±1 standard error in its estimate.

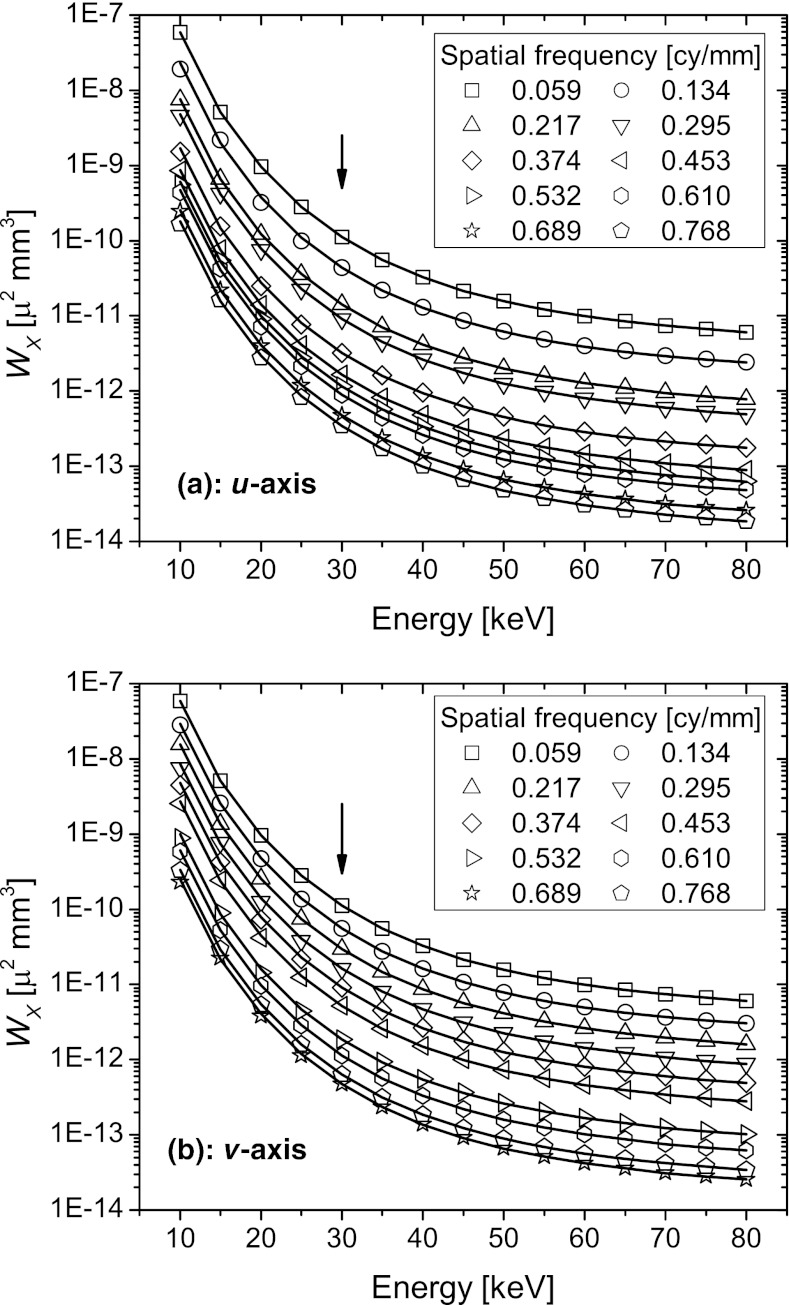
Figure 7 shows the 1D anatomic power spectra plotted as a function of x-ray photon energy at discrete spatial frequencies. The symbols represent the power spectra obtained through numerical simulations after transforming the f_g values to energy-dependent linear attenuation coefficients. The lines represent the theoretical prediction based on the scaling law, where the anatomic power spectrum at 30 keV (marked by an arrow) obtained from numerical simulations was used to determine the power spectra at other energies. Visually, excellent agreement between theory and numerical simulations is observed.

Figure 7.

The 1D anatomic power spectra along the u and v axes are plotted as a function of x-ray photon energy at discrete spatial frequencies. The symbols represent the power spectra obtained through numerical simulations after transforming the f_g values to linear attenuation coefficients. The lines represent the theoretical prediction based on the scaling law, where the anatomic power spectrum at 30 keV (marked by an arrow) obtained from numerical simulations was used to determine the power spectra at other energies. Excellent agreement between theory and numerical simulations is observed visually.

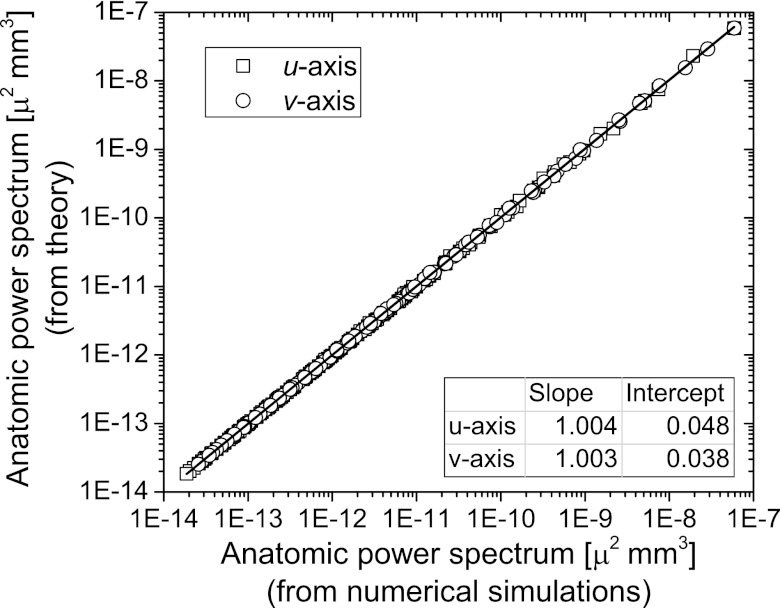
Figure 8 shows the linear regression analysis of the data presented in Fig. 7. The adjusted r² value was greater than 0.99 indicating good correspondence between numerical simulations and theory. The near-zero intercept and near-unity slope indicate good agreement between numerical simulations and theory.

Figure 8.

Linear regression analysis of the anatomic power spectrum from numerical simulations with that determined from theory. The adjusted r² value was greater than 0.99 indicating good correspondence between the theory and simulations. The near-zero intercept and near-unity slope indicated good agreement between theory and simulations.

DISCUSSION

The imaging geometry used to image mastectomy specimens in this study is different from that used during in vivo dedicated breast CT, as observed in Fig. 2. Specifically, the cone angle of 0° occurs near the nipple (apex of the specimen holder) in the setup used in this study, whereas in clinical prototype dedicated breast CT systems the 0° cone angle occurs close to the chest-wall. This implies that distribution of cone-beam artifacts is likely to be different in this study compared to that in in vivo breast CT. This may have contributed to our estimate of anatomic noise fit coefficients and could be a possible reason that the β value estimated in this study is different from that reported in prior studies with dedicated breast CT.^{6, 8} Future generations of dedicated breast CT systems may employ alternate image acquisition trajectories^{30, 31} or helical acquisition with photon-counting detectors^{32, 33, 34} that can mitigate cone-beam artifacts. Importantly, for a given imaging geometry, the key results from this study, viz., β is independent of x-ray photon energy, and K scales with x-ray photon energy are still valid.

While we attempted to position each mastectomy specimen within the specimen holder in an orientation representative of in vivo breast CT, it is likely that the spatial distribution of adipose and fibroglandular tissue may not be exactly representative of in vivo breast CT. In this study, the power spectrum was computed from numerical phantoms that were subjected to additional preprocessing steps including a correction for cupping artifacts²⁶ and anisotropic diffusion filtering²⁵ as well as segmentation, whereas prior studies^{6, 8} computed the power spectrum directly from the breast CT reconstructions. Also, the upper limit of the spatial frequency used to determine β in this study is different from prior studies.^{6, 8} All of these factors could have also contributed to our estimate of β being different from that reported in prior studies with dedicated breast CT.^{6, 8}

The presence of substantial noise power along the w-axis that corresponds to the cone-angle direction was observed in Fig. 4. Since the anatomic power spectrum was computed after subtraction of the average volume [Eq. 15], this noise source is stochastic. Further, the presence of this noise even at high spatial frequencies suggests that it is likely to be system noise.

In this study, we used a single volume of interest (VOI) from each specimen and the power spectrum was computed from ensemble average over all 20 specimens. While it is possible to compute the power spectrum using multiple VOIs from each specimen, we chose to use a single VOI from each specimen as it allows for the assumption that the samples are independent. We used an approach similar to that described by Burgess²² for 2D imaging to estimate the anatomical noise in 3D (i.e., over the ensemble of all breasts), so each spectrum is an independent sample drawn from the same random process, which is then averaged across samples to reduce the variance in the estimate.

Substituting adipose and fibroglandular tissues in Eq. 1 through Eq. 14, with any two tissues t1 and t2 that satisfy the condition μ_t1(E) ≠ μ_t2(E), it is readily observed that the scaling law for the anatomic power spectrum is valid. This could be of benefit for task-specific optimization of the x-ray photon energy for CT imaging of organs and anatomy that can be approximated by a two-component tissue model, e.g., lesion detection in brain approximated as comprising gray and white matter.

CONCLUSIONS

Current clinical prototype systems use substantially different kVp and filtration, and hence mean energy.^{35, 36} This work demonstrated that in dedicated breast CT, when the anatomic power spectrum is empirically determined at one x-ray photon energy, the anatomic power spectrum at any other energy can be determined by scaling its amplitude. The provided information allows for appropriate energy-dependent scaling of the anatomic power spectrum for task-specific optimization. While the study was focused on breast imaging, the described scaling law is also valid for any two-component model for the anatomy.