Abstract
In the primary walls of growing plant cells, the glucose polymer cellulose is assembled into long microfibrils a few nanometers in diameter. The rigidity and orientation of these microfibrils control cell expansion; therefore, cellulose synthesis is a key factor in the growth and morphogenesis of plants. Celery (Apium graveolens) collenchyma is a useful model system for the study of primary wall microfibril structure because its microfibrils are oriented with unusual uniformity, facilitating spectroscopic and diffraction experiments. Using a combination of x-ray and neutron scattering methods with vibrational and nuclear magnetic resonance spectroscopy, we show that celery collenchyma microfibrils were 2.9 to 3.0 nm in mean diameter, with a most probable structure containing 24 chains in cross section, arranged in eight hydrogen-bonded sheets of three chains, with extensive disorder in lateral packing, conformation, and hydrogen bonding. A similar 18-chain structure, and 24-chain structures of different shape, fitted the data less well. Conformational disorder was largely restricted to the surface chains, but disorder in chain packing was not. That is, in position and orientation, the surface chains conformed to the disordered lattice constituting the core of each microfibril. There was evidence that adjacent microfibrils were noncovalently aggregated together over part of their length, suggesting that the need to disrupt these aggregates might be a constraining factor in growth and in the hydrolysis of cellulose for biofuel production.
Growth and form in plants are controlled by the precisely oriented expansion of the walls of individual cells. The driving force for cell expansion is osmotic, but the rate and direction of expansion are controlled by the mechanical properties of the cell wall (Szymanski and Cosgrove, 2009). Expanding, primary cell walls are nanocomposite materials in which long microfibrils of cellulose, a few nanometers in diameter, run through a hydrated matrix of xyloglucans, pectins, and other polymers (Knox, 2008; Mohnen, 2008; Szymanski and Cosgrove, 2009; Scheller and Ulvskov, 2010). Native cellulose microfibrils are partially crystalline (Nishiyama, 2009; Fernandes et al., 2011). Formerly, primary wall cellulose was thought to have a unique crystal structure called cellulose IV1 (Dinand et al., 1996), but NMR evidence suggests the presence of forms similar to the better characterized cellulose Iα and Iβ crystalline forms together with large quantities of less ordered cellulose (Wickholm et al., 1998; Sturcová et al., 2004; Wada et al., 2004). Nevertheless, cellulose is much more ordered than any other component of the primary cell wall (Bootten et al., 2004), in keeping with its key role of providing strength and controlling growth.
The stiffness of the cell wall is greatest in the direction of the cellulose microfibrils, where growth is directional and the predominant microfibril orientation is usually transverse to the growth direction (Green, 1999; MacKinnon et al., 2006; Szymanski and Cosgrove, 2009). Expansion of the cell wall then requires either widening of the spacing between microfibrils (Marga et al., 2005) or slippage between them (Cosgrove, 2005), or both, and the microfibrils reorient toward the direction of growth (Anderson et al., 2010). Polymer cross bridges between microfibrils (McCann et al., 1990) are thought to resist these deformations of the cell wall nanostructure and, thus, to control the rate of growth. Until recently, most attention was focused on bridging xyloglucans, hydrogen bonded to microfibril surfaces (Scheller and Ulvskov, 2010). However, there is evidence that not all xyloglucans are appropriately positioned (Fujino et al., 2000; Park and Cosgrove, 2012a) and that other bridging polymers may be involved (Zykwinska et al., 2007). It has also been suggested that bundles of aggregated microfibrils, not single microfibrils, might be the key structural units in primary cell walls (Anderson et al., 2010), as in wood (Fahlén and Salmén, 2005; Fernandes et al., 2011). If so, single microfibrils could bridge between microfibril bundles. In summary, the growth of plant cells is not well understood, and we need more information on how cellulose orientation is controlled and on the nature of the bridging polymers, the cellulose surfaces to which these polymers bind, and the cohesion between microfibril surfaces that might mediate aggregation.
Cellulose microfibrils are synthesized at the cell surface by large enzyme complexes having hexagonal symmetry, sometimes called “rosettes” (Somerville, 2006). Each complex contains multiple cellulose synthases that differ between primary cell walls and wood, although the appearance of the complexes is similar (Somerville, 2006; Atanassov et al., 2009). The simultaneous synthesis, from the same end, of all the chains in a native cellulose microfibril is why they are parallel (Nishiyama et al., 2002, 2003), in contrast to the entropically favored antiparallel structure found in man-made celluloses like rayon (Langan et al., 2001). The number of chains in a microfibril and the number of cellulose synthases in the synthetic complex are evidently related. It is commonly assumed that the number of chains is divisible by six, matching the hexagonal rosette symmetry, and 36-chain models (Himmel et al., 2007) bounded by the hydrophilic [110] and [1-10] crystal faces, as in algal celluloses (Bergenstråhle et al., 2008), have been widely adopted. The assembly and orientation of cellulose are connected, as several cellulose synthase mutants have phenotypes defective in cellulose orientation and plant form as well as depleted in cellulose content (Paredez et al., 2008). In certain other mutant lines, the crystallinity of the microfibrils appears to be affected (Fujita et al., 2011; Harris et al., 2012; Sánchez-Rodríguez et al., 2012).
Therefore, a detailed understanding of the structure of primary wall cellulose microfibrils would help us to understand cellulose synthesis as well as the growth and structural mechanics of living plants (Burgert and Fratzl, 2009). Primary cell walls and their cellulose skeletons also affect food quality characteristics like the crispness of salad vegetables and apples (Malus domestica; Jarvis, 2011). When biofuels are produced from lignocellulosic biomass, lignification leads to recalcitrance (Himmel et al., 2007), but some of the cell types in Miscanthus spp., switchgrass (Panicum virgatum), and arable crop residues have only primary walls with no lignin, and recalcitrance then depends on the nature of the cellulose microfibrils (Beckham et al., 2011).
A relatively detailed structure has recently been proposed for the microfibrils of spruce (Picea spp.) wood (Fernandes et al., 2011), which are 3.0 nm in diameter, allowing space for only about 24 cellulose chains. Evidence from x-ray diffraction supported a “rectangular” shape (Matthews et al., 2006) bounded by the [010] and [200] faces. There was considerable disorder increasing toward the surface, and the microfibrils were aggregated into bundles about 15 to 20 nm across, with some, but not all, of the lateral interfaces being resistant to water (Fernandes et al., 2011). Disordered domains are a feature of other strong biological materials such as spider silk (van Beek et al., 2002).
Therefore, it is of interest whether any of these features of wood cellulose might also be found in the cellulose microfibrils of primary (growing) cell walls. It would be particularly useful to characterize the disorder known to be present in primary wall microfibrils, that is, to define how cellulose that is not measured as “crystalline” differs from crystalline cellulose. Many of the experiments leading toward a structure for wood cellulose were dependent on exceptionally uniform orientation of the cellulose microfibrils (Sturcová et al., 2004; Fernandes et al., 2011). However, in growing cell walls, the microfibrils are not uniformly oriented. When microfibrils are first laid down at the inner face of the primary cell wall, their orientation is normally transverse to the direction of growth, but as the cell wall expands, the microfibrils reorient so that the orientation distribution, integrated across the thickness of the expanded cell wall, becomes progressively closer to random (Cosgrove, 2005; MacKinnon et al., 2006).
This technical problem does not apply to the cell walls of celery (Apium graveolens) collenchyma, which are similar in composition to other primary cell walls but have their microfibrils oriented relatively uniformly along the cell axis (Sturcová et al., 2004; Kennedy et al., 2007a, 2007b). Some structural information on celery collenchyma cellulose has already been derived from spectroscopic and scattering experiments (Sturcová et al., 2004; Kennedy et al., 2007a, 2007b), confirming the disorder expected in a primary wall cellulose. Some of these experiments were analogous to what has been done on spruce cellulose (Fernandes et al., 2011), but insufficient data are available to specify the number of chains in each primary wall microfibril, the nature and location of the disorder, and the presence or absence of direct contact between microfibrils. Here, we report x-ray and neutron scattering and spectroscopic experiments addressing these questions and leading to a proposed structure for primary wall cellulose microfibrils. Characterizing a structure containing so much disorder presented unusual challenges, but disorder appears to be central to the enigmatic capacity of primary wall cellulose to provide high strength and yet to permit and control growth.
RESULTS
Microfibril Diameter and Spacing from Small-Angle Neutron Scattering
When collagen or cellulose microfibrils of fixed diameter are packed in arrays with some degree of regularity, small-angle diffraction of x-rays or neutrons (Bragg scattering) from the microfibrils themselves can be observed (Hulmes et al., 1995; Fernandes et al., 2011). This scattering is at smaller angles than conventional diffraction from crystal planes and is superimposed on small-angle scattering derived not from diffraction but from the texture and shape of the fibrils and the voids between them (the form factor). Unless the packing is regular enough to constitute a crystalline superlattice, only one Bragg peak is observed, corresponding to the center-to-center spacing of the fibrils (Hulmes et al., 1995; Kennedy et al., 2007a).
Using small-angle x-ray scattering (SAXS), a Bragg reflection was observed from cellulose microfibrils within intact cell walls of celery collenchyma. The microfibril spacing increased on hydration (Kennedy et al., 2007b). Modeling these results showed that the observed Bragg peak could be generated by a range of combinations of microfibril spacing and diameter. It was not possible, therefore, to derive the microfibril diameter unambiguously (Kennedy et al., 2007a).
In spruce wood, the microfibrils are too closely aggregated to provide adequate contrast for small-angle Bragg scattering. This problem was circumvented by deuterating the surface and using neutrons instead of x-rays (Fernandes et al., 2011). The nature of the contrast differs between x-ray and neutron sources. X-ray contrast depends mainly on local electron density, whereas neutron scattering contrast derives from local elemental composition and density. One advantage of this technique is the very different neutron scattering cross sections of hydrogen and deuterium, which allow for the introduction of contrast through, for example, deuterium exchange in deuterium oxide (D2O; Horikawa et al., 2009; Matthews et al., 2011).
An equatorial Bragg peak was readily visible in small-angle neutron scattering (SANS) images from spruce wood saturated with D2O (Fernandes et al., 2011). The intensity of the Bragg peak decreased and its distance (q) from the center of the diffraction pattern increased on drying, until in the SANS pattern from fully dry, deuterated wood the peak was faintly visible at q = 2.1 nm−1. The low contrast under these conditions was consistent with contact between adjacent, surface-deuterated microfibrils, so that the 3.0-nm center-to-center spacing corresponded essentially to the mean microfibril diameter (Fernandes et al., 2011).
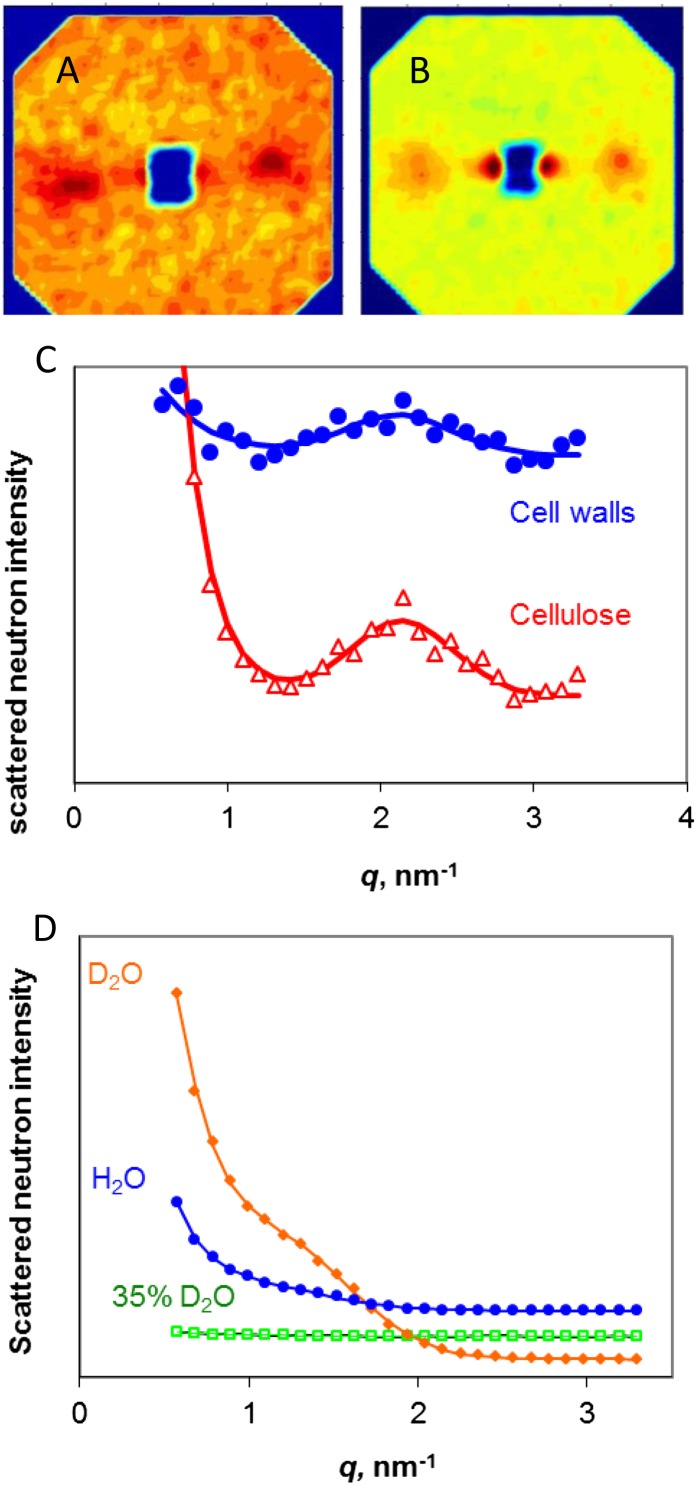
Similar SANS experiments were carried out on cell walls from celery collenchyma and on cellulose isolated from these cell walls (Fig. 1). A Bragg scattering peak in the region of q = 1 nm−1, superimposed on an exponential background from noncoherent scattering, was evident from both cell walls and isolated cellulose saturated with pure D2O, pure water, or a range of mixtures (Fig. 1; Supplemental Fig. S1). Consistent with scattering from cellulose rather than from other polymers, no Bragg peak was observed with the 35% [D2O]/[D2O + water] (v/v) mixture that matches the theoretical scattering length density of cellulose (Fig. 1).
Figure 1.
SANS from celery collenchyma cell walls and cellulose. A, SANS pattern for dry cell walls. B, SANS pattern for dry, isolated cellulose. In A and B, the fiber axis is vertical. C, Equatorial scattering profiles from cell walls and isolated cellulose. The fitted line is the sum of an exponential function corresponding to noncoherent scattering and a Gaussian function corresponding to the equatorial Bragg peak arising from diffraction from the packing arrangement of the microfibrils. D, Equatorial scattering profiles from cellulose saturated with water, D2O, or a 35% [D2O]/[D2O + water] (v/v) mixture matching cellulose in contrast. The vertical scale is greater than in C by a factor of 150. [See online article for color version of this figure.]
In contrast to spruce wood, dry celery cellulose gave a weak Bragg peak without deuteration of the microfibril surface. In the dry state, the Bragg peak was at q = 2.11 nm−1 for cellulose in the cell walls or q = 2.14 nm−1 for isolated cellulose (Fig. 1), corresponding to real-space center-to-center distances of 3.0 and 2.9 nm, respectively. The Bragg intensity was less than 1% of that observed after rehydration. This very low contrast was consistent with close packing of the microfibrils, probably with no other polymers between them over at least some of their length. The center-to-center distance should then approximate the mean microfibril diameter. Despite its low intensity, the Bragg peak was readily distinguishable in the SANS patterns because there was very little interference from incoherent scattering (Fig. 1).
In the hydrated state, the q value of the Bragg peak from the microfibrils in situ in the cell walls would correspond to a real spacing (d) of 7.1 ± 1.3 nm−1, while the q value of the Bragg peak from the hydrated cellulose would correspond to a real spacing of 6.0 ± 1.5 nm−1. These nominal d-spacings do not imply that all microfibrils separated to that extent on hydration. Hydration also greatly increased the SANS contrast by inserting water or D2O between the microfibrils and, in the case of D2O, by deuterating their surfaces and the noncellulosic polymers. It follows that in any distribution of microfibril spacings, the wider spacings would be greatly overrepresented in the SANS pattern. The nominal spacings observed after hydration slightly exceeded those estimated (Kennedy et al., 2007b) by SAXS, consistent with the different basis of x-ray contrast, but there was no difference between the spacings observed in the dry state with x-rays (Kennedy et al., 2007a) and with neutrons (Fig. 1). Although it was not possible to conclude from the x-ray data (Kennedy et al., 2007a) that the spacing observed in the dry state corresponded to microfibrils in direct contact with one another, this conclusion seems likely from the combined SAXS and SANS data. Hydration clearly separated the microfibrils, but probably to widely differing extents along their length (Kennedy et al., 2007b), depending perhaps on the affinity of the noncellulosic polysaccharides for water (Jarvis, 1992).
Microfibril Dimensions and Disorder from Wide-Angle X-Ray Scattering
Wide-angle x-ray or neutron scattering patterns from native cellulose are only well resolved enough for the structure to be solved crystallographically if the cellulose is exceptionally ordered and well oriented and if the microfibrils are thick enough to minimize the Scherrer broadening that results from limited numbers of lattice planes. Most of the celery collenchyma cellulose was relatively well oriented within the cell walls (Fig. 2). The wide-angle x-ray scattering (WAXS) contribution from a minor, isotropically oriented cellulose fraction was removed at the background subtraction stage. A substantial contribution from isotropic scattering by bound water was also removed during background subtraction. Scattering from water was identified by an experiment in which the water content was varied (Supplemental Fig. S2).
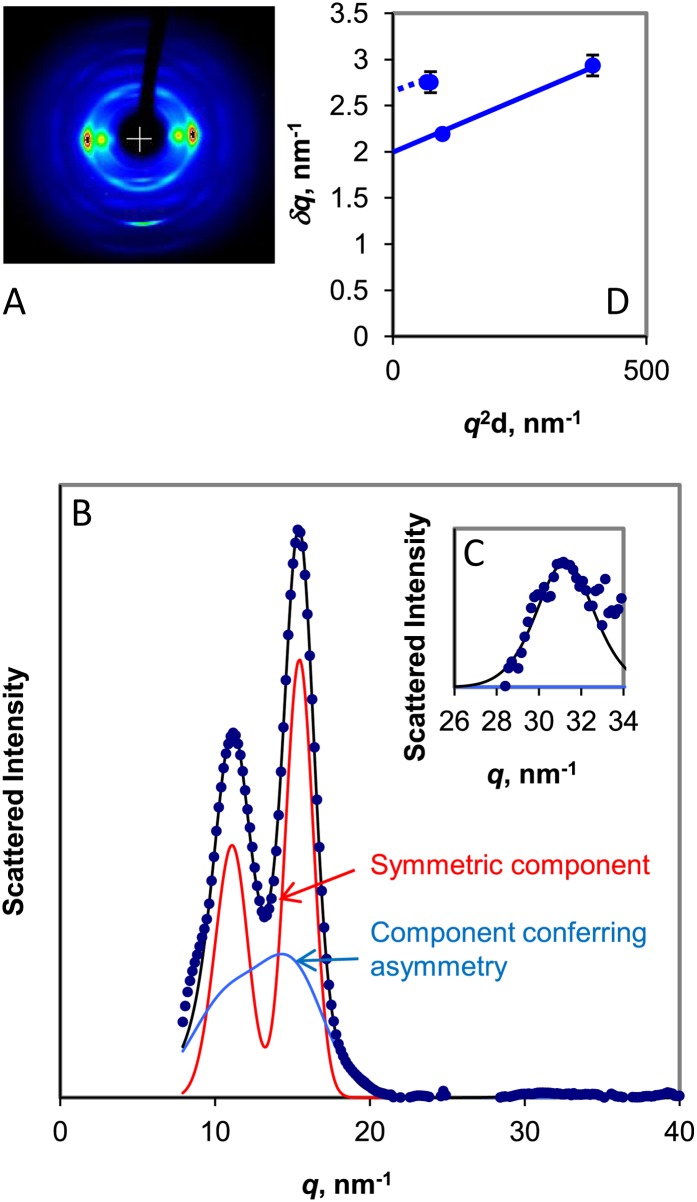
Figure 2.
A, WAXS image from celery collenchyma cell walls. The fiber axis is vertical. B, Equatorial WAXS profile of scattered intensity, with a symmetric fitted component and a component conferring asymmetry. C, 400 reflection, with vertical scale expanded 50×. D, Plot of δq against q2d for the principal equatorial reflections. The intercept of the line joining the 200 and 400 reflections was used to calculate the Scherrer dimension perpendicular to the [200] crystal plane, and an equal slope (dotted line) was used to derive an approximate mean intercept for the 1-10 and 110 reflections. [See online article for color version of this figure.]
The WAXS pattern from the well-oriented cellulose component was blurred in the radial direction by Scherrer broadening, disorder-related broadening, or both. The 200 reflection was at q = 15.5 nm−1, corresponding to somewhat greater interlayer spacing than in crystalline celluloses, and the 1-10 and 110 reflections were merged. These features have been observed in poorly oriented diffraction patterns from what has been called cellulose IV1 (Dinand et al., 1996) or disordered cellulose Iβ (Wada et al., 2004) in primary cell walls. For consistency, the Iβ lattice notation is used throughout this paper, but without any implication that this form presents the closest analogy to the average structure present.
Quantifying disorder and calculating Scherrer dimensions from the broadening of these reflections was made more difficult by the strong overlap between the 1-10 and 110 reflections and by the extremely low intensity of the 400 reflection, a qualitative indicator of greater lateral disorder than in spruce wood. With long data collection times (16–24 h), it was possible to obtain sufficient signal to noise to estimate the broadening of the 400 reflection. Hydration, by increasing the monoclinic angle and thus separating the 1-10 and 110 reflections, made it easier to model the respective widths of these two reflections in the diffraction pattern from spruce wood (Fernandes et al., 2011). In celery cellulose, however, hydration increased the [200] d-spacing slightly but did not significantly increase the monoclinic angle. The procedure of Fernandes et al. (2011) was used to separate out the effect of one form of lateral disorder that gives rise to radial peak asymmetry. Assuming that the remaining symmetric, radial widths of the 1-10 and 110 reflections were equal, the best-fit value was 22% greater than the radial width of the 200 reflection at a monoclinic angle of 95°. On this basis, the mean unit cell dimensions in the dry state were a = 0.81 nm, b = 0.80 nm, c = 1.03 nm (retaining the cellulose Iβ indexing for clarity even though a > b). Smaller monoclinic angles and greater widths, or vice versa, gave almost as close fits to the observed intensity profiles.
A further form of disorder that contributes, along with small lattice dimensions, to radial broadening has been modeled as “paracrystalline” (Fernandes et al., 2011), meaning that the width of the reflections increases with the square of the reflection order or with q2d. Using the best-fit data and plotting the width δq of the reflections against q2d as described (Fernandes et al., 2011), the widths of the symmetric components of the 200 and 400 reflections gave a residual disorder factor of g = 0.03 and a Scherrer dimension of 3.2 nm perpendicular to the ring planes in the dry state. The mean width of the 1-10 and 110 reflections lay clearly above the δq versus q2d plot for the 200 and 400 reflections. The implication is that the mean Scherrer dimension in the directions normal to the 1-10 and 110 lattice planes was smaller than the mean Scherrer dimension in the direction normal to the 200 lattice plane, as in spruce cellulose. However, the low intensity of the 400 reflection and the consequent difficulty of estimating the disorder-related contribution to the overall broadening made this conclusion less secure than for spruce cellulose.
Characterization of the Disordered Components by Deuteration and Wide-Angle Neutron Scattering
In the crystallographic study of cellulose Iα and Iβ (Nishiyama et al., 2002, 2003), the difference in neutron diffraction consequent on total, high-temperature deuteration of the hydroxyl groups was used to identify proton positions and hence hydrogen-bonding geometry. It should also be possible to exploit the strong difference between deuterium and proton scattering of neutrons to identify the scattering contribution of disordered regions accessible to deuteration under the milder, ambient temperature conditions used in the SANS and Fourier transform infrared (FTIR) experiments. As can be shown by FTIR (see below), hydroxyl groups on noncellulosic polysaccharides are accessible to deuteration, as are the outward-facing hydroxyls on cellulose surfaces unless these are blocked by aggregation (Horikawa et al., 2009). For disordered regions within microfibrils to admit D2O, they would need to have wider lattice spacings than crystalline cellulose (Matthews et al., 2011).
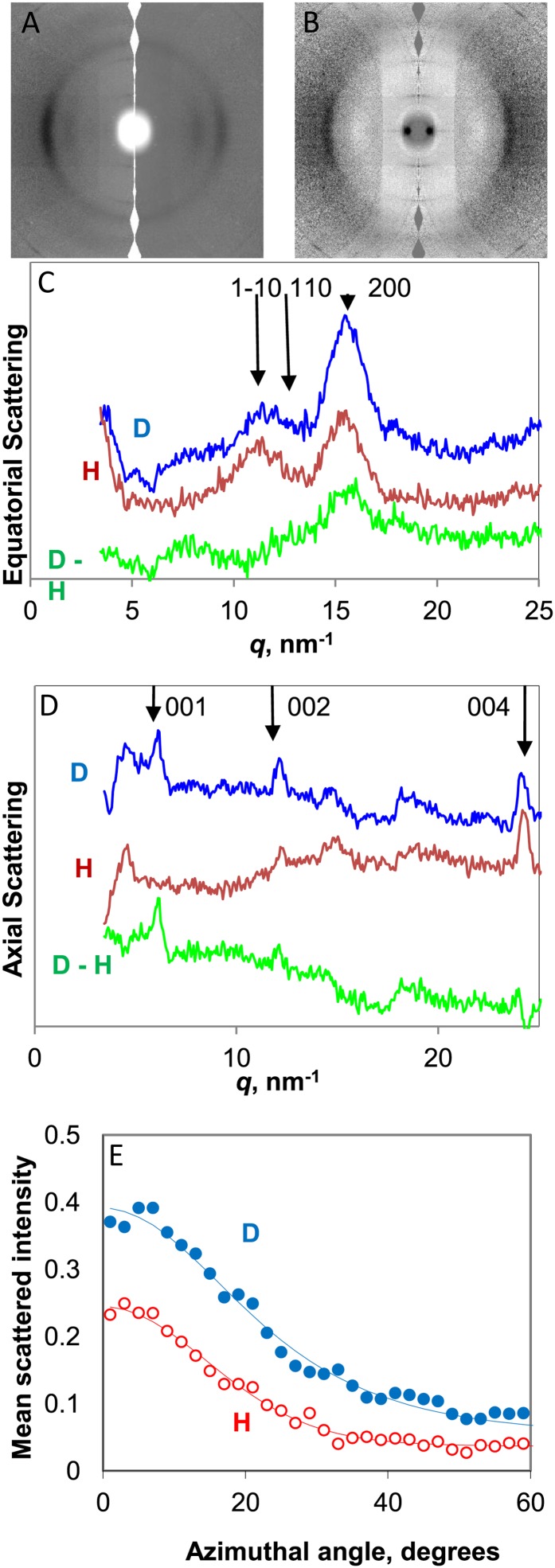
Figure 3A shows that there were visible changes in the neutron diffraction pattern on reversible, ambient-temperature deuteration. The changes included increased or decreased intensity of individual reflections, together with changes in diffuse scattering. In principle, the intensity change for any reflection can be positive, negative, or neutral depending on the effect of deuteration on the structure factor. For guidance, the intensities of the principal equatorial and axial reflections for cellulose Iβ in the native (H) and perdeuterated (D) forms were calculated using Shelxl-97 (Sheldrick, 2008) within the WinGX package (Farrugia, 1999), from a static model utilizing the published atomic coordinates (Nishiyama et al., 2002). Of the three principal equatorial reflections that define the lateral packing geometry of the cellulose chains, the effect of deuteration on intensity was predicted to be positive for 200 and strongly negative for 110 and 1-10. The 004 axial reflection was predicted to increase in intensity on deuteration, while the 001 reflection was absent in both D and H forms. These predictions agree with the observed neutron diffraction images for highly crystalline cellulose Iβ (Nishiyama et al., 2002).
Figure 3.
WANS from celery collenchyma cell walls. A, Scattering patterns in H form (right half) and after deuterium exchange of hydroxyl groups accessible to water (left half). The fiber axis is vertical. B, Difference scattering pattern (D − H). C, Equatorial scattering profiles from cell walls in H form, D form, and difference (D − H). D, Scattering profiles on the fiber axis from cell walls in H form, D form, and difference (D − H). E, Azimuthal scattering profiles across the 200 reflection. [See online article for color version of this figure.]
The observed effect of surface deuteration of the microfibrils was positive for the 200 and 004 reflections, negative for 110, and neutral for 1-10. The (D − H) subtraction profile for the equatorial reflections (Fig. 3B) showed that their positions and widths, corresponding to chains accessible to deuteration, were not perceptibly different from the fraction that did not deuterate. In the azimuthal direction, the equatorial intensity showed a broader underlying tail of orientation distribution in the D than in the H diffraction pattern (Fig. 3E), implying that some of the chains accessible to deuteration were less well oriented than the inaccessible cellulose chains.
On the fiber axis (Fig. 3D), the 004 reflection in the D form was centered at slightly lower q than in the H form, implying that some of the chains accessible to deuteration were more extended than the inaccessible chains. The difference in mean d-spacing was only about 0.5%, and the radial width of this reflection was similar in both D and H forms. The 002 reflection was stronger in the D form, and a 001 reflection, not present in the H diffraction pattern, appeared in the axial difference profile. The presence of this 001 reflection after deuteration implies that some of the deuterated chains did not have the same longitudinal stagger as either pure cellulose Iβ or cellulose Iα.
Near-isotropic changes in diffuse scattering on deuteration gave rise to a broad ring of increased intensity in the region 15 nm−1 < q < 20 nm−1, while below 15 nm−1, there was decreased diffuse intensity (Fig. 3B). The isotropic components responsible for these diffuse scattering features include noncellulosic components that exchange with D2O and small amounts of residual bound water.
Proton Spin-Diffusion Experiments and Spatial Relationships between Ordered and Disordered Chains
The rate at which nuclear magnetism equilibrates by spin diffusion between nanoscale domains can be used to estimate how far apart these domains are. Proton spin-diffusion experiments on this principle have been applied to wood (Newman, 1992; Altaner et al., 2006) and bacterial cellulose (Masuda et al., 2003). A two-dimensional (2D) representation of this experiment has been employed (Fernandes et al., 2011) to explore the disposition of ordered and disordered regions in spruce cellulose, making use of differences in their spatial separation from lignin. A quite different 13C spin-diffusion experiment on corn (Zea mays) stover (Foston et al., 2012) led to similar conclusions.
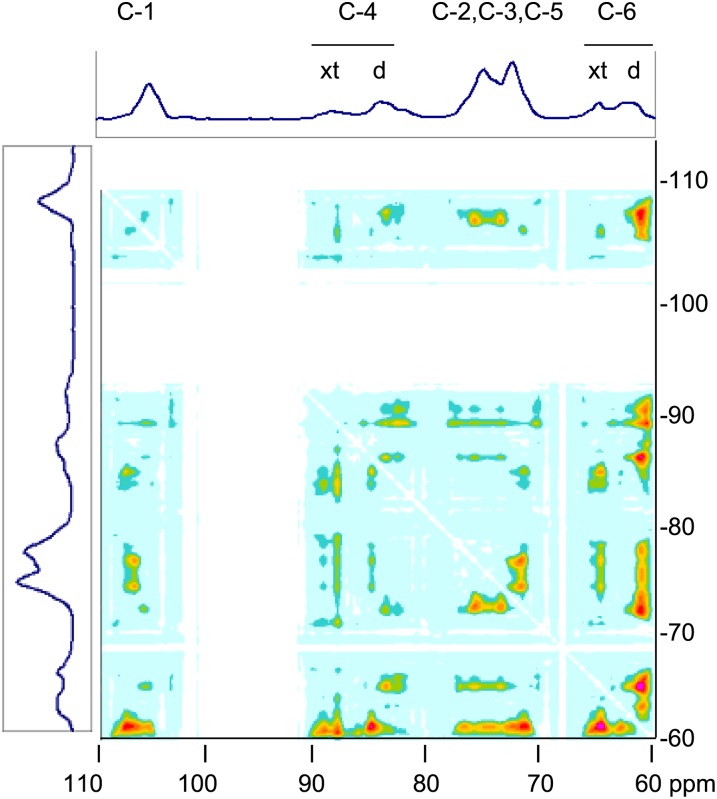
Celery collenchyma cellulose is not lignified but contains small, residual amounts of glucomannan and xyloglucan hemicelluloses, which having relatively high thermal mobility can be exploited instead of lignin as proton spin reservoirs. Figure 4 shows the 2D spectrum from this experiment. Cross peaks indicate domains that satisfy two conditions: (1) the domains differ in mobility and, hence, in magnetization at the start of the proton spin mixing period in the pulse sequence; and (2) the domains are sufficiently separated in space to require a measurable time, several milliseconds, to equilibrate in proton magnetization through spin diffusion. The signal assignments that follow are based on Sturcová et al. (2004).
Figure 4.
2D representation of a solid-state 1H spin-diffusion experiment on hydrated celery collenchyma cell walls monitored through the 13C spectrum. The 13C spectrum measured with cross polarization and magic-angle spinning is shown at top and side. Cross peaks in the 2D spectrum represent signals from 13C nuclei that are located in domains that differ in 1H spin-spin relaxation rate and are spatially separated. [See online article for color version of this figure.]
The one-dimensional 13C-NMR spectra were similar to those observed previously (Sturcová et al., 2004), with C-4 signals from crystalline cellulose (89–90 parts per million [ppm]) and disordered cellulose (84–85 ppm) in an approximate ratio of 1:2. In the 2D spectrum, cross peaks between C-4 of crystalline cellulose and C-4 of disordered cellulose were present but relatively weak. A cross peak between C-6 of crystalline cellulose (65 ppm) and C-4 of disordered cellulose (84–85 ppm) was also present. Cross peaks from hemicellulose C-1 (101 ppm) and C-4 (83 ppm) to crystalline cellulose C-4 were stronger than to disordered cellulose C-4, and cross peaks from hemicellulose C-1 and C-4 to crystalline cellulose C-6 were stronger still. The strongest cross peaks involved the C-2, C-5, and C-6 signals from disordered cellulose at 73, 75, and 62 ppm, but each of these signals also apparently contained a contribution from hemicelluloses and, therefore, could not be unambiguously interpreted.
These observations are consistent with models in which disordered and crystalline cellulose are not intermingled but are in close spatial proximity within each microfibril and hemicelluloses are located outside the microfibrils, probably partly outside each small bundle of microfibrils, but the difference in cross-peak intensity to crystalline and to disordered cellulose suggests that one group of hemicelluloses was in close association with microfibril surfaces.
Polarized Deuteration FTIR and Patterns of Hydrogen Bonding
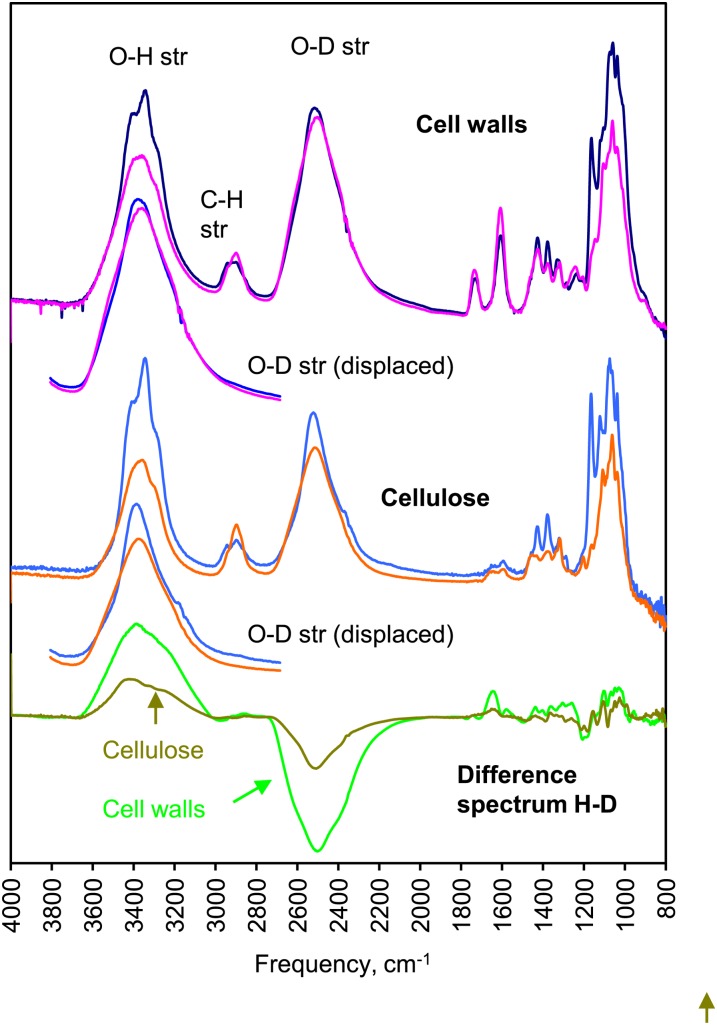
Polarized FTIR provides information on the direction of hydrogen bonds. FTIR studies on spruce wood showed that hydroxyl groups on disordered cellulose at microfibril surfaces were accessible to deuterium exchange, except where the microfibrils were tightly aggregated together. Hydroxyl groups on hemicelluloses were also accessible. Deuterium exchange moves the stretching band associated with each hydroxyl group to lower frequency by a factor of 1.34, due to the greater mass of the deuterium atom, but preserves the order of the bands because the structure is unchanged (Sturcová et al., 2003).
Figure 5 shows that deuteration of either celery collenchyma cell walls or isolated cellulose was extensive but less than the amount predicted from the 2:1 ratio of disordered to crystalline cellulose assessed using the C-4 signals in the NMR spectra. The pattern of O-D stretching bands is easiest to compare with the pattern of O-H stretching bands if the frequency scale is artificially shifted by the factor of 1.34 (Fig. 5). The two patterns were clearly different. The O-D stretching bands were less longitudinally oriented than the O-H stretching bands, showing that fewer hydrogen bonds in the deuterated fraction were directed along the microfibril axis and more were directed outward. As in spruce cellulose (Fernandes et al., 2011), deuteration removed intensity from a prominent shoulder at 3,400 cm−1 in the O-H stretching region, corresponding to hydroxyl groups more weakly hydrogen bonded and more outward directed than the mean. The maximum of the rather broad group of overlapping O-D stretching bands coincided, after shifting the frequency axis 1.34×, with this shoulder, which was originally assigned to an anomalous part of the cellulose Iα-like spectrum (Sturcová et al., 2004) but was later shown to correspond, in spruce cellulose, to inaccessible hydroxyl groups in disordered regions (Fernandes et al., 2011). Assignment to disordered domains, not cellulose Iα, is indicated by the evidence presented here. Only part of the intensity at 3,400 cm−1 was displaced by deuteration, implying that some of these disordered chains in celery collenchyma cellulose are accessible to deuteration and some are not.
Figure 5.
Polarized FTIR spectra of celery collenchyma cell walls and isolated cellulose subjected to vapor-phase deuterium exchange and dried without contact with water. Solid lines show longitudinal polarization, and dotted lines show transverse polarization. For comparison with the O-H stretching region (3,000–3,500 cm−1), the O-D stretching region (2,200–2,700 cm−1) is also shown with the wavelength scale increased by a factor of 1.34. Difference spectra (H − D) are shown below. [See online article for color version of this figure.]
DISCUSSION
Microfibril Structure
Cellulose that may loosely be called crystalline, and disordered cellulose different from the known crystalline forms cellulose Iα and Iβ, were identified by all the methods used. It does not follow that the same disordered fractions were observed by all these methods (i.e. that the chains identified as disordered differed in the same respects from the known crystalline forms). Conformational disorder, packing disorder, and disorder in hydrogen bonding were all observed.
The 13C-NMR spectra of celery collenchyma cellulose (Fig. 4) identified chains that differed in conformation from both cellulose Iα and cellulose Iβ, having some freedom of rotation around the C5-C6 bond and having the C-6 conformation dominated by the gauche-gauche (gg) and gauche-trans (gt) forms (Sturcová et al., 2004), as in spruce cellulose (Fernandes et al., 2011), although the gg-gt ratio differed considerably from spruce (Sturcová et al., 2004). The deuteration FTIR spectra of celery cellulose showed that some domains had hydrogen-bonding patterns different from those observed in cellulose Iα and cellulose Iβ, with reduced mean hydrogen-bonding strength (higher mean O-H stretching frequency) and less overall tendency toward axial hydrogen orientation. The change in H-bond orientation was evident both in chains accessible to deuterium exchange and in inaccessible chains and would be consistent with a move from the trans-gauche (tg) C-6 conformation found in crystalline cellulose to the gg and gt conformers. Similar observations on spruce cellulose were rationalized in terms of a model in which the core of each microfibril was occupied mainly by crystalline cellulose and the microfibril surface was occupied by cellulose chains with slightly different conformation and hydrogen bonding, some accessible to deuterium exchange and others rendered inaccessible by lateral aggregation of the microfibrils. A similar model would be consistent with the celery FTIR spectra (Fig. 5), earlier NMR data (Sturcová et al., 2004), and the spin-diffusion NMR data reported here (Fig. 4). From 13C spin-lattice relaxation NMR data (Viëtor et al., 2002), celery collenchyma cellulose has a higher proportion of the gg C-6 conformer than spruce cellulose. The unit cell dimensions differed considerably between these two kinds of cellulose, the mean intersheet spacing being greater in celery collenchyma cellulose and the axial dimension being slightly less. Molecular simulations have suggested links between C-6 conformation and lattice spacings (Matthews et al., 2012). As with spruce cellulose, it was not possible, and perhaps not meaningful, to distinguish between the Iα and Iβ cellulose forms by NMR in the presence of so much conformational disorder (Matthews et al., 2011).
Microfibril models with disordered surfaces have repeatedly been proposed on the basis of NMR data (Newman, 1992; Viëtor et al., 2002; Bergenstråhle et al., 2008), but it has been unclear how they should be reconciled with models derived from x-ray diffraction, which is more sensitive to chain-packing arrangements than to chain conformation or hydrogen bonding. The wide-angle neutron scattering (WANS) data (Fig. 3) showed that in domains accessible to deuteration, the chains were packed laterally in the same way and at almost the same mean spacings as in the crystalline regions, despite the differences in conformation and hydrogen bonding demonstrated by the spectroscopic experiments and despite considerable statistical variation in chain packing everywhere in the microfibril. Throughout each microfibril, the sheets of chains were stacked at wider mean spacing than in more crystalline celluloses. A further implication is that most of the chains accessible to deuteration were located at the microfibril surfaces rather than in “amorphous” microfibril segments occupying the whole width of the microfibril, because the chains within such segments would have to be loosely packed to permit water to enter.
From the 004 axial reflection, the deuteration-accessible chains appeared to be slightly more extended in the longitudinal direction than the inaccessible chains, perhaps due to twisting of the microfibrils. The longitudinal stagger was partially disrupted in the deuteration-accessible chains, adding to the difficulty of distinguishing between the Iα and Iβ forms.
A wide range of lateral chain spacings in the noncellulosic fraction, accessible to deuteration, may be deduced from the diffuse, nonoriented part of the neutron diffraction images. Water associated with the noncellulosic fraction scattered x-rays similarly to liquid water, suggesting a similar pair distribution function, but due to decreased thermal mobility, the magnitude of its contribution to the WAXS patterns was greater than expected for bulk liquid water.
Microfibril Diameter and Shape
The SANS data imply a microfibril diameter approximately equal to the center-to-center distance of 2.9 to 3.0 nm in the dry state. Assuming a circular cross section and allowing for the relatively loose chain packing observed by wide-angle scattering, this nominal diameter would correspond to 21 to 22 chains. The microfibrils are not, of course, circular, and the actual number of chains depends on the cross-sectional shape. The WANS observations confirmed that surface chains were positioned on the same disordered lattice as the interior chains and should be included in calculations of Scherrer dimensions from WAXS.
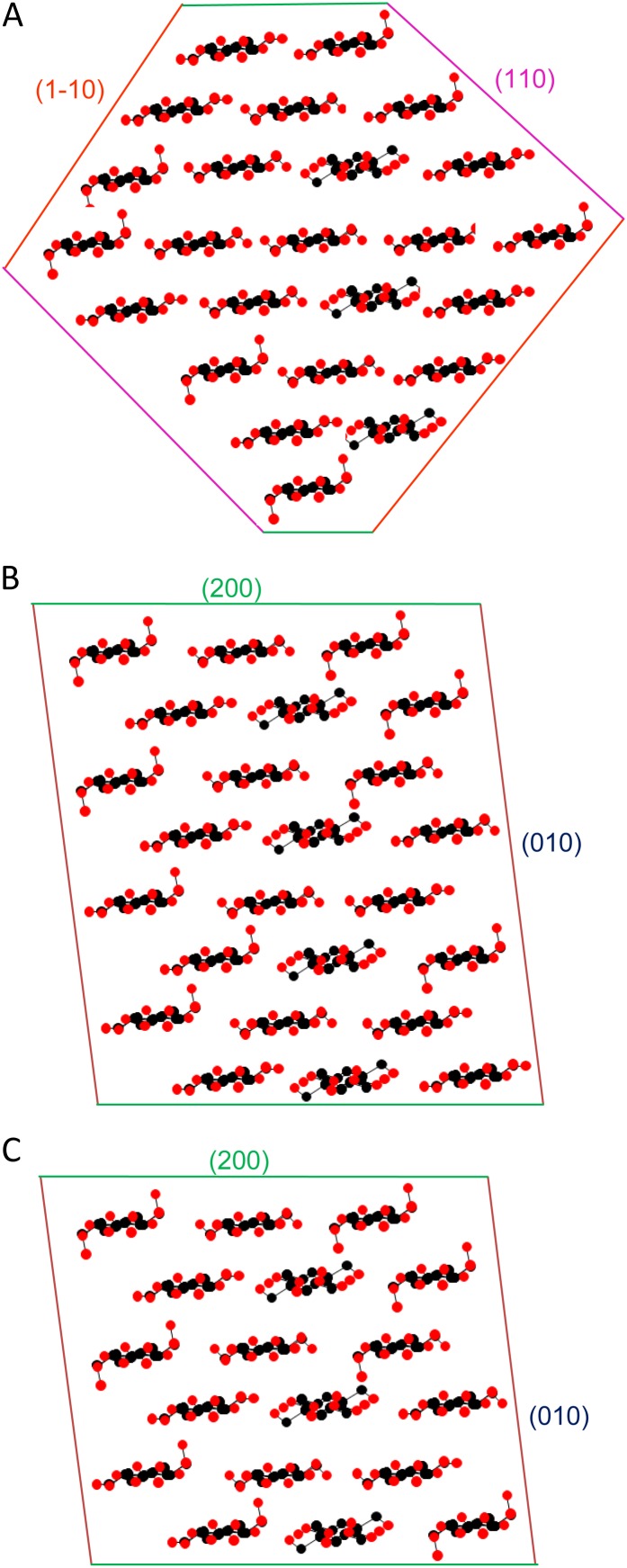
The SANS center-to-center distance and the transverse Scherrer dimensions were similar to those observed for spruce cellulose (Fernandes et al., 2011). The [200] Scherrer dimension was larger than the mean of the [1-10] and [110] dimensions, consistent with the rectangular microfibril model (Matthews et al., 2006; Fernandes et al., 2011), which has the relatively hydrophobic [200] crystal faces exposed top and bottom (Fig. 6) instead of the diagonal [1-10] and [110] crystal faces exposed in algal celluloses (Baker et al., 1997). However, the support for the rectangular rather than the diamond model is less secure than for spruce, due to the difficulty of correcting for disorder using the very weak 400 reflection and due to the problems inherent in estimating the individual widths of the overlapping 1-10 and 110 reflections. Given the extensive disorder observed, it is not even certain that primary wall microfibrils have cross sections of constant shape.
Figure 6.
Models for the cross section of celery collenchyma microfibrils. A, A 24-chain diamond-shaped model, 2.9 × 2.7 nm. B, A 24-chain rectangular model, 3.3 × 2.7 nm. C, An 18-chain rectangular model, 2.5 × 2.7 nm. The WAXS column lengths (Scherrer dimensions) after correction for disorder provide a means to distinguish between these models, with caution due to the difficulty of estimating the widths of the overlapped 1-10 and 110 reflections, the approximations involved in the disorder correction, and the possibility that the microfibril cross sections might vary. Calculated [200], [1-10], and [110] column lengths were as follows, respectively: model A, 2.5, 2.8, and 2.5 nm; model B, 3.2, 2.6, and 2.5 nm; model C, 2.4, 2.5, and 2.3 nm. The observed column lengths were as follow: [200], 3.2 nm; [1-10] and [110], mean of 2.5 nm. On this basis, the best-fit model was model B. [See online article for color version of this figure.]
A rectangular cross section with stacked sheets of three chains would be consistent with one-third of the chains, those in the central position in each sheet, being conformationally similar to crystalline celluloses as observed by NMR. The observation of a single small-angle Bragg peak is consistent with the slightly dispersed microfibril spacings that would be expected from roughly rectangular microfibrils, possibly twisted, in intermittent contact with one another. Either constant or slightly variable microfibril diameters could be accommodated, as could small numbers of microfibrils differing considerably from the dominant dimensions.
The number of chains per microfibril is relevant to the structure of the complexes that synthesize cellulose during growth. If the number of chains is a multiple of six, matching the geometry of the synthetic complex, then a stack of eight three-chain sheets (24 chains) would give the closest match to the 200 Scherrer dimension (Fig. 6B), as for spruce cellulose (Fernandes et al., 2011). However, in our case, the uncertainty is quite large and the level of packing disorder suggests that irregular and variable cross sections are possible. An 18-chain (6 × 3) model was not ruled out for spruce cellulose and would be consistent with the data presented here (Fig. 6C) if the 200 Scherrer dimension were augmented with additional hemicellulose chains, as suggested for spruce (Fernandes et al., 2011), or increased by stacking one microfibril on top of another for short distances.
Crystallinity
What is meant by “crystallinity” depends on the methods used to detect components that differ from crystalline cellulose. There was some degree of consistency between the spectroscopic methods in detecting chains differing in conformation from the accepted forms of crystalline cellulose and, hence, showing different patterns of hydrogen bonding. This included noncellulosic polysaccharides, and in the FTIR spectra, particularly, it was difficult to make a clear distinction between the contributions of the noncellulosic polysaccharides and some of the disordered cellulose.
The deuteration WANS experiments showed that these conformational differences had little influence on the packing of cellulose chains or on diffraction. The microfibril structure clearly contained a considerable amount of disorder in lateral chain packing, but this disorder was spread throughout the structure and was not restricted to the deuterium-accessible surfaces. Crystallinity assessed by diffraction methods is not the same thing as crystallinity assessed spectroscopically. In both cases, the apparent crystallinity would increase with microfibril diameter, but as a direct consequence of reduced Scherrer broadening in diffraction experiments and due to decreased surface-volume ratio in spectroscopic experiments that distinguish the surface chains.
Aggregation of Microfibrils
Aggregation of microfibrils into larger bundles is well established for conifer wood (Wickholm et al., 1998; Fahlén and Salmén, 2005; Fernandes et al., 2011). Fibrillar units with widths of 5 to 10 nm, sometimes up to 40 nm, have been observed by electron microscopy (McCann et al., 1990; Sugimoto et al., 2000), but their interpretation is complicated by the possible inclusion of noncellulosic polymers. The data reported here include two direct lines of evidence for the aggregation of primary wall microfibrils in collenchyma. The evidence from small-angle Bragg scattering of x-rays (Kennedy et al., 2007a) and neutrons showed clearly that aggregation existed. The range of microfibril spacings was difficult to infer because the scattered intensity increased strongly with separation of the microfibrils, so that well-separated microfibrils were overrepresented in the scattering patterns. The low SANS contrast in the dry state and the similarity of the SANS center-to-center distance to the mean WAXS Scherrer dimensions suggested that some microfibril segments remained in direct contact with one another, whereas other microfibril segments became well separated on hydration.
The deuteration FTIR spectra from both collenchyma cell walls and isolated cellulose included hydroxyl stretching bands centered on 3,400 cm−1, with neutral polarization. These hydroxyl stretching bands were assigned to hydroxyl groups distinct from all those of the Iα and Iβ crystalline forms of cellulose, more outward directed in orientation and partially, but not wholly, accessible to deuteration. Considering also the SANS and NMR data, the hydroxyl groups concerned may be attributed to microfibril surfaces. Because these surfaces were only partly accessible to D2O, it follows that that the microfibrils were aggregated together, for part of their length, with interfaces impermeable to water. These features were found in spruce wood, but there were also differences: spruce wood has different noncellulosic polymers, leading to apparently closer binding between microfibril surfaces and to stresses that distort the unit-cell geometry on hydration (Fernandes et al., 2011).
The 3,400 cm−1 hydroxyl stretching band in the FTIR spectrum, moved to 2,540 cm−1 by D2O exchange, was previously assigned incorrectly to an aberrant form of cellulose Iα (Sturcová et al., 2004) but appears to be a marker for surface chains and for the presence of microfibril aggregation if these surface chains are inaccessible to deuteration. This band was greatly reduced in intensity when celery collenchyma cellulose was subjected to hydrothermal annealing, which led to coalescence of the microfibrils into larger crystalline units with reduced surface-volume ratio (Sturcová et al., 2004). FTIR intensity at or near 3,400 cm−1 has been recorded in cell wall preparations from, for example, wild-type Arabidopsis (Arabidopsis thaliana; MacKinnon et al., 2006), suggesting that this form of aggregation is not a unique feature of celery collenchyma cellulose but is more widespread in primary cell walls.
Implications for Plant Growth
The size and structure of primary wall microfibrils give important clues concerning the nature of the enzyme complexes responsible for oriented cellulose synthesis and, hence, directional cell expansion. The expansion of plant cells requires disruption of the network of noncovalently cross-linked microfibrils in the cell wall. Understanding the topology of this network, therefore, is necessary, and recently, the accepted idea that the xyloglucans simply coat and link microfibril surfaces has been questioned (Bootten et al., 2004; Park and Cosgrove, 2012a). The NMR spin-diffusion data (Fig. 4) showed that some hemicellulose chains, probably xyloglucans, were located close to microfibril surfaces and thus probably lay between microfibrils, within microfibril aggregates. However, other microfibril segments appeared to be in direct contact without intervening polymers, illustrating the irregular nature of the aggregation that would be expected if the microfibrils are twisted and noncylindrical and implying that cellulose-cellulose as well as xyloglucan-cellulose interactions would have to be broken to separate aggregated microfibrils. Other mechanisms would be needed to separate one microfibril bundle from the next during growth by disrupting xyloglucan or other bridges between microfibril bundles (Anderson et al., 2010). The aggregation of microfibrils along part of their length, while other parts of their length remain free to separate or have other polysaccharides interposed, raises interesting questions about the action of expansins (Cosgrove, 2005) and about the way in which the action of certain glucan hydrolases interacts with that of xyloglucan-specific endoglucanase (Park and Cosgrove, 2012b).
Of interest is the high level of disorder at the interfaces most relevant to growth, between microfibrils and noncellulosic polymers and between one microfibril and the next. Examples of strong biological materials from the animal kingdom show that disordered domains can contribute to toughness (high fracture energy) under external stress (van Beek et al., 2002). In primary cell walls, resistance to fracture must be combined with the controlled, enzyme-mediated yielding, apparently at disordered interfaces, that permits growth.
Implications for Cellulose Degradation
The accessibility of cellulose microfibrils to cellulases is an important factor in the conversion of lignocellulose to biofuels and is still more important in the case of nonlignified biomass. Cellulose recalcitrance is often put down to crystallinity (Arantes and Saddler, 2010), and “decrystallization” is sometimes stated as an aim of pretreatment processes (Beckham et al., 2011), without full consensus on what these terms mean. The extent to which cellulose microfibrils have the relatively hydrophobic [200] face exposed will positively influence the initial stage of degradation by cellulases that bind specifically to this face (Dagel et al., 2011; Liu et al., 2011). It would be of interest to know more about the binding specificity of the GH61/CBM33 cellulose oxidases (Forsberg et al., 2011; Quinlan et al., 2011), some of which also bind to the same face (Li et al., 2012). Aggregation of cellulose microfibrils is a recalcitrance factor that deserves greater attention and that can now be approached through deuteration FTIR experiments.
MATERIALS AND METHODS
Materials
Collenchyma strands from mature celery (Apium graveolens) petioles were isolated, and cell walls and their cellulose fraction were prepared essentially as described (Sturcová et al., 2004) and stored dry. For details, see Supplemental Materials and Methods S1.
SANS
SANS experiments were carried out on beamline D11 at the Institut Laue-Langevin on celery collenchyma cell walls and isolated cellulose. For experimental details, see Supplemental Materials and Methods S1.
WAXS
X-ray diffraction patterns were collected at ambient temperature using a Rigaku R-axis/RAPID image plate diffractometer with a molybdenum x-ray emission line Kα (λ = 0.07071 nm) source. The beam was collimated to a diameter of 0.5 mm. Samples were 0.7 mm thick in the direction parallel to the beam, and their other dimensions exceeded the beam diameter. Diffraction patterns were collected in perpendicular transmission mode except for tilting experiments to measure the axial reflections. Distance from the center of the diffraction pattern was expressed as q = 4πsinθ/λ, where 2θ is the scattering angle. For further details of experimental and data processing methods (Fernandes et al., 2011), see Supplemental Materials and Methods S1.
WANS
Neutron diffraction was carried out on beamline D19 at the Institut Laue-Langevin at a mean neutron wavelength of 0.242 nm and a sample-to-detector distance of 0.756 m. Samples with dimensions of 25 × 15 × 1 mm were assembled from multiple aligned collenchyma strands and maintained at controlled water or D2O vapor pressure in a through-flow container with walls of aluminum foil. For details, see Supplemental Materials and Methods S1.
NMR
A 1H Goldman-Shen spin-diffusion experiment, with detection through the 13C spectrum after cross polarization, was carried out on celery collenchyma cell walls hydrated with 0.2 cm3 g−1 D2O. The experimental procedures and data analysis, including the 2D representation of the data, were as described (Fernandes et al., 2011).
Deuteration FTIR
Celery collenchyma cell walls and isolated cellulose were enclosed within a through-flow cell with barium fluoride windows and exchanged with D2O-saturated air until the spectra ceased to change. The gas line was then switched to nitrogen rigorously dried by passing through a dry 4A molecular sieve followed by phosphorus pentoxide (Sicapent; Aldrich). FTIR spectra were collected with a Thermo Nicolet Nexus spectrometer equipped with a Nicolet Continuum microscope attachment having a liquid nitrogen-cooled mercury cadmium telluride detector (Fernandes et al., 2011).
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Figure S1. Equatorial SANS profile of celery collenchyma cell walls and isolated cellulose.
Supplemental Figure S2. Contribution of water to WAXS patterns from celery collenchyma cell walls.
Supplementary Material
Acknowledgments
We thank Rigaku, Ltd., for an instrument loan and Fujiang Zhang for collecting some of the FTIR spectra.
Glossary
- SAXS
small-angle x-ray scattering
- D2O
deuterium oxide
- SANS
small-angle neutron scattering
- WAXS
wide-angle x-ray scattering
- WANS
wide-angle neutron scattering
- FTIR
Fourier transform infrared
- 2D
two-dimensional
- ppm
parts per million
References
- Altaner C, Apperley DC, Jarvis MC. (2006) Spatial relationships between polymers in Sitka spruce: proton spin-diffusion studies. Holzforschung 60: 665–673 [Google Scholar]
- Anderson CT, Carroll A, Akhmetova L, Somerville C. (2010) Real-time imaging of cellulose reorientation during cell wall expansion in Arabidopsis roots. Plant Physiol 152: 787–796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arantes V, Saddler JN. (2010) Access to cellulose limits the efficiency of enzymatic hydrolysis: the role of amorphogenesis. Biotechnol Biofuels 3: 4 [Google Scholar]
- Atanassov II, Pittman JK, Turner SR. (2009) Elucidating the mechanisms of assembly and subunit interaction of the cellulose synthase complex of Arabidopsis secondary cell walls. J Biol Chem 284: 3833–3841 [DOI] [PubMed] [Google Scholar]
- Baker AA, Helbert W, Sugiyama J, Miles MJ. (1997) High-resolution atomic force microscopy of native Valonia cellulose I microcrystals. J Struct Biol 119: 129–138 [DOI] [PubMed] [Google Scholar]
- Beckham GT, Matthews JF, Peters B, Bomble YJ, Himmel ME, Crowley MF. (2011) Molecular-level origins of biomass recalcitrance: decrystallization free energies for four common cellulose polymorphs. J Phys Chem B 115: 4118–4127 [DOI] [PubMed] [Google Scholar]
- Bergenstråhle M, Wohlert J, Larsson PT, Mazeau K, Berglund LA. (2008) Dynamics of cellulose-water interfaces: NMR spin-lattice relaxation times calculated from atomistic computer simulations. J Phys Chem B 112: 2590–2595 [DOI] [PubMed] [Google Scholar]
- Bootten TJ, Harris PJ, Melton LD, Newman RH. (2004) Solid-state 13C-NMR spectroscopy shows that the xyloglucans in the primary cell walls of mung bean (Vigna radiata L.) occur in different domains: a new model for xyloglucan-cellulose interactions in the cell wall. J Exp Bot 55: 571–583 [DOI] [PubMed] [Google Scholar]
- Burgert I, Fratzl P. (2009) Plants control the properties and actuation of their organs through the orientation of cellulose fibrils in their cell walls. Integr Comp Biol 49: 69–79 [DOI] [PubMed] [Google Scholar]
- Cosgrove DJ. (2005) Growth of the plant cell wall. Nat Rev Mol Cell Biol 6: 850–861 [DOI] [PubMed] [Google Scholar]
- Dagel DJ, Liu YS, Zhong LL, Luo YH, Himmel ME, Xu Q, Zeng YN, Ding SY, Smith S. (2011) In situ imaging of single carbohydrate-binding modules on cellulose microfibrils. J Phys Chem B 115: 635–641 [DOI] [PubMed] [Google Scholar]
- Dinand E, Chanzy H, Vignon MR. (1996) Parenchymal cell cellulose from sugar beet pulp: preparation and properties. Cellulose 3: 183–188 [Google Scholar]
- Fahlén J, Salmén L. (2005) Pore and matrix distribution in the fiber wall revealed by atomic force microscopy and image analysis. Biomacromolecules 6: 433–438 [DOI] [PubMed] [Google Scholar]
- Farrugia LJ. (1999) WinGX suite for small-molecule single-crystal crystallography. J Appl Cryst 32: 837–838 [Google Scholar]
- Fernandes AN, Thomas LH, Altaner CM, Callow P, Forsyth VT, Apperley DC, Kennedy CJ, Jarvis MC. (2011) Nanostructure of cellulose microfibrils in spruce wood. Proc Natl Acad Sci USA 108: E1195–E1203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forsberg Z, Vaaje-Kolstad G, Westereng B, Bunæs AC, Stenstrøm Y, MacKenzie A, Sørlie M, Horn SJ, Eijsink VGH. (2011) Cleavage of cellulose by a CBM33 protein. Protein Sci 20: 1479–1483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foston M, Katahira R, Gjersing E, Davis MF, Ragauskas AJ. (2012) Solid-state selective (13)C excitation and spin diffusion NMR to resolve spatial dimensions in plant cell walls. J Agric Food Chem 60: 1419–1427 [DOI] [PubMed] [Google Scholar]
- Fujino T, Sone Y, Mitsuishi Y, Itoh T. (2000) Characterization of cross-links between cellulose microfibrils, and their occurrence during elongation growth in pea epicotyl. Plant Cell Physiol 41: 486–494 [DOI] [PubMed] [Google Scholar]
- Fujita M, Himmelspach R, Hocart CH, Williamson RE, Mansfield SD, Wasteneys GO. (2011) Cortical microtubules optimize cell-wall crystallinity to drive unidirectional growth in Arabidopsis. Plant J 66: 915–928 [DOI] [PubMed] [Google Scholar]
- Green PB. (1999) Expression of pattern in plants: combining molecular and calculus-based biophysical paradigms. Am J Bot 86: 1059–1076 [PubMed] [Google Scholar]
- Harris DM, Corbin K, Wang T, Gutierrez R, Bertolo AL, Petti C, Smilgies D-M, Estevez JM, Bonetta D, Urbanowicz BR, et al. (2012) Cellulose microfibril crystallinity is reduced by mutating C-terminal transmembrane region residues CESA1A903V and CESA3T942I of cellulose synthase. Proc Natl Acad Sci USA 109: 4098–4103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himmel ME, Ding SY, Johnson DK, Adney WS, Nimlos MR, Brady JW, Foust TD. (2007) Biomass recalcitrance: engineering plants and enzymes for biofuels production. Science 315: 804–807 [DOI] [PubMed] [Google Scholar]
- Horikawa Y, Clair B, Sugiyama J. (2009) Varietal difference in cellulose microfibril dimensions observed by infrared spectroscopy. Cellulose 16: 1–8 [Google Scholar]
- Hulmes DJS, Wess TJ, Prockop DJ, Fratzl P. (1995) Radial packing, order, and disorder in collagen fibrils. Biophys J 68: 1661–1670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarvis MC. (1992) Control of thickness of collenchyma cell-walls by pectins. Planta 187: 218–220 [DOI] [PubMed] [Google Scholar]
- Jarvis MC. (2011) Plant cell walls: supramolecular assemblies. Food Hydrocoll 25: 257–262 [Google Scholar]
- Kennedy CJ, Cameron GJ, Sturcova A, Apperley DC, Altaner C, Wess TJ, Jarvis MC. (2007a) Microfibril diameter in celery collenchyma cellulose: x-ray scattering and NMR evidence. Cellulose 14: 235–246 [Google Scholar]
- Kennedy CJ, Sturcova A, Jarvis MC, Wess TJ. (2007b) Hydration effects on spacing of primary-wall cellulose microfibrils: a small angle x-ray scattering study. Cellulose 14: 401–408 [Google Scholar]
- Knox JP. (2008) Revealing the structural and functional diversity of plant cell walls. Curr Opin Plant Biol 11: 308–313 [DOI] [PubMed] [Google Scholar]
- Langan P, Nishiyama Y, Chanzy H. (2001) X-ray structure of mercerized cellulose II at 1 Å resolution. Biomacromolecules 2: 410–416 [DOI] [PubMed] [Google Scholar]
- Li X, Beeson WT, IV, Phillips CM, Marletta MA, Cate JHD. (2012) Structural basis for substrate targeting and catalysis by fungal polysaccharide monooxygenases. Structure 20: 1051–1061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu YS, Baker JO, Zeng YN, Himmel ME, Haas T, Ding SY. (2011) Cellobiohydrolase hydrolyzes crystalline cellulose on hydrophobic faces. J Biol Chem 286: 11195–11201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon IM, Sturcová A, Sugimoto-Shirasu K, His I, McCann MC, Jarvis MC. (2006) Cell-wall structure and anisotropy in procuste, a cellulose synthase mutant of Arabidopsis thaliana. Planta 224: 438–448 [DOI] [PubMed] [Google Scholar]
- Marga F, Grandbois M, Cosgrove DJ, Baskin TI. (2005) Cell wall extension results in the coordinate separation of parallel microfibrils: evidence from scanning electron microscopy and atomic force microscopy. Plant J 43: 181–190 [DOI] [PubMed] [Google Scholar]
- Masuda K, Adachi M, Hirai A, Yamamoto H, Kaji H, Horii F. (2003) Solid-state 13C and 1H spin diffusion NMR analyses of the microfibril structure for bacterial cellulose. Solid State Nucl Magn Reson 23: 198–212 [DOI] [PubMed] [Google Scholar]
- Matthews JF, Beckham GT, Bergenstrahle-Wohlert M, Brady JW, Himmel ME, Crowley MF. (2012) Comparison of cellulose I beta simulations with three carbohydrate force fields. J Chem Theory Comput 8: 735–748 [DOI] [PubMed] [Google Scholar]
- Matthews JF, Bergenstråhle M, Beckham GT, Himmel ME, Nimlos MR, Brady JW, Crowley MF. (2011) High-temperature behavior of cellulose I. J Phys Chem B 115: 2155–2166 [DOI] [PubMed] [Google Scholar]
- Matthews JF, Skopec CE, Mason PE, Zuccato P, Torget RW, Sugiyama J, Himmel ME, Brady JW. (2006) Computer simulation studies of microcrystalline cellulose Ibeta. Carbohydr Res 341: 138–152 [DOI] [PubMed] [Google Scholar]
- McCann MC, Wells B, Roberts K. (1990) Direct visualization of cross-links in the primary plant-cell wall. J Cell Sci 96: 323–334 [Google Scholar]
- Mohnen D. (2008) Pectin structure and biosynthesis. Curr Opin Plant Biol 11: 266–277 [DOI] [PubMed] [Google Scholar]
- Newman RH. (1992) Nuclear magnetic resonance study of spatial relationships between chemical components in wood cell walls. Holzforschung 46: 205–210 [Google Scholar]
- Nishiyama Y. (2009) Structure and properties of the cellulose microfibril. J Wood Sci 55: 241–249 [Google Scholar]
- Nishiyama Y, Langan P, Chanzy H. (2002) Crystal structure and hydrogen-bonding system in cellulose Ibeta from synchrotron x-ray and neutron fiber diffraction. J Am Chem Soc 124: 9074–9082 [DOI] [PubMed] [Google Scholar]
- Nishiyama Y, Sugiyama J, Chanzy H, Langan P. (2003) Crystal structure and hydrogen bonding system in cellulose I(alpha) from synchrotron x-ray and neutron fiber diffraction. J Am Chem Soc 125: 14300–14306 [DOI] [PubMed] [Google Scholar]
- Paredez AR, Persson S, Ehrhardt DW, Somerville CR. (2008) Genetic evidence that cellulose synthase activity influences microtubule cortical array organization. Plant Physiol 147: 1723–1734 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park YB, Cosgrove DJ. (2012a) Changes in cell wall biomechanical properties in the xyloglucan-deficient xxt1/xxt2 mutant of Arabidopsis. Plant Physiol 158: 465–475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park YB, Cosgrove DJ. (2012b) A revised architecture of primary cell walls based on biomechanical changes induced by substrate-specific endoglucanases. Plant Physiol 158: 1933–1943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinlan RJ, Sweeney MD, Lo Leggio L, Otten H, Poulsen J-CN, Johansen KS, Krogh KBRM, Jørgensen CI, Tovborg M, Anthonsen A, et al. (2011) Insights into the oxidative degradation of cellulose by a copper metalloenzyme that exploits biomass components. Proc Natl Acad Sci USA 108: 15079–15084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez-Rodríguez C, Bauer S, Hématy K, Saxe F, Ibáñez AB, Vodermaier V, Konlechner C, Sampathkumar A, Rüggeberg M, Aichinger E, et al. (2012) CHITINASE-LIKE1/POM-POM1 and its homolog CTL2 are glucan-interacting proteins important for cellulose biosynthesis in Arabidopsis. Plant Cell 24: 589–607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheller HV, Ulvskov P. (2010) Hemicelluloses. Annu Rev Plant Biol 61: 263–289 [Google Scholar]
- Sheldrick GM. (2008) A short history of SHELX. Acta Crystallogr A 64: 112–122 [DOI] [PubMed] [Google Scholar]
- Somerville C. (2006) Cellulose synthesis in higher plants. Annu Rev Cell Dev Biol 22: 53–78 [DOI] [PubMed] [Google Scholar]
- Sturcová A, His I, Apperley DC, Sugiyama J, Jarvis MC. (2004) Structural details of crystalline cellulose from higher plants. Biomacromolecules 5: 1333–1339 [DOI] [PubMed] [Google Scholar]
- Sturcová A, His I, Wess TJ, Cameron G, Jarvis MC. (2003) Polarized vibrational spectroscopy of fiber polymers: hydrogen bonding in cellulose II. Biomacromolecules 4: 1589–1595 [DOI] [PubMed] [Google Scholar]
- Sugimoto K, Williamson RE, Wasteneys GO. (2000) New techniques enable comparative analysis of microtubule orientation, wall texture, and growth rate in intact roots of Arabidopsis. Plant Physiol 124: 1493–1506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szymanski DB, Cosgrove DJ. (2009) Dynamic coordination of cytoskeletal and cell wall systems during plant cell morphogenesis. Curr Biol 19: R800–R811 [DOI] [PubMed] [Google Scholar]
- van Beek JD, Hess S, Vollrath F, Meier BH. (2002) The molecular structure of spider dragline silk: folding and orientation of the protein backbone. Proc Natl Acad Sci USA 99: 10266–10271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viëtor RJ, Newman RH, Ha MA, Apperley DC, Jarvis MC. (2002) Conformational features of crystal-surface cellulose from higher plants. Plant J 30: 721–731 [DOI] [PubMed] [Google Scholar]
- Wada M, Heux L, Sugiyama J. (2004) Polymorphism of cellulose I family: reinvestigation of cellulose IVI. Biomacromolecules 5: 1385–1391 [DOI] [PubMed] [Google Scholar]
- Wickholm K, Larsson PT, Iversen T. (1998) Assignment of non-crystalline forms in cellulose I by CP/MAS C-13 NMR spectroscopy. Carbohydr Res 312: 123–129 [Google Scholar]
- Zykwinska A, Thibault JF, Ralet MC. (2007) Organization of pectic arabinan and galactan side chains in association with cellulose microfibrils in primary cell walls and related models envisaged. J Exp Bot 58: 1795–1802 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.