Correct Estimation of Preferential Chromosome Pairing in Autotetraploids

Abstract

In recent work, a statistical model was proposed for the purpose of estimating parameters associated with quantitative trait locus (QTL) mapping and preferential pairing within a polyploidy framework. The statistical model contained several parameters that, when estimated from experimental data, supplied information about QTL, including a preferential pairing factor. Among the results reported were estimates of preferential pairing, many of which indicated high levels of preferential pairing (p = 0.60) that were inconsistent with biological expectations. By using the biological inconsistencies as our motivation, we present a reformulated statistical method for estimating preferential pairing, and use this method to reanalyze the same autotetraploid alfalfa data and to conduct a simulation study. Our results directly contradict the current findings of significant preferential pairing and affirm the traditional view of random chromosome segregation in alfalfa.

Polyploid species contain multiple sets of chromosomes, which can be derived from a single species (autopolyploids) or derived from distinct but related species (allopolyploids). Autopolyploids are expected to have polysomic inheritance due to similarity of homologous chromosomes and the ability of each homolog to pair with any other homolog during meiosis. Allopolyploids, on the other hand, often show disomic inheritance because related chromosomes contributed by the different species are only partially homologous (homoeologous) and either do not pair or pair only infrequently. The distinctions between autopolyploids and allopolyploids may be obscured if some sets of homoeologous chromosomes in allopolyploid species are very similar and pair more frequently, or if divergence of germplasm within autopolyploid species has lead to chromosome differentiation and preferred pairing configurations in hybrids of wide crosses. Thus, analytical methods to estimate the degree of preferential pairing would be useful for determining the mode of inheritance for each set of homologous or homoeologous chromosomes in polyploids. Preferential pairing has been used to denote the difference between the frequency of homologous pairing and homoeologous pairing, and estimated via mathematical models for autotetraploids performing multivalent pairing (Sybenga 1994, 1995). In keeping with the notation used in Sybenga (1994, 1995), p denotes preferential pairing factor, and P(A) the probability of an event A.

A method for mapping quantitative trait loci (QTLs) in polyploids was described by Ma et al. (2002) within the context of bivalent chromosome pairing. Their statistical model contained several parameters, that when estimated from experimental data, supplied associated QTL effects, including preferential pairing factor (p). Ma et al. (2002) reanalyzed data from a study of autotetraploid alfalfa (Medicago sativa, 2n = 4x = 32; Brouwer and Osborn 1999; Brouwer et al. 2000). They identified different associated QTL effects than were reported previously (Brouwer et al. 2000), and they obtained numerous high estimates of preferential pairing (p = 0.60). Their results disagree with results from previous studies showing tetrasomic inheritance in alfalfa based on genetic segregation data (for review, see McCoy and Bingham 1988). We question the estimates of preferential pairing provided in Ma et al. (2002), because different values of p were obtained from the same set of genotypes that had been grown in different environments (different years listed in Tables 1 and 2 of Ma et al. 2002). Estimates of p in mapping studies should be based only on marker genotype data and should not be influenced by environmental effects on phenotype.

In this article, we present a straightforward method for estimating preferential pairing that is based solely on genotypic data provided by pseudo-test backcross mapping experiments. This method is applied to the same alfalfa data set that was analyzed in Ma et al. (2002) and to a simulation study. Based on these analyses, we found no evidence for preferential pairing in the F₁ alfalfa genotype used to develop the mapping population.

RESULTS

Reanalysis of Autotetraploid Alfalfa Data

The preferential pairing factors were estimated for the seven chromosome sets of the B17 backcross experimental data (i.e., marker data from 101 progeny), and the results ranged from zero to 0.06 (Table 1). The estimated preferential pairing factors for the seven chromosome sets were close to zero, with a high proportion of negative estimates that were truncated to zero. It is likely that negative estimation was due to the small sample size (101 for this experiment) because recombination is a relatively rare event and a preferential pairing factor close to the extreme values (zero and two-thirds) also requires a larger sample size to produce a precise estimate (see below). We expect to see the relative frequency of estimates less than zero or greater than two-thirds to decrease as the sample size increases.

Table 1.

Estimated Preferential Pairing Factor for an F₁ Alfalfa Genotype Based on Segregation of 101 Backcross Progeny

Chromosome	p_esta	No. overb	No. underc	No. markers in group Ad	No. markers in group Be
1	0.0008	0	14	5	3
2	0.0227	0	22	4	7
3	0.0009	0	58	8	8
4	0.0000	0	22	5	6
5	0.0643	0	13	7	3
6	0.0000	0	8	3	3
8	0.0306	0	16	6	4

Note: F₁ alfalfa (Brouwer and Osborn 1999).

^aAverage of the estimated preferential pairing factors from alfalfa experimental data.

^bThe number of estimated preferential pairing factors larger than two-thirds.

^cThe number of negative estimated preferential pairing factors.

^dThe number of markers in homolog (or cosegregation group) A.

^eThe number of markers in homolog (or cosegregation group) B.

A Simulation Study

To determine the impact of underestimation and overestimation of preferential pairing p, and the power of this estimator, a simulation study was performed. Two markers were used in the simulation study. The genetic marker distance, d, ranged from 0.05 M (Morgan), 0.25 M, to 0.45 M. The true preferential pairing factor, p, was assigned four different values 0, 0.20, 0.40, and 0.666. The sample size, n, took values from the following set: {50, 100, 250, 500, 1000, 5000, and 10,000}. For each combination of genetic distance, preferential pairing factor, and sample size, 1000 data sets were simulated. The average of the 1000 estimates of the preferential pairing factor, the standard deviation of the 1000 estimates, the number of negative estimates, and the number of estimates greater than two-thirds are reported in Tables 2 and 3.

Table 2.

Estimated Preferential Pairing Factor With Two Simulated Markers in Repulsion When the True Preferential Pairing Factor is 0 or 0.20.

		pc= 0				p = 0.2
d(M)a	nb	p_estd	SEe	No. overf	No. underg	p_est	SE	No. over	No. under
0.45	50	0.182	0.008	83	524	0.282	0.009	161	356
	100	0.144	0.006	33	460	0.257	0.007	94	247
	250	0.094	0.004	0	478	0.232	0.006	23	172
	500	0.064	0.003	0	485	0.215	0.005	4	92
	1000	0.048	0.002	0	488	0.211	0.003	0	22
	5000	0.021	0.0009	0	482	0.203	0.002	0	0
	10000	0.013	0.0006	0	491	0.200	0.001	0	0
0.25	50	0.107	0.005	7	50	0.240	0.006	32	191
	100	0.081	0.004	0	455	0.217	0.005	9	94
	250	0.049	0.002	0	497	0.207	0.003	0	40
	500	0.034	0.002	0	482	0.203	0.002	0	5
	1000	0.025	0.001	0	476	0.204	0.002	0	0
0.05	50	0.060	0.003	0	489	0.211	0.004	0	75
	100	0.046	0.002	0	527	0.202	0.003	0	31
	250	0.027	0.001	0	495	0.199	0.002	0	0
	500	0.019	0.0009	0	547	0.200	0.001	0	0
	1000	0.013	0.0006	0	515	0.201	0.001	0	0

^aThe genetic distance between the two markers with unit Morgan (M).

^bThe sample size.

^cThe true value of the preferential pairing factor used in simulation.

^dThe average of 1000 estimated preferential pairing factors from 1000 simulated data sets.

^eThe standard error of the 1000 estimated preferential pairing factors.

^fThe number of estimated preferential pairing factors larger than two-thirds.

^gThe number of negative estimated preferential pairing factors.

Table 3.

Estimated Preferential Pairing Factor With Two Simulated Markers in Repulsion When the True Preferential Pairing Factor is 0.40 or 0.60

		pc= 0.4				p = 0.666
d(M)a	nb	p_estd	Stde	No. overf	No. underg	p_est	Std	No. over	No. under
0.45	50	0.374	0.008	252	210	0.503	0.007	463	82
	100	0.382	0.008	212	102	0.540	0.006	468	16
	250	0.399	0.006	113	31	0.582	0.004	518	0
	500	0.400	0.005	51	8	0.605	0.003	520	0
	1000	0.405	0.003	8	0	0.625	0.002	531	0
	5000	0.402	0.002	0	0	0.648	0.0009	530	0
	10000	0.400	0.001	0	0	0.652	0.0007	499	0
0.25	50	0.396	0.006	126	47	0.587	0.004	527	1
	100	0.399	0.005	71	6	0.611	0.003	566	0
	250	0.403	0.003	8	0	0.628	0.002	492	0
	500	0.400	0.002	0	0	0.637	0.001	496	0
	1000	0.402	0.002	0	0	0.647	0.0009	533	0
0.05	50	0.402	0.004	7	0	0.640	0.001	548	0
	100	0.400	0.003	0	0	0.648	0.001	438	0
	250	0.398	0.002	0	0	0.653	0.0006	523	0
	500	0.397	0.001	0	0	0.657	0.0004	446	0
	1000	0.400	0.0008	0	0	0.660	0.0003	469	0

^aThe genetic distance between the two markers with unit Morgan (M).

^bThe sample size.

^cThe true value of the preferential pairing factor used in simulation.

^dThe average of 1000 estimated preferential pairing factors from 1000 simulated data sets.

^eThe standard error of the 1000 estimated preferential pairing factors.

^fThe number of estimated preferential pairing factors larger than two-thirds.

^gThe number of negative estimated preferential pairing factors.

The performance of the estimator depends on the sample size, genetic distance, and true preferential pairing factor. In general, a larger sample size reduces both bias and variance of estimation. Furthermore, greater density of the genetic map can also improve the precision of the estimation. For example, when the true preferential pairing is zero, if the marker distance is 0.45 M, 10,000 individuals were needed to achieve an estimated value of 0.013 with standard error 0.0006, whereas with marker distance of 0.05 M, only 1000 individuals gave the same point estimation with standard error 0.0006. Also, as the preferential pairing factor approaches the margin (toward 0.0 or 0.667), both bias and variance of the estimator increase.

Because the sample size of the previously discussed alfalfa experiment was 101, we explored the results from the simulation study by using a sample size of 100. The true preferential pairing factors tend to be overestimated if the true preferential pairing factor is close to zero, or underestimated if the true preferential pairing factor is close to two-thirds. The extent of underestimation or overestimation increases as the marker distance increases, which means the true preferential pairing factor for each chromosome may be smaller than the estimated value (Table 1) when the sample size is 100. Based on these simulation results, and the estimates of p from the B17 backcross data, it is reasonable to assume random pairing of homologs in the (B17 × P13) F₁ for the seven sets of chromosomes analyzed.

DISCUSSION

Our findings contradict the work of Ma et al. (2002) pertaining to the estimation of preferential pairing for their reanalysis of the autotetraploid alfalfa data provided Osborn and colleagues (Brouwer and Osborn 1999, Brouwer et al. 2000), and reveal random pairing of homologs in the (B17 × P13) F₁ population. Our findings affirm the traditional view of random chromosome segregation in tetraploid alfalfa.

We find the biological interpretation of preferential pairing results as provided by Ma et al. (2002) to be inconsistent with the experimental design supplying the data. In this situation the experimental design dictates that the same genotype be grown in differing environments. Because preferential pairing depends only on the state of the genetic markers, or genotypic data, estimates of preferential pairing can be gained independent from any phenotypic information. Furthermore, because the same genetic material (i.e., genotypes) is grown in two different environments/years, there is no opportunity for genotypic variation; thus, estimates of preferential pairing, which are based solely on genotypic information, should be identical. The results of preferential pairing obtained by Ma et al. (2002) directly contradict both the experimental design and the traditional view of random chromosome segregation in alfalfa. Such a contradiction of biological expectation does not necessarily imply the statistical model itself of Ma et al. (2002) is incorrect, it merely indicates that the implementation of such a model to this experimental design and these data is incorrect.

The statistical model used by Ma et al. (2002) includes both genotypic and phenotypic data. Although the experimental design dictates no variation in the genotypic data, variation in the phenotype, as the result of environment, is almost certain and, as such, influences the estimates of preferential pair (p) when estimated for each year. Because preferential pairing factor (p) and marker configuration can be estimated independent from phenotype information (and variation), it is our opinion that both should be estimated based solely on marker genotype information.

After biological inconsistency, we turn to a more practical reason for the irregular estimates of preferential pairing obtained by Ma et al. (2002), namely, the algorithm and software program that were designed for an outcrossing experiment, yet applied to a data set from a pseudo-test backcross experiment. Specifically, in Ma et al.'s model, it was assumed that the QTL and two markers could be located on homologous or homoeologous chromosomes, and that the likelihood function included all possible progeny configurations under this assumption. If we consider that two chromosomes passed from one parent should be homologous rather than homoeologous, and also consider the fact that the SDRF markers were uniquely collected for each parent (B17 or P13), then the QTL and two markers from one parent could only be located on homologous chromosomes. The ramifications are that some of the progeny configuration probability matrices in Ma et al. (2002) do not fit the experimental scenario that represents these data and should not be considered when estimating preferential pairing.

We propose the estimation of preferential pairing factor based solely on genotypic data under pseudo-test backcross experiments. As gained from our approach and as implied by earlier work, the point estimate of preferential pairing close to zero for the alfalfa data at hand promotes the current view that random pairing applies. Although we realize that for different experimental designs the analytical formula for the point estimation may be different, our method of deriving the formula remains unchanged. Furthermore, if the estimated preferential pairing factor is significantly different from zero, we could then replace preferential pairing factor with the point estimate and treat it as a constant when mapping QTL. The separation of estimating preferential pairing factor from mapping QTL is a valid step because the meiotic process is not affected by QTL location or effect. Approaching the problem in this manner simplifies the statistical model, as well as reduces calculation complexity and time.

METHODS

A pseudo-test backcross population was developed previously and used to create a genetic linkage map of tetraploid alfalfa (Brouwer and Osborn 1999) and to identify QTL associated with winter hardiness and other related traits (Brouwer et al. 2000). Two genotypes, B17 and P13, representing extremes for each trait, were cross-pollinated. B17 was a single plant from the cultivar Blazer XL, and P13 was a single plant from PI 536535 that represents the Peruvian germplasm source of cultivated alfalfa. A single F₁ hybrid of the cross was back-crossed to each parent to create two populations each with 101 individuals. Each population was scored for 82 single-dose restriction fragment (SDRF) loci and measured for each trait in 2 years of replicated field trials. Only unique fragments that were present in one parent, absent in the other parent, and segregated in the backcross progeny were scored independently as dominant markers. Therefore, in each backcross population, the recurrent parent was noninformative.

We denote the four homologs of a chromosome in the F₁ plant as A, B, C, and D, where A and B derive from P13 and C and D come from B17 (Fig. 1). Assuming bivalent pairing, there are three possible pairing patterns: (1) homolog A pairs with homolog B, and C pairs with D; (2) homolog A pairs with C, and B pairs with D; and (3) homologs A and D pair, and B pairs with C. The first case involves pairing between homologs from the same parent, whereas the other two possibilities involve pairings between homologs from different parents. Although these parents are both members of cultivated alfalfa, Medicago sativa spp. sativa (Ma et al. 2002 incorrectly state that B17 was M. sativa spp. falcata), Blazer XL does have M. sativa spp. falcata germplasm in its pedigree, and Peruvian was identified as a genetically distinct germplasm (Kidwell et al. 1994). Thus, it is possible that these or other genomic differences between the parents could cause p of homologs from the same parent. A preferential pairing factor (0 ≤ p ≤ two-thirds) can be used to model the possibility that pairing of homologs from the same parent (P(a) = 1/3 + p) is more frequent than pairing of homologs from different parents (P(b) = P(c) = 1/3 – p/2; Wu et al. 2002).

Figure 1.

Pseudo-test backcross mating design with alfalfa parents B17 and P13.

Preferential pairing factor (p) can be estimated by using the marker genotype data for the backcross progeny because this distribution depends only on the preferential pairing factor, the parental marker linkage phase (coupling or repulsion), and the recombination fraction between markers. These last two factors can be determined from the segregation data. Consider two markers segregating in the B17 backcross population. Suppose two single-dose restriction fragment marker loci, M and N, present only in P13, were passed to the F₁ (F₁ genotypes of M/m/m/m or m/M/m/m, and N/n/n/n or n/N/n/n). Here, uppercase denotes the marker name, as well as the dominant allele (presence of the SDRF) and lowercase denotes the recessive allele (absence of the SDRF). There are four possible observable marker genotype classes in the B17 backcross progeny: neither marker is present, only M is present, only N is present, and both markers are present. The four events will be represented by Ø, M, N, and MN, respectively.

If M and N are linked in coupling and if we assume that all the dominant alleles are on homolog A, then homolog B, which contains recessive alleles, m and n, is equivalent to the two non-informative chromosomes passed from the recurrent parent B17, which also contain recessive alleles m and n. Therefore, for all the three possible pairing patterns, the marker genotype distribution of B17 backcross population is the same. Let r denote the recombination fraction between M and N, then P(Ø) = P(MN) = (1 – r) / 2, and P(M) = P(N) = r / 2. The fact that the marker genotype distribution does not depend on the preferential factor, p, factor means that p cannot be estimated based on progeny marker data if two markers are in coupling. The same argument follows naturally for all markers on a homolog (a cosegregation group), that is, because the marker genotype distribution does not depend on p, the p factor cannot be estimated (this point was not indicated in Ma et al. 2002).

If M and N are in repulsion, it can be shown that the distribution of observable marker genotype is given by 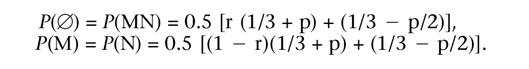Therefore, given the recombination fraction, r, we can estimate p simply by using the difference between observed marker presence/absence relative frequencies. If the estimated value is bigger than two-thirds, then two-thirds will be taken as the estimated value, and similarly if the estimated value is negative, then 0.0 will be taken as the estimated value. In a linkage group, when there is more than one pair of markers in repulsion, we can estimate p for each pair and use the average value as the estimate for p.