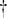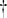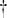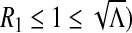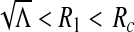Analysis of recruitment and industrial human resources management for optimal productivity in the presence of the HIV/AIDS epidemic

Abstract

The aim of this paper is to analyze the recruitment effects of susceptible and infected individuals in order to assess the productivity of an organizational labor force in the presence of HIV/AIDS with preventive and HAART treatment measures in enhancing the workforce output. We consider constant controls as well as time-dependent controls. In the constant control case, we calculate the basic reproduction number and investigate the existence and stability of equilibria. The model is found to exhibit backward and Hopf bifurcations, implying that for the disease to be eradicated, the basic reproductive number must be below a critical value of less than one. We also investigate, by calculating sensitivity indices, the sensitivity of the basic reproductive number to the model’s parameters. In the time-dependent control case, we use Pontryagin’s maximum principle to derive necessary conditions for the optimal control of the disease. Finally, numerical simulations are performed to illustrate the analytical results. The cost-effectiveness analysis results show that optimal efforts on recruitment (HIV screening of applicants, etc.) is not the most cost-effective strategy to enhance productivity in the organizational labor force. Hence, to enhance employees’ productivity, effective education programs and strict adherence to preventive measures should be promoted.

Introduction

The profitability of any organizational venture depends largely on the productivity of its workforce. The main determining factors include skill level, motivation, satisfaction, and schedule pressure. The question now is how would an ineffective employee recruitment policy affect the organization in the face of HIV/AIDS infection?

HIV/AIDS is not only a health issue but a substantial threat to socio-economic development, imposing a heavy burden on families, communities, and economies. The pandemic has affected most countries of the world. In 2003, UNAIDS estimated that 38 million people were HIV-positive worldwide of which about 26 million were workers between the ages of 15 and 49 (the most productive age group). This has great implications for families and economies in terms of employment, productivity, and labor-market changes [1].

In 2005, about 3.1 million people died from AIDS (acquired immunodeficiency syndrome) and 4.9 million people became infected with HIV, bringing the number to 40.3 million of people living with the virus across the world (UNAIDS 2005). HIV infection, which can cause AIDS, is a global problem and has shown a high degree of prevalence in populations all over Sub-Saharan Africa. The most susceptible individuals at risk of acquiring infection include people having sexual contacts with the HIV infected, homosexual and bisexual men, intravenous drug abusers, and persons transfused with contaminated blood.

HIV is preventable but not curable. Highly active antiretroviral therapy (HAART) is not a cure but the use of drugs to halt the decline in immune deficiency and prevent disease progression and death. ART suppresses viral replication and successful treatment helps in slowing or halting the disease progression, prevention of drug resistance, and improvement in the quality of life. Although the number of infected people receiving ART in low- and middle-income countries has increased dramatically, optimal disease management is not well defined. Despite substantial progress in the access to treatment, only 20% of adults who needed ART were receiving it [2] as of 2012.

There is still an intensive search going on for an anti-HIV vaccine. The use of chemotherapy is aimed at killing or halting the pathogen, but treatment that can boost the immune system can serve to help the body fight infection on its own [3]. The new treatments are aimed at reducing the viral population and improving the immune response. This brings new hope to the treatment of HIV infection and we are exploring strategies for such treatments using optimal control techniques.

A host of social, economic, cultural, and political factors facilitate the spread of HIV through populations. HIV spreads more widely where a wrong perspective or attitudes about HIV are common, for example, extensive organizational (office) sexual networks, where a person is having sex with more than one partner in an office location. Having multiple partners concurrently creates a node of transfer from one sexual network to another. Where sexual networks are smaller and more circumscribed, HIV can spread but less widely. The challenges posed by peoples’ attitude and ignorance to the disease dynamics call for a better understanding of its transmission and the development of effective and optimal strategies for the prevention and control of the spread of HIV/AIDS. Research has also shown that a behavioral or attitudinal change has a great influence on disease spread [4].

Most organizational workplaces recruit individuals without knowing their HIV/AIDS status or whether the individual would become an asset (productive) to the company or a liability (non-productive). The non-productive employees can be associated with their lifestyle (absenteeism, passive/aggressive behavior, not meeting deadlines, carefree attitude, and negative effect of multiple sexual partners) [5]. It is clear from various studies that interventions designed to support employment, or economic policy, or a national HIV/AIDS strategy cannot be implemented without considering the particular impact HIV and AIDS are having on the economically active and productive population [1]. As very little is known about the impact of HIV/AIDS on the labor force structure and productivity, this study then seeks to fill some of the gaps in this knowledge.

The impact of AIDS is significant on most economic sectors. For instance, agriculture, being the largest sector in most African economies, which accounts for a large portion of production and large employment opportunities, bears the brunt of HIV/AIDS. Studies performed in some countries have shown that AIDS will continue to have adverse effects on agriculture, including loss of labor supply and remittance income. The loss of a few workers at crucial periods of planting and harvesting can significantly reduce the size of the harvest [6]. AIDS-related illnesses and deaths to employees affect a firm by both increasing expenditures and reducing revenues. Expenditures are increased for health care costs, burial fees and training and recruitment of replacement employees. Revenues may be decreased because of absenteeism due to illness or attendance at funerals and time spent on training. Labor turnover can lead to a less experienced labor force that is less productive [7].

Mathematical models have been very useful tools in understanding the transmission dynamics of infectious diseases including HIV and in designing control measures to contain the diseases. Furthermore, they offer a better understanding of the epidemiological patterns for disease control as they provide short- and long-term predictions of HIV and AIDS incidence. Mathematical models have been used extensively in research into the epidemiology of HIV/AIDS to help improve our understanding of the major contributing factors.

Some of the notable studies include Anderson et al. [8], who presented a simple mathematical HIV transmission model to investigate the effects of various factors on the overall pattern of the AIDS epidemic. While Nikolaos et al. [9] proposed a detailed analysis of a dynamical model to describe the pathogenesis of HIV infection, and Christopher and Jorge [10] derived a simple two-dimensional SIS (susceptible-infected-susceptible) model with vaccination and multiple endemic states. Guihua and Zhen [11] studied the global dynamics of an SEIR (susceptible-exposed-infected-recovered) epidemic model in which latent and immune states were infective. Agraj et al. [12] proposed a mathematical model to study the effect of screening of unaware infectives on the spread of HIV infection. Mukandavire et al. [13] proposed and examined a deterministic model for the co-infection of HIV and malaria in a community.

Karrakchou et al. [14] investigated the fundamental role of chemotherapy treatment in controlling the virus reproduction in an HIV patient, while Adams et al. [15] derived HIV therapeutic strategies by formulating and analyzing an optimal control problem using two types of dynamic treatments. Gul et al. [16] studied the stability and optimal vaccination of an SIR epidemic model. Okosun et al. [4] investigated the effectiveness of HIV/AIDS preventive and treatment measures (treatment of HIV individuals, treatment of AIDS individuals, education campaign in the presence of carefree susceptibles) in reducing the spread of the disease. For optimal controls applied in other epidemic models, we refer the reader to [3, 17–19].

Very little or no attention has been paid to study models that incorporate classes of productive and non-productive individuals (susceptibles and infected) and that may be helpful in determining the productivity level of the labor force in organizations in the presence of HIV/AIDS. The model we consider in this paper is an improved dynamical system model but with the inclusion of a productive susceptible class, productive HIV-infected class, and time-dependent control parameters. We study and determine the possible impact of optimal education and HAART treatment for enhancing productivity on the spread of HIV. We carried out a detailed qualitative optimal control analysis of the resulting model and we determined the necessary conditions for optimal control of the disease using Pontryagin’s maximum principle in order to identify optimal strategies for controlling the spread of the disease.

Our main goal is to set up an optimal control problem related to the model. In order to do this, we use the following recruitment strategy: (effective screening of applicants) u₁, preventive measures (abstinence, being faithful, condom use) parameters on susceptibles u₃, education or educational parameter u₂ and HAART treatment parameter for individuals with HIV u₄ as time-dependent controls in the model. Hence, we investigate the role of productive susceptibles, productive infected, optimal education through counseling, mentoring, training, screening, educational campaigns, and HAART treatment of HIV/AIDS on the spread of HIV/AIDS.

The paper is organized as follows. In Section 2, we present a model consisting in ordinary differential equations (ODEs) that describes the dynamics of the disease and the underlying assumptions. The analysis of an endemic equilibrium is presented in Section 3. In Section 4 we use Pontryagin’s maximum principle to investigate the analysis of control strategies and to find the necessary conditions for the optimal control of the disease. In Section 5, we show the simulation results and then present the cost-effectiveness analysis in Section 6. Our conclusions are discussed in Section 7.

Model formulation

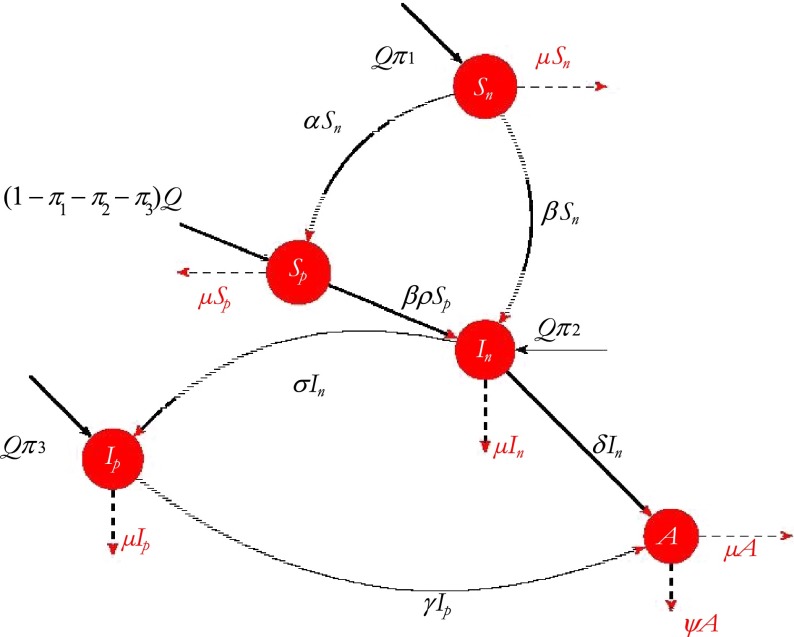
The model that we propose here is a standard compartmental model of HIV/AIDS in which we incorporated three time-dependent control measures simultaneously: (i) preventive measures (abstinence, being faithful, condom use), (ii) an education campaign, (iii) HAART treatment of HIV individuals for enhanced productivity. The model sub-divides the total human population at time t, denoted by N(t), into the following sub-populations of susceptible productive workers (S_p(t)), susceptible non-productive workers (S_n(t)), infected non-productive workers (I_n(t)), infected productive individuals on HAART treatment (I_p(t)), and that of full-blown AIDS individuals A(t), so that

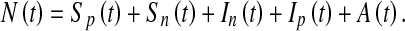The susceptibles are individuals who have not contracted the infection but may be infected through sexual contacts. The susceptible non-productive are individuals whose lifestyle places them at high risk of contracting the disease.

The organization recruits workers at the rate of Q, where the proportion of susceptible non-productive, infected non-productive and infected productive workers are recruited at rates π₁, π₂ and π₃ respectively. The parameter β is the per-capita contact rate for susceptible non-productive individuals. The susceptible productive workers have a per- capita contact rate of β₁ = ρβ < β, where ρ is the modification parameter due to the right value perception of the susceptible productive workers. When susceptible non-productive individuals are educated (through counseling, mentoring, or monitoring) and their attitude changes, they progress to the susceptible productive class at a rate u₂α, where u₂ is the education control effort. The infected non-productive individuals on the HAART treatment progress at a rate u₃σ to the infected productive individuals class, where σ is the proportion of the infected non-productive individuals on the HAART treatment for enhanced productivity and u₃ is the control effort on the HAART treatment to enhance productivity.

Infected non-productive workers not on the HAART treatment progress into the full-blown AIDS class at a rate δ, while γ is the rate of progression of infected productive individuals into full-blown AIDS, here γ < δ. The term η is the modification parameter due to the HAART treatment and right value perceptions of the infected productive individuals. The disease-induced death rate of AIDS individuals is denoted by ψ and μ is the natural mortality rate unrelated to HIV/AIDS. We also assume the AIDS class to be weakly sexually active and non-productive. We denote by τ the transmission probability of an AIDS individual infecting susceptible humans (Fig. 1).

Fig. 1.

Flow diagram for HIV/AIDS disease transmission

The resulting system of the equation for the constant control case is as follows:

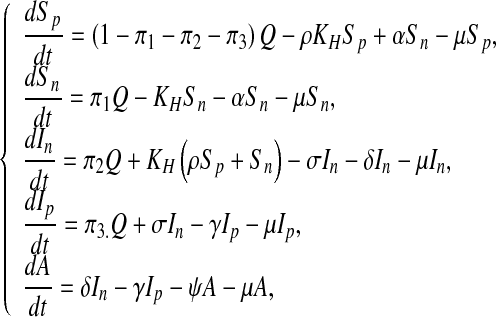1

where

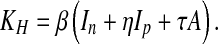Analysis of the endemic equilibrium

Calculating the endemic equilibrium point, we obtain

2

where

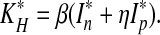The endemic equilibrium satisfies the following polynomial,

3

where

4

We shall examine the endemic equilibrium polynomial (3) under three scenarios; (i) when there is a recruitment of productive susceptibles only (i.e., π₁ = π₂ = π₃ = 0); (ii) when there is a recruitment of susceptibles only (i.e., 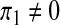, π₂ = π₃ = 0) and (iii) when there is a recruitment of productive individuals only (π₁ = π₂ = 0, ).

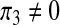The case of recruitment of productive susceptibles only (i.e., π₁ = π₂ = π₃ = 0)

Setting π₁ = π₂ = π₃ = 0, the DFE of the HIV/AIDS model (1) exists in the absence of the recruitment of infected individuals and is given by

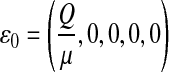and the endemic equilibrium coefficients then become

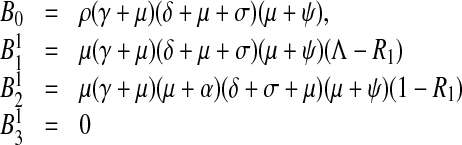5

where

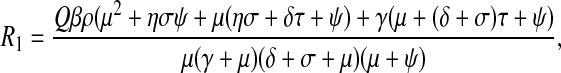6

is the basic reproductive number under this scenario and

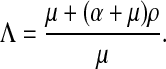7

Λ > 1 if and only if

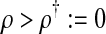We obtain the following result:

Proposition 1

1. if ρ ≥ ρ, then system (1) exhibits transcritical bifurcation.

2. if ρ < ρ, then system (1) exhibits backward bifurcation. That is, there exists R_c in (0, 1) such that

   • i.
     if 1 ≤ R₁ then (1) has one endemic equilibrium point.
   • ii.
     if R_c < R₁ < 1 then (1) has two endemic equilibrium points.
   • iii.
     if R₁ = R_c then (1) has one endemic equilibrium point.
   • iv.
     if R₁ < R_c then (1) has no endemic equilibrium points.

Proof

1. If ρ ≥ ρ then Λ ≥ 1. In this case, we have the following

   • i.
     If R₁ > 1, then B₂ < 0. In this case, (3) has a unique positive solution.
   • ii.
     If R₁ ≤ 1, then B₂ ≥ 0 and B₁ ≥ 0 (because . This, together with B₀ > 0, imply that (3) has no positive solution.
2. If ρ < ρ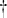, then Λ < 1. In this case, we have

   • i.
     If R₁ ≥ 1, then B₂ ≤ 0, which implies that (3) has a unique positive solution.
   • ii.
     If 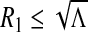, then B₁ ≥ 0 and B₂ > 0. This implies that (3) has no positive solution.
   • iii.
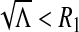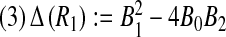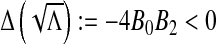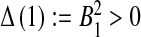     If , we consider the discriminant of . One can see that and . Therefore, there exists 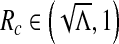such that Δ (R_c) = 0 and Δ < 0 for 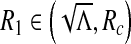and Δ > 0 for R₁ ∈ (R_c, 1). In this case, we have

     1. If then (3) has no positive solution.
     2. If R₁ = R_c then Δ = 0 and B₁ < 0. This implies that (3) has one positive solution.
     3. If R_c < R₁ < 1 then (3) has two real solutions that are positive since B₂ > 0 and B₁ < 0.□

Proposition 1 establishes the existence of two endemic equilibria for Λ in (R_c, 1).

The case of the recruitment of susceptibles only (i.e., 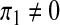, π₂ = π₃ = 0)

Setting 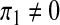, π₂ = π₃ = 0, the DFE of the HIV/AIDS model (1) exists in the absence of the recruitment of infected individuals and is given by

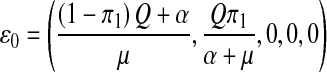The endemic equilibrium coefficients become

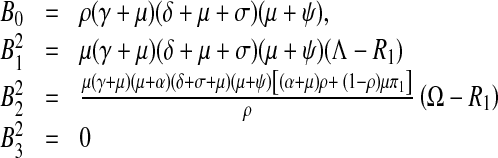8

where

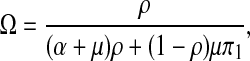9

The proof is similar to (5) above if Ω = 1. But Ω = 1 if and only if

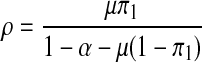Hence, the model exhibits a backward bifurcation in the presence of the recruitment of non-productive susceptibles.

The case of the recruitment of productive individuals only (π₁ = π₂ = 0, )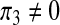

Setting π₁ = π₂ = 0, 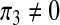the coefficients of the endemic equilibrium (3) become,

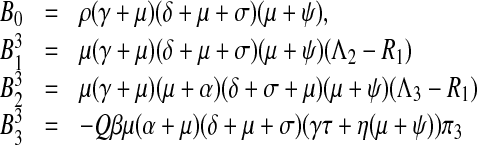10

here

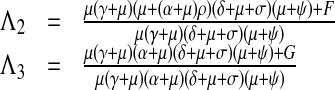11

F = Qβρ(γ(μ(1 − τ) + ψ) + (1 − η)μ(μ + ψ) + δ(μτ − η(μ + ψ))) π₃, G = Qβ((α + μ)ρ(μ(1 − τ) + ψ + (1 − η)μ(μ + ψ) + δ(μτ − η(μ + ψ))) − μ(δ + μ + σ)(γτ + η(μ + ψ))) π₃.

By Routh–Hurwith criteria, the roots of (10) have negative real parts if and only if B₀ > 0, 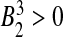and 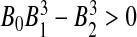. It is clear from (10) that 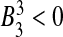, so the disease free equilibrium is unstable.

Numerically, we shall show that periodic solutions bifurcate from the endemic equilibrium, implying that the endemic equilibrium is unstable (Fig. 2).

Fig. 2.

Simulations of system (1) for Q = 100, μ = 0.04, π₃ = 0.03, γ = 0.288, ρ = 0.2, σ = 0.04, δ = 0.8, α = 0.81. (a) is the solution of I_p versus time (days) and (b) is I_n versus time t, (c) is the projected I_n − I_p phase plane of the phase space and in (d) we use Q = 10 while all other parameters remain the same

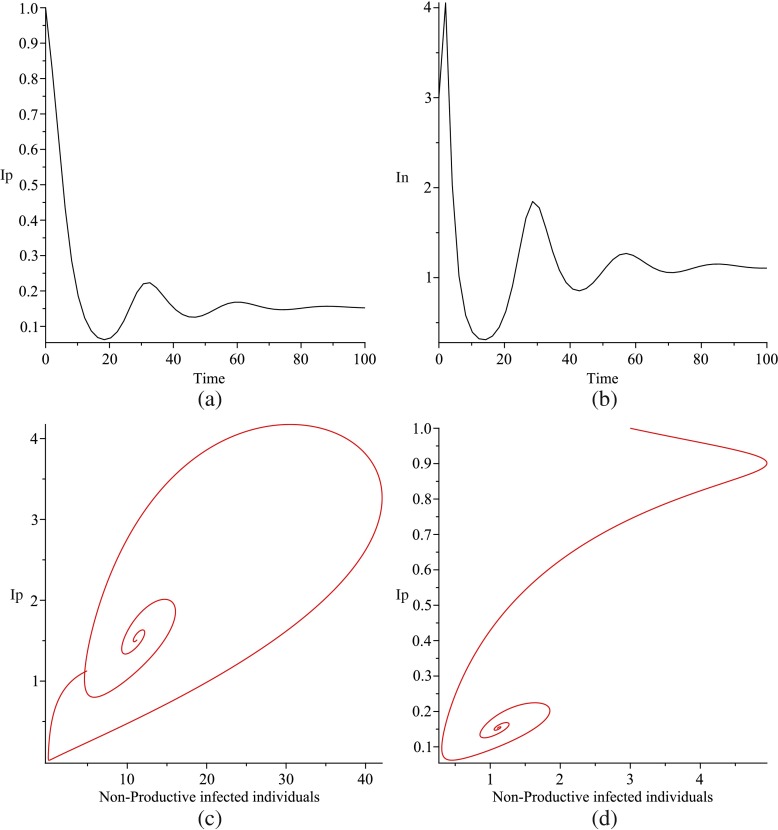
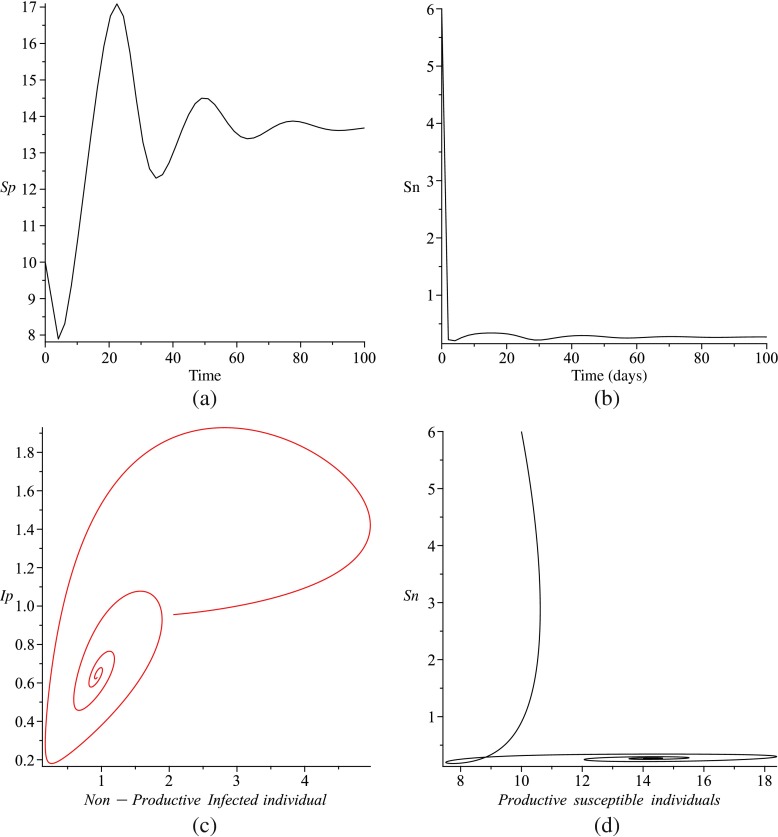
In Fig. 3c, the endemic equilibrium loses its stability and the periodic solutions bifurcate from the endemic equilibrium. This is an explicit example of the existence of a Hopf bifurcation using ρ as a bifurcation parameter and variation of initial values of state variables.

Fig. 3.

Simulations of system (1) for Q = 100, μ = 0.04, π₃ = 0.03, γ = 0.288, ρ = 0.02, σ = 0.04, δ = 0.8, α = 0.81. (a) is the solution of S_p versus time (days) and (b) is S_n versus time t. (c) is the projected I_p − I_n phase plane space and (d) is the projected S_n − S_p phase plane of the phase space

Sensitivity analysis

Due to uncertainties associated with the estimation of certain parameter values, it is useful to investigate how sensitive the basic reproductive number is with respect to its parameters. This will also allow us to identify the parameters that cause the most reduction in R₁ and therefore determine the control measure that is the most effective in controlling the disease. For this, we compute the normalized forward sensitivity index of the reproduction number with respect to these parameters. This index measures the relative change in a variable with respect to relative changes in its parameters (see [20] for the application of this index to a malaria transmission model).

Definition

The normalized forward sensitivity index of a variable, h, that depends differentiably on a parameter, l, is defined as:

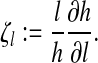The sensitivity index of R₁ with respect to β and Q is equal to 1. For the other parameters, we obtain

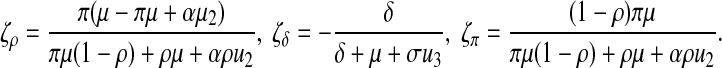As μ, α, γ and σ have complex expressions, we find the sensitivity indices using the parameter values in Table 2 that are always constant (even though their expressions depend on u₂, u₃). Therefore, we calculate the sensitivity indices of π, μ, ρ, α, γ, η, σ, δ. Their values are given in Table 1.

Table 2.

Description of variables and parameters of the HIV/AIDS model (1)

Parameter	Description	Value	Ref
β	Probability of susceptible non-productive contact with infectives	0.344	[12]
μ	Natural mortality unrelated to HIV/AIDS	0.02	[12]
ψ	AIDS-related death	1	[12]
ρ	Modification parameter due to productivity mindset	0.02	[12]
δ	Rate of progression into AIDS	0.1	[12]
σ	Proportion of infected non-productive workers on the HAART treatment	0.002	Assumed
π	Proportion of susceptible non-productive workers recruited	0.002	Assumed
α	Proportion of educated susceptible non-productive workers	0.034	Assumed
η	Modification parameter on infected productive class contact rate	0.4	Assumed
b1	Cost per blood unit screened	$15.30	[27]
b2	Cost per person educated	$12.01, 47.13	[26, 27]
b3	Cost per unit condom	$1.09	[27]
b4	Cost of drug per person reached	$964.83	[27]

Table 1.

Sensitivity indices of R₁

Parameter	Parameter description	Sensitivity index
ρ	Modification parameter	+0.96
δ	Progression to AIDS	−0.82
μ	Mortality rate	−0.38
π	Proportion of non-productive susceptibles recruited	+0.035
u2	Control effort through education	−0.0221
α	Education rate	−0.02215
u3	Control effort on susceptibles	−0.0128
σ	HAART treatment rate	−0.0128
η	Modification parameter on the infected productive	+0.00362
γ	Progression to full-blown AIDS from the infected productive	−0.00329

The interpretation of the sensitivity index values of R₁ given in Table 1 is that an increase/decrease of 1% in any of the parameter values in the first column results in a percentage increase/decrease given by the corresponding value in the third column.

The table above implies that a decrease in the modification parameter due to productivity mindset ρ or an increase in the progression rate to AIDS δ has a positive impact in controlling HIV/AIDS in the community. The parameters are arranged from the most sensitive to the least sensitive, the most sensitive parameters are the transmission and recruitment rates β and Q. Since 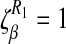, increasing (or decreasing) the transmission probability rate β by 10% increases (or decreases) R₁ by 10%. Similarly, increasing (or decreasing) the recruitment rate, Q, by 10% increases (or decreases) R₁ by 10%. Increasing (or decreasing) the modification parameter rate ρ by 10% increases (or decreases) R₁ by 9.6%. In the same way, increasing (or decreasing) the progression to AIDS rate δ by 10% decreases (or increases) R₁ by 8.1%.

In the next section, we determine the necessary conditions for optimal control of the recruitment regime for effective productivity within the organization by using Pontryagin’s maximum principle.

Analysis of optimal control

We now incorporate time-dependent controls into the model (1) to obtain the following,

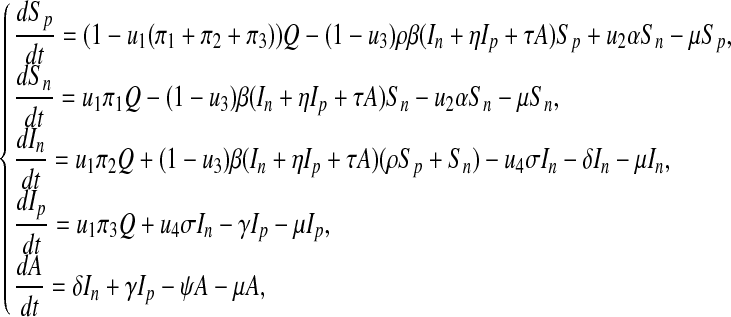12

where u₁, u₂, u₃, u₄ are time-dependent controls. u₁ is the control effort to minimize the recruitment of non-productive and infected individuals (e.g., screening, etc), u₂ is the education/monitoring control on the non-productive susceptible in order to enhance its productivity, u₃ is a preventative control measure on the susceptible from becoming infected with HIV/AIDS and u₄ is the treatment strategy on the non-productive infected individuals.

We investigate the optimal level of effort that would be needed to control the disease and ensure productivity, which is to minimize the number of non-productive susceptibles and infectious individuals and the cost of applying the controls u₁, u₂, u₃ and u₄ over a finite time interval. We achieve this by defining the objective functional J by choosing a quadratic cost on the controls, which is similar to other literature on epidemic controls [3, 15, 17, 18, 21].

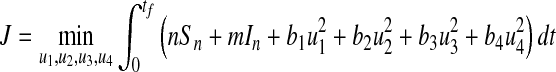13

where n, m, b₁, b₂, b₃, b₄ are positive weights. The term 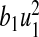is the cost of control efforts on minimizing the recruitment of non-productive and infected individuals, 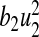is the cost of control efforts on education/monitoring of non-productive susceptibles, 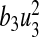is the cost of control efforts on the preventive control on susceptibles and 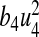is the cost of control efforts on the treatment of non-productive infected individuals. With the given objective function J(u₁, u₂, u₃, u₄), our goal is to minimize the number of susceptible non-productive individuals S_n, while minimizing the cost of controls u₁(t), u₂(t), u₃(t) and u₄(t). We seek an optimal control quadruple and 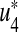such that

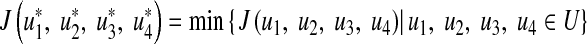14

where U = {(u₁, u₂, u₃, u₄) such that u₁, u₂, u₃, u₄ is measurable with 0 ≤ u_i ≤ 1 and i = 1, 2, 3, 4 for t ∈ [0, t_f ]} is the control set. The necessary conditions that an optimal pair (u^∗, x^∗), where 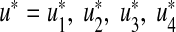and 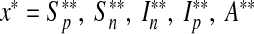, must satisfy come from Pontryagin’s maximum principle [22]. This principle converts (12) and (13) into a problem of minimizing pointwise Hamiltonian H, with respect to u₁, u₂, u₃ and u₄

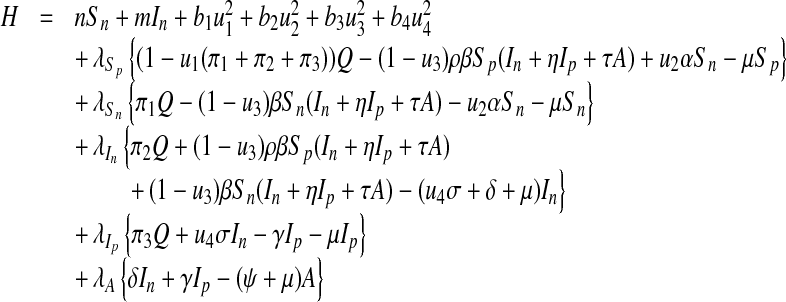15

where 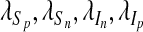and λ_A are the adjoint variables or co-state variables. By applying Pontryagin’s maximum principle [22] and the existence result for the optimal control from [23], we obtain

Proposition 2

For the optimal control quadruples 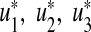and that minimize J(u₁, u₂, u₃, u₄) over U, then there exist adjoint variables 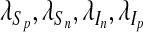, λ_A satisfying

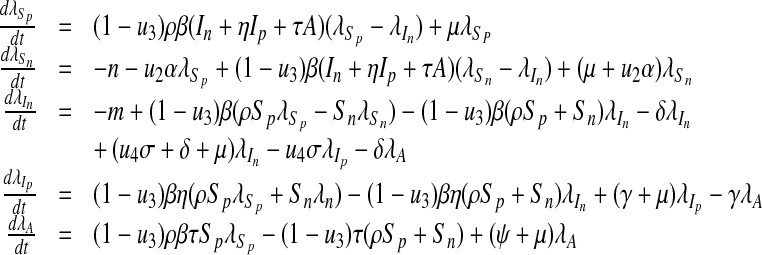16

and with transversality conditions

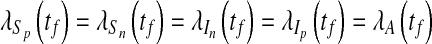17

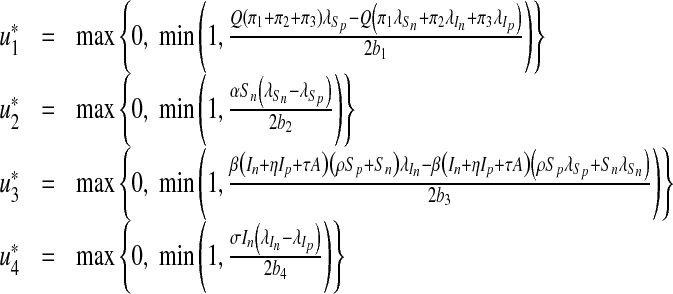18

Proof

From Corollary 4.1, Fleming and Rishel [23] gave the existence of an optimal control due to the convexity of the integrand of J with respect to u₁, u₂, u₃ and u₄, a priori boundedness of the state solutions and the Lipschitz property of the state system with respect to the state variables [23]. The differential equations governing the adjoint variables are obtained by differentiation of the Hamiltonian function evaluated at the optimal control.

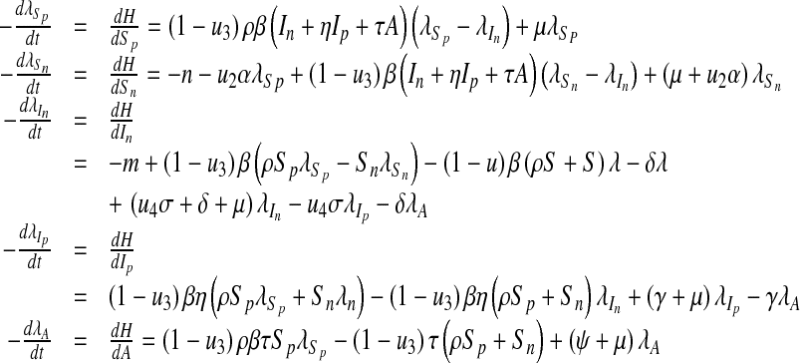19

Furthermore, by equating to zero the derivatives of the Hamiltonian with respect to the controls we obtain (see Lenhart and Workman [24])

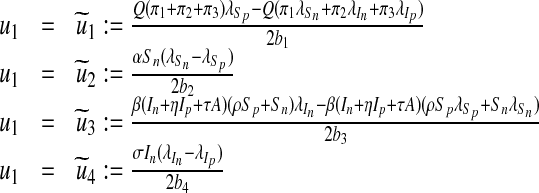20

By standard control arguments involving the bounds on the controls, we conclude

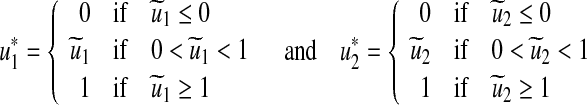21

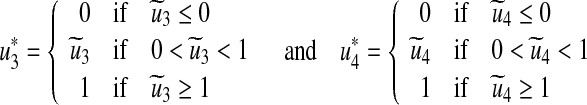22

Due to the a priori boundedness of the state system, the adjoint system and the resulting Lipschitz structure of the ODEs, we obtain the uniqueness of the optimal control for small t_f. The uniqueness of the optimal control follows from the uniqueness of the optimality system that consists in (16) and (17) with characterization (18). There is a restriction on the length of the time interval in order to guarantee the uniqueness of the optimality system.

This smallness restriction on the length of time is due to the opposite time orientations of (16) and (17); the state problem has initial values and the adjoint problem has final values. This restriction is very common in control problems [3, 17, 18, 21].□

Numerical results and discussion

In this section, we examine a deterministic model with non-productive susceptibles and we study numerically the effects of prevention, education, and the HAART treatment on the spread of HIV/AIDS. The optimal control is obtained by solving the optimality system, consisting in the state and adjoint systems. An iterative scheme is used for solving the optimality system. We start to solve the state equations with a guess for the controls over the simulated time using the fourth-order Runge–Kutta scheme. Because of transversality conditions (17), the adjoint equations are solved by a backward fourth-order Runge–Kutta scheme using the current iteration’s solutions of the state equations. Then the controls are updated by using a convex combination of the previous controls and the values from the characterizations (18). This process is repeated and iterations stopped if the values of the unknowns at the previous iterations are very close to the ones at the present iterations [24].

We explore a simple model with screening, prevention, education, and treatment as control measures to study the effects of control practices and transmission of HIV. We use various combinations of the four controls, three controls and two controls at a time. This is done under the following scenarios to compare numerical results.

• Strategy A: Using screening (u₁) and education (u₂) without prevention (u₃ = 0) and no treatment of infectives (u₄ = 0)

• Strategy B: Using screening (u₁) and treatment of infectives (u₄) without education (u₂ = 0) and no prevention (u₃ = 0)

• Strategy C: Using screening (u₁) and prevention (u₃) without education (u₂ = 0) and no treatment of infectives (u₄ = 0)

• Strategy D: Using education (u₂) and prevention (u₃) without screening (u₁ = 0) and no treatment of infectives (u₄ = 0)

• Strategy E: Using education (u₂) and treatment of infectives (u₄) without screening (u₁ = 0) and no prevention (u₃ = 0)

• Strategy F: Using prevention (u₃) and treatment of infectives (u₄) without screening (u₁ = 0) and no education (u₂ = 0)

• Strategy G: Using screening (u₁), education (u₂) and prevention (u₃) with no treatment of infectives (u₄ = 0)

• Strategy H: Using screening (u₁), education (u₂) and treatment of infectives (u₄) with no prevention (u₃ = 0)

• Strategy I: Using screening (u₁), prevention (u₃) and treatment of infectives (u₄) with no education (u₂ = 0)

• Strategy J: Using education (u₂), prevention (u₃) and treatment of infectives (u₄) with no screening (u₁ = 0)

• Strategy K: Using all four control measures (u₁, u₂, u₃ and u₄)

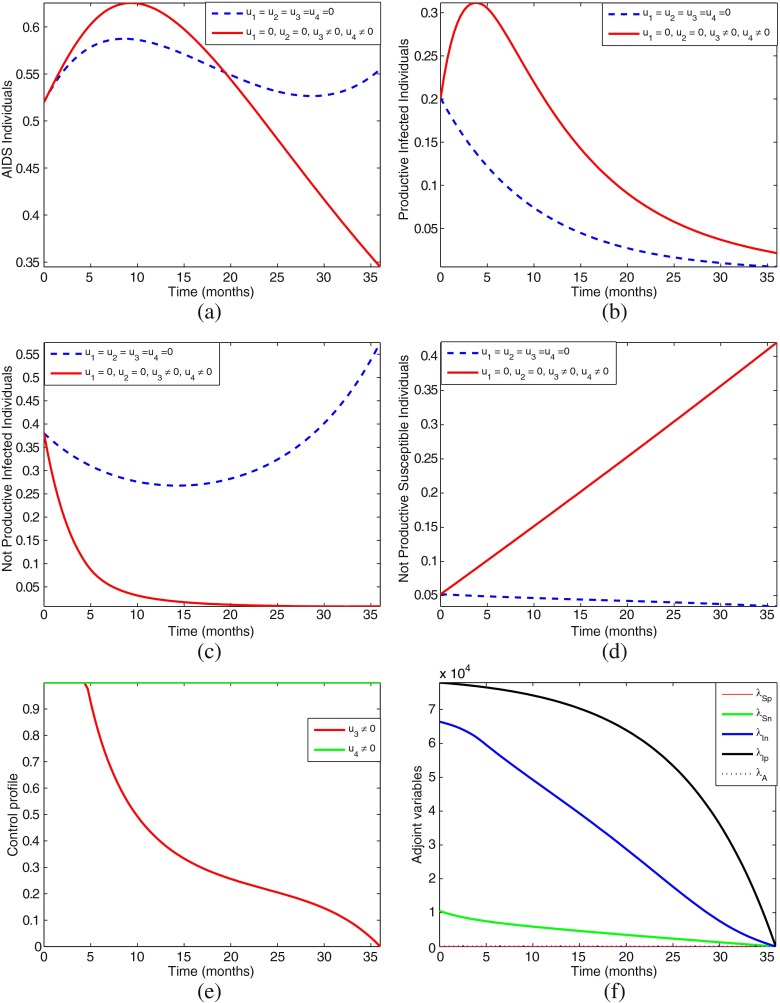
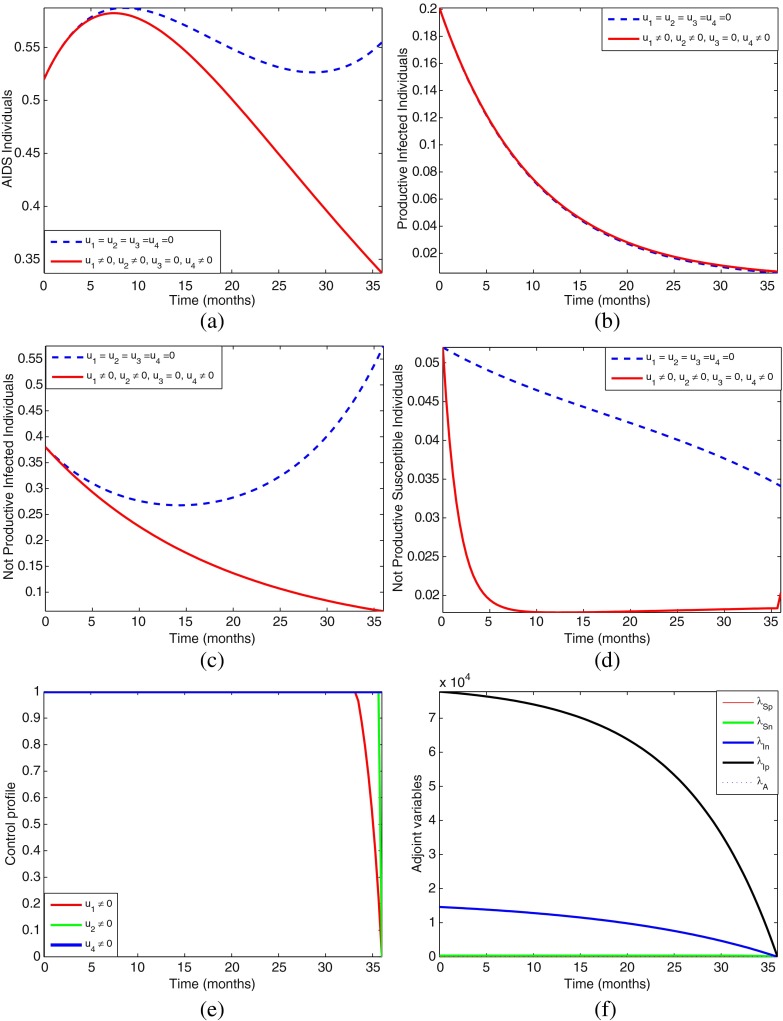
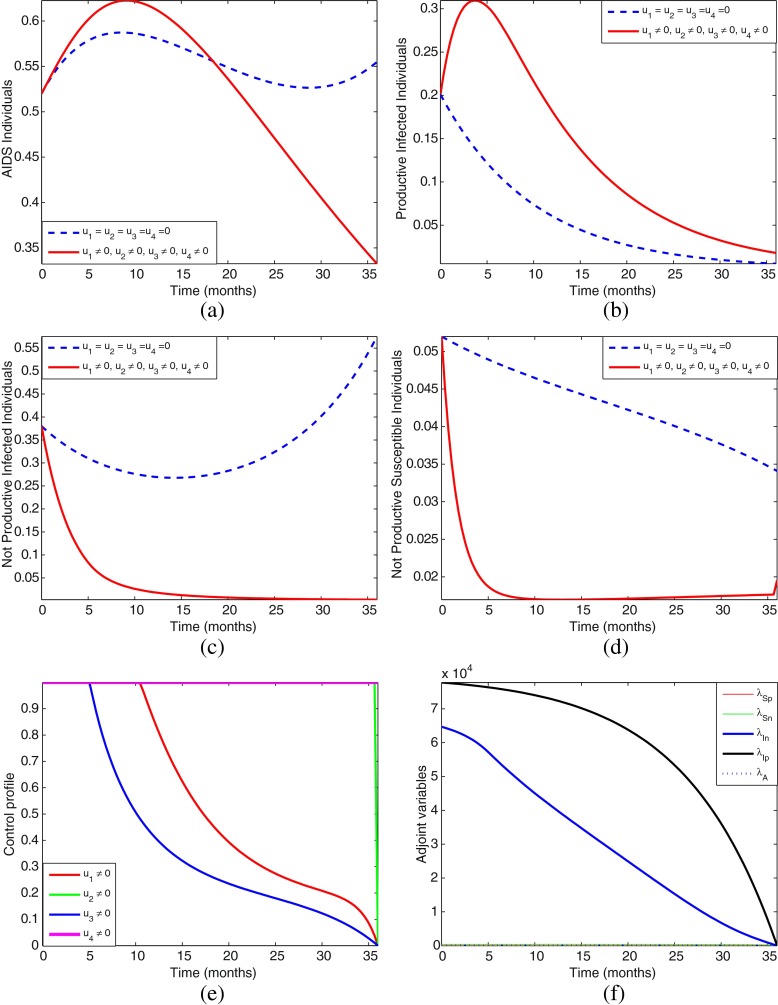
However, because of space, we shall only present numerical simulations for the four most effective strategies, that is, strategies D, F, H, and K.

• Strategy D: Using education (u₂) and prevention (u₃) without screening (u₁ = 0) and no treatment of infectives (u₄ = 0)

• Strategy F: Using prevention (u₃) and treatment of infectives (u₄) without screening (u₁ = 0) and no education (u₂ = 0)

• Strategy H: Using screening (u₁), education (u₂) and treatment of infectives (u₄) with no prevention (u₃ = 0)

• Strategy K: Using all four control measures (u₁, u₂, u₃ and u₄)

From the numerical simulations, Figs. 4, 5, 6, and 7, we can see that one cannot easily conclude which control strategy gives optimal results. Most of the strategies produce almost a similar pattern and effects, therefore we need to further ascertain which of these four most effective strategies is the most cost-effective and efficient. In the next section, we carry out the cost-effectiveness analysis.

Fig. 4.

Simulations of the model showing the effect of control strategy D on HIV/AIDS transmission. The control profile suggests control u₂ to be at the upper bound for 36 months before dropping gradually to the lower bound, while control u₃ to be at the upper bound for just 5 months before dropping gradually to the lower bound

Fig. 5.

Simulations of the model showing the effect of control strategy F on HIV/AIDS transmission. The control profile suggests control u₃ be at the upper bound for just 4 months before dropping gradually to the lower bound and control u₄ to be maintained at the upper bound throughout the intervention period

Fig. 6.

Simulations of the model showing the effect of control strategy H on HIV/AIDS transmission. The control profile suggests control u₁ and u₂ to be at the upper bound for 33 months and 36 months before dropping gradually to the lower bound, respectively, while control u₄ to be maintained at the upper bound throughout the intervention period

Fig. 7.

Simulations of the model showing the effect of control strategy K on HIV/AIDS transmission. The control profile suggests control u₁ and u₂ to be at the upper bound for 11 months and 36 months before dropping gradually to the lower bound, respectively, while control u₃ to be at the upper bound for just 5 months before dropping gradually to the lower bound and control u₄ to be maintained at the upper bound throughout the intervention period

Cost-effectiveness analysis

To quantify the cost-effectiveness of the control measures, we examine the cost-effectiveness ratio of the strategies so that we can draw our conclusions. There are three types of cost-effectiveness ratios: (1) Average Cost-Effectiveness Ratio (ACER), which deals with a single intervention and evaluates that intervention against its baseline option (e.g., no intervention or current practice). It is calculated by dividing the net cost of the intervention by the total number of health outcomes prevented by the intervention. (2) Marginal Cost-Effectiveness Ratio (MCER) for the assessment of the specific changes in cost and effect when a program is expanded or contracted. (3) Incremental Cost-Effectiveness Ratio (ICER) used to compare the differences between the costs and health outcomes of two alternative intervention strategies that compete for the same resources and is generally described as the additional cost per additional health outcome (see [25]).

We assume that the costs of the controls are directly proportional to the number of controls deployed. This assumption is based on the understanding that the primary goal of providing preventive measures, education programs, and treatment of infective individuals is to reduce infection.

We calculated the total number of infections averted by estimating the difference between the total infectious individuals without control and the total infectious individuals with control. We used the parameter values in Table 2. The total cost in ($) USD is calculated by estimating the cost of controls 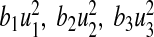and 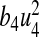over time, respectively.

For the purpose of our study, we consider the incremental cost-effectiveness ratio (ICER). It allows us to compare the cost-effectiveness of the combination of at least two of the control strategies, screening, prevention, education, and treatment of infective individuals. In ICER, when comparing two competing intervention strategies incrementally, one intervention should be compared with the next-less-effective alternative. The ICER numerator includes the differences in intervention costs, averted disease costs, costs of prevented cases, and averted productivity losses if applicable. The ICER’s denominator is the difference in health outcomes (e.g., total number of infection averted, number of susceptibility cases prevented).

Based on the model simulation results, we rank the strategies in order of increasing effectiveness

Strategies	Total infections averted	Total costs ($)	ICER
No strategy	0	0	–
Strategy H	22.328	$242070	10841.544
Strategy F	23.856	$57468	−120812.83

The ICER is calculated as follows:

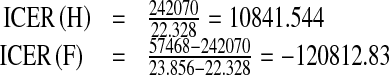The comparison between strategies H and F shows a cost savings of $120812.83 for strategy F over strategy H. The negative ICER for strategy F indicates that strategy H is more costly and less effective than strategy F. Therefore, strategy H is excluded from the set of alternatives so it does not consume limited resources.

We recalculate the ICER

Strategies	Total infections averted	Total costs ($)	ICER
Strategy F	23.856	$57468	2408.95
Strategy K	24.522	$17339	− 59804.77

The comparison between strategies F and K shows a cost savings of $59804.77 for strategy K over strategy F. Similarly, the high ICER for strategy F indicates that strategy F is more costly and less effective than strategy K. Therefore, strategy F is excluded from the set of alternatives so it does not consume limited resources.

We recalculate the ICER

Strategies	Total infections averted	Total costs ($)	ICER
Strategy K	24.527	$17339	706.935
Strategy D	24.972	$16266	− 2411.236

The comparison between strategies K and D shows a cost savings of $2411.236 for strategy D over strategy K. Similarly, the high ICER for strategy K indicates that it is more costly and less effective than strategy D. Therefore, strategy K is excluded from the set of alternatives so it does not consume limited resources.

With this result, we conclude that strategy D (combination of education and preventive measures) has the least ICER and therefore is the more cost-effective strategy.

Conclusions

In this paper, we derived and analyzed a deterministic model for the transmission of the HIV/AIDS disease to examine the recruitment effect of the following, non-productive susceptible individuals, non-productive infected individuals, productive susceptible individuals, and productive infected individuals into an organizational workforce. We carried out a stability analysis of the equilibrium and the model was found to exhibit backward and Hopf bifurcations under different scenarios. Furthermore, we also performed an optimal control analysis of the model. Using Pontryagin’s maximum principle we derived and analyzed the conditions for optimal control of the disease with an effective HAART and ABC treatment regime and education of non-productive susceptible and infectious individuals. The results also suggest that the effective recruitment strategy, education/monitoring of employees to ensure productivity, has a significant impact in reducing the non-productivity of an infected employee (labor force) in the presence of HIV/AIDS. From the cost-effectiveness analysis, the results suggest that it is not cost-effective to screen applicants for HIV infection during recruitment and that the effective education/monitoring of employees and adherence to preventive measures against infection is the most cost-effective strategy to combat the spread of HIV/AIDS.