Anomalies in the motion dynamics of long-flagella mutants of Chlamydomonas reinhardtii

Abstract

Chlamydomonas reinhardtii has long been used as a model organism in studies of cell motility and flagellar dynamics. The motility of the well-conserved ‘9+2’ axoneme in its flagella remains a subject of immense curiosity. Using high-speed videography and morphological analyses, we have characterized long-flagella mutants (lf1, lf2-1, lf2-5, lf3-2, and lf4) of C. reinhardtii for biophysical parameters such as swimming velocities, waveforms, beat frequencies, and swimming trajectories. These mutants are aberrant in proteins involved in the regulation of flagellar length and bring about a phenotypic increase in this length. Our results reveal that the flagellar beat frequency and swimming velocity are negatively correlated with the length of the flagella. When compared to the wild-type, any increase in the flagellar length reduces both the swimming velocities (by 26–57%) and beat frequencies (by 8–16%). We demonstrate that with no apparent aberrations/ultrastructural deformities in the mutant axonemes, it is this increased length that has a critical role to play in the motion dynamics of C. reinhardtii cells, and, provided there are no significant changes in their flagellar proteome, any increase in this length compromises the swimming velocity either by reduction of the beat frequency or by an alteration in the waveform of the flagella.

Electronic supplementary material The online version of this article (doi:10.1007/s10867-012-9282-8) contains supplementary material, which is available to authorized users.

Introduction

Eukaryotic flagella and cilia have a conserved ‘9+2’ axoneme and they constitute propulsion units that are essential for motility, sensory perception, and development [1]. The axoneme comprises a cyclical arrangement of nine microtubule doublets (A and B) and a central pair of microtubules connected by a radial spoke scaffold consisting of the head and the stalk. Motors (dyneins) are present on the inner and outer surface of the A tubule. During motion, a typical C. reinhardtii axoneme exhibits repetitive bends, each with an emergence and propagation component. The actual motion starts from an inherent propulsive force that brings about an activation of the chemo-mechanical dynein arms that convert chemical energy to mechanical energy and thereby causes the microtubules in the doublet to slide along each other’s length [2]. Such sliding is converted into bending by the restraining action of an anchored structure present in the basal bodies and nexin links [3–5]. Highly coordinated flagellar action gives rise to waveforms with beat frequencies of 60–80 Hz. While microtubule sliding and bending are well documented, insights into the physics that governs repetitive bending remain elusive. Current understanding relies on one of the following viewpoints: the ‘switch-point’ mechanism, curvature control, the central pair/spoke axis hypothesis, dyneins acting as oscillators to co-ordinate movement [6], systems involving motors and springs [7], or the geometric clutch model [8].

Several flagellar mutants have been isolated that have contributed significantly towards the understanding of the function of axonemes. To gain insights into the ‘breast-stroke’ motility [1, 9–11], mutants in the radial spokes [10], the central pair microtubules [12], dynein arms [8, 13–16], striated fibers [17], basal bodies [18–20], and a battery of these [21] have been useful. Two types of dynein arm mutants have been used to show that the outer dynein arms provide power to the flagellar beat while the inner arm dyneins are essential for normal motility [13, 14]. Correlating molecular aberrations in the axoneme to the biophysics that governs motility requires quantification of axonemal motility in terms of parameters such as swimming velocity, flagellar beat frequency, wave amplitude, and bend angles of the waves in a number of cells and axonemes. Aberrations in the flagella (with proteins missing from the central pair of microtubules, radial spokes and dynein arms) have led us to believe that several proteins play a vital role in the flagellar motion dynamics and show that this micromachine operates as a gear [21].

In this study, we probe how flagellar length affects the motion dynamics of C. reinhardtii cells, specifically the swimming velocity, beat frequency, waveform, and swimming trajectory, since it is of significance to question how motility would be affected if the number of force-generators were increased. The answer is not intuitive because by increasing flagellar length one increases the number of dyneins that are present in the organelles but, at the same time, it may be that longer flagella experience higher viscous drag and a difference in bending moments along the length. Chlamydomonas reinhardtii flagella have two distinct waveforms: an asymmetrical, cilia-like, forward breast-stroke and a symmetrical, flagellar, reverse-swimming one. In the present study, we focus on probing the forward motion. Long flagellated cells exhibit reduced beat frequencies, aberrant waveforms, and meandering swimming trajectories. We demonstrate that it is this increased length that has a critical role to play in the motion dynamics of C. reinhardtii cells.

Results and discussion

Flagellar lengths, swimming velocities, and beat frequencies

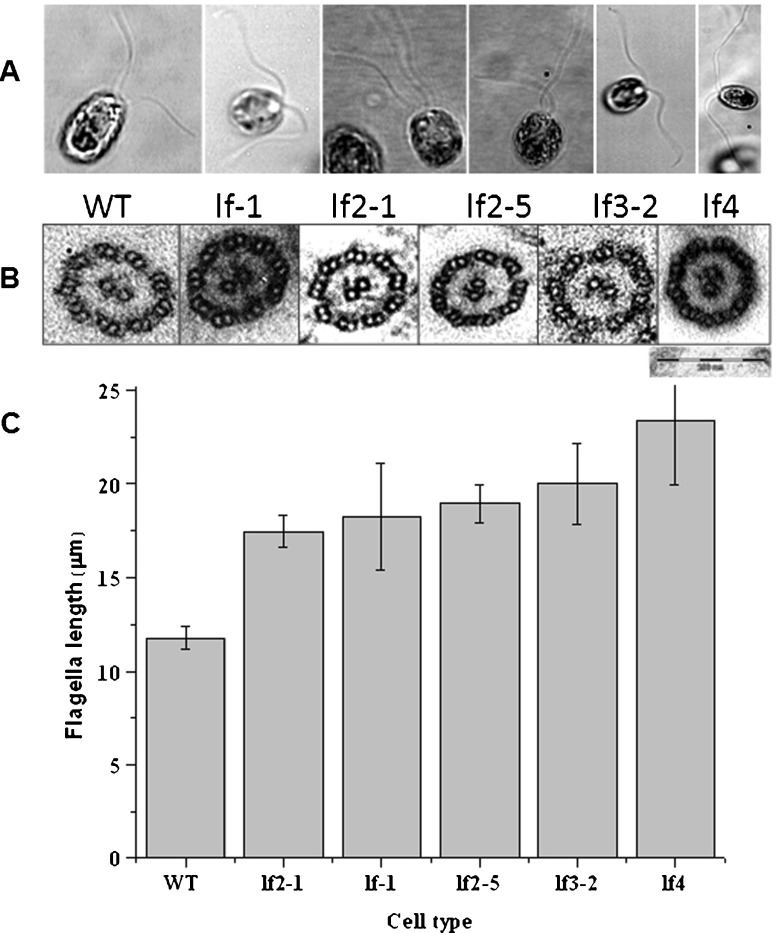
Our observations of a large number of live, swimming C. reinhardtii wild-type (WT, CC-125) cells enable us to summarize the following facets of cell motility: each cell swims in a breast-stroke fashion; the swimming trajectory is helical; most cells tend to beat with a synchronous breast-stroke, as previously reported [9]; each flagellum waveform exhibits a specific amplitude and bend angle; and each flagellum bend originates near the cell body and then propagates along the flagellum. We probe how increasing the number of dynein arms affects flagellar dynamics. We have used long-flagella mutants (Table 1 and Fig. 1a) that are aberrant in a single protein to measure swimming velocities, beat frequencies, and waveforms. The flagellar-length measurements yielded values that are consistent with those reported earlier [22–28]. The ultrastructural details of these mutants do not show any apparent aberration in the axonemes (Fig. 1b; viewed at 50,000× using a TEM) as compared to the WT.

Table 1.

Flagellar-length mutants used in the current study with the relevant information as cited in literature

Cell type	Allele	Protein (kDa)	Phenotype	Flagella length (μm)	Reference
WT	–	–	Normal length flagella	10 to 12	[29]
CC-802	lf1-1	88	Flagella 3× WT	Never exceeds 32	[27]
			Re-grows very slowly after amputation
			Novel protein - Glycine-rich
CC-803	lf2-1	38	Unequal length flagella and do not regenerate their flagella. Results in a truncated protein product (Cyclin-dependent PK)	18 to 22	[26, 28]
CC-2287	lf2-5	26	Retains partial functions, hypomorphic, regenerates with normal kinetics	17 ± 2.2	[28]
CC-3662	lf3-2	133	Flagella 1.5–2×, <15% of the population with stumpy flagella, 30–80% with long flagella; novel protein (contains an amber mutation, truncated product)	19 to 24	[28]
lf4	lf4	63	Null mutants of lf4 show almost two-fold increase in the lengths of the flagella; gene encodes a MAPK	23 to 28	Gift from P. A. Lefebvre [25]

Fig. 1.

A Images of WT and long-flagella mutants depicting differences in flagellar length. B TEM of axonemes from WT and long-flagella mutants, magnification 50,000×, Bar = 200 nm. C Flagellar length (in μm) of WT and long-flagella mutant cells. Cells were stained with iodine (see text) to enhance contrast and facilitate measurement

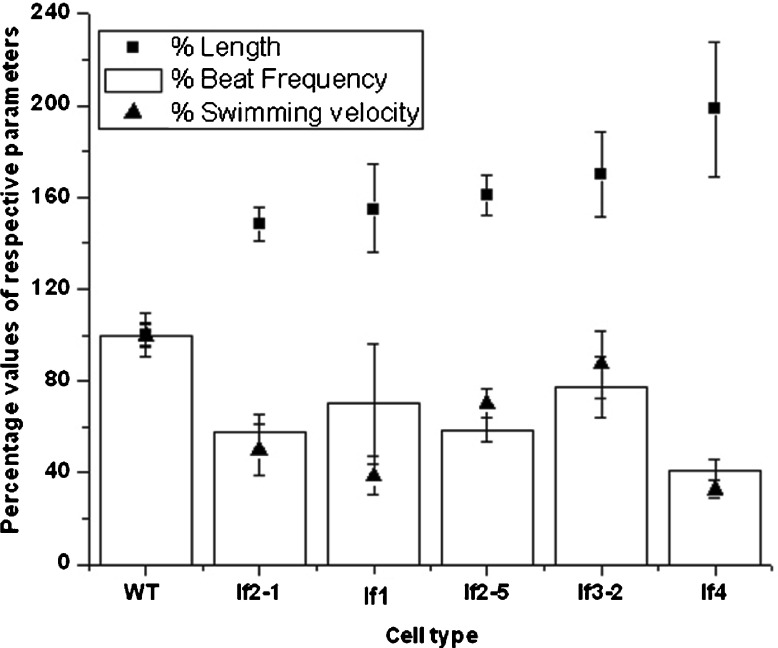
Swimming velocities and beat frequencies were determined from videographs and were statistically verified (Table 2; Fig. 2). The beat frequencies and swimming velocities vary with cell type, with the WT showing the highest values. The swimming velocity of lf3-2 was closest to that of the WT (87% that of average WT velocity). The next closest to the WT was lf2-5; its swimming velocity was 70% that of the WT. lf2-1, an allele of lf2-5, on the other hand, swam 50% slower than the WT, possibly because lf2-5 is a hypomorphic mutant and is known to retain partial function when compared to lf2-1. Both the alleles show identical beat frequencies and ~9% difference in their flagellar lengths (average ~18 μm) while swimming velocities differed by ~29%. The swimming velocity of lf1 was ~39% that of the WT; lf4 swam the slowest (33% of the WT).

Table 2.

Mean (standard deviation) values for flagella length, beat frequency, and swimming velocity against cell type

Cell types	Final length	Beat frequency (Hz)	Swimming velocity (μm/s)
CC 125WT	11.8 (0.6)	62.0 (2.7)	156.5 (14.6)
lf 1	18.7 (2.3)	43.6 (16.5)	60.8 (13.3)
lf2-1	17.5 (0.8)	36.1 (4.5)	78.3 (17.9)
lf2-5	19.0 (1.0)	36.4 (3.3)	110.2 (10.2)
lf3-2	20.0 (2.2)	48.1 (8.2)	136.8 (22.9)
lf4	23.4 (2.8)	25.7 (2.8)	51.3 (6.0)

Fig. 2.

Flagellar length (μm), swimming velocities (μm/s), and beat frequencies (Hz) of WT and mutant cells. The various values for the WT were fixed at 100% and the values for the mutants were calculated as a percentage of the WT

Prior to one-way analysis of variance (ANOVA), the data sets for beat frequency and swimming velocity underwent outlier analyses and tests for violation of normality assumptions. Some observations were found to be outliers and were removed both from the swimming velocity and beat frequency data sets. Further, a logarithmic transformation was made on the beat-frequency data set so that normality assumptions were satisfied. The one-way analysis of variance results, indicated that, the effect of cell type on beat frequency (F = 38778, df = 6, 129, p < 0.0001) and swimming velocity (F = 982.4, df = 6, 90, p < 0.0001) were significant. To examine differences among cell types, each mutant was compared with the WT separately for beat frequency and swimming velocity. For both variables, there were significant differences between the mutants and WT (Table 3). Simple regression results showed that the effect of flagellar length on the logarithm of the beat frequency is statistically significant (F = 145.4, df = 1, 124, p < 0.0001).

Table 3.

Pair-wise comparisons for wild-type against each cell type for beat frequency and swimming velocity

Variable	Pair-wise comparisons	99.50% Confidence interval for difference in means
Beat frequency	WT vs. lf 1	0.013 to 0.218*
	WT vs. lf2-1	0.457 to 0.595*
	WT vs. lf2-5	0.449 to 0.582*
	WT vs. lf3-2	0.171 to 0.325*
	WT vs. lf4	0.819 to 0.953*
Swimming velocity	WT vs. lf 1	83.583 to 107.841*
	WT vs. lf2-1	65.056 to 91.287*
	WT vs. lf2-5	34.402 to 58.233*
	WT vs. lf3-2	5.295 to 34.073*
	WT vs. lf4	93.616 to 116.783*

*Significant at the Bonferroni significance level of 0.005

From the regression equation in Table 4, we see that the beat frequency decreases by 0.056 units for every one unit increase in flagellar length. The correlation coefficient between beat frequency and flagellar length is − 0.73. Similarly, from the regression results for swimming velocity, we see that the effect of flagellar length on swimming velocity is statistically significant (F = 79.445, df = 1, 94, p < 0.0001). The regression equation in Table 4 shows that the swimming velocity of these mutants decreases by 6.64 units for every one unit increase in flagellar length. Flagellar length and swimming velocity are negatively correlated with a coefficient of − 0.68. Using the two fitted regression equations in Table 4, we compute the percentage changes in the beat frequency and swimming velocity when comparing each cell type with the WT with respect to flagellar length (see Table 5). The mean flagellar length for each cell type from Table 2 is used to compute the percentage changes. We observe from Table 5 that, an increase in flagellar length reduces the swimming velocities (between 26 and 57%) as well as the beat frequencies (8–16%) of the mutant cells. Assuming that longer flagella imply a larger number of dynein arms, the inference from our results is that, an increase in the force-generating molecules does not lead to a proportional increase of swimming speed.

Table 4.

Fitted regression models of the form y=a+bx, for the relationship between beat frequency and flagella length, and between swimming velocity and flagella length

Model	Regression equation	p value	R2
Beat frequency (beatfreq) vs. flagella length (fl)	Log (Beatfreq) = 4.708–0.056 fl	<0.0001	53.6%
Swimming velocity (swimvel) vs. flagella length (fl)	Swimvel = 214.231–6.641 fl	<0.0001	45.8%

Table 5.

Percentage change in beat frequency and swimming velocity while comparing each cell type to the wild-type with respect to flagella length. The percentage changes were obtained using the regression equations (Table 4) and the mean flagella length (Table 2) for each cell type

Wild-type vs. mutant	Percentage change in beat frequency	Percentage change in swimming velocity
WT vs. lf 1	9.5	35.7
WT vs. lf2-1	7.8	26.1
WT vs. lf2-5	9.9	34.6
WT vs. lf3-2	11.2	33.2
WT vs. lf4	16.0	56.6

Flagellar mutants of C. reinhardtii exhibit zero or reduced swimming velocities [10, 17, 27–32] and from recent work [21, and references therein], it appears established that reduction in swimming velocity may be attributed to the reduced beat frequencies and alteration in waveform. Our observations with the two alleles of lf2 (viz. lf2-1 and lf2-5) are noteworthy; with ~9% difference in their flagellar lengths, they have almost equal beat frequencies but a 29% difference in their swimming velocities. Measured beat frequencies for mutants were always less than those for the WT; the least values were for lf4 and the highest (closest to the WT frequency) was for the lf3-2 mutant. We note that lf4 possesses the longest flagella, it has the lowest beat frequency and its swimming velocity is ~33% that of the WT. Table 5 shows the percentage changes in beat frequency and swimming velocity, where the comparison is with respect to the WT cells. It is clear that an increase in flagellar length reduces swimming velocities (by 26–57%) as well as beat frequencies (by 8–16%) for all mutants.

Comparing waveforms of long-flagella mutants with the wild-type

We recorded flagellar waveform patterns to observe the correlation of beat frequency to beat symmetry/asymmetry. Montages generated from high-speed videographs are shown in Fig. 3 such that the montage for each cell type corresponds to one complete beat cycle. The first and last image slices of each cell type depict the same flagellar position; the time gap between two successive slices of a montage was kept constant. As expected, wild-type cells exhibited typical waveforms [16] where both moving flagella were in the same plane and the angle of motion remained unchanged. Also, the origin and propagation of the flagellar bends were as expected (Fig. 3a). For lf3-2 mutants, the power and recovery strokes followed a pattern identical to the WT and the cell angle did not change with motion. Nonetheless, the time taken to complete one beat cycle was 10–15% longer than for the WT (Fig. 3e). Interestingly, it was only in this mutant that the flagella exhibited two troughs and two crests. Although the waveform of lf2-5 appeared similar to the WT, the major qualitative differences observed were as follows: (i) an asynchrony between the two flagella, while one showed a forward stroke, the other did not appear to make any significant movement; (ii) the flagellum that took the first forward stroke formed a ‘knot-like’ structure (see arrow in Fig. 3d), which gave rise to a propulsive force for the next flagellum to move and also assume a ‘knot-like’ geometry. Such a ‘two-knotted’ structure was observed in ~90% of these mutant cells. The mutant lf2-1, an allele of lf2-5, exhibited a similar beat frequency and followed almost a similar waveform as that of lf2-5 but did not form the ‘knot-like’ structure. However, it showed asynchronous tumbling in the beats of the two flagella (Fig. 3c). Along the same lines, lf4 cells also tumbled, the flagella beat asynchronously and their waveforms were very different form those of the WT (Fig. 3f). The lf1 mutant also exhibited a strange waveform: it formed knots and the flagella beat one at a time (see arrow, Fig. 3b) and these cells changed their angle of movement with each flagellar beat. While we are unable to decipher the precise origin of the knot-forming phenomena, we think that the knot-like loops, which subtend very large angles and appear longer than normal bends, seem to have an aberrant coordination between bending at their distal end and unbending at their proximal end. Such cells tumbled at times and the expected waveform was not achieved. The lf4 mutants tumbled with every beat, stuck to the cover-slip more often than other cells and their flagella beat asynchronously. Some cells also displayed a flutter-kick motion (see Supplementary videos). The lf2-1 flagella did not complete a waveform, flutter kicking was observed in a few cells and their flagella beat very asynchronously. In the lf3-2 mutant, an asymmetric beating was observed but there was no flutter-kick motion; about 5% of such cells self-rotated. The lf2-5 mutant also showed asymmetric beating but the waveform was usually completed. The flagella exhibited the flutter-kick motion and bent to form characteristic loops (as in lf2-1 and lf1 mutants). An observation common to both the alleles of lf2 (lf2-1 and lf2-5) was that the flagella had a higher propensity of adhering to the cover-slip and were so delicate as to break upon gentle shearing.

Fig. 3.

Waveforms of WT and long-flagella mutants. Real-time movies were used to generate montages for all the cell types; each montage corresponds to one complete flagella-beat cycle. The time-stamps are provided on each slice of a montage. The arrows indicate a ‘knot-like’ structure. (A = WT; B = lf1; C = lf2-1; D = lf2-5; E = lf3-2; F = lf4)

The observed differences in the lf1 and lf4 waveforms indicate that the two flagella are differentially controlled. It is a known fact now that C. reinhardtii flagella show asymmetry in the molecular arrangement of the proteins binding to the nine microtubule doublets [33]. Since the eight inner-arm dynein heavy chains regulate and determine flagellar waveform, we believe that these are intact and functional in lf3-2, lf2-5 and lf2-1 but may have some biochemical defect in lf1 and lf4.

Comparing motion trajectories of long-flagella mutants with the wild-type

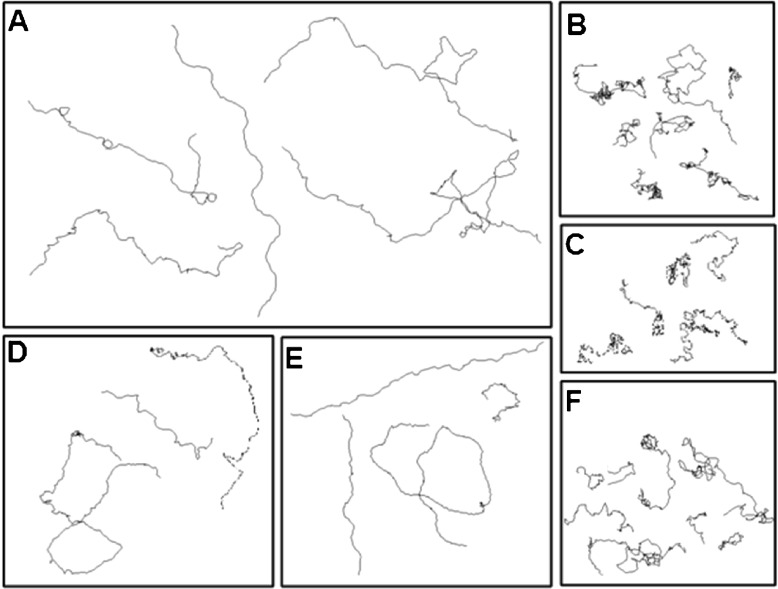
We tracked the swim paths of WT and mutant cells and typical results are shown in Fig. 4. Wild-type cells demonstrated the standard, wavy and helical-type paths with loop formation [34]. For lf2-5 and lf3-2, swim paths and waveforms were closest to those of WT, with swimming velocities being 70% and 88%, respectively, of the WT. On the other hand, cells tumbled while swimming in cases where the flagella beat asynchronously (lf1, lf2-1, and lf4); moreover, the waveforms exhibited knot-like structures and swimming velocities were 39%, 50%, and 33%, respectively, of WT. They all showed irregular swim paths with reference to (i) the distance traveled, (ii) the number of turns taken, and (iii) the helicity of the motion. Such swim paths did not result in significant forward motion although there was considerable random motion (Fig. 4b, c, f).

Fig. 4.

Trajectory analyses of WT and the long-flagella mutants. Real-time movie clips of translationally moving cells were captured and converted to individual frames. The motion of each cell was considered as a ‘trajectory’, and its movement was traced using TRACKER software. (A = WT; B = lf1; C = lf2-1; D = lf2-5; E = lf3-2; F = lf4)

The speed of a motile cell is essentially a balance between the propulsive force generated by its flagellum, a reflection of the flexural rigidity, and the drag from the surrounding fluid. Distances moved by individual cells were deduced from the ratio of swimming velocities to beat frequencies. Compared to WT (2.52 μm), distances traveled per beat were larger in the case of lf2-5 (3.03 μm), lf3-2 (2.84 μm), and lf4 (2.00 μm) and less in the case of lf1 (1.39 μm) and lf2-1 (2.17 μm). This indicates that lf2-5, lf3-2, and lf4 mutants generate a higher propulsive force compared to WT, lf2-1 and lf1, and that more of the flagellar energy goes into rotation of the cell body in the cells in Fig. 4b, c & f, while less energy goes into forward propulsion. Whether this is a function of the flagellar length is unclear.

Materials and methods

Materials

All chemicals used were of analytical grade and obtained from Amresco International, USA, Sisco Research Laboratories, India, and Qualigens, India. Chlamydomonas reinhardtii WT and mutant strains were obtained from ‘The Chlamydomonas Stock Center’ (http://www.chlamy.org) and maintained by regular transfers in TAP medium (both solid and liquid conditions). Table 1 summarizes the mutants and their phenotype. lf4 was a kind gift from Paul Lefebvre, University of Minnesota, USA.

Cell culture conditions and sample preparation

Cells (WT and mutants) were grown and maintained following procedures that have been described earlier [21, 35, 36]. Each experiment lasted 10–15 min wherein several real-time movie clips were recorded over a field of view that typically contained 9–25 motile cells.

Axoneme preparation for TEM

Wild-type or mutant cells were grown to a density of 5 ×10⁶/ml and flagella and axonemes were prepared as per Witman [37]. In brief, cells were washed in 10 mM HEPES (pH 7.4), re-suspended in HMDS (4% sucrose) and deflagellated using 50 mM dibucaine. After observation of deflagellation, ice-cold HMDS (4% sucrose) with 2 mM PMSF and 2 mM EGTA were added. Cells were spun at 1,800 g and underlaid with HMDS (25% sucrose). Supernatant with flagella was collected and spun at full speed, re-suspended in HMDEK, and an equal volume of 1% NP-40 (Loba Chemicals, India) in HMDEK was added. Axonemes were pelleted down at full speed and washed with HMDEK to remove residual detergent. The axonemes were fixed o/n in 1% glutaraldehyde in a 100 mM cacodylate buffer (pH 7.4) at 4 °C, followed by washing twice in a cacodylate buffer and treated with 1% OsO₄ for 1 h at RT, dehydrated in an ethanol gradient and treated with 1% uranyl acetate for 1 h. Samples were then processed through an Araldite gradient and finally embedded in Araldite. Thin sections of 70 nm were cut on a Leica EM UC7 ultramicrotome, mounted on grids and observed on a Carl Zeiss Libra 120 TEM.

Flagellar length measurements

C. reinhardtii WT and mutant cells were stained for viewing the flagella. One part of Lugol’s iodine (6% potassium iodide and 4% iodine crystals) was added to three parts of cell suspension and observed under 100× magnification. Images of fixed C. reinhardtii cells with stained flagella were captured using a Nikon 90i microscope. Flagellar lengths were measured from these images using ImageJ software.

Measuring the swimming velocity

10 μl of cells were loaded onto a glass cover slip and observed under a 10× objective, affording a large field of view (295.6 ×270.7 μm). Each video was converted to individual frames and the distance covered by a given cell was analyzed using image processing software. A red filter helped avoid any complications that would arise due to phototaxis. Self-rotating cells and those that were stuck to the cover-slips were avoided in all the quantifications.

Beat frequency measurements

10 μl of cells were loaded onto a cover-slip and observed under a 100× oil-immersion objective. Real-time movies were recorded using a high-speed (700-Hz frame rate) camera that enabled direct determination of flagellar beat frequencies of live, free-swimming cells in TAP medium at room temperature (23–24 °C). For each of the 20 cells analyzed from both groups, the mean was determined from five individually calculated frequencies. The camera used was a PCO Dimax (Germany) with a resolution of 1104 ×1104 pixels.

Flagellar tracings for the waveform patterns

Real-time movie clips were used to generate montages for all the cell types; each montage in turn corresponded to one complete beat cycle. The time intervals between each slice of the montage were as follows: WT (1.19 ms), lf1 (1.19 ms), lf2-1 (1.85 ms), lf2-5 (3.39 ms), lf3-2 (1.19 ms), lf4 (3.03 ms).

Statistical analysis of data

Descriptive statistics were computed for variables such as flagellar length, beat frequency, and swimming velocity and corresponding box plots were studied. One-way analysis of variance (ANOVA) was used to study the effect of cell types on the beat frequency and swimming velocity. If the main effect of the cell type was found to be statistically significant, it was followed by pair-wise comparisons to determine the difference between the cell types. Two separate simple linear regression models of the form y = a + bx were fitted to study the relationship of flagellar length with beat frequency and swimming velocity. The variable x was the flagellar length in our study, while the parameters a and b are the intercept and slope of the fitted line, respectively. Based on the fitted regression models, percentage changes in beat frequency and swimming velocity were computed for a given increase in flagellar length. Pair-wise associations between flagellar length and beat frequency and flagellar length and swimming velocity were evaluated using Pearson correlation. A p value of less than 0.05 was taken as statistically significant.

Concluding remarks

The somewhat unexpected result to emerge from our systematic experiments is that flagellar length is not directly proportional to swimming velocity, waveform patterns, or beat frequencies. The flagellar length in Chlamydomonas is optimized in the WT for efficient locomotion and, even in the absence of defects, longer flagella detract from the efficiency. It appears clear that the motility dynamics of flagella rely on a mechanism that is more intricate than simple reliance on the number of dyneins that are present. Since the ultrastructural details of most mutants remain unprobed, one obvious conclusion may be that the inner dynein arms in these mutants may be near normal while the outer dynein arms may be either reduced in number or aberrant [13, 14]. It remains to be shown whether the outer dynein arm proteins are either absent and/or reduced in their ATPase activity. Our studies also reveal that, irrespective of the beat frequency, the swimming speed is essentially normal if the waveform is normal: the waveform seems to be the decisive factor in determining an optimal swimming speed. We have observed that lf1, lf2, and lf4 flagellar waveforms show serious deviations from the WT waveform. This points the way to further work involving an in vitro microtubule-sliding assay with isolated axonemes so as to examine the possible role of the central pair in modulating dynein activity on specific doublet microtubules [38–40]. A closer look at mutant cell shapes is, therefore, warranted. It is also important to note that the propulsive force required to move the cells is either not enough in lf1, lf2, and lf4 mutants, or the ATP required for the propulsive force is limited. Also, given that there are different dynein arms in the proximal region compared to the distal portion, one needs to study the ratio of the kinds of dynein arms. Experiments to address these issues are being initiated in our laboratory.