Dosimetric comparison between the microSelectron HDR ¹⁹²Ir v2 source and the BEBIG ⁶⁰Co source for HDR brachytherapy using the EGSnrc Monte Carlo transport code

Abstract

Manufacturing of miniaturized high activity ¹⁹²Ir sources have been made a market preference in modern brachytherapy. The smaller dimensions of the sources are flexible for smaller diameter of the applicators and it is also suitable for interstitial implants. Presently, miniaturized ⁶⁰Co HDR sources have been made available with identical dimensions to those of ¹⁹²Ir sources. ⁶⁰Co sources have an advantage of longer half life while comparing with ¹⁹²Ir source. High dose rate brachytherapy sources with longer half life are logically pragmatic solution for developing country in economic point of view. This study is aimed to compare the TG-43U1 dosimetric parameters for new BEBIG ⁶⁰Co HDR and new microSelectron ¹⁹²Ir HDR sources. Dosimetric parameters are calculated using EGSnrc-based Monte Carlo simulation code accordance with the AAPM TG-43 formalism for microSlectron HDR ¹⁹²Ir v2 and new BEBIG ⁶⁰Co HDR sources. Air-kerma strength per unit source activity, calculated in dry air are 9.698×10^-8 ± 0.55% U Bq^-1 and 3.039×10^-7 ± 0.41% U Bq^-1 for the above mentioned two sources, respectively. The calculated dose rate constants per unit air-kerma strength in water medium are 1.116±0.12% cGy h^-1U^-1 and 1.097±0.12% cGy h^-1U^-1, respectively, for the two sources. The values of radial dose function for distances up to 1 cm and more than 22 cm for BEBIG ⁶⁰Co HDR source are higher than that of other source. The anisotropic values are sharply increased to the longitudinal sides of the BEBIG ⁶⁰Co source and the rise is comparatively sharper than that of the other source. Tissue dependence of the absorbed dose has been investigated with vacuum phantom for breast, compact bone, blood, lung, thyroid, soft tissue, testis, and muscle. No significant variation is noted at 5 cm of radial distance in this regard while comparing the two sources except for lung tissues. The true dose rates are calculated with considering photon as well as electron transport using appropriate cut-off energy. No significant advantages or disadvantages are found in dosimetric aspect comparing with two sources.

Introduction

This study comprises EGSnrc[1] Monte Carlo based dosimetry in accordance with AAPM TG-43U1[2] protocol for new BEBIG ⁶⁰Co HDR source model Co0. A86 (Eckert and Ziegler BEBIG GmbH, Germany) and microSelectron HDR ¹⁹²Ir source model 105.002 “v2” (Nucletron, Netherlands). The aim of this study was to compare the various dosimetry parameters as well as TG- 43U1[2] parameters for two sources. Meanwhile, some authors have published the relevant dosimetry data with different methodology for both sources. Richter et al.[3] have reported a comparison of ⁶⁰Co and ¹⁹²Ir sources using EGS-Ray[4] Monte Carlo based calculations and only photon emission has been considered for the simulations. Recently Selvam et al.[5] have published EGSnrc[1] Monte Carlo based dosimetry data except anisotropy function for BEBIG ⁶⁰Co HDR source. Moreover, Ballester et al.[6] and Granero et al.[7] have reported GEANT4 based Monte Carlo dosimetry data in accordance with TG-43[2] formalism for the same source. On the other hand, Daskalov et al.[8] have published dosimetry data for microSelectron HDR ¹⁹²Ir sources using MCPT Monte Carlo transport code. Collision kerma is used to approximate the absorbed dose calculation. Furthermore, Borg et al.[9] and Taylor et al.[10,11] have reported TG-43 dosimetry parameters for same source using BrachyDose[12] EGSnrc based Monte Carlo transport code.

In this work, the EGSnrc[1] Monte Carlo code system is used to calculate the TG-43[2] parameters with similar methodology for two sources. The true dose rates are calculated with considering photon as well as electron transport. The calculated radial dose function and anisotropy function values for both sources are compared. The calculated air-kerma strength and dose rate constant are compared with other published data for the sources. The absorbed dose is calculated in different tissues related to the same dose in water for both sources and the results are compared to estimate the relative heterogeneity effect.

Materials and Methods

Monte Carlo models of microSelectron-HDR ¹⁹²Ir v2 source and BEBIG ⁶⁰Co HDR source

The microSelectron HDR ¹⁹²Ir source consists of pure iridium metal having density 22.39 g cm^-3. A source cylinder having diameter 0.065 cm and length 0.36 cm contains the radioactive ¹⁹²Ir material distributed uniformly inside it. The source core is encapsulated with an AISI 304 steel capsule which has outer diameter 0.09 cm, inner diameter 0.065 cm, and length 0.45 cm and is connected to a 0.2 cm long steel cable having diameter of 0.07 cm. The thickness of the capsule on the opposite end of the steel cable is 0.02 cm and side of the iridium core toward the cable is 0.07 cm.[9] Figure 1a shows the geometry of the real microSelectron-HDR ¹⁹²Ir v2 source whose model used in the Monte Carlo calculations is shown in Figure 1b. The cylindrical geometric model is an approximation of the real geometry of the sources.

Figure 1.

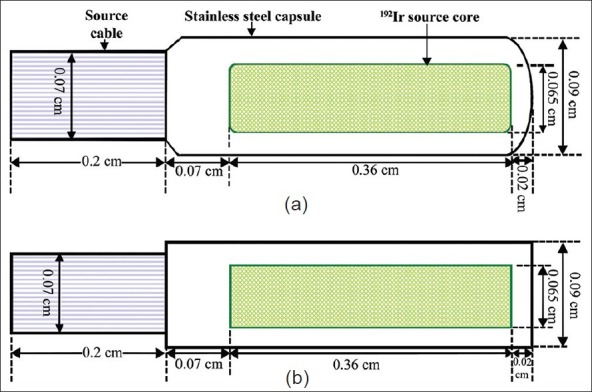
(a) Schematic diagram of the microSelectron-HDR Ir-192 v2 source and (b) the model diagram of the source used in Monte Carlo calculations. Dimensions shown are in centimetres and not to be scale

The BEBIG ⁶⁰Co HDR source consists of pure cobalt metal (density of 8.9 g cm^-3) and is kept inside the source cylinder having diameter 0.05 cm and length 0.35 cm. Radioactive ⁶⁰Co material is uniformly distributed inside it. As of the previous case the source core is encapsulated, but now with an AISI 316L steel capsule (outer diameter = 0.1 cm, inner diameter = 0.07 cm). The capsule is 0.5 cm long and connected to a 0.2 cm long steel cable. The capsule thickness is 0.075 cm on the longitudinal sides of the ⁶⁰Co source core and the thickness of axial side is 0.015 cm. There is an air gap of 0.01cm around the axial side of the active source core.[13] Figure 2(a) shows the geometry of the real BEBIG ⁶⁰Co HDR source and Figure 2(b) shows the model of it used in the Monte Carlo simulations.

Figure 2.

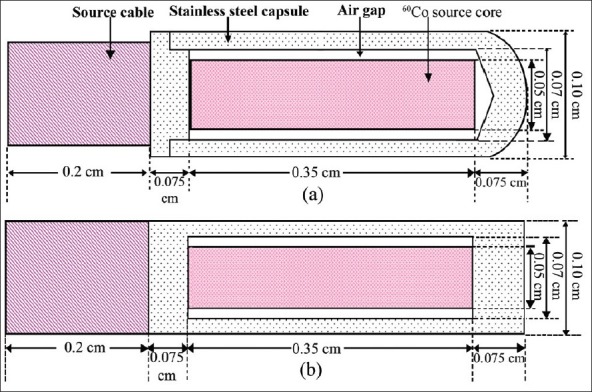
(a) Schematic diagram of the new BEBIG Co-60 HDR source and (b) the model diagram of the source used in Monte Carlo calculations. Dimensions shown are in centimetres and not to be scale

Medium

For the calculation of air-kerma strengths the sources are positioned at the center of a cylindrical container having 200 cm diameter and in dry air of mass density 0.001205 g cm^-3 (pressure = 1 atm. and temperature = 20°C). Following the recommendation of TG-43² for absorbed dose calculations, the density of water was taken as 0.998 g cm^-3 at 22°C. Several tissues are used as media for absorbed dose calculations. The ICRU density correction files[14] are used to make the pegs4 input files. Some human tissue equivalent materials are shown in Table 1 are simulated to investigate the absorbed dose difference for BEBIG ⁶⁰Co and microSelectron HDR v2 sources.

Table 1.

Human equivalent tissue materials which are used in Monte Carlo simulation for the calculation of tissue dependent absorbed dose for the sources

Monte Carlo simulations

The EGSnrc code system[1] used in the present work is widely accepted Monte Carlo simulation code for coupled electron-photon transport. Its current energy range of applicability is considered to be 1 keV to 10 GeV. It is an extended and improved version of the EGS4 package[1] originally developed at Stanford Linear Accelerator Center (SLAC).[15] In particular, it incorporates significant improvements in the implementation of the condensed history technique for the simulation of charged particle transport and better low energy cross sections.[14] In this study, the latest version of the code is used for calculations of photon fluence and absorbed dose to water.

The half-life for ¹⁹²Ir is 73.825 days and as an average one-decay will result in the emission of 1 electron and 2.363 photons.[9] The decay of ¹⁹²Ir radionuclide occurs through 4.7 % electron capture and 95.3 % β^- transitions followed by γ transitions and k- and L-shells X-rays.[9] “¹⁹²Ir_ bare_1993” spectrum and “¹⁹²Ir_beta” spectrum are used as input photon spectrum and as beta spectrum respectively presented by Duchemin et al.[16] for all Monte Carlo calculations of microSelectron_HDR ¹⁹²Ir source. The half-life of ⁶⁰Co radionuclide is 5.27 years and one-decay will result of emission of two photon spectrums with energy of 1.17 MeV and 1.33 MeV.[13] The “bareco60” spectra file is used for all the subsequent Monte Carlo calculations of BEBIG ⁶⁰Co HDR source. The number of history used for all calculations is 10⁹. The bound Compton scattering, PE angular sampling, Raleigh scattering and atomic relaxations are considered as transport parameters. Variance reduction techniques are avoided in the calculations.

Calculation of air-kerma strength

Air-kerma strength, S_k is a measure of brachytherapy source strength which is specified in terms of air-kerma rate, at a point along the transverse axis of the source in free space.[2] It is defined as the product of air-kerma rate, 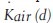at a calibration distance, d, in free space, measured along the transverse bisector of the source and the square of the distance, d:[9]

The total air-kerma is related to the photon fluence by

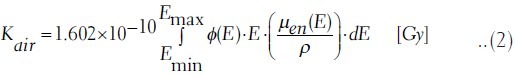
where, Φ(E) [MeV^-1 cm^-2] is the photon fluence per unit energy at energy E [MeV] and 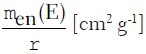is the mass energy-absorption coefficient at the same energy E. The factor 1.602 × 10^-10 is required to convert K_air from MeV g^-1 into Gy.

The total air-kerma is calculated from the equation below[9]:

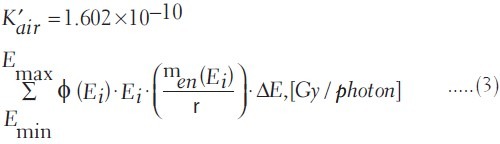
Here, E_i is the mid-point of each energy bin and ΔE is the bin size. The air-kerma rate 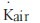in [Gy/s] of source activity A in [Bq] and number of photon per decay, N_p is determined from:

The air-kerma strength per unit source activity is then calculated using equation (1) and dividing it by the activity A:

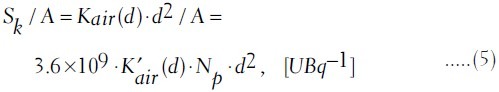
Here, the unit of S_k is denoted by the symbol U, and U = 1 μGy m²h^-1=1 cGy cm²h^-1.

The air-kerma per initial particle is calculated at a distance 100 cm from the center of the source as per AAPM TG-43 recommendation inside dry air medium.[2] The mass energy-absorption coefficient, 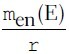for dry air are taken from the latest NIST compilation.[17] The user-code FLURZnrc[1] is used to calculate the differential fluence spectrum, Φ′(E) in the calculation grid per initial photon in the simulation. The photon fluence spectrum in 5 keV[2] intervals was scored along the transverse axis for the point of 100 cm distance. The cut-off energy for photon and electron transport are 0.001 MeV and 2 MeV. In the present work, bare iridium source data (Ir192_bare_1993. spectrum) is used as spectra file for simulation to calculate the differential fluence spectrum for microSelectron HDR v2 source. The beta spectrum is not considered in the calculation of air-kerma strength in accordance with the TG-43 protocol.[2] But both the spectra are used in the dose rate calculations for the source. Similarly, bare cobalt-60 spectrum (bareco60. spectrum) is used to simulate for the BEBIG ⁶⁰Co source in the calculation of air-kerma strength and also dose rate.

To estimate the air-kerma strength, the source is kept in a 2 × 2 × 2 m³ air cylinder and kerma is scored for a 0.2 cm thick and 0.1 cm high cylindrical ring cell, located along the transverse source axis. The number of 10[9] histories is simulated to obtain air-kerma strength for both sources. Whereas Borg et al.[9] calculated air-kerma strength as same methodology for 50 cm distance for microSelectron HDR ¹⁹²Ir v2 source. Selvam et al.[5] have calculated using same user code with photon fluence spectrum in 10 keV interval at 100 cm distance in a 1 cm thick and 0.5 cm height of voxel size for new BEBIG ⁶⁰Co HDR source. Moreover, Sahoo et al.[13] calculated the air-kerma strength at 100 cm distance using MCNP code for new BEBIG ⁶⁰Co HDR source.

Calculations of absorbed dose rate

For the absorbed dose rate calculation the source is positioned at the centre of a cylindrical water phantom of volume π × 1² × 2 m³. In order to provide adequate spatial resolution, the cells are 0.01 cm thickness for <2 cm, 0.05 cm for 2 cm < r < 5 cm, 0.1 cm for 5 cm < r < 10 cm and 0.2 cm for r > 10 cm from the source.[11] The dose rate values are calculated in different positions of the water phantom with polar co-ordinate for different position of the water phantom. The user-code DOSRZnrc[1] is used to calculate D_photon and D_electron for subsequent calculation of the true dose Ḋ_true is using the equation (6):[18]

Ḋ_true = 3.6×10⁵ (N_p×D_photon+D_electron)/(S_k/A)[cGy h^–1U¹]      …‥(6)

where D_photon is the total dose produced by photons, D_electron is that due to electrons, S k/A is air-kerma strength per unit source activity in [U Bq^-1]. The factor 3.6 × 10⁵ is required to convert the dose rate per unit air-kerma strength per unit source activity in [cGy U^-1] to the dose rate per unit air-kerma strength. The values of N_p for ¹⁹²Ir and ⁶⁰Co are 2.363 ± 0.3%⁹ and 2, respectively.[13] The true dose rate is calculated for all points of interest and these values are used to calculate TG-43 parameters[2] e.g., dose rate constant, radial dose function and anisotropy function. The cut-off energy for photon and electron transport are 0.001 MeV and 0.521 MeV, respectively, as maintained in the dose rate calculations for all radial distances. Daskalov et al.[8] simulated for new microSelectron HDR ¹⁹²Ir source using MCPT based Monte Carlo transport code and collision kerma is used to approximate the absorbed dose, whereas secondary electron transport was not considered for calculation. Taylor et al.[10,11] have reported TG-43 parameter's value for same source using EGSnrc based BrachyDose[12] Monte Carlo transport code without considering electron transport. Granero et al.[7] and Richter et al.[3] calculated the dosimetry parameters using Monte Carlo based transport code GEANT4 and EGS-Ray,[4] respectively, for new BEBIG ⁶⁰Co HDR source and the authors used 10 keV cut-off energy in the simulation for photon and electron. Selvam et al.[5] calculated absorbed dose to water using DOSRZnrc user code[1] of EGSnrc for the same source with cut-off energy 0.001 MeV and 0.521 MeV for photon and electron transport, respectively. The authors also calculated collision kerma to approximate the absorbed dose close to the source (up to 1 cm) and electron rage rejection technique (ESAVE =2 MeV) is used for rest of the calculations.

Results and Discussion

Air-kerma strength, S_k

The calculated value of air-kerma strength per unit source activity is found to be 9.698 × 10^-8 ± 0.55% U Bq^-1 for new microSlectron HDR ¹⁹²Ir v2 source. The source is also simulated at the point of 100 cm distance from the source centre of a cylindrical air phantom. This value is in good agreement with results (=9.737 ± 0.009 × 10^-8 U Bq^-1) obtained by Hong et al.[18] at an average value from 2 to 50 cm distances with 0.2% contribution from bremsstrahlung. The extracted results at 50 cm distance without bremsstrahlung contribution was 9.694 ± 0.037 × 10^-8 U Bq^-1. The results also agree well with the observed results (9.71 × 10^-8 ± 0.4% U Bq^-1) of Borg and Rogers[9] for air-kerma strength per unit source activity for the microSlectron HDR ¹⁹²Ir v2 source at 50 cm distance from the source centre. It's worth mentioning that thier methodology has been adopted in the present cases also.

The value of air-kerma strength per unit source activity for BEBIG ⁶⁰Co HDR source is found to be 3.039 × 10^-7 ± 0.41% U Bq^-1. All the parameters are set as like the previous case of calculation of the microSlectron HDR ¹⁹²Ir v2 source. Selvam et al.[5] obtained the value (=3.043 × 10^-7 U Bq^-1) using same code with 10 keV interval of fluence spectrum. The value is about 0.13% higher than the value obtained from this study probably due to higher size of calculation grid. In this case also the results are again in good agreement with Monte Carlo based MCNP results of 3.04 × 10^-7 ± 0.05% U Bq^-1 by Sahoo et al.[13]

Dose rate constant, Λ

Dose rate constants, Λ, are calculated by dividing the dose to water per unit source activity in a (0.1 mm)³ voxel centred at the reference position, (1 cm, 90°), in the π × 100² × 200 cm³ cylindrical water phantom, by the air-kerma strength per unit source activity. The contribution of primary electron is accounted for in all the calculations related to microSlectron HDR ¹⁹²Ir v2 source. The value of Λ for microSlectron HDR ¹⁹²Ir v2 source is found to be 1.116 ± 0.12% cGy h^-1 U^-1. This result agrees well with the result of Taylor et al.[10] (=1.109 ± 0.18% cGy h^-1 U^-1) and Hong et al.[18] (=1.112 ± 0.51% cGy h^-1 U^-1).

The calculated value of Λ for BEBIG ⁶⁰Co HDR source is found to be 1.097 ± 0.12% cGy h^-1 U^-1 whereas Selvam et al.[5] have reported the dose rate constant value (=1.097 cGy h^-1 U^-1) using FLURZnrc-based[1] calculation of collision kerma to approximate the dose. This is also in good agreement with GEANT4 Monte Carlo based published results of 1.087 ± 0.011% cGy h^-1 U^-1 by Granero et al.[7]

Radial dose function, g_L(r) and anisotropy function,G_L(r, θ)

The radial dose function, g_L(r) accounts for dose fall- off on the transverse-plane due to photon scattering and attenuation in water medium. The function is also influenced by the geometry factor, G_L(r, θ) and the anisotropy factor, F(r, θ). The geometry factor depends on the physical parameters of the source, i.g., the length and the radius of the source. An identical construction of of the sources can ensure same geometry factors. The isodose curve is influenced by the anisotropy factor in clinical dose distribution. These two functions are essential for comparing different brachytherapy sources.

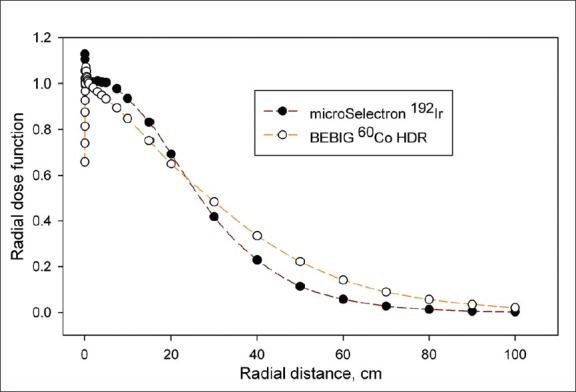
The Figure 3 shows the comparison of radial dose functions from 0.06 cm to 100 cm radial distance and the Figure 4 does the same for distance from 0.06 cm to 2 cm. The values of radial dose function for ⁶⁰Co source is about 2.4% lower than ¹⁹²Ir at 2 cm radial distance (Manchester Point A) and the values are also found to be lower 7.5%, 9.3% and 10.3% for the point of 5 cm, 7.5 cm and 10 cm respectively. The values of radial dose function of ⁶⁰Co source are also lower than that of the ¹⁹²Ir source in the range from 0.06 cm -0.17 cm. The values are, however, found higher in the range from 0.18 cm -1 cm and above 22 cm of radial distance. The higher values of radial dose function are found for ¹⁹²Ir source at the distance shorter than 0.17 cm may be the dose by electron contribution. The values are found to be less by 7% averagely using ECUT =2 MeV.[19] The radial dose function for ⁶⁰Co source is linearly fall-off from 1 cm to 7.5 cm of radial distances.

Figure 3.

Comparison of radial dose function for microSelectron HDR ¹⁹²Ir and BEBIG ⁶⁰Co HDR sources from 0.06 cm to 100 cm of radial distances

Figure 4.

Comparison of radial dose function for microSelectron HDR ¹⁹²Ir and BEBIG ⁶⁰Co HDR sources from 0.06 cm to 2 cm of radial distances

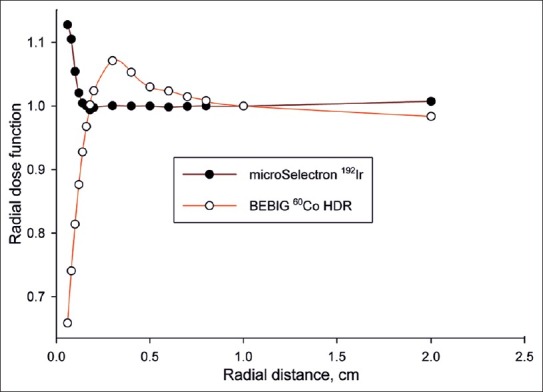
The anisotropy factors of BEBIG ⁶⁰Co HDR source are comparatively higher at the longitudinal sides of the source with the values of microSelectron HDR ¹⁹²Ir source. It is also sharply increases with the radial distances to the longitudinal side of the BEBIG ⁶⁰Co source comparatively with the value of microSlectron ¹⁹²Ir v2 source. These factors for the cable connecting side of the BEBIG ⁶⁰Co source are quite low compared to that of the other side and the values show an increase with the radial distance. The Figures 5 to 8 compare the anisotropy factors for 2 sources at radial distances 1 cm, 3 cm, 5 cm and 10 cm.

Figure 5.

Comparison of anisotropy function for 1 cm of radial distance

Figure 8.

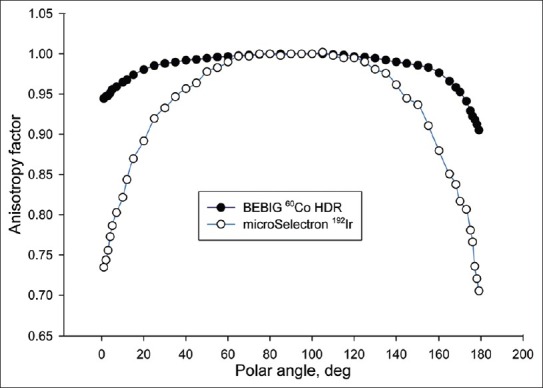
Comparison of anisotropy function for 10 cm of radial distance

Figure 6.

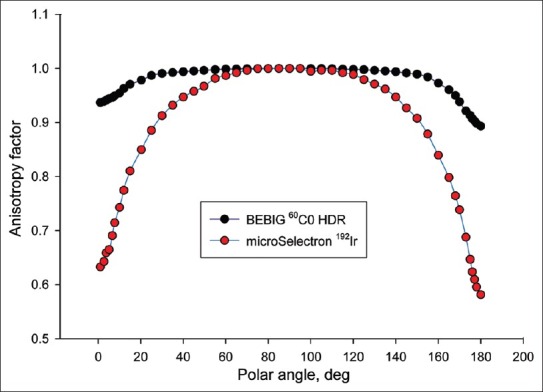
Comparison of anisotropy function for 3 cm of radial distance

Figure 7.

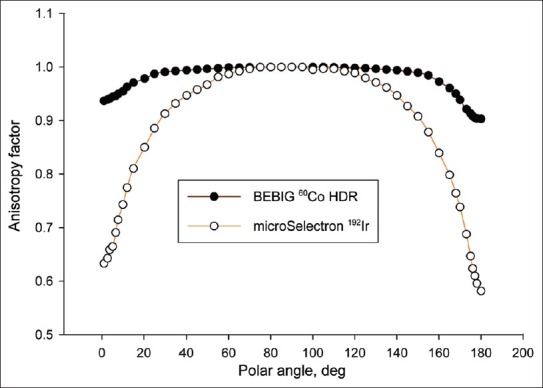
Comparison of anisotropy function for 5 cm of radial distance

Absorbed dose difference

A cylindrical phantom was constructed with the respective tissue equivalent materials [Table 1] for simulation. The absorbed doses are calculated at different radial distances. The absorbed dose of water at discrete distances has been used as reference dose for the calculation of relative dose differences. The Figure 9 shows the relative absorbed dose differences between ⁶⁰Co and ¹⁹²Ir sources. Significant dose differences are noted for compact bone tissue up to 8 cm and more than 10 cm radial distances. Maximal absorbed dose differences are, however, observed in lung tissue: The results being about 30.8% at 0.2 cm, and 12.45% at 1 cm. As is expected the difference decreases with increase in radial distances. Tissue dependence of absorbed dose has been calculated with vacuum phantom for water, breast, compact bone, blood, lung, thyroid, soft tissue, testis and muscle. No significant tissue dependence in absorbed dose is noted at 5 cm of radial distance by comparing BEBIG ⁶⁰Co HDR to microSlectron HDR ¹⁹²Ir v2 sources except for the lung tissues. Figure 10 shows the differences comparing them with the absorbed dose of water.

Figure 9.

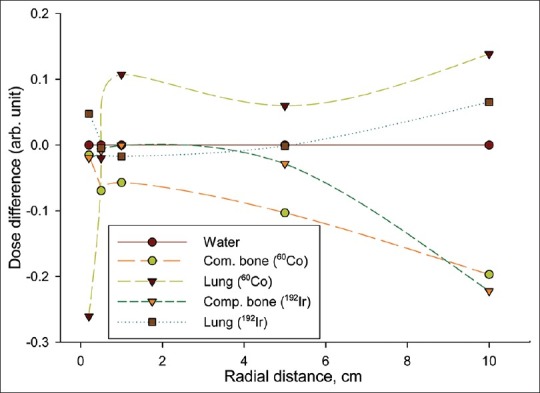
Relative absorbed dose difference for compact bone and lung with water

Figure 10.

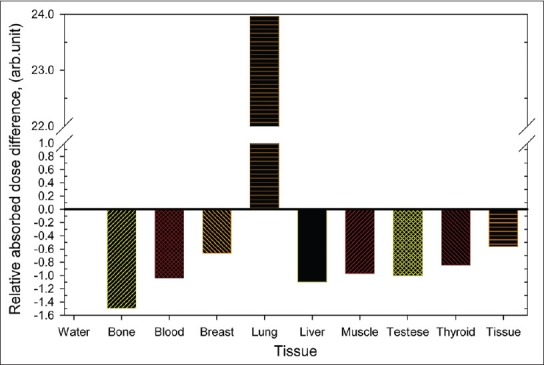
Relative absorbed dose difference for deferent tissue materials at 5 cm radial distance

The investigations of ⁶⁰Co and ¹⁹²Ir sources have shown approximately identical dose distribution. Negligible differences are noted in radial dose distribution as well as negligible absorb dose differences with various tissues. A significant difference appears in absorbed dose at the close surface of the iridium source (132 times higher than the dose of 1 cm of radial distance from the source centre)[19] probably due to the contribution of primary electron. These differences are minimal when the calculation is done with KERMA approximation.[19] In case of ⁶⁰Co source, the absorbed dose is about 74 times higher[19] than the dose of 1 cm of radial distance.

Conclusions

The values of anisotropy function at the longitudinal sides of the BEBIG ⁶⁰Co HDR source are relatively higher than microSelectron HDR ¹⁹²Ir source and the isodose lines will be not exactly identical due to this effect for these region. Treatment planning system performs to adjust the isodose distribution using dwell time positioning technology in clinical relevant situation. The radial dose function characterize the dose fall-off on the transverse plane of the source. The higher dose region for ¹⁹²Ir source and lower dose region for ⁶⁰Co source (<0.17 cm from the source centre) may be situated inside the applicators and rest of the region up to 1 cm, the radial dose fall-off will be dependent on the nature of the applicator. The applicators commonly use for cervical site; these region again may be situated inside the applicators. The differences of the radial dose function <1 cm for 2 sources may be effectual for narrow catheter based intracavitary or interstitial brachytherapy. The small difference of radial dose function (within the therapeutic range of radial distance) has a possibility to make a negligible difference in isodose distribution in clinical applications.