Abstract
Prostate Dynamic-Contrast-Enhanced (DCE) MRI often exhibits fast and extensive global contrast reagent (CR) extravasation - measured by Ktrans, a pharmacokinetic parameter proportional to its rate. This implies that the CR concentration ([CR]) is high in the extracellular, extravascular space (EES) during a large portion of the DCE-MRI study. Since [CR] is detected indirectly, through water proton signal change, the effects of equilibrium transcytolemmal water exchange may be significant in the data and thus should be admitted in DCE-MRI pharmacokinetic modeling. The implications for parameter values were investigated through simulations, and analyses of actual prostate data, with different models. Model parameter correlation and precision were also explored. A near-optimal version of the exchange-sensitized model was found. Our results indicate that ΔKtrans (the Ktrans difference returned by this version and a model assuming exchange to be effectively infinitely fast) may be a very useful biomarker for discriminating malignant from benign prostate tissue. Using an exchange-sensitized model, we find that the mean intracellular water lifetime (τi) - an exchange measure - can be meaningfully mapped for the prostate. Our results show prostate glandular zone differences in τi values.
Keywords: Dynamic-Contrast-Enhanced, water exchange, contrast reagent, prostate cancer
INTRODUCTION
The use of (Dynamic-Contrast-Enhanced) DCE-MRI to study prostate disease began almost 15 years ago (1) and has increased significantly since then. Recent reviews include (2-5): the Bonekamp, Macura paper (4) is particularly recommended. As a consequence of this effort, the indications for DCE-MRI prostate studies have been proliferating. Recent contributions include (6-11).
The vast majority of mathematical models used for quantitative DCE-MRI are variants of the nuclear medicine radiotracer pharmacokinetic paradigm (4): we refer to this as the standard model (SM). However, we have pointed out a fundamental problem in the SM (12). For T1 -weighted 1H2O signals, the bases for DCE-MRI, “tracerization” carries the incorrect corollary that inter-compartmental water molecule exchange be assumed effectively infinitely fast throughout the course of the DCE-MRI acquisition - the fast-exchange-limit [FXL] MR condition. Though the contrast reagent (CR) plays the role of the tracer molecule, the MR signal comes from the water molecule and most water is in intracellular spaces inaccessible to CR. The classic tracer molecule is also the signal molecule: its compartmentalization is not encoded into the signal. However, the CR compartmentalization is intrinsic to the DCE-MRI 1H2O signal because the water compartmentalization is intrinsic. Thus, there are two molecular probes, CR and H2O, inherent in DCE-MRI. The shutter-speed pharmacokinetic model (SSM) was developed to shift from the tracer paradigm by allowing finite inter-compartmental water exchange kinetics (12-15). Relieving the FXL constraint of the SM can lead to remarkable performance by the SSM. With an SSM DCE-MRI follow-up to mammography, it is now possible to contemplate elimination of most if not all of the more than 70% of breast biopsy procedures that yield negative pathology reports (13,14,16,17).
The SSM is a “homogeneous” model [as is the SM] (12): i.e., it assumes “well-mixed” compartments. There is a family of more highly parameterized “inhomogeneous” models (12) that can describe data just as well as the SSM. However, for a given number of compartments, each is less parsimonious.
In this contribution, we explore aspects of the pharmacokinetic modeling of in vivo prostate DCE-MRI data. These include: relative parameter influence, acquisition exchange (shutter-speed effect) sensitivity, applicable exchange conditions, parameter uncertainty, parameter correlation, and parameter pertinence. These help explain the success and limitations of the SSM. It is not surprising that if one uses a relatively exchange-insensitive acquisition sequence, shutter-speed effects are small (18). However, because they afford a greater signal to noise (S/N) ratio, most prostate DCE-MRI acquisitions reported in the literature produce data that are rather exchange-sensitive. And yet, all studies but one (19) have used SM analyses.
The single application of the SSM to prostate DCE-MRI so far reported (19) is quite encouraging. It shows trends very similar to those we see for breast malignancy. In a companion paper, we report our own preliminary experience comparing shutter-speed analyses of prostate DCE-MRI data with pathology analyses of biopsy core specimens (20). Also as with breast cancer, SSM promises high specificity in distinguishing malignant from benign prostate tissue.
THEORY
Starting from the Bloch Equation for longitudinal relaxation, the 2nd generation Shutter-Speed Model (SSM2) calculates the temporal DCE-MRI signal (magnetization) change. It considers all three water populations (sites) [blood, interstitium, and intracellular] and can be manipulated to provide insights into parameter influences (12). The mathematical expression of the model is best made in matrix form (12), Equation (1), where: M ≡ (Mb, Mo, Mi)T is the three-element
| (1) |
| (2) |
compartmental water magnetization vector, C represents the equilibrium (physiological steady-state) condition [C = (M0b/T1b, M0o/T1o, M0i/T1i)T], and X is the exchange matrix, Equation (2). The quantities R1b, R1o, and R1i are the intrinsic T1 relaxation rate constants [≡(T1)−1] for the blood, interstitial, and intracellular compartmental water magnetizations (signals), respectively. [R1b = r1p(1 − h)[CRp] + R1b0 and R1o = r1o[CRo] + R1o0; where r1p and r1o and [CRp] and [CRo] are the plasma and interstitial CR relaxivities and concentrations, respectively, R1b0 and R1o0 are the pre-CR 1H2Ob and 1H2Oo rate constants, and h is the capillary hematocrit.] The compartmental water mole fractions (populations), pb, po, and pi, are proportional to their corresponding magnetizations and volume fractions. The quantities τb, τo, and τi are the average compartmental water molecule lifetimes (τb and τi are the reciprocals of their respective unidirectional efflux rate constants). Each is directly proportional to a 1D compartmental size measure and inversely proportional to the compartmental boundary water permeability. During a DCE-MRI experiment, R1b and R1o will vary with [CRp], and [CRo], respectively. The transcytolemmal longitudinal shutter-speed, Toi−1(t), is |R1o(t) − R1i| (12). The relationship between these [CR] values is given by Kety-Schmidt pharmacokinetic rate law, Equation (3), where Ktrans = kepve [kep and ve are the unidirectional rate constant for passive CR intravasation and the extracellular, extravascular volume fraction quantities, respectively]. For the gradient-recalled-echo (GRE) acquisition pulse sequence, the NMR steady-state solution for Eq. (1)
| (3) |
is given (12) as Equation (4): where I is the Identity matrix, TR is the steady-state pulse repetition time, α the read pulse flip angle, and M0 the initial magnetization vector.
| (4) |
SSM2 provides valuable insights into DCE-MRI pharmacokinetics that will aid both pulse sequence optimization and pharmacokinetic modeling. This includes approach simplification and choice of acquisition and fitting parameters. When CR extravasation is high, as often seen in the prostate, SSM2 can be simplified to ignore a distinct blood volume contribution (pb): i.e., pb + po ≡ pe. Thus, a two-site exchange (2SX) model can be used. For this, a phenomenological expression, (with apparent relaxation rate constants, R1S,L and , and fractional populations, aS,L [aS + aL = 1]) has a closed-form expression, Equation (5), where
| (5) |
, and is thus commonly used (13). The subscripts S and L designate the components with the smaller and larger T1,2 values, respectively. R1S, R1L and aS/(aS + aL) can be expressed in terms of the intrinsic system parameters as in Equations (6) and (7). The transverse relaxation factors, , are often assumed
| (6) |
| (7) |
to be unity. Three 2SX conditions are characterized as follows:
the fast-exchange-limit [FXL], R1 = poR1o + piR1i;
the fast-exchange-regime [FXR], R1 = R1L(because aS → 0 [as determined by Eq. (7)]; i.e., aL 1); and
the slow-exchange regime [SXR], which requires the use of Eqs. (5) - (7).
The 1st generation of the SSM (SSM1) can be made to span these 2SX conditions (13,15), but the matrix version, SSM2 [Eqs. (1-3)], does it more succinctly.
When transverse relaxation signal loss becomes significant [i.e., the Eq. (5) factors < 1], the apparent normalized MRI signal is less than the sum aL + aS defined by Eq. (7). When two R1 values are not observed, the 2SX system is in either the FXL, the FXR, or the SXR condition with, we presume, disproportionate transverse quenching of aS. In contrast to the standard model (FXL-constrained, FXL-c), the SSM1 thus simplifies R1 to the dominant apparent rate constant, R1L. The non-linear [CR]-dependence of R1 is evident from the expression for R1L, Eq. (6), the smaller (only) apparent rate constant (12). Below, we present evidence for disproportionate transverse relaxation quenching of DCE-MRI data from prostate tissue.
MATERIALS AND METHODS
Patient Population
The study was approved by both the Portland VA Medical Center (PVAMC) and the Oregon Health & Science University (OHSU) institutional review boards (IRBs). Here, we report on two of thirteen male subjects [60 (± 8.4) yr] [mean (± standard deviation)]. Results from all 13 are reported in (20). All presented to the PVAMC with clinical indications for a prostate biopsy procedure (i.e., elevated serum PSA and/or an abnormal digital rectal examination). A prior biopsy was an exclusion criterion. Each was referred for biopsy as standard care and volunteered for our DCE-MRI protocol before that procedure occurred. All participants gave written informed consent. Consequent to his biopsy findings, one subject further elected prostatectomy in his clinical treatment plan.
MRI
All Prostate MRI data were acquired with a Siemens TIM Trio (3T) system. RF transmission utilized the instrument whole body coil, while reception employed a combination of flexible body and spine matrix coils. Multi-slice T2-weighted images (Turbo Spin Echo, TR/TE/FA, 5000 ms/102 ms/90°) were acquired for anatomic contrast and region-of-interest (ROI) selection. A near proton density (PD) image of the prostate gland was obtained using a 3D FLASH pulse sequence with a 256*144*16 matrix size and a 360*203 mm2 transverse field-of-view (FOV), resulting in a nominal in-plane resolution of (1.4)2 mm2. Other parameters were: slice thickness, 3 or 3.2 mm; TR/TE/FA, 200 ms/1.56 ms/8°. For DCE-MRI, the same FLASH sequence was run with the only differences being TR = 5.0 ms and a 15° flip angle, which yielded a 6.28 s imaging inter-sampling interval. The total DCE-MRI acquisition time was ten and a half minutes. A bolus of 0.1 mmol/kg Prohance (Bracco, Inc.) was administered in an antecubital vein ~ 38 s after commencing the DCE-MRI acquisition. It was delivered in 5 to 10 s, at 3.0 mL/s, followed by a 20 mL saline flush. We measured the arterial input function (AIF) from a femoral artery within the FOV. An individual AIF time-course was measureable for each subject except one, due to severe motion during the DCE acquisition. A population-averaged AIF based on six subjects was used for this subject.
An array of external receive RF coils was used for this work. Although an endorectal receive coil provides excellent signal, it has the disadvantages of: 1) yielding a very small FOV - limited to the pelvic region very near the prostate gland - which a) hinders radiation planning, and b) inhibits experimental MR AIF measurement from a large blood vessel, 2) distorting the gland from its shape in the absence of the coil, which would be that presented for radiation, and 3) increasing patient discomfort [fasting (or enema) and mild sedation are often used]. Since a possible outcome of the SSM DCE-MRI prostate protocol may be to shift a fraction of therapy from prostatectomy to radiation treatment, we have employed the surface RF coil array. As we will see, it provides quite sufficient MR signal.
Prostate Biopsy and Pathology
Each subject underwent a standard ten core prostate biopsy procedure performed using (exclusively) ultrasound guidance, subsequent to the DCE-MRI acquisition. Pathology examinations of biopsy core specimen fragments revealed Gleason scores ranging from 6 to 8. No subject had a prostate biopsy prior to the research MRI.
DCE-MRI Analyses
An ROI boundary was manually drawn around an area in a DCE-MR image for each of the 13 subjects. Its location had been outlined on a T2-weighted image slice by a radiologist (not involved in DCE-MRI data processing) using hypointensity and morphology criteria, and pathology laterality. The DCE-MRI analyses were then performed by a different researcher. DCE-MRI pharmacokinetic modeling employed the standard model (SM) and the first generation shutter-speed model [SSM(FXR-a); FXR-allowed]. As presented in our breast DCE-studies (13,14,21), the only difference between SM and SSM(FXR-a) is the allowance for finite transcytolemmal water exchange kinetics in SSM. The SM intrinsically assumes τi to be effectively zero. The AIF time-course was obtained from a small ROI within a femoral artery that was clearly visible within the image FOV. To minimize inflow effect-introduced AIF uncertainties, each individual AIF was recursively amplitude adjusted until the ve(SM) parameter from obturator muscle reference tissue (18,22) ROI DCE data converged to 0.11, with a tolerance of ~ 0.005. Since the PD-weighted image still carries some weak (mixed) relaxation weighting, a numerical approach is employed to obtain the PD image based on the average of DCE baseline images and that of the PD-weighted image; with proton density and T1 as the only variables. This allowed R10 (R1 before CR arrival) mapping and thus [since R1o0 = (R10 − piR1i)/(1 − pi)] elimination of R1o0 from Eqs. (6,7).
All data fitting used nonlinear least square methods with an in-house software package written in Matlab (MathWorks, Natick, MA, USA). The computation time for an ROI (or a single voxel) fitting with each model is under one second on a dual–core Windows XP personal computer.
RESULTS
DCE-MRI Pharmacokinetic Analyses
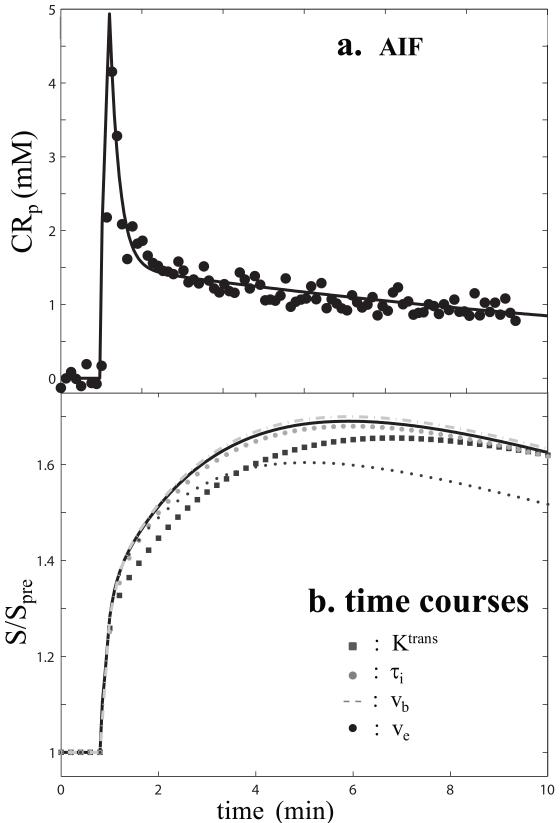
Figure 1a shows a 4 minute post-CR injection transverse DCE pelvic image slice (#6) from subject No. 12. [A different subject is shown in Fig. 1 of (20).] The image is viewed from the inferior perspective, and has the anterior side up. Figure 1b shows a T2-weighted image of the same slice. Based on the Fig. 1b image, four ROIs, representing suspicious (40 pixels) and normal appearing gland (NAG) (24 pixels) prostate tissues, obturator muscle (73 pixels) tissue, and the femoral artery (5 pixels) used to obtain the arterial input function (AIF), are indicated with arrows and white borders in the Fig. 1c zoomed Fig. 1a image section. Following the DCE-MRI study, a 10-core trans-rectal prostate biopsy procedure was conducted on the subject. The 10 biopsy needles were inserted so as to representatively (“geographically”) sample the entire gland (mostly) peripheral zone. The pathology analyses indicated malignant adenocarcinoma in all five biopsy core specimens obtained from the left (right in image) of the prostate, with a Gleason number 7 (3 + 4), and benign tissue (NAG) in all five core specimens from the right peripheral zone. The Fig. 1f inset shows the AIF (in the form of the plasma CR concentration, [CRp]) for the subject, determined from the femoral artery S/Spre time-course, using muscle as reference tissue to adjust the amplitude (18,23,24).
Figure 1.
An axial pelvic DCE-MR image slice is shown for one subject in panel a. Panel b shows a T2-weighted image of the same slice. Panel c zooms on the panel a image, and indicates ROIs chosen from panel b image inspection. Panels d, e, and f plot DCE-MRI time-courses (points) from the suspicious, normal-appearing-gland (NAG), and muscle panel c ROIs, respectively. The panel f inset shows the time-course from the panel c femoral arterial input function (AIF) ROI. The solid curves represent SSM(FXR-a) [Eq. (5), ] fittings, the lower dashed curves, SM(FXL-c) [Eqs. (1)-(4), τb = τi → 0] fittings, and the upper dashed curves SM expectations for the SSM-returned Ktrans and ve parameter values. Pathology analyses of biopsy specimens acquired subsequent to the DCE-MRI revealed malignant tissue in the left prostate peripheral zone, in or near the suspicious ROI on the right side of the image.
The Fig. 1d points trace the normalized (S/Spre) time-course for the suspicious Fig. 1c ROI, which was on the same side as the retrospectively-confirmed malignancy. The solid curve represents the best fitting with the SSM(FXR-a) model while the black dashed curve is that with the SM(FXL-c) analysis. The signature mismatch (temporally correlated residuals) of the FXL fitting is the same as we have previously reported for breast malignancy (13,16,21,25). It is more noticeable here due to the larger Ktrans value, and reflects systematic SM model insufficiency. This is also indicated by the parameter values returned by these fittings: Ktrans(SSM) = 0.63 min−1; Ktrans(SM) = 0.23 min−1; ve(SSM) = 0.64; ve(SM) = 0.27; and τi(SSM) = 400 ms. [r1o was set as 3.8 (mM)−1s−1] It is even more clearly indicated with the gray dashed curve, expected by SM(FXL-c) (i.e., with τi → 0) for the SSM(FXR-a)-returned Ktrans and ve values. Analogous results for the NAG Fig. 1c prostate ROI are shown in Fig. 1e. The maximum enhancement is not very different from that of the suspicious ROI (Fig. 1d). The differences in the S/Spre time-courses for the suspicious (Fig. 1d) and NAG (Fig. 1e) ROIs are seen to be mainly in their shapes. Propitiously, the SSM is especially sensitive to this property (15). Consequently, the Fig. 1e SM/data mismatch is not as great as in Fig. 1d, though still noticeable: Ktrans(SSM) = 0.23 min−1, Ktrans(SM) = 0.17 min−1, ve(SSM) = 0.63, ve(SM) = 0.37, and τi(SSM) = 260 ms. Finally, the analogous plots for the Fig. 1c muscle ROI are shown in Fig. 1f. The SM/data mismatch is not large: Ktrans(SSM) = 0.087 min−1, Ktrans(SM) = 0.054 min−1, ve(SSM) = 0.16, ve(SM) = 0.09, and τi(SSM) = 710 ms. With decreasing Ktrans values, the shutter-speed (water exchange) effects in these DCE data decrease - the gray dashed curves are increasingly closer to the points, reflecting the decreasing SSM(FXR-a) - SM(FXL-c) parameter differences. This is exactly as predicted by shutter-speed theory (12), and observed in breast DCE-MRI (13,14,16,17,21).
Determining Parameter Influence
A strength of SSM2 is that it covers the entire range of DCE-MRI CR extravasation kinetics, from very leaky tumor (fast extravasation) to normal brain (almost no extravasation) tissues. In these different situations, the various pharmacokinetic parameters may have drastically different influences on the tissue DCE-MRI time-courses (12,23).
Parameter influence (sensitivity) can be understood from simulations using SSM2. It is best that the most influential parameters be identified (or even ranked) prior to pharmacokinetic model fitting. The simplest way to do this is to generate a time-course based on fixed parameter values. We illustrate this concept in Figure 2 for a case with small Ktrans magnitude. The AIF used for this simulation (Fig. 1f inset) was determined from the ROI marked in Fig. 1c, and is shown in Fig. 2a. The parameters po = 0.4, Ktrans = 0.04 min−1, and , for TR = 5 ms, and FA = 15°, give rise to the solid (“true”) tissue curve in Fig. 2b. With all other values remaining unchanged, the influence of a particular parameter can be investigated by adjusting its magnitude by a certain percentage (26) and generating a new signal time-course. Four of these are plotted in Fig. 2b for each of Ktrans, po (~ ve), pb (~ vb), and τi decreased by 20%. The absolute differences between the true and “altered” time-courses measure the influence of the parameter altered. This represents a univariate approach for local parameter sensitivity estimates. Given the smoothly varying nature of the measured signal defined in Eq. (4), it is expected that parameter influences will vary smoothly as well. For the relatively high CR extravasation anticipated in the prostate, it is expected that Ktrans and ve are the two most dominant parameters (12). The influences of τi and vb are smaller. For the particular case shown in Fig. 2, τi is more influential than vb.
Figure 2.
Panel a shows the points comprising the Fig. 1f inset AIF time-course. The solid curve is the empirically fitted AIF. The solid (“true”) curve in panel b shows the SSM(3S2X)-calculated [Eqs. (1)-(4)] tissue time-course for this AIF with: Ktrans = 0.04 min−1, po = 0.4, , TR = 5 ms, and FA = 15°. The other four time-courses have the same parameter values except with a decrease of the one indicated by 20%. This represents a univariate investigation of parameter influence.
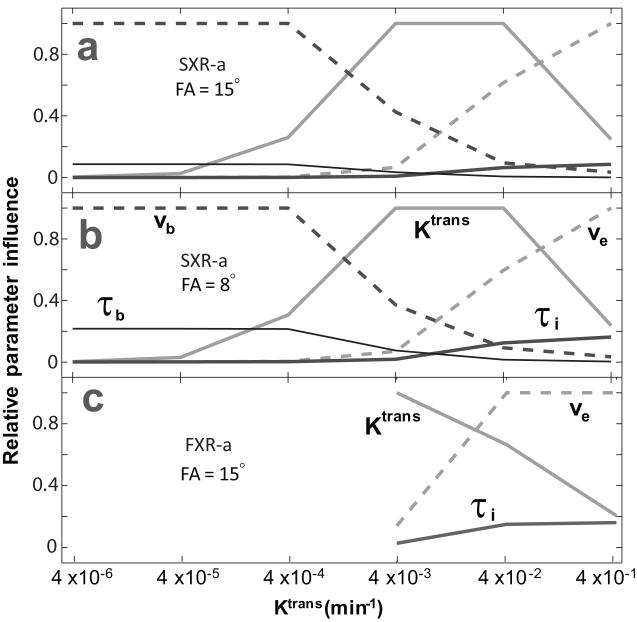
The Ktrans-dependences of relative parameter influences are displayed in Figure 3, for ten-minute DCE-MRI data acquisition windows. Figure 3a displays the relative parameter influences for six Ktrans values, spanning five orders of magnitude mimicking in vivo behaviors from intact blood brain barrier (BBB, left) to very leaky tumor (right), when FA = 15°. The ordinate is the relative influence (= |ΔA/A|, where ΔA = Aaltered − Atrue, and A is the area under the S/Spre time-course, with baseline S/Spre =1, integrated out to 10 min.). Except for Ktrans, the values of all other parameters remained the same as for the Fig. 2 true curve. The influences of vb and τb decrease with increasing Ktrans, those of ve and τi increase with increasing Ktrans, and Ktrans itself remains one of the two most influential parameters as long as there is detectable CR extravasation. For cancer DCE-MRI, Ktrans is normally in the 10−3 to 10−1 min−1 range, where the influences of transcytolemmal water exchange and blood volume fraction can be similar. As expected (13), relative parameter influences will also depend on the MRI acquisition pulse sequence parameters in addition to the acquisition window. Figure 3b shows the analog of Fig. 3a except that the read pulse flip angle is decreased from 15° to 8°. The relative influences of the two exchange parameters, τb and τi, are seen to be increased. We will consider this below. Such analyses, based on SSM2, provide valuable insight into DCE-MRI experimentation, including the optimization of DCE-MRI pulse sequence parameters.
Figure 3.
Panel a shows the Ktrans-dependences of the relative influences of the parameters indicated. The ordinate is |ΔA/A|, where ΔA ≡ Aaltered − Atrue, and A is the area under a Fig. 2 tissue curve. The SXR-a approximation is used, with FA = 15°. Panel b shows the situation when FA = 8°. Panel c shows relative influences when the FXR-a approximation is used, with FA = 15°.
The Influence of τi
The parameter analysis suggests that τi could be influential in prostate DCE-MRI pharmacokinetic modeling. Given its crucial role in breast cancer detection (13,14,16,21), and its important ability to measure cell membrane ion pumping activity (27), τi is a highly desirable new imaging biomarker. Since this water exchange measure is not one of the two most influential quantities, parameter interdependences might hinder its direct extraction. However, disproportionate signal quenching due to transverse relaxation may enhance the influence of τi (13,14). This is not considered in the simplest SSM2 or in Figs. 2 and 3. Importantly, simulations using the FXR-a version [, in Eq. (5)] of SSM1 with FA = 15° exhibit very similar parameter influences, with enhanced water exchange sensitivity, as the Fig. 3b SSM2 8° results. These are shown in Fig. 3c. In the FXR-a approximation, vb and τb are essentially undefined. Thus, Fig. 3c spans only the Ktrans magnitudes where they would be non-influential.
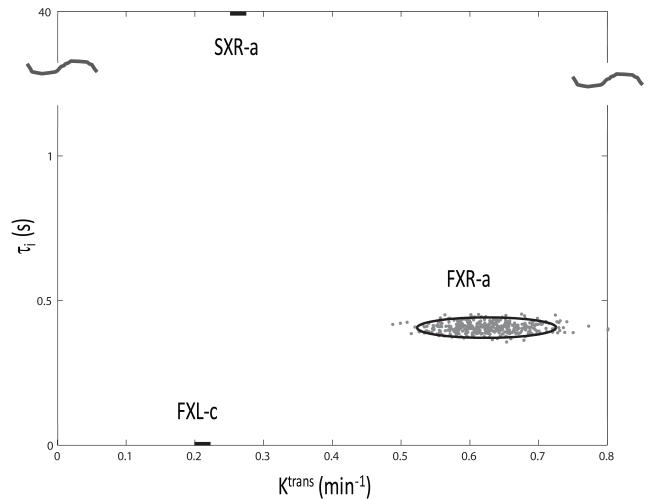
Figure 4 summarizes a simulation designed to demonstrate the results of this. It tests the compatibility of pharmacokinetic model constraints with prostate DCE-MRI data. Monte Carlo calculations similar to those in a previous report (28) were implemented. These were based on the Fig. 1d suspicious ROI time-course and comprised FXL-constrained (two parameter), FXR-allowed (three parameter), and SXR-allowed (three parameter) fittings. These three approximations were described above. In this context, R1L [Eq. (6)] can be thought of as representing mostly 1H2Oi and R1S as representing much of 1H2Oo and 1H2Ob. [The SSM2 considers all three signals 1H2Oi, 1H2Oo, and 1H2Ob distinctly (12,23,28), and for the large Ktrans values here, the system might reach the SXR condition (13,14) if there were no signal quenching.] Four hundred simulation runs were carried out. For each, a new random noise (Gaussian distribution about zero) contribution was added to each Fig. 1d time-course data point. This was done so that each simulated time-course had a smaller S/N (roughly equal to that from a single voxel) than the actual ROI data (Fig. 1d points) and that the simulated data carry no bias from a potential model. Randomly generated initial guess Ktrans, ve, and (in two cases) τi, values (28) were used for each fitting of each of the 400 simulated time courses. Figure 4 exhibits the fitting-returned space of τi (ordinate) and Ktrans (abscissa). The 400 gray points largely within the FXR-a oval have the coordinates of the final fitted values. The initial guesses spanned the plot ranges. The oval encloses two SDs of the fitting-returned values. The FXL-c oval, at τi = 0, is only one dimensional (horizontal bar) because the SM assumes that τi is effectively zero. The mean Ktrans value returned is seen to be 0.21 (± 0.01) min−1. The bar length equals four SDs. The value of ve is 0.28 (± 0.013) (not shown in Fig. 4). Fitting the same 400 data time-courses with FXR-a returns a mean Ktrans value of 0.61 (± 0.05) min−1, and a ve = 0.62 (± 0.02). Figure 4 shows that the τi value returned by FXR-a is 0.41 (± 0.02) s. The uncertainty is less than 10%.
Figure 4.
The 2D τi/Ktrans parameter space for three different modelings of the Fig. 1d suspicious ROI points. Each oval (two are 1D) has radii equal to 2SD of the parameter values returned from 400 Monte Carlo fittings with starting magnitudes randomly distributed over the entire plot. [The fitting points (gray) are shown for the FXR-a analysis.] The three models are labeled: the SM(FXL-c) approach [Eqs. (1)-(4), τb = τi → 0]; the SSM(FXR-a) approach [Eq. (5), ] fittings; and the SSM(SXR-a) approach [Eqs. (5) - (7), ]. The FXL-c and SXR-a ovals are one dimensional. In the former, the τi value is constrained to be effectively zero. In the latter, the τi values returned are all pegged at the upper bound, 40 s, of the SSM(SXR-a) τi iteration (note the ordinate scale break). Neither of these τi values is realistic. In contrast, the mean τi value returned by FXR-a is 0.41 (± 0.02) s, which is quite reasonable.
If the R1S term was contributing proportionately [“reporting,” Eqs. (5)-(7)], fitting the same data with SXR-a would be expected to change the returned τi and Ktrans values only slightly from the FXR-a magnitudes (13). However as we see, Ktrans reverts back to 0.26 (± 0.01), closer to its FXL-c value, the value of ve returned is 0.37 (± 0.002), and τi rises to 40 s, the upper bound set for the iterative fitting algorithm (note the ordinate scale break): it is “pegged.” Once again, the oval is a 1D bar. We have observed this behavior also for in vivo human malignant breast tumor (13,14) and myocardial muscle (28) tissues. A τi value of 40 s is no more reasonable than a τi value of zero (13,14). For a typical cell membrane water permeability coefficient [PW = 1.4 × 10−4 cm/s], a 40 s τi value would correspond to a 336 μm diameter [d = 6PW τi] for a cell approximated as a sphere (13). This is impossibly large. This suggests that the R1S contribution (1H2Oo and 1H2Ob signals mostly) is very disproportionately small, if not completely absent - most likely due to transverse relaxation “quenching” (13,14). Accounting for it, as the SXR-a does, when it is not actually reporting, over-weights it and seems to cause systematic errors in Ktrans and ve. [SXR-a does work well for cell suspension NMR experiments – where the cell density is much less than tissue, and the R1S contribution can be evident (27,29).] On the other hand, the FXR-a returned value of τi, 400 ms, is quite reasonable (12,13). Furthermore, FXR-a often yields a better match to the experimental time-course (Figs. 1d, 1e, and 1f). Thus, we will henceforth demonstrate the capabilities of FXR-a as a practical tool for prostate DCE-MRI data. In effect, we are using the τi magnitude as a model selection criterion.
Parameter Correlations and Uncertainties
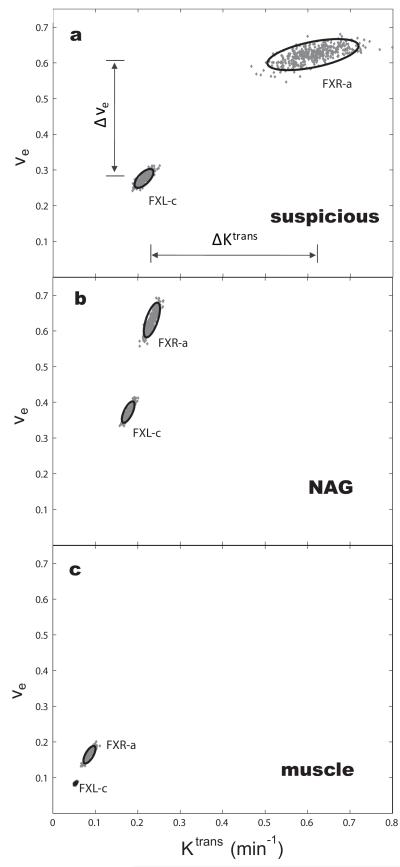
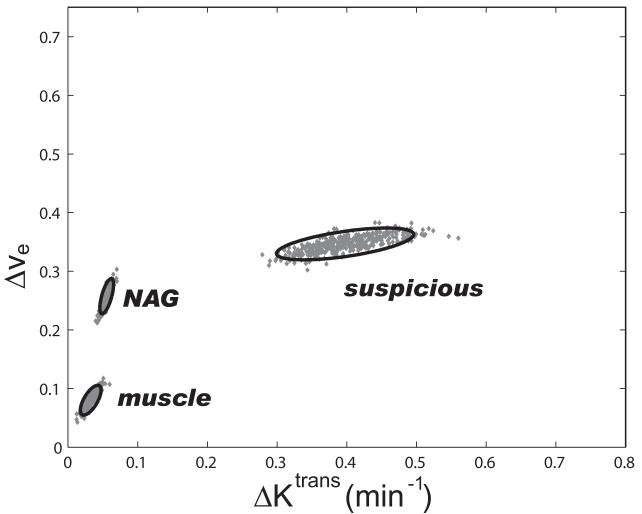
Besides model and data agreement from a fitting, it is important to estimate any correlation between parameters varied, and also the parameter uncertainty resulting from the fitting process itself. To these ends, Monte Carlo simulations similar to those of Fig. 4 were carried out. These were applied to the data points of each of the three Fig. 1 time-courses (Figs. 1d, 1e, and 1f). The Figure 5 panels show ve vs. Ktrans plots: the 800 gray points in each panel have the coordinates of the final fitted values - the initial guesses spanned the plot ranges. Two point clusters are shown for each tissue ROI: one for the SM(FXL-c) fitting, with two parameters [Ktrans and ve] varied, and one for the SSM(FXR-a) fitting, with three parameters [Ktrans, ve, and τi] varied. All panels have the same scales, so the results can be readily compared. The two standard deviation (SD) ellipses are also superimposed (28). In the suspicious prostate tissue (panel a), the difference between the Ktrans values returned by the SSM(FXR-a) and SM(FXL-c) fittings is large: ΔKtrans = 0.38 min−1. Analogous to what we find for breast tumors (13,14,16,17,21), it is more than six times larger than for the NAG prostate tissue (panel b), where it is 0.06 min−1. Indeed, the ΔKtrans parameter is very useful for discriminating malignant from benign prostate tissue (20). For the obturator muscle tissue (panel c), the ΔKtrans value is even smaller, 0.03 min−1. As far as the effect on the Ktrans parameter is concerned, the exchange systems in the NAG and muscle tissues remain in, or close to, the FXL condition during most of DCE time-course. This is true despite the fact that the maximum contrast enhancements of NAG and suspicious ROIs are similar: it is the difference in time-course shapes (compare Figs. 1d and 1e) that is important here. The 2SD ellipses show that, for these ROIs and for this subject, the ΔKtrans parameter is significantly nonzero for the suspicious prostate tissue, and the Δve parameter is significantly nonzero for all three tissues. The latter point is made evident in Figure 6, which shows the plot of ΔKtrans vs. ve (ΔKtrans and Δve; defined as SSM - SM) for the Fig. 5 results. With Fig. 6 having exactly the same scale as that of Fig. 5 (though the quantities differ), the ellipse sizes suggest some cancellations of other systematic errors in the pharmacokinetic fittings. The sources of these may include, but are not limited to: 1) fixed parameter errors (e.g., h, r1 values); 2) AIF timing and amplitude uncertainties (since the same AIF is used for the SSM/SM fitting pair); and 3) (adjusted) parameter correlations. It is worth noticing that the separation of the center of the suspicious tissue ΔKtrans cluster from that of the NAG tissue [ΔKtranssuspic − ΔKtransNAG] (i.e., Δ[ΔKtrans]) is very similar to that of the FXR-a suspicious and NAG tissue clusters in Figs. 5a,b [Ktrans(FXR)suspic − Ktrans(FXR)NAG]. This suggests better discrimination by the ΔKtrans biomarker. The drastically different parameter values for these tissue types from pharmacokinetic analyses that differ only in their water exchange kinetics assumptions exhibit mostly the effects of that exchange, which are unique to DCE-MRI pharmacokinetics.
Figure 5.
The 2D ve/Ktrans parameter spaces showing 400 Monte Carlo SSM(FXR-a) [Eq. (5), ] fittings (points) and SM(FXL-c) [Eqs. (1)-(4), τb = τi → 0] fittings (points) of the three Fig. 1d-f time-course points: suspicious (a), NAG (b), and muscle (c). The Δ biomarkers, Δve and ΔKtrans, are defined in panel a. It is seen that ΔKtrans is significantly large for only the suspicious ROI: malignancy was subsequently found on the same side of the prostate as this ROI.
Figure 6.
The 2D Δve/ΔKtrans parameter space showing the differences (points) of 400 Monte Carlo SSM(FXR-a) [Eq. (5), ] fittings and SM(FXL-c) [Eqs. (1)-(4), τb = τi → 0] fittings of the three Fig. 1d-f ROI time-course points: suspicious, NAG, and muscle. It is seen that ΔKtrans is significantly large for only the suspicious ROI: malignancy was subsequently found on the same side of the prostate as this ROI.
Two Parameter Fittings
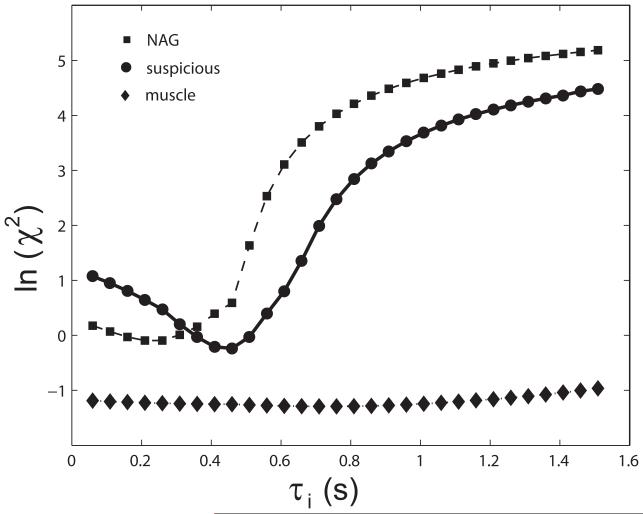
For tissues with low CR extravasation, the interstitial [CR] may not reach a level that transcytolemmal water exchange appears to slow significantly (12,15), and thus a three parameter FXR-a fitting carries larger uncertainty with little benefit (18). However, a two parameter SSM(FXR-a) fitting with τi held fixed, but at some reasonable nonzero value, can be beneficial when S/N is small. Figure 7 exemplifies this approach for evaluating τi. Two parameter fittings using SSM(FXR-a) analyses at 30 different fixed τi values were performed on the three Fig. 1 data sets. The natural logarithms of the goodness of fitting chi square statistic, χ2 = Σ [Sdata(t) − Smodel(t)]2, for these are plotted vs. the τi value. The fixed τi that yields the smallest χ2 represents the most likely τi value. For the three tissue types shown in Fig. 1, both suspicious and NAG tissues show well defined τi minima supporting the significance of the SSM(FXR-a) three parameter fittings of Figs. 1, 4, and 5. For the obturator muscle ROI, however, τi is not as readily accessible (i.e., greater uncertainty). The results in Fig. 7 suggest that for the three tissue ROIs chosen for this subject, τi is ~450 ms, ~250 ms, and ~ 750 ms for the suspicious and normal-appearing prostate tissues and the obturator muscle tissue, respectively. The latter is similar to values we have reported for other muscle tissues (25). It is important to note that for the smallest Ktrans value, that of the muscle ROI, the τi minimum “washes out” toward the FXL side, i.e., τi →0. Thus, the τi value becomes less determinate, and approaches zero, not because τi is actually small [it is ~750 ms], but because Ktrans is small.
Figure 7.
The τi-dependence of the natural logarithm of the fitting goodness measure, χ2, for data from the three (Fig. 1c-f) ROIs: suspicious, NAG, and muscle. The model used was SSM(FXR-a) [Eq. (5), ], but with only two parameters (Ktrans and ve) varied. The τi parameter was held fixed at each value on the abscissa. The minimum χ2 values are seen at τi = 450, 250, and 750 ms for suspicious, NAG, and muscle, respectively; with increasing uncertainties.
τi Mapping
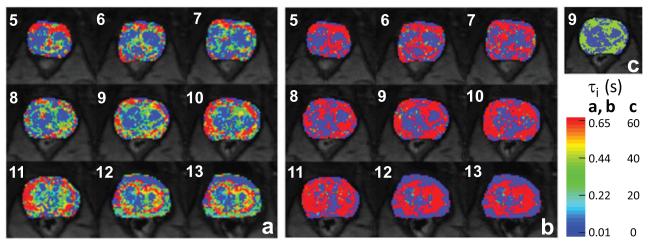
All of the results above are for ROI-averaged signal data. When the S/N is sufficient, one can apply analyses to signals on a pixel-by-pixel basis, and produce DCE-MRI parametric maps (13-16,21,23). Figure 8 shows zoomed τi color maps overlaid on a central set of nine post-contrast axial pelvic DCE image slices of a different subject (No. 8). No malignancy was found in any of the ten subsequent biopsy core specimens. The Fig. 8a maps result from FXR-a analyses, while those of Fig. 8b result from SXR-a analyses. The color scale is the same for Figs. 8a and 8b. Conspicuous peripheral/central zone contrast is evident in most slices. Many transitional/central zone (TZ/CZ) pixels have very small τi values - effectively zero in some cases. In the FXR-a maps, the τi values for a majority of peripheral zone (PZ) (and possibly fibromuscular stroma) pixels are in the 300-800 ms range: (thus a number of PZ pixels exceed the color scale maximum). From literature physiological NMR studies for cell suspensions (27,29), where τi can be measured with greater precision, these values are very reasonable and support the τi parameter interpretation. The (spatial) correlation with known tissue structure (i.e., PZ) supports τi significance.
Figure 8.
Nine axial prostate image slice τi parametric maps are shown for a different subject, whose subsequent biopsy specimens revealed no malignancy. The maps in panel a were produced with the SSM(FXR-a) model [Eq. (5), ], while those in panel b come from the SSM(SXR-a)model [Eqs. (5) - (7), ]. They have the same color scale. The peripheral zone (PZ) τi values in the panel b maps are each pegged at the color scale upper limit, 0.65 s. The slice 9 map in panel c is the same as in panel b, except that the color scale is changed. It is clear that in panel c the PZ τi values are each pegged at 40 s, the upper bound of the SSM(SXR-a) τi iteration. Thus, the PZ τi values in panel b are unrealistic. Good PZ/central zone, transition zone contrast is seen in each panel a image slice.
Figures 8b and 8c show the mapping equivalent of the Fig. 4 evidence for disproportionate 1H2Oo and 1H2Ob signal transverse relaxation quenching. The SXR-a maps in Fig. 8b exhibit PZ τi values that are uniformly above the color scale maximum (which is the same as for Fig. 8a). When the color scale maximum is raised considerably (Fig. 8c, for slice 9), we see that SXR-a returns peripheral zone τi values overwhelmingly approaching the upper bound set for the iterative fitting, 40 s. This is just as unreasonable for this non-malignant prostate tissue as it is for the malignant tissue ROI analyzed in Fig. 4. These τi values are pegged. Though there is spatial correlation in the (essentially binary) Fig. 8c map, it is not reasonable that all PZ τi values be identical. That is, one does not expect a correct map to be binary. This spatial correlation further supports that the SXR-a incompatibility with the data is due to selective signal quenching rather than to some complicated parameter correlation. In conclusion, Figs. 4 and 8 each strongly indicates the incompatibility of the SXR-a model with prostate DCE-MRI data.
DISCUSSION
Extensive effort has been devoted to developing prostate DCE-MRI through the last decade (2-5). Still, MR imaging of prostate cancer remains largely a research endeavor because it has lacked the specificity required for clinical relevance. Prostate DCE-MRI time-course data often present noticeable enhancement even for benign tissues. This means that there is a relatively diminished time-course signature difference between benign and malignant tissues based solely on qualitative, visual inspection of the plots. Depending on the pharmacokinetic paradigm used to model such data, this often results in non-significant pharmacokinetic parameter discrimination.
Importantly, most current prostate quantitative DCE-MRI time-course analyses employ some variant of the SM which ignores inter-compartmental water exchange effects, an aspect unique to MRI. Using SSM2, we have shown that water exchange effects are CR extravasation dependent and can be significant in prostate DCE. Accounting for these with the FXR-a version of SSM1 results in greater benign/malignant parameter separation, and this could represent a significant advance for prostate cancer detection (20).
Further enhancement of water exchange sensitivity can be achieved through MRI data acquisition optimization. The results presented here suggest that the influence of τi on prostate DCE-MRI data is significant, and potentially biomedically very useful. However, all of the results were obtained with TR = 5 ms and FA = 15°. [Most prostate DCE-MRI data in the literature resulted from somewhat similar T1 relaxation weighting. Thus, there were almost certainly exchange effects present in those data, which were missed by the SM analyses used.] Figure 3b suggests that, in future acquisitions, data τi-sensitivity can be enhanced by reducing FA to ~8°. A balance of this enhanced τi-sensitivity against the slightly sacrificed S/N and reduced DCE-MRI dynamic range has to be determined. Unproductively, exchange-sensitivity as well as S/N can also be diminished by data acquisition adjustment (20).
We have shown that, due to the heavy CR extravasation, τi can often be readily mapped using the FXR-a SSM approximation. We find this parameter to be elevated in the peripheral zone (PZ), where most cancers are found: there, τi is often in the range of hundreds of ms, most influential to DCE-MRI pharmacokinetic modeling. Furthermore, the “cold” centers in the Fig. 8a τi maps suggest that while PZ cell membrane water exchange systems depart their FXLs during the CR passage, TZ/CZ systems generally do not. A very small returned τi value (e.g., in the TZ/CZ) does not necessarily mean that τi is actually small, however. It could mean that the systems did not depart the FXLs sufficiently for τi to be determinate (τi → 0 in the FXL). But, this happens for small CR extravasation (Fig. 3), and TZ/CZ Ktrans values are rather large, 0.3 min−1 (20). This suggests that TZ/CZ τi values actually are small. If the TZ/CZ cells are not unusually small in size, this in turn suggests that they have high metabolic activities – possibly because glucose also extravasates more rapidly from the leakier TZ/CZ capillaries (27).
It is interesting to note that prostate glandular duct spaces are particularly abundant in the peripheral zone (11). It is thought that, in the normal prostate, these spaces may be inaccessible to CR (11,30). If so, then the ductules will appear to the model as a fractional population of larger cells. Though this might affect ve, it might particularly increase τi in the normal PZ (as we do see); if the duct spaces are larger than the parenchymal cells (11). However, the ductules are lined with epithelial cells, and there could also be active cycling of water across the epithelium (27,31), which would prevent τi from being too large. It is thought that, in advanced cancer CR can enter the duct (11,30). This might be expected to make PZ ve and τi smaller in malignant foci. Perhaps the decreased tumor core τi observed in our SSM parametric mapping (20) reflects this. Alternatively, this may represent a cellular metabolic response to a more rapid glucose extravasation in the tumor core. The latter’s Ktrans values are large (20), and Ktrans measures the extravasation rate of CR. Any peri-endothelial CR extravasation surely also signals adventitious glucose extravasation through the same pathway. The molecular size of glucose is slightly smaller than that of CR, and they are of similar hydrophilicities. These observations certainly bear further investigation.
The simplified FXR-a model provides both the strength and a limitation of current work. On the one hand, FXR-a gives the same result as FXL-c when τi is actually small and/or when the interstitial CR concentration is small (e.g., obturator muscle, Fig. 1f) due to sluggish extravasation. But, it readily detects exchange effects (Figs. 1d, 1e, 4-8). Thus, it is an exchange-sensitized analysis. On the other hand, the FXR-a approximation assumes effectively complete quenching of the faster relaxing phenomenological component. The τi values returned by the SXR-a analyses in Figs. 4 and 8 suggest this is almost the case in prostate tissue. This obviously requires further investigation, which can be approached both by simulation and experiment.
CONCLUSIONS
Using a water exchange-sensitized pharmacokinetic model (FXR-a), we demonstrate the effect of non-zero τi on other pharmacokinetic parameters with simulations and with data analyses. This shows that ΔKtrans could be a very useful biomarker for benign/malignant tissue discrimination. In the companion paper (20), we show that the ROI-averaged ΔKtrans value correlates with the number of ipsilateral (to the ROI) biopsy cores found positive for adenocarcinoma by pathology (a measure of disease extent) and with the independent determination of the Gleason score for disease severity. We also demonstrate that τi maps themselves exhibit prostate zone contrast, with very interesting pathophysiologic implications.
Highlights.
Prostate pharmacokinetic MRI data were modeled w. & w/o water exchange.
Model parameter influence/correlation was investigated using real/simulated data.
The model contrast agent extravasation rate difference detects malignancy.
Gland anatomical zones show mean intracellular water molecule lifetime differences.
ACKNOWLEDGEMENTS
Grant Support: Medical Research Foundation of Oregon (XL), NIH: RO1-EB00422 (CSS), RO1-NS40801 (CSS,WDR), computational support provided by an administrative supplement NIH UL1RR024140-04S1, and RSNA Research and Education Foundation: Research Medical Student Grant #RMS0801 (FS).
We thank Dr. Charles Thomas for continued support and encouragement.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- [1].Jager GJ, Ruijter ET, van de Kaa CA, de la Rosette JJ, Oosterhof GO, Thornbury JR, Ruijs SH, Barentsz JO. Dynamic TurboFLASH subtraction technique for contrast-enhanced MR imaging of the prostate: correlation with histopathologic results. Radiology. 1997;203:645–652. doi: 10.1148/radiology.203.3.9169683. [DOI] [PubMed] [Google Scholar]
- [2].Franiel T, Hamm B, Hricak H. Dynamic contrast-enhanced magnetic resonance imaging and pharmacokinetic models in prostate cancer. European radiology. 2011;21:616–626. doi: 10.1007/s00330-010-2037-7. [DOI] [PubMed] [Google Scholar]
- [3].McMahon CJ, Bloch BN, Lenkinski RE, Rofsky NM. Dynamic contrast-enhanced MR imaging in the evaluation of patients with prostate cancer. Magn Reson Imaging Clin N Am. 2009;17:363–383. doi: 10.1016/j.mric.2009.01.013. [DOI] [PubMed] [Google Scholar]
- [4].Bonekamp D, Macura KJ. Dynamic contrast-enhanced magnetic resonance imaging in the evaluation of the prostate. Top Magn Reson Imaging. 2008;19:273–284. doi: 10.1097/RMR.0b013e3181aacdc2. [DOI] [PubMed] [Google Scholar]
- [5].Alonzi R, Padhani AR, Allen C. Dynamic contrast enhanced MRI in prostate cancer. Eur J Radiol. 2007;63:335–350. doi: 10.1016/j.ejrad.2007.06.028. [DOI] [PubMed] [Google Scholar]
- [6].Oto A, Kayhan A, Jiang Y, Tretiakova M, Yang C, Antic T, Dahi F, Shalhav AL, Karczmar G, Stadler WM. Prostate cancer: differentiation of central gland cancer from benign prostatic hyperplasia by using diffusion-weighted and dynamic contrast-enhanced MR imaging. Radiology. 2010;257:715–723. doi: 10.1148/radiol.10100021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Alonzi R, Taylor NJ, Stirling JJ, d’Arcy JA, Collins DJ, Saunders MI, Hoskin PJ, Padhani AR. Reproducibility and correlation between quantitative and semiquantitative dynamic and intrinsic susceptibility-weighted MRI parameters in the benign and malignant human prostate. J Magn Reson Imaging. 2010;32:155–164. doi: 10.1002/jmri.22215. [DOI] [PubMed] [Google Scholar]
- [8].Eyal E, Bloch BN, Rofsky NM, Furman-Haran E, Genega EM, Lenkinski RE, Degani H. Principal component analysis of dynamic contrast enhanced MRI in human prostate cancer. Invest Radiol. 2010;45:174–181. doi: 10.1097/RLI.0b013e3181d0a02f. [DOI] [PubMed] [Google Scholar]
- [9].Franiel T, Ludemann L, Rudolph B, Lutterbeck E, Hamm B, Beyersdorff D. Differentiation of prostate cancer from normal prostate tissue: role of hotspots in pharmacokinetic MRI and histologic evaluation. AJR Am J Roentgenol. 2010;194:675–681. doi: 10.2214/AJR.09.3233. [DOI] [PubMed] [Google Scholar]
- [10].Turkbey B, Thomasson D, Pang Y, Bernardo M, Choyke PL. The role of dynamic contrast-enhanced MRI in cancer diagnosis and treatment. Diagn Interv Radiol. 2010;16:186–192. doi: 10.4261/1305-3825.DIR.2537-08.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Noworolski SM, Vigneron DB, Chen AP, Kurhanewicz J. Dynamic contrast-enhanced MRI and MR diffusion imaging to distinguish between glandular and stromal prostatic tissues. Magn Reson Imaging. 2008;26:1071–1080. doi: 10.1016/j.mri.2008.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Li X, Rooney WD, Springer CS. A unified magnetic resonance imaging pharmacokinetic theory: intravascular and extracellular contrast reagents. Magn Reson Med. 2005;54:1351–1359. doi: 10.1002/mrm.20684. Erratum: Magn Reson Med 2006; 55:1217. [DOI] [PubMed] [Google Scholar]
- [13].Li X, Huang W, Morris EA, Tudorica LA, Seshan VE, Rooney WD, Tagge I, Wang Y, Xu J, Springer CS. Dynamic NMR effects in breast cancer dynamic-contrast-enhanced MRI. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:17937–17942. doi: 10.1073/pnas.0804224105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Huang W, Li X, Morris EA, Tudorica LA, Seshan VE, Rooney WD, Tagge I, Wang Y, Xu J, Springer CS. The magnetic resonance shutter speed discriminates vascular properties of malignant and benign breast tumors in vivo. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:17943–17948. doi: 10.1073/pnas.0711226105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Yankeelov TE, Rooney WD, Li X, Springer CS. Variation of the relaxographic “shutter-speed” for transcytolemmal water exchange affects the CR bolus-tracking curve shape. Magn Reson Med. 2003;50:1151–1169. doi: 10.1002/mrm.10624. [DOI] [PubMed] [Google Scholar]
- [16].Huang W, Tudorica LA, Li X, Thakur SB, Chen Y, Morris EA, Tagge IJ, Korenblit M, Rooney WD, Koutcher JA, Springer CS. Discrimination of benign and malignant breast lesions by using shutter-speed dynamic-contrast-enhanced MR imaging. Radiology. 2011;261:394–403. doi: 10.1148/radiol.11102413. doi:0010.1148/radiol.1102413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Springer CS, Tudorica LA, Li X, Thakur S, Morris EA, Oh KY, Kettler MD, Chen Y, Tagge IJ, Hemmingson SL, Korenblit M, Grinstead JW, Laub G, Koutcher JA, Huang W. Meta-population breast cancer screening with the ΔKtrans DCE-MRI parameter. Proc Int Soc Magn Reson Med. 2011;19:3097. [Google Scholar]
- [18].Buckley DL, Kershaw LE, Stanisz GJ. Cellular-interstitial water exchange and its effect on the determination of contrast agent concentration in vivo: dynamic contrast-enhanced MRI of human internal obturator muscle. Magn Reson Med. 2008;60:1011–1019. doi: 10.1002/mrm.21748. [DOI] [PubMed] [Google Scholar]
- [19].Lowry M, Zelhof B, Liney GP, Gibbs P, Pickles MD, Turnbull LW. Analysis of prostate DCE-MRI: comparison of fast exchange limit and fast exchange regimen pharmacokinetic models in the discrimination of malignant from normal tissue. Invest Radiol. 2009;44:577–584. doi: 10.1097/RLI.0b013e3181b4c1fe. [DOI] [PubMed] [Google Scholar]
- [20].Li X, Priest RA, Woodward WJ, Tagge IJ, Siddiqui F, Huang W, Rooney WD, Beer TM, Garzotto MG, Springer CS. Feasibility of Shutter-Speed DCE-MRI for improved prostate cancer detection. Magn Reson Med. doi: 10.1002/mrm.24211. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Li X, Huang W, Yankeelov TE, Tudorica A, Rooney WD, Springer CS. Shutter-speed analysis of contrast reagent bolus-tracking data: Preliminary observations in benign and malignant breast disease. Magn Reson Med. 2005;53:724–729. doi: 10.1002/mrm.20405. [DOI] [PubMed] [Google Scholar]
- [22].Landis CS, Li X, Telang FW, Molina PE, Palyka I, Vetek G, Springer CS. Equilibrium transcytolemmal water-exchange kinetics in skeletal muscle in vivo. Magn Reson Med. 1999;42:467–478. doi: 10.1002/(sici)1522-2594(199909)42:3<467::aid-mrm9>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- [23].Li X, Rooney WD, Varallyay CG, Gahramanov S, Muldoon LL, Goodman JA, Tagge IJ, Selzer AH, Pike MM, Neuwelt EA, Springer CS. Dynamic-contrast-enhanced-MRI with extravasating contrast reagent: rat cerebral glioma blood volume determination. J Magn Reson. 2010;206:190–199. doi: 10.1016/j.jmr.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Kovar DA, Lewis M, Karczmar GS. A new method for imaging perfusion and contrast extraction fraction: input functions derived from reference tissues. J Magn Reson Imaging. 1998;8:1126–1134. doi: 10.1002/jmri.1880080519. [DOI] [PubMed] [Google Scholar]
- [25].Yankeelov TE, Rooney WD, Huang W, Dyke JP, Li X, Tudorica A, Lee JH, Koutcher JA, Springer CS. Evidence for shutter-speed variation in CR bolus-tracking studies of human pathology. NMR in Biomedicine. 2005;18:173–185. doi: 10.1002/nbm.938. [DOI] [PubMed] [Google Scholar]
- [26].Hamby DM. A comparison of sensitivity analysis techniques. Health Phys. 1995;68:195–204. doi: 10.1097/00004032-199502000-00005. [DOI] [PubMed] [Google Scholar]
- [27].Zhang Y, Poirier-Quinot M, Springer CS, Balschi JA. Active trans-plasma membrane water cycling in yeast is revealed by NMR. Biophys J. 2011;101:2833–2842. doi: 10.1016/j.bpj.2011.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Li X, Springer CS, Jerosch-Herold M. First-pass dynamic contrast-enhanced MRI with extravasating contrast reagent: evidence for human myocardial capillary recruitment in adenosine-induced hyperemia. NMR in Biomedicine. 2009;22:148–157. doi: 10.1002/nbm.1293. [DOI] [PubMed] [Google Scholar]
- [29].Labadie C, Lee JH, Vetek G, Springer CS. Relaxographic imaging. J Magn Reson B. 1994;105:99–112. doi: 10.1006/jmrb.1994.1109. [DOI] [PubMed] [Google Scholar]
- [30].Noworolski SM, Reed GD, Kurhanewicz J. A novel luminal water model for DCE MRI of prostatic tissues. Proc Int Soc Magn Reson Med. 2011;19:50. [Google Scholar]
- [31].Zeuthen T. Water-transporting proteins. J Membr Biol. 234:57–73. doi: 10.1007/s00232-009-9216-y. [DOI] [PubMed] [Google Scholar]