A scoping review of malaria forecasting: past work and future directions

Abstract

Objectives

There is a growing body of literature on malaria forecasting methods and the objective of our review is to identify and assess methods, including predictors, used to forecast malaria.

Design

Scoping review. Two independent reviewers searched information sources, assessed studies for inclusion and extracted data from each study.

Information sources

Search strategies were developed and the following databases were searched: CAB Abstracts, EMBASE, Global Health, MEDLINE, ProQuest Dissertations & Theses and Web of Science. Key journals and websites were also manually searched.

Eligibility criteria for included studies

We included studies that forecasted incidence, prevalence or epidemics of malaria over time. A description of the forecasting model and an assessment of the forecast accuracy of the model were requirements for inclusion. Studies were restricted to human populations and to autochthonous transmission settings.

Results

We identified 29 different studies that met our inclusion criteria for this review. The forecasting approaches included statistical modelling, mathematical modelling and machine learning methods. Climate-related predictors were used consistently in forecasting models, with the most common predictors being rainfall, relative humidity, temperature and the normalised difference vegetation index. Model evaluation was typically based on a reserved portion of data and accuracy was measured in a variety of ways including mean-squared error and correlation coefficients. We could not compare the forecast accuracy of models from the different studies as the evaluation measures differed across the studies.

Conclusions

Applying different forecasting methods to the same data, exploring the predictive ability of non-environmental variables, including transmission reducing interventions and using common forecast accuracy measures will allow malaria researchers to compare and improve models and methods, which should improve the quality of malaria forecasting.

Article summary.

Article focus

• Accurate predictions of malaria can provide public health and clinical health services with the information needed to strategically implement prevention and control measures.

• The diversity in forecasting accuracy measures and the use of scale-dependent measures limits the comparability of forecasting results, making it difficult to identify the optimal predictors and methods for malaria forecasting.

• The objective was to identify and assess methods, including predictors, used to forecast malaria.

Key messages

• When performing forecasting, it is important to understand the assumptions of each method as well as the associated advantages and disadvantages.

• Common accuracy measures are essential as they will facilitate the comparison of findings between studies and methods.

• Applying different forecasting methods to the same data and exploring the predictive ability of non-environmental variables, including transmission reducing interventions, are necessary next steps as they will help determine the optimal approach and predictors for malaria forecasting.

Strengths and limitations of this study

• The strength of this review is that it is the first review to systematically assess malaria forecasting methods and predictors, and the recommendations in the review, if followed, should lead to improvement in the quality of malaria forecasting.

• A limitation of a literature review is that unpublished methods, if any, are omitted from this review.

Introduction

In 1911, Christophers¹ developed an early-warning system for malaria epidemics in Punjab based on rainfall, fever-related deaths and wheat prices. Since that initial system, researchers and practitioners have continued to search for determinants of spatial and temporal variability of malaria to improve systems for forecasting disease burden. Malaria forecasting is now conducted in many countries and typically uses data on environmental risk factors, such as climatic conditions, to forecast incidence for a specific geographic area over a certain period of time.

Malaria can be forecasted using an assortment of methods and significant malaria predictors have been identified in a variety of settings. Our objective was to identify and assess methods, including predictors, used to forecast malaria. This review is intended to serve as a resource for malaria researchers and practitioners to inform future forecasting studies.

Methods

We included in our scoping review studies that forecasted incidence, prevalence or epidemics of malaria over time. Whereas a systematic review is guided by a highly focused research question, a scoping review covers a subject area comprehensively by examining the extent, range and nature of research activity on a topic.² The studies had to use models that included prior malaria incidence, prevalence or epidemics as a predictor. A description of the forecasting model and an assessment of the forecast accuracy were requirements for inclusion. Studies were restricted to human populations and to autochthonous transmission settings. We excluded studies that provided only spatial predictions, exploratory analysis (eg, assessing temporal correlations), mortality predictions and/or individual-level transmission modelling. Commentaries, descriptive reports or studies that did not include original research were also excluded. In addition, for studies that were related (eg, the same setting and the same methods with different time periods), the study with the most comprehensive data was included in the review.

A review protocol was developed and electronic search strategies were guided by a librarian experienced in systematic and scoping reviews. Papers were identified using medical subject headings and key word combinations and truncations: (‘forecast*’ or ‘predictive model*’ or ‘prediction model*’ or ‘time serie*’ or ‘time-serie*’; AND ‘malaria*’). The searches were not restricted by year or language although our searches were restricted by the historical time periods of the databases. The citation searches began on 18 April 2011 and the final citation search was conducted on 29 May 2012. We searched the following databases: CAB Abstracts (1910–2012 Week 20), EMBASE (1947–2012 28 May), Global Health (1910–April 2012), MEDLINE (1948−May Week 3 2012), ProQuest Dissertations & Theses (1861–29 May 2012) and Web of Science (1899–28 May 2012). We performed manual searches of the Malaria Journal (2000–29 May 2012) and the American Journal of Tropical Medicine and Hygiene (1921–May 2012). Grey literature was also searched using Google Scholar, based upon the same key words used to search the databases. In addition, the websites of the WHO and the US Agency for International Development were also examined for any relevant literature. To ensure that all appropriate references were identified, hand searching of reference lists of all included studies was conducted and any potentially relevant references were incorporated into the review process.

The citations were imported into EndNote X5 (Thomas Reuters) for management. Two main reviewers (KZ and AV) examined all citations in the study selection process with the exception of articles in Chinese, which were reviewed by a third reviewer (ZS). The first stage of review involved each reviewer independently identifying potentially relevant studies based upon information provided in the title and abstract. If it was uncertain whether to include or exclude a study during the first stage of review, the citation was kept and included in the full article review.

The second stage of review involved each reviewer independently identifying potentially relevant studies based upon full article review; data abstraction occurred for those articles that met the inclusion criteria. From each study, we abstracted the following: setting, outcome, covariates, data source(s), time-frame of observed data, forecasting and model evaluation methodologies, final models and associated measures of prediction accuracy. Quality of the included studies was not assessed as the objective was to conduct a scoping review and not a systematic review. Any discordance among the reviewers regarding inclusion or exclusion of studies or with respect to the information abstracted from the included studies was resolved by consultation with another author (DB).

Results

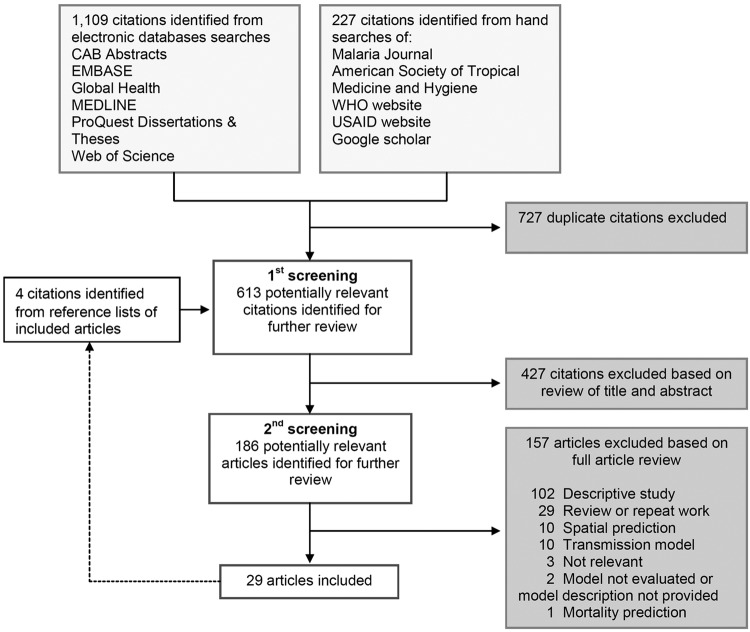
Our search identified 613 potentially relevant articles for the scoping review after duplicate citations were removed (figure 1). We identified 29 different studies that met our inclusion criteria for this review; they are described briefly in table 1. Malaria forecasting has been conducted in 13 different countries with China as the most frequent site of malaria forecasting. The size of the geographic region of study ranged from the municipal level to larger administrative divisions such as country and provinces or districts. Almost all of the studies (97%) used health clinic records of malaria infections from the general population as their data source for malaria infections, with one study using cohort data. Eleven (38%) of the 29 studies used laboratory confirmation of malaria cases (microscopy and/or rapid diagnostic tests), seven (24%) used clinical confirmation and two (7%) used a mixture of clinical and microscopic confirmation. Nine studies did not state whether they used clinical or microscopic confirmation of malaria.

Figure 1.

Flow of literature searches and screening process.

Table 1.

Characteristics of malaria forecasting studies included in review (n=29)

Authors (reference)	Population and setting	Model specifics	Malaria outcome	Number of data points used for training/testing	Evaluation measure
Regression forecasting studies
Adimi et al3	Community health post data from 2004 to 2007 for 23 provinces in Afghanistan; clinical confirmation	23 linear regressions (1 for each province); included autoregressive, seasonal and trend parameters	Monthly cases	31/6 (varied between provinces but last 6 months used only for testing)	Root mean squared error and absolute difference
Chatterjee and Sarkar4	Municipal data for 2002–2005 for Chennai (city), India; microscopic confirmation	Logistic regression; polynominal and autoregressive parameters	Monthly slide positivity rate	36/1	95% CI (for predicted value and compared to observed)
Gomez-Elipe et al5	Health service data from 1997 to 2003 for Karuzi Province, Burundi; clinical confirmation	Linear regression; adjusted for population, lagged weather covariates, autoregressive and seasonal parameters	Monthly incidence	60/24; 1 month ahead forecasts	95% CI, correlation, p value trend line of difference (between predicted and observed)
Haghdoost et al6	District health centre data from 1994 to 2001 for Kahnooj District, Iran; microscopic confirmation	Separate Poisson regressions for Plasmodium vivax and Plasmodium falciparum; population offset, lagged weather covariates, seasonality and trend parameters	10-day cases	213/73	Average percent error
Rahman et al7	Hospital data from 1992 to 2001 for all divisions of Bangladesh; clinical confirmation	Four linear regressions (1 for each administrative division and one for all of Bangladesh); environmental covariate for weeks of highest correlation	Yearly cases	10, 1 year was removed from series at a time	Root mean squared error and relative bias (observed-predicted)
Roy et al8	Municipal data for Chennai (city) (2002–2004) and Mangalore (city) (2003–2007), India; microscopic confirmation	Two linear regressions (one for each city); adjusted for population, lagged weather covariates, autoregressive term, interaction terms, polynomial terms	Monthly SPR (Chennai), monthly cases (Mangalore)	28/8 (Chennai), 48/12 (Mangalore); 1 month ahead	95% CI
Teklehaimanot et al9	Health facility data from 1990 to 2000 for all districts in Ethiopia; microscopic confirmation	10 Poisson regressions (one for each district); lagged weather covariates, autoregressive term, time trend and indicator covariates for week of the year	Weekly cases	572 (varied between districts, training and testing); 52 weeks (year) were removed from series at a time; 1–4 week ahead forecasts	Compared performance of alerts from predicted versus observed cases (using potentially prevented cases)
Xiao et al10	Medical and health unit data from 1995 to 2007 for Hainan Province, China; microscopic confirmation	Poisson regression; lagged weather covariates, autoregressive term	Monthly incidence	144/12	T-test (predictive value significantly different than actual)
Yacob and Swaroop11	Medical data from 1944 to 1996 for all health districts in Punjab; clinical confirmation	19 linear regressions (1 for each district); include coefficients of correlation between rainfall and epidemic figures from 1914 to 1943	Seasonal epidemic figure*		Coefficient of correlation (between actual and predicted epidemic figure)
Yan et al12	Municipal data from 1951 to 2001 for Chongquin (city), China	Linear regression; logarithm curve	Yearly cases	50/1	Visual inspection of predicted within range of actual values
ARIMA forecasting studies
Abeku et al13	Health clinics data from 1986 to 1999 for 20 areas in Ethiopia; mixture of microscopic and clinical confirmed	20 models (1 for each area) compared approaches: Overall average, seasonal average, seasonal adjustment, ARIMA	Monthly cases	168/12 (varied between areas but last 12 months only used for testing); 1–12 month ahead forecasts	Average forecast error
Briët et al14	Health facility data from 1972 to 2005 for all districts in Sri Lanka; microscopic confirmation	25 models (1 for each district) compared approaches: Holt-Winters, ARIMA (seasonality assessed with fixed effects or harmonics) and SARIMA; lagged weather covariates	Monthly cases of malaria slide positives	180/204 (varied between districts but approximately 50% of series reserved for testing); 1–4 month ahead forecasts	Mean absolute relative error
Liu et al15	Data from 2004 to 2010 for China	SARIMA	Monthly incidence	72/12	Visual (plot of predicted vs observed)
Wangdi et al16	Health centre data from 1994 to 2008 for seven districts in Bhutan; microscopic and antigen confirmation	Seven models (one for each district): SARIMA and ARIMAX; lagged weather covariates	Monthly cases	144/24	Mean average percent error
Wen et al17	Data from 1991 to 2002 for Wanning County, China	SARIMA	Monthly incidence	252/12	95% CI
Zhang et al18	CDC data from 1959 to 1979 for Jinan (city) China; clinical confirmation	SARIMA; lagged weather covariates	Monthly cases	84/120 (removed 1967 and 1968 from series)	Visual (plot of predicted vs observed)
Zhou et al19	Data from 1996 to 2007 for Huaiyuan County, China; microscopic and clinical confirmation	SARIMA	Monthly incidence	108/12	Average error
Zhu et al20	Data from 1998 to 2007 for Huaiyuan and Tongbai counties, China	SARIMA	Monthly incidence rates	84/24; 1–12 month ahead forecasts	95% CI and error
Mathematical forecasting studies
Gaudart et al21	Data from cohort of children from 1996 to 2000 in Bancoumana (municipality), Mali from 1996 to 2006; microscopic confirmation	VSEIRS model	Monthly incidence rate	60 (training and testing); 15 day, 1 month, 2 month, seasonal forecasts	Mean absolute percentage error and root mean squared error
Laneri et al22	Health centre data (passive and active surveillance) for Kutch (1987–2007) and Balmer (1985–2005) Districts, India; microscopic confirmation	2 models (one for each district); compared two types of VSEIRS model to linear and negative binominal regressions	Monthly incidence for parameter estimation; seasonal totals (Sept−Dec) for epidemic forecasting	240 (training and testing); 1 to 4 months ahead forecasts	Weighted mean square error and prediction likelihood
Neural network forecast studies
Cunha et al23	Ministry of Health data from 2003 to 2009 for Cornwall (City), Brazil; microscopic confirmation	Compared neural network to linear regression	Monthly cases	72/12; 3, 6 and 12 months forecasts	Absolute error and mean square error
Gao et al24	Data from 1994 to 1999 for Honghe State, China	Neural network	Monthly incidence	48/12	Percent error
Kiang et al25	Hospital and clinic data from 1994 to 2001 for 19 provinces, Thailand; microscopic confirmation	19 neural networks (1 for each province); various architectures used (varied by province)	Monthly incidence	84/12	Root mean square error
Other forecasting methods
Fang et al26	Data from 1956 to 1988 for Xuzhou (City), China	Grey and Grey Verhulst models (1,1)	Yearly incidence	30/2	Percent error
Gao et al27	Data from 1998 to 2005 for Longgang District, China	Grey model (1,1)	Yearly incidence	6/1	Error and percent error
Guo et al28	Data from 1988 to 2010 China	Grey model (1,1)	Yearly incidence	21/2	Visual (plot of predicted vs observed)
Gill29	Medical data from 1925 to 1926 for health districts in Punjab; clinical confirmation	29 forecasts consisting of visual inspection of rainfall, spleen rates and epidemic potential†	Seasonal epidemic (yes/no)		Qualitative comparison of prediction (presence of epidemic) to epidemic figure
Medina et al30	Community health centre data from 1996 to 2004 (14 centres) for Niono District, Mali; clinical confirmation	Multiplicative Holt-Winters model, age-specific rates (three age groups); compared to seasonal adjustment method	Monthly malaria consultation rates	36/72; 2 and 3-month ahead forecasts; one step ahead forecasts	Mean absolute percentage error and 95% CI
Xu and Jin31	Data from 2000 to 2005 for Jiangsu Province, China	Grey model	Yearly cases	4/1	Visual (plot of predicted vs observed number of cases)

*Seasonal epidemic figure is the ratio of October incidence to mean spring incidence.

†Epidemic potential is the coefficient of variability of fevers during the month of October for the periods of 1868–1921.

ARIMA, auto-regressive integrated moving average; ARIMAX, auto-regressive integrated moving average with exogenous input; SARIMA, seasonal auto-regressive integrated moving average; SPR, slide positivity rate; VSEIRS, vector-susceptible-exposed-infected-recovered-susceptible model.

Forecasting studies

The forecasting approaches included statistical modelling, mathematical modelling and machine-learning methods (table 2). The statistical methods included generalised linear models, Auto-Regressive Integrated Moving Average (ARIMA) models³² and Holt-Winters models.³³ The mathematical models were based upon extensions of the Ross-MacDonald susceptible-infected-recovered (SIR) malaria transmission model.³⁴ Other authors predicted malaria incidence using neural networks, a machine-learning technique.³⁵

Table 2.

Summary of malaria forecasting methods (n=29)

Forecasting method	Number of studies (reference)
GLM	123–12 22 23
ARIMA	713, 14 15–20
Grey methods	426–28 31
Smoothing methods*	313 14 30
Neural networks	323, 24, 25
Mathematical models	221 22
Visual	129

References in bold indicate multiple comparisons. ARIMA, auto-regressive integrated moving average; GLM, generalised linear model.

*Includes Holt - (Holt-Winters) Winters, seasonal average, seasonally adjusted average and simple average.

Twelve studies (41%) included in the review used generalised linear models to forecast malaria counts, rates or proportions through linear, Poisson or logistic regression. All but one of the regression models included climate-related covariates such as rainfall, temperature, vegetation and/or relative humidity.¹² Typically, the weather covariates were lagged, to account for the delayed effects of weather on malaria infections. Two studies^{4 8} explored the effects of including covariates as higher-order polynomials. Several of the studies used a generalised linear model approach to time series analysis by including previous (lagged) malaria incidence as an autoregressive covariate in the model. Some models included terms for season or year to account for seasonal and annual variations.

Seven studies (24%) used forecasting approaches based on ARIMA modelling with some including a seasonal component (SARIMA). While not explicitly stated, many studies used a transfer function model, also known as ARIMAX. Typically, these ARIMA-based models incorporated various meteorological series as covariates although one study also included data on the malaria burden in neighbouring districts.¹⁴

Four studies (14%) from China used the Grey method for malaria forecasting, none of which incorporated predictors other than malaria incidence.^{26–28 31} There were two studies (7%) that used mathematical models.^{21 22} Gaudart et al²¹ included a vector component in a SIR-type model and used data from a cohort of children, remote sensing data, literature and expert opinions of entomologists and parasitologists. The study by Laneri et al²² used a vector-susceptible-exposed-infected-recovered-susceptible (VSEIRS) model although they incorporated two different pathways from recovery to susceptibility that were based upon different timescales (seasonal and interannual), mimicking different transmission intensities. They found that rainfall had a significant effect on the interannual variability of epidemic malaria and including rainfall as a predictor improved forecast accuracy. The parameters in their models were based on literature as well as laboratory findings.

We identified three studies (10%) that used neural networks in their analyses, and each study used different input data and a unique network structure.^23–25 Two of the studies used weather variables to predict malaria incidence.^{24 25} Gao et al²⁴ also included evaporation and sunshine hours to predict malaria incidence; two variables that were not included in any other study.

As shown in table 3, climate-related predictors were used consistently in forecasting models, with the most common predictors being rainfall, relative humidity, temperature and normalised difference vegetation index. One study accounted for the effect of malaria incidence in neighbouring districts, but it was not a significant predictor and was excluded from the final model.¹⁴ The mathematical models included non-time varying parameters such as the reporting fraction of cases (proportion of malaria cases in a population that is reported to public health), average life expectancy and several vector characteristics, which are listed in table 4.

Table 3.

Time varying predictors considered in malaria forecasting models

Predictor	Number of studies (reference)
Rainfall
Total rainfall	113–6 9 10 14 16 18 22 25
Average rainfall	28 24
Rainy day index*	114
Number of rainy days/month	124
Humidity
Average relative humidity	76 8 10 16 18 24 25
Minimum humidity	14
Maximum humidity	14
Temperature
Maximum air temperature	84–6 9 10 16 18 24
Minimum air temperature	74 5 9 10 16 18 24
Average air temperature	48 10 24 25
Average LST	23 25
Temperature condition index	17
Vegetation
Average NDVI	23 5
Maximum NDVI	221 25
Vegetation condition index	17
Other environmental predictors
Average air pressure	218 24
Average air evaporation	124
Sunshine hours	124
Other
Malaria in neighbouring districts	114
Population	14

*Rainy day index: the number of days per month when rainfall was larger than zero divided by the number of days that a reading for rainfall was available.

LST, land surface temperature; NDVI, normalised difference vegetation index.

Table 4.

Parameters included in the mathematical forecasting models

Predictor	References
Vector
Mean developmental delay	22
Number of bites per night	21
Probability of a susceptible becoming infected after one single bite from a contagious human	21
Mortality per day	21
Density	21
Length of gonotrophic cycle	21
Time lag of NDVI influence	21
Lowest NDVI value to influence behaviour
Humans
Probability of a susceptible human becoming infected after one single infected bite	21
Probability of becoming susceptible after being resistant	21, 22
Probability of acquiring contagiousness	21, 22
Probability of losing contagiousness	21, 22
Average human life expectancy	22
Infectivity of quiescent cases relative to full-blown infections	22
Other
Reporting fraction*	22

*Reporting fraction is the fraction of malaria cases in the population that are reported to public health.

NDVI, normalised difference vegetation index.

Evaluation methods

Authors used different approaches to evaluate the accuracy of forecasting models. A typical approach was to segment the data into a model building or training portion with the other portion (the ‘holdout’ sample) used for model validation or assessing forecast accuracy. The cross-validation approach used by Rahman et al⁷ and Teklehaimanot et al⁹ excluded 1 year of data at a time, the model was fit to the remaining data, forecast errors (prediction residuals) were computed using data from the missing year and then this process was repeated for subsequent years. The accuracy of the predictions was then estimated from the prediction residuals. Some of the studies used all the available data to fit a model and did not reserve data for assessing forecast accuracy.^{21 22}

Studies compared the forecasts to observed values using various measures: mean-squared error, mean relative error, mean percentage error, correlation coefficients, paired t tests (between predicted and observed values), 95% CI (of predicted values and determined if observed values fell within the interval) and visualisations (eg graphical representations of observed and predicted values).

Comparison of forecasting methods

We could not compare the forecast accuracy of models from different studies due to the lack of common measures and the lack of scale-independent measures. However, we briefly discuss the findings from studies that compared different methods within a single study.

Abeku et al¹³ found that their ARIMA models provided the least accurate forecasts when compared with variations of seasonal averages, and the most accurate forecasts were produced by the seasonal average that incorporated deviations from the last three observations (SA₃). In contrast, Briet et al¹⁴ found that the most accurate model varied by district and forecasting horizon, but the SARIMA approach tended to provide the most accurate forecasts, followed by an ARIMA model with seasonality modelled using a sine term, then Holt-Winters, with the SA₃ providing the least accurate forecasts. They also considered independent time series, such as rainfall and malaria cases in neighbouring districts, in the models. Medina et al³⁰ determined that their Holt-Winters method provided more accurate forecasts and the accuracy did not deteriorate as rapidly as with the SA₃ method. Cunha et al²³ found that their neural network provided more accurate predictions across all three forecast horizons (3, 6 and 12 months) when compared with a logistic regression model.

Discussion

Malaria forecasting can be an invaluable tool for malaria control and elimination efforts. A public health practitioner developed a simple forecasting method, which led to the first early-warning system of malaria.¹ Forecasting methods for malaria have advanced since that early work, but the utility of more sophisticated models for clinical and public health decision making is not always evident. The accuracy of forecasts is a critical factor in determining the practical value of a forecasting system. The variability in methods is the strength of malaria forecasting, as it allows for tailored approaches to specific settings and contexts. There should also be continued effort to develop new methods although common forecasting accuracy measures are essential as they will help determine the optimal approach with existing and future methods.

When performing forecasting, it is important to understand the assumptions of forecast models and to understand the advantages and disadvantages of each. Forecast accuracy should always be measured on reserved data and common forecasting measures should be used to facilitate comparison between studies. One should explore non-climate predictors, including transmission reducing interventions, as well as different forecasting approaches based upon the same data.

Differences between forecasting methods

The regression approach to time series prediction attempts to model the serial autocorrelation in the data through the inclusion of autoregressive terms and/or sine and cosine functions for seasonality. Generalised linear regression models are used commonly and their main advantages are their flexibility and the intuitive nature of this approach for many people relative to ARIMA models. For example, the temporal dynamics observed in time series plots can be feasibly managed in generalised linear models by including several cyclic factors, interaction terms and numerous predictors.³⁶ The main disadvantages are that generalised linear models do not naturally account for correlation in the errors³⁷ and the models may need to be complex to capture all the dynamics of the relationship within a series and between two or more series.³⁸ Failure to accurately model serial autocorrelation may bias the estimation of the effect of predictors as well as underestimate the standard errors. Crucially, regression model residuals must be examined for autocorrelation and it was not always evident that this occurred in the studies we identified using this method. In addition, it was not apparent if any remedial measures were used to account for the effect of autocorrelation on estimates of variance, for example, re-estimating standard errors using heteroskedasticity and autocorrelation consistent (HAC) estimators.³⁹

ARIMA models are designed to account for serial autocorrelation in time series; current values of a series can be explained as a function of past values and past shocks.³⁸ With ARIMA models, once the series have been detrended through differencing, any remaining seasonality can be modelled as part of additional autoregressive or moving average parameters of a SARIMA model. A rule of thumb is that 50 observations are a minimal requirement for ARIMA models,³⁷ whereas SARIMA models require longer time series. The transfer function model, ARIMAX, extends ARIMA by also including as predictors current and/or past values of an independent variable. An advantage of ARIMA models versus GLMs is that ARIMA models naturally represent features of temporal patterns, such as seasonality and autocorrelation. As with generalised linear regression models, the residuals of ARIMA models need to be examined for residual correlation. Also, when incorporating an input series into the model, prewhitening should occur prior to the cross-correlation assessment for the transfer function models. Prewhitening is when the residuals from an ARIMA model for the input series are reduced to ‘white noise’ and the same ARIMA model is applied to the output series.³⁷ The authors did not always report that they prewhitened the series prior to assessing cross-correlations. The relationship between the two resulting residual series is then estimated by the cross-correlation function. Without prewhitening, the estimated cross-correlation function may be distorted and misleading.

Four studies from China used the Grey method for malaria forecasting.^{26–28 31} This forecasting method is essentially a curve-fitting technique based on a smoothed version of the observed data.^{40 41} The Grey model appears most useful in predicting malaria when using a very short time series and when there is a strong linear trend in the data. This is due to the nature of the GM(1,1) model which will always generate either exponentially increasing or decreasing series.⁴² Its value in malaria prediction beyond that of the simpler statistical modelling approaches is yet to be determined.

The approach to prediction differs between mathematical models and other approaches such as generalised linear models, ARIMA and Grey models. The Ross-Macdonald mathematical model divides the population under study into different compartments such as SIR, and uses differential equations to model the transition over time of individuals from one group to another. By using differential equations, these models can represent explicitly the dynamics of malaria infection, mosquito populations and human susceptibility. The disadvantages of mathematical models include the difficulty in finding appropriate, setting-specific data for the parameters. Also, the computational complexity of these models increases with the number of parameters, resulting in the omission of relevant features of malaria dynamics for the model to be manageable.⁴³

A neural network is a machine-learning method that connects a set of inputs (eg, weather covariates) to outputs (eg, malaria counts).⁴⁴ The connection between inputs and outputs are made via ‘neurons’ and the number of links and corresponding weights are chosen to give the best possible fit to the training data. Neural networks have been proven to be useful in their capacity to handle non-linear relationships as well as a large number of parameters, and also their ability to detect all possible interactions between predictor variables.⁴⁵ Mathematical models and neural networks are able to capture thresholds or limits on malaria transmission, which cannot be readily captured by statistical approaches. For example, in generalised linear models, a small decrease in the temperature leads to a small decrease in malaria incidence. Neural networks and mathematical models can express explicitly that there will be no malaria transmission below a certain temperature. The disadvantages of neural networks include difficulties in determining how the network is making its decision and its greater computational burden,⁴⁶ both of which depend upon the number of input parameters included in the model. In addition, neural networks have a greater susceptibility to overfitting⁴⁵ and several thousand observations are typically required to fit a neural network with confidence.⁴⁶ Malaria time series are unlikely to contain several thousands of observations, perhaps unless the observations are aggregated over time (eg, monthly) and location (eg, national level).

Researchers have examined many forecasting methods, but published articles tend to describe the application of a single method to a unique dataset. Direct comparison of methods would be easier if multiple malaria forecasting methods were applied to the same data. This approach would allow the identification of methods that provide the most accurate short-term, intermediate-term and long-term forecasts, for a given setting and a set of predictors. It would also allow the exploration of gains in forecast accuracy by using a weighted combination of forecasts from several models and/or methods.⁴⁷

Malaria predictors

It has been suggested that climate and meteorological predictors have greater predictive power when modelling malaria incidence in areas with unstable transmission compared to areas with stable endemicity.⁴⁸ It is interesting to note that nearly all of the models focused narrowly on a small number of environmental predictors despite the importance of other predictors of malaria incidence, such as land use, bednets, indoor residual spraying and antimalarial resistance. Forecast accuracy may be weakened if transmission-reducing interventions are not considered in the models.

Forecast evaluation

Model selection based upon model-fitting criteria, such as Akaike's information criterion, Bayesian information criterion or the coefficient of determination, are standard measures considered when choosing a regression model. Using such measures to guide forecast model selection may result in selecting models with a greater number of parameters and ‘over-fitting’, which tends to result in inaccurate forecasts.⁴⁹ For the purposes of forecasting, visualisations of forecasts compared to observations and forecast accuracy measures, such as the mean absolute forecast error, provide more direct and intuitive model selection criteria.

When choosing how much of the series to reserve for testing the model, it is recommended to reserve at least as much as the maximum forecast horizon.⁵⁰ Cross-validation is a more efficient use of data than partitioning a data set into train and test segment, although it is more computational intensive. It is recommended in cross-validation that only prior observations be used for testing a future value.⁵⁰

Various direct measures were used to estimate forecasting error. Absolute measures, such as the mean absolute error (MAE), are relevant for measuring accuracy within a particular series but not across series because the magnitude of the MAE depends on the scale of the data.⁵¹ percent errors, such as mean absolute percent error (MAPE), are scale-independent but are not recommended when the data involve 0 counts as MAPE cannot be calculated with 0 values. Also, the MAPE places a heavier penalty on forecasts that exceed the observed compared to those that are less than the observed.⁵² In economics, a measure called mean absolute scaled error (MASE) has been recommended as an accuracy measure for forecasting.⁵¹ We recommend incorporating MASE into malaria forecast evaluation as this evaluation measure will facilitate comparison between studies. We also recommend reporting MAE as it allows an intuitive interpretation of the errors. In addition, MAPE should be reported and a constant such as 1 could replace the 0 values in the series, allowing the calculation of MAPE. An advantage of MAPE as that it considers scale variance. For example, if we observed 70 counts of malaria but predicted 60, MAPE would be 14.3, MAE 10 and MASE 0.7. If we observed 15 counts of malaria but predicted 5, MAPE would be 66.7, MAE 10 and MASE 0.7. MAPE and MASE could be used to compare findings across series and studies, and also compared to one another to understand if and how they differ in their ranking of forecast accuracy. The MAE, MAPE and MASE should be provided as site-specific measures for each forecasting horizon, as summary measures for each site, and finally as summary measures for each forecasting horizon across all sites (within a study).

Conclusion

Accurate disease predictions and early-warning signals of increased disease burden can provide public health and clinical health services with the information needed to strategically implement prevention and control measures. Potential barriers to their usefulness in public health settings include the spatial and temporal resolution of models and accuracy of prediction. Models that produce coarse forecasts may not provide the precision necessary to guide targeted intervention efforts. Additionally, technical skill and lack of readily available data may reduce the feasibility of model utility in practise, which should be considered in developing malaria forecasting models if the intent is to use these models in clinical or public health settings. Applying different forecasting methods to the same data, exploring the predictive ability of non-environmental variables, including transmission-reducing interventions, and using common forecast accuracy measures will allow malaria researchers to compare and improve models and methods, and lead to the improvement in the quality of malaria forecasting.