Abstract
Spatial dispersion of action potential duration (APD) is a substrate for the maintenance of cardiac fibrillation, but the mechanisms are poorly understood. We investigated the role played by spatial APD dispersion in fibrillatory dynamics. We used an in vitro model in which spatial gradients in the expression of ether-à-go-go-related (hERG) protein, and thus rapid delayed rectifying K+ current (IKr) density, served to generate APD dispersion, high-frequency rotor formation, wavebreak and fibrillatory conduction. A unique adenovirus-mediated magnetofection technique generated well-controlled gradients in hERG and green fluorescent protein (GFP) expression in neonatal rat ventricular myocyte monolayers. Computer simulations using a realistic neonatal rat ventricular myocyte monolayer model provided crucial insight into the underlying mechanisms. Regional hERG overexpression shortened APD and increased rotor incidence in the hERG overexpressing region. An APD profile at 75 percent repolarization with a 16.6 ± 0.72 ms gradient followed the spatial profile of hERG-GFP expression; conduction velocity was not altered. Rotors in the infected region whose maximal dominant frequency was ≥12.9 Hz resulted in wavebreak at the interface (border zone) between infected and non-infected regions; dominant frequency distribution was uniform when the maximal dominant frequency was <12.9 Hz or the rotors resided in the uninfected region. Regularity at the border zone was lowest when rotors resided in the infected region. In simulations, a fivefold regional increase in IKr abbreviated the APD and hyperpolarized the resting potential. However, the steep APD gradient at the border zone proved to be the primary mechanism of wavebreak and fibrillatory conduction. This study provides insight at the molecular level into the mechanisms by which spatial APD dispersion contributes to wavebreak, rotor stabilization and fibrillatory conduction.
Key points
Spatial dispersion of action potential duration is a substrate for the maintenance of cardiac fibrillation, but the mechanisms are poorly understood.
The rapid delayed rectifying K+ current (IKr) that flows through sarcolemmal ether-à-go-go-related (hERG) channels plays a fundamental role in the control of rotor frequency and localization during atrial and ventricular fibrillation, although IKr is heterogeneously distributed throughout the heart chambers.
Using a novel magnetofection technique to induce regional overexpression of hERG, we have investigated the mechanisms by which regional gradients in IKr control rotor localization, frequency and wavebreak during fibrillation.
Our study establishes a mechanistic link between regional IKr heterogeneity, action potential duration and patterns of wavebreak in fibrillation.
Knowledge that ion channel gradients are important in the mechanism of cardiac fibrillation should lead to improved therapy.
Introduction
Clinical and experimental evidence supports the hypothesis that fibrillation results from the activity of a small number of high-frequency re-entrant sources (rotors) localized in one cardiac chamber (atrium or ventricle), with fibrillatory conduction to the contralateral chamber (Samie et al. 2001; Narayan et al. 2012). As shown in animals and in man, waves emanating from rotors propagate throughout the atria or ventricles, where they undergo intermittent block and wavebreak, generating highly complex patterns of local electrical activation (Jalife, 2000; Narayan et al. 2012). Wavebreak, which resembles turbulence in water, is known as ‘fibrillatory conduction’ (Jalife et al. 1998). Arguably, understanding the ionic mechanisms involved in the formation of wavebreaks and fibrillatory conduction should prove useful in developing therapies to prevent and/or terminate life-threatening tachyarrhythmias.
Spatial dispersion of cardiac electrophysiological properties is likely to play a major role in establishing spatially distributed gradients of fibrillatory frequency across the cardiac chambers. More specifically, during fibrillation, chamber-specific differences in excitability, action potential duration (APD) and refractoriness are likely to be the cause of stabilization of rotors in one cardiac chamber, with fibrillatory conduction in the contralateral chamber (Samie et al. 2001). Sarcolemmal potassium currents are known to be strong modulators of excitability, APD, rotor frequency and ventricular fibrillation (VF) dynamics (Samie et al. 2001; Muñoz et al. 2007; Noujaim et al. 2007b). The inwardly rectifying potassium current (IK1) and its spatial heterogeneity are thought to play important roles in the mechanisms of rotor stability and frequency in the atria (Cha et al. 2005) and the ventricles (Samie et al. 2001; Noujaim et al. 2007b). On the contrary, overexpression of the slow delayed rectifier current (IKs) was found to increase fibrillatory conduction in cardiomyocyte monolayers while not increasing rotor frequency (Muñoz et al. 2007).
More recently, we investigated the consequences of overexpressing the α-subunit of the human ether-à-go-go-related (hERG) channel, which is coded by KCNH2, is responsible for the rapid delayed rectifier current (IKr) and helps to establish the action potential duration and morphology. We showed that upregulation of IKr increases rotor frequency in a manner that depends on its APD-shortening effects (Hou et al. 2010). Mutations in KCNH2 have been associated with human short and long QT syndrome and heterogeneous APD (Gaita et al. 2003; Brugada et al. 2004; Perrin et al. 2008). In contrast, viral transfer of the KCNH2 mutant G628S associated with long QT syndrome eliminated AF in a porcine model by prolonging atrial APD (Amit et al. 2010). Heterogeneity of IKr is found transmurally and from apex to base in the ventricles of ferret hearts (Brahmajothi et al. 1997). It is also found transmurally in basal left ventricular tissue of guinea-pig hearts and in canine wedge preparations modelling long QT syndrome type 2, as well as between the pulmonary veins and left atrium in the dog (Bryant et al. 1998; Charles Antzelevitch, 2001; Cha et al. 2005).
Here we focus on the role of spatial APD heterogeneity in the mechanisms of wavebreak and fibrillatory conduction. Given that IKr is important in the control of the APD and that APD dispersion is thought to be important in cardiac fibrillation, we surmised that generating hERG gradients in a well-controlled environment may recreate the arrhythmogenic substrate that results in wavebreak and rotor formation.
Our central hypothesis is that in the presence of a spatial APD gradient, wavebreak and fibrillatory conduction occur when high-frequency waves generated in the short APD region propagate towards and impinge on the boundary with the long APD region, but not the reverse. To test this hypothesis, we used heterogeneous hERG expression as a tool and reduced the complex problem of fibrillatory propagation in the three-dimensional heart to a two-dimensional model. We used a novel regionally heterogeneous magnetofection of adenovirus containing the hERG cDNA sequence into neonatal rat ventricular myocyte (NRVM) monolayers. The results may provide important information about the nature of arrhythmias in the heart and how we may better prevent and treat them in future.
Methods
Ethical approval
All experiments were conducted following National Institutes of Health guidelines. All experiments were approved by the University Committee on the Use and Care of Animals at the University of Michigan and the Department of Laboratory Animal Resources. All euthanasia was performed following the recommendations of the University Committee on the Use and Care of Animals and the Department of Laboratory Animal Resources and the Committee for the Humane Use of Animals. Please see the Online Supplemental Material for details on the ethical aspects, experimental methodology, solutions, viral vectors, biochemical assays and the optical mapping and patch-clamp equipment.
Myocyte isolation, culture, magnetofection and optical mapping
We created NRVM monolayers as previously described (Rohr et al. 2003; Muñoz et al. 2007). Cells were plated on human type IV collagen (Sigma)-coated 35 mm culture dishes at a density of 1 × 106 cells per monolayer. Magnetofection was performed on day 2 in culture to infect monolayers with either Ad-hERG-GFP which contains a fused cDNA sequence of hERG (α-subunit) with the sequence green fluorescent protein (GFP) or an adenovirus encoding for GFP (Ad-GFP; Hou et al. 2010; Fig. S1). Each virus was first complexed to ViroMag Magnetofection nanoparticles (Boca Scientific, FL, USA), a product normally used for increasing infection efficiency (Kadota et al. 2005). A volume of 0.5 μl of ViroMag was complexed with 1 × 108 viral particles in 200 μl Hank's Buffered Salt Solution (HBSS) (Sigma) for 15 min, then raised to a final transduction volume of 2 ml per monolayer. As illustrated in Fig. S1, each monolayer was exposed to a Super Magnetic Plate (Boca Scientific) for 1.5 ± 0.5 min in the presence of the magnetofection solution. Whole-infected monolayers were placed entirely over the magnet, while regionally infected monolayers were created by exposing only half of the lower surface area of the dish containing the monolayer to the magnet. The magnetofection solution was then removed, and monolayers were washed twice with and returned to media containing 5% fetal bovine serum and given an additional 48 h to express protein. Uninfected control monolayers were treated in a similar manner using HBSS for 1.5 ± 0.5 min.
Experiments were conducted at an additional 46–50 h after magnetofection. Optical mapping using di-8-ANNEPPS (4-{2-[6-(dibutylamino)-2- naphthalenyl]-ethenyl}-1-(3-sulfopropyl)pyridinium inner salt, 40 μmol l−1; Molecular Probes) was conducted as previously described (Muñoz et al. 2007; Hou et al. 2010) and in the Online Supplementary material. Quiescent monolayers received repetitive stimuli (duration, 5 ms; strength, twice diastolic threshold) applied by a thin extracellular bipolar electrode at increasing frequencies, starting at 1 Hz, until loss of 1:1 capture or initiation of sustained re-entry. Movies 5 s in duration were obtained at 200 frames s−1 (LabWindows Acquisition, National Instruments, Austin, TX, USA) using an 80 × 80 pixel CCD camera (SciMeasure Analytical Systems, Decatur, GA, USA). Signals were amplified, filtered and digitized for offline analysis. No electromechanical uncouplers were used. Dominant frequency (DF) maps, APD maps, regularity index (RI) maps and conduction velocity (CV) measurements were done as previously described (Morley et al. 1999; Zaitsev et al. 2000; Kalifa et al. 2006). The activation ratio (AR; dubbed n:m ratio) is a ratio between the number of activations in the uninfected and the infected regions; thus, n:m was calculated as the number of activations in the distal or uninfected region of the monolayer (n) divided by the number of activations in the proximal or infected region (m). The number of activations in a given region was determined by three 1 s time–space plots taken along parallel lines at ¼, ½ and ¾ of the way within each dish perpendicular to the gradient. Figure S2 shows examples of time–space plots taken at the ½ location. During rotor analysis in the wholly uninfected and infected monolayers, distal and proximal regions were arbitrarily assigned; in regional infections, distal refers to uninfected region and proximal refers to infected regions. The average DF and RI and their respective standard error maps were created in Matlab (Mathworks, Natick, MA, USA).
Fluorescence microscopy
We imaged monolayers on day 4 in culture before optical mapping using a Nikon Eclipse Ti confocal microscope (Nikon Instruments Inc., Melville, NY, USA). Composite images were taken over 9 mm × 14 mm, with length perpendicular to the gradient. Images were analysed in Matlab, and best fits were determined using Origin 7.0 (OriginLab, Wellesley Hills, MA, USA).
Statistical analyses
For statistical analyses, we used one-way ANOVA with a Bonferroni correction (Origin 7.0). Values are expressed as means ± SEM. A value of P < 0.05 was considered significant. Contingency table tests and χ2 analyses were conducted where appropriate; N refers to the number of dissociations and n to the number of monolayers.
Computer simulations
We used a mathematical model for the NRVM adapted to experimental data, as previously described in detail (Hou et al. 2010), with minor modifications. To simulate an NRVM monolayer of tissue, we used a two-dimensional disc-shaped sheet with a Cartesian mesh of 352 × 352 nodes having a spatial resolution of 100 μm that contained a 35 mm diameter disc-shaped active domain in its centre, with a non-diffusive outer domain boundary. The area outside the monolayer (the black peripheral region) was implemented with passive and non-diffusive nodes for ease of integration. The membrane model at each node was solved by the finite volume method, with a time step of 10 μs and no-flux boundary conditions, as described previously by Zlochiver et al. (2008). The maximal conductance of IKr (GKr) was either set as homogeneous [whole GKr, 1 × GKr (uninfected) or 5 × GKr (infected)] or varied spatially across the model (regional GKr model). To simulate the spatial gradient in GKr expression along the model, we implemented the Boltzmann best fit of the hERG-GFP fluorescence data obtained in the experiments for all the groups (Fig. 1B an Fig. S3). A native level of GKr was used in the ‘uninfected’ region (1×). The value of GKr was increased over a range from one to 20 times basal levels within the ‘infected region’ of the model. Re-entry was induced via an S1–S2 cross-field stimulation protocol. The DF, DF profiles and n:m ratios were determined as in experiments (see Online Supplemental material and Tables S1–S3 for further details).
Figure 1. Spatial gradient in human ether-à-go-go-related gene (hERG) expression.
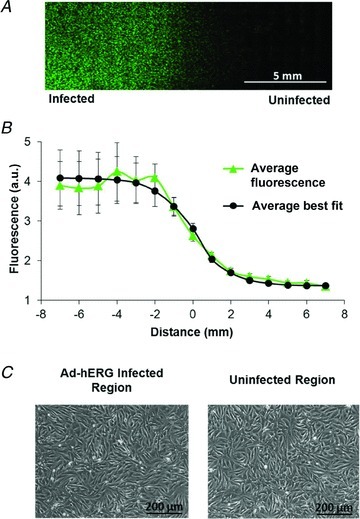
A, fluorescence image across 16 mm at the centre of a monolayer regionally overexpressing hERG with a GFP tag. B, average fluorescence gradient and best fit with a slope factor (dx) = 0.97 ± 0.12 mm (n = 6, x0 of best fit is set to 0). C, phase contrast images of infected and uninfected regions show full myocyte confluency and structural homogeneity.
Results
Regional IKr expression model
Regional magnetofection allows for the creation of confluent, electrically coupled monolayers with regional differences in hERG channel expression. Figure 1A shows a representative fluorescence image across 16 mm at the centre of a regionally infected monolayer expressing GFP-tagged hERG channels (Ad-hERG) in the left side only. In Fig. 1B, the non-uniform hERG expression across six monolayers follows a characteristic Boltzmann distribution, with a gradient at the centre of the monolayers; best fit of the averaged fluorescence showed approximately fourfold more fluorescence in the infected than in the uninfected region and a slope factor of 0.97 ± 0.12 mm at the gradient location (border zone). In Fig. 1C, contrast micrographs from the infected and uninfected regions confirm the presence of uniform myocyte confluency and distribution across the monolayer.
We used a bipolar electrode in the infected region to pace the monolayer at 1 Hz and characterize its electrophysiological properties. The APD map shown in Fig. 2A confirms that regional Ad-hERG infection generates well-demarcated APD heterogeneity, with an APD75 gradient of 16.6 ± 0.72 ms. In Fig. 2B, the average and best fit for both fluorescence (grey lines) and APD50 (black lines) as a function of distance have been represented; again, 0 mm is the central location within the monolayer. Representative optical action potentials and average APD at 50 and 75 percent repolarization (APD50 and APD75) (Fig. 2C) demonstrate that the regional infection generated significant APD heterogeneity. The upstroke velocity of these traces was significantly faster than repolarization (Figure S4A). In the top graph of Fig. 2D, APD75 was the same in the uninfected (UN) and whole-Ad-GFP-infected (W-GFP) monolayers, but APD75 in the whole-Ad-hERG-infected (W-hERG) monolayers was significantly shorter than the other two. In the bottom graph, APD75 in the infected region of the regionally infected hERG (R-hERG) monolayers was significantly shorter than in the infected region of the regionally infected GFP (R-GFP) monolayers. We did not observe any regional APD differences within UN, W-GFP, R-GFP or W-hERG. A non-significant APD difference between the R-GFP and UN groups was observed. Analysis of APD50 showed similar results. Additionally, optical mapping-based analysis of wave propagation in uninfected, whole-infected and regionally infected monolayers during 1 Hz pacing demonstrated no significant differences in CV among groups (Figure S4B).
Figure 2. Distribution of action potential duration (APD) during pacing at 1 Hz.
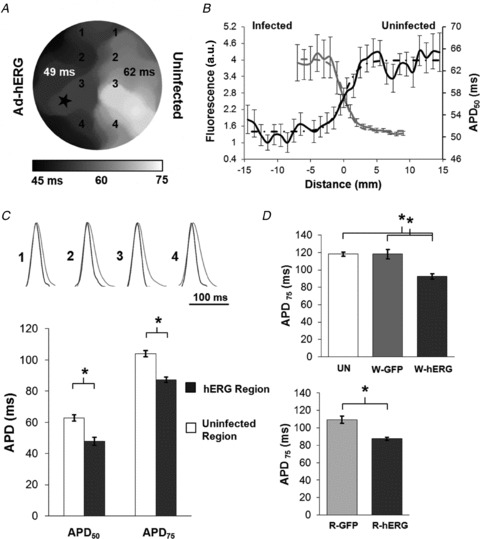
A, APD50 map shows regional APD heterogeneity (paced from star). B, APD50 profile perpendicular to infection border superimposed on Ad-hERG-GFP profile. C, top, superimposed representative optical action potentials in infected (black) and uninfected regions (grey), with pixel locations indicated on the APD map in A. C, bottom, mean ± SEM APD50 (n = 3, P = 0.009) and APD75 (APD at 75% repolarization, n = 3, P = 0.003) in infected and uninfected regions. D, mean ± SEM APD75 values for homogeneous (top) and infected region of heterogeneous monolayers (bottom). D, top, UN (uninfected; n = 11); W-GFP (whole-Ad-GFP infected; n = 7); W-hERG (whole-Ad-hERG infected; n = 9); *P < 0.0005. D, bottom, R-GFP (regionally Ad-GFP infected; n = 9); R-hERG (regionally Ad-hERG infected; n = 3); *P = 0.015.
Rotors in heterogeneous monolayers
Single or multiple rotors were observed in any given monolayer group. Dominant rotors were defined as those being the most stable, having the longest lifespan and presenting the maximal DF (DFmax). Figure 3A (top) shows snapshots of dominant rotors in a whole-Ad-hERG-infected monolayer (left; DFmax, 14 Hz) and in the infected region of a regional Ad-hERG-infected monolayer (right; DFmax, 14.8 Hz). Time–space plots in the centre show that in the W-hERG monolayer the waves emanating from the rotor propagated unobstructed throughout the field of view. In contrast, waves from a rotor of similar DFmax in the infected region of the regionally infected monolayer underwent intermittent blockade and wavebreak as they impinged upon the border zone on their way to the uninfected region (Movie S1). In those cases, slower and often short-lived rotors were observed within the uninfected region; therefore, while 1:1 propagation was maintained throughout the whole-infected monolayer (left), the Ad-hERG gradient in the regionally infected monolayer resulted in a 4:3 n:m pattern of propagation from the infected to the uninfected region. As shown by the DF maps (at the bottom of Fig. 3A), pixel-by-pixel power spectral analysis of the 5 s movies yielded a DF gradient of 3.2 Hz in the regionally infected monolayer because of a reduced activation rate to 11.6 Hz in the uninfected region. Similar results were obtained when high-frequency pacing (15 Hz) in the infected region was used to compare wave propagation in regionally infected vs. whole-infected monolayers (Fig. S2). As demonstrated in Figure 3, the presence of the Ad-hERG expression gradient can generate wavebreak, block or delay when waves emanating from the infected region enter the longer APD border zone.
Figure 3. Rotor activity and propagation of waves.
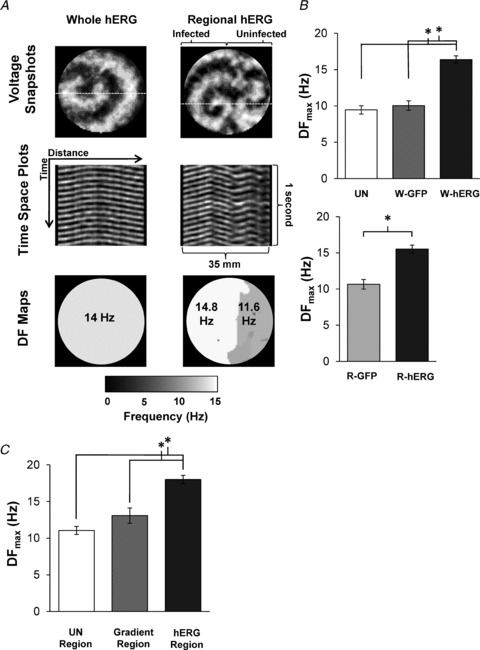
A, top, snapshots of dominant rotors in W-hERG (left) and R-hERG monolayers (right). A, centre, time–space plots taken at the dashed lines in the snapshots. Uniform propagation in the whole-hERG monolayer (left), and 4:3 pattern in the R-hERG monolayer. A, bottom, dominant frequency (DF) maps. Note the 3.2 Hz gradient between infected and uninfected regions. B, DFmax values. There were no significant differences between uninfected (n = 12) and W-GFP (n = 4); however, both were significantly different from W-hERG (n = 45) *P < 5 × 10−9. The DFmax of R-hERG monolayers (n = 64) was significantly higher than for R-GFP monolayers (n = 7; P = 0.005). C, hERG gradient results in DFmax gradient. The DFmax in the Ad-hERG-infected region (n = 37) was at significantly higher frequencies than in the gradient (n = 12) and uninfected regions (n = 15); *P < 5 × 10−9.
Values of DFmax were not significantly different between uninfected (UN), W-GFP and R-GFP (Fig. 3B). Likewise, the values of DFmax in W-hERG and R-hERG monolayers were the same; however, both were significantly higher than in control groups. A non-significant difference in DFmax between the R-GFP and UN groups was observed. This strongly suggests a dependence of DFmax on IKr density. Frequency analysis of the dominant rotors based on their location within the regionally infected Ad-hERG monolayers demonstrates that the level of hERG expression is a strong determinant of both the local DFmax and the DFmax gradients across the monolayer.
Incidence and localization of rotors generating fibrillatory conduction
Many rotors appeared spontaneously, presenting an opportunity to determine whether the level of IKr expression modulated the incidence of spontaneously occurring rotors (Table S4). Overall, the incidence of spontaneous rotor activity was different among hERG-overexpressing and control groups (P = 0.005, χ2 analysis). For uninfected, W-GFP and R-GFP groups, the percentage of spontaneous rotors (the ratio of the number of monolayers with spontaneous rotors to the number of total monolayers of any given group) was similar, being 39% (12/31), 25% (4/16) and 35% (7/20), respectively. For the W-hERG group, it was 74% (45/62), suggesting that IKr overexpression alone generates spontaneous rotor activity. However, the R-hERG group had an even higher proportion of spontaneous rotors at 84.2% (64/76) of the time, which suggests that regional IKr overexpression may be an independent promoter of spontaneous rotor activity and appears to be a factor in the initiation of arrhythmias.
Dominant rotors and DFmax sites were homogeneously distributed and did not show any regional preference in the uninfected, W-GFP, R-GFP or W-hERG monolayers. Also, in the presence of a single rotor these monolayers did not generate wavebreak patterns or fibrillatory conduction even during high-frequency activity. When more than one rotor was present, annihilation occurred by collision of wavefronts generated by each of the rotors, but this did not generate significant DF heterogeneity.
In R-hERG monolayers, the dominant rotors showed a preference to localize stably within the infected region. Dominant rotors were seen within the infected region (57.8%), the gradient region (18.8%) and the uninfected region (23.4%) in 64 monolayers (P < 0.0001; χ2 analysis).
Regional hERG heterogeneity with rotors localized within the infected region was the only condition which generated patterns of wavebreak and fibrillatory conduction. We did not observe wavebreaks in R-hERG monolayers when the dominant rotor was localized within the border zone or the uninfected region. Average DF and standard error (SE) maps of R-hERG monolayers with rotors localized within the infected region (n = 37) clearly divide the monolayer into two halves (Fig. 4A); the infected half has DFs ∼16 Hz and the uninfected half ∼12 Hz, with intermediate levels at the border zone. The SE is much larger in the infected than in the uninfected half, probably due to a varying level of IKr overexpression in the infected half. In contrast to the heterogeneous DF map in Fig. 4A, when rotors localized in the uninfected half or in W-hERG-infected monolayers the DF maps were uniform (see Fig. S5A).
Figure 4. Dominant frequency gradients across heterogeneous monolayers.
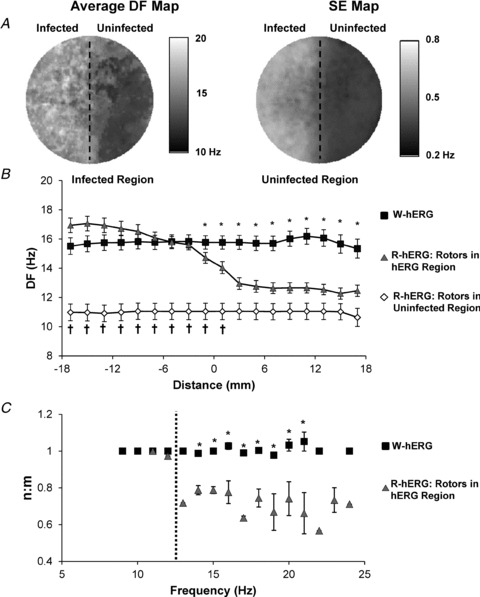
A, average DF and standard-error (SE) maps (n = 37). The DF distribution divides the monolayer into two halves. The SE is much larger in the infected than in the uninfected half. B, spatial DF profiles for rotors in the infected (triangles, n = 37) and uninfected regions (diamonds, n = 15) of R-hERG monolayers. The values for R-hERG with rotors in the infected region is significantly different from W-hERG (*P < 0.05) and from R-hERG with rotors in the uninfected region (†P < 0.05). The halfway transition point of the DF profile in the R-hERG monolayers occurred within the gradient region. C, values of n:m for W-hERG (squares, n = 45) and R-hERG monolayers (triangles, n = 37) as a function of dominant rotor frequency. The dashed line is the frequency at which wavebreak begins n:m was significantly greater in W-hERG monolayers than in R-hERG monolayers from 14–21 Hz (*P < 0.05).
To quantify the consequences of IKr heterogeneity and rotor location further, we collected average DF profiles perpendicular to the border zone. Only rotors that localized within the infected region of the R-hERG monolayers produced wavebreaks (Fig. 4B, triangles); this resulted in a DF gradient profile (see also Fig. 3A and Fig. S5B and C). The DF changed gradually in space from values similar to those in the W-hERG monolayers (Fig. 4B, squares) to those similar to DFs when the rotor was in the uninfected region (Fig. 4B, diamonds). The halfway transition point (xo) occurred approximately at the centre of the border zone (18.5 mm from the uninfected edge of the dish (left) or at −1 mm along the x-axis in Fig. 4B). The DF transition depended on the precise location of the dominant rotor and on whether two or more dominant rotors coexisted. Multiple dominant rotors in the infected region yielded a heterogeneous DF profile, with a larger slope factor than for single dominant rotors which had a sharper DF transition (Fig. S5C).
To determine the frequency dependence of wavebreak, we characterized the proximal-to-distal activation ratios (n:m) over a range of rotor frequencies (Fig. 4C). The n:m for W-hERG and R-hERG with rotors localized in the uninfected region remained at 1.00 ± 0.005 (n = 45; 9–24 Hz) and 1.00 ± 0.005 (n = 15; 7.5–12.9 Hz). However, when rotors in the infected region had frequencies of 12.9 Hz or higher, complex patterns of activation developed, ranging from AR = 0.72 (i.e. m:n = 3:2; infected:uninfected) at 12.9 Hz to 0.57 (m:n = 5:3) at 22 Hz. Other intermediate ARs were also observed, including 0.79 (m:n = 5:4) and 0.66 (m:n = 20:13). Finally, we observed a declining trend in n:m as the spontaneous rotor frequency increased to 24 Hz. Altogether, regional gradients in Ad-hERG resulted in intermittent wavebreak and significantly variable n:m when the frequency of rotors in the infected region ranged between 13 and 24 Hz.
Next, we calculated the regularity index (RI), taken from the power spectrum defined as the power under the DFmax divided by the total power (Zaitsev et al. 2000; Kalifa et al. 2006), to determine where wavebreaks and fractionation occurred most frequently in the R-hERG monolayers. Figure 5A shows a phase map in which a rotor in the infected region was accompanied by fibrillatory conduction towards the uninfected region. Three pixels were sampled for RI analysis, as follows: pixel 1, near the core of the dominant rotor, showed a frequency of 14.8 Hz and a relatively high RI at 0.72; pixel 2, at the border zone, also showed a frequency of 14.8 Hz, but its RI was appreciably reduced (0.53); and pixel 3, in the uninfected region, showed a reduced frequency (11.7 Hz) but a high RI (0.71). The spectrum at pixel 2 clearly shows two peaks, each corresponding to the frequency of activation within the infected and uninfected regions. Average RI and SE maps (Fig. 5B) demonstrate that there is a substantial area within the border zone (horizontal dashed line) which consistently has reduced RI of about 0.4 or lower. The RI profiles (Fig. 5C) perpendicular to the border zone taken for single dominant rotors in the infected (green) and uninfected regions (red) show that: (i) regularity is higher when the rotors are in the uninfected region compared with the infected region; and (ii) irregular activity at the centre of the border zone (−2.5 to 3.5 mm on the x-axis or 15–21 mm from the infected edge of the monolayer) is greatest when the rotors reside within the hERG-infected region.
Figure 5. Single rotors and regularity index (RI) gradients.
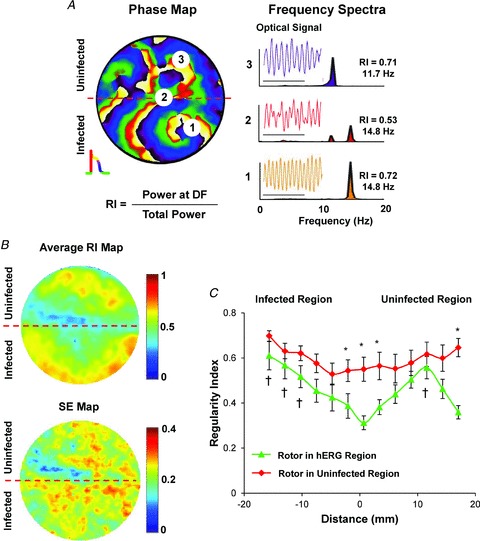
A, left, colour phase map. A rotor in the infected region resulted in fibrillatory conduction in the uninfected region. The map shows pixel locations 1–3 used for RI analysis. A, right, single pixel time series and power spectra for pixels 1–3. B, average RI and SE maps (n = 10) show reduced RI at the border zone (dashed red line). C, spatial RI profiles perpendicular to the border zone for single dominant rotors in the infected (triangles, n = 10) and uninfected regions (diamonds, n = 12; *P < 0.05). The RI is high when the rotors are in the uninfected region. The RI is lowest at the border zone when the rotor resides within the infected region. †P < 5 × 10−5 between minimal RI (18.5 mm).
Mechanisms of wavebreak and fibrillatory conduction: computer simulations
Experimental data obtained from the regional hERG overexpression suggest that rotor acceleration and fibrillatory conduction are consequences of the non-uniform IKr current density distribution, which results in significant APD dispersion. To support this idea and to investigate the mechanisms of fibrillatory conduction further, we used a two-dimensional mathematical model of NRVM electrical activity (see Online Supplementary materials for details). Figure 6A shows a snapshot (left) and time–space plot (right) of rotor activity in a monolayer model with a regional fivefold increase in GKr in the rotor region. Similar to the experiments, a stable rotor at 15.0 Hz in the region of increased GKr (‘infected’ region) generated wavefronts that blocked intermittently at the border zone and resulted in a 3:2 m:n pattern (n:m = 0.67) of propagation in the region of nominal GKr (‘uninfected region’), which closely reproduced the experimental results (n:m at 15 Hz is 0.79 ± 0.02; n = 4).
Figure 6. Simulations showing dependence of APD and maximal diastolic potential (MDP) on conductance of IKr (GKr) factor in the ‘infected region’.
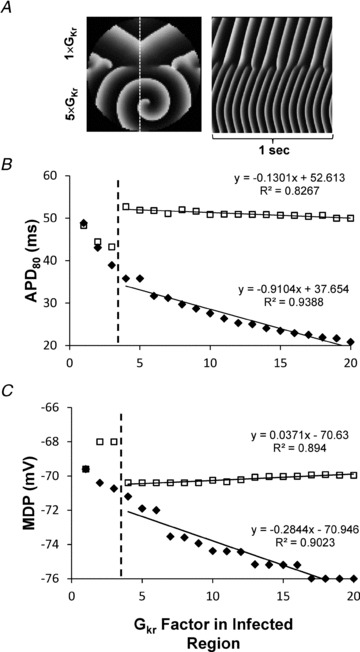
A, snapshot (left) and time–space plot (right) taken at the dotted vertical line showing rotor activity in the infected region (GKr = 5×). At 15 Hz, rotor activity generated wavefronts that transformed at the border zone into a 3:2 (infected:uninfected) pattern. B, APD at 80% repolarization (APD80) in the infected (diamonds) and uninfected regions (squares) as a function of GKr factor in infected region. There was an initial transient decrease of APD80 in uninfected region (2–3 × GKr). C, MDP vs. GKr factor in the infected region. The MDP transiently depolarizes in the uninfected region when GKr = 2–3× in the infected region. Dashed lines, critical value of GKr at which wavebreak occurred.
To determine the respective roles of regional APD and maximal diastolic potential (MDP) in the mechanism of fibrillatory conduction, we first examined their dependence on GKr in the infected region. In Fig. 6B, APD80 decreases as GKr increases, as expected (Hou et al. 2010). In the uninfected region (open squares), the APD at 80% repolarization (APD80) decreases somewhat at GKr values below the wavebreak point (dashed line). Beyond that point, 1:1 propagation (n:m = 1.0) cannot be maintained. Consequently, APD80 in the uninfected region increases stepwise from 42 to ∼50 ms, while APD80 in the infected region (filled diamonds) decreases linearly with the GKr increase. In Fig. 6C, the MDP in the infected region hyperpolarizes monotonically from −69.5 mV at GKr = 1 to about −76 mV at 20 × GKr. At the same time, the MDP in the uninfected region varies non-monotonically; when the GKr in the infected region changes from 1 to 2×, the uninfected region depolarizes slightly to about −68 mV, probably due to the increased DF during 1:1 activation of that region. At the wavebreak point, 1:1 activation is lost, and the MDP in the uninfected region changes abruptly to a relatively stable level of approximately −70 mV. Hence, the next step was to test the relationship between APD dispersion and the MDP distribution in the generation of fibrillatory conduction.
We conducted additional simulations to separate the roles of APD and MDP in the generation of wavebreaks. In Fig. 7, we clamped the MDP of each monolayer at incremental predetermined depolarized values while allowing APDs, DFmax and ARs to vary spontaneously. In Fig. 7A, MDP profiles along the length of the monolayer ranged from the unclamped values (5 × GKr region, −72 mV; 1 × GKr region, −70 mV) to −62 mV. The unclamped, −72 and −71 mV clamped profiles resulted in non-uniform MDPs, with the more negative values in the 5 × GKr region. All other conditions resulted in a uniform MDP profile as the clamped values rose to −70 mV and above (the MDP in the 1 × GKr regions). The DF profiles, shown in Fig. 7B, correspond to each clamped MDP value. It is clear that: (i) DF in the 5 × GKr region is not sensitive to MDP values more negative than −68 mV (values which are close to those in the 1 × GKr region); and (ii) DF gradients exist for MDPs up to −67 mV, which allow for rotor DFmax of ∼14.6 Hz in the 5 × GKr region. In addition, as the MDP clamp value changes to more depolarized levels, the location of wavebreak shifts to the right; i.e. towards the 1 × GKr region. It is only when the MDP is clamped at −66 mV or more positive voltages that the driving rotor is forced to slow to ∼13.7 Hz, at which point wavebreaks and fibrillatory conduction are no longer possible, and the uninfected-to-infected n:m becomes 1.0. Figure 7C shows the manner in which rotor DFmax (black) and n:m values change as the clamped MDP depolarizes. Between −72 and −67 mV rotor DFmax remains high, and wavebreaks at the border zone result in fibrillatory conduction with an n:m of ∼0.6. At −66 mV, DFmax begins to decline, wavebreak ceases and n:m becomes equal to 1.0.
Figure 7. Maximal diastolic potential and the control of DFmax gradients.
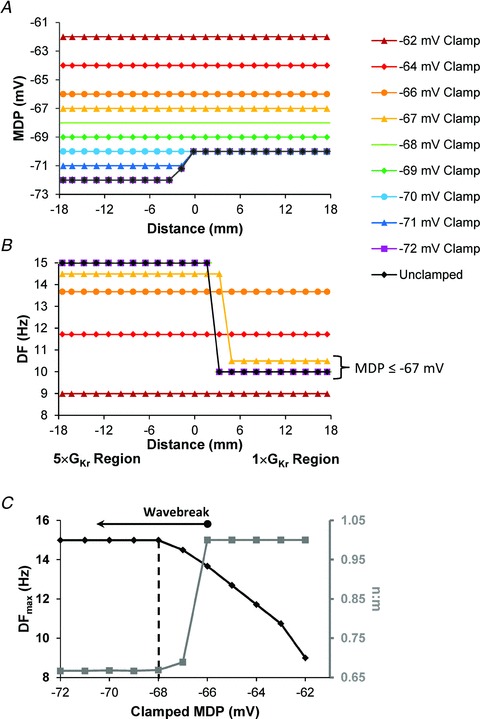
A, MDP was clamped at varying predetermined values. The APD and activation ratio were allowed to change. The MDP ranged from the unclamped values (5 × GKr, −72 mV; 1 × GKr, −70 mV) to −62 mV. B, spatial DF profiles correspond to MDP as indicated. The DF in the 5 × GKr region is insensitive to MDPs more negative than −67 mV, remaining at 14.7 Hz. The rotor frequency decreases when clamped MDP is less negative than −66 mV and wavebreak ceases. C, rotor DFmax (black) and n:m change (grey) change as functions of MDP in the infected region. For MDP of −68 mV and more negative, DF and n:m remain constant.
It is important to stress that in the unclamped condition (Fig. 7A, black diamonds), appreciably different MDPs would be expected to contribute to the genesis of wavebreak, in part by establishing different APD values in the two regions. However, wavebreak and fibrillatory conduction continued to occur at clamped MDPs of −70 to −67 mV, which are equal to, or slightly more positive than, the MDP of the unclamped 1 × GKr region. This suggests that an MDP gradient is not essential to generate wavebreak (see also Fig. S6).
We demonstrated in Fig. 6B (see above) the strong dependence of APD80 on GKr in the numerical NRVM model. In Fig. 8A, we demonstrate a similar strong dependence of rotor DFmax on APD80. As shown in Fig. 6B, there is a critical level of GKr (and APD) at which 1:1 propagation across the border zone is no longer possible. Thus, we conducted a set of simulations over a range of GKr values to determine whether the model predicts a critical level of DFmax at which wavebreak should occur. In Fig. 8B, DF is plotted as a function of GKr in the infected region. Consistent with recent experimental and simulation data (Muñoz et al. 2007; Hou et al. 2010), DF in the infected region (filled diamonds) increases linearly as GKr increases up to 20×. The uninfected region (open squares) is activated in a 1:1 manner up to a rotor frequency of ∼13.7 Hz, corresponding to 3 × GKr in the infected region (vertical dashed line). Beyond that line, intermittent wavebreaks at the border zone resulted in sharp DF reduction in the uninfected region, with stabilization at 10.2–11.3 Hz, regardless of the DF values in the infected region. Figure 8C demonstrates the manner in which the ARs across the border zone change with the DFmax of the rotor in the infected region. Altogether, the numerical data predict a critical rotor DFmax in the infected region at which wavebreak and fibrillatory conduction should occur. Such predictions are clearly borne out of the experimental results in which n:m ratios <1 reproducibly appear at a critical DFmax breakpoint of ∼14 Hz (see Fig. 4).
Figure 8. Critical dependence of wavebreak and fibrillatory conduction on DF gradient.
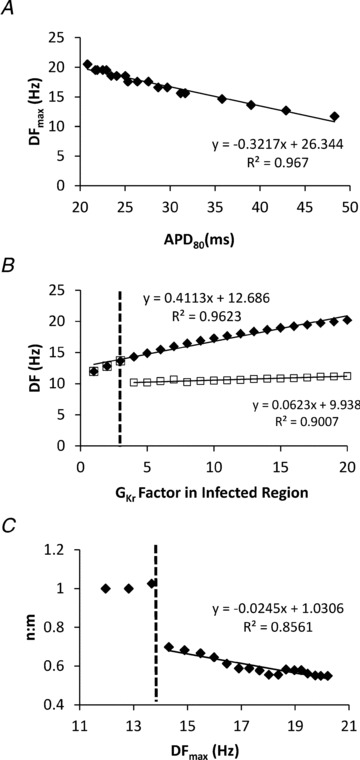
A, rotor DFmax depends strongly on APD80. B, DF in infected (diamonds) and uninfected regions (squares) as functions of GKr in infected region. Vertical dashed line shows the level of GKr at which wavebreaks occur. C, values of n:m across the border zone as a function of DFmax in the infected region at varying levels of GKr in the infected region. Vertical dashed line shows critical rotor DFmax (∼14 Hz) at which wavebreak occurs.
Discussion
Major results of the study
We have investigated the mechanisms by which gradients in IKr density contribute to the mechanisms of high-frequency rotor formation, wavebreak and fibrillatory conduction in heterogeneous cardiac tissues. Gradients in hERG and GFP expression were created in NRVM monolayers using adenovirus-mediated magnetofection, which allowed accurate spatial control of protein distribution. Computer simulations using a realistic NRVM monolayer model provided mechanistic insight, which greatly clarified experimental results. Our main findings were as follows. (i) Regional increase in IKr density shortened the APD and increased the incidence of rotor formation in the Ad-hERG-infected region. (ii) An APD75 gradient profile of 16.6 ± 0.72 ms followed the distribution profile of hERG-GFP across the monolayer; conduction velocity was not significantly altered by Ad-hERG infection. (iii) Rotors in the Ad-hERG-infected region whose DFmax was ≥12.9 Hz resulted in wavebreak at the interface (border zone) between infected and non-infected regions; when the DFmax was <12.9 Hz or the rotors resided in the uninfected region, the DF distribution was uniform. (iv) The higher the rotor DFmax in the infected region, the lower the regularity at the border zone. (v) In computer simulations, the regional increase in IKr led to both regional APD abbreviation and MDP hyperpolarization. However, the steep APD gradient at the border zone was the primary mechanism of wavebreak and fibrillatory conduction in this model. Overall, our study provides insight into the molecular mechanisms by which non-uniform distribution of a major repolarizing potassium channel results in rotor stabilization, APD dispersion and fibrillatory conduction.
Magnetofection enables controlled spatial gradients in ion channel expression
Regional magnetofection can be used to generate structurally homogeneous but electrically heterogeneous monolayers to investigate the role of spatial gradients in ion channels in the mechanism of cardiac fibrillation. Magnetofection is a relatively new technique that is used primarily to enhance cellular infection efficiency (Cheng et al. 2010). Our novel use of magnetofection produced well-controlled gradients in Ad-hERG-GFP expression in the form of a Boltzmann profile spanning over a distance of hundreds of NRVMs (∼5 mm), with a slope factor of ∼1 mm. We submit that such a gradual transition of ion channel distribution is much more realistic from the physiological and pathophysiological standpoint than the previous model of ionic heterogeneity, which generates gradients that are ∼50 μm, approximately 100 times steeper that those we have created here (Sekar et al. 2009). Our approach enabled us to demonstrate, for the first time, that regional IKr heterogeneity is an arrhythmogenic substrate, which increases the probability of spontaneous rotor formation and promotes wavebreak and fibrillatory conduction from regions of high to low IKr density. The approach is readily applicable to the study of other channels and channel-associated proteins and might prove useful in in vivo experimental studies on the pathophysiological consequences of heterogeneous ion channel expression.
Gradients of IKr and APD dispersion in the heart
Spatially distributed heterogeneity of IKr has been observed in a number of animal models and is associated with APD dispersion. In myocytes from the basal subendocardium of the guinea-pig heart, IKr is decreased by a factor of 0.6 with respect to the subepicardium (Bryant et al. 1998). Both apical-to-basal and transmural gradients in the density of IKr channels have been reported in the ferret heart (Brahmajothi et al. 1997). However, IKr distribution in the canine ventricles remains controversial. One study reported hERG expression to differ by as much as 3.3-fold on the epicardum of the left vs. right ventricles (Stoll et al. 2008). Another study reported a more than twofold transmural gradient (Obreztchikova et al. 2006). Yet another study found that although treatment with IKr blockers revealed regional APD prolongation, in basal conditions there were no gradients in IKr (Charles Antzelevitch, 2001). Moreover, in canine wedge preparations, d-sotalol generated transmural APD heterogeneity and resulted in the generation of spontaneous as well as stimulation-induced Torsades de pointes (Charles Antzelevitch, 2001). In canine atria, IKr density differed by ∼20% between cells from the posterior wall of the left atrium and the pulmonary veins (Cha et al. 2005). Unfortunately, none of the above studies showing regional differences gave an idea of how abrupt the transitions were from one region to the other. Nevertheless, based on the limited information available it is reasonable to estimate that the spatial differences correspond to gradual gradients spanning over a few millimetres.
Spatial dispersion of K+ channels and cardiac fibrillation
Cardiac fibrillation may depend on the presence of a small number of high-frequency re-entrant sources (Jalife & Gray, 1996; Vaidya et al. 1999; Samie et al. 2001; Noujaim et al. 2007a). Spiral wavefronts emanating periodically away from such sources may encounter functional, temporal and/or anatomical tissue heterogeneities and result in wavebreak with multiple wavelet formation (Samie et al. 2001). The wavelets undergo irregular spatiotemporal patterns of fibrillatory conduction (Jalife, 1998; Jalife, 2000). In the isolated guinea-pig heart, the presence of a fast and stable rotor driving fibrillatory activity has been demonstrated to correlate with gradients in IK1 density between the left and right ventricles (Samie et al. 2001). Hou et al. (2010) demonstrated that overexpression of hERG in an NRVM system stabilizes and accelerates rotors. Reduction of IKr in pig atria by transfection of the G628S-hERG mutant significantly reduced the ability to induce atrial fibrillation by burst pacing (Amit et al. 2010). Thus, there is a link between fibrillatory frequency and APD. However, details regarding the relationship between the spatial organization of excitation and the spatial IKr distribution were lacking. Here we demonstrate that regional IKr heterogeneity can be a mechanism of rotor formation, wavebreak and fibrillatory conduction. Importantly, only rotors localized within higher hERG expression regions and whose frequency exceeded ∼13 Hz resulted in wavebreaks and fibrillatory conduction. On the contrary, no fibrillatory activity was observed in cases in which a single driving rotor resided in lower IKr regions or in uniformly infected monolayers, regardless of the frequency of the rotors. While hERG overexpression does not transiently hyperpolarize the MDP in all cell types (Nuss et al. 1999; Hua et al. 2004), in NRVMs it has been shown previously both to transiently hyperpolarize the MDP and to abbreviate APD; both these factors contribute to rotor acceleration (Hou et al. 2010). Our numerical results indicate that spatial APD dispersion induced by MDP heterogeneity alone does not result in fibrillatory conduction; therefore, in these monolayers, regional IKr heterogeneity leading to APD dispersion is the primary mechanism of the fibrillatory activity.
Clinical relevance
Ion channel gradients have been suggested to exist in the atria of patients with atrial fibrillation (Caballero et al. 2010; Voigt et al. 2010). This, together with the recent demonstration by Narayan et al. (2012) that atrial fibrillation in humans may be the result of long-standing rotors with fibrillatory conduction to the surrounding atrium, strongly supports the conclusion that rotors are the primary drivers of atrial fibrillation, at least in some patients. Most importantly, brief radiofrequency ablation at or near the centre of rotation alone acutely terminated atrial fibrillation (Narayan et al. 2012). This provides a solid rationale for investigating the mechanisms of wavebreak, rotor formation and fibrillatory conduction. While our results cannot be extrapolated directly to the clinical situation, they demonstrate that heterogeneity in the atrium in the form of spatially distributed APD gradients constitutes a likely arrhythmogenic substrate, in which waves emanating at high frequency from either focal or re-entrant sources results in the turbulent electrical activation that manifests as fibrillatory conduction.
Gain-of-function mutations in IKr abbreviate the QT interval and generate heterogeneous APD shortening and refractoriness (Gaita et al. 2003; Brugada et al. 2004). In contrast, it was reported recently that viral transfer of a hERG mutant (KCNH2-G628S) associated with long QT syndrome eliminated atrial fibrillation in a porcine model by prolonging atrial APD (Amit et al. 2010). As both gain- and loss-of-function mutations in hERG exacerbate APD heterogeneity, spatially distributed hERG gradients may be highly relevant to understanding the mechanisms of these arrhythmias. It is important to note, however, that the APD gradient secondary to heterogeneous hERG expression is by no means the only substrate conducive to wavebreak and high-frequency rotor formation leading to fibrillatory conduction. We have previously shown, in a similar monolayer model overexpressing KvLQT1 and minK (proteins responsible for IKs), that IKs-mediated postrepolarization refractoriness can also promote wavebreak formation and fibrillatory conduction during rapid pacing or sustained high-frequency re-entry by a completely different mechanism (Muñoz et al. 2007). In agreement with such data, Shimizu & Antzelevitch (2000) found that the IKr blocker d-sotalol increased transmural inhomogeneity in APD and was proarrhythmic, while an IKs blocker uniformly increased APD and was proarrhythmic only after the addition of isoprenaline. Taken together, these findings suggest that APD heterogeneity and/or postrepolarization refractoriness are both important but separate determinant factors in the mechanisms of wavebreak, rotor formation and fibrillatory conduction. Consequently, investigating the functional effect of individual and multiple overlapping ionic gradients in both normal and diseased hearts should lead to a better understanding of the mechanism.
Limitations
Several limitations should be considered. First, cardiac fibrillation occurs in a complex three-dimensional structure, and our study was performed in a simplified monolayer system. Nevertheless, we focused on ionic mechanisms of fibrillatory activity. Our methods thus provide a well-controlled model system to study the role of cellular and ionic heterogeneities in the generation of fibrillatory conduction. Such heterogeneities would be very difficult to study in the whole heart. Second, the effect of regional hERG overexpression was examined using NRVMs whose electrical properties are vastly different from those of human myocytes and have slower CV. Clearly, the α-subunit of hERG channels expressed in rodent myocytes differs functionally from adult human channels additionally containing the β-subunit KCNE2 (MiRP1). Nevertheless, we (Zlochiver et al. 2008; Hou et al. 2010; Deo et al. 2011) and others (Sekar et al. 2009) have demonstrated that the uniform and heterogeneous NRVM models recapitulate many of the observations in whole adult hearts. Third, we did not address the potential effects that hERG overexpression may have on other transmembrane currents. However, based on our experimental and numerical results, we are confident that regional hERG overexpression was an appropriate tool to generate predictable and quantifiable APD gradients. Wavebreak and fibrillatory conduction occur when high-frequency waves generated in the short APD region propagate towards and impinge on the boundary with the long APD region, but not the reverse. Fourth, magnetofection may introduce unidentified effects on the electrophysiology of the cells. Yet, we feel reassured that this technique did not adversely affect our preparations. Magnetofection of Ad-GFP in the monolayers did not produce any effects on CV, APD or rotor frequency. Finally, varying levels of hERG overexpression were not studied, and conclusions regarding changes in IKr density rely on computer simulations.
Acknowledgments
We thank Dr Zhengfeng Zhou (Oregon Health and Science University) for the use of his adenoviral construct. This work was supported by NIH grants P01-HL039707 and P01-HL087226, and the Leducq Foundation.
Glossary
- Ad-GFP
adenovirus encoding for GFP
- Ad-hERG-GFP or Ad-hERG
adenovirus encoding for hERG with GFP tag
- APD
action potential duration
- APD50
APD at 50% repolarization
- APD75
APD at 75% repolarization
- APD80
APD at 80% repolarization
- AR
activation ratio
- CV
conduction velocity
- DF
dominant frequency
- GFP
green fluorescent protein
- GKr
maximal conductance of IKr
- hERG
human ether-à-go-go-related gene
- IKr
rapid delayed rectifying K+ current
- MDP
maximal diastolic potential
- NRVM
neonatal rat ventricular myocyte
- R-GFP
regionally infected with Ad-GFP
- R-hERG
regionally infected with Ad-hERG
- RI
regularity index
- UN
uninfected
- W-GFP
wholly Ad-GFP infected
- W-hERG
wholly Ad-hERG infected
Author contributions
Experimental and computational studies were conducted at the Center of Arrhythmia Research at the University of Michigan. J.J. and O.B. were involved in the conception and design of experiments and drafting and critically revising the manuscript. S.M. and T.H. were involved in aspects of the experimental design. C.C. was involved in the collection, analysis and interpretation of data. K.C. was involved in the experimental design, collection, analysis and interpretation of data as well as drafting and revising the manuscript. All Authors approved the final version of the manuscript.
Translational perspective
Spatial dispersion of refractoriness is considered a hallmark for the initiation and maintenance of cardiac fibrillation. Here we tested the hypothesis that dispersion of refractoriness in the form of a well-demarcated action potential duration (APD) gradient results in wavebreak and fibrillatory conduction when high-frequency waves generated in the short APD region propagate towards and impinge on the boundary with the long APD region, but not the reverse. Ion channel gradients, generating regional APD heterogeneity, have been suggested to exist in the atria of patients with atrial fibrillation. This, together with the recent demonstration that both atrial fibrillation and ventricular fibrillation in humans may result from long-standing rotors with fibrillatory conduction to the surrounding tissues, strongly supports the conclusion that rotors are the primary drivers of cardiac fibrillation, at least in some patients. Additionally, gain- and loss-of-function mutations in hERG associated with long and short QT syndromes exacerbate APD heterogeneity, suggesting that spatially distributed hERG gradients may be highy relevant to understanding the mechanisms of these arrhythmias. Therefore, while our results cannot be extrapolated directly to the clinical situation, they demonstrate that heterogeneity in the atria or ventricles in the form of spatially distributed APD gradients constitutes a likely arrhythmogenic substrate, in which waves emanating at high frequency from either focal or re-entrant sources results in the turbulent electrical activation which manifests as fibrillatory conduction.
Supplementary material
Online Supplement
References
- Antzelevitch C, Nesterenko VV, Muzikant AL, Rice JJ, Chen G, Colatsky T. Influence of transmural repolarization gradients on the electrophysiology and pharmacology of ventricular myocardium. Cellular basis for the Brugada and long-QT syndromes. Phil Trans R Soc Lond A. 2001;359:1201–1216. [Google Scholar]
- Amit G, Kikuchi K, Greener ID, Yang L, Novack V, Donahue JK. Selective molecular potassium channel blockade prevents atrial fibrillation. Circulation. 2010;121:2263–2270. doi: 10.1161/CIRCULATIONAHA.109.911156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brahmajothi MV, Morales MJ, Reimer KA, Strauss HC. Regional localization of ERG, the channel protein responsible for the rapid component of the delayed rectifier, K+ current in the ferret heart. Circ Res. 1997;81:128–135. doi: 10.1161/01.res.81.1.128. [DOI] [PubMed] [Google Scholar]
- Brugada R, Hong K, Dumaine R, Cordeiro J, Gaita F, Borggrefe M, Menendez TM, Brugada J, Pollevick GD, Wolpert C, Burashnikov E, Matsuo K, Wu YS, Guerchicoff A, Bianchi F, Giustetto C, Schimpf R, Brugada P, Antzelevitch C. Sudden death associated with short-QT syndrome linked to mutations in HERG. Circulation. 2004;109:30–35. doi: 10.1161/01.CIR.0000109482.92774.3A. [DOI] [PubMed] [Google Scholar]
- Bryant SM, Wan X, Shipsey SJ, Hart G. Regional differences in the delayed rectifier current (IKr and IKs) contribute to the differences in action potential duration in basal left ventricular myocytes in guinea-pig. Cardiovasc Res. 1998;40:322–331. doi: 10.1016/s0008-6363(98)00133-3. [DOI] [PubMed] [Google Scholar]
- Caballero R, de la Fuente MG, Gómez R, Barana A, Amorós I, Dolz-Gaitón P, Osuna L, Almendral J, Atienza F, Fernández-Avilés F, Pita A, Rodríguez-Roda J, Pinto A, Tamargo J, Delpón E. In humans, chronic atrial fibrillation decreases the transient outward current and ultrarapid component of the delayed rectifier current differentially on each atria and increases the slow component of the delayed rectifier current in both. J Am Coll Cardiol. 2010;55:2346–2354. doi: 10.1016/j.jacc.2010.02.028. [DOI] [PubMed] [Google Scholar]
- Cha TJ, Ehrlich JR, Zhang L, Chartier D, Leung TK, Nattel S. Atrial tachycardia remodeling of pulmonary vein cardiomyocytes: comparison with left atrium and potential relation to arrhythmogenesis. Circulation. 2005;111:728–735. doi: 10.1161/01.CIR.0000155240.05251.D0. [DOI] [PubMed] [Google Scholar]
- Cheng K, Li TS, Malliaras K, Davis DR, Zhang Y, Marban E. Magnetic targeting enhances engraftment and functional benefit of iron-labeled cardiosphere-derived cells in myocardial infarction. Circ Res. 2010;106:1570–1581. doi: 10.1161/CIRCRESAHA.109.212589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deo M, Sato PY, Musa H, Lin X, Pandit SV, Delmar M, Berenfeld O. Relative contribution of changes in sodium current vs intercellular coupling on reentry initiation in 2-dimensional preparations of plakophilin-2-deficient cardiac cells. Heart Rhythm. 2011;8:1740–1748. doi: 10.1016/j.hrthm.2011.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaita F, Giustetto C, Bianchi F, Wolpert C, Schimpf R, Riccardi R, Grossi S, Richiardi E, Borggrefe M. Short QT Syndrome: a familial cause of sudden death. Circulation. 2003;108:965–970. doi: 10.1161/01.CIR.0000085071.28695.C4. [DOI] [PubMed] [Google Scholar]
- Hou L, Deo M, Furspan P, Pandit SV, Mironov S, Auerbach DS, Gong Q, Zhou Z, Berenfeld O, Jalife J. A major role for HERG in determining frequency of reentry in neonatal rat ventricular myocyte monolayer. Circ Res. 2010;107:1503–1511. doi: 10.1161/CIRCRESAHA.110.232470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hua F, Johns DC, Gilmour RF., Jr Suppression of electrical alternans by overexpression of HERG in canine ventricular myocytes. Am J Physiol Heart Circ Physiol. 2004;286:H2342–H2351. doi: 10.1152/ajpheart.00793.2003. [DOI] [PubMed] [Google Scholar]
- Jalife J. Ventricular fibrillation: mechanisms of initiation and maintenance. Annu Rev Physiol. 2000;62:25–50. doi: 10.1146/annurev.physiol.62.1.25. [DOI] [PubMed] [Google Scholar]
- Jalife JDM, Davidenko J, Anumonwo J. Basic Cardiac Electrophysiology for the Clinician. New York: Futura Publishing Co. Inc; 1998. [Google Scholar]
- Jalife J, Gray R. Drifting vortices of electrical waves underlie ventricular fibrillation in the rabbit heart. Acta Physiol Scand. 1996;157:123–131. doi: 10.1046/j.1365-201X.1996.505249000.x. [DOI] [PubMed] [Google Scholar]
- Kadota S, Kanayama T, Miyajima N, Takeuchi K, Nagata K. Enhancing of measles virus infection by magnetofection. J Virol Methods. 2005;128:61–66. doi: 10.1016/j.jviromet.2005.04.003. [DOI] [PubMed] [Google Scholar]
- Kalifa J, Tanaka K, Zaitsev AV, Warren M, Vaidyanathan R, Auerbach D, Pandit S, Vikstrom KL, Ploutz-Snyder R, Talkachou A, Atienza F, Guiraudon G, Jalife J, Berenfeld O. Mechanisms of wave fractionation at boundaries of high-frequency excitation in the posterior left atrium of the isolated sheep heart during atrial fibrillation. Circulation. 2006;113:626–633. doi: 10.1161/CIRCULATIONAHA.105.575340. [DOI] [PubMed] [Google Scholar]
- Morley GE, Vaidya D, Samie FH, Lo C, Delmar M, Jalife J. Characterization of conduction in the ventricles of normal and heterozygous Cx43 knockout mice using optical mapping. J Cardiovasc Electrophysiol. 1999;10:1361–1375. doi: 10.1111/j.1540-8167.1999.tb00192.x. [DOI] [PubMed] [Google Scholar]
- Muñoz V, Grzeda KR, Desplantez T, Pandit SV, Mironov S, Taffet SM, Rohr S, Kléber AG, Jalife J. Adenoviral expression of IKs contributes to wavebreak and fibrillatory conduction in neonatal rat ventricular cardiomyocyte monolayers. Circ Res. 2007;101:475–483. doi: 10.1161/CIRCRESAHA.107.149617. [DOI] [PubMed] [Google Scholar]
- Nanthakumar K, Jalife J, Massé S, Downar E, Pop M, Asta J, Ross H, Rao V, Mironov S, Sevaptsidis E, Rogers J, Wright G, Dhopeshwarkar R. Optical mapping of Langendorff-perfused human hearts: establishing a model for the study of ventricular fibrillation in humans. Am J Physiol Heart Circ Physiol. 2007;293:H875–H880. doi: 10.1152/ajpheart.01415.2006. [DOI] [PubMed] [Google Scholar]
- Narayan SM, Patel J, Mulpuru S, Krummen DE. Focal impulse and rotor modulation ablation of sustaining rotors abruptly terminates persistent atrial fibrillation to sinus rhythm with elimination on follow-up: a video case study. Heart Rhythm. 2012;9:1436–1439. doi: 10.1016/j.hrthm.2012.03.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noujaim SF, Berenfeld O, Kalifa J, Cerrone M, Nanthakumar K, Atienza F, Moreno J, Mironov S, Jalife J. Universal scaling law of electrical turbulence in the mammalian heart. Proc Natl Acad Sci U S A. 2007a;104:20985–20989. doi: 10.1073/pnas.0709758104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noujaim SF, Pandit SV, Berenfeld O, Vikstrom K, Cerrone M, Mironov S, Zugermayr M, Lopatin AN, Jalife J. Up-regulation of the inward rectifier K+ current (IK1) in the mouse heart accelerates and stabilizes rotors. J Physiol. 2007b;578:315–326. doi: 10.1113/jphysiol.2006.121475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuss HB, Marban E, Johns DC. Overexpression of a human potassium channel suppresses cardiac hyperexcitability in rabbit ventricular myocytes. J Clin Invest. 1999;103:889–896. doi: 10.1172/JCI5073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obreztchikova MN, Patberg KW, Plotnikov AN, Ozgen N, Shlapakova IN, Rybin AV, Sosunov EA, Danilo P, Jr, Anyukhovsky EP, Robinson RB, Rosen MR. IKr contributes to the altered ventricular repolarization that determines long-term cardiac memory. Cardiovasc Res. 2006;71:88–96. doi: 10.1016/j.cardiores.2006.02.028. [DOI] [PubMed] [Google Scholar]
- Perrin MJ, Subbiah RN, Vandenberg JI, Hill AP. Human ether-a-go-go related gene (hERG) K+ channels: function and dysfunction. Prog Biophys Mol Biol. 2008;98:137–148. doi: 10.1016/j.pbiomolbio.2008.10.006. [DOI] [PubMed] [Google Scholar]
- Rohr S, Flückiger-Labrada R, Kucera JP. Photolithographically defined deposition of attachment factors as a versatile method for patterning the growth of different cell types in culture. Pflugers Arch. 2003;446:125–132. doi: 10.1007/s00424-002-1000-0. [DOI] [PubMed] [Google Scholar]
- Samie FH, Berenfeld O, Anumonwo J, Mironov SF, Udassi S, Beaumont J, Taffet S, Pertsov AM, Jalife J. Rectification of the background potassium current: a determinant of rotor dynamics in ventricular fibrillation. Circ Res. 2001;89:1216–1223. doi: 10.1161/hh2401.100818. [DOI] [PubMed] [Google Scholar]
- Sekar RB, Kizana E, Cho HC, Molitoris JM, Hesketh GG, Eaton BP, Marbán E, Tung L. IK1 heterogeneity affects genesis and stability of spiral waves in cardiac myocyte monolayers. Circ Res. 2009;104:355–364. doi: 10.1161/CIRCRESAHA.108.178335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimizu W, Antzelevitch C. Effects of a K+ channel opener to reduce transmural dispersion of repolarization and prevent torsade de pointes in LQT1, LQT2, and LQT3 models of the long-QT syndrome. Circulation. 2000;102:706–712. doi: 10.1161/01.cir.102.6.706. [DOI] [PubMed] [Google Scholar]
- Stoll M, Quentin M, Molojavyi A, Thamer V, Decking UK. Spatial heterogeneity of myocardial perfusion predicts local potassium channel expression and action potential duration. Cardiovasc Res. 2008;77:489–496. doi: 10.1093/cvr/cvm060. [DOI] [PubMed] [Google Scholar]
- Vaidya D, Morley GE, Samie FH, Jalife J. Reentry and fibrillation in the mouse heart. A challenge to the critical mass hypothesis. Circ Res. 1999;85:174–181. doi: 10.1161/01.res.85.2.174. [DOI] [PubMed] [Google Scholar]
- Voigt N, Trausch A, Knaut M, Matschke K, Varró A, Van Wagoner DR, Nattel S, Ravens U, Dobrev D. Left-to-right atrial inward rectifier potassium current gradients in patients with paroxysmal versus chronic atrial fibrillation. Circ Arrhythm Electrophysiol. 2010;3:472–480. doi: 10.1161/CIRCEP.110.954636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaitsev AV, Berenfeld O, Mironov SF, Jalife J, Pertsov AM. Distribution of excitation frequencies on the epicardial and endocardial surfaces of fibrillating ventricular wall of the sheep heart. Circ Res. 2000;86:408–417. doi: 10.1161/01.res.86.4.408. [DOI] [PubMed] [Google Scholar]
- Zhou Z, Gong Q, Ye B, Fan Z, Makielski JC, Robertson GA, January CT. Properties of HERG channels stably expressed in HEK 293 cells studied at physiological temperature. Biophys J. 1998;74:230–241. doi: 10.1016/S0006-3495(98)77782-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zlochiver S, Muñoz V, Vikstrom KL, Taffet SM, Berenfeld O, Jalife J. Electrotonic myofibroblast-to-myocyte coupling increases propensity to reentrant arrhythmias in two-dimensional cardiac monolayers. Biophys J. 2008;95:4469–4480. doi: 10.1529/biophysj.108.136473. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


