Network Inference and Biological Dynamics

Abstract

Network inference approaches are now widely used in biological applications to probe regulatory relationships between molecular components such as genes or proteins. Many methods have been proposed for this setting, but the connections and differences between their statistical formulations have received less attention. In this paper, we show how a broad class of statistical network inference methods, including a number of existing approaches, can be described in terms of variable selection for the linear model. This reveals some subtle but important differences between the methods, including the treatment of time intervals in discretely observed data. In developing a general formulation, we also explore the relationship between single-cell stochastic dynamics and network inference on averages over cells. This clarifies the link between biochemical networks as they operate at the cellular level and network inference as carried out on data that are averages over populations of cells. We present empirical results, comparing thirty-two network inference methods that are instances of the general formulation we describe, using two published dynamical models. Our investigation sheds light on the applicability and limitations of network inference and provides guidance for practitioners and suggestions for experimental design.

1 Introduction

Networks of molecular components such as genes, proteins and metabolites play a prominent role in molecular biology. A graph G = (V, E) can be used to describe a biological network, with the vertices V identified with molecular components and the edges E with regulatory relationships between them. For example, in a gene regulatory network [3, 13], nodes represent genes and edges transcriptional regulation, while in a protein signaling network [61], nodes represent proteins and edges may represent the enzymatic influence of the parent on the biochemical state of the child, for example via phosphorylation. In many biological contexts, including disease states, the edge structure of the network may itself be uncertain (e.g. due to genetic or epigenetic alterations). Then, an important biological goal is to characterize the edge structure (often referred to as the “topology” of the network) in a context-specific manner, that is, using data acquired in the biological context of interest (e.g. a type of cancer, or a developmental state). Advances in high-throughput data acquisition have led to much interest in such data-driven characterization of biological networks. Statistical approaches play an increasingly important role in these “network inference” efforts. From a statistical perspective, the goal can be viewed as making inference regarding the edge structure E in light of biochemical data y. Since aspects of biological dynamics may not be identifiable at steady-state, time-varying data is usually preferred, and this is the setting we focus on here. In many applications the data y arise from “global perturbation” of the cellular system, for example by varying culture conditions or stimuli. The extent to which networks can be characterized using global perturbations remains poorly understood, since it is likely that such data expose only a subspace of the phase space associated with cellular dynamics.

The importance of network inference in diverse biological applications, from basic biology to diseases such as cancer, has spurred vigorous activity in this area. Many specific methods have been proposed, in the statistical literature as well as in bioinformatics and bioengineering, with some popular approaches reviewed in [5, 24, 34, 38]. Graphical models play a prominent role in this literature, as does variable selection. A distinction is often made between statistical and “mechanistic” approaches [28]. The former is usually used to refer to models that are built on conventional regression formulations and variants thereof, while the latter usually refers to models that are explicitly rooted in chemical kinetics, e.g. systems of coupled ordinary differential equations (ODEs). This distinction is somewhat artificial, since it is possible in principle to carry out formal statistical network inference based on mechanistic models (e.g. systems of ODEs), although this remains challenging [60].

Many network inference schemes are based on formulations that are closely related in terms of the underlying statistical model. For example, vector autoregressive (VAR) models (including Granger causality-related approaches as special cases) [7, 40, 42, 46, 63], linear dynamic Bayesian networks (DBNs) [29], and certain ODE-based approaches [4, 35, 44] are intimately related, being based on linear regression, but with potentially differing approaches to variable selection. In recent years, several empirical comparisons of competing network inference schemes have emerged, including [2, 5, 22, 52, 57]. Assessment methodology has received attention, including attempts to automate the generation of large scale biological network models for automatic benchmarking of performance [37, 55]. In particular the Dialogue for Reverse Engineering Assessments and Methods (DREAM) challenges [48] have provided an opportunity for objective empirical assessment of competing approaches. At the same time developments in synthetic biology have led to the availability of gold standard data from hand-crafted biological systems, such that the underlying network is known by design [9, 10, 41]. However relatively little attention has been paid to the (sometimes contrasting) assumptions of the statistical formulations underlying these network inference schemes.

Inferential limitations due to estimator bias and nonidentifiability remain incompletely understood. It is clear that chemical reaction networks (CRNs; these are graphs that give detailed descriptions of individual reactions comprising the overall system) underlying biological networks are not in general identifiable [11]. Indeed, there exist topologically distinct CRNs which produce identical dynamics under mass-action kinetics. Moreover even when the true network structure is known, reaction rates themselves may be nonidentifiable. However, mainstream descriptions of biological networks, e.g. gene regulatory or protein signaling networks, are coarser than CRNs. Such networks are useful because they are closely tied to validation experiments in which interventions (e.g. RNA interference or inhibitors) target network vertices. For example, inference of an edge in a gene regulatory network corresponds to the qualitative prediction that intervention on the parent will influence the child (via transcription factor activity). It remains unclear to what extent such biological network structure can be usefully identified from various kinds of data. On the other hand [58, 59] discuss a number of general issues relating to stochastic modeling for systems biology, but do not discuss network inference per se in detail. This paper complements existing empirical work by focusing on statistical issues associated with linear models commonly used in network inference applications.

Network inference methods can be viewed as generating hypotheses about cell biology. Yet the link between biochemical networks at the cellular level and network inference as applied to bulk or aggregate data (i.e. data that are averages over large numbers of cells) from assays such as microarrays remains unclear. In applications to noisy time-varying data there is uncertainty in the predictor variables of the same order of magnitude as uncertainty in the responses, yet often only the latter is explicitly accounted for. Moreover, the treatment of time intervals in discretely observed data remains unclear, with contradictory approaches appearing in the literature. Most high-throughput assays, including array based technologies (e.g. gene expression or protein arrays), as well as single-cell approaches (e.g. FACS-based) involve destructive sampling, i.e. cells are destroyed to obtain the molecular measurements. The impact of the resulting nonlongitudinality upon inference does not appear to have been investigated.

The contributions of this paper are threefold. First, we explore the connection between biological networks at the cellular level and the linear statistical models that are widely used for inference. Starting from a description of stochastic dynamics at the single-cell level we describe a general statistical approach rooted in the linear model. This makes explicit the assumptions that underlie a broad class of network inference approaches. This also clarifies the relationship between “statistical” and “mechanistic” approaches to biological networks. Second, we explore how a number of published network inference approaches can be recovered as special cases of the model we arrive at. This sheds light on the differences between them, including how different assumptions lead to quite different treatments of the time step. Third, we present an empirical study comparing 32 different approaches that are special cases of the general model we describe. To do so, we simulate stochastic dynamics at the single-cell level from known networks, under global perturbation of two published dynamical models. This enables a clear assessment of the network inference methods in terms of estimation bias and consistency, since the true data-generating network is known. Furthermore, the simulation accounts for both averaging over cells, nonlongitudinality due to destructive sampling and the fact that only a subspace of the dynamical phase space is explored. Using this approach, we investigate a number of data regimes, including both even and uneven sampling, longitudinal and nonlongitudinal data and the large sample, low noise limit. We find that the net effect of predictor uncertainty, nonlongitudinality and limited exploration of the dynamical phase space is such that certain network estimators fail to converge to the data-generating network even in the limits of large datasets and low noise. However, we point to a simple formulation which might represent a default choice, delivering promising performance in a number of regimes.

An implication of our analysis is that uneven time steps may pose inferential problems, even when using models that apparently handle the sampling intervals explicitly. We therefore investigate this case by carrying out network inference on unevenly sampled data using a variety of statistical models. We find that the ability to reconstruct the data-generating network is much reduced in all cases, with some approaches faring better than others. Since biological data are often unevenly resolved in time, this observation has important implications for experimental design.

The remainder of this paper is organized as follows. We begin in Section 2 with a description of stochastic dynamics in single-cells and show how a series of assumptions allow us to arrive at a statistical framework rooted in the linear model. Section 3 contains an empirical comparison of several inference schemes, addressing questions of performance and consistency in a number of regimes. In Section 4 we discuss our results and point to several specific areas for future work.

2 Methods

The cellular dynamics that underlie network inference are subject to stochastic effects [17, 32, 39, 49, 53]. We therefore begin our description of the data-generating process at the level of single cells and then discuss the relationship to aggregate data of the kind acquired in high-throughput biochemical assays. We then develop a general statistical approach, rooted in the linear model, for data from such a system observed discretely in time. We discuss inference and show how a number of existing approaches can be recovered as special cases of the general model we describe. Our exposition clarifies a number of technical but important distinctions between published methodologies, which until now have received little attention.

2.1 Data-generating process

2.1.1 Stochastic dynamics in single cells

Let $\mathbf{X}=(X_1,\dots ,X_P)\in \mathcal{X}$ denote a state vector describing the abundance of molecular quantities of interest, on a space $\mathcal{X}$ chosen according to physical and statistical considerations. The components of the state vector (e.g. mRNA, protein or metabolite levels) are identified with the vertices of the graph G that describes the biological network of interest. In this paper the “expression levels” X(t) of a single cell at time t are modeled as continuous random variables that we assume satisfy a time-homogenous stochastic delay differential equation (SDDE)

$$d\mathbf{X}=\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\right)dt+\mathbf{g}\left({\mathcal{F}}_{\mathbf{X}}\right)d\mathbf{B}$$ (1)

where f, g are drift and diffusion functions respectively, ${\mathcal{F}}_{\mathbf{X}}\left(t\right)=\{\mathbf{X}\left(s\right):s\le t\}$ is the natural filtration (the history of the state vector X) and B denotes a standard Brownian motion. A continuous state space $\mathcal{X}$ is appropriate as a modeling assumption only if the copy numbers of all molecular components are sufficiently high. This is thought to be the case for the biological systems considered in this paper, but in general the stochasticity due to low copy number will need to be encoded into inference [49]. The edge structure E of the biological network G is defined by the drift function f, such that $(i,j)\in E\iff f_j\left(\mathbf{X}\right)$ depends on X_i.

We further assume that the functions f, g are sufficiently regular and depend only on recent history ${\mathcal{F}}_{\mathbf{X}}\left([t-\tau ,t]\right)$. For example in the context of gene regulation τ might be the time required for one cycle of transcription, translation and binding of a transcription factor to its target site; the characteristic time scale for gene regulation. This is a finite memory requirement and can be considered a generalization of the Markov property. Equivalently, this property codifies the modeling assumption that the observed processes are sufficient to explain their own dynamics; that there are no latent variables. It is common practice to take τ = 0, in which case the process defined by Eqn. 1 is Markovian. This stochastic dynamical system with phase space $\{(\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\right),\mathbf{X}):\mathbf{X}\in \mathcal{X}\}$ forms the basis of the following exposition.

2.1.2 Aggregate data

A variety of experimental techniques, including notably microarrays and related assays, capture average expression levels ${\mathbf{X}}^{\left(N\right)}≔{\sum }_{k=1}^N{\mathbf{X}}^k∕N$ over cells, where X^k denotes the expression levels in cell k. This paper does not consider effects due to inter-cellular signaling, which are typically assumed to be negligible. Then averaging sacrifices the finite memory property (a generalization of the fact that the sum of two independent Markov processes is not itself Markovian). However it is usually possible to construct a finite memory approximation of the form

$$d{\mathbf{X}}^{\left(N\right)}={\mathbf{f}}^{\left(N\right)}\left({\mathcal{F}}_{{\mathbf{X}}^{\left(N\right)}}\right)dt+{\mathbf{g}}^{\left(N\right)}\left({\mathcal{F}}_{{\mathbf{X}}^{\left(N\right)}}\right)d{\mathbf{B}}^{\left(N\right)}$$ (2)

using a so-called “system size expansion” [56]. Approximations of this kind derive from a coarsening of the underlying state space, assuming that the new state vector X^(N) captures every quantity relevant to the dynamics. The statistical models discussed in this paper rely upon coarsening assumptions in order to control the dimensionality of state space.

Using the mild regularity conditions upon cellular stochasticity g the laws of large numbers gives that in the large sample limit the sample average ${\mathbf{X}}^{\infty }:={\text{lim}}_{N\to \infty }{\mathbf{X}}^{\left(N\right)}=\mathbb{E}\left(\mathbf{X}\right)$ equals the expected state of a single cell (almost surely). We note that the relationship between the single-cell dynamics as it appears in Eqn. 1 and this deterministic limit may be complicated, since in general $\mathbb{E}\left(\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\right)\right)\ne \mathbf{f}\left({\mathcal{F}}_{\mathbb{E}\left(\mathbf{X}\right)}\right)$. However for linear f, say for simplicity f ≡ f(X) = AX, we have

$$\begin{array}{cc}\hfill d{\mathbf{X}}^{\left(N\right)}=\frac{1}{N}\sum _{k=1}^{N}d{\mathbf{X}}^k& =\frac{1}{N}\sum _{k=1}^N(\mathbf{f}\left({\mathcal{F}}_{{\mathbf{X}}^k}\right)dt+\mathbf{g}\left({\mathcal{F}}_{{\mathbf{X}}^k}\right)d{\mathbf{B}}^k)\hfill \\ \hfill & =\frac{1}{N}\sum _{k=1}^N{\mathbf{AX}}^{k}dt+\frac{1}{N}\sum _{k=1}^N\mathbf{g}\left({\mathcal{F}}_{{\mathbf{X}}^k}\right)d{\mathbf{B}}^k\hfill \\ \hfill & =\mathbf{A}\left(\frac{1}{N}\sum _{k=1}^N{\mathbf{X}}^k\right)dt+{\mathbf{R}}^{\left(N\right)}\hfill \\ \hfill & ={\mathbf{AX}}^{\left(N\right)}dt+{\mathbf{R}}^{\left(N\right)}=\mathbf{f}\left({\mathcal{F}}_{{\mathbf{X}}^{\left(N\right)}}\right)dt+{\mathbf{R}}^{\left(N\right)}\hfill \end{array}$$ (3)

where ${\mathbf{R}}^{\left(N\right)}≔{\sum }_k\mathbf{g}\left({\mathcal{F}}_{{\mathbf{X}}^k}\right)d{\mathbf{B}}^k∕N\to 0$ almost surely as N → ∞, and so $d{\mathbf{X}}^{\infty }∕dt=\mathbf{f}\left({\mathcal{F}}_{{\mathbf{X}}^{\infty }}\right)$. In other words, the average over large numbers of cells shares the same drift function as the single cell, so that inference based on averaged data applies directly to single cell dynamics. Otherwise this may not hold, that is $d{\mathbf{X}}^{\infty }∕dt=d\mathbb{E}\left(\mathbf{X}\right)∕dt=\mathbb{E}\left(\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\right)\right)\ne \mathbf{f}\left({\mathcal{F}}_{\mathbb{E}\left(\mathbf{X}\right)}\right)=\mathbf{f}\left({\mathcal{F}}_{{\mathbf{X}}^{\infty }}\right)$. This has implications when using nonlinear forms, such as Michaelis-Menten or Hill kinetics, to describe the behavior of a large sample average; these nonlinear functions are derived from single cell biochemistry and may not apply equally to the large sample average X^∞. The error entailed by commuting drift and expectation may be assessed using the multivariate Feynman-Kac formula for ${\mathbf{X}}^{\infty }=\mathbb{E}\left(\mathbf{X}\right)$ [45].

In practice the observation process may be complex and indirect, for example measurements of gene expression may be relative to a “housekeeping” gene, assumed to maintain constant expression over the course of the experiment. Moreover the details of the error structure will depend crucially on the technology used to obtain the data. To limit scope, this article assumes the averaged expression levels X^∞(t) are observed at discrete times t = t_j (0 ≤ j ≤ n) with additive zero-mean measurement error as Y(t_j) = X^∞(t_j) + w_j, where the w_j are independent, identically distributed uncorrelated Gaussian random variables.

2.2 Discrete time models

Network inference is usually carried out using coarse-grained models (Eqn. 2) that are simpler and more amenable to inference than the process described by Eqn. 1. Here, informed by the foregoing treatment of cellular dynamics, we develop a simple network inference model for data observed discretely in time. We clarify the assumptions of the statistical model, and show how several published approaches can be recovered as special cases.

2.2.1 Approximate discrete time likelihood

Network inference entails statistical comparison of networks $G\in \mathcal{G}$, where $\mathcal{G}$ denotes the space of candidate networks. The space $\mathcal{G}$ may be large (naively, there are 2^P×P possible networks on P vertices), although biological knowledge may provide constraints. Network comparisons require computation of a model selection score for each network that is considered, which in turn entails use of the likelihood (e.g. maximization of information criteria, or integration over the likelihood in the Bayesian setting). Therefore, exploration over large model spaces is often only feasible given a closed-form expression for the likelihood (or preferably for the model score itself).

However the likelihood for a SDDE model (Eqn. 2) is not generally available in closed form. There has been recent research into computationally efficient approximate likelihoods for fully observed, noiseless diffusions [26], but it remains the case that the most efficient (though least accurate) closed-form approximate likelihood is based on the Euler-Maruyama discretization scheme for stochastic differential equations (SDEs), which in the more general SDDE case may be written as (henceforth dropping the superscript N)

$$\mathbf{X}\left(t_j\right)\approx \mathbf{X}\left(t_{j-1}\right)+{\Delta }_j\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\left(t_{j-1}\right)\right)+\mathbf{g}\left({\mathcal{F}}_{\mathbf{X}}\left(t_{j-1}\right)\right)\Delta {\mathbf{B}}_j$$ (4)

where ΔB_j ~ N(0, Δ_jI) and Δ_j = t_j – t_j–1 is the sampling time interval. Incorporating measurement error into this so-called Riemann-Itô likelihood [12] requires an integral over the hidden states X which would destroy the closed-form approximation. Therefore the observed, nonlongitudinal data y are directly substituted for the latent states X, yielding the (triply) approximate likelihood

$$\begin{array}{cc}\hfill \mathcal{L}\left(\theta \right)& =\prod _{j=1}^n\mathcal{N}(\mathbf{y}\left(t_j\right);\mu \left(t_j\right),\Sigma \left(t_j\right))\hfill \\ \hfill \mu \left(t_j\right)& =\mathbf{y}\left(t_{j-1}\right)+{\Delta }_j\mathbf{f}\left({\mathcal{F}}_{\mathbf{y}}\left(t_{j-1}\right)\right)\hfill \\ \hfill \Sigma \left(t_j\right)& ={\Delta }_j\mathbf{g}\left({\mathcal{F}}_{\mathbf{y}}\left(t_{j-1}\right)\right)\mathbf{g}{\left({\mathcal{F}}_{\mathbf{y}}\left(t_{j-1}\right)\right)}^{\prime }.\hfill \end{array}$$ (5)

Here $\mathcal{N}(•;\mu ,\Sigma )$ denotes a Normal density with mean μ and covariance Σ. Implicit here is that the functions f, g depend on ${\mathcal{F}}_{\mathbf{y}}$ only through time lags which coincide with the measurement times t_j–1.

Thus $\mathcal{L}$ may be obtained from a state-space approximation to the original SDDE model (Eqn. 2). Despite reported weaknesses with the Riemann-Itô likelihood [12, 26] and the poorly characterized error incurred by plugging in nonlongitudinal observations, this form of approximate likelihood is widely used to facilitate network inference (Eqns. 5-6 correspond to a Gaussian DBN for the observations y, generalized to allow dependence on history). This is due both to the possibility of parameter orthogonality, allowing inference to be performed for each network node separately, and the possibility of conjugacy, leading to a closed-form marginal likelihood π(y|G).

2.2.2 Linear dynamics

Kinetic models have been described for many cellular processes [10, 51, 54, 59]. However, statistical inference for these often non-linear models may be challenging [58, 59, 60]. Moreover, there is no guarantee that conclusions drawn from cellular averages will apply to single cells, because as noted above the deterministic behavior seen in averages may not coincide with the single cell drift. However, linear dynamics satisfy $\mathbb{E}\left(\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\right)\right)=\mathbf{f}\left({\mathcal{F}}_{\mathbb{E}\left(\mathbf{X}\right)}\right)$ exactly, so that conclusions drawn from verages apply directly to single cells. For notational simplicity consider the Markovian τ = 0 regime. A Taylor approximation of the cellular drift f about the origin gives

$$\mathbf{f}\left(\mathbf{X}\right)\approx \mathbf{f}\left(0\right)+D\mathbf{f}{\mid }_{\mathbf{x}=0}\mathbf{X}$$ (6)

where Df is the Jacobian matrix of f. The constant term can be omitted (f(0) = 0), since absent any regulators there is no change in expression. Then, the Jacobian Df captures the dynamics approximately under a linear model. Furthermore, the absence of an edge in the network G implies a zero entry in the Jacobian, that is $(i,j)\notin E\Rightarrow {\left(D\mathbf{f}\right)}_{ji}=0$. Obtaining the Jacobean at x = 0 therefore does not imply complete knowledge of the edge structure E. We note that the general SDDE case is similar but with additional differentiation required for the additional dependencies of f. Henceforth we write equations for the simpler Markovian model, although they hold more generally.

One may ask whether the restriction to linear drift functions allows the computational difficulties associated with inference for continuous time models to be avoided, since in the Markovian (τ = 0) case both the SDE (Eqn. 1) and limiting ordinary differential equation (ODE) have exact closed form solutions. In the ODE case, for example, X(t) = exp(At)X₀ and under Gaussian measurement error the likelihood has a closed form as products of terms $\mathcal{N}(\mathbf{y}\left(t_j\right);\text{exp}\left(\mathbf{A}{t}_j\right){\mathbf{X}}_0,\mathbf{M})$ where the parameters θ = (A, X₀, M) include the model parameters A, initial state vector X₀ and the measurement error covariance M. Unfortunately evaluation of the matrix exponential is computationally demanding and inference for the entries of A must be performed jointly since in general exp(A) does not factorize usefully. It therefore remains the case that inference for continuous time models is computationally burdensome, even when the models are linear.

2.2.3 The dynamical system as a regression model

The Jacobian Df with entries ${\left(D\mathbf{f}\right)}_{i,j}=\partial f_i∕\partial x_j{\mid }_{\mathbf{x}=0}$ is now the focus of inference. We can identify the Jacobian with the unknown parameters in a linear regression problem by modeling the expression of gene p using

$$\left[\begin{array}{c}\hfill d{X}_p\left(t_1\right)\hfill \\ \hfill ⋮\hfill \\ \hfill d{X}_p\left(t_n\right)\hfill \end{array}\right]\approx \left[\begin{array}{ccc}\hfill X_1\left(t_0\right)\hfill & \hfill \dots \hfill & \hfill X_P\left(t_0\right)\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill X_1\left(t_{n-1}\right)\hfill & \hfill \dots \hfill & \hfill X_P\left(t_{n-1}\right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\left(Df\right)}_{p,1}\hfill \\ \hfill ⋮\hfill \\ \hfill {\left(Df\right)}_{p,P}\hfill \end{array}\right]$$ (7)

where the gradients dX_p(t_j) are approximated by finite differences, in this case (X_p(t_j) – X_p(t_j–1))/Δ_j. Our notation for finite differences should not be confused with the differentials of stochastic calculus. More generally for processes with memory the matrix may be augmented with columns corresponding to lagged state vectors and the vector (Df)_p,• augmented with the corresponding derivatives of the drift function f with respect to these lagged states. To avoid confusion we write A for Df when discussing parameters, since the drift f is unknown. Similarly, design matrices will be denoted by B to suppress the dependence on the random variables X. So Eqn. 7 may be written compactly as

$$d{\mathbf{X}}_p\approx \mathbf{B}{A}_{p,•}^{\prime }.$$ (8)

Inference for the parameters A_p,• may be performed independently for each variable p. Whilst Eqn. 8 is fundamental for inference, one can equivalently consider the dynamically intuitive expression

$$d\mathbf{X}\left(t_j\right)\approx \mathbf{A}{B}_{j,•}^{\prime }.$$ (9)

An interesting issue arises from the dual interpretation of the regression model as a dynamical system (Eqn. 9), because there are natural restrictions on A to avoid the solution tending to infinity. For instance if the sampling interval Δ is constant then we require $\mathbb{R}\left(\lambda \right)\le 0$ for each eigenvalue λ of A + ΔI. The inference schemes which we discuss do not account for this, because the condition forces a nontrivial coupling between rows A_p,•, jeopardizing parameter orthogonality.

Finally, the generative model is specified by substituting noisy, nonlongitudinal observables Y for latent variables X into Eqn. 9 and stating the dependence of the approximation error on the sampling interval Δ_j. Under uncorrelated Gaussian measurement error we arrive at a model

$$d\mathbf{Y}\left(t_j\right)\sim N(\mathbf{A}{B}_{j,•}^{\prime },h\left({\Delta }_j\right)\mathcal{D}({\sigma }_1^2,\dots ,{\sigma }_P^2))$$ (10)

where $h:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ is a variance function that must be specified and $\mathcal{D}\left(\mathbf{v}\right)$ represents the diagonal matrix induced by the vector v.

There are a number of ways in which this regression is non-standard. For example, the substitution of (nonlongitudinal) observations for latent variables is clearly unsatisfactory because the linear regression framework does not explicitly allow for uncertainty in the predictor variables B. It is unclear whether this introduces bias or leads to an overestimate of the significance of results. Moreover, it is unclear how to choose the variance function h, since the Euler-Maruyama approximation (Eqn. 4) is only valid for small sampling intervals Δ_j, but in this regime the responses dY(t_j) are dominated by measurement error, such that the data may carry little information. These issues are investigated in Sections 3 and 4 below.

2.3 A unifying framework

Eqn. 10 describes a class of models with specific instances characterized by choice of design matrix B and variance function h. Since any such model corresponds to the linear regression Eqn. 7, the task of determining the edge structure of the network, or equivalently the location of non-zero entries in the Jacobian A, can be cast as a variable selection problem.

A number of specific network inference schemes can now be recovered by fixing the design matrix and variance function and coupling the resulting model with a variable selection technique. A selection of published network inference schemes that can viewed in this way is presented in Table 1. One might see these schemes classed as VAR models [7, 42, 46, 63], DBNs [25, 29], or ODE-based approaches [4, 35, 44], although as we have demonstrated this classification disguises their shared foundation in the linear model.

Table 1.

A nonexhaustive list of network inference schemes rooted in the linear model. The examples from literature demonstrate the statistical features indicated, but may differ in some aspects of implementation. The symbol ∅ denotes the VAR(q) model which lacks a variance function.

Design matrix B	Variance function h(Δ) ∝	Variable selection	Example
Standard	Δ – 2	Ridge regression	[4] Bansal and di Bernardo, “TSNIB”
Standard with lagged predictors	∅	Group LASSO	[7] Bolstad et al.
Quadratic	∅	Conjugate Bayesian with network prior	[25] Hill et al.
Standard	∅	Information criteria	[29] Kim et al.,
Non-linear (Hill) basis functions	1	AIC with backstepping	[35] Li and Chen
Standard	1	Conditional independence tests	[36] Li et al. “DELDBN”
Standard	∅	Semi-conjugate Bayesian	[42] Morrissey et al.
Standard	Δ – 2	SVD and pseudoinverse	[44] Nam et al. “LEARNe”
Standard	∅	Multi-stage analytic shrinkage approach	[46] Opgen-Rhein and Strimmer
Standard and non-linear with lagged predictors	∅	Granger causality	[63] Zou and Feng

As shown in Table 1, the variance functions h, and therefore sampling intervals Δ_j, are not treated in a consistent way in the literature. In the special case of even sampling times Δ_j = Δ, a model is characterized only by its design matrix. If the standard design matrix is used then the entire family of models

$$\frac{\mathbf{Y}\left(t_j\right)-\mathbf{Y}\left(t_{j-1}\right)}{\Delta }\sim N(\mathbf{AY}\left(t_{j-1}\right),h\left(\Delta \right)\mathcal{D}({\sigma }_1^2,\dots ,{\sigma }_P^2))$$ (11)

reduces to a linear VAR(1) model

$$\mathbf{Y}\left(t_j\right)\sim N(\stackrel{‒}{\mathbf{A}}\mathbf{Y}\left(t_{j-1}\right),\mathcal{D}({\stackrel{‒}{\sigma }}_1^2,\dots ,{\stackrel{‒}{\sigma }}_P^2))$$ (12)

where Ā = ΔA + I and ${\stackrel{‒}{\sigma }}_p^2={\Delta }^{2}h\left(\Delta \right){\sigma }_p^2$. More generally the VAR(q) model is prevalent in the literature (see Table 1), yet it does not explicitly handle uneven sampling intervals. This is a potentially important issue since uneven sampling is commonplace in global perturbation experiments, with high frequency sampling used to capture short term cellular response and low frequency sampling to capture the approach to equilibrium. We discuss the importance of modeling using a variance function, and whether a natural choice for such a function exists in Section 4 below. In addition we explored whether inference may be improved through the use of either nonlinear basis functions or lagged predictors to capture respectively nonlinearity and memory in the underlying drift function is unclear. Section 3 presents an empirical investigation of these issues.

2.4 Inference

An appealing feature of the discrete time model is that parameters corresponding to different variables are orthogonal in the Fisher sense:

$$\mathcal{L}\left(\theta \right)=\prod _{p=1}^P\mathcal{L}(A_{p,•},{\sigma }_p)$$ (13)

As a consequence network inference over $\mathcal{G}$ may be factorized into P independent variable selection problems. For definiteness we focus on just two approaches to variable selection, the Bayesian marginal likelihood and AIC, but note that many other approaches are available, including those listed in Table 1, and can be applied here in analogy to what follows. Below we assume the response vector dy_ph^–1/2 and the columns of the design matrix Bh^–1/2 are standardized to have zero mean and unit variance, but for clarity subsume this into unaltered notation.

2.4.1 Bayesian variable selection

For simplicity, the variance function is initially taken to be constant (h = 1). We set up a Bayesian linear model conditional on a network G using Zellner's g-prior [62], that is with priors $A_{p,•}\mid {\sigma }_p^2\sim N(0,{\sigma }_p^{2}n{\left({{\mathbf{B}}_p}^{\prime }{\mathbf{B}}_p\right)}^{-1})$ and $\pi \left({\sigma }_p^2\right)\propto 1∕{\sigma }_p^2$ where B_p is the design matrix B with non-predictors removed according to G. We note that while the g-prior is a common choice, alternatives may offer some advantages [14, 19].

Let m_p be the number of predictors for variable p in the network G. Integrating the likelihood (induced by Eqn. 10) against the prior for $(A_{p,•},{\sigma }_p^2)$ produces the following closed-form marginal likelihood

$$\pi (\mathbf{y}\mid G)\propto \prod _p{\left(\frac{1}{1+n}\right)}^{m_p∕2}{\left[d{\mathbf{y}}_p^{\prime }d{\mathbf{y}}_p-\left(\frac{n}{1+n}\right)\widehat{d}{\mathbf{y}}_p^{\prime }\widehat{d}{\mathbf{y}}_p\right]}^{-n∕2}$$ (14)

where $\widehat{d}{\mathbf{y}}_p={\mathbf{B}}_p{\left({{\mathbf{B}}_p}^{\prime }{\mathbf{B}}_p\right)}^{-1}{{\mathbf{B}}_p}^{\prime }d{\mathbf{y}}_p$. These formulae extend to arbitrary variance functions h by substituting $\mathbf{B}\mapsto \mathbf{B}{h}^{1∕2}$, $d\mathbf{y}\mapsto d\mathbf{y}{h}^{1∕2}$. Network inference may now be carried out by Bayesian model averaging, using the posterior probability of a directed edge from variable i to variable j:

$$\mathbb{P}\left(i\text{regulates}j\right)=\sum _G\frac{\pi (\mathbf{y}\mid G)\pi \left(G\right)}{\sum _{G^{\prime }}\pi (\mathbf{y}\mid G^{\prime })\pi \left(G^{\prime }\right)}\mathbb{I}\{(i,j)\in E\left(G\right)\}.$$ (15)

In experiments below, we take a network prior which, for each variable p is uniform over the number of predictors m_p up to a maximum permissible in-degree d_max, that is $\pi \left(G\right)\propto {\prod }_p{\left(\begin{array}{c}\hfill P\hfill \\ \hfill m_p\hfill \end{array}\right)}^{-1}\mathbb{I}\{m_p\le d_{\text{max}}\}$, but note that richer subjective network priors are available in the literature [43]. Finally, a network estimator Ĝ is obtained by thresholding posterior edge probabilities: $(i,j)\in E\left(\widehat{G}\right)\iff \mathbb{P}\left(i\text{regulates}j\right)>∊$. For small maximum in-degree d_max, exact inference by enumeration of variable subsets may be possible. Otherwise, Markov chain Monte Carlo (MCMC) methods can be used to explore an effectively smaller model space [16, 21]. In the experiments below we use exact inference by enumeration.

2.4.2 Variable selection by corrected AIC

Again, consider a constant variance function (h = 1); rescaling as described above recovers the general case. The usual maximum likelihood estimates ${\widehat{A}}_{p,•}={\left({{\mathbf{B}}_p}^{\prime }{\mathbf{B}}_p\right)}^{-1}{{\mathbf{B}}_p}^{\prime }d{\mathbf{y}}_p$ and ${\widehat{\sigma }}_p^2=\frac{1}{n}{\sum }_j{(d{\mathbf{y}}_p\left(t_j\right)-\widehat{d}{\mathbf{y}}_p\left(t_j\right))}^2$ induce closed forms $C_p{\widehat{\sigma }}_p^{-n}$ for the maximized factors of the likelihood function, where C_p is a constant not depending on the choice of predictors. Corrected AIC scores [8] for each variable p are then

$$AI{C}_c(p,G)=n\text{log}\left({\widehat{\sigma }}_p^2\right)+2m_p+\frac{2m_p(m_p+1)}{n-m_p-1}.$$ (16)

Again we consider all models with maximum permissible in-degree d_max. Lowest scoring models are chosen for each variable in turn, inducing a network estimator Ĝ.

3 Results

In this Section, we present empirical results investigating the performance of a number of network inference schemes that are special cases of the general formulation described by Eqn. 10. Objective assessment of network inference is challenging [48], since for most biological applications the true data-generating network is unknown. We therefore exploit two published dynamical models of biological processes, namely Cantone et al. [10] and Swat et al. [54], described in detail in Supplemental Information (SI). The first is a synthetic gene regulatory network built in the yeast Saccharomyces cerevisiae. This five gene network and associated delay differential equations (DDEs) has received attention in computational biology [9, 41], and has been shown to agree with gold-standard data (at least under an $\mathbb{E}\left(\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\right)\right)\approx \mathbf{f}\left({\mathcal{F}}_{\mathbb{E}\left(\mathbf{X}\right)}\right)$ assumption). Cantone et al. consider two experimental conditions; “switch-on” and “switch-o ”. In this paper “switch-on” parameter values were used to generate data. The Swat model is a gene-protein network governing the G₁/S transition in mammalian cells. The model has a nine dimensional state vector and, unlike Cantone, is Markovian. We note that this model has not been directly verified in the manner of Cantone but is based on a theoretical understanding of cell cycle dynamics. There is undoubtedly bias from this essentially arbitrary choice of dynamical systems but a comprehensive sampling of the (vast) space of possible networks and dynamics is beyond the scope of this paper.

3.1 Experimental procedure

3.1.1 Simulation

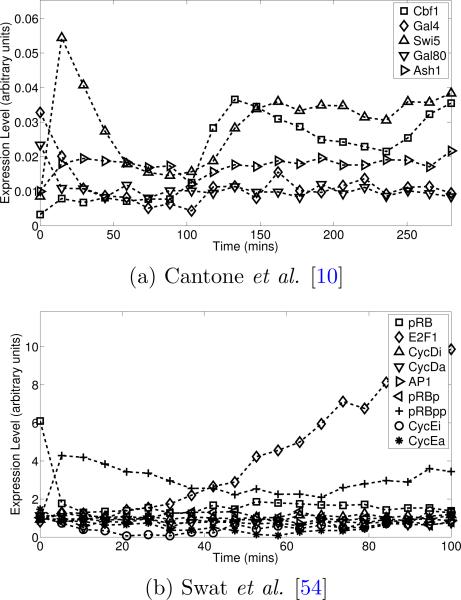
We consider global perturbation data by initializing the dynamical systems from out of equilibrium conditions. This is a common setting for network inference approaches, but the limitations of inference from such data remain incompletely understood. For each dynamical system f, trajectories X^k of single cell expression levels were obtained as solutions to the SDDE Eqn. 1 with drift f and uncorrelated diffusion $\mathbf{g}\left(\mathbf{X}\right)={\sigma }_{\text{cell}}\mathcal{D}\left(\mathbf{X}\right)$ (representing multiplicative cellular noise). Trajectories were obtained by numerically solving SDDEs with heterogeneous initial conditions using the Euler-Maruyama discretization scheme (Eqn. 4). MATLAB R2010a code for all simulation experiments is available in the SI. To mimic destructive sampling and consequent nonlongitudinality, solutions were regenerated at each time point. We are interested in data that are averages over a large number N of single-cell trajectories. However, the computational cost of solving N × n SDDEs to produce each data set is prohibitive. Therefore, only a smaller number N* << N of cells were simulated and a larger sample N then obtained by bootstrapping, i.e. re-sampling from the N* trajectories with replacement. In practice N* should be taken sufficiently large such that a negligible change in experimental outcome results from further increase in N*. Initial conditions for single cell trajectories varied with standard deviation σ_cell. Finally, uncorrelated Gaussian noise of magnitude σ_meas was added to simulate a measurement process with additive error. In the experiments presented below, N = 10, 000, N* = 30 and n = 20 time points are taken within the dynamically interesting range (0-280 minutes for Cantone and 0-100 minutes for Swat). Measurement error and cellular noise are set to give signal-to-noise ratios $\langle \mathbf{X}\rangle ∕{\sigma }_{\text{meas}}\approx 10,\langle \mathbf{X}\rangle ∕{\sigma }_{\text{cell}}\approx 10$ (here $\langle \mathbf{X}\rangle$ represents the average expression levels of the variables X over all generated trajectories). Fig. 1 shows typical datasets for the two dynamical systems.

Figure 1.

Two published dynamical systems models of cellular processes were used to generate datasets. Single cell trajectories were generated from an SDDE model (Eqn. 1) and averaged under measurement noise and nonlongitudinality due to destructive sampling. (a) Data generated from (a model due to) Cantone et al. [10], describing a synthetic network built in yeast. (b) Data generated from Swat et al. [54], a theory-driven model of the G₁/S transition in mammalian cells.

3.1.2 Inference schemes

The following inference schemes were assessed 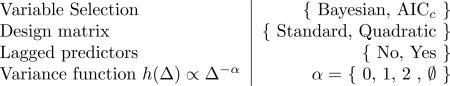For the design matrix “quadratic” refers to the augmentation of the predictor set by the pairwise products of predictors, the simplest nonlinear basis functions. For the variance function the symbol ∅ is used to denote the VAR(q) model, which formally lacks a variance function. “Lagged predictors = Yes” indicates augmentation of the predictor set with lagged observations (a lag of ≈ 28 mins is used for Cantone and ≈ 10 mins for Swat). There are heuristic justifications for each of the candidate variance functions. For example the function with α = 2 appears for small Δ_j when an exact Euler approximation and additive measurement error are assumed [4], whereas α = 1 is reminiscent of the Euler-Maruyama discretization Eqn. 4.

3.1.3 Empirical assessment

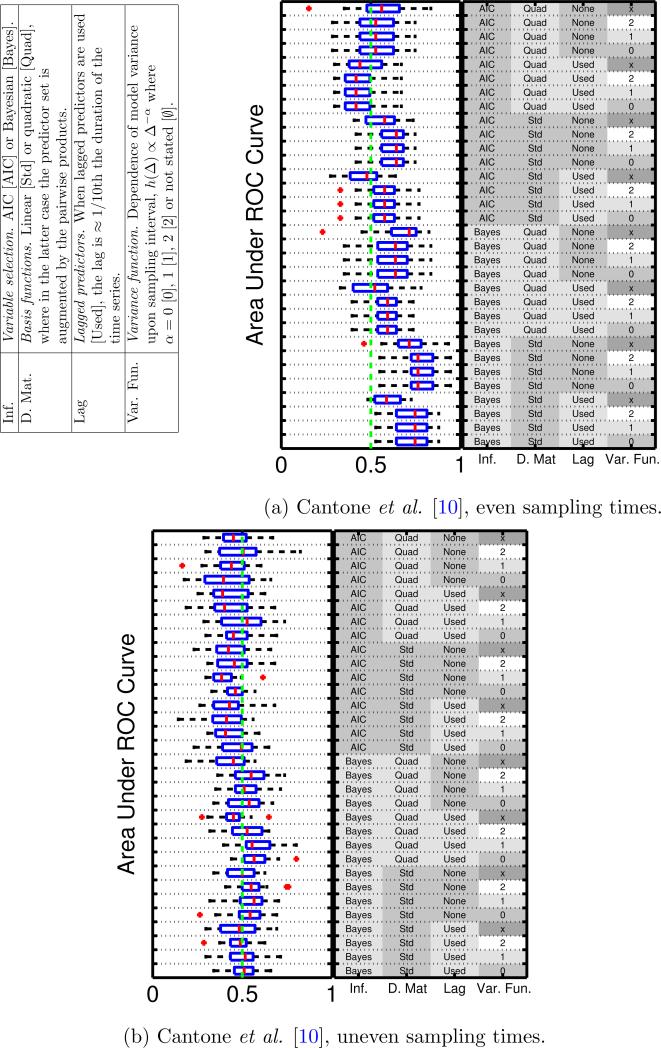
The performance of each inference scheme is quantified by the area under the receiver operating characteristic (ROC) curve (AUR), averaged over 20 datasets [18]. This metric, equivalent to the probability that a randomly chosen true edge is preferred by the inference scheme to a randomly chosen false edge, summarizes, across a range of thresholds, the ability to select edges in the true data-generating graph. Results presented below use a computationally favorable in-degree restriction d_max = 2. In order to check robustness to d_max all experiments were repeated using d_max = 3, with no substantial changes in observed outcome (SFig. 6).

3.2 Empirical results

3.2.1 Even sampling interval

Fig. 2(a) displays box-plots over AUR scores for the Cantone dynamical system under even sampling intervals. Note that under even sampling, for an otherwise identical scheme, changing variance function does not a ect the model, leading to identical AUR scores for schemes which differ only in variance function. (An exception to this is the VAR model, since the parameters A carry a subtly different meaning, which under a Bayesian formulation leads to a translation of the prior distribution and in the information criteria case changes the definition of the predictor set.)

Figure 2.

An empirical comparison of network inference schemes. Simulated experiments based on published dynamical systems allow benchmarking of performance in terms of area under ROC curves (AUR; higher scores correspond to better network inference performance).¹⁶ (a) Even sampling intervals. (b) Uneven sampling intervals.

Despite the presence of nonlinearities and memory in the cellular drift f, neither the use of quadratic basis functions nor the inclusion of lagged predictors appear to improve performance in terms of AUR. In order to verify that quadratic predictors are sufficiently nonlinear and that lagged predictors are sufficiently delayed, we repeated the investigation using both cubic predictors and using a delay twice as long. Results (SFigs. 3,4) demonstrate that no improvement to the AUR scores is achieved in this way.

Corresponding results for the Swat model are shown in SFig. 2. Here we find that none of the methods performs well.

We also performed inference using biochemical data from the experimental system reported in Cantone et al. [10] (specifically the “switch-on” dataset therein). AUR scores obtained using this data (SFig. 5) were in close agreement with those obtained using synthetic data (Fig. 2(a)), suggesting that the results of the simulations are relevant to real world studies.

3.2.2 Uneven sampling intervals

Many biological time-course experiments are carried out with uneven sampling intervals. We therefore repeated the analysis above with sampling times of 0, 1, 5, 10, 15, 20, 30, 40, 50, 60, 75, 90, 105, 120, 140, 160, 180, 210, 240 and 280 minutes. Fig. 2(b) displays the AUR scores so obtained. We find that all the methods perform worse in the uneven sampling regime, with no method performing significantly better than random. Corresponding results for the Swat model are shown in SFig. 7. Again, here we find that none of the methods performs well.

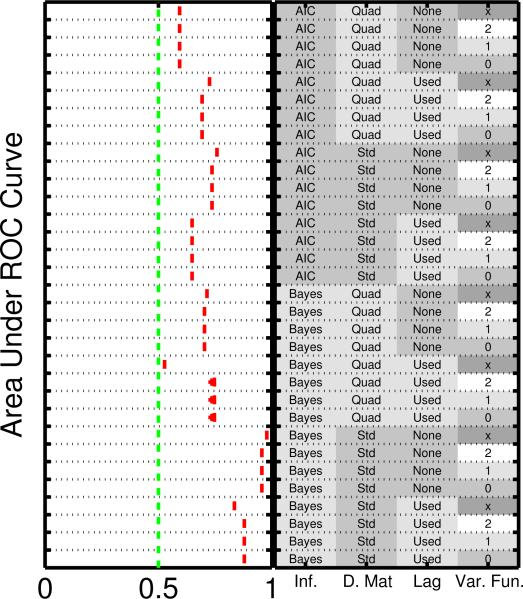
3.2.3 Consistency

Fig. 3 displays AUR scores for Cantone for a large number of evenly sampled time points (n = 100), and the limiting case of zero measurement noise and zero cellular heterogeneity (σ_meas = 0, σ_cell = 0, even sampling intervals). Consistency (in the sense of asymptotic convergence of the network estimate to the data-generating network) may be unattainable due to the nonidentifiability resulting from limited exploration of the dynamical phase space. This lack of surjectivity means that in many cases inference cannot possibly reveal the full data-generating graph, although as we have seen network inference can nonetheless be informative. From Fig. 3 we see that the Bayesian schemes using linear predictors approach AUR equal to unity, and in this sense show empirical consistency with respect to network inference. However, some of the other methods do not converge to the correct graph even in this limit.

Figure 3.

Investigation of empirical consistency of network estimators, using the Cantone [10] model with even sampling intervals. Area under ROC curves are shown in the large dataset, zero cellular heterogeneity and zero measurement noise limits.

4 Discussion

The analyses presented here were aimed at better understanding statistical network inference for biological applications. We showed how a broad class of approaches, including VAR models, linear DBNs and certain ODE-based approaches, are related to stochastic dynamics at the cellular level. We discuss a number of these aspects below and close with some views on future perspectives for network inference, including recommendations for practitioners.

4.1 Time intervals

We found that uneven sampling intervals posed problems, even for methods that explicitly accounted for the sampling interval. Further insight may be gained from an error analysis of the approximations indicated in Section 2.2. Assuming the true large sample process obeys dX^∞/dt = F(X^∞), we have that under an observation process with independent additive Gaussian measurement error Y(t) ~ N(X^∞(t), M) an expansion for the variance $\mathbb{V}(d\mathbf{Y}-\mathbf{F}\left(\mathbf{Y}\right))$ over a time interval Δ is given by

$$\mathbf{M}{\Delta }^{-2}+(\mathbf{I}{\Delta }^{-1}+D\mathbf{F})\mathbf{M}{(\mathbf{I}{\Delta }^{-1}+D\mathbf{F})}^{\prime }+\dots$$ (17)

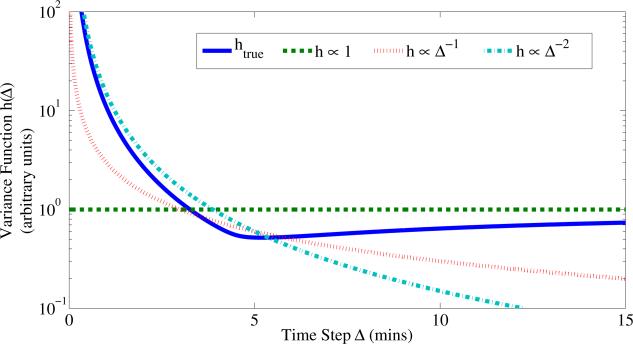
(see SI for details). Recall that the model family in Eqn. 10 approximates this variance by $h\left(\Delta \right)\mathcal{D}({\sigma }_1^2,\dots ,{\sigma }_P^2)$ where h(Δ) = Δ^–α. From this perspective it is clear that each variance function we considered captures only partial variation due to Δ. It is therefore not surprising that performance suffers in the uneven sampling regime, which requires the variance function to apply equally to large Δ as to small Δ. Moreover, a natural choice of variance function driven by Eqn. 17 is not possible, since this would require knowledge of the unknown process F. The implication for experimental design is that absent specific reasons for uneven sampling, it may be preferable to collect data at regular intervals.

Fig. 4 displays an approximation to the true variance function for the Cantone model (see SI). Observe that for small sampling intervals Δ the true curvature is best captured by a functional approximation of the form $h\left(\Delta \right)\propto {\Delta }^{-\alpha }$ with α = 1, 2, whereas for intervals larger than 10 mins (which are more common in practice) the flat approximation $h\left(\Delta \right)\propto 1$ correctly captures the asymptotic behavior. In applications where high frequency sampling is infeasible the flat variance function might be a sensible choice. To understand whether difficulties related to sampling intervals disappear in the large sample limit, we repeated the empirical consistency analysis under uneven sampling (SFigs. 11,12). Interestingly, we found that none of the methods appeared to be empirically consistent, and that the choice of variance function is influential. However, unevenly sampled data are common in biology and it may be the case that in some settings, the existence of multiple time scales (e.g. signaling, transcription, accumulating epigenetic alterations) mean that unevenly sampled data are nonetheless useful. Our findings suggest that care should be taken in the uneven sampling regime.

Figure 4.

Variance functions used in literature provide partial approximation to the “true” functional form for Cantone et al. [10]. For small time steps a power law Δ^–α provides a good approximation, but for larger time steps a constant variance function may be more appropriate. In practice the precise form of h_true will be unknown.

4.2 Interventional data

The Cantone data are favorable in the sense that gene profiles show interesting time-varying behavior under global perturbation, exploring a large proportion of the dynamical phase space. However such behavior is dependent on the specific dynamical system and is not displayed by the Swat model, which has a much larger phase space, being a nine-dimensional dynamical system. This may help explain the poor performance of all the methods on this latter model using global perturbation data and perhaps reinforces the intuitive notion that dynamics that are favorable (in this informal sense) facilitate network inference. In some cases, perturbation data are available in which individual variables are inhibited (e.g. by RNA interference, gene knockouts or inhibitor treatments). Such data have the potential to explore much more of the dynamical phase space, including regions which cannot be accessed without direct inhibition of specific molecular components. This is an important consideration because the statistical estimators described in Section 2.4 take the form

$$\widehat{\mathbf{A}}={\langle D\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\right)\rangle }_{\mathbf{X}\in \mathcal{R}}$$ (18)

where the average is over the region $\mathcal{R}\subseteq \mathcal{X}$ in state space visited during the experiments. Clearly if the region $(\mathbf{f}\left({\mathcal{F}}_{\mathcal{R}}\right),\mathcal{R})$ is only a small subspace of phase space then the estimate Eqn. 18 will be poor compared to one based on the entire phase space ${\widehat{\mathbf{A}}}^{\ast }={\langle D\mathbf{f}\left({\mathcal{F}}_{\mathbf{X}}\right)\rangle }_{\mathbf{X}\in \mathcal{X}}$.

To investigate the added value of interventional treatments for network inference, we repeated both the Cantone and Swat analyses with an ensemble of datasets obtained by inhibiting each variable in turn; this gave 5 and 9 datasets for Cantone and Swat respectively. Whilst no improvement to the Cantone AUR scores was observed (SFig. 15), there was improved performance for Swat (SFig. 16). This suggests that global perturbations are insufficient to explore the Swat dynamical phase space, and supports the intuitive notion that intervention experiments may be essential for inference regarding larger dynamical systems. Nevertheless AUR scores remain far from unity. This may be because the Swat drift function contains complex interaction terms which single interventions alone fail to elucidate. An important problem in experimental design will be to estimate how much (possibly combinatorial) intervention is required to achieve a certain level of network inference performance.

We considered precise artificial intervention of single components in silico. However, biological interventions may be imprecise and imperfect. For example, RNA interference achieves only incomplete silencing of the target and small-molecule inhibitors may have off-target effects. Moreover, at present such interventions are not instantaneous nor truly exogenous. This means that in many cases the system itself may be changed by the intervention, rendering resulting predictions inaccurate for the native system of interest. There remains a need for novel statistical methodology capable of analyzing time-course data under biological interventions. Existing literature in causal inference [47] and related work in graphical models [15] are relevant, but in biological applications it may also be important to consider the mechanism of action of specific interventions.

4.3 Non-linear models

We focused on linear statistical models. Clearly, linear models are inadequate in many cases. For example [50] demonstrate the benefit of a nonlinear model based on Michaelis-Menten chemical kinetics for inference of transcription factor activity. However, network inference based on nonlinear ODEs remains challenging [60]. Alternatively Äijö and Lähdesmäki [1] consider the use of a non-parametric Gaussian process (GP) interaction term in the regression, which is naturally more flexible than linear regression using finitely many basis functions. This may help to overcome the linearity restriction, but introduces additional degrees of freedom, including the GP covariance function and associated hyperparameters. Whilst a thorough comparison of such approaches was beyond the scope of this article, the potential utility of nonparametric interaction terms is worthy of investigation. In this study we observed that neither the use of predictor products nor lagged predictors led to improved performance; this may reflect nontrivial coupling between cellular dynamics and the observed data.

4.4 Single-cell data

In the future it may become possible to measure single cell expression levels X^k non-destructively (e.g. by live cell imaging), producing truly longitudinal datasets. It is interesting to consider how such data may impact upon the performance of regression-based network inference. Under independent additive Gaussian measurement error Y(t) ~ N(X^k(t), M) an expansion for the single cell variance $\mathbb{V}(d\mathbf{Y}-\mathbf{f})$ over a time interval Δ, in analogy with Eqn. 17, is given by

$$\mathbf{M}{\Delta }^{-2}+(\mathbf{I}{\Delta }^{-1}+D\mathbf{F})\mathbf{M}{(\mathbf{I}{\Delta }^{-1}+D\mathbf{F})}^{\prime }+{\Delta }^{-1}{\mathbf{gg}}^{\prime }+\dots$$ (19)

(see SI). Thus a (single) longitudinal single cell dataset contains less information about the drift f than aggregate data (Eqn. 17) due to cellular stochasticity g. However, multiple longitudinal datasets may jointly contain more information than a single aggregate dataset. To empirically test the utility of such data, we carried out network inference using 10 such longitudinal single-cell datasets on both the Cantone and Swat models, observed at even intervals with the same magnitude of measurement error as aggregate data. Results (SFig. 13,14) show a small improvement to the mean AUR scores, but reduction by a factor of about two in the variance of these scores (compared with the corresponding non-longitudinal data), implying that the network estimators may be converging to an incorrect network. Bias may occur when the cellular drift f is not well approximated by a linear function, as is the case for the Swat model. Consider the idealized scenario where f ≡ f(X) is Markovian and it is possible to observe longitudinal, single cell expression levels. Under these apparently favorable circumstances even estimators obtained after a thorough exploration of state space may not offer good approximations, i.e. ${\widehat{\mathbf{A}}}^{\ast }\not\approx D\mathbf{f}{\mid }_{\mathbf{x}=0}$. As a toy example consider the cellular drift

$$\mathbf{f}:{[0,1]}^2\to \mathbb{R},\mathbf{f}\left(\mathbf{X}\right)=\left(\begin{array}{c}\hfill {\left(2\pi \right)}^{-1}\text{sin}\left(2\pi X_2\right)\hfill \\ \hfill {\left(2\pi \right)}^{-1}\text{sin}\left(2\pi X_1\right)\hfill \end{array}\right)$$ (20)

which is not well approximated by a linear function over the state space $\mathcal{X}={[0,1]}^2$. In this case averaging leads to cancellation

$$\begin{array}{cc}\hfill {\widehat{\mathbf{A}}}^{\ast }={\langle D\mathbf{f}\left(\mathbf{X}\right)\rangle }_{\mathbf{X}\in \mathcal{X}}& ={\langle \left(\begin{array}{cc}\hfill 0\hfill & \hfill \text{cos}\left(2\pi X_2\right)\hfill \\ \hfill \text{cos}\left(2\pi X_1\right)\hfill & \hfill 0\hfill \end{array}\right)\rangle }_{\mathbf{X}\in {[0,1]}^2}\hfill \\ \hfill & =0\ne \left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right)=D\mathbf{f}{\mid }_{\mathbf{x}=0}\hfill \end{array}$$ (21)

so that no interactions are inferred. Under such circumstances network inference is no longer possible using the naïve linear regression approach. This suggests that network inference rooted in non-linear models may be needed to fully exploit longitudinal single-cell data in the future. A related line of work addresses heterogeneity of the drift function in time by coupling DBNs with change point processes [27, 31, 33]. A promising direction would be piecewise linear regression modeling for network inference applications, where the heterogeneity appears in the spatial domain.

4.5 High-dimensions and missing variables

We focused on the simplest possible case of fully observed, low-dimensional systems. There is a rich literature in high-dimensional variable selection and related graphical models [40, 23, 20] which applies equally to the regression models described here. The issues raised in this paper remain relevant in the high-dimensional setting. However in practice even high-dimensional observations are likely to be incomplete, since it is not currently possible to measure all relevant chemical species. Therefore, inferred relationships between variables may be indirect. This may be acceptable for the purpose of predicting the outcome of biochemical interventions (e.g. inhibiting gene or protein nodes), but limits stronger causal or mechanistic interpretations. Latent variable approaches are available [6], but model selection can be challenging and remains an open area of research [30]. We note also that the missing variable issue for biological networks is arguably more severe than in, say, economics or epidemiology, insofar as measured variables may represent only a small fraction of the true state vector, often with little specific insight available into the nature of the missing variables or their relationship to observations. Further work is required to better understand these issues in the context of inference for biological networks.

4.6 Future perspectives

We found that a simple linear model could successfully infer network structure using globally perturbed time-course data from the Cantone system. It is encouraging that inference based only on associations between variables, none of which were explicitly intervened upon, can in some cases be effective. Interventional designs should further enhance prospects for network inference. On the other hand, theoretical arguments, and the results we showed from the Swat system, emphasize that in some cases network structure may not be identifiable, even at the coarse level required for qualitative biological prediction. On balance, we believe that network inference can be useful in generating biological hypotheses and guiding further experiment. However, the concerns we raise motivate a need for caution in statistical analysis and interpretation of results. At the present time, we do not believe network inference should be treated as a routine analysis in bioinformatics applications, but rather as an open research area that may, in future, yield standard experimental and statistical protocols.

Some specific recommendations that arise from the results presented here are:

• A default model. Our results suggest that a reasonable default choice of model for typical applications uses the standard design matrix with no lagged predictors and a flat variance function, corresponding to the linear model

  $$d\mathbf{Y}\left(t_j\right)\sim N(\mathbf{AY}\left(t_{j-1}\right),\mathcal{D}({\sigma }_1^2,\dots ,{\sigma }_P^2)).$$ (22)

  Coupled with the Bayesian variable selection scheme outlined in Section 2.4.1, this simple model produced empirically consistent network estimators for Cantone using evenly sampled global perturbation data (Fig. 3).

• Diagnostics and validation. It is clear that network inference does not enjoy general theoretical guarantees and that the ability to successfully elucidate network structure depends on details of the specific system under study. Therefore careful empirical validation on a case-by-case basis is essential. This should include statistical assessment of model fit, robustness and predictive ability and where possible systematic validation using independent interventional data.

• Experimental design. We suggest sampling evenly in time as a default choice. Interventional designs may be helpful to effectively explore larger dynamical phase spaces. However, to control the burden of experimentally exploring multiple time points, molecular species, interventions, culture conditions and biological samples, adaptive designs that prune experiments based on informativeness for the specific biological setting may be helpful [60].

In conclusion, linear statistical models for networks are closely related to models of cellular dynamics and can shed light on patterns of biochemical regulation. However, biological network inference remains profoundly challenging, and in some cases may not be possible even in principle. Nevertheless, studies aimed at elucidating networks from high-throughput data are now commonplace and play a prominent role in biology. For this reason there remains an urgent need for both new methodology and theoretical and empirical investigation of existing approaches. Furthermore, there remain many open questions in experimental design and analysis of designed experiments in this setting.