Radiobiological description of the LET dependence of the cell survival of oxic and anoxic cells irradiated by carbon ions

Abstract

Light-ion radiation therapy against hypoxic tumors is highly curative due to reduced dependence on the presence of oxygen in the tumor at elevated linear energy transfer (LET) towards the Bragg peak. Clinical ion beams using spread-out Bragg peak (SOBP) are characterized by a wide spectrum of LET values. Accurate treatment optimization requires a method that can account for influence of the variation in response for a broad range of tumor hypoxia, absorbed doses and LETs. This paper presents a parameterization of the Repairable Conditionally-Repairable (RCR) cell survival model that can describe the survival of oxic and hypoxic cells over a wide range of LET values, and investigates the relationship between hypoxic radiation resistance and LET. The biological response model was tested by fitting cell survival data under oxic and anoxic conditions for V79 cells irradiated with LETs within the range of 30–500 keV/µm. The model provides good agreement with experimental cell survival data for the range of LET investigated, confirming the robustness of the parameterization method. This new version of the RCR model is suitable for describing the biological response of mixed populations of oxic and hypoxic cells and at the same time taking into account the distribution of doses and LETs in the incident beam and its variation with depth in tissue. The model offers a versatile tool for the selection of LET and dose required in the optimization of the therapeutic effect, without severely affecting normal tissue in realistic tumors presenting highly heterogeneous oxic and hypoxic regions.

INTRODUCTION

The increased interest in setting up ion facilities for cancer treatment around the world is the result of the positive clinical experience based on continuous experimental, clinical and fundamental research. The encouraging results from the most experienced ion therapy centres in Heidelberg (Germany), Chiba and Hyogo (Japan) support the potential of carbon ions in terms of physical dose distributions and increased radiobiological effectiveness [1, 2]. Carbon ion beams are characterized by well-defined range, narrow penumbra and pronounced Bragg peak that generally result in an improved target conformity and better sparing of normal tissues compared to electron, photon and proton beams. In addition to good physical properties, carbon ion beams also have an increased relative biological effectiveness (RBE) in the tumor compared to conventional photon and proton beams. The RBE varies with the linear energy transfer (LET) of the ions and this has to be taken into account when optimizing ion treatments.

The oxygen effect of radiation is also highly dependent on LET. In photon radiation therapy, tumor hypoxia is a common cause for treatment failure, since photons generally have a very low LET and are inefficient in killing hypoxic cells [3, 4]. For high LET radiation the direct action is dominant [5, 6]. Furthermore, radical scavenger experiments have shown that the contribution of indirect action under hypoxic conditions is lower than that under oxic conditions [7]. Therefore light ion radiation therapy has a greater effect on hypoxic tumors than photon therapy [4]. The clinical benefit of using carbon ions when treating hypoxic tumors has been shown recently in a clinical study by Nakano et al. [8].

The increased biological effect in the presence of oxygen is usually quantified as the oxygen enhancement ratio (OER), the ratio of the doses required to achieve the same survival under hypoxic and oxic irradiation conditions. The dependence of OER on LET has been studied in vitro for different ion types [9–13]. The study by Furusawa et al. (2000) [11], revised in 2012 [12], presented a systematic investigation of cell survival for several ion types, cell lines, LETs and dose levels in both oxic and hypoxic conditions. They found that for carbon ions with low LET, OER is about 2.5–3, which is comparable to OER of photons. At very high LETs, beyond 200 keV/µm, the influence of oxygen becomes almost negligible and hence OER decreases to 1.

The physical and radiobiological properties of ion beams has led to the current practice in which the treatment is delivered in only a few relatively large fractions of radiation. Therefore, in order to accurately predict the response to ion therapy, a mathematical model able to describe the survival of cells over a large range of doses and LET is required. The current models used in Heidelberg (Germany), Chiba or Hyogo (Japan) are mainly based on the linear quadratic (LQ) cell survival model, which is rather accurate for doses per fraction employed in the conventional treatment schedules for low LET radiotherapy, but might be less accurate in reproducing the shape of the survival curve at higher doses where it becomes almost exponential. Furthermore, the LQ model is not able to describe the response in cases of low-dose hypersensitivity without slight modifications [14]. In order to overcome these possible limitations, Lind and co-workers have proposed the repairable-conditionally reparable (RCR) damage model [15]. The RCR model was further developed by taking into account not only the dose but also the LET dependence of cell survival [4, 16]. The LET parameterized RCR model was able to accurately fit the cell survival data reported by Furusawa et al. [11] for HSG, V79 and T1 cells irradiated with carbon ion beams under oxic conditions.

In order to model the response of tumors with both oxic and hypoxic sub-compartments irradiated with carbon ion beams of different LETs, a further development of the current model is required to explicitly account for the oxygen effect dependence on LET. This model will therefore open the possibility of selecting the optimum LET to overcome the tumor resistance caused by hypoxia, thus allowing the biological optimization of particle therapy based on individual measurements of tumor oxygenation.

It is the aim of this present paper to describe a parameterized RCR model that can describe cell survival for oxic as well as hypoxic cells at different LETs, and to determine the relationship between hypoxic radioresistance and LET. The resulting model was tested by its ability to fit the comprehensive experimental data set reported by Furusawa et al. [11, 12].

MATERIALS AND METHODS

The RCR damage model [4, 15] is a cell survival model that specifically takes into account repair processes and distinguishes between potentially and conditionally repairable damage. The surviving fraction of cells after a dose D is given by:

(1)

The first term in equation 1 gives the fraction of cells that have not been hit or damaged and therefore survive. The parameter a is therefore related to the hit cross-section and the initial mean number of damage events per unit dose. The second term corresponds to the fraction of cells that have been damaged and subsequently been correctly repaired. The parameter b specifically describes the maximum amount of damage that can be repaired per unit dose. Parameter c gives the loss of repair due to more complex damage. All a, b and c parameters are given in units of effect per Gy. Being the sum of two exponentials as a dual Poisson process, the equation is flexible enough to accurately describe both the low dose hypersensitivity, the shoulder of the survival curve and the exponential part of the cell survival curve at high doses.

The initial RCR model was further developed by Wedenberg et al. [16] and Brahme [4], who derived expressions for the dependence of the parameters a, b and c on LET for cells irradiated under oxic conditions. The generalized equation giving the surviving fraction of oxic cells after a dose D is:

(2)

where the LET dependence of a_ox, b_ox and c_ox are given by:

(3)

(4)

(5)

(6)

Equations 3–6 accurately describe the LET dependence of the RBE [4]. The parameters a₀, a₁, , , , 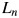and in the above equations are free parameters depending on both the intrinsic radiosensitivity of the cells and the ion type. The variation of the survival with the oxygenation status of the cells is a further development of the RCR model. The decreased cell kill under anoxic conditions can similarly be described by an anoxic version of Equation 2:

(7)

where the anoxic parameters in the first approximation are given by:

and is a dose modification factor closely related to OER.

The oxygen-mediated cell kill decreases with increasing LET due to a decreasing radical dependent cell kill and an increased direct effect. The LET dependence of is assumed to be similar to that analytically derived by Brahme for OER [4] and is given by:

(8)

where _min, _max are the limit values at high and low LET and is the LET where is reduced to 37% of its maximum value. The minimum value for corresponds to the minimum oxygen enhancement ratio at very high LETs and it generally approaches unity (1.0), while the maximum value for is similar to the oxygen enhancement ratio corresponding to irradiation under anoxic conditions with low LET electrons and X-rays.

The model described by Equations 2 and 7 was tested by fitting cell survival data for Chinese hamster V-79 cells irradiated with LETs in the range of 30–500 keV/µm. The available 23 oxic and 23 hypoxic datasets were obtained by irradiating the cells with ¹²C in vitro at an average of five dose levels, ranging from 1–25 Gy [11,12]. The parameters in Equations 3–6 and 8 were obtained by the simultaneous fit of the oxic and hypoxic datasets with Equations 2 and 7. The validity of the proposed model with the parameters resulting from the fitting of the data described above was tested by comparing the predicted cell survival fraction with the actual experimentally-derived data points for two LET values which were not used in the fitting. The experimental data on which the model was tested belong to the same dataset used by Furusawa et al. [11,12] and correspond to Chinese hamster cells, V79, irradiated in aerobic and hypoxic conditions with ¹²C ions with dose-averaged LET of 88 keV/µm and 151.5 keV/µm.

The model parameters were determined by minimizing the square of the error between the experimental data and the analytical survival curves on a logarithmic scale. Several constraints related to the radiobiological interpretation of the RCR parameters were imposed, as originally suggested by Lind et al. [15]. Thus, a(L) > c(L) since the total amount of damage has to be larger than the amount of potentially repairable damage. It was further assumed that a(L) > b(L) to avoid surviving fractions larger than 1. It was also assumed that for doses around 2 Gy the hypersensitivity is no longer evident and thus the constraint a < b/2 + c was set to avoid concave survival curves.

To test the robustness of the fit, the parameters of the curve describing the as a function of LET were also determined by calculating for each LET separately in order to assess the influence of the fitting approach. In order to investigate how strongly the estimation of the oxic parameters is influenced by the simultaneous fit, Equations 2–6 were also fitted separately to the oxic dataset for comparison. The goodness-of-fit was estimated by the root mean square deviation, RMSD, and by the Pearson product-moment correlation coefficient, r². Since the surviving cell fraction is represented on a logarithmic scale, the RMSD values were calculated as the deviation of the logarithm of the experimental data from the logarithm of the calculated cell survival.

RESULTS

Figure 1 shows the result of the simultaneous fit of the cell survival data for Chinese hamster V79 cells irradiated in vitro with ¹²C ions under oxic and anoxic conditions for a selection of nine different LETs ranging from 30–501.5 keV/μm. The difference between the oxic and hypoxic curves decreases rapidly with increasing the LET beyond 100 keV/μm.

Fig. 1.

Survival curves for V79 cells irradiated with carbon ions in oxic (red curves) and hypoxic conditions (blue curves) for nine different LETs as resulting from the simultaneous fit of the whole set of experimental data with Equations 2–7.

Experimental data are shown as scattered points (red symbols for oxic conditions, blue symbols for hypoxic conditions)

The simultaneous fitting approach appears to provide a good fit of the cell survival data for the whole range of LET values investigated. The root mean square deviation of the logarithm of the experimental cell survival from the analytical calculation, RMSD, for the oxic curves was 0.51 and for the hypoxic curves 0.41. The Pearson product-moment correlation coefficient, r², was 0.95 for the oxic data and 0.96 for the hypoxic data respectively. It should also be noted that the decrease of the hypoxic resistance for high LET does not influence the overkill effect that is evident at very high LET. Indeed, the slope of the cell survival curve increases with increasing LET, reaching a maximum for 142 keV/μm in oxic conditions and 276 keV/μm in hypoxic conditions, and then decreases for higher LET. It is interesting to note that the optimum LET for cell inactivation is different for the cells irradiated in oxic and in hypoxic conditions.

The fitting parameters a₀, a₁, , , , 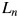and corresponding to the cell survival curves shown in Fig. 1 are given in Table 1.

Table 1.

a₀, a₁, b₁, c₀, c₁, L_n and L_d resulting from the simultaneous fit of the oxic and anoxic cell survival data shown in Fig. 1

a0 (1/Gy)	a1 (1/Gy)	b1 (1/Gy)	c0 (1/Gy)	c1 (1/Gy)	Ln (keV/ μm)	Ld (keV/ μm)
5.7	1.3	2.0	5.7	0.2	423	86

Figure 2 shows the derived relationship between as a function of LET, resulting from the simultaneous fit of oxic and hypoxic data for all LETs (solid line) and from the separate fitting for one LET value at a time (dotted line) for all the 23 oxic and 23 hypoxic datasets obtained by irradiating the V79 cells with ¹²C ions with LETs in the range of 30–500 keV/µm. The two curves almost coincide, indicating that the fitting approach does not affect in a substantial manner the shape or the parameters of the (L) curve. The oxygen enhancement ratio, i.e. the ratio of doses in oxic and hypoxic conditions required for obtaining a survival fraction of 10% (as determined for the same dataset used by Furusawa et al. [11, 12] using the LQ model for fitting the experimental points), is also shown in Fig. 2 in the form of scattered points for each LET. Although OER values as a function of LET follow the shape of the (L) curve, it should be noted that OER and values are quite different, especially in the low LET range.

Fig. 2.

Õ for different LETs as resulting from the simultaneous fit of all the experimental data points (full line) and from the separate fit at each LET value (dashed line).

The corresponding OER values determined by Furusawa et al. [11] by LQ fit at 10% survival is also plotted as scattered points.

The parameters for 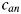(L) resulting from the simultaneous fit of oxic and hypoxic data for all LETs and from the separate fitting for one LET value at a time are given in Table 2.

Table 2.

Õ_min, Õ_max and L_O parameters resulting from the separate and simultaneous fit

Fitting approach	Õmin	Õmax	LÕmax(keV/µm)
Separate	1.14	2.97	105
Simultaneous	1.10	2.92	114

The LET dependence of the parameters , and of the RCR model is presented in Fig. 3, along with the corresponding anoxic parameters. It can thus be seen that dividing the oxic parameters by (L) results in about three times lower values for low LETs, as expected from experience with photon and other low LET radiations. For very high LETs, above 300 keV/µm, the oxic and hypoxic parameters follow almost the same curve due to the fact that the oxygen effect, and hence the value, become close to unity as the direct action of the radiation becomes dominant.

Fig. 3.

The RCR parameters 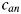, 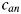and 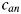(red line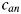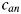) and , and 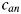, (blue line) as a function of LET resulting from the simultaneous fit to the whole data set.

The difference in shape between a_ox, b_ox and c_ox parameters is described by Equations 3–5. One could observe that a_ox, and c_ox have similar expressions resulting in an increase in value with an increase in LET followed by a decrease, while b_ox is only decreasing with an increase in LET. The trend for a_an, b_an and c_an results from the combination of the LET dependence of a_ox, b_ox and c_ox and Õ. It should be noted in Fig. 2 that Õ has a rapid decrease between approximately 60–110 keV/μm, while in the same LET interval a_ox, and c_ox increase with LET and b_ox decreases. This leads to the different appearance of the curves for a_an, c_an and b_an compared to those of the oxic parameters.

In order to assess the influence of the simultaneous fit and its robustness with respect to the oxic data, Equations 2–6 were fitted to the oxic dataset exclusively. The resulting parameters were the same as for the simultaneous fit to the whole dataset. The only exception was L_n that decreased from 423 keV/µm to 396 keV/µm, but this led to negligible changes in the, and parameters.

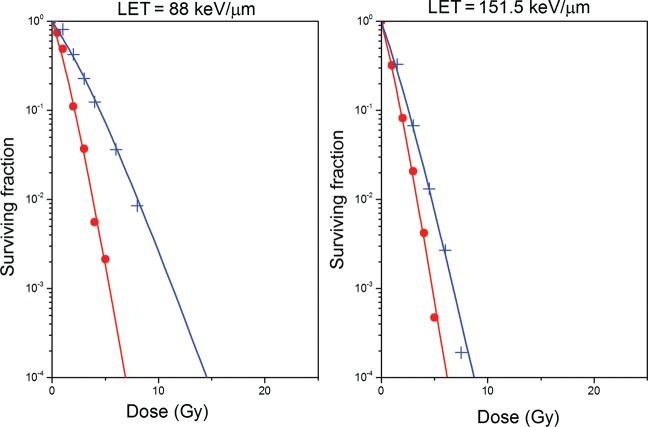
In order to test the ability of this newly parameterized version of the RCR model to predict clonogenic cell survival for oxic and hypoxic cells irradiated with ¹²C ions with a broad range of LET values, Equations 2–7 were used, together with the parameters given in Table 1, to calculate the surviving fraction of cells assuming that irradiation was performed with ¹²C ions with LET of 88 keV/µm and 151.5 keV/µm, respectively. The resulting cell survival curves are shown in Fig. 4. The scatter points in Fig. 4 correspond to actual experimental data points determined by Furusawa et al. [11, 12] for the same cell line and irradiation conditions. As one can see, the predicted and the actual cell survival for both LET values agree well for oxic and anoxic conditions.

Fig. 4.

Survival curves for V79 cells irradiated with carbon ions in oxic (red curves) and hypoxic conditions (blue curves) for two different LETs predicted by the RCR parameterized model described by Equations 2–7.

Experimental data are shown as scattered points (red symbols for oxic conditions, blue symbols for hypoxic conditions).

The robustness of the parameterization approach proposed in this study has also been tested for other ion species for which cell survival data is available. Thus, the model has been able to describe cell survival data for Ne ions (Fig. 5) within the limit of the differences reported experimentally by Furusawa et al. [11, 12]. It should be noted, however, that these findings do not undermine the value of the proposed parameterization. Indeed, differences in the determination of the effective LET, or even variations in the parameters describing track structure variations of different ion beams, may lead to different cell survival parameters, as demonstrated experimentally by Furusawa et al. [11, 12].

Fig. 5.

Survival curves for V79 cells irradiated with neon ions in oxic (red curves) and hypoxic conditions (blue curves) for different LETs predicted by the RCR parameterized model described by Equations 2–7.

Experimental data are shown as scattered points (red symbols for oxic conditions, blue symbols for hypoxic conditions).

DISCUSSION

This paper presents an accurate parameterization of the RCR model that can simultaneously describe the variation with LET of cell survival under oxic and hypoxic conditions. The a, b and c parameters of the RCR model have been expressed as functions of LET in order to be able to illustrate the influence of a broad range of ionization densities, which is of considerable importance in the attempt to accurately describe the response of cells to light ion beams. In a clinical set-up, tumors and normal tissues are irradiated with low and high LET from the plateau and respectively the Bragg peak, and therefore there is a need to be able to accurately predict cell survival for a broad range of LET for a given ion type.

The first term in the RCR model accounts for the cells that survive due to fact that they are not hit by radiation, the a parameter being therefore related to the probability of cell hit and the initial mean number of damage events per unit dose. The second term in the RCR model accounts for the two main repair pathways of mammalian cells, Non Homologous End Joining (NHEJ), responsible mainly for potentially repairable damage, and Homologous Recombination processes (HR), accounting for the conditionally repairable damage. The b parameter describes the maximum amount of damage that can be repaired per unit dose, and the c parameter is related to the inactivation cross-section of the cell [4, 16]. Thus, the expression proposed for c as a function of LET is able to reproduce the increase of the inactivation cross-section with an increase in LET of up to about 120 keV/μm, where the overkill effect sets in due to the clustering of the DNA damage, but also the increasing probability of radical-radical recombination at very high LET. The expression for the parameter a as a function of LET can be explained based on the fact that the probability that a given cell is hit, which is proportional to a, has to be larger than the probability that the cell is both hit and inactivated which is proportional to c, at any LET. Therefore, the equation describing the variation of a with LET will be similar to that for c, fulfilling at the same time the condition a > c at any LET. However, the difference between parameters a and c should decrease with increasing LET due to the fact that with increasing LET there is an increased probability that the cells that are hit are also inactivated. This also relates to the b parameter, which describes the amount of repairable damage at increasing LET values. The equation proposed for b reflects the fact that with increasing LET the DNA damage becomes more severe and it is more difficult for the cell to repair. Consequently, the parameter b decreases with increasing LET, which also leads to better reproducing the almost exponential shape of the cell survival curve at high LET.

The parameterization of the RCR model presented in this paper also accounts for the variation with LET of cell survival depending on oxygenation status of the cells at the time of irradiation. By analogy with the well known concept of OER, used for quantifying the effect of oxygen on cell survival compared to irradiation performed in hypoxic conditions, a dose modifying factor, , for the parameters describing the cell survival for hypoxic cells was introduced. The model was found to fit quite accurately both the oxic and the hypoxic experimental cell survival data over a broad range of LETs. The derived parameters appear to be little influenced by the approach used to derive them. The resulting model is therefore expected to accurately predict the cell survival of mixed populations of oxic and hypoxic cells irradiated with ¹²C beams in the clinically relevant range of LETs.

The relationship between and LET was determined by fitting a multi-parameter function to the largest available experimental dataset resulting from ¹²C irradiation of cells in vitro, as found in the literature. The relationship is representative for the cell line under investigation, V79, assuming that the systematic uncertainties of the underlying experiments were negligible. However, it should be mentioned that the original cell survival experiment indicated a similar relationship between OER and LET for both V79 and HSG cells. Hence, the relationship between and LET could possibly be extended to describe cell lines other than V79. However, differences in the shape of cell survival curves between different cell lines should be taken into account.

Another aspect that has to be considered regarding the extrapolation of these results to cells irradiated in vivo comes from the survival data used in this study that was obtained with cells irradiated in monolayers. However, it should be mentioned that data exist for spheroids irradiated with carbon ions of different energies. Thus, Staab et al. [14] used V79 spheroids and reported OER values similar to those of monolayer cells irradiated in glass dishes for different LETs. Thus, it appears that OER, defined as a ratio of isosurvival doses, is only weakly dependent on the system used to derive it. However, there might still be small differences between the absolute responses of the systems used to determine OER.

The model presented in this paper is therefore expected to accurately predict the biological response for mixed populations of oxic and hypoxic cells irradiated with ¹²C beams in the clinically relevant range of LETs. This is an important aspect for developing successful ion treatments, since it has been shown that tumors contain subpopulations of hypoxic cells and that their presence has been associated with poor outcome for treatments with low LET radiation [17–19]. Reduced hypoxic protection from an OER of around 3.0 to about 1.6–2.0 for high LET radiation could therefore be used for a more accurate description of the effects of tumor hypoxia.

An important factor to take into account for predictions of clinical tumor response is that therapeutic high LET beams often contain a mixture of high and low LET component. Thus, for optimal results one would have to consider both the distribution of LETs in the incident beam and its variation with depth in tissue as well as the distribution of hypoxia. Treatment optimization under such conditions would require accurate models explicitly describing the relationship between cell survival, tumor cure, dose and effective LET for both the oxic and hypoxic compartments of the clinical tumors. The parameterized cell survival model addresses all these issues and could therefore be used for LET optimization of light ion therapy of hypoxic tumors [20–22]. Bassler et al. [23] has recently presented an analysis of dose- and LET-painting with particle therapy, taking into account the variation of the LETs along the ion track and assuming a fixed OER calculated at 10% survival as a dose-modifying factor for each LET in the distribution. In a very recent paper Brahme [4] presented not only the possibility of determining the optimal LET with respect to cell killing for tumors with different degrees of oxygenation but also the ion type and even the optimal combination of low, medium and high LET radiation. This was based on OER modeling as a function of LET.

The LET parameterized RCR model including the Õ(L) as presented in this study can thus be used for the accurate selection of LET and the dose required in the optimization of light ion therapy with respect to cell killing in realistic tumors presenting oxic and hypoxic regions.