Microsecond simulations of the folding/unfolding thermodynamics of the Trp-cage mini protein

Abstract

We study the unbiased folding/unfolding thermodynamics of the Trp-cage miniprotein using detailed molecular dynamics simulations of an all-atom model of the protein in explicit solvent, using the Amberff99SB force field. Replica-exchange molecular dynamics (REMD) simulations are used to sample the protein ensembles over a broad range of temperatures covering the folded and unfolded states, and at two densities. The obtained ensembles are shown to reach equilibrium in the 1 μs per replica timescale. The total simulation time employed in the calculations exceeds 100 μs. Ensemble averages of the fraction folded, pressure, and energy differences between the folded and unfolded states as a function of temperature are used to model the free energy of the folding transition, ΔG(P,T), over the whole region of temperature and pressures sampled in the simulations. The ΔG(P,T) diagram describes an ellipse over the range of temperatures and pressures sampled, predicting that the system can undergo pressure induced unfolding and cold denaturation at low temperatures and high pressures, and unfolding at low pressures and high temperatures. The calculated free energy function exhibits remarkably good agreement with the experimental folding transition temperature (T_f = 321 K), free energy and specific heat changes. However, changes in enthalpy and entropy are significantly different than the experimental values. We speculate that these differences may be due to the simplicity of the semi-empirical force field used in the simulations and that more elaborate force fields may be required to describe appropriately the thermodynamics of proteins.

Introduction

The Trp-cage mini protein is a designed peptide that behaves like larger globular proteins ¹. This protein is stabilized by a hydrophobic core containing a Trp amino acid, which hydrogen bonds to a distant backbone carbonyl, and by an ion pair. Structurally the Trp-cage is composed of an alpha helix, a 3-10 helix and a polyproline II segment. The folding is cooperative, and occurs in the microsecond timescale². The Trp-cage miniprotein has also served as an ideal model in computational studies where force fields^3-5and modeling techniques ^{6,7, 8}have been benchmarked against detailed structural¹, thermodynamics⁹, kinetics^{2, 10-12}, and design^13-16 data. Up to date multiple studies describing the folding of Trp-cage using atomic force fields with implicit and explicit solvent ^{3, 6-8, 17-25} have successfully reproduced the structure of the folded state with excellent accuracy. Here we report the equilibrium thermodynamics of the Trp-cage mini protein that have been calculated with the recently developed Amberff99SB (ff99SB) force field ⁴ and compare with thermodynamic studies ⁹. We find that the ff99SB force field and the TIP3P water model accurately describe the thermodynamics of the system and predict a folding transition at 48 C, and the specific heat of the transition. These results contrast with extreme stability and high folding temperature (T_f ~ 450K) predicted by the Cornell et al. force field (ff94)²⁶ and obtained by us in similar calculations^{18, 24}. We show that the ff99SB significantly improves the description of folding thermodynamics of the protein. However, the enthalpy and entropy changes during the folding/unfolding transition are underestimated by at least a factor of two. Here we characterize the folding thermodynamics and structural ensembles of the protein as a function of temperature.

Methods

We used replica exchange molecular dynamics (REMD) to model the configurational ensemble of a system composed of the 20 amino acid Trp-cage (Ac-NLYIQWLKDGGPSSGRPPPS-Nme), with charged Lys, Arg and Asp sidechains, one Na⁺, two Cl⁻ ions to neutralize the system, and 2635 TIP3P water molecules²⁷. Electrostatics interactions were modeled using PME using a cubic 36×36×36 grid and van der Waals interactions were truncated at 1.0 nm. A grid size of 0.12 nm was used for the PME. Following the results of Cooke and Schmidler regarding the ergodicity of the sampling in REMD²⁸, the equations of motion were integrated using the stochastic dynamics with coupling time of 1.0 ps, and using a 2 fs time step. Simulations are done using GROMACS and the ff99SB forcefield⁴. REMD simulations are done at constant volume, in a cubic box of 4.42 nm, corresponding to the volume of the system at pressure, P=1atm, and temperature, T=300 K—obtained from a 10 ns NPT simulation. We simulated 40 systems with temperatures 280.0, 284.1, 288.2, 292.4, 296.7, 301.1, 305.6, 310.2, 314.9, 319.7, 324.6, 329.6, 334.7, 340.0, 345.4, 351.0, 356.6, 362.5, 368.4, 374.6, 380.9, 387.3, 394.0, 400.8, 407.8, 415.1, 422.5, 430.1, 438.0, 446.0, 454.3, 462.8, 471.6, 480.6, 489.8, 499.3, 509.0, 519.0, 529.2 and 539.7 K. Temperatures were selected such that an exchange rate of 0.15 is obtained ²⁹. REMD simulations were started from random unfolded states (we label this as “unfolded initial conditions” (UIC)) and from the folded state of the protein (we label this as “folded initial conditions” (FIC)).The UIC states were generated by starting from an extended all-PPII conformation, which gets slightly compacted after running a short (25 ps) simulation in the gas phase at 300 K, as described in previous calculations²⁴. The resulting systems were solvated with a pre-equilibrated box of TIP3P water molecules at 300 K. Simulations were extended for 1 μs /replica for UIC and 0.5 μs for FIC. The length of the simulations is dictated by the relaxation behavior (of approximately 200 ns) of the system. Previous ff94 simulations were extended to 200 ns, since they showed fast (30 ns) relaxation time²⁴. Configurations were collected for further analysis every 1 ps. Analysis presented here use the last 0.5 μs and 0.25 μs for the UIC and FIC simulations, respectively. To fit the thermodynamics of the Trp cage over a broad range of T and P we also simulated the system at high average pressure over the same temperatures. The initial configuration for this simulation was the folded state (since it reaches steady state faster than simulation started from the unfolded state), but the volume was reduced such that the average pressure at 310 K is 400 MPa. The initial state of the system was obtained from a 10 ns NPT simulation. The REMD simulation was extended for 1 μs /replica and the last 0.5 μs are used for calculating averages.

To obtain a pressure-temperature stability diagram we fit the calculated fraction folded, the average pressure, and average potential energy, and free energy differences as a function of temperature. Here we combine the averages calculated for the protein under different conditions. The free energy difference between the folded and unfolded state as a function of P and T can be written as

$$\Delta G(T,P)=\Delta G_u^0-\Delta S_u^0(T-T_0)-\Delta C_p\left[T\left(\mathrm{Log}\left(\frac{T}{T_0}\right)-1\right)+T_0\right]+\Delta V_u^0(P-P_0)+\frac{1}{2}\Delta {\beta }_u^0{(P-P_0)}^2+\Delta {\alpha }_U^0(P-P_0)(T-T_0)$$ [1]

where ΔC_P is the heat capacity, ΔS⁰ _U is the entropy, ΔG⁰ _U is the Gibbs free energy, Δβ⁰ _U is the compressibility change, ΔV⁰ _U is the volume change, and Δα⁰ _U is the expansivity change upon unfolding of the protein³⁰. The superscript 0 in the coefficients indicate that the coefficients are calculated at a reference T₀ (298 K) and P₀ (0.1 MPa= 1 atm). Each one the six coefficients in this expansion is a measurable thermodynamic quantity. The system free energy difference is fitted by minimizing a χ² function as a function of the expansion coefficients. The χ² function is given by

$$x^2={\Sigma }_i{\left[\frac{\Delta G_i-\Delta G(T_i,P_i)}{\sigma \Delta G_i}\right]}^2+{\Sigma }_i\left[\frac{\Delta x_i^{\text{foided}}-\Delta x(T_i,P_i)}{\sigma \Delta x_i}\right]+{\Sigma }_i{\left[\frac{\Delta E_i-\Delta E(T_i,P_i)}{\sigma \Delta E_i}\right]}^2$$ [2]

Here σ_ΔYi is the uncertainty in the average of Y (where Y is the energy, free energy or fraction folded), x_i^folded is the fraction of molecules folded at the state i, and ΔG_i, ΔE_i are the free energy, and energy changes, respectively, calculated from ensemble averages. ΔE_i is the average potential energy. The index i labels the replica states. Each replica state samples a temperature T_i, at constant system volume. ΔG(T_i, P_i), ΔV(T_i, P_i), and ΔE(T_i, P_i) are the fitted functions evaluated for each of the replicas states (T_i, P_i ), and P_i is the average pressure. The volume change is defined as the partial derivative of the Gibbs free energy with respect to P (at constant temperature),

$$\Delta V(P,T)={\left(\frac{\partial \Delta G(P,T)}{\partial P}\right)}_T=\Delta V_u^0+\Delta {\alpha }_u^0(T-T_0)+\Delta {\beta }_u^0(P-P_0)$$ [3]

The enthalpy is given by ΔH_i =ΔE_i + P_iΔV_i. The average energy is given by

$$\Delta E(T,P)=\Delta H-P\Delta V=\Delta G(T,P)+T\Delta S(T,P)-P\Delta V(T,P)$$ [4]

where.

$$\Delta S(T,P)=-{\left(\frac{\partial \Delta G(T,P)}{\partial T}\right)}_p.$$ [5]

Then, the energy difference is given by

$$\Delta E(T,P)=\Delta G_u^0+T_0\Delta S_U^0-\Delta V_u^0{P}_0+\Delta C_p(T-T_0)-\Delta {\alpha }_U^0(\mathit{PT}-P_0{T}_0)-\Delta {\beta }_u^0(P^2-P_0^2)$$ [6]

The free energy, ΔG(P,T) is calculated from the fraction of folded states, x^folded, obtained from the sampling and is related to the free energy of folding by

$$\Delta G_i(T_i,P_i)=-\mathit{RT}\mathrm{Log}\left[\frac{1-x_i^{\text{folded}}}{x_i^{\text{folded}}}\right]$$ [7]

Here R is the gas constant. Uncertainties in fraction folded, free energy, and energy are calculated from five, 100 ns segments for low and high average pressure simulations. The length of the segments, 100 ns, are taken to be about twice the correlation time of the number of folded replicas as a function of time. Fittings are done in Mathematica using steepest descent and Newton-Raphson minimization algorithms.

We estimate the correlation time, τ_c, of the number of folded replicas from the time correlation functions, c(t). We obtained two estimates of the correlation time. One by integrating the correlation function over time, ${\tau }_c=\text{Max}\left[{\int }_0^t{\mathit{dt}}^{\prime }c\right(t^{\prime }\left)\right]$, until a maximum is reached and taking this maximum to be an upper bound for the correlation time. Another estimate was obtained by assuming that the errors are Gaussian distributed, and calculating the integral ${\tau }_c={\int }_0^{\omega }{\mathit{dt}}^{\prime }{c}^2\left(t^{\prime }\right)$³¹. Both estimates give τ_c~ 50 ns. We use segments of twice that time, 100 ns, to estimate uncertainties in the averages. We found that even 1 μs simulation is not long enough to obtain better estimates of the correlation of a slowly varying function, like the number of folded replicas as a function of time.

Results

Steady state equilibrium of the system

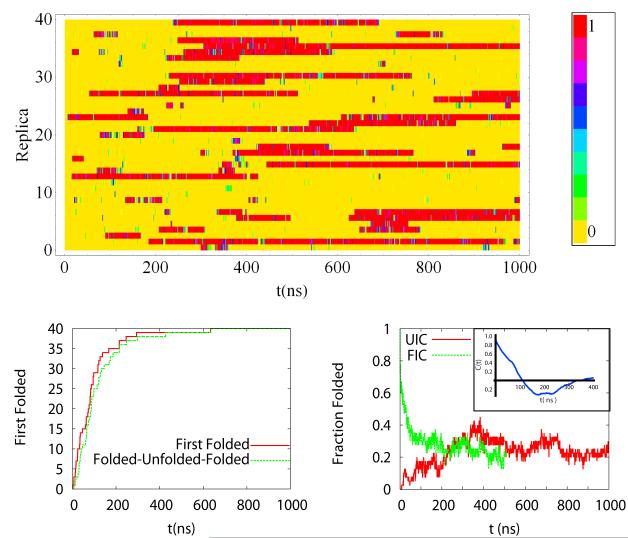
First we establish that the ensemble averages have reached a steady state by monitoring the rate at which replicas reach the folded state, unfold and refold (Figure 1a), the average number of replicas that are folded as a function of simulation time (figure 1b), and the time history of the folding probability of each replica (Figure 1c). We distinguish folded from unfolded based on the rmsd distance of the configuration from the folded state reported in the PDB (NMR Structure #1 (PDB-code 1L2Y)). A configuration is considered folded if rmsd < 0.22 nm. We will justify this choice later in the manuscript, using the distribution of rmsd at various temperatures. To identify possible dependence of the results on initial conditions, we performed two simulations starting from the folded initial configurations (FIC) and unfolded initial configurations (UIC). For simulations with UIC all replicas have folded after 0.60 μs. The refolding curve monitors the rate at which replicas refold after leaving the folded basin and reaching an rmsd > 0.6 nm from the folded state. This curve shows a short delay from the first folded time curve, illustrating that the averages obtained in long timescale simulations are not sensitive to initial conditions. Figure 1b shows that the number of folded replicas in the UIC and FIC converge after 0.20 μs. The number of folded replicas shows a long correlation time of 50 ns. Similar calculations for ff94 showed that all replicas folded after 30 ns—which is an order of magnitude faster than for the ff99SB calculations presented here and therefore require that the ff99SB calculations be extended to the μs timescale. The time evolution of the fraction of time, within 1 ns time blocks, that a given replica samples the folded state, shown in Figure 1c, shows that replicas remain folded for hundreds of nanoseconds, which explain the slow relaxation time of the total number of folded replicas. Figure S8 shows a figure similar to Figure 1, for the high density REMD simulations.

Figure 1. Time evolution of the REMD trajectories.

A) Fraction of the time that each replica (1-40) spends in the folded state (rmsd<0.22 nm) over 1 ns time block averages. All replicas were started from an unfolded configuration. B) First folding time for replicas along the folding trajectory (red line). The profile shows an exponential growth with exponent of the order on 100 ns. The green line shows the first time a replica has folded, unfolded past 0.6 nm, and refolded. The curve is very similar to the first folding time, expect for a time delay of tens of ns. C) Fraction of replicas that are folded at any time during the simulation as a function of time (red line(UIC) and green line(FIC)). All replicas, at different temperatures are averaged together. We also show the fraction of replicas that are folded for a simulation in which all replicas were started in the folded state. The two ensembles show similar averages after 200 ns. The blue curve in the inset of c) is the time correlation function of the fraction folded time-history shows. Estimates of the correlation time for the fraction for replicas folded are 50 ns. We use simulation segments if twice this time, 100 ns, to estimate uncertainties in the averages.

Structural characterization of the ensembles

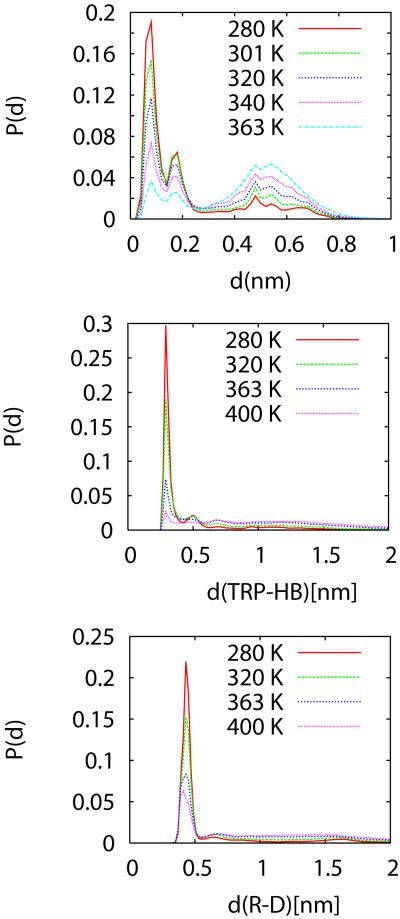
The structural ensembles of the protein are characterized using different order parameters. In general, not all order parameters are equally suited to describe the folding/unfolding equilibrium. In particular, the folding thermodynamics of proteins is not strictly two-state and different order parameters will monitor changes differently, as is the case when using experimental probes. Ideally, an order parameter should be related to a measurable quantity like the fluorescence quenching or the strength of a circular dichroism (CD) or infrared (IR) bands, but these quantities cannot be easily calculated from the protein configurations³². Here we will use geometrical parameters related to the protein structure as order parameters. Figures 2a-c show ensemble averages of the rmsd, a parameter that reports globally on the protein structure, and two single amino acid contacts that report on the local structure of the protein: the Trp-to backbone hydrogen bond distance (to the Arg carbonyl), and the Asp-Arg ion pair distance distributions, at various temperatures. The rmsd distance distributions, shown in Figure 2a, exhibit two large peaks for rmsd below 0.22 nm; one at 0.06 nm and another at 0.18 nm. We assign these two peaks, characterized by rmsd<0.22 nm, as the folded state, consistent with our previous results using ff94^{18, 24}. A peak at 0.52 nm builds up at higher Ts, correspond to the unfolded state. The smallest distance to the PDB structure 1 is 0.029 nm, the largest is 1.2 nm. An analysis of the 38 structures deposited in the 1L2Y PDB file shows that these structures are at an average of 0.72 nm, with a standard deviation of 0.022 nm¹. The minimum distance between structures in the NMR ensemble is 0.0227 nm and the maximum is 0.150 nm. The NMR ensemble and the distribution centered at 0.066 nm are very similar.

Figure 2.

Temperature dependence of distributions of a) rmsd, b) Trp Nε to Asp backbone carbonyl hydrogen bond, and c) Arg- Asp ion pair distances. All distances are in nm.

In addition to the rmsd distance, we also monitor the presence of a hydrogen bond between the Nε atom of the Trp sidechain and the backbone carbonyl Oxygen of Asp. The distance distributions at various temperatures shown in Figure 2b show a large peak centered at 0.3 nm, a smaller centered at 0.5 nm and a broad distribution for larger distances. The intensity of the 0.3 nm peak decreases drastically with increasing temperature, showing that we could also monitor this hydrogen bond to differentiate the folded and unfolded state. Another interaction that is associated with the stability of the mini protein is the Arg-Asp ion pair ^{1, 18}. The distance distributions for this ion pair (Figure 1c) exhibit a similar behavior as the other distributions in Figure 2 in that the large peak at 0.43 nm decrease quickly in magnitude with increasing temperature. Figure 3 shows the superposition of structures belonging to the two folded substates. The main differences among the structures in the basin are in the turn (Pro 12- Ser13-Ser-14-Gly15) region and the N and C termini. The substates with larger rmsd present in the folded basin also have a sub-population in which the Trp-Nε H-bond (supplementary Figure S9) is near 0.5 nm. In the thermodynamic analysis shown below we assume that the folding/unfolding transition is two-state. This is consistent with the thermodynamic analysis of Trp-cage ⁹; but not with the fluorescence experiments¹¹, which may be affected by the large reporter group attached to the protein.

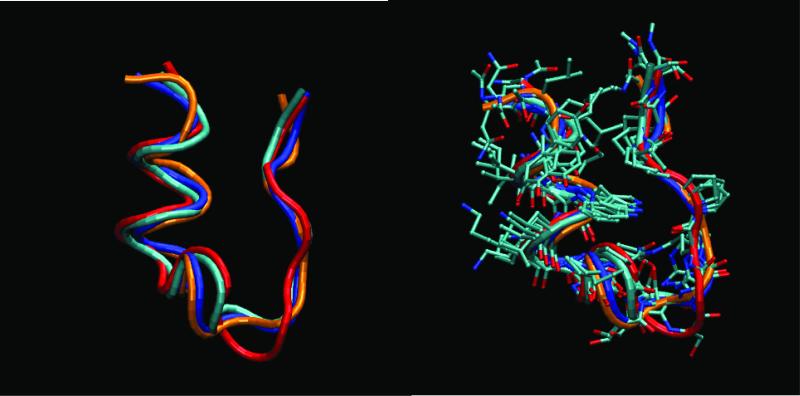
Figure 3. Superposition of representative structures belonging to the folded basins. Four representative structures are obtained by clustering the structures sampled at the lowest temperature (280K), during the last 10 ns of the REMD simulation.

The top most populated clusters correspond to structures at 0.075 nm (48%), 0.69 nm (7%), 0.15 nm (6%), 0.17 nm (5%), and 0.21 nm (4%) from structure 1 of the NMR ensemble. Cluster 2 is assigned as an unfolded state. The plots show the superposition of the structures in the folded basin (rmsd < 0.22 nm). We used the Daura clustering method implemented in Gromacs⁴⁸. A) Tube representation of the backbone. B) All non hydrogen atoms. The structures representative of the top four clusters in the folded basins are labeled in cyan first cluster), blue (third cluster), red (fourth cluster), and orange (fifth cluster). The main differences in the structures are in the 3-10 turn (Pro 12- Ser13-Ser-14-Gly15) region and the N and C termini.

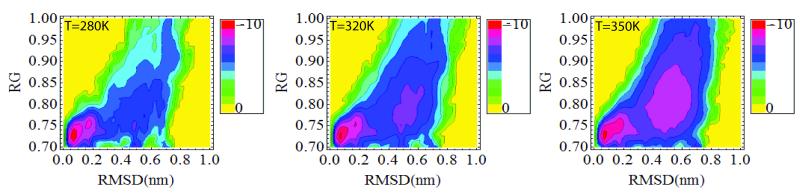
Figure 4 shows the 2-dimensional contours of conditional probabilities of rmsd and the radius of gyration (R_g) of the molecule. These contours show that the system samples two basins, one describing the folded state (low R_g and rmsd) and another distribution centered at rmsd ~ 0.6 nm and R_g ~0.8 nm, corresponding to the unfolded state. The unfolded state basin is not highly populated at low temperature, but as the temperature increases above 315 K it dominates the weight of the distribution. Within this order parameter representation the folding/unfolding thermodynamics of the Trp-cage is two-state like. An analysis of the distributions for rmsd < 0.22 nm show that two substates compose this basin. Figure s10 show time history of the rmsd vs. time for selected trajectories. Transitions between these two substates occur with a mean residence time in either state of 0.1 ns. Given the quick interconversion between these two states we consider them to belong to one folded basin.

Figure 4. Contour maps of the free energy of the Trp-cage as a function of the rmsd and the radius of gyration (R_g) at 280K, 320K and 350K.

The contour shows that the system occupies two main basins- - one corresponding to the folded state (low rmsd and compact states) and another at larger rmsd > 0.4 nm and less compact, corresponding to the unfolded state. At even higher temperatures the system becomes extended and only the large rmsd and R_g basin is occupied. The folded basin for low rmsd and R_g has two basins (substates) at low temperature. The legends use a logarithmic scale, with -10 corresponding to the highest probability and 0 to the lowest.

Equilibrium thermodynamics

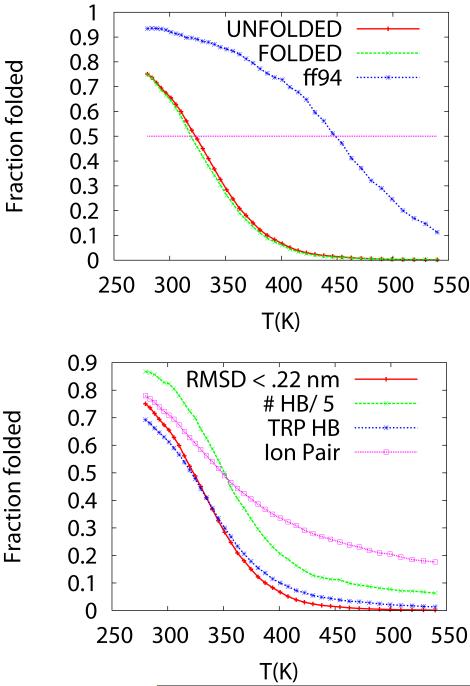
Based on the decomposition of the free energy as a function of various order parameters we can describe the thermodynamics of the system as a function of temperature, assuming the thermodynamics is two-state. We find that a convenient parameter to characterize the population of folded and unfolded states is the rmsd from the folded state. Figure 5a shows the fraction of configurations that are folded as a function of temperature. We see that the fraction of folded reaches a value near 75% at the lowest sampled temperature. The fraction folded reaches 50% (i.e., equilibrium between folded and unfolded) at T= T_f=321 K (48 C), and decreases rapidly as a function of temperature. Here T_f defines the folding temperature. A similar (almost indistinguishable curve) is obtained for simulations stated from folded or unfolded states, as described in figure 1c. As a reference, we also show the fraction folded profile obtained using the ff94 force field obtained previously ^{18, 24}. The f94 force field yields a much more stable folded state, with higher occupancy at low temperature (90%) and T_f ~ 420 K.

Figure 5. Fraction of replicas folded as a function of temperature.

A) Comparison of the fraction of Trp-cage protein folded as a function of temperature for two different force fields—ff99SB (red and green curves) and ff94 (blue curve). The folding profiles for the ff99SB are practically indistinguishable for REMD simulation starting from completely unfolded states (red) and folded states (green). The ff99SB profiles cross the 50% fraction folded at T=321 K, in close agreement with experimental data (T_exp = 317 K). However, the calculated fraction of folded states is lower than measured values at low T. B) Fraction folded as a function of other order parameters that are representative of the folded Trp-cage folded structure. These parameters are rmsd (red curve--folded is rmsd< 0.22 nm), fraction of a Trp-Nε – Asp backbone carbonyl hydrogen bond (blue curve-- d < .4 nm), Arg-Asp ion pair (magenta curve -- d<0 .6 nm), and number of alpha helical amino acids (divided by five to fit the same scale in the plot, green curve). An alpha helical amino acid is an amino acid with three consecutive phi-psi angles in the alpha helical region ( ϕ= −60 +/− 30 Deg. and φ = −47+/− 30 Deg) ⁴⁹. The maximum number of alpha helical segments observed is ten.

Similar thermodynamic profiles can be obtained using other order parameters. For example, monitoring the population of the hydrogen bond between the Trp Nε to the Arg backbone carbonyl oxygen (labeled Trp-Hb) shows a very similar behavior as the rmsd order parameter. That is, the rmsd and hydrogen bond are formed at low temperature and the probability of forming the hydrogen bond decrease significantly as temperature is increased slightly. Figure 5b shows the fraction of the ensemble that forms the Trp-HB (d < 0.40 nm), the Arg-Asp ion pair (d< 0.6 nm), and the total number of alpha helical amino acids. The thermodynamic profile obtained with the Trp-HB is very similar to the one obtained with the rmsd. However, we see that the Arg-Asp ion pair and alpha helical formation persist at temperatures above T_f, and the thermodynamics profile obtained using this order parameter will be different than for the rmsd or Trp-HB parameters, described above. For this small protein, the ion pairs can be present even when the system is unfolded.

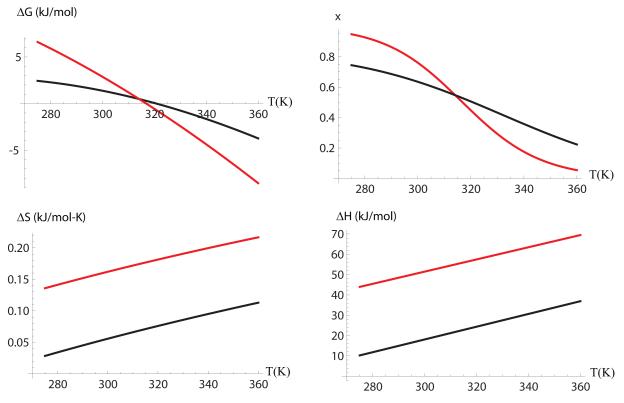
The free energy difference between the unfolded and the folded states are described by Eqn. 1, with the coefficients described in Table 1. The specific heat, ΔC_p, entropy, ΔS(T), and free energy ΔG₀, differences have been measured for Trp-cage by Streicher et al. ⁹, and reported at T=298K and P=0.1 MPa. The reported experimental values are also shown in Table 1. We find that the fitted changes in specific heat and folding temperature are in close agreement with experiments. The calculated free energy difference is underestimated by less than 2 kJ/mol. Figure 6 shows a comparison of the calculated and the experimentally measured free energy, enthalpy and entropy as a function of temperature. We find a significant differences between the calculated and measured entropy and enthalpy changes upon folding—which differ by close to a factor of two, but in such a way that there is a balance between the entropy and enthalpy that gives ΔG =0 at 321 K vs. 317 K obtained in experiments.

Table 1. Thermodynamics Parameters for Trp-cage.

Thermodynamic parameters describing the P-T stability diagram³⁰.

	Calculated	Experimental
T0,P0	298 K, 0.1 MPa	298 K, 0.1 MPa
Δα(kJ/mol)	0.027	not available
Δβ(kJ/mol-MPa2)	−0.025	not available
ΔV0 (ml/mol)	−1.94	not available
ΔS (kJ/mol-K)	0.053	0.16
ΔCp (kJ/mol-K)	0.314	0.30+/− 0.1
ΔG0 (kJ/mol)	1.49	3.2
Tf (K)	321	317

Figure 6. Comparison of the computed (solid line) and measured (dotted line).

a) Free energy, b) fraction folded, c) entropy and d) enthalpy, as a function of temperature.

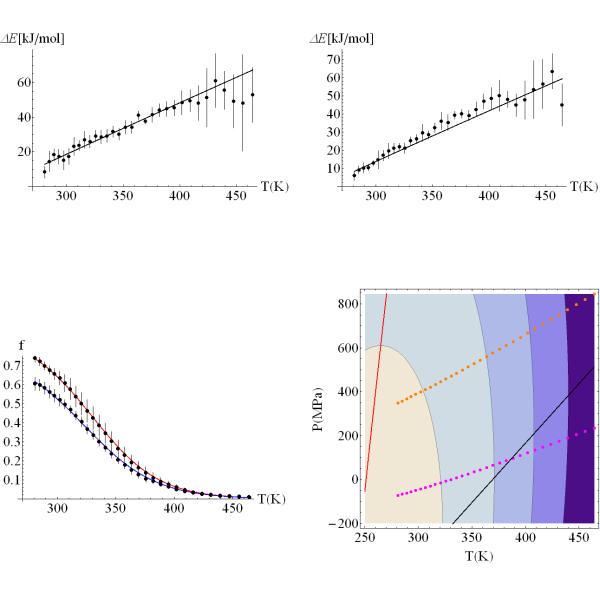
Figure 7 shows the fitting of the energy difference upon unfolding at low (a) and high (b) densities. Notice that the fitted curve is almost linear over a broad range of temperatures. The large error bars at high temperatures are due to the lack of statistics for folded states at very temperatures (T > 400K). Figure 6c shows the fraction of folded proteins as a function of temperature for the systems at low and high density (high average pressure). The curve shows that pressure destabilizes the protein. Pressure destabilization of the folded protein comes as a combination of many effects. On one hand, pressure will favor the state with lowest volume. There are three ways of reducing the volume of a protein: (i) by reducing the amount of free volume (cavities) in the folded state, (ii) by inserting water molecules into the hydrophobic core of the protein³³, and (iii) by increasing the water density around non-polar groups exposed to the solvent^{24, 34-36}. The net equilibrium will be determined by the balance of these interactions in the folded and unfolded states. From our free energy fits, the net volume change between the unfolded and folded state, ΔV_U⁰, is – 2ml/mol, favoring the unfolded state. This small volume is consistent with the small hydrophobic core of the trp-cage. Figure 6c shows the pressure-temperature (P-T) stability diagram for the trp-cage. The ΔG(T,P)=0 curve is elliptical, suggesting that the protein can be denatured at low pressure by increasing the temperature (heat denaturation), or by increasing the pressure, at constant low temperature (e.g., 298K). We also see a region of ΔS(T,P)<0, which is characteristic of cold denaturation, at high pressures and low temperatures.

Figure 7. Stability of the Trp-cage protein as function of temperature and pressure.

A) Average energy difference between unfolded and folded state ensembles calculated at various temperatures for a system at low pressure. B) Average energy difference between unfolded and folded state ensembles calculated at various temperatures for a system at high pressure. The uncertainties are calculated over five, 100 ns long, time segments. C) Fraction of the ensemble folded as a function of temperature. The two curves show the results obtained from simulations at low and high average pressures. The solid lines are the best χ² fit of the thermodynamics of the system, following a fitting procedure described in the text. The parameters describing the changes in Gibbs free energy are shown in table 1. D) Pressure-Temperature stability diagram for the Trp-cage protein. The contours for ΔG(P,T)=0 (contour closer to P=0 and T=320K), −5, −10,−15 kJ/mol are elliptical. The free energy profile shows small pressure dependence and the protein will require high pressures to unfold at low temperatures. The dotted lines represent the states sampled during the REMD simulations at low (blue) and high (red) densities. The black solid line represents the ΔV=0 isochore. The red solid line represents ΔS=0. All states above this curve decrease stability upon cooling, and have higher entropy in the folded state than in the unfolded state.

Discussion and conclusions

We have used molecular dynamics simulations to describe the folding/unfolding equilibrium thermodynamics for the Trp-cage mini protein in water. The calculations exploit the use of enhanced sampling methods to accelerate the sampling of configurations while maintaining a Boltzmann distribution for the ensemble of configurations obtained. Comparison of the calculated folded state with the NMR structure show that the ensemble of structures obtained are as close as 0.029 nm and that they share all secondary structural features and tertiary contacts characteristic of the Trp-cage (e.g., Arg-Asp ion pair, Trp-to-backbone hydrogen bond). The R_g of the unfolded state is slightly larger than for the unfolded state, but only at very high temperatures are non-collapsed states sampled. This is in agreement with photochemically induced NMR pulse labeling experiments showing that non-native contacts between the Trp sidechain protons and other sidechains exist in the unfolded state³⁷.

The obtained configuration ensembles were analyzed within a two-state thermodynamics assumption to determine the pressure-temperature stability map of the system. This analysis describes an elliptical P-T diagram in which the protein can be unfolded via increases in pressure and/or temperature. The elliptical P-T diagrams have been observed for globular proteins ^38-40. For the Trp-cage we find that the pressure effects are small. This may be a reflection of the fact that the protein does not have a large hydrophobic core, which when disrupted in the unfolded state, it helps lower the overall volume of the system ³³. At 298 K and 0.1 MPa the volume change ΔV₀ is negative and small (~ −2 ml/mol). The MD simulations and modeling of the thermodynamics provides a model which is in excellent quantitative agreement with experiments⁹. We find that the specific heat and free energy differences and folding temperature agree with experimental values to a degree unexpected for the model. Previous calculations of the thermodynamics using the ff94 force field produced similar results for the specific heat changes, but gave the folding temperature at high values (~450K)²⁴. The ff99SB force field used here gives much better results for the folding temperature. Comparison of MD simulations with NMR order parameter measurements have also shown that the ff99SB force field describes better, when compared to experiments, the dynamics of globular proteins ⁴¹. However, studies of the helix coil transition on model peptides have shown that the ff99SB force field fails to form thermodynamically stable helices at room temperature ⁴². Given that the Trp-cage has a large helical segment, we could have expected that the ff99SB would not have folded. However, we find that for non-Ala based sequences and in the presence of tertiary interactions, stable alpha helices are formed for the Trp-cage. The alpha helices are stable approximately 50 K above the folding T. The importance of tertiary contacts has been highlighted by Neidigh et al.¹. When the three C-terminal pro-residues were removed from the Trp-cage construct, the N-terminal part of the peptide did show not any significant protection of the amide protons from H/D exchange¹. We would like to point at another difference, structurally distinguishing the unfolded ensembles of the ff94 and ff99SB models: ff99SB shows an about a factor of four to five reduced helical content, compared to ff94 at the lowest temperatures²⁴. The residues involved in forming the N-terminal helix are significantly exploring beta, PPII and left-handed-helical parts of the backbone conformation space when in the unfolded state. We conjecture that this greater conformational diversity is a key factor for the dramatically slower convergence of the ff99SB REMD simulations.

A puzzling result we obtained is that the entropy and enthalpy changes upon folding are at least a factor of two smaller than the measured values. Here we estimate the entropies from the temperature dependence of the fitted free energies and not from the ensembles. Entropy and enthalpy changes upon unfolding are typically an order of magnitude larger than the corresponding free energy differences⁴³ and entropies cannot be calculated directly from average energies and free energies since the errors in average energy are as large as ΔG. Calculations based on minimalist models ⁴⁴ and all atom models ²⁴ show, in agreement with experiments, that the entropy and enthalpies are approximately one order of magnitude larger than the free energies⁴⁴. All atom calculations of enthalpies using molecular dynamics simulations of an RNA tetraloop hairpin also underestimated the enthalpy of the transition⁴⁵. Best and Hummer optimized the dihedral angle energy terms of the ff99SB force field such that calculations could reproduce the known stability of alpha helices at a given temperature⁴². They found that, although they can reproduce the free energy at a given T, they could not get the correct temperature dependence. In the case of alpha helical peptides it was also found that the entropy and enthalpies were underestimated by a factor of two. Best and Hummer have speculated that the smaller enthalpy and entropy changes may be a consequence of the simplicity of the energy model used in atomic simulations, in which hydrogen bonds are represented by Coulomb interactions and do not have a bonding character, and electronic polarizability are not explicitly included. We speculate that models that include directional hydrogen bonding terms, as they are used in structure prediction programs, may give a better description of the entropy and enthalpy differences ^{46, 47}. Interestingly, the underestimates in entropy and enthalpy are correlated such that the free energy differences are reasonably small and the folding transition temperature is close to the measured value. If we assume that the directional hydrogen bonding is responsible for the lower enthalpy—how do we justify the decrease in entropy? We can argue that non-directional hydrogen bonds allow for more flexibility in the hydrogen bonds without much change in energy. If we use a directional hydrogen bond term the energy will change upon hydrogen bond bending and the entropy of the folded state will be reduced. The reduction in entropy of the folded state will lead to a decrease in the stability of the folded state, unless a stronger binding energy is also used. Assuming that the directional hydrogen bonds have no effect in the entropy of the unfolded state, we could, qualitatively, account for the increase in energy and larger increase in entropy changes upon unfolding. Directional hydrogen bonds, if used in the solvent model, will change the hydrophobic effect on folding by increasing solvent structure and, presumably, decreasing H-bonding between the protein and the solvent. These changes in the hydrophobic effect could also contribute to changes in entropy and enthalpy. A careful parameterization of the effect of directional hydrogen bonds will be needed such that the net changes in entropy and enthalpy cancel out in the free energy difference and give similar folding temperatures and free energy differences, as we obtained with the current force field. Based on the close agreement with experimental folding temperature, specific heat and free energy differences, it could be argued that the ff99SB force field gives a better description of the thermodynamics than the ff94. However, there are differences in enthalpy and entropies, and as a consequence the lack of sharp changes in the fraction of molecules in the folded state that will need to be addressed in future parameterizations of empirical force fields. The effect of water model (e.g., TIP3P vs. TIP4P) on the folding/unfolding of the Trp-cage will be described in another publication.

Supplementary Material

Supp Fig 1

Figure s8- Time evolution of the REMD trajectories for the high pressure REMD simulation. A) Fraction of the time that each replica (1-40) spends in the folded state (rmsd <0.22 nm) over 1 ns time averages. All replicas were started from a folded configuration. B) First folding time after unfolding to rmsd > 0.6 nm for replicas along the trajectory (red line). The profile shows an exponential growth with exponent of the order on 100 ns. C) Fraction of replicas that are folded at any time during the simulation as a function of time (red line). All replicas, at different temperatures are averaged together. The inset curve on c) is the time correlation function of the fraction folded time-history. The correlation time for the fraction for replicas folded is ~50 ns. We use simulation segments of twice this time, 100 ns, to estimate uncertainties in the averages for the simulations at high pressure.

Supp Fig 2

Figure S9. Contour maps of the free energy ΔG(rmsd,R_g) (top panel), ΔG(rmsd,d _Trp-HB) (middle panel), ΔG(rmsd,d _Ion-pair) (bottom panel), at 280K, 320K and 350K. The contours show that the system occupies two main basins- -one corresponding to the folded state and another to the unfolded state. However, the bottom contours show that the ion-pair distance distribution for formed pairs (d _Ion-pair < 0.6 nm) persists at temperatures when the system is mostly unfolded (rmsd as large as 0.8 nm). For comparison, the top panel reproduces the results in Figure 4.

Supp Fig 3

Figure S10. Time histories of the rmsd vs. time for selected replica trajectories. Transitions between the folded basins occur frequently. The blue dashed line marks the rmsd < 0.15 nm substate. The green dashed line marks the 0.15 < rmsd < 0.22 substate. The mean residence time in the rmsd < 0.15 nm basin is 0.10 ns. The mean residence time in folded (rmsd < 0.4) basin is close to 100 ns. Given the minor structural differences and the fast inter conversion between the two folded substates, we consider the thermodynamics of the trp-cage to be two-state. However, the kinetics may not be two-states.