A Stability Analysis of a Modified Version of the Chi-Square Ratio Statistic: Implications for Equivalence Testing of Aerodynamic Particle Size Distribution

Abstract

Demonstration of equivalence in aerodynamic particle size distribution (APSD; e.g., by comparing cascade impactor (CI) profiles) constitutes one of key in vitro tests for supporting bioequivalence between test (T) and reference (R) orally inhaled drug products (OIDPs). A chi-square ratio statistic (CSRS) was previously proposed for equivalence testing of CI profiles. However, it was reported that the CSRS could not consistently discriminate between equivalent and inequivalent CI profiles. The objective of the overall project was to develop a robust and sensitive methodology for assessing equivalence of APSD profiles of T and R OIDPs. We propose here a modified version of the CSRS (mCSRS) and evaluated systematically its behavior when T and R CI profiles were identical. Different scenarios comprising CI profiles with different number of deposition sites and shapes were generated by Monte-Carlo simulation. For each scenario, the mCSRS was applied to 20,000 independent sets of 30 T and 30 R CI profiles that were identical. Different metrics (including mean and median) of the distribution of 900 mCSRSs (30 T × 30 R) were then evaluated for their suitability as a test statistic (i.e., independent of the number of sites and shape of the CI profile) for APSD equivalence testing. The median of the distribution of 900 mCSRSs (MmCSRS) was one regardless of the number of sites and shape of the CI profile. Hence, the MmCSRS is a robust metric for CI profile equivalence testing when T and R CI profiles are identical and potentially useful for APSD equivalence testing.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-012-9410-1) contains supplementary material, which is available to authorized users.

INTRODUCTION

The Food and Drug Administration (FDA)’s current thinking for establishing bioequivalence (BE) of orally inhaled drug products (OIDPs) is based upon the aggregate weight of scientific evidence. In this approach, demonstration of equivalence in aerodynamic particle size distribution (APSD) constitutes one key in vitro tests for supporting BE between test (T) and reference (R) OIDPs (1). APSD is assessed through multistage cascade impaction—a method evaluating the size distribution of the emitted dose on the basis of size-dependent particle inertia with an Andersen cascade impactor or a next-generation impactor. This test provides an important in vitro performance attribute, as APSD is believed to affect the total and regional deposition of drug(s) in the lung and therefore influence the safety and efficacy of OIDPs. For comparing cascade impactor (CI) profiles of T and R products, an accurate, sensitive, and robust statistical method comparing APSD profiles across the relevant deposition sites is desirable. Besides other proposed methods (2,3), a chi-square ratio statistic (CSRS) was proposed by the FDA for equivalence testing of CI profiles in the June 1999 Draft Guidance for Industry: Bioavailability and Bioequivalence Studies for Nasal Aerosols and Nasal Sprays for Local Action (4) and discussed by Cheng and Shao (5) that allowed univariate cumulative assessment of the entire multivariate CI profiles. The computational form of the 1999 CSRS is given in Eq. 1.1

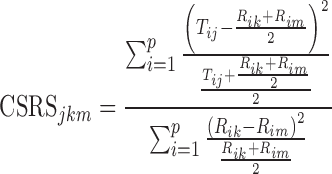1

where p represents the number of deposition sites of the CI profile, T_ij represents the normalized deposition (i.e., by dividing the absolute deposition on each individual site by the total deposition on all sites under consideration (percent)) on the ith site (i = 1, …, p) of the jth CI profile (j = 1, …, n_T) of the T sample, R_ik and R_im represent the normalized deposition on the ith site of the kth and mth CI profile (k ≠ m = 1, …, n_R) of the R sample, respectively. n_T and n_R represent the number of CI profile samples that were obtained from the T and R product, respectively. The kth and mth CI profile are two different samples obtained from the same R product (e.g., different units from the same batch or different batches of the R product). The Product Quality Research Institute (PQRI) “Aerodynamic Particle Size Distribution Profile Comparisons Working Group” (WG) evaluated the suitability of the CSRS to discriminate between equivalent and inequivalent APSD profiles by applying the CSRS on all individual deposition sites (e.g., amount of drug deposited in the actuator of the metered-dose inhaler, in the mouthpiece adaptor, within the throat, and on the CI stages including the filter) and a constant critical value (i.e., a cutoff value for equivalence testing). The PQRI WG concluded that the CSRS could not consistently discriminate between equivalent and inequivalent CI profiles (6–8). However, no alternative approach was proposed at that time.

In particular, the PQRI WG demonstrated that the behavior of the CSRS was dependent on the shape and the number of deposition sites of the CI profile (7). Since the “stability” of the CSRS increased as the number of deposition sites of the CI profiles increased, the PQRI WG concluded that the CSRS could not be applied to a reduced number of deposition sites of the CI profile (e.g., deposition sites that may be more related to lung deposition; 7,8). This non-applicability to a reduced number of deposition sites was one of the major limitations of the CSRS since the CSRS was demonstrated to be more sensitive to changes in high deposition sites (e.g., throat or preseparator), which may not be relevant for the performance of an OIDP with respect to lung deposition.

The objective of this study was to develop a robust and sensitive methodology for assessing equivalence of APSD profiles of T and R OIDPs. We proposed a modified version of the CSRS (mCSRS, Eq. 2) and evaluated systematically its behavior when T and R CI profiles were identical or differed from each other on single or multiple deposition site(s). The results of this evaluation are published as a series of three articles. In this article, (part I), the computational form of the mCSRS is introduced and the behavior of the mCSRS, when T and R CI profiles are identical, is characterized and hypothesized to be robust.2 Subsequent publications will continue to characterize the behavior of the mCSRS. In the second article (part II), the behavior of the mCSRS when T and R CI profiles differ from each other on a single or multiple deposition site(s) will be characterized. In the third article (part III), a stepwise APSD equivalence testing procedure is proposed that uses the mCSRS within a series of statistical tests. The sensitivity and robustness of this overall procedure is evaluated by categorizing 55 “representative” CI profile scenarios (8–10), which were judged by the PQRI WG members as equivalent or inequivalent.

Definition of a Modified Version of the CSRS

The computational form of the mCSRS is given in Eq. 2.

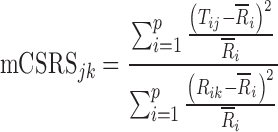2

where p was defined above, T_ij and R_ik represent the normalized deposition on the ith site of the jth CI profile (j = 1, …, n_T) of the T sample and on the ith site of the kth CI profile (k = 1, …, n_R) of the R sample, respectively, n_T and n_R are defined above, and 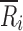represents the sample mean on the ith stage of all R CI profiles. Similar to the CSRS (Eq. 1), the numerator and denominator of the mCSRS represent a measure of the T-to-R and R-to-R distance, respectively. By design, for a constant denominator, the numerator of the mCSRS increases with increasing difference in mean deposition between T and R CI profiles and with increasing variability of the T product, and decreases with decreasing variability of the T product. Hence, the mCSRS rewards or penalizes the T product for having a lower or higher variability than the R product, respectively. Unlike for the computation of the CSRS, where a triplet of CI profiles (i.e., one T and two distinct R CI profiles) is required, the mCSRS only requires sampling of a pair of CI profiles (i.e., one T and one R profile).

Comparison to Pearson’s chi-square statistic for goodness-of-fit tests (11; Eq. 3) shows a similarity between Pearson’s chi-square statistic and both the numerator and denominator of the mCSRS.

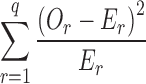3

where q represents the number of cells (translates into the number of deposition sites in a CI profile), O_r represents the observed cell count (translates into percentage of drug on ith deposition site of T or R CI profiles) in the rth cell (m = 1, …, q) and E_r represents the expected cell count in the rth cell (translates to true percentage of drug on the ith deposition site of the R CI profile). Whereas Pearson’s chi-square statistic compares observations to expectations (true values), both the numerator and denominator of the mCSRS compare individual CI profiles (T and R, respectively) to the average CI profile of the R product. In the context of BE, however, 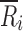(Eq. 2) can be viewed as an estimator for the expected (true) deposition on the ith site of both the T and R product. Hence, both numerator and denominator of the mCSRS compare, in some sense, observations (i.e., two individual CI profiles (T and R)) to expectations .

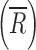The similarity of both the numerator and the denominator of the mCSRS (Eq. 2) and Pearson’s chi-square statistic (Eq. 3) was expected to result in a favorable distributional behavior of the mCSRS, namely that of an approximate F distribution (12), when certain criteria are met (see “Discussion” section).3

METHODS

The behavior of the mCSRS was evaluated and compared to that of the CSRS with respect to the capability to conclude equivalence when T and R CI profiles are identical (i.e., the same set of CI profiles is used for both T and R) under a wide range of possible situations (i.e., CI profiles differ in the shape of the overall profiles and variability on the sites). This was done as a robust test statistic for the mCSRS should be independent of the shape and number of deposition sites when T and R CI profiles are identical.

All evaluations were based upon simulated CI profiles (see below). This allowed evaluating the performance of the mCSRS in all theoretically conceivable CI profile scenarios. CI profile simulations and all computations were performed in the statistical software “R” (13). Computationally intensive simulation algorithms were run on “Betsy”, a high performance scientific computer provided by the FDA/Center for Devices and Radiological Health/Office of Science and Engineering Laboratories Scientific Computing Laboratory. The “Betsy” cluster is comprised of 110 IBM system ×3650 M2 8-core diskless compute nodes each containing eight Intel(R) Xeon(R) CPUs at 2.67 GHz with shared RAM of 24 GB per node. The “Betsy” cluster was equipped with “R” version 2.10.1.

The simulated CI profiles used for this evaluation were constructed based on a so-called “beta distribution approach” that was introduced by the PQRI WG and used for their initial evaluation of the CSRS when T and R CI profiles were identical (7). Details about this CI profile simulation approach were described by the PQRI WG (7). Briefly, rank-ordered CI profiles (i.e., deposition sites were ordered according to their decreasing magnitude of normalized drug deposition (percent of drug on an individual deposition site relative to total amount of drug on the entire CI profile; see Fig. 1 and Electronic Supplementary Material (ESM))) were modeled by controlling three parameters, the shape of the profile (uniform to maximally skewed), the standard deviation on the first deposition site (low to high), and the linear change of the coefficient of variation (CV) across sites (no change to maximum change). Furthermore, normally distributed deposition on each site4 and no intersite correlation were assumed in this approach. Eight extreme CI profile scenarios (“beta scenarios”; Table I, Fig. 1, and ESM) could therefore be modeled by systematically changing each of the three parameters (shape, standard deviation of first site, and change in CV). In addition, these eight scenarios were applied for CI profiles comprising 13, 8, and 4 deposition sites to cover a wide range of CI setups. Thus, a total number of 24 CI profile scenarios were evaluated. CI profiles were simulated in units of mass deposition and, subsequently, normalized by dividing the mass on individual sites by the total mass of all deposition sites.

Fig. 1.

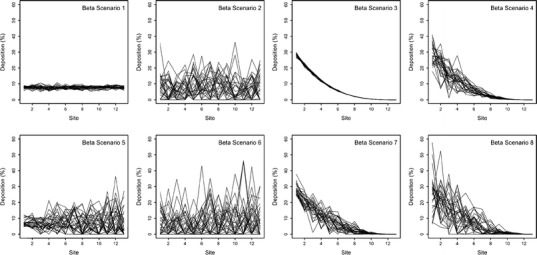
Representative CI profile plots (rank-ordered, see “Methods” sections) of “beta scenarios” 1–8 for 13 deposition sites

Table I.

“Beta Scenarios”, Profile Shape: Shape of the Rank-Ordered CI Profile (for Uniform and Skewed Profiles the Beta Parameter of the Beta Distribution was Set to 1 and 4, Respectively)

Beta Scenario	Profile Shape	SD First Stage	Change in CV
1	Uniform	Low	Low
2	Uniform	High	Low
3	Skewed	Low	Low
4	Skewed	High	Low
5	Uniform	Low	High
6	Uniform	High	High
7	Skewed	Low	High
8	Skewed	High	High

SD First Stage standard deviation of the first stage of the rank-ordered CI profile (low, 1; high, 10); Change in CV magnitude of increase in coefficient of variation from the first to the last stage of the rank-ordered CI profile (low, 0; high, 15). Detailed information on the parameters values is available elsewhere (7)

For each of the 24 scenarios, a set of 30 CI profiles was generated based upon the respective mean and standard deviation of the rank-ordered (see above) CI profiles. If a negative deposition on a site was simulated, its value was set to 0.001 mcg. This value was selected as it could possibly represent a reasonable lower limit of quantification on a deposition site (see “Discussion” section). The set of 30 CI profiles was then used as both T and R CI profiles. The number of T and R CI profiles was in accordance with the recommendations in the June 1999 Draft Guidance for Industry: Bioavailability and Bioequivalence Studies for Nasal Aerosols and Nasal Sprays for Local Action and the analysis of the PQRI working group (4,7,8). The mCSRS (Eq. 2) was then applied to all 900 possible pairs (30 T × 30 R) comprising one T and one R CI profile and, consequently, the distribution of the 900 mCSRSs was obtained. Six metrics, the 5th, 10th, 50th (median), 90th, 95th percentiles and the mean of the distribution of the 900 mCSRSs, were then calculated. These six metrics were potential candidates for a test statistic for the mCSRS and should provide some information about the distributional behavior of the mCSRS. This procedure was replicated 20,000 times and the averages (of the 20,000 replicates) of each of the six metrics were determined for each of the 24 scenarios. Furthermore, the averages of the six metrics of the distribution of the 900 mCSRSs were compared to their theoretical equivalents of an F distribution (12). This comparison was performed since it was expected that the distribution of the 900 mCSRSs is approximately an F distribution when certain criteria are met (see “Discussion” section).

The same analysis was performed for the CSRS. However, the CSRS (Eq. 1) was applied to all 13050 (30 T × 0.5 × (30 × 29) R) possible triplets comprising one T and two distinct R profiles. It should be noted that this evaluation of the CSRS differed slightly (see “Discussion” section) from the algorithm that was originally proposed (14). This alteration was needed in order to directly compare the performance of the mCSRS with that of the CSRS.

RESULTS

mCSRS

For each of the 24 scenarios (eight profile shapes for 13, 8, and 4 deposition sites), the averages (n = 20,000) of each of the six metrics (see above) and their theoretical equivalents of the respective F distribution are presented in Tables II, III, and IV. All six metrics were viable candidates for a robust and sensitive metric for comparing T and R CI profiles. The median of the distribution of 900 mCSRSs (MmCSRS) was equal to one regardless of the shape and the number of stages of the CI profiles. All other metrics varied across CI profiles with a different shape and number of deposition sites. Numerical comparison of the empirical percentiles/means (Tables II, III, and IV) and visual comparison of the histograms (examples shown for eight deposition stages, Figs. 2 and 3) of the distributions of the 900 mCSRSs to those of the respective F distribution show a certain agreement for the uniformly shaped beta scenarios (i.e., #1, 2, 5, and 6, Fig. 1 and ESM). For those scenarios, the similarity between the empirical percentiles/mean of the distribution of the 900 mCSRSs and those of the respective F distribution was confirmed by a Kolmogorov–Smirnov test (15; results not shown).

Table II.

Distribution (Percentiles and Mean) of mCSRS (900 Pairs) Across the Eight “Beta Scenarios”

Beta scenario	P5	P10	P50	P90	P95	Mean
1	0.38	0.47	1.00	2.16	2.70	1.20
2	0.36	0.45	1.00	2.23	2.81	1.22
3	0.24	0.32	1.00	3.17	4.44	1.50
4	0.21	0.29	1.00	3.56	5.12	1.62
5	0.36	0.46	1.00	2.22	2.81	1.22
6	0.36	0.45	1.00	2.26	2.86	1.22
7	0.31	0.40	1.00	2.55	3.36	1.31
8	0.27	0.36	1.00	2.85	3.86	1.40
F(12,12)	0.37	0.47	1.00	2.15	2.69	1.20

Thirteen deposition sites, identical sets of 30 T and 30 R CI profiles. Represented as the average (n = 20,000); F(12,12): theoretical percentiles and expected value of the f distribution with 12 numerator and 12 denominator degrees of freedom.

P5 5th percentile, P10 10th percentile, P50 median, P90 90th percentile, P95 95th percentile

Table III.

Distribution (Percentiles and Mean) of mCSRS (900 Pairs) Across the Eight “Beta Scenarios”

Beta scenario	P5	P10	P50	P90	P95	Mean
1	0.27	0.37	1.00	2.79	3.81	1.39
2	0.26	0.35	1.00	2.95	4.11	1.45
3	0.14	0.22	1.00	4.77	7.58	2.12
4	0.13	0.21	1.00	5.07	8.18	2.25
5	0.24	0.34	1.00	3.07	4.38	1.49
6	0.27	0.36	1.00	2.83	3.88	1.41
7	0.20	0.28	1.00	3.63	5.35	1.68
8	0.18	0.26	1.00	3.95	5.96	1.80
F(7,7)	0.26	0.36	1.00	2.78	3.79	1.40

Eight deposition sites, identical sets of 30 T and 30 R CI profiles. Represented as the average (n = 20,000); F(7,7): theoretical percentiles and expected value of the f distribution with seven numerator and seven denominator degrees of freedom

P5 5th percentile, P10 10th percentile, P50 median, P90 90th percentile, P95 95th percentile

Table IV.

Distribution (Percentiles and Mean) of mCSRS (900 Pairs) Across the Eight “Beta Scenarios”

Beta scenario	P5	P10	P50	P90	P95	Mean
1	0.12	0.20	1.00	5.51	9.94	2.94
2	0.10	0.17	1.00	6.32	11.62	3.40
3	0.04	0.08	1.00	13.98	34.43	22.41
4	0.04	0.08	1.00	14.28	35.22	26.49
5	0.08	0.14	1.00	7.72	14.60	4.30
6	0.10	0.17	1.00	6.21	11.49	3.34
7	0.06	0.12	1.00	9.83	23.76	11.56
8	0.05	0.10	1.00	11.07	26.54	11.59
F(3,3)	0.11	0.19	1.00	5.39	9.28	3.00

Four deposition sites, identical sets of 30 T and 30 R CI profiles. Represented as the average (n = 20,000); F(3,3): theoretical percentiles and expected value of the f distribution with three numerator and three denominator degrees of freedom

P5 5th percentile, P10 10th percentile, P50 median, P90 90th percentile, P95 95th percentile

Fig. 2.

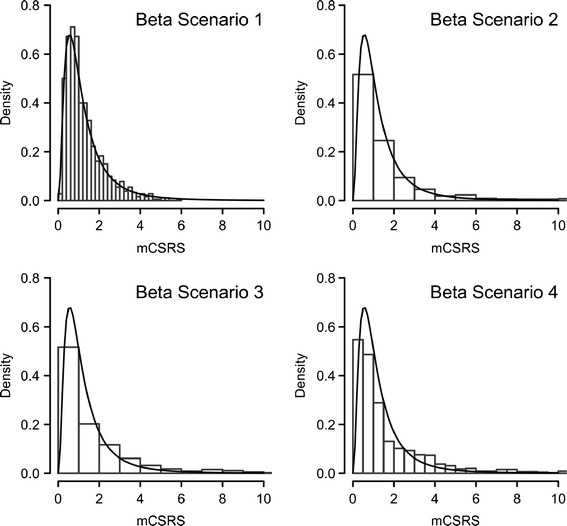
Comparison of distribution of the 900 mCSRSs (histogram) and F distribution with seven numerator and seven denominator degrees of freedom (solid line) for “beta scenarios” 1–4 and eight deposition sites, representative examples are displayed

Fig. 3.

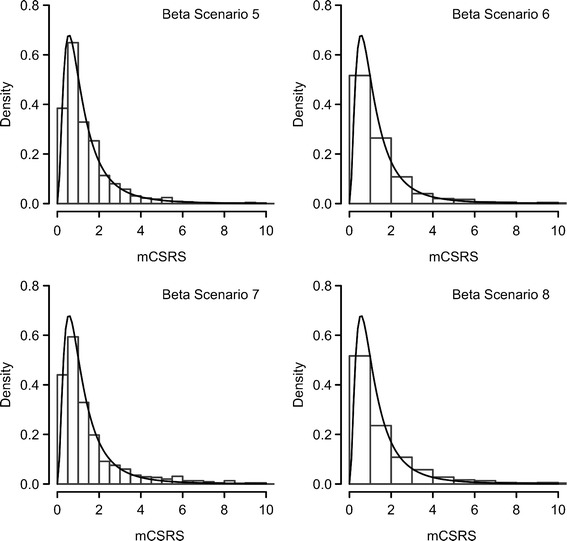
Comparison of distribution of the 900 mCSRSs (histogram) and F distribution with seven numerator and seven denominator degrees of freedom (solid line) for “beta scenarios” 5–8 and eight deposition sites, representative examples are displayed

CSRS

For each of the 24 scenarios, the averages (n = 20,000) of each of the six metrics of the distribution of 13050 CSRSs and their theoretical equivalents of the respective F distribution are presented in Tables V, VI, and VII. None of the metrics (5th, 10th, 50th, 90th (P90), 95th (P95) percentiles and the mean) returned the same value (in average) across the 24 beta scenarios. The median of the distribution of 13,050 original CSRS was close to 0.7 (in average) and varied the least across the 24 scenarios when compared with the other metrics. Numerical comparison of the empirical percentiles/mean of the distribution of 13,050 CSRSs to those of the respective F distribution did not show any similarities (Tables V, VI, and VII), which was confirmed by a Kolmogorov–Smirnov test (results not shown).

Table V.

Distribution (Percentiles and Mean) of CSRS (13500 Triplets) Across the Eight “Beta Scenarios”

Beta scenario	P5	P10	P50	P90	P95	Mean
1	0.25	0.26	0.71	1.58	1.99	0.86
2	0.30	0.35	0.76	1.47	1.78	0.86
3	0.17	0.24	0.69	2.31	3.25	1.08
4	0.17	0.22	0.68	2.43	3.50	1.12
5	0.28	0.33	0.75	1.60	2.02	0.90
6	0.31	0.36	0.79	1.49	1.80	0.89
7	0.22	0.27	0.70	1.91	2.55	0.96
8	0.23	0.27	0.71	1.91	2.53	0.96
F(12,12)	0.37	0.47	1.00	2.15	2.69	1.20

Thirteen deposition sites, identical sets of 30 T and 30 R CI profiles. Represented as the average (n = 20,000); F(12,12): theoretical percentiles and expected value of the F distribution with 12 numerator and 12 denominator degrees of freedom.

P5 5th percentile, P10 10th percentile, P50 median, P90 90th percentile, P95 95th percentile

Table VI.

Distribution (Percentiles and Mean) of CSRS (13500 Triplets) Across the Eight “Beta Scenarios”

Beta scenario	P5	P10	P50	P90	P95	Mean
1	0.20	0.25	0.70	2.03	2.77	1.00
2	0.22	0.27	0.71	1.87	2.50	0.96
3	0.11	0.17	0.67	3.41	5.42	1.53
4	0.10	0.16	0.67	3.49	5.60	1.57
5	0.18	0.24	0.70	2.28	3.28	1.11
6	0.25	0.30	0.74	1.84	2.43	0.98
7	0.14	0.20	0.67	2.69	4.01	1.23
8	0.14	0.20	0.68	2.70	4.04	1.24
F(7,7)	0.26	0.36	1.00	2.78	3.79	1.40

Eight deposition sites, identical sets of 30 T and 30 R CI profiles. Represented as the average (n = 20,000); F(7,7): theoretical percentiles and expected value of the F distribution with seven numerator and seven denominator degrees of freedom

P5 5th percentile, P10 10th percentile, P50 median, P90 90th percentile, P95 95th percentile

Table VII.

Distribution (Percentiles and Mean) of CSRS (13500 Triplets) Across the Eight “Beta Scenarios”

Beta scenario	P5	P10	P50	P90	P95	Mean
1	0.09	0.15	0.67	3.83	6.64	2.11
2	0.08	0.14	0.65	4.01	7.05	2.26
3	0.03	0.06	0.63	9.22	20.78	24.01
4	0.03	0.06	0.63	9.28	21.02	18.07
5	0.06	0.11	0.62	5.63	10.80	3.46
6	0.08	0.14	0.65	3.95	7.04	3.04
7	0.04	0.09	0.64	6.60	14.19	11.08
8	0.04	0.08	0.63	7.14	15.57	14.69
F(3,3)	0.11	0.19	1.00	5.39	9.28	3.00

Four deposition sites, identical sets of 30 T and 30 R CI profiles. Represented as the average (n = 20,000); F(3,3): theoretical percentiles and expected value of the F distribution with three numerator and three denominator degrees of freedom

P5 5th percentile, P10 10th percentile, P50 median, P90 90th percentile, P95 95th percentile

DISCUSSION

Comparison of the mCSRS (Eq. 2) to Pearson’s chi-square statistic for goodness-of-fit tests (Eq. 3) indicates a similarity between Pearson’s chi-square statistic for goodness-of-fit tests and both the numerator and denominator of the mCSRS (see above). If the population mean depositions (true values) on all sites of the R CI profile (E[R_i]) and T CI profile (E[T_i]) were known and under the assumption of identical T and R CI profiles (i.e., E[R_i] = E[T_i]), the mCSRS (Eq. 2) could be expressed as

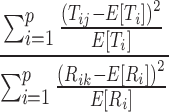4

In this case, both the numerator and the denominator of Eq. 4 have the same form as Pearson’s chi-square statistic for goodness-of-fit tests (Eq. 3) and are expected to follow approximately a chi-square distribution (with degrees of freedom = number of sites (p) − 1) when only a few low deposition sites are present5 (11,16). Furthermore, numerator and denominator are independent of each other (17) and have the same degrees of freedom. Thus, under the assumption of identical T and R CI profiles, Eq. 4 is expected to follow an approximate F distribution (with numerator and denominator degrees of freedom = number of stages − 1; 12,18). Since Eq. 4 and the mCSRS measure the same quantity under the assumption of identical T and R CI profiles, the distribution of the mCSRS is expected to be related to an F distribution under this assumption.

The behavior of the mCSRS when T and R CI profiles were identical was evaluated using CI profiles that were generated by simulation. These simulations assumed that drug deposition on a site is normally distributed. This assumption was based upon analysis of actual CI data that suggested normal distribution. Furthermore, it allowed comparison of the results with those of the PQRI working group that also assumed a normal distribution during data generation (7). However, this procedure resulted in simulation of negative depositions. Those negative values were, subsequently, converted to 0.001 mcg (see “Methods” section). Analysis of actual CI data suggested that an amount of 0.001 mcg could represent a reasonable lower limit of quantification on a deposition site on a CI profile. Setting the negative values to zero would have been an alternative option that is not expected to have affected the results (see below). However, it might be a worthwhile discussion on how to deal with CI data that contain a lot of zero (below lower limit of quantification) deposition sites. The number of negative amounts was dependent on the total number of deposition sites (4, 8, or 13; data not shown). If the drug was deposited on a total of four sites, negative simulation data averaged 1.1% (0–5.93%) while deposition of the same dose on 13 sites resulted in average in 13% (0–31%) negative data. It is unlikely that this procedure (simulations assuming normal distribution and using 0.001 mcg as default value for negative data) would affect the conclusions drawn from these simulations. First, we assumed that T and R CI profiles were identical and, thus, potential interferences should cancel out. Second, the numerical value of the selected test statistic (MmCSRS) was one regardless of the shape and the number of deposition sites of the CI profiles (Tables II, III, and IV), both of which affected the percentage of negative results. Hence, the method of data generation does not invalidate the conclusions of this work.

It must be also noted that all CI profiles were generated by assuming that the deposition between two sites is not correlated. Furthermore, all evaluations were performed for a sample size of 30 T and 30 R CI profiles, which is in accordance with the recommendations in the June 1999 Draft Guidance for Industry: Bioavailability and Bioequivalence Studies for Nasal Aerosols and Nasal Sprays for Local Action and the analysis of the PQRI working group (4,7,8). Since T and R CI profiles were identical throughout this analysis of the mCSRS, it is not expected that these assumptions would affect the conclusion regarding the behavior of the mCSRS in this case. However, the influence of varying both factors will be a subject of the forthcoming articles when T and R profiles differ in their properties.

One limitation of the CSRS was its non-applicability to a reduced number of deposition sites (e.g., deposition sites that may be more related to lung deposition) since the “stability” of the test statistic, which was specified in the original algorithm and was related to the mean of the distribution of CSRSs (14), was dependent of the number of depositions sites of the CI profiles (7,8; see “Introduction” section). The current analysis of the behavior of the CSRS when the set of T and R CI profiles were identical confirmed the dependency of the mean of the distribution of 13,050 CSRSs on the number of deposition sites and shape of the CI profile (Tables V, VI, and VII). Since the algorithm of the original CSRS specified obtaining a bootstrap estimate of the mean of a distribution of 500 randomly sampled triplets (14) rather than obtaining metrics from the distribution of all possible 13,050 triplets, direct numerical comparison of the results in this article to those of the original algorithm might differ slightly. However, the different algorithms did not affect the conclusions. Interestingly, it appeared that the median of the distribution of 13,050 CSRSs, which was close to 0.7, is the most robust metric across the 24 scenarios (Tables V, VI, and VII).

On the other hand, the MmCSRS was equal to one in all 24 scenarios (Tables II, III, and IV). Hence, the MmCSRS is independent of the shape and number of deposition sites of the CI profile when the sets of T and R CI profiles are identical and, thus, is applicable to CI profiles with a reduced number of deposition sites. Furthermore, the MmCSRS returns a for ratios correct value of one when sets of T and R CI profiles are identical. All other metrics (e.g., P90 or P95) varied across the 24 scenarios and, thus, were not considered as potential test statistics for APSD equivalence testing. It must be noted that those percentiles (e.g., P90 or P95) were not evaluated as potential metrics for constructing confidence intervals for APSD equivalence testing based on the mCSRS. A method for constructing confidence intervals for the MmCSRS will be introduced and discussed in a forthcoming publication (part III).

It is desirable for a new statistical metric to follow a known distribution. If certain criteria are met, the distribution of the 900 mCSRSs is expected to follow an approximate F distribution (see above). Indeed for CI profiles with only a few or no low deposition sites (beta scenarios 1, 2, 5, and 6, Fig. 1 and ESM), the similarity between the distribution of 900 mCSRSs and the F distribution was empirically confirmed by numerical comparison of the six metrics (see above) of the distribution of the 900 mCSRSs to their theoretical equivalents of the respective F-distribution (Tables II, III, and IV) and by visual inspection of the histograms of the distributions of the 900 mCSRSs (Figs. 2 and 3). Comparison of those metrics for more skewed CI profiles (i.e., more low deposition sites are present) indicated that the agreement between the distribution of 900 mCSRS and the F distribution is worsening (Tables II, III, and IV). However, the MmCSRS remains stable.

Even though the characteristic, that the distribution of the 900 mCSRS seems to be approximately F distributed when T and R CI profiles are identical and only a few low deposition sites are present, seems to be a desirable feature, it might not be of any practical relevance as realistic CI profiles are very likely to show several low deposition sites. Nonetheless, the MmCSRS is not affected by these distributional considerations and is equal to one for all 24 scenarios regardless of the number of deposition sites and shape of the CI profiles.

On the other hand, numerical comparison of the six metrics of the distribution of 13,050 CSRSs to their theoretical equivalents of the respective F distribution (Tables V, VI, and VII) shows that the CSRS does not follow an approximate F distribution in any of the cases under consideration. These results support findings of a more detailed analysis of the CSRS, its relationship to the F distribution, and a discussion on independence of its numerator and denominator (19).

Since the 24 scenarios covered in this evaluation are expected to cover all possible CI profiles, the robustness of the MmCSRS was demonstrated in cases when the T and R CI profiles are identical. Thus, this result suggests that the MmCSRS is a potential test statistic for APSD equivalence testing.

CONCLUSIONS

The current analysis suggests that MmCSRS is independent of the shape and number of deposition sites of a CI profile and is equal to one when T and R CI profiles are identical. Hence, the MmCSRS is a robust metric and, thus, is potentially useful as test statistic for APSD equivalence testing. Moreover, the MmCSRS could be applied to CI profiles comprising a reduced number of deposition sites (e.g., sites that may be more relevant for lung deposition). The behavior of the MmCSRS when T and R CI profiles differ from each other on a single or multiple deposition site(s) will be evaluated in a forthcoming article (part II) in order to better understand the suitability of the MmCSRS for APSD equivalence testing.

Electronic supplementary material

Below is the link to the electronic supplementary material.