Interactions of Everolimus and Sorafenib in Pancreatic Cancer Cells

Abstract

Everolimus targets the mammalian target of rapamycin, a kinase that promotes cell growth and proliferation in pancreatic cancer. Sorafenib inhibits the Raf-mitogen-activated protein kinase, vascular endothelial growth factor, and platelet-derived growth factor pathways, thus inhibiting cell growth and angiogenesis. Combinations of these two agents are under evaluation for therapy of several cancers. This study examined the effects of everolimus and sorafenib on proliferation of the pancreatic cancer cell lines MiaPaCa-2 and Panc-1. Cell growth inhibition was evaluated in vitro for a range of concentrations of the drugs alone and in combination. Maximum inhibition capacity (I_max) and potency (IC₅₀) were determined. The data were analyzed to characterize drug interactions using two mathematical analysis techniques. The Ariens noncompetitive interaction model and Earp model were modified to accommodate alterations in the inhibition parameters of one drug in the presence of another. Sorafenib alone inhibited growth of both cell lines completely (I_max = 1), with an IC₅₀ of 5–8 μM. Maximal inhibition by everolimus alone was only 40% (I_max = 0.4) in both cell lines, with an IC₅₀ of 5 nM. Slight antagonistic interaction occurred between the drugs; both analytic methods estimated the interaction term Ψ as greater than 1 for both cell lines. The in vitro data for two pancreatic cancer cell lines suggest that a combination of these two drugs would be no more efficacious than the individual drugs alone, consistent with the drug interaction analysis that indicated slight antagonism for growth inhibition.

INTRODUCTION

Pancreatic cancer is the fourth leading cause of cancer-related deaths in the USA (1). Gemcitabine-based chemotherapy is the standard of care for this disease, and erlotinib (Tarceva®) was shown recently to improve survival slightly when added to gemcitabine therapy (2). Pancreatic cancers display numerous genetic mutations; 90% of tumors show activating mutations in the Ras–Raf signaling pathway (3), leading to activation of downstream signaling such as the mitogen-activated protein kinase (MAPK) (4,5) and PI3k-Akt-mammalian target of rapamycin (mTOR) pathways (6–9), which promote cell proliferation, angiogenesis, and survival. Sorafenib (Nexavar®, BAY 43-9006) is a multikinase inhibitor that has activity in vitro and in vivo against a variety of solid tumors (10,11). It inhibits the MAPK, vascular endothelial growth factor, and platelet-derived growth factor pathways, and has shown anti-proliferative and pro-apoptotic activity in pancreatic cancer cell lines (12). Everolimus is an inhibitor of mTOR, which regulates cell proliferation and apoptosis (13,14). It has anti-proliferative activity in vitro and in vivo in pancreatic cancer models (15,16).

The MAPK and PI3k-Akt-mTOR pathways demonstrate cross-talk, in that inhibition of one can result in compensatory responses in the other (17–19). The combination of MAPK inhibitors with inhibitors of the PI3k-Akt-mTOR pathway in solid tumors has been speculated as a viable option and has proved effective in human melanoma and hepatocellular carcinoma (20–23). Our hypothesis is that concurrent inhibition of the compensatory pathways will lead to a synergistic effect in pancreatic cancer cells. We tested this hypothesis by investigating the in vitro anti-proliferative capacity of everolimus and sorafenib on pancreatic tumor cell lines MiaPaCa-2 and Panc-1 and quantified the interaction between them.

The nature and extent of drug interactions are usually evaluated using computational approaches. Mathematical modeling is particularly important in oncology because drugs are often given as combinations. In many situations, there is insufficient pharmacological detail to support mechanistic mathematical models. In these cases, empirical models based on Loewe additivity have been used widely. Another commonly used technique is isobologram analysis (24), which evaluates the nature of interaction between two drugs at any given effect level (e.g., IC₅₀ or IC₉₀). Curve-shift analysis is a technique that provides visual analysis of drug combination data, the concentration–response curves of drugs alone and in combination plotted to reveal a shift in the IC₅₀ (25). These methods are two-dimensional techniques used to facilitate analysis of combination data obtained in vitro. Three-dimensional analysis approaches have also been developed, as proposed by Greco et al. (26) for in vitro data, wherein the isobologram analysis is adapted to allow all the data from combination studies to be fitted into a single equation and to provide a statistical summary parameter describing the nature and extent of interactions.

Where possible to apply, mechanistic models are superior for characterizing drug interactions from in vivo studies. A simple model based on the assumption that two drugs exert their effect by interacting competitively with enzymes or receptors was given by Gaddum (27). A noncompetitive interaction equation was developed by Ariens and Simonis (28). Chakraborty et al. adapted these competitive and noncompetitive interaction models to provide a quantitative summary as a three-dimensional interaction surface using a single interaction parameter Ψ (29). The Ψ value signifies the degree to which cell sensitivity increases or decreases when one drug is combined with another. The three-dimensional surface also allows for visual inspection of the drug combination data. Drug interactions relevant to indirect response models were explored by Earp et al., who explored numerous scenarios depending on the mechanisms of combined drug action (30). The Earp et al. mechanistic models can be used for data obtained in vitro by modifying them for steady-state conditions. In this study, we have modified and evaluated two mechanistic methods to quantify the nature and extent of interaction.

METHODS

Reagents and Cell Lines

Everolimus and sorafenib p-toluenesulfonate salt were purchased from LC Laboratories (Woburn, MA). Stock solutions of the drugs were prepared in dimethylsulfoxide (DMSO) and stored at −20°C. The prepared everolimus stock was 2.08 mM, and the sorafenib stock was 20 mM. When diluted to the final working concentrations in experiments, the DMSO concentration was below 0.1% v/v, which did not perturb cell growth. The pancreatic adenocarcinoma cell lines MiaPaCa-2 and Panc-1 were obtained from American Type Culture Collection and maintained in Dulbecco’s Modified Eagle’s Medium (Cellgro, Manassas, VA) supplemented with 10% heat-inactivated fetal bovine serum (Atlanta Biological, Lawrenceville, VA).

In Vitro Growth Inhibition Assay

Panc-1 cells were plated in 24-well plates at 2.0 × 10⁴ cells per well in a volume of 1 mL, and MiaPaCa-2 cells were plated at 1.0 × 10⁴ cells per well. After overnight incubation at 37°C to permit cells to adhere, cells were treated with drugs in triplicate. Cells were exposed to everolimus at final concentrations of 0.01 to 1,000 nM and to sorafenib at final concentrations of 0.1 to 20 μM. Drug interaction experiments included at least 14 different combinations of drug concentrations spanning the entire range of relevant concentrations. Controls included cells incubated in drug-free medium, as well as cells incubated with DMSO at a final concentration of 0.1% (v/v), which exceeded the final DMSO concentration in any drug-treated wells. Drug exposure was 48 h for MiaPaCa-2 cells and 72 h for Panc-1 cells, after which cells were washed with Dulbecco’s phosphate-buffered saline (Sigma-Aldrich, St. Louis, MO), removed from the plates with 1% trypsin–0.53 mM EDTA, and counted using a Coulter Counter (Beckman Coulter, Hialeah, FL).

Pharmacodynamic Analysis

The cell counts obtained for each drug concentration were normalized relative to the growth of control (vehicle-treated) cells using:

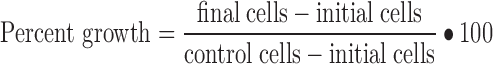1

where final cells is the cell count per well after drug exposure, initial cells is the average number of cells per well at the start of drug exposure, and control cells is the average cell count for wells containing drug-free medium. All model parameters were fitted to the individual cell numbers for each of the triplicate wells exposed to each drug concentration.

Analysis of Single Drug Effects

The concentration-dependent growth inhibition response R of cells for each drug concentration was modeled using the sigmoidal Hill function:

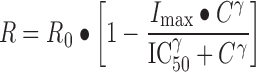2

where R₀ is the cell number when no drug is present, I_max is the maximum possible inhibition caused by the drug, C is the drug concentration, IC₅₀ is the drug concentration causing 50% of the maximum effect, and γ is the Hill coefficient.

Analysis of Combination Drug Effects

Drug combination effects were analyzed by two approaches. One pharmacodynamic model used was proposed originally by Ariens and Simonis (31,32) for noncompetitive interaction and later modified to express the intensity of possible interaction as a drug potency term (Ψ) (29). A value of Ψ < 1 signifies synergism, Ψ = 1 indicates additivity, and Ψ > 1 denotes antagonism. The equation assumes R₀ percent growth as percent of control in the absence of the drug, which was estimated from the data rather than fixing it to a value of 100.

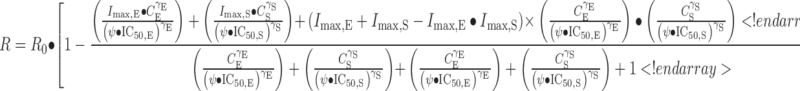3

where R is the cell count, C_E and C_S are concentrations of everolimus and sorafenib, and IC_50,E and IC_50,S are the drug concentrations producing 50% of the maximum inhibitory effect for each drug.

The second pharmacodynamic model employed was a previously described mechanistic model (30), which combines the indirect effect of the drugs on the growth process in order to evaluate interactions of the drugs according to the mechanisms of action of each. The drugs used in this study exert their effects on cells by inhibiting the processes that control their growth. Therefore, a form of the model indicating inhibition of cell growth by both drugs was used. The original model assumes the Hill coefficient γ to be 1, and it also assumes the baseline growth to be 100% of the control growth. The γ reflects the steepness of the concentration–response curve. We modified the previously described equation (30) to account for γ values other than 1 and also estimated the baseline growth of cells (R₀) rather than fixing it to 100%. For combinations, one drug might alter the actions of the other, thus exerting either antagonism or synergism. We introduced the term Ψ, which expresses alterations in the IC₅₀ or I_max of either drug when given in combination. The modified equation for noncompetitive interactions between two drugs that exert inhibitory effects is:

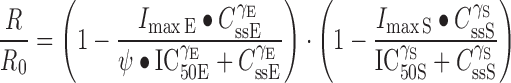4

where R is response at steady state, R₀ is the response when no drug is present, and I_max, IC₅₀, and γ have the same meaning as above. Values for these parameters are obtained from the analysis of single drug effects. The C_ss is the drug concentration to which cells are exposed. The equation was fitted to the data obtained from drug combination experiments to obtain the values of R₀, and the results from this method of analysis were compared to the other methods.

Model fitting and parameter estimation was performed using ADAPT 5 (33) with the maximum likelihood method. Naive-pooled data from all replicate studies were used in the analysis with a linear variance model:

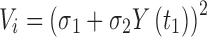5

where V_i is the variance of the response at the ith time point (t_i), and Y(t_i) represents the response at time t_i predicted from the model. Variance parameters σ₁ and σ₂ were estimated together with system parameters during fittings. The goodness-of-fit criteria included visual inspection of the fitted curves, the sum of squared residuals, Akaike Information Criteria (AIC), Schwarz Criterion (SC), and Coefficients of Variation (CV%) of the estimated parameters. All results were expressed as estimates along with their CV%.

RESULTS

Cell Growth Inhibition by Everolimus and Sorafenib

Growth Inhibition as Single Agents

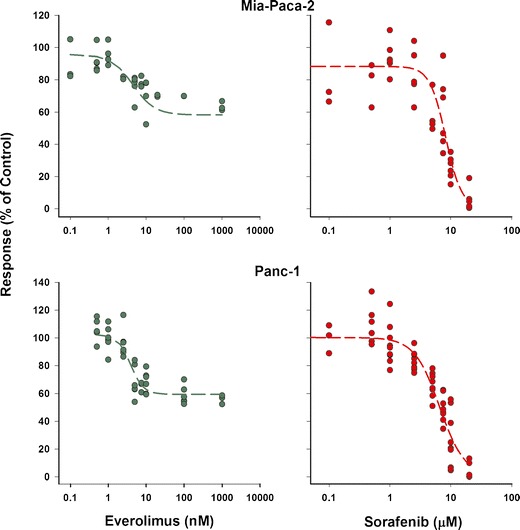
The concentration–growth inhibition response curves of the MiaPaCa-2 and Panc-1 pancreatic cancer cell lines to everolimus and sorafenib as single agents are shown in Fig. 1, along with the fit to the data of Eq. 2. The fitted parameters for analysis of the single drugs are listed in Table I. Overall, the Panc-1 cell line was slightly more sensitive to the drugs compared to MiaPaCa-2. The IC₅₀ for sorafenib was 8.29 μM in MiaPaCa-2 and 6.58 μM in Panc-1 cells, whereas the IC₅₀ for everolimus was 4.51 nM in MiaPaCa-2 and 3.87 nM in Panc-1 cells. At the highest concentrations, sorafenib was more efficacious (I_max = 1) than everolimus, as the latter did not suppress cell growth completely (I_max = 0.4), thus leaving a nonresponsive cell population. The γ for everolimus was 1.52 in MiaPaCa-2 and 2.53 in Panc-1 cells, whereas for sorafenib, γ was 3.3 in MiaPaCa-2 and 2.1 in Panc-1cells.

Fig. 1.

Cell growth inhibition by everolimus and sorafenib as single agents on two pancreatic cancer cell lines. Symbols represent experimental data, and lines show fitted curves

Table I.

Parameters for Individual Everolimus and Sorafenib Effects on Pancreatic Cancer Cells

Cell line	Drug	R 0 (%) (CV%)	IC50 (CV%)	I max (CV%)	γ (CV%)
MiaPaCa-2	Everolimus	95.67 (3.43)	4.51 (32.16) nM	0.39 (12.31)	1.52 (46.31)
	Sorafenib	88.31 (4.81)	8.29 (6.25) μM	1.00 (Fixed)	3.3 (20.57)
Panc-1	Everolimus	102.5 (2.85)	3.87 (13.83) nM	0.41 (6.45)	2.53 (27.23)
	Sorafenib	100.3 (2.49)	6.58 (5.51) μM	1.00 (Fixed)	2.1 (12.38)

Growth Inhibition of Combined Agents

Cells were exposed to a range of concentrations of the two drugs in order to investigate the cell growth inhibitory effects of drug combinations. Model-fitting approaches were used to determine the nature and intensity of the interactions between the two drugs. Two analysis approaches were applied to the drug combination data. Figure 2 shows the observed data for MiaPaCa-2 cells along with a three-dimensional response surface based upon analysis of the combination data using the Ariens–Chakraborty equation (29). The analysis yielded a Ψ value of 1.20 for MiaPaCa-2 and 1.01 for Panc-1, with good precision (Table II). Because the Ψ value is slightly greater than 1, it suggests the drugs are modestly antagonistic. The response surface is created using the final estimates for IC₅₀, I_max, γ, and Ψ. The response surface shown in Fig. 2 represents the three-dimensional model prediction for a Ψ value of 1.20 with MiaPaCa-2 cells. The 95% confidence interval for Ψ in MiaPaCa-2 cells is 1.09–1.29, and for Panc-1 cells, it is 0.95–1.2. Therefore, the estimates of Ψ are significantly different from 1.0 for MiaPaCa-2, but not for Panc-1.

Fig. 2.

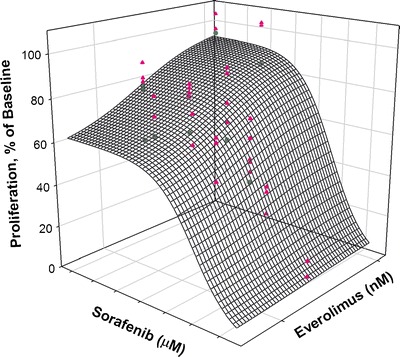
Fitted response surface using the Ariens–Chakraborty method for drug combination data for MiaPaCa-2 cells. The mesh surface represents a model fitting for Ψ = 1.20, which is the value of the interaction parameter derived from the analysis of the data. The triangles are data above the surface, and the circles are data below the surface

Table II.

Parameters for Everolimus and Sorafenib Interactions on Pancreatic Cancer Cells

Cell line	Modified Ariens method			Modified Earp method
	R 0 (%)	Potency (Ψ)	AIC/SC	R 0 (%)	Potency (Ψ)	AIC/SC
MiaPaCa-2	96.93 (2.29)	1.20 (4.25)	746/755	99.15 (2.54)	1.48 (26.39)	760/770
Panc-1	110.8 (2.33)	1.01 (4.18)	1,135/1,146	109.7 (1.99)	1.06 (15.63)	1,134/1,146

AIC Akaike Information Criteria, SC Schwarz Criterion

Both drugs decrease growth of cells by inhibiting proliferative pathways. Therefore, the Earp equation can be modified to indicate alteration of IC₅₀ or I_max of either drug when cells are exposed to a drug combination. We evaluated models in which IC₅₀ of either drug was altered due to the presence of the other drug. Figure 3 shows the three-dimensional response surface predicted for the drug combination as analyzed and predicted using the modified Earp equation (Eq. 4). The estimate of Ψ, indicating the effect of sorafenib on the IC₅₀ of everolimus, was 1.48 for MiaPaCa-2 and 1.06 for Panc-1 cells. The estimate of Ψ, representing the effect of everolimus on the IC₅₀ of sorafenib, was 1.2 for MiaPaCa-2 and 1.1 for Panc-1 cells (Table II). The surface shown in Fig. 3 represents the model prediction of response with a value of Ψ of 1.48 for MiaPaCa-2 cells. The fitting with the modified Ariens–Chakraborty model was better than obtained with the modified Earp model, as was evident both visually and based upon the AIC, SC, and r² values.

Fig. 3.

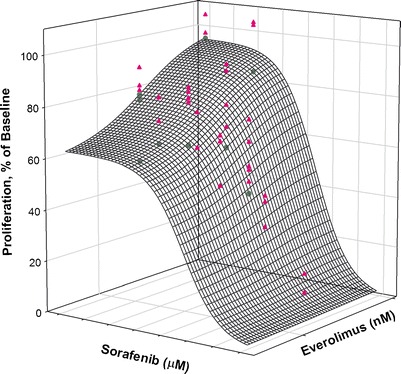
Fitted response surface using the modified Earp method with drug combination data for MiaPaCa-2 cells. The mesh surface is the model prediction for a value of Ψ = 1.48, which is the value derived by analysis of the data. The triangles are data above the surface, and the circles are data below the surface

DISCUSSION

There exists a dire need for effective therapy of pancreatic cancer, as the majority of the patients have limited treatment options. Numerous molecularly targeted agents have been developed and are in clinical evaluation for treatment of cancers having genetic aberrations that may confer vulnerability to interdiction of specific signaling pathways. However, molecularly targeted drugs often have shown disappointing clinical activity as single agents, owing to the lack of sufficient “pathway addiction” to the signaling axis that is inhibited, as well as the development of compensatory mechanisms (17–19). Therefore, the combination of molecularly targeted agents that are mechanistically complementary in order to overcome resistance to monotherapy may represent a more effective strategy. The Ras–Raf–MAPK pathway, which is activated in 90% of pancreatic cancer patients, is involved in cell growth and angiogenesis. Therefore, sorafenib, an inhibitor of this pathway, was selected for investigation. Everolimus was chosen here as a mechanistically complementary agent. It inhibits mTOR, which is involved in cell growth, proliferation, and apoptosis. Interactions between these signaling pathways are known (17,19,34), so simultaneous molecular targeting would be expected to provide a synergistic action, thereby overcoming resistance. The combination of sorafenib and everolimus (or its analog rapamycin) has shown synergistic activity in vitro and in vivo against melanoma (20,21) and hepatocellular carcinoma (22).

Multiple mathematical models are available for evaluation of potential drug interactions arising from combination drug treatments (35). In this study, we modified appropriate mechanistic models to interpret data obtained for a combination of two agents that may be mechanistically complementary.

The data necessary to evaluate the nature of drug interactions were obtained by measuring the inhibitory effects of everolimus and sorafenib individually on the growth of two pancreatic cancer cell lines. These two cell lines contain activating Kras mutations as well as mutations in the TP53, CDKN2A, and SMAD4 genes, which are involved in the regulation of proliferation in normal cells (36). The two drugs, individually or in combination, did not exert any anti-proliferative effects on BXPC-3, a third pancreatic cancer cell line that lacks the Kras mutation (36) (data not shown).

The analysis of single-agent data provided quantitative measures of drug potency, steepness of the concentration–response relationship, and maximal cancer cell growth inhibition. For combinations of the two drugs, isobologram analysis (not shown) suggested a slight antagonistic interaction between them. Modeling of the data was used to analyze the nature of the interaction quantitatively. Previously published methods do not account for baseline variability; the baseline plays an important role in pharmacodynamic analysis, as it contains variability, as do all experimental data points (37). To address this issue, all data, including that for drug-free controls, were fitted by the model. This contrasts with the traditional approach of normalizing data by the drug-free controls, which obscures the contribution of errors in baseline data to the drug concentration–response analysis. Thus, the best-fitted R₀ values were obtained by estimation, as an alternative to normalizing experimental data by an assumed error-free average of data for drug-free controls.

The results from all methods used to evaluate drug interaction indicated a slight antagonistic interaction between the two drugs on the tumor cell lines in vitro. Application of the equation developed by Earp et al. (30) incorporates inhibitory effects of each drug. Here, the conceptual incorporation of Ψ into the approach enables the determination of whether combining two drugs results in a change in the sensitivity of the individual drug effects (IC₅₀ and I_max). Alterations in IC₅₀ (Table II) and I_max (not shown) of each drug were investigated. Based upon the known pharmacology of the two agents, it is difficult to decipher mechanisms of interactions and which parameters were altered upon combination of the agents. But, from the parameter estimates and indicators of model fits, it appears that the model in which an alteration of IC₅₀ for everolimus is hypothesized provided the best fit. Nonetheless, all models suggested slight antagonistic drug interaction.

Everolimus and sorafenib are cytostatic agents and differ in their sites of action upon cell cycle progression. Everolimus inhibits a key enzyme involved in cell growth and proliferation and arrests cells in the late G1 phase. In contrast, sorafenib inhibits cells from transitioning into the G1 phase of the cell cycle. The observed antagonistic effect observed in vitro could be attributed to drug arrest of cells in one phase, thereby rendering fewer cells susceptible to the full inhibitory potential of a second drug that affects drugs in a subsequent cycle phase.

In vitro testing of oncology drugs provides an opportunity to investigate mechanisms of drug interaction that may be difficult to identify in vivo. In vitro studies allow for rapid assessment of the nature and mechanisms of interactions, and the development of model-based analysis of in vitro results can provide key quantitative parameters relating to cell-level drug effects that can be applied to the subsequent analysis of in vivo drug combination interactions. The results of this study indicate absence of synergistic interaction between everolimus and sorafenib on pancreatic cancer cells, and additional studies that explored the sequence in which cells were exposed to the drug yielded no evidence of enhanced effects of the combination (data not shown).

In contrast, in vivo xenograft experiments, in which mice bearing low-passage, patient-derived pancreatic cancer explants were treated with combined sorafenib and everolimus, exhibited supra-additive (synergistic) antitumor effects (D.K. Pawaskar, R.M. Straubinger, G.J. Fetterly, B.H. Hylander, E.A. Repasky, W.W. Ma, and W.J. Jusko; Synergistic Interactions Between Sorafenib and Everolimus in Pancreatic Cancer Xenografts in Mice; unpublished). The lack of direct synergistic interactions of the two-drug combination on the rapidly dividing tumor cells observed here in vitro suggests that in vivo efficacy of the combination may arise from a significant contribution of drug effects on the supporting tumor vasculature, tumor stromal cells, and the tumor microenvironment. This finding not only underscores the necessity for testing of drug combinations in vivo, but also suggests that key insights into the interpretation of therapeutic data may be gained by quantitative analysis of drug interaction data from in vitro studies.

In conclusion, everolimus and sorafenib inhibit distinct but interrelated signaling pathways and exert their effects in different phases of the cell cycle. The results suggest that pharmacological interactions between sorafenib and everolimus in pancreatic cancer cells in vitro are no more than additive and possibly slightly antagonistic. Modeling was used to analyze and summarize quantitatively the nature of the interaction. Similar results were observed for both analytic methods. The mechanistic model that hypothesized that the combination alters the IC₅₀ of everolimus was the best fitting. The results also suggest that tumors in vivo represent a highly dynamic system, in which drug combinations affect multiple cellular signaling processes and exert a spectrum of effects in addition to those upon the tumor cells themselves, such as inhibition of angiogenesis or modulation of tumor stromal interactions. The approaches developed here for quantitative analysis of drug combination effects upon tumor cells in vitro can yield valuable information for the interpretation of therapeutic results obtained in preclinical pancreatic cancer models.