Abstract
The pharmacokinetic (PK) behavior of inhaled drugs is more complicated than that of other forms of administration. In particular, the effects of certain physiological (mucociliary clearance and differences in membrane properties in central and peripheral (C/P) areas of the lung), formulation (as it relates to drug deposition and particle dissolution rate), and patient-related factors (lung function; effects on C/P deposition ratio) affect the systemic PKs of inhaled drugs. The objectives of this project were (1) to describe a compartmental model that adequately describes the fate of inhaled corticosteroids (ICS) after administration while incorporating variability between and within subjects and (2) based upon the model, to provide a freely available tool for simulation of PK trials after ICS administration. This compartment model allows for mucociliary removal of undissolved particles from the lung, distinguishes between central and peripheral regions of the lung, and models drug entering the systemic circulation via the lung and the gastrointestinal tract. The PK simulation tool is provided as an extension package to the statistical software R (‘ICSpkTS’). It allows simulation of PK trials for hypothetical ICS and of four commercially available ICS (budesonide, flunisolide, fluticasone propionate, and triamcinolone acetonide) in a parallel study design. Simulated PK data and parameters agreed well with literature data for all four ICS. The ICSpkTS package is especially suitable to explore the effect of changes in model parameters on PK behavior and can be easily adjusted for other inhaled drugs.
KEY WORDS: compartment model, inhaled corticosteroids, pharmacokinetics, trial simulation
INTRODUCTION
Inhaled corticosteroids (ICS) are first-line medications for asthma treatment and a therapy option in the management of chronic obstructive pulmonary disease (1,2). A better understanding of pharmacokinetic (PK) properties that influence pulmonary selectivity of ICS has helped increase the efficacy and reduce systemic side effects of novel ICS (3,4). However, the effects of certain physiological, formulation, and patient-related factors on the systemic PKs of ICS remain poorly understood. For instance, changes in the lung physiology and anatomy during the course of a pulmonary disease affect the PK behavior of some ICS while that of others is unchanged (5,6). Similarly, the aerodynamic particle size distribution and regional lung deposition patterns (central-to-peripheral airways) affect the systemic PKs of some ICS but not that of others (7). Differences in dissolution rates do not only affect the time to reach the maximum plasma concentration (tmax) and the maximum plasma concentration (Cmax) but also the area under the plasma concentration time profile (AUC). Thus, the PK behavior of inhaled drugs is much more complicated than that of traditional forms of administration. Moreover, changes in formulation and delivery device and comparison of different ICS in the same device are often challenging.
Clinical trial simulation (8) is a powerful tool for evaluating the outcomes of clinical or PK studies in a time and cost-efficient way before resources are invested in conducting the actual studies. A trial simulation model generates realistic data by specifying a mathematical model that adequately describes the functional relationship between the variable of interest and time (deterministic part of the model; here, PK profile of ICS) and by incorporating variability between and within subjects (random part of the model). This project was interested in providing such a simulation tool that allows incorporation of relevant physiological and formulation factors into the model and is able to predict the effects of changes in such parameters on systemic PKs without having to perform actual PK studies.
A freely available tool for simulation of PK trials after administration of ICS is provided that enables the user to explore the relationship between certain physiological (e.g., differentiation between central and peripheral lung regions, different pulmonary absorption rates between central and peripheral lung regions (9,10), and presence of mucociliary clearance mechanism in central lung regions (11)), formulation (e.g., aerodynamic particles size distribution of the aerosol determining regional lung deposition patterns and dissolution properties of the ICS), and patient-related factors (e.g., variability between and within subjects and differences in lung physiology between healthy subjects and patients) and the systemic PKs of ICS. The PK trial simulation tool is provided as an extension package (“Inhaled Corticosteroids Pharmacokinetic Trial Simulation“ (ICSpkTS)) to the statistical software R (12) and is available for download viahttp://www.cop.ufl.edu/pc/research/areas-of-research/inhaled-glucocorticoids/icspkts-r-extension/. The ICSpkTS package enables the users to simulate PK trials for any ICS (currently available or hypothetical) delivered via different inhalers and different physiological settings in healthy subjects or patients by allowing the users to specify their own model parameters. Furthermore, the ICSpkTS package contains specific modules for some of the commercially available ICS (budesonide (BUD), flunisolide (FLU), fluticasone propionate (FP), and triamcinolone acetonide (TA)).
This PK trial simulation tool for ICS represents an innovation compared with previously published ICS PK models (3) and deterministic ICS PK simulation tools (13) as it allows simulation of PK trials by integrating variability between and within subjects and distinguishes between central and peripheral regions of the lung.
This paper is structured as follows. First, a compartment model (Fig. 1) that incorporates physiological, formulation, and patient-related factors of inhalation therapy (see above) is characterized. Second, a closed-form expression for the plasma concentration time profile after ICS administration is derived based upon the compartment model (deterministic part of the PK trial simulation model). The availability of a closed-form expression of the underlying mathematical model is beneficial for time-efficient simulation. Third, the structure of the random part of the PK trial simulation model (i.e., between-subject variability (BSV) and within-subject variability (WSV)) is specified. Fourth, literature estimates of model parameters (i.e., typical values and associated variability terms (BSV and WSV)) for the drug-specific modules of the PK trial simulation tool are summarized. Fifth, the performance of the drug-specific modules of the ICSpkTS package is checked by comparing model simulated plasma concentration time profiles to actual plasma concentration data and/or literature data following administration of BUD, FLU, FP, and TA. In the Discussion, possible applications, the practical relevance, and limitations of the ICSpkTS package are debated. In the Appendix, the structure and functions of the PK trial simulation tool and its modules are briefly explained by two hands-on examples.
Fig. 1.
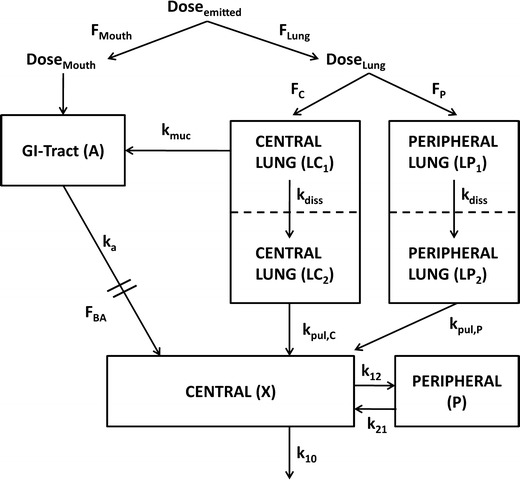
Compartment model for characterization of plasma concentration after administration of ICS. F Lung fraction of the emitted dose that is deposited in the lung, F Mouth fraction of the emitted dose that is deposited in the oropharynx, F C fraction of the lung dose that is deposited in central regions of the lung (LC1), F P fraction of the lung dose that is deposited in peripheral regions of the lung (LP1), LC 2 compartment representing central lung regions where the drug is dissolved, LP 2 compartment representing peripheral lung regions where the drug is dissolved, F BA oral bioavailability, k muc mucociliary clearance, k a drug absorption from the gut into the systemic absorption, k diss dissolution of drug particles, k pul,C drug absorption from central lung regions into the systemic circulation (central body compartment), k pul,P drug absorption from peripheral lung regions into the systemic circulation, k 12 and k 21 drug distribution between central and peripheral body compartments; k 10 drug elimination from the systemic circulation. All rate constants (k) were assumed to be first-order processes
COMPARTMENT MODEL
Figure 1 displays a compartment model that adequately describes the fate of an ICS by incorporating physiological and formulation-related aspects for inhalation therapy and patient factors. In detail, an inhaled drug particle, according to its aerodynamic particle size distribution, is deposited in the oropharynx (DoseMouth), is deposited in the lung (DoseLung), or is exhaled. The fraction of the emitted dose that is exhaled is negligible and was, thus, disregarded in the compartment model. It is pragmatic to distinguish the dose deposited in the lung into a fraction deposited in central lung regions and a fraction deposited in peripheral lung regions, given the impact of the physiological differences between the two regions on the fate of an inhaled drug (14). Even though in vitro/in vivo correlation between aerodynamic particle size distribution and regional lung deposition patterns has been established infrequently if ever, it is widely accepted that larger particles are more likely to be deposited in the oropharynx and central lung regions and smaller particles are more likely to be deposited in peripheral lung regions (15). Both central and peripheral lung regions were separated in one compartment where undissolved particles are present (LC1 and LP1) and one compartment where particles are in solution (LC2 and LP2). In detail, drug particles deposited in central lung regions (LC1) are either cleared by the mucociliary clearance mechanism (kmuc) or will dissolve in the bronchial fluids (kdiss), pass through the pulmonary cells in the central lung regions (LC2) and be absorbed into the systemic circulation (kpul,C) (11). Drug particles deposited in peripheral lung regions (LP1) dissolve (kdiss), pass through the pulmonary cells in the peripheral lung regions (LP2), and are absorbed into the systemic circulation (kpul,P). The model allows explicitly for different absorption rate constants for drug absorption from the central and peripheral lung regions if this distinction is justified (9,10). The fraction of the drug that is deposited in the oropharynx and the fraction that is removed by mucociliary clearance will be swallowed and can be absorbed systemically (ka) through the gastrointestinal tract (A) depending upon the oral bioavailability (FBA) of the drug. The amount of drug that reaches the systemic circulation will be distributed throughout the body (k12 and k21) and eliminated (k10) according to its PK properties. The model was parameterized in terms of CL and VC, where CL represents the systemic clearance (in liters per hour) of the ICS, VC represents the volume of distribution (in liters) of the central body compartment, and k10 = CL/VC. Patient factors are incorporated into the model by allowing for variability in the model parameters between and within subjects.
PLASMA CONCENTRATION TIME PROFILE CLOSED-FORM EXPRESSION
A closed-form expression for the plasma concentration time profile after ICS administration was judged as beneficial for time-efficient PK trial simulation. This expression was derived based on a system of differential equations (Eqs. 1–7) describing the fate of an ICS in the compartment model (Fig. 1)
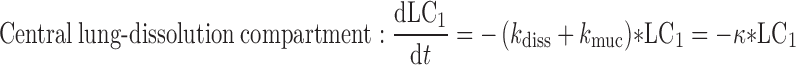 |
1 |
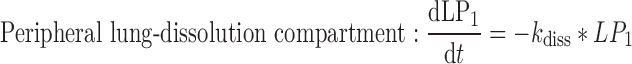 |
2 |
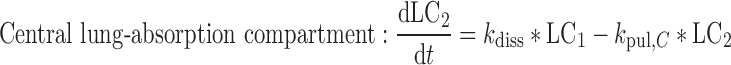 |
3 |
 |
4 |
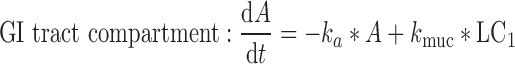 |
5 |
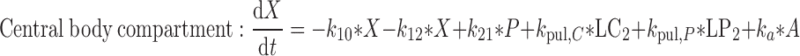 |
6 |
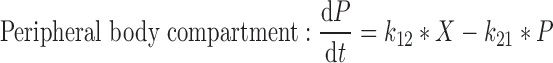 |
7 |
where t represents the time (in hours), LC1, LP1, LC2, LP2,A, X, and P represent the amount of drug at time point t in the dissolution compartment of the central lung, dissolution compartment of the peripheral lung, solution compartment of the central lung, solution compartment of the peripheral lung, GI absorption compartment, central body compartment, and peripheral body compartment, respectively. The first-order rate constants kdiss, kpul, C, kpul, P, kmuc, ka, k12, k21, and k10 were defined above. The assumption that the mucociliary clearance is a first-order process, which seems to be justified for healthy subjects or mild-asthmatic patients (16), was made for mathematical convenience. The system of differential equations was then solved using Laplace integration methods (17). Details are given in the Appendix. Hence, a closed-form expression for the plasma concentration time profile (Ct) after administration of an ICS and thus the deterministic part of the PK trial simulation model is given by
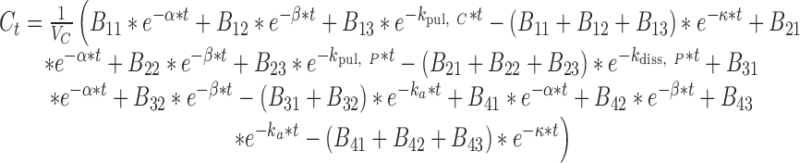 |
8 |
where all terms that were not introduced above are defined in the Appendix.
RANDOM STRUCTURE OF PK MODEL—BETWEEN AND WITHIN-SUBJECT VARIABILITY
After log transformation, individual PK parameters (e.g., FLung, CL, and VC) were assumed to follow a multivariate normal distribution with population mean vector θ and variance–covariance matrix Ω where the elements of θ represent the typical values (population averages) and the diagonal element of Ω represents the BSV (in terms of variance) of the PK parameters. The off-diagonal elements of Ω, representing the covariance between the PK parameters, are zero. Hence, all individual PK parameters are independent of each other and follow a lognormal distribution.
An exponential error model was selected as residual error model.
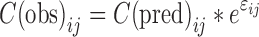 |
9 |
where C(obs)ij and C(pred)ij represent the observed and predicted plasma concentration at the jth time point in the ith subject, respectively, and εij are assumed to be independent and identically distributed normal random variables with mean equal to zero and variance σ2.
DRUG-SPECIFIC MODULES—LITERATURE-BASED PARAMETER ESTIMATES
The ICSpkTS tool contains four specific modules for PK trial simulation after administration of the ICS BUD, FLU, FP, and TA. Estimates for the typical value parameters are given in Table I and are in accordance with a previously published deterministic PK model (18) (unless otherwise stated in Table I). It should be noted that literature estimates for both the pulmonary dissolution and absorption processes were not available. Therefore, it was assumed that literature estimates of the “pulmonary absorption rate” rather represent the dissolution than the absorption process. This assumption that the dissolution process is the rate-limiting step seems reasonable given the lipophilic character of ICS and the fast pulmonary absorption of lipophilic substances (9,10). Furthermore, an educated guess of 0.5 for the fraction of the lung dose that is deposited in central lung regions (i.e., central to peripheral lung deposition (C/P) ratio equals 1) was used as a default value in all four modules. This C/P ratio is a common value within the estimates reported in the literature for some of the formulations/drugs that are included in the simulation tool. For some other formulations/drugs, however, literature estimates were not available. Furthermore, literature data on C/P ratios need to evaluate critically due to a lack of validated scintigraphy data (19) (see also Discussion). Therefore, a C/P ratio of 1 was used without further differentiation for all four drug-specific modules. Estimates for the BSV and WSV terms either varied across the literature or were not available. Hence, BSV estimates for all parameters and WSV were set to default values of 20% and 30% (expressed as coefficient of variation (CV)), respectively, in all four drug-specific modules. However, the users can adjust the BSV and WSV parameters and typical value parameters if desired.
Table I.
Typical value parameters for the BUD, FLU, FP, and TA modules of the PK trial simulation tool
| Parameter | Unit | BUDa (DPI) | FLU (MDI) | FPa (DPI) | TAa (MDI) |
|---|---|---|---|---|---|
| θ (F Lung) | 0.3b | 0.24b | 0.16b | 0.15b | |
| θ (F C) | 0.5b, g | 0.5b, g | 0.5b, g | 0.5b, g | |
| θ (F BA) | 0.11 | 0.2 | 0e | 0.23 | |
| θ (k muc) | h−1 | 0.938b (14) | 0.938b (14) | 0.938b (14) | 0.938b (14) |
| θ (k diss) | h−1 | 17.8b | 14b | 0.189f | 1.2b |
| θ (k pul,C) | h−1 | 10c | 10c | 10c | 10c |
| θ (k pul,P) | h−1 | 20c | 20c | 20c | 20c |
| θ (k a) | h−1 | 0.45 (20) | 14 | –e | 0.91 (21,22) |
| θ (CL) | L/h | 85 | 55 | 73 | 39 |
| θ (V C) | L | 100 | 70 | 31 | 154 |
| θ (k 12) | h−1 | 20.01 | 0.41 | 1.78 | –d |
| θ (k 21) | h−1 | 11.06 | 0.82 | 0.09 | –d |
Typical value parameters are based upon a publication by Krishnaswami et al. (18) unless otherwise stated (reference(s) in parenthesis). Further literature references that are related to the selection of the typical value parameters are given as additional references. BSV and WSV terms are set (by default) to values of 20% and 30% (expressed as CV%), respectively, and can be changed by the user
BUD budesonide, FLU flunisolide, FP fluticasone propionate, TA triamcinolone acetonide, DPI dry powder inhaler, MDI metered-dose inhaler
aAdditional references: BUD (23–29), FP (30–33), and TA (34)
bParameters are set to literature estimates but can be changed by user. The default values for θ (F Lung) represent specific values for the inhalers (i.e., BUD (Turbohaler), FLU (MDI), FP (Diskus), and TA (MDI))
cParameters are arbitrarily chosen to represent fast absorption of dissolved lipophilic substances and to account for possible faster absorption from peripheral lung regions and can be changed by the user
dOne compartment body model seems to be more suitable to describe PK of TA
eThe oral bioavailability of FP is <1% and negligible for the plasma concentration time profile
fThe dissolution rate constant (k diss) for the FP module is based upon unpublished in vitro dissolution data and PK analysis of unpublished FP data
gLiterature estimates for F C (i.e. central vs. peripheral lung (C/P) deposition ratio) ratio for the different formulations are either not available or not applicable for the model (see Discussion). Thus, an educated guess of 0.5 (i.e., C/P deposition ratio of 1) was used as a default value for the modules
PERFORMANCE CHECK OF THE DRUG-SPECIFIC MODULES OF PK TRIAL SIMULATION TOOL
Methods
For all modules, the literature-based model parameters (Table I) were used to generate 1,000 plasma concentration time profiles after inhalation of a single dose of 1,000, 500, 250, and 100 mcg BUD, FP, FLU, and TA, respectively.
For BUD and FP, these simulated plasma concentration time profiles were used to check the performance of the BUD and FP modules of the PK trial simulation tool by comparing the simulated data to PK data from four studies where healthy subjects received BUD and FP delivered via their respective dry powder inhalers (studies I (30), II (35), III (36), and IV (37)). Individual plasma concentration time profiles were available for study I. For studies II–IV, only certain PK metrics (e.g., AUC0−t, Cmax, and tmax) were available from the literature. Using the simulated plasma concentration time data, 90% prediction intervals were constructed by cutting off the lower and upper 5% of the simulated plasma concentrations per time point. For both, BUD and FP, the 90% prediction intervals were then visually compared with data from 14 healthy subjects that received a single dose of 1,000 mcg BUD and 500 mcg FP, respectively (study I). Moreover, typical PK metrics (i.e., AUC0–inf, AUC0−t, Cmax, tmax, and the terminal half-life) were calculated for the simulated data and compared with those of studies I–IV. AUC and Cmax values from studies II–IV were normalized to the simulated dose of 1,000 (BUD) and 500 mcg (FP) to match the administered dose of the simulated data and study I.
For FLU and TA, where individual plasma concentration time data were not available, simulated (n = 1,000) AUC0−inf, Cmax, and tmax were compared with those (after dose adjustment) from literature (38–44) to check the performances of the FLU and TA modules.
Results
Figures 2 and 3 display the visual comparison of the simulated plasma concentrations (90% prediction intervals) to those of the 14 healthy subjects (study I) for BUD and FP, respectively. Comparison of the PK metrics of the simulated data to those of studies I–IV is given in Tables II and III for BUD and FP, respectively. For FLU and TA, the results of the performance checks are displayed in Table IV.
Fig. 2.
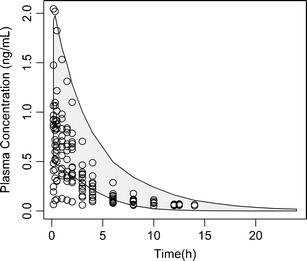
Validation of BUD module of the ICSpkTS R extension package. Empty circles, observed plasma concentration after inhalation of a single dose of 1,000 mcg BUD (n = 14) (30). Grey-shaded area, 90% prediction interval based upon simulated plasma concentrations after inhalation of a single dose of 1,000 mcg BUD (n = 1,000) using the BUD module of the ICSpkTS R extension package
Fig. 3.
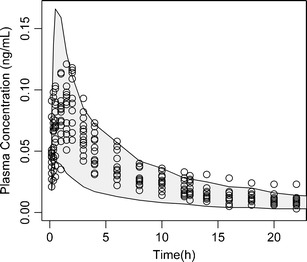
Validation of FP module of the ICSpkTS R extension package. Empty circles, observed plasma concentration after inhalation of a single dose of 500 mcg FP (n = 14) (30). Grey-shaded area, 90% prediction interval based upon simulated plasma concentrations after inhalation of a single dose of 500 mcg FP (n = 1,000) using the FP module of the ICSpkTS R extension package
Table II.
Performance check of BUD module of the ICSpkTS R extension package
| Simulated data | Study I—Moellmann et al. (30) | Study II—Harrison et al. (35) | Study III—Mortimer et al. (36) | Study IV—Dalby et al. (37) | |
|---|---|---|---|---|---|
| n | 1,000 | 14 | 12 | 20 | 26 |
| C max (ng/mL) | 1.39 (27.2) | 0.89 (54.3) | 2.02 (−) | 2.09 (49) | 2.26 (−) |
| t max (h) | 0.65 (92.3) | 0.41 (84.3) | – | 0.21 (114) | 0.5 (−) |
| AUC0–24 (ng mL−1 h) | 4.74 (27.2) | 2.56 (60.0) | – | – | – |
| AUC0–inf (ng mL−1 h) | 4.77 (27.4) | 2.84 (56.3) | – | – | – |
| AUC0−5/6 a (ng mL−1 h) | 3.63 (26.4) | – | – | 3.59 (41.4) | – |
| AUC0−8 (ng mL−1 h) | 4.06 (25.9) | – | 5.39 (−) | – | – |
| AUC0−10 (ng mL−1 h) | 4.32 (25.9) | – | – | – | 3.3 (106.4) |
| Terminal t 1/2 (h) | 2.62 (39.3) | 2.97 (48.4) | – | – | – |
Comparison of PK metrics (mean (CV%)) from simulated data using the PK trial simulation tool and literature. Only data from healthy subjects were used from literature. AUC and C max data from literature were normalized to the simulated dose of 1,000 mcg
n number of subjects
aAUC0−5 for simulated data and AUC0−6 for literature data
Table III.
Performance check of FP module of the ICSpkTS R extension package
| Simulated data | Study I—Moellmann et al. (30) | Study II—Harrison et al. (35) | Study III—Mortimer et al. (36) | Study IV—Dalby et al. (37) | |
|---|---|---|---|---|---|
| n | 1,000 | 14 | 12 | 20 | 26 |
| C max (ng/mL) | 0.11 (37.7) | 0.10 (19.8) | 0.07 (−) | 0.06 (58.3) | 0.1 (−) |
| t max (h) | 0.89 (65.4) | 1.36 (44.4) | – | 1.21 (75.2) | 1 (−) |
| AUC0−24 (ng mL−1 h) | 0.56 (31.0) | 0.66 (23.2) | – | – | – |
| AUC0−inf (ng mL−1 h) | 0.63 (32.1) | 0.78 (33.7) | – | – | – |
| AUC0−5/6 a (ng mL−1 h) | 0.31 (32.3) | – | – | 0.20 (57.5) | – |
| AUC0−8 (ng mL−1 h) | 0.36 (33.3) | – | 0.36 (−) | – | – |
| AUC0−10 (ng mL−1 h) | 0.41 (31.7) | – | – | – | 0.75 (42.5) |
| Terminal t 1/2 (h) | 6.77 (30.4) | 8.05 (53.1) | – | – | – |
Comparison of PK metrics (mean (CV%)) from simulated data using the PK trial simulation tool and literature. Only data from healthy subjects were used from literature. AUC and C max data from literature were normalized to the simulated dose of 500 mcg
n number of subjects
aAUC0−5 for simulated data and AUC0−6 for literature data
Table IV.
Performance check of FLU and TA modules of the ICSpkTS R extension package
| FLU—simulated data | FLU—literature data (40–43) | TA—simulated data | TA—literature data (38,39,44) | |
|---|---|---|---|---|
| Mean | Range | Mean | Range | |
| C max (ng/mL) | 1.30 | 0.81–2.39 | 0.18 | 0.12–0.25 |
| t max (h) | 0.33 | 0.09–0.2 | 2.01 | 1.59–3.67 |
| AUC0−inf (ng mL−1 h) | 1.92 | 1.52–4.28 | 0.90 | 0.69–1.92 |
Comparison of PK metrics from simulated data using the PK trial simulation tool (mean) and literature (range of means). AUC0−inf and C max data from literature were normalized to the simulated dose of 250 and 100 mcg for FLU and TA, respectively
DISCUSSION
A freely available tool for simulation of PK trials for ICS has been developed as an extension package to the software R. In its current form, the model allows simulation of plasma concentration time profiles after administration of (1) two different hypothetical ICS and (2) two different formulations of four different ICS (BUD, FLU, FP, and TA) in a parallel study design. Two detailed examples about the functions and outputs of the ICSpkTS package are provided in the Appendix. Briefly, for all five modules (hypothetical ICS, BUD, FLU, FP, and TA), the user can specify certain PK model parameters (typical values, BSV, and WSV) for both drugs (ICS) or both formulations of either BUD, FLU, FP, and TA, the time points at which plasma samples are obtained, and the number of subjects. The ICSpkTS packages then simulates the outcome of a PK trial based upon the specified parameters values and returns 90% confidence intervals for geometric means ratio of the two drugs/formulations for both AUC and Cmax and generates a plot displaying the average plasma concentration time profiles. Optionally, output tables containing, e.g., individual or average plasma concentration can be generated.
In the module for simulation of PK trials for hypothetical ICS, the users can specify all typical value parameters whereas certain typical value parameters (e.g., CL, VC, k12, k21, and ka) are fixed to literature values in the drug-specific modules (BUD, FLU, FP, and TA) (Table I). Since literature estimates for most of the BSV and WSV parameters were either inconsistent or not available (e.g., distribution rate constants) BSV and WSV parameters were set to default values of 20% and 30% (CV), respectively, in all modules. These values represent reasonable estimates for some parameters (e.g., BSV for CL and volume of distribution is commonly between 20% and 30% (31)). The authors are aware that a BSV of 20–30% might not be representative for all model parameters. However, given the scarcity of reliable literature information on BSV and WSV, suggesting certain default values for those model parameters and giving the users the options to adjust them to their beliefs and needs seems appropriate.
Moreover, the module for hypothetical ICS of the ICSpkTS R extension package could be applied for simulation of PK trials of non-ICS by adjusting the model parameters to represent other inhaled drugs.
The PK trial simulation tool is based upon a compartmental model that is able to incorporate relevant physiological aspects of the lung (difference in absorption rate from central and peripheral lung regions and mucociliary removal of particles from central lung regions), physicochemical properties of the drug (dissolution rate and deposition characteristics, such as pulmonary deposition efficiency, central vs. peripheral deposition), and patient factors (reduction of mucociliary clearance rate constant or changes in deposition efficiency, see Hands-on Example 1: ICS). It must be emphasized that while the model can adjust for such factors, the underlying model is neither a physiologically based PK model nor does it directly link the deposition profile of the drug particles in the lung to its physicochemical properties (see below). The purpose of the model is to adequately reflect plasma concentration time profiles of ICS while allowing certain features of inhalation therapy (e.g., C/P ratio and mucociliary removal of undissolved drug particles in the central lung) to be considered. In addition, the variability between and within subjects of all PK parameters is considered. The PK trial simulation tool and the compartment model itself represent an extension of previously published inhalation models by Byron (14), Gonda (45), and Hochhaus et al. (3). Specifically, the models by Byron and Gonda focused rather on the kinetics in the respiratory tract and not in plasma and did not consider variability. The model by Hochhaus et al. did not distinguish between central and peripheral regions of the lung and did not allow for variability between and within subjects.
In the current form of the PK trial simulation tool, the user needs to specify deposition characteristics such as the emitted dose, the pulmonary deposited dose, and the C/P ratio. The authors are aware that particle deposition in the lung could be modeled with higher resolution using analytical equations for particle deposition efficiencies and specific flow conditions or computational fluid and particle dynamics methods (46). However, addition of such tools into the model would be of little benefit, as the purpose of the simulation tool is to model plasma and not regional lung concentration profiles after ICS administration. Since little is known about differences in the pulmonary absorption rates between different regions of the lung (other than some evidence pointing towards faster absorption from peripheral lung regions (9,10), which is already incorporated into the model), higher regional resolution for particle deposition exceeding central and peripheral regions, as generally provided by deposition models (46) would not affect the PK profile as the particles would still dissolve/be absorbed according to the same rate constants.
Nonetheless, users could easily link these particle deposition models (46) with this PK trial simulation tool by translating the outputs of the deposition models into inputs of the simulation tool (i.e., fraction of the emitted dose that is deposited in the lung and the pulmonary fraction that is deposited in central or peripheral regions of the lung). Similarly, model parameters could be adjusted to include specific patient groups if known relationships between disease state and pulmonary deposition characteristics are known (36,47). Furthermore, suitable in vitro deposition models, such as cascade impaction (48) or systems able to assess the dissolution rate of inhalable drug fraction (49) might be used to predict in vivo lung deposition or dissolution behavior. Indeed, we incorporated in vitro dissolution rate constants into the FP model (as the dissolution rate for this but not the other ICS was slow enough to be measured with sufficient accuracy in the in vitro setting (unpublished data). However, it needs to be realized that in vitro/in vivo correlation between CI profiles and regional lung deposition, as well as in silico/in vivo correlations remain generally to be established. A more detailed in vitro-based prediction of particle deposition in the lung would definitely be incorporated in future extensions of the current version of the PK trial simulation tool, once validated models are available.
The module that allows PK trial simulation after administration of hypothetical ICS should be considered as the main tool of this extension package as it allows the users to specify all model parameters based upon their own data, beliefs, and/or needs (see above). Nonetheless, modules for four specific ICS (BUD, FLU, FP, and TA) were included in the simulation tool for convenience. For these modules, a set of default values for the model parameters is provided (Table I). Whereas drug-related PK parameters (i.e., CL, VC, k12, and k21) are fixed to literature values, the users can adjust formulation-related parameters (e.g., lung deposition parameters and dissolution rate constants). This enables the users, first, to explore the effect of different formulations or patient groups on the PK of a specific ICS and, second, to change the default values to values that would be supported by their data if needed. The default values for the typical value parameters of the drug-specific modules are based upon published literature data or unpublished experimental data (Table I) unless that for the C/P ratio and the pulmonary absorption rate constants. Even though literature data on the C/P ratio is available for ICS (23–26,39), differences in the C/P ratio have been described for different formulations of a given drug and for different patient groups (19). Because of the large variability in such estimates, the fact that no validated scintigraphy methods have been agreed on, and the lack of estimates for other ICS, an educated guess of 1 was used for the C/P ratio of healthy volunteers. However, the users can easily adjust these default values (see above). In addition, only general estimates for differences in the absorption rate across pulmonary membranes have been described in the literature (9,10). For glucocorticoids, differences in the absorption rates for central and peripheral sections of the lung have only resulted in semi-quantitative estimates. Again, educated guesses resulted in the choices of 10 and 20 h−1 as pulmonary absorption rate constants for the central and peripheral regions of the lung, respectively. However, the user can change these defaults estimates if the properties of a specific drug require it.
To ensure that the model and the selected model parameters are valid, the predictive performance of the BUD, FLU, FP, and TA modules was checked by comparing simulated PK data and resulting metrics to those of actual studies.
The performances of the BUD and FP modules of the ICSpkTS R extension package were checked by comparing simulated data to PK data from four studies where healthy subjects received BUD and FP delivered via their respective dry powder inhalers (see above). For FP, the simulated plasma concentrations predict the outcomes of the studies I–IV adequately with respect to mean and variability of both the individual plasma concentration profiles (study I, Fig. 3) and the PK metrics (studies I–IV, Table III). The model overestimated somewhat the variability in Cmax compared with that of study I (CV%—37.7 vs. 19.8), while the variability in Cmax for study III was underestimated (58.3 CV%). tmax of the simulated data (0.89 h) is smaller than that of studies I, III, and IV (1–1.32 h). This might indicate that the selected dissolution rate constant (kdiss) of the FP module is slightly too large or that the literature-based compartmental micro-constants (k12 and k21) need adjustment (18). The predicted AUCs are in very good agreement with the range of observed AUCs in the four FP studies (Table 3), also indicating that the mucociliary clearance rate constant (which affects the AUC of slowly dissolving drugs) is reasonable.
For BUD, the overall predictive performance of the simulated data is not quite as good as that of FP but still satisfactory (Table II and Fig. 2). There was, however, a tendency of the simulation to slightly overestimate plasma concentrations of study I (the 90% prediction interval overestimated somewhat the observed plasma concentrations from study I; see Fig. 2). This is also reflected in the increased AUC0–inf of the simulated data compared with that of study I (ratio of simulated vs. observed mean AUC0–inf equals 1.67; Table II). However, this was not an indicator for a poor predictive performance of the BUD module, as a much better agreement between the PK metrics of the simulated data and those of studies II–IV was observed (average ratio of simulated vs. observed mean AUCs equals 1.02; range, 0.75–1.31; Table II). The simulated mean Cmax (1.39 ng/mL) was within the range of observed mean values (0.89–2.26 ng/mL; Table II), although some tendency to lower concentrations and later tmax values (tmax, simulated, 0.65 h (mean) and tmax, observed, 0.21–0.5 h (range of means)) was observed. This difference in tmax might suggest that the dissolution rate constant of the BUD module (kdiss = 17.8 h−1) might be too small.1 For most of the published BUD PK data after inhalation, however, the dissolution/absorption rate is difficult to determine since the peak concentrations occur very early (often at the time point where the first plasma sample was obtained). Similarly, it is almost impossible to correctly estimate dissolution rates in vitro for such fast dissolving drugs.
The predictive performances of both the FLU and TA modules were both satisfactory as the simulated mean AUC0–inf, Cmax, and tmax were in good agreement with those of the published data (Table IV). In particular, the means of simulated PK metrics were within the range of the means of the literature data with exception of tmax of the FLU module.
In summary, the predictive performances of all modules were satisfactory, in particular when considering that model parameters are either based upon different sources of literature data, in vitro data, or educated guesses (see Table I for more details). The slight differences between the predicted and observed Cmax and tmax (see above) is very likely due to the uncertainty that is involved when estimating the pulmonary dissolution rates of the ICS, especially when this process is very fast, such as observed for BUD and FLU. All modules, including those for BUD and FP, explicitly allow the users to adjust the pulmonary dissolution rates as well as other deposition parameters to their own beliefs. Hence, parameters established by the user can be easily incorporated. Furthermore, the general module of this PK trial simulation package, in which the users can change all model parameters, has been provided to allow the highest degree of flexibility. Overall, the drug-specific modules of the ICSpkTS package should be considered as tools for simulating PK trials for specific ICS without having to perform literature research on the input parameters that also allow adjustment of the model parameters if needed.
The ICSpkTS package allows the user to examine the effect of certain physiological, formulation, and patient-related factors on the systemic PKs of ICS while incorporating variability between and within subjects. For instance, the PK trial simulation tool could be used to compare two identical formulations in different patient populations by altering the model parameters that are related to lung anatomy and physiology (i.e., C/P ratio and the mucociliary clearance rate constant). Furthermore, the PK trial simulation tool could be applied to compare the PK behavior of two different formulations of the same ICS that differ in their dissolution rates and/or aerodynamic particle size distribution (central-to-peripheral airways) and to explore the effect of these differences on the AUC and Cmax. In the Appendix, these two possible applications of the ICSpkTS package are used as hands-on examples to explain how to use the different modules of the PK trial simulation tool.
Introductory videos showing how to download and install R, how to install the ICSpkTS R extension package, and how to operate the ICSpkTS package can be downloaded viahttp://www.cop.ufl.edu/pc/research/areas-of-research/inhaled-glucocorticoids/icspkts-r-extension/.
The ICSpkTS could be further extended to allow for simulation of more complicated study designs (e.g., cross-over designs) or could be used as a basis for a PK/pharmacodynamics (PD) model by linking the plasma concentrations to the suppression of the endogenous cortisol release (50). Moreover, Eqs. 12 and 13 could be used for predicting the pulmonary drug concentrations after ICS administration that could then be linked to a PD model of a pulmonary biomarker. Such a pulmonary PKPD model could be useful for evaluating the effect of different ICS or different formulations of the same ICS on their pulmonary efficacy.
CONCLUSIONS
A freely available tool for PK clinical trial simulation after ICS administration was provided as an extension package (ICSpkTS) to the software R based upon a compartment model that describes the fate of an ICS after inhalation. In its current form, the ICSpkTS package is a valuable tool for exploring the effect of changes in model parameters, which could represent physiological, formulation, and patient-related factors on PK behavior of ICS while taking variability between and within subjects into account.
ACKNOWLEDGMENTS
We would like to thank Saskia Fuhrmann, Uta Schilling, and especially Bhargava Kandala, for all their assistance with this project.
Appendix
Laplace transformation (17) of Eqs. 1–7 and rearrangements yields
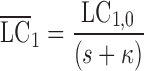 |
10 |
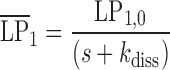 |
11 |
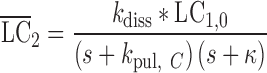 |
12 |
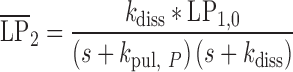 |
13 |
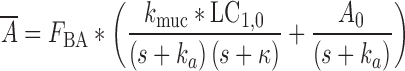 |
14 |
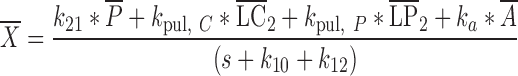 |
15 |
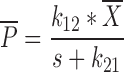 |
16 |
where s represents the Laplace operator, FBA was defined above, and LC1,0, LP1,0, and A0 denote the initial amount of drug in the dissolution compartments of the central and peripheral lung, and the GI absorption compartment, respectively. Particularly,
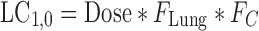 |
17 |
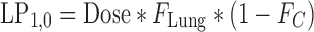 |
18 |
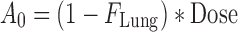 |
19 |
where Dose is the by-the-inhaler-emitted dose, FLung is the fraction of the emitted dose that is deposited in the lung, and FC is the fraction of the lung dose that is deposited in central lung regions. Substitution of Eq. 10–14 and Eq. 16 into Eq. 15 and defining α * β = k10 * k21 and α + β = k10 + k12 + k21 yields
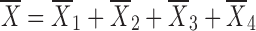 |
20 |
where
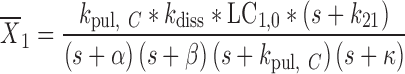 |
21 |
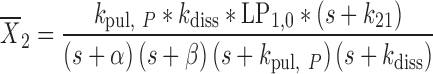 |
22 |
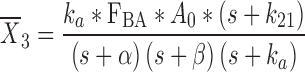 |
23 |
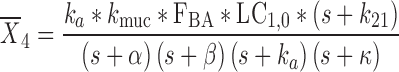 |
24 |
Anti Laplace transformation (17) of Eq. 20 yields
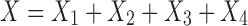 |
25 |
where
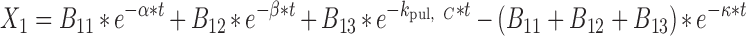 |
26 |
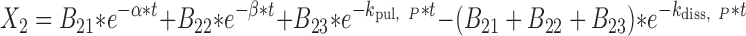 |
27 |
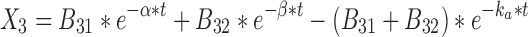 |
28 |
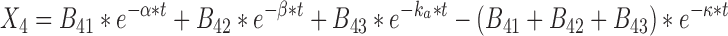 |
29 |
and
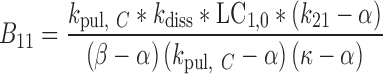 |
30 |
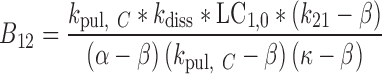 |
31 |
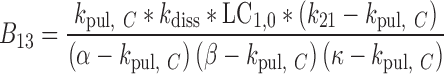 |
32 |
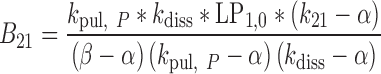 |
33 |
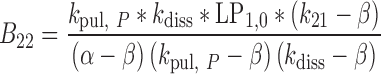 |
34 |
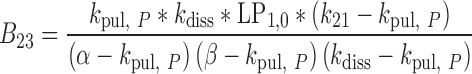 |
35 |
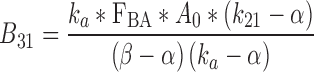 |
36 |
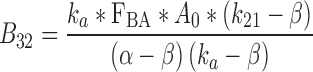 |
37 |
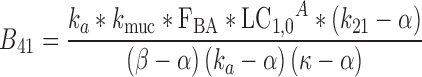 |
38 |
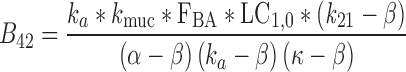 |
39 |
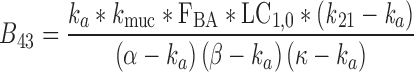 |
40 |
ICSpkTS R EXTENSION PACKAGE—HANDS-ON EXAMPLES
The structure and functions of the ICSpkTS extension package are briefly explained in form of two hands-on examples. In the first example, the ICS module of the ICSpkTS package is introduced by a case study comparing the AUC and Cmax in healthy subjects and asthmatic patients. In the second example, the effect of having two FP formulations that differ in their pulmonary dissolution rate constant on the PK behavior is used to explain the FP module. Further details and functions of the ICSpkTS package can be found in the official documentation (available via http://www.cop.ufl.edu/pc/research/areas-of-research/inhaled-glucocorticoids/icspkts-r-extension/) and/or by accessing the official R help files.
HANDS-ON EXAMPLE 1: ICS
Running the following code in R will simulate a PK trial when 500 mcg of an hypothetical ICS are administered to 25 subjects per treatment group (healthy subjects (situation A) vs. asthmatic patients (situation B)) and plasma samples are obtained at 0.17, 0.33, 0.5, 1, 1.5, 2, 3, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, and 24 h after administration. The asthmatic patients are modeled by increasing the fraction of drug that is deposited in the central regions of the lung and by lowering the mucociliary clearance rate constant.
#####################################################
#Number of Subjects (n) per Group
#####################################################
n.subjects = 25
#####################################################
#Time points (h) where plasma samples are obtained
#####################################################
Time = c(0.17,0.33,0.5,1,1.5,2,3,4,6,8,10,12,14,16,18,20,22,24)
#####################################################
#Situation A-Model Parameters-Typical Values (TV) and
#Between-Subject Variability (BSV)
#####################################################
Dose.A = 500
TV.FLung.A = 0.2
TV.FC.A = 0.5
TV.FBA.A = 0.1
TV.kdiss.A = 0.3
TV.kmuc.A = 0.5
TV.kpulC.A = 0.4
TV.kpulP.A = 0.4
TV.ka.A = 0.65
TV.CL.A = 49
TV.VC.A = 87
TV.k12.A = 0.1
TV.k21.A = 0.05
BSV.FLung.A = 0.2
BSV.FC.A = 0.2
BSV.FBA.A = 0.2
BSV.kdiss.A = 0.2
BSV.kmuc.A = 0.2
BSV.kpulC.A = 0.2
BSV.kpulP.A = 0.2
BSV.ka.A = 0.2
BSV.CL.A = 0.2
BSV.VC.A = 0.2
BSV.k12.A = 0.2
BSV.k21.A = 0.2
#####################################################
#Situation B-Model Parameters-Typical Values (TV) and
#Between-Subject Variability (BSV)
#####################################################
Dose.B = 500
TV.FLung.B = 0.2
TV.FC.B = 0.8
TV.FBA.B = 0.1
TV.kdiss.B = 0.3
TV.kmuc.B = 0.25
TV.kpulC.B = 0.4
TV.kpulP.B = 0.4
TV.ka.B = 0.65
TV.CL.B = 49
TV.VC.B = 87
TV.k12.B = 0.1
TV.k21.B = 0.05
BSV.FLung.B = 0.2
BSV.FC.B = 0.2
BSV.FBA.B = 0.2
BSV.kdiss.B = 0.2
BSV.kmuc.B = 0.2
BSV.kpulC.B = 0.2
BSV.kpulP.B = 0.2
BSV.ka.B = 0.2
BSV.CL.B = 0.2
BSV.VC.B = 0.2
BSV.k12.B = 0.2
BSV.k21.B = 0.2
#####################################################
#Within Subject Variability (WSV)
#####################################################
WSV = 0.3
#####################################################
#PK Trial Simulation
#####################################################
ICS(plots = FALSE,tables = FALSE)
The following output displaying the AUC and Cmax for both healthy subjects and asthmatic patients and 90% confidence intervals of the geometric means ratios (healthy/asthmatic) for both AUC and Cmax is generated by the ICSpkTS package.
Simulation was successful
AUC-Means (Arithmetic Means):
Situation A-Situation B
[1] 2.23 1.96
Cmax-Means (Arithmetic Means):
Situation A-Situation B
[1] 0.43 0.34
AUC-90% Confidence Interval (Geometric Mean Ratio):
[1] 0.99 1.28
Cmax-90% Confidence Interval (Geometric Mean Ratio):
[1] 1.04 1.39
Furthermore, a graph showing the average plasma concentration time profiles for both healthy subjects and asthmatic patients is created (Fig. 4).
Fig. 4.
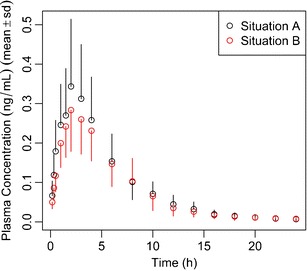
Hands-on example 1, ICS module, simulation of a PK trial after administration of 500 mcg of a hypothetical ICS to 25 subjects per treatment group (healthy subjects (situation A) vs. asthmatic patients (situation B)), and plasma samples are obtained at 0.17, 0.33, 0.5, 1, 1.5, 2, 3, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, and 24 h after administration. Asthmatic patients are modeled by increasing the fraction of drug that is deposited in the central regions of the lung and by lowering the mucociliary clearance rate constant
HANDS-ON EXAMPLE 2: FP
Running the following code in R will simulate a PK trial when 500 mcg FP are administered to 35 subjects per formulation group (formulation A and B differ in their dissolution rate constants, B dissolves 3-fold faster) and plasma samples are obtained at 0.17, 0.33, 0.5, 1, 1.5, 2, 3, 4, 6, 8, 10, 12, 16, 20, and 24 h after administration.
#####################################################
#Number of Subjects (n) per Group
#####################################################
n.subjects = 35
#####################################################
#Time points (h) where plasma samples are obtained
#####################################################
Time = c(0.17,0.33,0.5,1,1.5,2,3,4,6,8,10,12,16,20,24)
#####################################################
#Formulation A-Model Parameters-Typical Values (TV) # and Between-Subject Variability (BSV)
#####################################################
Dose.A = 500
TV.FLung.A = 0.16
TV.FC.A = 0.5
TV.kdiss.A = 0.302
TV.kmuc.A = 0.938
TV.kpulC.A = 10
TV.kpulP.A = 20
BSV.FLung.A = 0.2
BSV.FC.A = 0.2
BSV.kdiss.A = 0.2
BSV.kmuc.A = 0.2
BSV.kpulC.A = 0.2
BSV.kpulP.A = 0.2
BSV.CL.A = 0.2
BSV.VC.A = 0.2
BSV.k12.A = 0.2
BSV.k21.A = 0.2
#####################################################
#Formulation B-Model Parameters-Typical Values (TV) and
#Between-Subject Variability (BSV)
#####################################################
Dose.B = 500
TV.FLung.B = 0.16
TV.FC.B = 0.5
TV.kdiss.B = 0.9
TV.kmuc.B = 0.938
TV.kpulC.B = 10
TV.kpulP.B = 20
BSV.FLung.B = 0.2
BSV.FC.B = 0.2
BSV.kdiss.B = 0.2
BSV.kmuc.B = 0.2
BSV.kpulC.B = 0.2
BSV.kpulP.B = 0.2
BSV.CL.B = 0.2
BSV.VC.B = 0.2
BSV.k12.B = 0.2
BSV.k21.B = 0.2
#####################################################
#Within-Subject Variability (WSV)
#####################################################
WSV = 0.3
#####################################################
#PK Trial Simulation
#####################################################
FP(plots = FALSE,tables = FALSE)
The following output displaying the AUC and Cmax for both formulations and 90% confidence intervals of the geometric means ratios (A/B) for both AUC and Cmax is generated by the ICSpkTS package.
Simulation was successful
AUC-Means (Arithmetic Means):
Formulation A-Formulation B
[1] 0.71 0.73
Cmax-Means (Arithmetic Means):
Formulation A-Formulation B
[1] 0.20 0.38
AUC-90% Confidence Interval (Geometric Mean Ratio):
[1] 0.85 1.09
Cmax-90% Confidence Interval (Geometric Mean Ratio):
[1] 0.45 0.60
Moreover, a graph showing the average plasma concentration time profiles for both formulations is generated (Fig. 5).
Fig. 5.
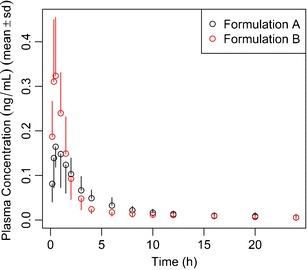
Hands-on example 2, FP module, simulation of a PK trial when 500 mcg FP are administered to 35 subjects per formulation group (formulations A and B differ in their dissolution rate constants; B dissolves 3-fold faster), and plasma samples are obtained at 0.17, 0.33, 0.5, 1, 1.5, 2, 3, 4, 6, 8, 10, 12, 16, 20, and 24 h after administration
Footnotes
Other reasons such as variability in systemic distribution micro-constants (k12 and k21) across studies cannot be excluded.
REFERENCES
- 1.Global Initiative for Asthma. Global strategy for asthma management and prevention. http://www.ginasthma.org/uploads/users/files/GINA_Report_2011.pdf. Accessed 12 June 2012.
- 2.Global Initiative for Chronic Obstructive Lung Disease. Global strategy for the diagnosis, management, and prevention of chronic obstructive pulmonary disease. http://www.goldcopd.org/uploads/users/files/GOLD_Report_2011_Jan21.pdf. Accessed 12 June 2012. [DOI] [PubMed]
- 3.Hochhaus G, Mollmann H, Derendorf H, Gonzalez-Rothi RJ. Pharmacokinetic/pharmacodynamic aspects of aerosol therapy using glucocorticoids as a model. J Clin Pharmacol. 1997;37:881–892. doi: 10.1002/j.1552-4604.1997.tb04262.x. [DOI] [PubMed] [Google Scholar]
- 4.Hochhaus G. New developments in corticosteroids. Proc Am Thorac Soc. 2004;1:269–274. doi: 10.1513/pats.200402-007MS. [DOI] [PubMed] [Google Scholar]
- 5.Brutsche MH, Brutsche IC, Munawar M, Langley SJ, Masterson CM, Daley-Yates PT, et al. Comparison of pharmacokinetics and systemic effects of inhaled fluticasone propionate in patients with asthma and healthy volunteers: a randomised crossover study. Lancet. 2000;356:556–561. doi: 10.1016/S0140-6736(00)02581-2. [DOI] [PubMed] [Google Scholar]
- 6.Singh SD, Whale C, Houghton N, Daley-Yates P, Kirby SM, Woodcock AA. Pharmacokinetics and systemic effects of inhaled fluticasone propionate in chronic obstructive pulmonary disease. Br J Clin Pharmacol. 2003;55:375–381. doi: 10.1046/j.1365-2125.2003.01758.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Harrison LI, Novak CC, Needham MJ, Ratner P. Comparative pulmonary function and pharmacokinetics of fluticasone propionate and salmeterol xinafoate delivered by two dry powder inhalers to patients with asthma. J Aerosol Med Pulm Drug Deliv. 2011;24:245–252. doi: 10.1089/jamp.2011.0884. [DOI] [PubMed] [Google Scholar]
- 8.Holford NH, Kimko HC, Monteleone JP, Peck CC. Simulation of clinical trials. Annu Rev Pharmacol Toxicol. 2000;40:209–234. doi: 10.1146/annurev.pharmtox.40.1.209. [DOI] [PubMed] [Google Scholar]
- 9.Brown RA, Jr, Schanker LS. Absorption of aerosolized drugs from the rat lung. Drug Metab Dispos. 1983;11:355–360. [PubMed] [Google Scholar]
- 10.Schanker LS, Mitchell EW, Brown RA., Jr Species comparison of drug absorption from the lung after aerosol inhalation or intratracheal injection. Drug Metab Dispos. 1986;14:79–88. [PubMed] [Google Scholar]
- 11.Edsbacker S, Wollmer P, Selroos O, Borgstrom L, Olsson B, Ingelf J. Do airway clearance mechanisms influence the local and systemic effects of inhaled corticosteroids? Pulm Pharmacol Ther. 2008;21:247–258. doi: 10.1016/j.pupt.2007.08.005. [DOI] [PubMed] [Google Scholar]
- 12.R Development Core Team. R: A language and environment for statistical computing. http://www.r-project.org/. Accessed 12 June 2012.
- 13.Wu K, Blomgren AL, Ekholm K, Weber B, Edsbaecker S, Hochhaus G. Budesonide and ciclesonide: effect of tissue binding on pulmonary receptor binding. Drug Metab Dispos. 2009;37:1421–1426. doi: 10.1124/dmd.108.026039. [DOI] [PubMed] [Google Scholar]
- 14.Byron PR. Prediction of drug residence times in regions of the human respiratory tract following aerosol inhalation. J Pharm Sci. 1986;75:433–438. doi: 10.1002/jps.2600750502. [DOI] [PubMed] [Google Scholar]
- 15.Lee SL, Adams WP, Li BV, Conner DP, Chowdhury BA, Yu LX. In vitro considerations to support bioequivalence of locally acting drugs in dry powder inhalers for lung diseases. AAPS J. 2009;11:414–423. doi: 10.1208/s12248-009-9121-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.O’Riordan TG, Zwang J, Smaldone GC. Mucociliary clearance in adult asthma. Am Rev Respir Dis. 1992;146:598–603. doi: 10.1164/ajrccm/146.3.598. [DOI] [PubMed] [Google Scholar]
- 17.Gibaldi M, Perrier D. Pharmacokinetics. 2. New York: Informa Healthcare; 1982. pp. 419–424. [Google Scholar]
- 18.Krishnaswami S, Hochhaus G, Derendorf H. An interactive algorithm for the assessment of cumulative cortisol suppression during inhaled corticosteroid therapy. AAPS PharmSci. 2000;2:28–37. doi: 10.1208/ps020322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Clark AR. Understanding penetration index measurements and regional lung targeting. J Aerosol Med Pulm Drug Deliv. 2012;25:179–187. doi: 10.1089/jamp.2011.0899. [DOI] [PubMed] [Google Scholar]
- 20.Moellmann HW, Hochhaus G, Tromm A, Froehlich P, Moellmann AC, Krieg M, et al. Pharmcokinetics and pharmacodynamics of budesonide pH-modified release capsules. In: Moellmann HW, May B, et al., editors. Glucocortocoid therapy in chronic inflammatory bowel disease. Norwell: Kluwer; 1996. pp. 107–120. [Google Scholar]
- 21.Derendorf H, Hochhaus G, Rohatagi S, Mollmann H, Barth J, Sourgens H, et al. Pharmacokinetics of triamcinolone acetonide after intravenous, oral, and inhaled administration. J Clin Pharmacol. 1995;35:302–305. doi: 10.1002/j.1552-4604.1995.tb04064.x. [DOI] [PubMed] [Google Scholar]
- 22.Rohatagi S, Hochhaus G, Mollmann H, Barth J, Galia E, Erdmann M, et al. Pharmacokinetic and pharmacodynamic evaluation of triamcinolone acetonide after intravenous, oral, and inhaled administration. J Clin Pharmacol. 1995;35:1187–1193. doi: 10.1002/j.1552-4604.1995.tb04045.x. [DOI] [PubMed] [Google Scholar]
- 23.Borgstrom L. Deposition patterns with Turbuhaler. J Aerosol Med. 1994;7:S49–S53. doi: 10.1089/jam.1994.7.Suppl_1.S-49. [DOI] [PubMed] [Google Scholar]
- 24.Borgstrom L, Bondesson E, Moren F, Trofast E, Newman SP. Lung deposition of budesonide inhaled via Turbuhaler: a comparison with terbutaline sulphate in normal subjects. Eur Respir J. 1994;7:69–73. doi: 10.1183/09031936.94.07010069. [DOI] [PubMed] [Google Scholar]
- 25.Pitcairn G, Reader S, Pavia D, Newman S. Deposition of corticosteroid aerosol in the human lung by Respimat Soft Mist inhaler compared to deposition by metered dose inhaler or by Turbuhaler dry powder inhaler. J Aerosol Med. 2005;18:264–272. doi: 10.1089/jam.2005.18.264. [DOI] [PubMed] [Google Scholar]
- 26.Wildhaber JH, Devadason SG, Wilson JM, Roller C, Lagana T, Borgstrom L, et al. Lung deposition of budesonide from turbuhaler in asthmatic children. Eur J Pediatr. 1998;157:1017–1022. doi: 10.1007/s004310050990. [DOI] [PubMed] [Google Scholar]
- 27.Ryrfeldt A, Andersson P, Edsbäcker S, Tönnesson M, Davies D, Pauwels R. Pharmacokinetics and metabolism of budesonide, a selective glucocorticoid. Eur J Respir Dis Suppl. 1982;122:86–95. [PubMed] [Google Scholar]
- 28.Thorsson L, Edsbacker S, Conradson TB. Lung deposition of budesonide from Turbuhaler is twice that from a pressurized metered-dose inhaler P-MDI. Eur Respir J. 1994;7:1839–1844. doi: 10.1183/09031936.94.07101839. [DOI] [PubMed] [Google Scholar]
- 29.Kallen A, Thorsson L. Drug disposition analysis: a comparison between budesonide and fluticasone. J Pharmacokinet Pharmacodyn. 2003;30:239–256. doi: 10.1023/A:1026123317752. [DOI] [PubMed] [Google Scholar]
- 30.Mollmann H, Wagner M, Krishnaswami S, Dimova H, Tang Y, Falcoz C, et al. Single-dose and steady-state pharmacokinetic and pharmacodynamic evaluation of therapeutically clinically equivalent doses of inhaled fluticasone propionate and budesonide, given as Diskus or Turbohaler dry-powder inhalers to healthy subjects. J Clin Pharmacol. 2001;41:1329–1338. doi: 10.1177/00912700122012913. [DOI] [PubMed] [Google Scholar]
- 31.Thorsson L, Edsbacker S, Kallen A, Lofdahl CG. Pharmacokinetics and systemic activity of fluticasone via Diskus and pMDI, and of budesonide via Turbuhaler. Br J Clin Pharmacol. 2001;52:529–538. doi: 10.1046/j.0306-5251.2001.01493.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mackie AE, Ventresca GP, Fuller RW, Bye A. Pharmacokinetics of intravenous fluticasone propionate in healthy subjects. Br J Clin Pharmacol. 1996;41:539–542. doi: 10.1046/j.1365-2125.1996.36110.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Krishnaswami S, Hochhaus G, Mollmann H, Barth J, Derendorf H. Interpretation of absorption rate data for inhaled fluticasone propionate obtained in compartmental pharmacokinetic modeling. Int J Clin Pharmacol Ther. 2005;43:117–122. doi: 10.5414/cpp43117. [DOI] [PubMed] [Google Scholar]
- 34.Berridge MS, Lee Z, Heald DL. Pulmonary distribution and kinetics of inhaled [11C]triamcinolone acetonide. J Nucl Med. 2000;41:1603–1611. [PubMed] [Google Scholar]
- 35.Harrison TW, Tattersfield AE. Plasma concentrations of fluticasone propionate and budesonide following inhalation from dry powder inhalers by healthy and asthmatic subjects. Thorax. 2003;58:258–260. doi: 10.1136/thorax.58.3.258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mortimer KJ, Tattersfield AE, Tang Y, Wu K, Lewis S, Hochhaus G, et al. Plasma concentrations of fluticasone propionate and budesonide following inhalation: effect of induced bronchoconstriction. Br J Clin Pharmacol. 2007;64:439–444. doi: 10.1111/j.1365-2125.2007.02856.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dalby C, Polanowski T, Larsson T, Borgstrom L, Edsbacker S, Harrison TW. The bioavailability and airway clearance of the steroid component of budesonide/formoterol and salmeterol/fluticasone after inhaled administration in patients with COPD and healthy subjects: a randomized controlled trial. Respir Res. 2009;10:104. doi: 10.1186/1465-9921-10-104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Argenti D, Shah B, Heald D. A study comparing the clinical pharmacokinetics, pharmacodynamics, and tolerability of triamcinolone acetonide HFA-134a metered-dose inhaler and budesonide dry-powder inhaler following inhalation administration. J Clin Pharmacol. 2000;40:516–526. doi: 10.1177/00912700022009134. [DOI] [PubMed] [Google Scholar]
- 39.Hirst PH, Pitcairn GR, Richards JC, Rohatagi S, Gillen MS, Newman SP. Deposition and pharmacokinetics of an HFA formulation of triamcinolone acetonide delivered by pressurized metered dose inhaler. J Aerosol Med. 2001;14:155–165. doi: 10.1089/08942680152484090. [DOI] [PubMed] [Google Scholar]
- 40.Mollmann H, Derendorf H, Barth J, Meibohm B, Wagner M, Krieg M, et al. Pharmacokinetic/pharmacodynamic evaluation of systemic effects of flunisolide after inhalation. J Clin Pharmacol. 1997;37:893–903. doi: 10.1002/j.1552-4604.1997.tb04263.x. [DOI] [PubMed] [Google Scholar]
- 41.Nolting A, Sista S, Abramowitz W. Flunisolide HFA vs flunisolide CFC: pharmacokinetic comparison in healthy volunteers. Biopharm Drug Dispos. 2001;22:373–382. doi: 10.1002/bdd.274. [DOI] [PubMed] [Google Scholar]
- 42.Nolting A, Sista S, Abramowitz W. Single-dose study to compare the pharmacokinetics of HFA flunisolide and CFC flunisolide. J Pharm Sci. 2002;91:424–432. doi: 10.1002/jps.10030. [DOI] [PubMed] [Google Scholar]
- 43.Richards J, Hirst P, Pitcairn G, Mahashabde S, Abramowitz W, Nolting A, et al. Deposition and pharmacokinetics of flunisolide delivered from pressurized inhalers containing non-CFC and CFC propellants. J Aerosol Med. 2001;14:197–208. doi: 10.1089/08942680152484126. [DOI] [PubMed] [Google Scholar]
- 44.Zaborny BA, Lukacsko P, Barinov-Colligon I, Ziemniak JA. Inhaled corticosteroids in asthma: a dose-proportionality study with triamcinolone acetonide aerosol. J Clin Pharmacol. 1992;32:463–469. doi: 10.1002/j.1552-4604.1992.tb03863.x. [DOI] [PubMed] [Google Scholar]
- 45.Gonda I. Drugs administered directly into the respiratory tract: modeling of the duration of effective drug levels. J Pharm Sci. 1988;77:340–346. doi: 10.1002/jps.2600770413. [DOI] [PubMed] [Google Scholar]
- 46.Hofmann W. Modelling inhaled particle deposition in the human lung—a review. J Aerosol Sci. 2011;42:693–724. doi: 10.1016/j.jaerosci.2011.05.007. [DOI] [Google Scholar]
- 47.Mortimer KJ, Harrison TW, Tang Y, Wu K, Lewis S, Sahasranaman S, et al. Plasma concentrations of inhaled corticosteroids in relation to airflow obstruction in asthma. J Clin Pharmacol. 2006;62:412–419. doi: 10.1111/j.1365-2125.2006.02712.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Byron PR, Hindle M, Lange CF, Longest PW, McRobbie D, Oldham MJ, et al. In vivo–in vitro correlations: predicting pulmonary drug deposition from pharmaceutical aerosols. J Aerosol Med Pulm Drug Deliv. 2010;23(Suppl 2):S59–S69. doi: 10.1089/jamp.2010.0846. [DOI] [PubMed] [Google Scholar]
- 49.Son Y-J, Horng M, Copley M, McConville JT. Optimization of an in vitro dissolution test method for inhalation formulations. Dissolution Technologies. 2010;1–8:6–13. [Google Scholar]
- 50.Rohatagi S, Bye A, Mackie AE, Derendorf H. Mathematical modeling of cortisol circadian rhythm and cortisol suppression. Eur J Pharm Sci. 1996;4:341–350. doi: 10.1016/S0928-0987(96)00174-1. [DOI] [Google Scholar]


