ANALYSIS AND CLASS VALIDATION OF A MEASURE OF PARENTAL VALUES PERCEIVED BY EARLY ADOLESCENTS: AN APPLICATION OF A LATENT CLASS MODEL FOR RANKINGS

Abstract

A Parental Values scale, in which students ranked the top 5 of 10 items in terms of how important they perceived the items as being to their parents, was analyzed using a latent class ranking model. A model with three latent classes was considered adequate, based on the Bayesian information criterion and the interpretability of the results. The three classes were interpreted as consisting of students who perceive their parents as valuing personal happiness, those who perceive their parents as valuing concern for others, and those who perceive their parents as valuing academics and attending a good college. Some evidence as to the validity of the latent classes was obtained by comparing scores on a Parental Expectations scale; the scores were higher for the academic latent class as compared to the other two classes. The analysis suggests which items might be useful in a revised version of the scale.

Adjustment difficulties increasingly documented among relatively affluent suburban youth have been viewed as stemming partly from high pressures to achieve. To examine the degree to which youngsters perceive such pressures, a 10-item instrument was developed as part of an ongoing research program involving adaptation among suburban youth (Luthar & Becker, 1999; Luthar & D’Avanzo, 1999). The instrument was designed to ascertain the degree to which the adolescents viewed their parents as valuing their accomplishments (5 items), such as academic achievement, versus personal and social adaptation (5 items), such as being honest and kind to others. Adolescents were asked to select and rank the top-5 items that they thought were most important to their parents. Thus, the data consist of incomplete rankings in that only 5 of the 10 items were ranked.

The approach via rankings overcomes some difficulties that arise with ratings (e.g., Likert-type scales). For example, in an earlier pilot study (of a scale with more items), adolescents were asked to rate each item from 1 to 5, indicating the degree to which they perceived their parents as valuing each item (with 1 = not, 2 = little, 3 = somewhat, 4 = very, and 5 = extremely). Many individuals tended to rate all the items highly (e.g., using only 4 or 5), which in hindsight is not surprising, considering that the values being rated were all desirable. In this case, requiring the adolescents to rank the items might be more informative, with the patterns of rankings providing a more detailed picture of their perceptions. Other advantages of rankings over ratings, such as allowing one to avoid arbitrary decisions as to the number and labels of response categories, have been noted by Böckenholt (1996) and Linacre (1989).

To analyze the Parental Values scale, we use a choice model for ranking data. The parameters of the model can be interpreted as indicating how the adolescents perceive their parents as valuing the items. The simple ranking model is somewhat limited, however, in that it treats the participants as being a homogeneous group in the sense that the adolescents are all seen as perceiving their parents’ values in the same way. It seems more likely that there will be heterogeneity among the participants; indeed, a basic reason for developing the scale was to detect different latent groups (achievement versus personal) and, subsequently, to determine if group membership is related to aspects of students’ psychosocial adjustment. A latent class version of the ranking model recognizes heterogeneity in that it allows for two or more subgroups, with adolescents in the same subgroup perceiving their parents as having the same value structure and adolescents in different subgroups perceiving their parents as having a different value structure. To obtain evidence as to the validity of the latent classes, we compare, across the classes, scores on a Parental Expectations scale that was also completed by the adolescents.

Ranking Models

Descriptive and model-based approaches to ranking data are reviewed by Marden (1995); Critchlow, Fligner, and Verducci (1991) review many ranking models discussed in psychology; chapters in Fligner and Verducci (1993) discuss extensions and applications; and Critchlow (1985) discusses partial rankings. The model used here is referred to as the Plackett-Luce model by Marden (1995), and the latent class version is discussed by Croon and Luijkx (1993; also see Croon, 1989). The model accounts for the probability of any ordering with parameters that can be interpreted as indicating the value adolescents perceive their parents would associate with each item. The model is based on a simple, psychologically plausible view of the ranking process and has the advantages of being easy to apply to partial rankings and being readily extended to include latent classes.

For the Parental Values scale, participants rank the top 5 of 10 items, so the data consist of incomplete rankings (i.e., only rankings for the top-5 items are obtained). The ranks for the remaining items can be viewed as being censored in that it is only known that they are ranked less than 5. Another way to view the data is in terms of orderings, in which the ordering indicates which item was ranked first, which item was ranked second, and so on. If the items are arbitrarily labeled from 1 to n, and if m out of n of the items are ranked, with m ≤ n – 1 (the rankings are complete if m = n – 1 and incomplete if m < n – 1), then an ordering of the items can be written as (i, j, k, . . . l), where i gives the number of the item ranked as 1, j the number of the item ranked as 2, with i ≠ j, and so on. For example, if the top 5 out of 10 items are ranked, then (3, 9, 1, 6, 4) would indicate that Item 3 is ranked 1, Item 9 is ranked 2, and so on. Note that the variables are rankings, and the levels of the variables are the item numbers.

Probability models for the orderings follow from models of the ranking process. One approach views the ranking process as being sequential. The basic idea is that the item ranked as 1 is first chosen from the set of n items, followed by the object ranked as 2, which is chosen from the remaining n – 1 items, followed by the item ranked as 3, which is chosen from the remaining n – 2 items, and so on. This is a simple view of the ranking process that, in our view, is plausible for early adolescents, whereas some other approaches to rankings, although potentially useful, seem too cognitively demanding to expect of early adolescents. For example, another model considered in the latent class context, the Pendergrass-Bradley (PB) model (see Croon & Luijkx, 1993), arises from the view that the ranking process consists of all possible paired comparisons of the items, which would involve 45 paired comparisons for the 10 items used here (the all-pairwise-comparisons view of the ranking process is more generally known as the Babington-Smith model, of which PB is a special case for ranking three out of n [see Marden, 1995]); Croon and Luijkx (1993) noted that, for their example, the PB model gave results similar to the Bradley-Terry-Luce model (BTL) (Bradley & Terry, 1952; Luce, 1959).

Given a sequential view of the ranking process and assuming that successive choices are made independently, the probability of any ordering can be written as the product of conditional probabilities. For example, if the top-three choices are ranked, then the probability of the ordering (i, j, k) can be written as

$$p(i,j,k)=p(i)p(j\mid i)p(k\mid ij),$$

where p(i) is the probability of ranking item i first, with the choice being made from the set of n items; p(j|i) is the probability of ranking item j second given that object i was ranked first, with i ≠ j and the choice being made from the remaining n – 1 items; and p(k|i, j) is the probability of ranking item k third, given i and j (note that p(k|i, j) = p(k|j, i)).

The above probabilities can in turn be written in terms of a choice model, such as the BTL model noted above. The BTL model assigns a positive number to each item so that the probability of choosing the ith item out of a set of n items can be written as

$$p(i)=\frac{exp(a_i)}{{\sum }_{j}exp(a_j)},$$

where exp is the exponential function and exp(a_i) are positive values assigned to each item, namely, their utilities, and so the model is sometimes referred to as a strict utility model. For identification purposes, a constraint on the a_i, such as Σa_i = 0, is necessary. Using the BTL model for the conditional probabilities shown above, and assuming that the parameters are the same across the stages, the probability of any ordering can then be written in terms of the model parameters. For example, if the top three out of n items are ranked, then the probability of any ordering is

$$p(i,j,k)=\frac{exp(a_i)}{{\sum }_{S}exp(a_s)}\times \frac{exp(a_j)}{{\sum }_{R}exp(a_r)}\times \frac{exp(a_k)}{{\sum }_{Q}exp(a_q)},$$

where S is the original set of n objects, R is the subset of n – 1 objects remaining after the first choice, and Q is the subset of n – 2 objects remaining after the first and second choices. As an example, if the top three of five items are ranked, then the probability of the ordering (3, 5, 1) can be written as

$$p(3,5,1)=\frac{exp(a_3)}{exp(a_1)+exp(a_2)+exp(a_3)+exp(a_4)+exp(a_5)}\times \frac{exp(a_5)}{exp(a_1)+exp(a_2)+exp(a_4)+exp(a_5)}\times \frac{exp(a_1)}{exp(a_1)+exp(a_2)+exp(a_4)}.$$

The three terms are for the three independent successive choices, with the BTL model giving the probability of choosing an item from the current subset, as reflected by the changes in the denominator. The model can be fit using software for log-linear models that allows one to specify structural zeros, which are cells of the multiway table that are necessarily empty (see Agresti, 1990); structural zeros arise in ranking models because orderings in which the same object appears more than once, such as (3, 3, 1), cannot occur.

Latent class models

The latent class version of the model allows the parameters (the a_i) to differ across the latent classes; Croon and Luijkx (1993) present, for ranking models, details for the general case; general aspects of latent class analysis are discussed by McCutcheon (1987) and Dayton (1998). For the case of ranking three out of n items, the latent class version of the model can be written as

$$p_c(i,j,k)=\frac{exp(a_{ic})}{{\sum }_{S}exp(a_{sc})}\times \frac{exp(a_{jc})}{{\sum }_{R}exp(a_{rc})}\times \frac{exp(a_{kc})}{{\sum }_{Q}exp(a_{qc})},$$ (1)

where p_c(i, j, k) is the probability of the ordering (i, j, k) for latent class c, exp(a_ic) is the utility of the ith item ranked first for the cth latent class, exp(a_jc) is the utility of the jth item ranked second for the cth latent class, exp(a_kc) is the utility of the kth item ranked third for the cth latent class, and the usual sum to zero constraints apply. In the present application, the latent classes represent homogeneous subgroups of adolescents who perceive their parents’ values in the same way.

With the assumption that the nonempty latent classes are mutually exclusive and exhaustive, the probability of the ordering (i, j, k) is simply the sum across the C latent classes of p_c(i, j, k) times the class size,

$$p(i,j,k)=\sum _{c=1}^{C}p(c)p_c(i,j,k),$$ (2)

where p(c) is the size of latent class c with Σ_c p(c) = 1. Using Equation 1 for p_c(i, j, k) in Equation 2 completes the model. The model can be fit using software that allows one to specify latent class log-linear models with structural zeros, such as LEM (Vermunt, 1997). The latent class ranking model is used here to explore the structure of the adolescents’ responses to the items of the Parental Values scale.

Method

Participants

Two hundred ninety-five sixth- and seventh-grade students in a suburban town in the Northeast completed the Parental Values scale. One participant did not give his or her top-five rankings and was dropped, giving a sample size of 294.

Participants in this study were of upper socioeconomic status. Median family income in the town served by this school was $98,459, and 79.7% of households had at least one parent with a bachelor’s degree (Beuhring, Saewyc, Stern, & Resnick, 1996). The mean age of the students who participated (except for 2 students who did not report their age) was 12.23 years (SD = 0.80); 54% were boys and 46% were girls.

The Parental Values scale was administered as part of a larger survey examining risk and resilience in suburban early adolescents (Luthar & Becker, 1999). This measure and several other questionnaires assessing aspects of psychosocial development were administered to students in a group format over the course of two class periods.

Materials

The Parental Values scale consists of the 10 items shown in Table 1. The items were developed with the goal of distinguishing between achievement values and personal values, with achievement values seen as connoting high emphasis on performance and accomplishments and, thus, a potential risk factor for the development of emotional difficulties. Five of the items (1, 3, 4, 9, 10) were considered as reflecting personal values, and the other five (2, 5, 6, 7, 8) were seen as reflecting performance values.

Table 1.

Parameter Estimates for Three-Class Model

Item	Class 1	Class 2	Class 3
1. That you are respectful to others	1.393	1.951	0.277
3. That you are honest	1.756	2.064	0.650
4. That you always try to help others in need	0.037	0.396	−1.362
9. That you are kind to others	0.815	1.080	−0.331
10. That you are generally happy with yourself and your life	5.248	0.671	0.848
2. That you attend a good college	−0.663	−0.327	1.130
5. That you make a lot of money in the future	−3.720	−1.981	−0.973
6. That you excel academically	−0.331	0.018	1.605
7. That you are a leader in school	−2.095	−1.187	−1.224
8. That you shine in extracurricular activities	−2.441	−2.684	−0.620
Class sizes	.436	.241	.323

Note. Class 1 = happiness; Class 2 = concern for others; Class 3 = academic.

Statistical Analysis

The software LEM, which is freely available at http://cwis.kub.nl/~fsw_1/mto/, was used to fit the model. LEM is a general program for categorical data analysis that can be used to fit many types of models, such as log-linear models, generalized linear models, latent class models, and LISREL-like models for categorical dependent variables; for examples of fitting the ranking model considered here and its latent class extension, see the files Cro89_3a.inp and Cro89_3b.inp provided with the LEM examples (for examples discussed by Croon, 1989). LEM offers several algorithms to obtain maximum likelihood estimates, one of which is a version of the EM algorithm (see Vermunt, 1997) that was used here. The model can be specified in terms of the conditional probabilities shown above, with a multinomial logit model for the conditional probabilities, as in Equation 1.

For the analyses reported herein, the eigenvalues of the information matrix were all greater than zero for models with from one to four classes, but, for the five-class model, one or more eigenvalues were close to zero, which suggests an identification problem. Multiple runs with different starting values were performed; local solutions were sometimes encountered, particularly for the five-class model. Convergence for models with three or more latent classes was, in general, quite slow (e.g., up to several hours on a personal computer running at 450 MHz).

Results

The usual likelihood ratio and chi-square goodness-of-fit statistics are not useful in this situation because of the sparseness of the data; that is, there are 10 × 9 × 8 × 7 × 6 = 30,240 possible orderings, so with 294 observations, there are many empty and low-frequency cells. Information criteria, however, are useful for selecting among models with sparse data (Lin & Dayton, 1997; Sclove, 1987). Table 2 shows, for models with one to five latent classes, the log likelihoods, the number of parameters, and goodness-of-fit criteria, specifically, the Bayesian information criteria (BIC) and Akaike’s information criteria (AIC), both of which are discussed in categorical textbooks, such as Agresti (1990), as well as a version of the AIC with a small sample bias correction (AIC_c) recommended by Burnham and Anderson (1998; although the correction was derived for a normal linear model, Burnham and Anderson provide a reference in which it was useful for a product multinomial model). BIC, AIC, and AIC_c all include a penalty for the number of parameters; they provide information similar to that given by cross-validation with a single sample (see Browne & Cudeck, 1989; Burnham & Anderson, 1998; Cudeck & Browne, 1983; Dayton, 1998). The values reported herein are based on the −2 log likelihoods, with smaller values indicating better fit (BIC = −2 log L + p × log N, where L is the likelihood, p is the number of parameters, and N is the number of observations; AIC = −2 log L + 2p, and for AIC_c, 2p is multiplied by the correction factor N/(N − p − 1)).

Table 2.

Log Likelihood and Information Criteria for the Latent Class Ranking Model

Number of Classes	Number of Parameters	Log Likelihood	BIC	AIC	AICc
1	9	−2459.666	4970.48	4937.33	4937.97
2	19	−2334.718	4777.42	4707.44	4710.21
3	29	−2279.764	4724.35	4617.53	4624.12
4	39	−2253.263	4728.18	4584.53	4596.81
5	49	−2241.512	4761.52	4581.02	4601.11

Note. BIC = Bayesian information criterion; AIC = Akaike’s information criterion; AIC_c = Akaike’s information criterion with small sample correction.

Table 2 shows that BIC is smallest for the three-class model, AIC decreases up to five latent classes, and the sample size corrected AIC_c is smallest for the four-class model. Dayton (1998) noted that BIC tends to favor less complex models (i.e., fewer parameters) than AIC, and that appears to be the case here as well (Cudeck & Browne, 1983, made a similar observation with respect to the performance of AIC and BIC as compared to cross-validation for the multivariate normal situation). Overall, the information criteria suggest a three- or four-class model. We present parameter estimates for both the three- and four-class models and focus on the three-class model, which has a simple interpretation in terms of an academic latent class versus two similar (personal) latent classes.

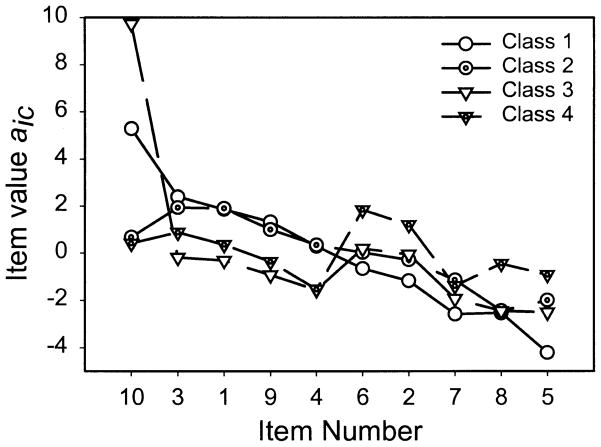
Table 1 shows, for the three-class model, the maximum likelihood estimates of the class sizes and the 30 estimated a_ic (10 for each of the three latent classes, with a sum to zero constraint within each latent class). The table shows that the estimates of the class sizes are .436 for Class 1, .241 for Class 2, and .323 for Class 3. Figure 1 is a plot of the estimates of the 10 a_ic for each item, separately for each latent class; the abscissa is ordered by the values obtained for Class 1. The table and figure together show that, for latent classes 1 and 2, the five personal items were valued highest, followed by the achievement items. Thus, the two classes behave in a way consistent with the initially hypothesized personal values class in that students in both classes tended to rank personal items above performance items. The two latent classes appear to differ primarily with respect to Item 10, which is concerned with personal happiness, with students in Class 1 seeing their parents as valuing personal happiness most highly, followed by being honest, respectful of others, kind to others, helping others, and the five academic items, and students in Class 2 considering their parents as valuing being honest first, followed by being respectful, kind, happy, helpful, and the five academic items. The figure also suggests a difference between Classes 1 and 2 with respect to Item 5, which is concerned with making a lot of money, with those in Class 1 tending to place it as last and those in Class 2 tending to place it as second to last. Apart from that, Figure 1 shows that the two classes are quite similar.

Figure 1.

Plot of the estimated a_ic, separately for each latent class, for the three-class model. The abscissa is ordered by the values obtained for latent Class 1.

The pattern for Class 3 differs considerably from that for the other two. Students in this class see their parents as valuing academic success (Item 6) and attending a good college (Item 2) most highly and valuing helping others (Item 4) and being kind to others (Item 9) relatively less than the other two classes (i.e., Items 4 and 9 tend to be ranked lower). Thus, to some extent, this group corresponds to the academic achievement group initially hypothesized in that the results suggest a latent class whose parents primarily value academic success, with concern for others valued less. In sum, Class 3 appears to be a performance latent class consisting of students who see their parents as valuing academic achievement highly, and Classes 1 and 2 appear to be personal latent classes consisting of students whose parents value concern for others and personal happiness.

The results for the four-class model are also informative. Figure 2 is a plot of the estimates of the 10 a_ic for each item and latent class. The plot suggests two latent classes similar to those found above, namely, an academic class and a personal class. More specifically, Classes 1 and 2 in Figure 2 suggest a class of students who see their parents as valuing the five personal items above the academic items, with the two classes differing with respect to the happiness item. Classes 3 and 4 in Figure 2 suggest a class of students who see their parents as valuing academics (Items 2 and 6) over some of the personal items, with the classes again split with respect to the happiness item. Thus, as for the three-class model, the scale partly achieves the goal of distinguishing between performance and personal latent classes, with the happiness item appearing to be responsible for further splits among these classes.

Figure 2.

Plot of the estimated a_ic, separately for each latent class, for the four-class model.

The two- and three-class models were also examined separately for each gender and grade (i.e., sixth and seventh grade). Some problems were encountered because of the small sample sizes; for example, the eigenvalues of the information matrix indicated identification problems for the three-class model for females (n = 134). Overall, the estimated a_i again suggested a pattern of academic versus personal classes across the grades and genders. Another approach would be to introduce grade and gender as covariates in the ranking model and compare fits for a heterogeneous model (different a_ic across gender and grade) to partially heterogeneous and completely homogeneous models, but the sparseness of the present data precludes these analyses.

Assignment to Latent Classes and Reliability

Given the estimated model parameters, the posterior probabilities of membership in each of the latent classes can be computed, and each adolescent can be classified into the class with highest probability. A nonparametric measure of the reliability of the classifications, lambda, can be obtained from the posterior probabilities. Lambda gives the relative reduction in prediction error; Clogg (1995) and Clogg and Manning (1996) discuss and illustrate lambda’s use in latent class analysis; Dayton (1998) notes that there is an upward bias for lambda (and the estimated proportion correctly predicted) because estimation and classification are performed on the same data. For the latent class ranking model considered here, lambda can be viewed as a measure of the reliability of the classifications based on the rankings as a set. It is the following:

$$\lambda =\frac{P_c-maxp(X_c)}{1-maxp(X_c)},$$

where max p(X_c) is the largest class size, and P_c is the proportion correctly predicted. Lambda corrects for the fact that one can correctly predict a percentage of cases equal to the largest class size simply by assigning all cases to that class. In the present case, the largest estimated class size is .436. The estimated proportion correctly predicted is .876, computed by multiplying the observed frequencies for each response pattern by the modal posterior probabilities (Clogg, 1995, noted that lambda can be computed using either observed or expected frequencies). The estimate of lambda is (.876 – .436)/ (1 – .436) = .78, so the rankings as a set are 78% reliable.

Validation of the Latent Classes

To obtain evidence as to the validity of the latent classes for the three-class solution, we examined the scores on a Parental Expectations scale across the latent classes, with each adolescent classified into a latent class using the modal posterior probabilities. The Parental Expectations scale consists of five items from the Multidimensional Perfectionism Scale (Parker & Stumpf, 1995), in particular, (a) My parents set very high standards for me, (b) My parents want me to be the best at everything, (c) Only outstanding performance is good enough in my family, (d) My parents expect excellence from me, and (e) My parents have higher expectations for my future than I have. It seems reasonable to expect that adolescents in the academic latent class should report higher parental expectations as compared to adolescents in the other two classes.

Table 3 shows the results for an analysis of variance (ANOVA) with the parental expectation score as the dependent variable and gender, grade, and latent class assignment (from the posterior probabilities) as factors. Note that this analysis does not take into account errors in the latent classifications, so the p values should be interpreted cautiously. The table shows that the mean parental expectation scores differ across the latent classes and grades (i.e., the p values are less than .05) but not across gender; the interactions are also not significant. The effect size measure η², using guidelines given by Cohen (1988) (.01 = small effect size, .06 = medium effect size, .14 = large effect size), indicates a small effect size for grade (η² = .025) and a medium to large effect size for latent class (η² = .091). The lower portion of Table 3 shows the means and standard errors of the parental expectation scores for each latent class separately for each grade. The means are highest for the academic class (Class 3) and lowest for the personal happiness class (Class 1), with the other class in between, and this pattern appears for both sixth and seventh graders. Within each latent class, the means tend to be higher for the seventh graders than for the sixth graders. Thus, adolescents in the academic latent class (Class 3) report the highest parental expectations, whereas adolescents in the happiness latent class (Class 1) report the lowest, and seventh graders report higher parental expectations than sixth graders. The results provide evidence as to the validity of the classifications obtained from the latent class ranking model, in that parental expectations tend to be reported as being higher by those in the latent class interpreted as emphasizing academics and achievement.

Table 3.

Analysis of Variance and Means for Parental Expectations Scores for the Three-Class Model

Source	df	F	p Value	η2
Gender	1	0.22	.637	.001
Grade	1	7.10	.008	.025
Latent class (3)	2	14.09	<.001	.091
Gender × Grade	1	2.06	.152	.007
Gender × Latent Class	2	0.06	.947	.007
Grade × Latent Class	2	1.06	.347	<.001
Grade × Gender × Latent Class	2	1.06	.347	.007
	Sixth Graders		Seventh Graders
	M	SE	M	SE
Class 1	12.41	0.40	12.87	0.50
Class 2	13.13	0.62	15.38	1.02
Class 3	15.04	0.62	16.20	0.74

Note. η² is an effect-size measure; Cohen (1988) suggests .01 = small effect size, .06 = medium effect size, and .14 = large effect size.

Alternative Scoring Procedures

A simple way to use the scale would be to tally the number of personal items that each student ranked as top five. Table 4 shows a cross-tabulation of the number of items ranked as top five (with possible values of 0–5) and the latent classes that adolescents are assigned to based on the modal posterior probabilities from the latent class analysis. The table shows that those who chose two or fewer personal items all fall into the academic latent class, those who chose four or five personal items were largely in one of the two personal classes, and those who chose three items are split among the academic and personal classes. Thus, a simple tally is to some extent useful for classifying students. The main limitation of tallying is that it is not clear where to categorize those with a score of three (the latent class model classifies these cases based on the pattern of rankings).

Table 4.

Number of Personal Items Ranked as Top Five Versus Assigned Latent Class for the Three-Class Model

Class	Number of Personal Items Ranked as Top Five
	1	2	3	4	5
1 (happy)	0	0	23	64	54
2 (concern)	0	0	12	35	12
3 (academic)	10	29	53	2	0

Discussion

The latent class ranking model used in the present study provides an informative summary of the rankings and items, suggesting that the scale goes part way toward identifying a latent class of adolescents whose parents emphasize achievement and, in particular, academic performance as reflected by grades and getting into a good college, in contrast to a latent class who view their parents as valuing concern for others more highly. Adolescents in the academic latent class also reported higher parental expectations than adolescents in the other classes, and this pattern appeared for both sixth and seventh graders.

With respect to further development of the scale, the analysis suggests which items might be useful in a revised version of the instrument. As our primary interest is in distinguishing the academic latent class from others, the items concerned with academics and concern for others will be kept, whereas the happiness and concern for money items, which seemed to be responsible for further subclasses not of substantive interest, will be dropped.