Abstract
The dimerization domain of the yeast transcription factor GCN4, one of the first coiled-coil proteins to be structurally characterized at high resolution, has served as the basis for numerous fundamental studies on α-helical folding. Mutations in the GCN4 leucine zipper are known to change its preferred oligomerization state from dimeric to trimeric or tetrameric; however, the wild-type sequence has been assumed to encode a two-chain assembly exclusively. Here we demonstrate that the GCN4 coiled-coil domain can populate either a dimer or trimer fold, depending on environment. We report high-resolution crystal structures of the wild-type sequence in dimeric and trimeric assemblies. Biophysical measurements suggest populations of both oligomerization states under certain experimental conditions in solution. We use parallel tempering molecular dynamics simulations on the microsecond timescale to compare the stability of the dimer and trimer folded states in isolation. In total, our results suggest that the folding behavior of the well-studied GCN4 leucine-zipper domain is more complex than was previously appreciated. Our results have implications in ongoing efforts to establish predictive algorithms for coiled-coil folds and the selection of coiled-coil model systems for design and mutational studies where oligomerization state specificity is an important consideration.
INTRODUCTION
It has been estimated that ~3% of the protein-encoding regions across known genomes specify sequences that adopt α-helical coiled-coil folds.1 Coiled-coil proteins play diverse roles in nature, including cellular scaffolding, oligomerization domains, and mediators of transmembrane signaling.2,3 The importance of coiled coil proteins in biology, along with their emerging role in the preparation of designed biomaterials,4 has motivated extensive efforts to elucidate the fundamental relationship between sequence and folding behavior in this common quaternary structure.
The basic sequence pattern of the coiled coil has a simplicity that belies the ubiquity and importance of the folding motif. α-Helices are defined by a repeat of 3.6 residues per turn; thus, two helical turns comprise a ~7 residue “heptad”. In a canonical α-helical coiled-coil sequence, positions a and d in several adjacent abcdefg heptad repeats are hydrophobic (i.e., (XOOXOOO)n sequence repeat where X is hydrophobic and O is polar). When such a sequence adopts an α-helical fold, it forms an amphiphilic structure with a hydrophobic stripe along one face of the helix. Burial of the hydrophobic stripes in two or more such helices can drive their assembly to form a rope-like superhelical quaternary structure with a slight left-handed twist.
The precise shape complementarity of residues packed together at the hydrophobic interface is a critical determinant of coiled-coil folding. Moreover, inter- or intra-helix polar contacts involving core residues or flanking e/g heptad positions can tune folding and assembly behavior. As a result of the complex interplay among these forces, closely related coiled-coil sequences can give rise to folding patterns that vary in gross structural properties such as oligomerization state (dimer, trimer, etc.),5–7 topology (parallel or antiparallel),8 and specificity (homotypic or heterotypic association).9 A particular challenge in elucidating the folding behavior of coiled coils is that the above properties of the quaternary structure can vary widely without significant changes in the helical structure of individual chains.
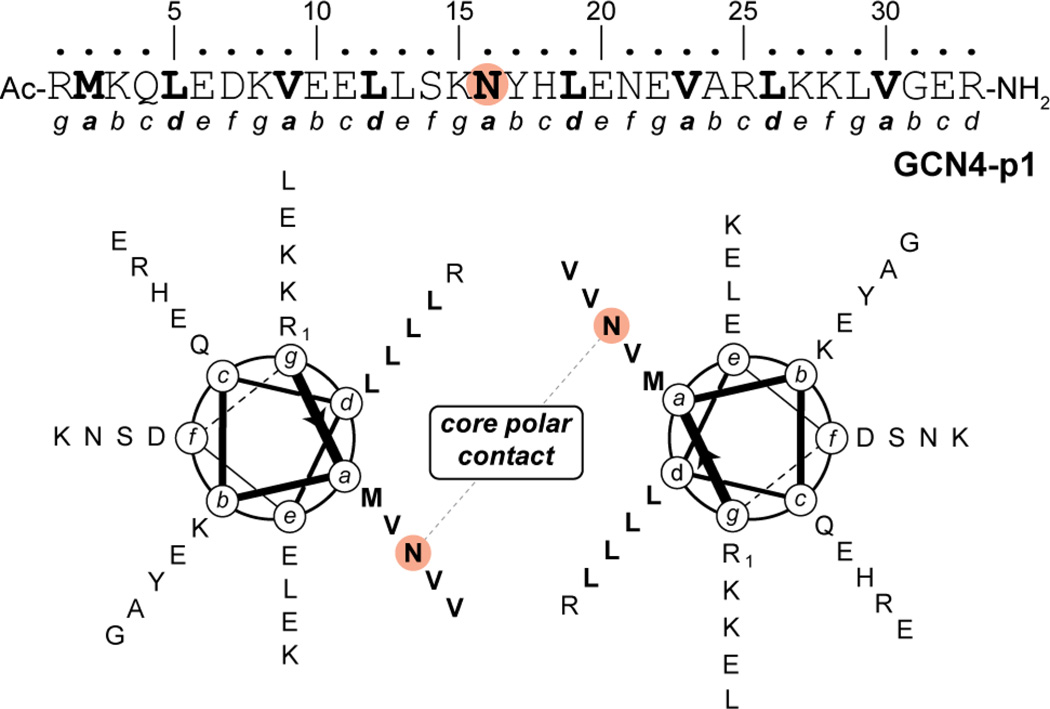
One of the earliest and most thoroughly studied α-helical coiled-coil protein sequences is the dimerization domain of the yeast transcription factor GCN4.10,11 The 33-residue GCN4 leucine zipper (often referred to as “GCN4-p1”) is a canonical coiled coil sequence with Val and Leu residues predominating at a and d heptad positions, respectively (Figure 1). A single polar Asn residue found at a central a position plays a key role in dictating folding through formation of an inter-chain polar contact in the otherwise hydrophobic core of the dimer.12–14 In more than two decades since it was first reported, the GCN4-p1 leucine-zipper domain has been the basis for numerous fundamental studies on α-helical coiled-coil protein folding. Although mutations are known to change its oligomerization state,5,12–16 the wild-type sequence has generally been assumed to exclusively specify a dimer. In a landmark 1993 paper, it was shown that mutations at a/d heptad positions in GCN4-p1 alter the preferred oligomerization state of the sequence.5 For example, a mutant with Ile at all a core positions and Leu at all d core positions (GCN4-pIL) formed a dimer, while switching to Leu at all a positions and Ile at all d positions (GCN4-pLI) led to a tetramer. Perhaps most intriguing in that study was the observation that the Val at a, Leu at d hydrophobic core of the native sequence was poorly discriminating between dimer and trimer in the absence of the single core Asn.
Figure 1.
Primary sequence of GCN4-p1 and helical wheel diagram for the GCN4-p1 dimeric coiled coil. Residue Asn16, which is involved in an inter-helix polar contact in the otherwise hydrophobic core of the dimer, is highlighted.
We report here that the native GCN4 leucine zipper domain (GCN4-p1) can adopt either a dimeric or trimeric coiled-coil fold, depending on environment. High-resolution crystal structures show how the core Asn16 residue is accommodated into each oligomerization state. Biophysical measurements suggest populations of both dimeric and trimeric assemblies in solution under certain experimental conditions. Microsecond molecular dynamics (MD) simulations provide insights into the relative stabilities of the two folded states in isolation. These simulations involved the application of parallel tempering, which is a special case of the replica exchange enhanced sampling method. By making optimal use of GPU hardware, our simulations are at least ten times longer than previous replica exchange simulations of the GCN4-p1 domain, its mutants, and fragments.17–20 Other computational studies of related systems have been limited to single-point energy calculations21 and short, standard MD simulations (up to 100 ns).22,23 Thus, the MD simulations we report are the most extensive to date involving the leucine-zipper fold.
MATERIALS AND METHODS
Peptide Synthesis and Purification
Peptides were synthesized by Fmoc solid-phase methods using manual microwave-assisted protocols24 or in automated fashion on a Protein Technologies Tribute Automated Synthesizer. NovaPEG Rink Amide resin was used to prepare the C-terminal carboxamide, and Fmoc-Arg(Pbf)-Wang 100–200 mesh polystyrene resin was used to prepare the C-terminal carboxylic acid. Peptides were cleaved from resin by treatment with 94% trifluoroacetic acid, 2.5% water, 2.5% ethanedithiol and 1% triisopropylsilane solution for 2 to 4 hours. After the peptide was cleaved from resin, it was precipitated from the filtered cleavage solution by addition of ~40 mL cold diethyl ether. The precipitate was pelleted by centrifugation, and the ether decanted. The peptide pellet was suspended in a mixture of 0.1% TFA in water and 0.1% TFA in acetonitrile for purification. Peptides were purified by HPLC on a C18 preparative column using gradients between 0.1% TFA in water and 0.1% TFA in acetonitrile. HPLC fractions containing the product were combined, frozen, and lyophilized. Peptide identity was confirmed by mass spectrometry using a Voyager DE Pro MALDI-TOF instrument calibrated with external standards (monoisotopic [M+H]+ m/z for GCN4-p1 C-terminal carboxamide: obsd. = 4034.7, calc. = 4036.2; GCN4-p1 C-terminal carboxylic acid: obsd. = 4038.6, calc. = 4037.2). All samples used for biophysical analysis were >95% pure by analytical HPLC on a C18 column.
Crystallization, Diffraction Data Collection, and Structure Determination
Crystallization was carried out using the hanging drop vapor diffusion method. Drops were prepared by mixing 0.7 µL of peptide stock (10 mg/mL in water) with 0.7 µL of buffer and allowed to equilibrate at room temperature over a well containing 0.7 mL of buffer solution. Crystals of the GCN4-p1 dimer were obtained from a well buffer composed of 0.1 M sodium acetate pH 4.6, 0.1 M sodium citrate tribasic dihydrate pH 5.6, and 25% w/v PEG 4000. A single crystal was flash frozen in liquid N2 after being soaked in the above buffer supplemented with 25% v/v glycerol. Crystals of the GCN4-p1 trimer were obtained from a well buffer composed of 0.2 M ammonium sulfate, 0.1 M MES monohydrate pH 6.5 and 30% w/v PEG monomethylether 5000. A single crystal was flash frozen in liquid N2 after being soaked in the above buffer supplemented with 10% v/v glycerol. The GCN4-p1 C-terminal carboxylic acid dimer was crystallized in 0.3 M sodium acetate pH 4.6, 0.1 M sodium citrate tribasic dihydrate pH 5.6, and 20% w/v PEG 4000. A single crystal was flash frozen in liquid N2 after being soaked in the parent buffer supplemented with 25% v/v glycerol. The GCN4-p1 C-terminal carboxylic acid trimer was crystallized by mixing 0.7 µL of a 20 mg/ml stock solution and 0.2 µL of the buffer described above for the C-terminal carboxamide trimer. A single crystal was flash frozen in liquid N2 after being soaked in the parent buffer supplemented with 10% v/v glycerol. Diffraction data were collected on Rigaku Saturn 944 CCD using CuKα radiation. d*TREK was utilized to index, integrate, and scale the collected data.
Structure refinement was carried out using CCP4.25 Phaser was used for molecular replacement, and previously published GCN4 coiled-coil derivatives were used as models; the dimer and trimer structures were solved using PDB entries 2ZTA11 and 1IJ2,14 respectively. A combination of refinement programs were used to complete the structure: Refmac26 for automated refinement, Coot27 for manual model building, ARP/wARP28 for solvent building, and Phenix29 for construction of composite omit maps. Phenix was also used to compare the metric symmetry between the trimer crystal forms of the C-terminal carboxamide (Table 1) and C-terminal carboxylic acid (P21, a = 34.6 Å, b = 58.5 Å, c = 101.3 Å, γ = 90.5°); this analysis indicated a shared primitive cell between the two lattices. Superhelix parameters and cavity volume were calculated using the TWISTER30 and the CASTp server,31 respectively. Buried surface area values were calculated using the PISA server.32 Coordinates and structure factors for the refined dimer and trimer structures were deposited in the PDB under accession codes 4DMD and 4DME.
Table 1.
Crystallographic Data Collection and Refinement Statistics.
| GCN4p1 dimer | GCN4p1 trimer | |
|---|---|---|
| space group unit cell | C2 | C2 |
| a, b, c (Å) | 83.4, 30.5, 27.8 | 61.2, 34.4, 78.1 |
| α, β, γ (°) | 90, 104.5, 90 | 90, 139.7, 90 |
| data collection | ||
| resolution (Å) | 40.4–2.0 (2.07–2.00) | 50.5–2.2 (2.28–2.20) |
| Rmerge (%) | 5.8 (25.3) | 9.4 (22.1) |
| I / σ(I) | 15.5 (2.2) | 9.7 (3.2) |
| completeness (%) | 99.8 (100.0) | 99.5 (100.0) |
| redundancy | 3.8 (2.4) | 2.7 (2.8) |
| refinement | ||
| resolution (Å) | 40.4–2.00 | 50.54–2.20 |
| no. reflections | 4432 | 5198 |
| Rwork / Rfree (%) | 23.5 / 26.5 | 22.6 / 28.7 |
| no. atoms | 567 | 903 |
| avg. B factor (Å2) | 23.9 | 24.7 |
| rmsd | ||
| bond lengths (Å) | 0.016 | 0.010 |
| bond angles (°) | 1.8 | 1.4 |
Gel Permeation Chromatography
GPC was carried out on a Superdex 75 10/300 column (10 × 300 mm, 24 mL bed volume, 13 µm average particle size, GE Healthcare). The column was equilibrated with 0.15 M NaCl in 0.05 M sodium phosphate, pH 7.0. Peptides were loaded onto the column (100 µL sample at 100 µM concentration in equilibration buffer) and eluted at a flow rate of 0.8 mL/min (Figure S1). A molecular weight calibration curve was obtained by fitting the elution volumes of 1 mg/mL solutions of BSA, ovalbumin, aprotinin, a 17-residue synthetic peptide (Ac-YEAAAKEAAAKEAAAKA-NH2), and vitamin B12.
Circular Dichroism Spectroscopy
Measurements were taken on an Olis DSM17 CD Spectrometer using 0.1 cm quartz cuvettes. Peptide concentration was determined by UV absorbance at 276 nm (ε = 1450 M−1 cm−1) from the single Tyr residue in the GCN4-p1 sequence.33 Samples of 100 µM peptide in buffer were prepared and scanned from 200 nm to 260 nm in 1 nm increments, an integration time of 5 seconds and a bandwidth of 2 nm at 20°C. A buffer blank was subtracted from each spectrum and baseline molar ellipticity at 260 nm was set to zero. Variable temperature CD was taken by monitoring molar ellipticity at 222 nm from 20–96°C in 4°C increments with a 2 minute equilibration time between data points and an integration time of 5 seconds. Thermal melt data was fit to a two-state unfolding model34,35 to obtain the melting temperature (Tm). Although the GCN4-p1 folding equilibrium is concentration dependent, this analysis is sufficient for qualitative comparison of folded stability at a fixed concentration.
Concentration-Dependent Circular Dichroism
A 400 µM solution of peptide was prepared in 10 mM phosphate buffer, 6 M urea, pH 7.0. Serial two-fold dilutions were made into 10 mM phosphate buffer, 6 M urea, pH 7.0 to generate nine samples with peptide concentrations ranging from 400 µM to 1.56 µM. Samples from 400 µM to 100 µM were measured in 1 mm quartz cuvettes, 50 µM to 6.25 µM in 2 mm quartz cuvettes, and 3.125 µM to 1.56 µM in 5 mm quartz cuvettes. Buffer solution used for the dilutions was taken from a common stock. CD measurements of each sample were performed on an Olis DSM17 Circular Dichroism Spectrometer. Molar ellipticity of the samples was monitored at 222 nm at 20.0°C using a 2 nm bandwidth and a 5 second integration time. Three independent samples of each concentration were measured to obtain the reported molar ellipticities and accompanying error bars (standard deviation of the mean).
The concentration-dependent molar ellipticities were fit to a previously published model,36 which assumes a simple two-state transition:
| (eq. 1) |
| (eq. 2) |
| (eq. 3) |
| (eq. 4) |
where Ptot, Pmon and Pn are the concentration of total peptide, the monomer, and the n-mer respectively, K is the dissociation constant, and n is the number of the molecules in the associated state. The concentration dependence of molar ellipticity is described by the following equations:
| (eq. 5) |
| (eq. 6) |
| (eq. 7) |
| (eq. 8) |
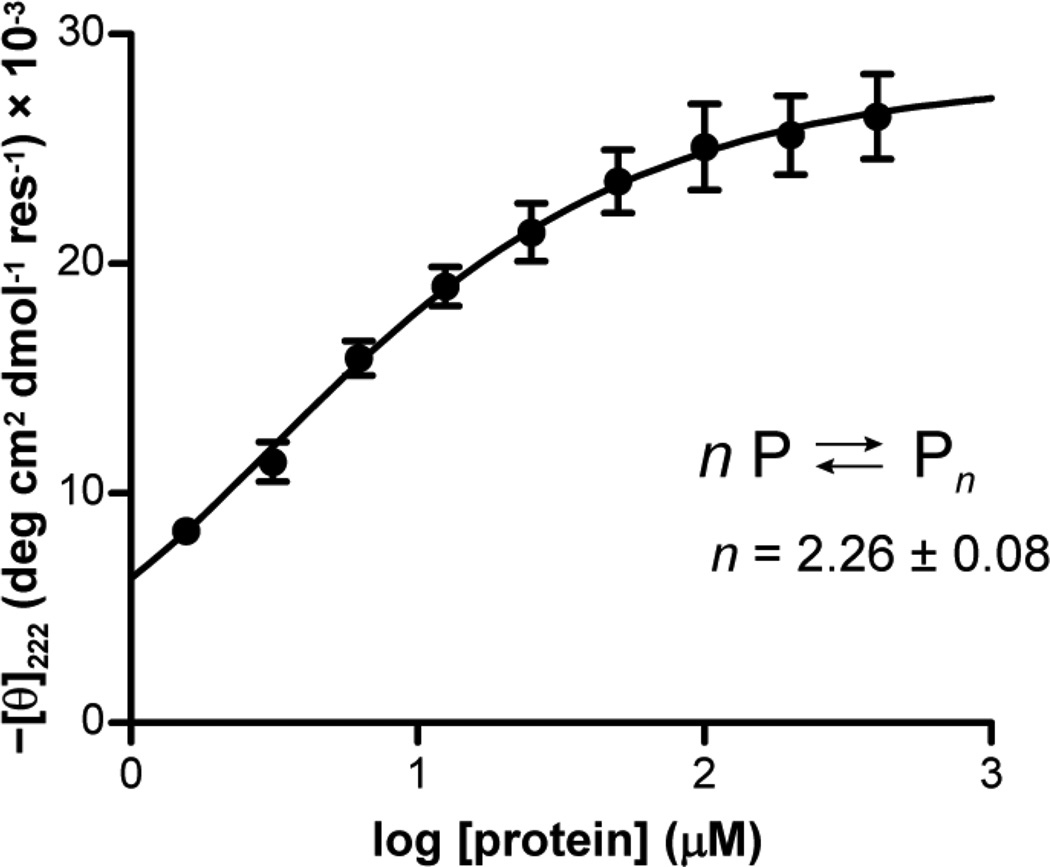
in which [θfold] is the mean molar ellipticity of the folded peptide, [θcoil] is the mean molar ellipticity of the random coil, and f is the mole fraction of peptide in the state specified by the subscript. The value for [θcoil] was determined experimentally from a thermal melt of GCN4-p1 in 10 mM phosphate buffer, pH 7.0, 6 M urea. The limiting value after complete thermal denaturation was used as the value for [θcoil]. Using non-linear least-squares regression methods in Mathematica (Wolfram Research), the best fit parameters values for the K, n, and [θfold] were determined by fitting the data to eq. 8 and using eq. 4 to determine Pmon. In the fit, each data point was weighted by 1/σ2, where σ is the standard deviation from the three independent measurements. The parameters obtained were [θfold] = 28.1 ± 0.56, log K = 0.88 ± 0.01, n = 2.26 ± 0.08. Following the precedent for the use of the above protocol to probe coiled-coil oligomerization states,36 the Hill coefficient (n) was allowed to float in the fit. The fact that the value of n obtained is greater than 2.0 suggests that the concentration-dependent folding of GCN4-p1 under the conditions of the experiment does not follow a simple monomer–dimer equilibrium.
Sedimentation Equilibrium Measurements
Sedimentation equilibrium measurements were carried out using a Beckman Coulter Model XL-A Analytical Ultracentrifuge. GCN4-p1 was prepared by simple dissolution in one of four buffers and used without further manipulation; the initial concentrations in each buffer were determined from spectra as recorded in the centrifuge using an extinction coefficient of 1490 M−1 cm−1 at 280 nm. The buffers were (A) 0.05 M phosphate, 0.15 M NaCl, pH 7.0 with peptide concentrations of 89, 220, and 415 µM; (B) 0.1 M sodium acetate, 0.1 M sodium citrate tribasic, pH 5.3, 245 µM GCN4-p1; (C) 0.2 M ammonium sulfate, 0.1 M MES, pH 6.6, 269 µM GCN4-p1; (D) 10 mM phosphate, 6 M urea, pH 7.0, 267 µM GCN4-p1. Buffer densities at 20°C were computed using density increment functions37 as 1.010, 1.004, 1.012, and 1.102 g/mL respectively (a contribution for MES buffer was not available but it is likely that the ammonium sulfate is the dominant contributor). The partial specific volume of GCN4-p1 (0.748 cm3 g−1) was calculated using consensus values reported for the amino acid residues with a correction applied for the acetyl and carboxamide end groups.38,39 In the presence of denaturing concentrations of urea, the partial specific volume can be corrected for specific interactions of urea and water with the protein;40 this corrections leads to an effective partial specific volume of 0.764 cm3 g−1 for GCN4-p1. However, the data presented here suggest that the protein is in a mostly folded state in 6 M urea, so that the true value may lie closer to 0.748 cm3 g−1. The molecular weight of GCN4-p1 is 4038 Da including the terminal blocking groups.
Approximately 100 µL of a peptide solution was placed in one sector of a 1.2 cm path length, charcoal filled epon centerpiece with ~110 µL of the corresponding buffer added to the reference sector. Gradients were monitored at a nominal wavelength of 276 nm. Samples were spun at various speeds at 20°C until gradients collected 3 or more hours apart were superimposable. The equilibrium data were analyzed following an approach similar to that described by Laue41 using software written by D.R.M. for Igor Pro (Wavemetrics, Inc., Lake Oswego, OR).
Under all buffer conditions, a single macromolecular species with a small contribution from non-sedimenting absorbance (see supplemental information) was able to describe the data. The weight average molecular weights derived from global fits of data in each buffer are summarized in Table 2. The variations are likely a reflection of the computed nature of the partial specific volume in various salts. Figure S2 shows a plot of the logarithm of the measured absorbance (after subtracting the fitted non-sedimenting absorbance) as a function of squared radial distance from the center of rotation; in such plots, a single species manifests as a series of straight lines with slopes proportional to the weight average molecular weight. The solid lines are based on the fitted weight average molecular weights shown in Table 2 and well account for the available data.
Table 2.
Sedimentation Equilibrium results for GCN4-p1 under different buffer conditions.
| Buffer | MWobs (Da)a | MWobs/MWcalcb |
|---|---|---|
| 0.05 M phosphate, 0.15 M NaCl, pH 7.0 | 8339 ± 22 | 2.07 ± 0.01 |
| 0.1 M sodium acetate, 0.1 M sodium citrate, pH 5.3 | 7546 ± 42 | 1.87 ± 0.01 |
| 0.1 M MES, 0.2 M (NH4)2SO4, pH 6.6 | 8276 ± 57 | 2.05 ± 0.01 |
| 0.05 M phosphate, 6 M urea, pH 7.0 | 8069 ± 66 | 2.00 ± 0.02 |
Weight average molecular weight (MWobs) from fits to a single-species model using computed densities and a partial specific volume of 0.748 mL g−1. Errors represent least squares fitting errors in the fitted parameter;
ratio of the weight average molecular weight to the molecular weight based on the peptide sequence (MWcalc).
Parallel tempering molecular dynamics simulations
To determine the melting temperatures (Tm) of the dimer and trimer folded states of the GCN4-p1 leucine zipper in isolation, we used parallel tempering molecular dynamics (MD) simulations.42–44 Parallel tempering is a widely used replica exchange enhanced sampling technique that involves simultaneously performing “replica” simulations of the system at different temperatures with the aim of making configurations at higher temperatures available to simulations at lower temperatures and vice versa. During the course of these simulations, the conformations at two different temperatures Ti and Tj are swapped at regular intervals according to the Metropolis-type criterion with a probability of:
Where β = (kBT)−1 and U is the potential energy. MD simulations at each of the replica temperatures were simulated for 1 µs using the OpenMM 4.0 software45–48 on the XSEDE Forge GPU cluster. Replicas were exponentially spaced at temperatures from 37 to 177 °C (18 replicas for the dimer and 24 replicas for trimer), resulting in an aggregate simulation time of 18 µs and 24 µs for the dimer and trimer, respectively. After the first 1 ns, exchanges were attempted every 5 ps among all replicas using the Gibbs sampling scheme.49 Velocities were reassigned from the Maxwell-Boltzmann distribution after every exchange attempt. The overall exchange acceptance ratio was ~13% for the dimer and ~11% for the trimer. Conformations were sampled every 5 ps. To allow for sufficient equilibration of the system, only the last 900 ns of each parallel tempering simulation was subjected to analysis. We obtained ~100 and ~50 ns/day for the dimer and trimer, respectively, using one NVIDIA Fermi M2070 GPU per replica (total of 18 GPUs for the dimer and 24 GPUs for the trimer).
To estimate Tm values of the dimer and trimer, three approaches were applied, each using a different order parameter to monitor unfolding in the parallel tempering simulations. In the first approach, an unfolded conformation was defined as having a Cα rmsd from the crystal structure that is more than one standard deviation above the average value at 37 °C in the simulations. The three C-terminal residues that were missing in the crystal structure of the dimer were not included in the rmsd calculations. In the second approach, a conformation was considered unfolded if the number of helical residues was more than one standard deviation below the average value at 37 °C (helical residues were defined as having φ = −60 ± 30 and ψ = −47 ± 3050). Finally, in the third approach, an unfolded conformation was defined as having at least one of the chains dissociated (i.e., beyond van der Waals distance of 4.5 Å). For each approach, the average fraction unfolded was plotted vs. temperature and the temperature of 50% unfolding was considered as the melting temperature.
To compute the folding free energies of the dimer and trimer at the temperatures of interest, we applied the multistate Bennett acceptance ratio (MBAR) method51 to our parallel tempering simulations as implemented in the PyMBAR package (https://simtk.org/home/pymbar). This method is equivalent to the weighted histogram analysis method52 in the limit of infinitesimally thin histogram bins with the additional feature of providing a means to directly calculate statistical uncertainties in the free energy differences. In this method, the dimensionless free energy at thermodynamic state i, f̂i, is estimated by solving the following equation in a self-consistent fashion:
where K is the total number of replicas in the system, Nj is the number of uncorrelated samples for each replica j, and ui is the reduced potential energy for conformation xjn. The difference in free energies can then be calculated as Δf̂ij = f̂j − f̂i where i and j are the two thermodynamics states of interest (i.e. folded and unfolded), respectively. Folding free energies were estimated using snapshots collected every 5 ns. The extent of folding was monitored using order parameters with non-discrete values (i.e. Cα rmsd and the helical content). Folding free energies at temperatures that were not included among the temperate replicas of the parallel tempering simulations (i.e. below 37 °C) were estimated by extrapolation using the MBAR method.51 Uncertainties at each temperature were estimated by the asymptotic covariance matrix of the MBAR estimating equations.51
MD simulations at each of the replica temperatures were performed using the AMBER ff99SB force field,53 generalized Born implicit solvent (OBC model II; igb=5)54 with a surface-area dependent term,55 and physiological salt concentration of 150 mM as implemented in the AMBER 11 molecular dynamics package.56 Constant temperature was maintained for each of the replicas using the Langevin thermostat. To accelerate unfolding and refolding events, we used a reduced solvent viscosity (collision frequency of 1 ps−1). All hydrogen bonds to heavy atoms were constrained using the SHAKE algorithm57 (relative geometrical tolerance of 10−6), enabling the use of a 2-fs time step. To increase the frequency of refolding events, a square-well distance restraint with a spring constant of 20 kcal mol−1 Å −2 was applied between the Cα atoms of the N-terminal arginine residues in each monomer (two for the dimer and three for the trimer) to keep these atoms within 45 Å of each other, resulting in the same effective concentration of monomers for each simulation.
Starting structures for the simulations of the dimer and trimer folded states were prepared using the LEAP module in the AmberTools 1.5 package.56 Heavy atom coordinates were taken from the crystal structures of the corresponding oligomeric form. The three C-terminal residues of the dimer had not been resolved in the crystal structure and were added using the PyMol visualization software.58 Crystallographic water molecules were removed and hydrogen atoms were added using the protonation states present in solution at pH=7. The removal of the two buried water molecules in the trimer crystal structure (Figure 3C) appears to not substantially affect the stability of the trimer within our implicit solvent model as the structure remained folded in the 500 ns-long standard MD simulation at 20 °C (Cα rmsd values of 2.0 ± 0.4 Å relative to the crystal structure, Figure S8). No cutoff for non-bonding interactions was used. To relieve unfavorable interactions, each starting structure was subjected to energy minimization in two stages, with position restraints applied to the heavy atoms in the first stage and no position restraints in the second stage.
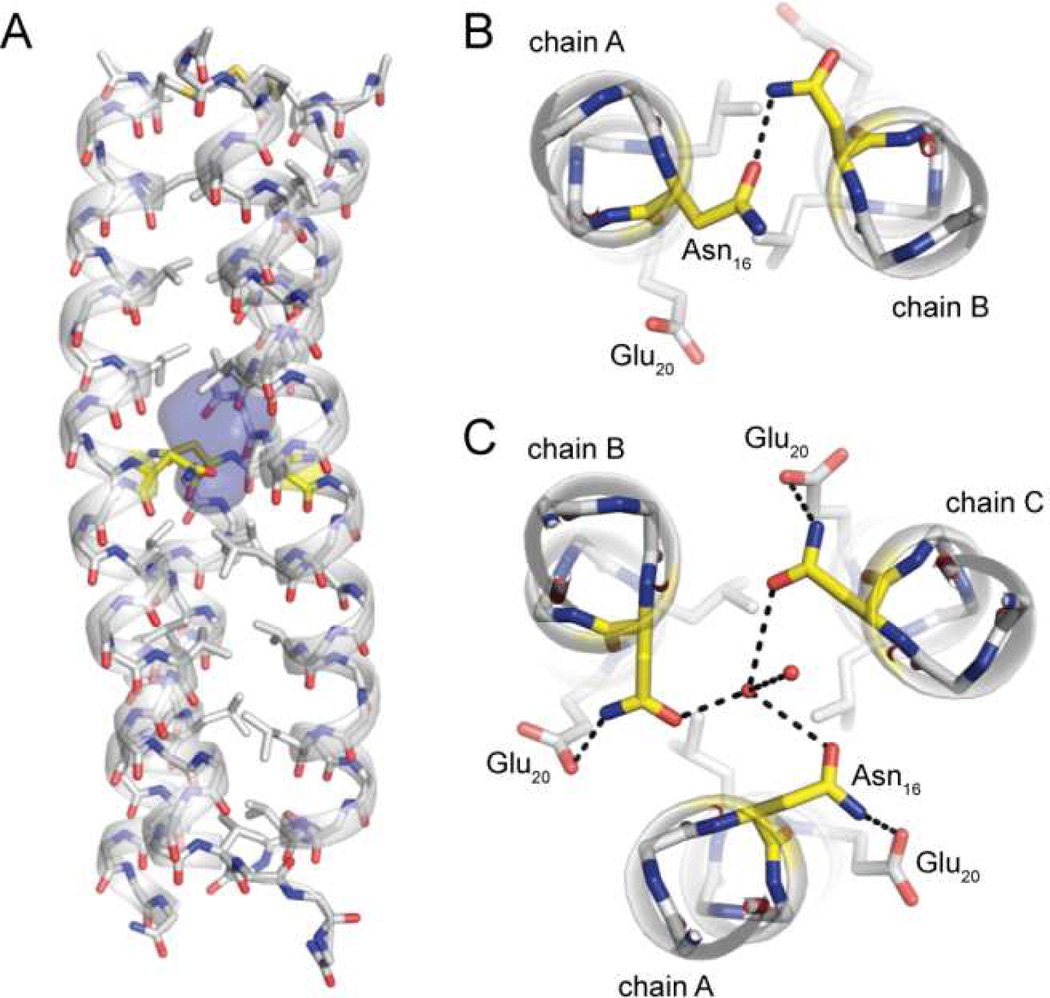
Figure 3.
(A) A water-filled cavity is present in the hydrophobic core of the GCN4-p1 trimer. Sticks are shown for all backbone atoms as well as side-chains of hydrophobic core residues; carbons in Asn16 are colored yellow. (B,C) Polar interactions involving core residue Asn16 in the GCN4 p1 dimer (B) and trimer (C) helix bundle; two ordered water molecules resolved in the buried cavity are shown as spheres.
RESULTS
Crystal Structure and Analysis
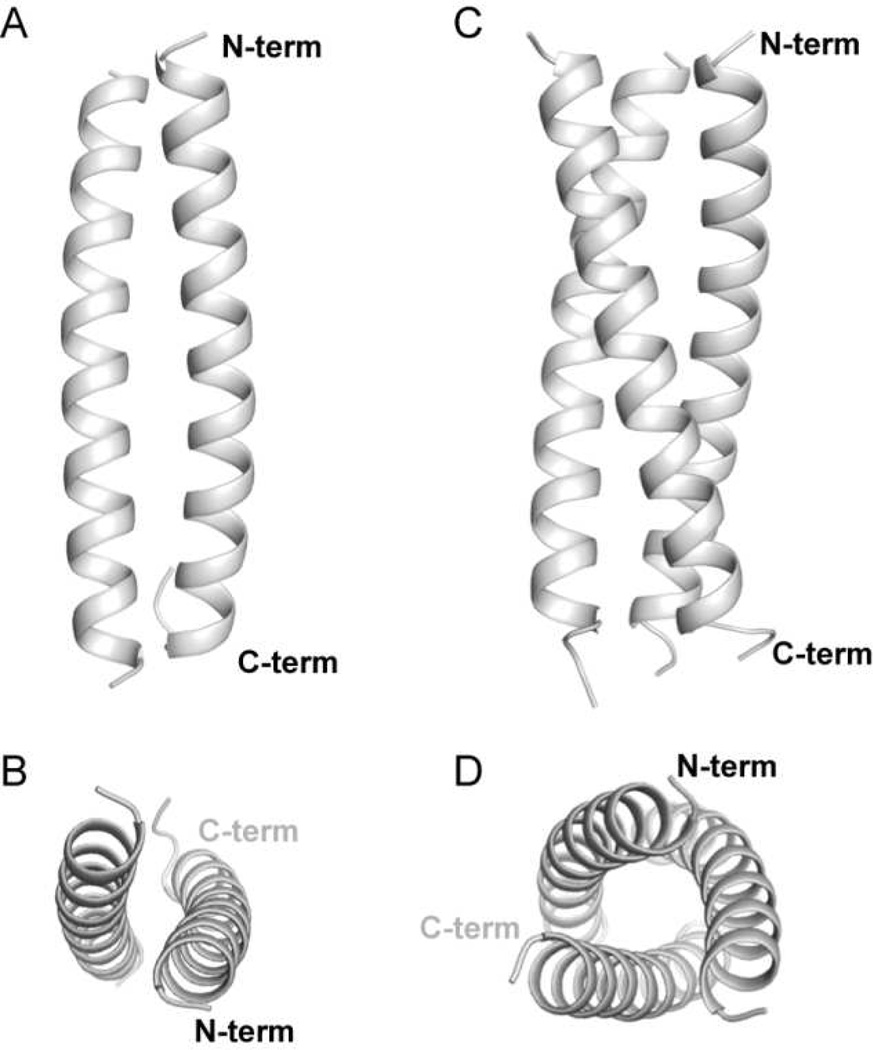
Crystallization efforts yielded diffraction-quality crystals of GCN4-p1 in two different forms. From indexing, it was clear that neither corresponded to the lattice first reported for the native GCN4 leucine-zipper sequence in a dimer fold.11 We obtained X-ray diffraction data for each crystal form and solved the structures to 2.0 Å and 2.2 Å (Table 1). The higher resolution data set was readily solved by molecular replacement with a model of the previously published GCN4-p1 dimeric coiled coil (Figure 2A–B, the asymmetric unit is the dimer). For the other crystal system, the dimer failed to give a reasonable solution. Molecular replacement performed with a single α-helix as the search model placed three chains in the asymmetric unit in a parallel arrangement. We repeated the molecular replacement with a trimeric coiled coil formed by a known sequence variant of GCN4-p1,14 which led to the refined structure reported here (Figure 2C–D, the asymmetric unit is the trimer).
Figure 2.
Cartoon representations of the crystal structures of the wild-type GCN4-p1 coiled coil domain in a dimeric (A,B) and trimeric (C,D) oligomerization state.
Although the crystal packing in our GCN4-p1 dimer structure differed from that previously observed for the same sequence in a different lattice (PDB 2ZTA),11 the coiled-coil quaternary folds were found to be virtually identical (Cα rmsd of 0.53 Å). The main differences between the two structures are in the conformation of a few solvent-exposed side chains and the C-terminal tail; this segment of GCN4-p1 tends to be disordered past Gly31 and was not consistently resolved in electron density.
Residue Asn16 is known to be a key determinant of oligomerization state specificity in GCN4-p1.11–14 This hypothesis is supported in the literature by (1) the involvement of this side chain in an intermolecular polar contact in the otherwise hydrophobic core of the dimer interface11 (Figure 3B) and (2) the observation that mutation of just Asn16 can lead to a change in the favored oligomerization state.12–15 We examined Asn16 in the trimer structure of the wild-type sequence in an effort to gain insight into how this side chain was accommodated in the core of the trimeric coiled coil (Figure 3). The interface between chains in the GCN4-p1 dimer is tightly packed (total buried surface area 1810 Å2). The close packing is largely retained in the trimer (total buried surface area 4000 Å2); however, the switch in oligomerization state is accompanied by formation of a 112 Å3 cavity in the vicinity of Asn16 (Figure 3A). Although the pocket is isolated from solvent, we observed two ordered water molecules filling it in the crystal structure (Figure 3C). One of the two core waters appears to be stabilized by hydrogen-bonds to the three Asn16 carboxamide oxygen atoms lining the cavity, while the other is involved in an inter-water polar contact. A matching shift of the e-position Glu20 residues between the dimer and trimer folds leads to three new intrachain polar contacts to the Asn carboxamide (Figure 3C). These flanking polar interactions may help to stabilize the Asn16 side chains in a conformation that effectively binds the core water.
There are six known single-residue mutations of GCN4-p1 that lead to a trimeric oligomerization state: replacement of Asn16 with Ala, Val, Ser, Thr, Gln, or (S)-2-aminobutyric acid (Abu).12–15 Four of the former have been structurally characterized at high resolution, so we compared the wild-type trimer structure to each of these mutants (Table 3). Backbone Cα overlay for residues 1–30 revealed significant structural homology between the five coiled coils; rmsd values varied from 0.55–0.80 Å. The closest match was to the fold of the Asn16→Thr sequence variant. Idealized superhelix parameters,59 calculated from backbone Cα positions, show that the wild-type trimer is more tightly wound than any of the point mutants, indicated by its smaller superhelical pitch.
Table 3.
Comparison of the wild-type GCN4-p1 coiled-coil trimer structure to known trimer-forming mutants.
| GCN4p1 mutanta |
|||||
|---|---|---|---|---|---|
| wt | N16→S | N16→T | N16→Q | N16→X | |
| Cα rmsd to wt (Å) | n/a | 0.80 | 0.55 | 0.63 | 0.67 |
| Superhelix parameter | |||||
| radius (Å) | 6.3 | 6.4 | 6.3 | 6.5 | 6.5 |
| rise per residue (Å) | 1.44 | 1.47 | 1.44 | 1.45 | 1.46 |
| pitch (Å) | 130 | 153 | 139 | 140 | 143 |
wt is wild-type trimer structure reported here; other structures were published previously (Asn16→Ser, PDB 1IJ3; Asn16→Thr, PDB 1IJ2; Asn16→Gln, PDB 1ZIM; Asn16→Abu, PDB 1ZIJ); Abu = (S)-2-aminobutyric acid;
rmsd values calculated from overlay to wild-type using Cα atoms in residues 1–30.
The GCN4-p1 peptide used to obtain the two structures described above has a C-terminal carboxamide, whereas the previously published crystal structure of the same sequence was reported for the C-terminal carboxylic acid. GCN4-p1 and its variants tend to be disordered past the flexible Gly31 residue, so we deemed it unlikely that such a small change at Arg33 would be responsible for the trimer fold observed. To test this assumption, we synthesized a sample of GCN4-p1 with a C-terminal carboxylic acid and attempted to grow crystals using the same two buffers that gave rise to the dimer and trimer crystal forms described above. Using the acetate-based dimer buffer, we were able to obtain a crystal of the C-terminal acid that diffracted with the same unit cell and symmetry as the C-terminal amide dimer. Using the MES-based trimer buffer, we obtained a crystal form that was crystallographically related to that of the C-terminal amide trimer; the lattice had lower symmetry, however, leading to three crystallographically independent trimeric coiled coils in the asymmetric unit. Neither C-terminal acid structure was refined. Overall, these data suggest the identity of the C-terminal functional group has no bearing on the ability of the GCN4-p1 sequence to adopt a dimer vs. trimer fold.
Solution Biophysical Characterization
We performed a series of experiments to further investigate the folding behavior of GCN4-p1 in solution. To our knowledge, no prior study has shown direct biophysical evidence for the trimer fold we saw in the crystal; however the assumption of a simple two-state unfolding transition has been questioned.60 Our goals in these experiments were to test prior observations that the dimer is the favored fold in benign buffer at pH 7 and to look for measurable population of trimer under other experimental conditions.
We carried out analytical gel-permeation chromatography (GPC) to examine the association state of GCN4-p1 in pH 7 phosphate. We compared the wild-type sequence to GCN4-pII, a known mutant that adopts a trimeric fold.5,61 Each peptide eluted as a single peak (Figure S1). Calibration of the column with protein molecular weight standards showed that the elution volume of GCN4-p1 corresponded to an apparent molecular weight slightly larger than expected for the dimer (MWapp/MWcalc = 2.3), while GCN4-pII had an elution volume that exactly matched the expected trimer. Given the resolution limitations of GPC as an analytical tool for sizing small globular proteins, the 15% deviation from the MW expected for the dimer was not deemed significant within the uncertainty of the measurement.
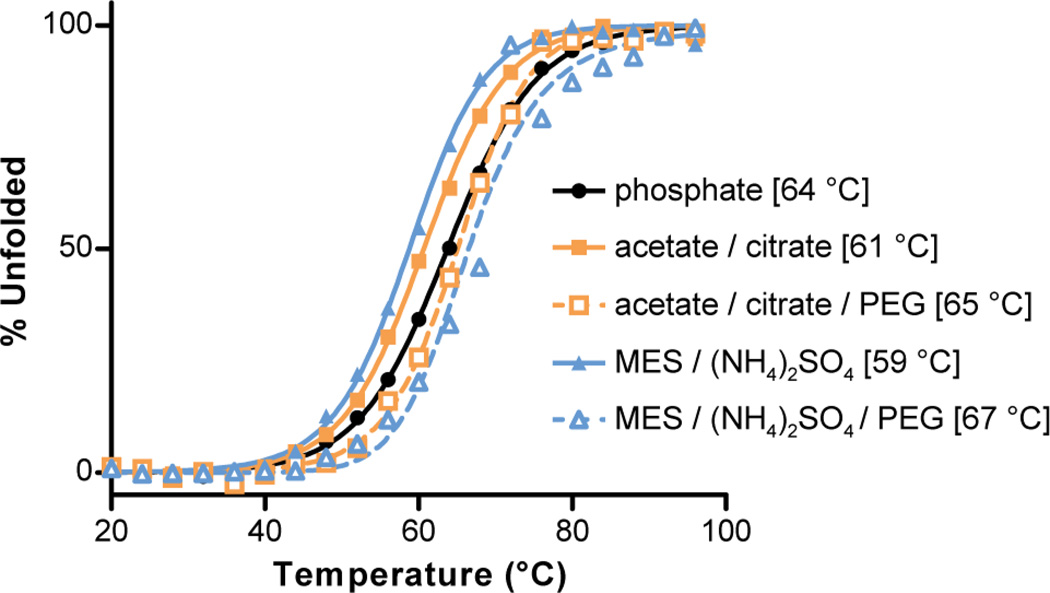
A circular dichroism (CD) spectrum and thermal melt for a 100 µM solution of GCN4-p1 in pH 7 phosphate buffer were consistent with prior data.10 This measurement served as a baseline for comparison of the folded stability of the peptide in the buffers that gave rise to the dimer and trimer crystal forms (Figure 4). We carried out CD thermal melts on 100 µM peptide solutions in the two crystallization conditions with and without added PEG to isolate possible effects of pH/salt from those of the precipitant. The data showed that the GCN4-p1 coiled coil was slightly destabilized by the pH and/or salt content of the two crystallization buffers relative to pH 7 phosphate. More striking was the consistent increase in coiled-coil folded stability that accompanied addition of PEG; the increase in Tm was more pronounced in the trimer buffer (ΔTm = +8 °C) than in the dimer buffer (ΔTm = +4 °C).
Figure 4.
Circular dichroism thermal melts for GCN4-p1 in different buffers. Solution conditions from top to bottom in the legend: 10 mM phosphate, pH 7; 0.1 M sodium acetate, 0.1 M sodium citrate, pH 5.3; 0.1 M sodium acetate, 0.1 M sodium citrate, 25% w/v PEG 4000, pH 5.3; 0.2 M ammonium sulfate, 0.1 M MES, pH 6.6; 0.2 M ammonium sulfate, 0.1 M MES, 30% w/v PEG 5000 monomethylether, pH 6.6. Curves are shown for fits to a two-state unfolding transition, with melting temperatures (Tm) indicated in brackets. The outlier point at 72 °C in sample (5) was observed in two independent experiments; the origin is not clear, but its presence does not impact the Tm from the fit.
Concentration-dependent folded population can be used to determine oligomerization state in proteins where folding requires self-assembly. Folding and self-assembly are known to be coupled in GCN4-p1;10 however, the folded state is too stable to allow for a complete titration under concentrations accessible to CD analysis. We therefore performed a titration under partially denaturing conditions, a method developed previously for the specific purpose of determining the preferred oligomerization state of coiled-coil peptides.36 We measured the concentration-dependent molar ellipticity of GCN4-p1 at 222 nm in 10 mM phosphate buffer, 6 M urea, pH 7 (Figure 5). The concentration of urea used was determined empirically to give the best range of folded population in the concentration range of peptide used in the experiment. A fit of the CD titration data to a model where the number of chains in the associated state (n) was allowed to float36 gave a value of n = 2.26 ± 0.08. A non-integer value of n does not correspond to a physically real folded state; however, the fact that n is greater than 2.0 suggests that the concentration-dependent folding behavior of GCN4-p1 does not follow a simple monomer–dimer equilibrium under the conditions of the experiment.
Figure 5.
Concentration-dependent molar ellipticity of GCN4-p1 at 20 °C in 10 mM phosphate, 6 M urea, pH 7. The curve is the best fit of the data to a self-association model of monomer to n-mer, where n is allowed to float (see methods).
To further probe the self-assembly behavior of GCN4-p1 under different buffer conditions, we carried out sedimentation equilibrium measurements in four buffers: (A) pH 7 phosphate, (B) the dimer crystallization buffer without PEG, (C) the trimer crystallization buffer without PEG, and (D) the partially denaturing urea-containing buffer used for CD titration. Over the concentration range accessible in these experiments, the analysis suggests a single macromolecular species in all buffer conditions (Figure S2). Using a computed partial specific volume, the weight average molecular weight under each condition matches that expected for the dimer (Table 2). There is some uncertainty as to treatment of data obtained in 6 M urea. In the presence of high concentrations of urea corrections to the partial specific volume are needed to account for preferential interactions of the urea and water.40 Application of a known method for this correction leads to a MWobs/MWcalc of 2.22, in accord with the concentration-dependent CD analysis. However, the method for partial specific volume correction was originally developed to provide correct molecular weights under denaturing conditions, which is not the case here. Thus, the dimeric form of the peptide appears to best describe the oligomeric state under all the buffer conditions tested.
Parallel Tempering Molecular Dynamics
In an effort to compare the relative stabilities of the GCN4-p1 dimer and trimer oligomerization states in isolation, we carried out parallel tempering MD simulations in implicit solvent on the microsecond timescale. The simulations appear converged according to three criteria. One criterion is the “end-to-end” transition time (τend), which represents the speed of diffusion of a replica in temperature space62 and reflects the quality of mixing among replicas.49,63–66 Our transition times are significantly shorter than the length of the simulations, resulting in a large number of round trips (184 and 135 for the dimer and trimer, respectively), with all replicas visiting most of the temperatures (Figure S3, Table S1). Another criterion for convergence is the number of chain reassociations, as the simulations should sample many dissociation and association events for accurate determination of the melting temperature. Overall, 2355 and 1791 rebinding events were observed for the dimer and trimer, respectively. The average time scale for the rebinding events (total simulation time divided by the total rebinding events) was ~8 ns for the dimer and ~13 ns for the trimer, allowing each replica to sample 125 and 75 transitions on average for the dimer and trimer simulations, respectively. Finally, obtaining converged estimates of the melting temperatures required simulation times (>100 ns, Figure S4) more than ten times longer than previous replica exchange MD simulations on related systems.17,18
To estimate the difference in melting temperatures between the dimer and trimer forms, we used three different order parameters to monitor the extent of unfolding: Cα rmsd from the crystal structure, helical content, and chain dissociation (see Methods). The two association states show melting temperatures that are identical within experimental error, regardless of the order parameter employed (Table 4, Figure S5). It is worth noting that the absolute values of the observed melting temperatures are artificially high due to the use of an implicit solvent model.67–70 This systematic overestimation of Tm does not interfere with our goal to ascertain the relative stabilities of the dimer and trimer forms by MD simulations. The results obtained indicate that there is no significant difference in melting temperatures for the two oligomerization states under the conditions of the simulations.
Table 4.
Melting temperatures for the dimer and trimer oligomerization states determined by parallel tempering MD simulations.
| Order parametera | Tm (°C)b | |
|---|---|---|
| Dimer | Trimer | |
| Cα RMSD | 156 ± 4 °C | 155 ± 8 °C |
| Fraction helicity | 157 ± 4 °C | 165 ± 5 °C |
| Chain dissociation | 163 ± 4 °C | 165 ± 5 °C |
Method employed to quantify folded population (see text);
temperature for 50% unfolding as determined by the indicated order parameter.
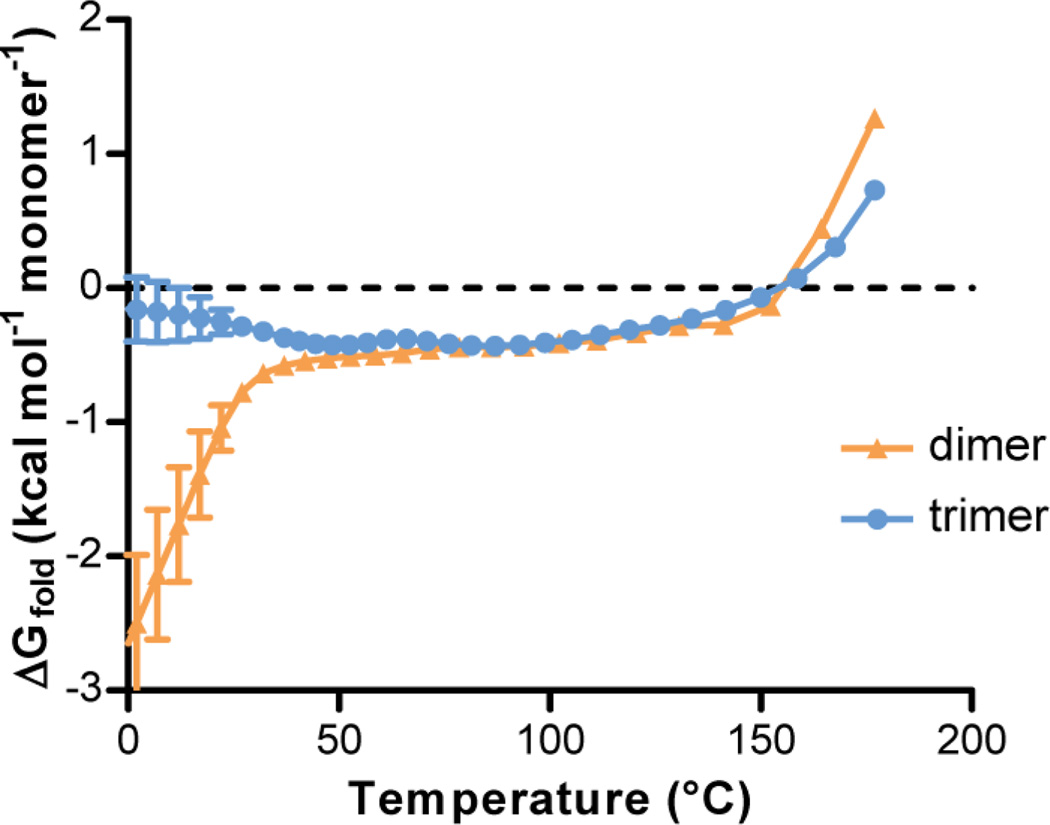
We also characterized the relative folding free energies of the dimer and trimer at different temperatures ranging from 0 to 180 °C. The extent of folding was monitored using two different order parameters: Cα rmsd (Figure 6) and the helical content (Figure S6). Regardless of the order parameter, we observe similar qualitative trends. At temperatures below ~45 °C, the dimeric form is more stable than the trimeric form. As the temperature increases from ~45 to ~155 °C (near their melting temperatures), the dimeric and trimeric forms appear to be similar in stability, indicating that both forms can exist in solution at these temperatures. The enhanced thermal stability of the trimeric form is consistent with the greater buried surface area relative to dimer observed in the crystal structure.
Figure 6.
Folding free energies of the dimer vs. the trimer computed from parallel tempering simulations at various temperatures. For these computations, conformations were collected every 5 ns (total of 180 conformations at each temperature). The folded state was defined based on Cα rmsd from the crystal structure. Uncertainties are computed as described in Methods.
To identify the key conformational states that are populated by the dimer and trimer, we generated potential of mean force (PMF) surfaces of each oligomer as a function of Cα rmsd and number of inter-chain residue contacts at the temperature of each replica in the parallel tempering simulations (Figure S7). Each simulation predominantly populates its starting state (dimer or trimer) at the lowest temperature (37 °C), with some extent of unfolding as evident by the large Cα rms deviations from the corresponding crystal structure. The apparent partial unfolding at low temperatures in the simulations is consistent with prior experimental results suggesting that the temperature-induced unfolding of the leucine zipper consists of several transitions, with the first transition starting at temperatures as low as 0 °C and the last transition involving cooperative unfolding / dissociation of the monomers.60 Our simulation model appears to be reasonable, as found by standard molecular dynamics simulations of each oligomer for 500 ns at 20 °C during which the oligomers remained folded the entire time (Cα rmsd values of 2.3 ± 0.9 Å for the dimer and 2.0 ± 0.4 Å for the trimer, Figure S8). Upon increasing the temperature, our simulations of the trimeric form reveal a dimer intermediate (with ~60 inter-chain residue contacts) that becomes increasingly populated (Figure S7). This result suggests the temperature-induced denaturation of the trimer may involve a dimeric intermediate.
DISCUSSION
Collectively, the data we report here show that the GCN4 leucine-zipper (GCN4-p1) can populate either a dimeric or trimeric coiled-coil fold depending on environment. Consistent with extensive prior work, we found the dimer fold is favored under most conditions examined, including pH 7 phosphate and pH 5.3 acetate/citrate, with added PEG or without. In a buffer composed of pH 6.6 MES/(NH4)2SO4 with added PEG, however, we obtained a high-resolution crystal structure of wild-type GCN4-p1 in a trimeric fold. We also saw evidence for some population of trimeric coiled coil in solution under partially denaturing conditions by concentration-dependent CD analysis, although sedimentation equilibrium measurements suggest a single dimer species. Parallel tempering molecular dynamics simulations starting from the two experimentally determined crystal structures suggest that while the dimer is the dominant form at low temperatures, the folding free energy of the dimer and trimer states are similar at temperatures well below Tm. Furthermore, our simulations reveal that refolding events of the trimer involve a dimeric intermediate. It is possible that the small energy gap between the dimer and trimer states could be closed or swapped through minor changes to environmental conditions.
The strongest direct evidence for the trimeric state of GCN4-p1 we have obtained is the high-resolution crystal structure. The possibility exists that crystal contacts present in the trimer lattice may influence the equilibrium between dimer and trimer in solution, effectively selecting a single species over the course of crystallization. The previous assumption presupposes some non-trivial amount of the trimer already present. Thus, it is informative to examine what about the trimer experimental conditions may shift the equilibrium toward a trimeric fold. High protein concentration would be expected to promote trimer formation by Le Chatelier’s principle. The lack of observed deviation from the ideal single-species model in any of the sedimentation equilibrium measurements (Figure S2) suggests that concentration alone is not sufficient to generate measurable amounts of trimer in solution up to the concentration accessible in the experiment. Concentration in the crystallization drops is higher than in the biophyiscal measurements; however, the same concentration of peptide (~2 mM) led to either a dimer or trimer fold in the crystal lattice, depending on buffer conditions. The above analysis suggests that something about the trimer crystallization buffer must be important.
Sedimentation equilibrium measurements suggest that the buffer/salt components from the trimer crystallization conditions do not lead to a measurable amount of trimer in solution; however, the PEG from the crystallization buffer was omitted to prevent complications from a sedimenting buffer component. PEG is commonly used as a non-ionic precipitating agent in protein crystallization but also as a “crowding agent,” a chemical additive that simulates the highly crowded environment proteins experience in a cell. The role of crowding in protein folding thermodynamics has been the subject of intensive study.71,72 Theoretical calculations suggest that crowding increases the association affinity of a macromolecular oligomerization event and that the extent of stabilization increases dramatically with the number of monomers in the assembly (i.e., a crowding-based increase in Ka will be more pronounced in a trimer vs. dimer).72 The addition of PEG stabilizes the GCN4-p1 folded state, as evidenced by CD thermal melts. The extent of stabilization is more pronounced in the trimer crystallization buffer than the conditions that favor dimer, suggesting the possibility that the addition of PEG has shifted the equilibrium toward trimer under the appropriate buffer conditions. Crowding alone cannot be responsible for the observed trimer fold, however, since a similar concentration of non-ionic precipitant was present in conditions that gave rise to the dimer crystal structure. We hypothesize that the effect of PEG as a crowding agent coupled with the buffer conditions work in concert to shift the GCN4-p1 equilibrium toward trimer under the conditions where we obtained the crystal structure in this oligomerization state.
The above data suggest that the native GCN4 leucine zipper is on the verge of two folded coiled-coil oligomerization states, the dimeric fold observed in prior studies and the trimeric structure that we report here. The favored state is dependent on context. In partially denaturing buffers, the trimer may form to some extent, although the dimer is still favored. Crowding by addition of PEG, similar to the crowded environment of a cell interior, can favor trimer formation under certain conditions. The potential biological relevance of this observation is strengthened by a prior study that showed the GCN4 leucine zipper can act as a functional substitute for the oligomerization domain of heat shock transcription factor (HSF), a trimeric DNA-binding protein.73 In that study, GCN4-HSF chimeras with the leucine zipper from GCN4 and DNA binding region from HSF were able to bind three-box DNA segments with affinity similar to wild-type HSF. These observations led the authors to propose that DNA binding might enforce stoichiometry and alter the preferred oligomerization state by bringing a defined number of GCN4 leucine-zipper domains in close proximity. Our results suggest that the crowded cell environment, as well as the templating effect of the DNA, may be responsible for the functional equivalence of the GCN4-HSF chimera to wild-type HSF.
The hydrophobic core composition of GCN4-p1 (Val at a heptad positions and Leu at d heptad positions) has long been known to be poorly discriminating between dimeric and trimeric oligomerization states.5,13,74 A variant with this core (GCN4-pVL) forms a mixture of the two assemblies in solution.5 The introduction of an a-position Asn residue to the Val at a, Leu at d context (to generate native GCN4-p1) shifts the equilibrium toward dimer; however, our results show that the trimer state is still accessible to the wild-type protein under appropriate conditions. Recent bioinformatics analyses have quantified the ability of different amino acid residues to discriminate between dimer and trimer oligomerization states when placed in the hydrophobic core of coiled-coil proteins.75 Consistent with prior work, a-position Asn residues were found to favor dimeric states, although the control exerted is not absolute. A search of an online repository of coiled coil structures76 reveals nine a-position Asn residues in parallel, homotrimeric coiled-coil proteins (Table S2). In most of these cases, a pocket exists in the hydrophobic core in the vicinity of the Asn that is occupied by an ordered water or ion – similar to the water-filled pocket we observed in the GCN4-p1 trimer. Presumably, this pocket contributes to the destabilization of the trimer state relative to the dimer (where the core is well-packed).
In summary, we have reported here that the folding behavior of the GCN4 dimerization domain, a canonical and well-studied coiled coil, is more complex than was previously appreciated. High-resolution crystal structures show the wild-type sequence can adopt a dimeric or trimeric fold, depending on environment. Biophysical measurements suggest populations of both oligomerization states in the presence of crowding agents and possibly under partially denaturing conditions. Parallel tempering molecular dynamics simulations suggest that the dimer and trimer folds are quite close in energy. The microsecond time scales involved make these the most extensive set of simulations on the GCN4 leucine zipper published to date. Our findings have implications in ongoing efforts to establish predictive algorithms for coiled-coil folds and the selection of model systems for design and mutational studies where oligomerization state specificity is an important consideration. Moreover, our results provide further evidence for the complexity of folding behavior in even the simplest coiled-coil proteins. One take home message is the potential importance of environmental conditions in determining the preferred oligomerization state. By necessity, most biophysical studies of protein folding are carried out in dilute aqueous solution at or below room temperature; however, it is important to consider the potential consequences of using such biophysical observations to infer association behavior in the complex and crowded cellular environment.
Supplementary Material
ACKNOWLEDGMENT
We thank the University of Pittsburgh and the National Science Foundation (CAREER award DMR-1149067 to W.S.H. and MCB-0845216 to L.T.C.) for funding. This work used an NSF XSEDE allocation to W.S.H. (TG-MCB110174) and L.T.C. (TG-MCB100109) on the Forge GPU cluster and the University of Pittsburgh’s Center for Simulation and Modeling Linux Cluster. We are grateful for helpful discussions with Dr. John Chodera and his assistance with using the OpenMM package and MBAR method. Sedimentation equilibrium studies were performed at the University of Wisconsin - Madison Biophysics Instrumentation Facility, which was established with support from the University of Wisconsin - Madison and grants BIR-9512577 (NSF) and S10 RR13790 (NIH).
ABBREVIATIONS
- CD
circular dichroism
- HPLC
high-performance liquid chromatography
- HSF
heat-shock transcription factor
- MALDI-TOF
matrix-assisted laser desorption ionization time of flight
- MBAR
multistate Bennett acceptance ratio
- MD
molecular dynamics
- MES
2-(N-morpholino)ethanesulfonic acid
- PEG
polyethylene glycol
- PMF
potential of mean force
- TFA
trifluoroacetic acid
- UV
ultraviolet
Footnotes
Supporting Information. Figures S1–S8, Table S1, and supplementary text. This material is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- 1.Rackham OJL, Madera M, Armstrong CT, Vincent TL, Woolfson DN, Gough J. The evolution and structure prediction of coiled coils across all genomes. J. Mol. Biol. 2010;403:480–493. doi: 10.1016/j.jmb.2010.08.032. [DOI] [PubMed] [Google Scholar]
- 2.Lupas AN, Gruber M. The structure of α-helical coiled coils. Adv. Protein Chem. 2005;70:37–78. doi: 10.1016/S0065-3233(05)70003-6. [DOI] [PubMed] [Google Scholar]
- 3.Woolfson DN, Bartlett GJ, Bruning M, Thomson AR. New currency for old rope: From coiled-coil assemblies to α-helical barrels. Curr. Opin. Struct. Biol. 2012;22:432–441. doi: 10.1016/j.sbi.2012.03.002. [DOI] [PubMed] [Google Scholar]
- 4.Marsden HR, Kros A. Self-assembly of coiled coils in synthetic biology: Inspiration and progress. Angew. Chem. Int. Ed. 2010;49:2988–3005. doi: 10.1002/anie.200904943. [DOI] [PubMed] [Google Scholar]
- 5.Harbury PB, Zhang T, Kim PS, Alber T. A switch between two-, three-, and four-stranded coiled coils in GCN4 leucine-zipper mutants. Science. 1993;262:1401–1407. doi: 10.1126/science.8248779. [DOI] [PubMed] [Google Scholar]
- 6.Liu J, Zheng Q, Deng Y, Cheng CS, Kallenbach NR, Lu M. A seven-helix coiled coil. Proc. Natl. Acad. Sci. USA. 2006;103:15457–15462. doi: 10.1073/pnas.0604871103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zaccai NR, Chi B, Thomson AR, Boyle AL, Bartlett GJ, Bruning M, Linden N, Sessions RB, Booth PJ, Brady RL, Woolfson DN. A de novo peptide hexamer with a mutable channel. Nat. Chem. Biol. 2011;7:935–941. doi: 10.1038/nchembio.692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Oakley MG, Hollenbeck JJ. The design of antiparallel coiled coils. Curr. Opin. Struct. Biol. 2001;11:450–457. doi: 10.1016/s0959-440x(00)00232-3. [DOI] [PubMed] [Google Scholar]
- 9.Schnarr NA, Kennan AJ. Peptide tic-tac-toe: Heterotrimeric coiled-coil specificity from steric matching of multiple hydrophobic side chains. J. Am. Chem. Soc. 2002;124:9779–9783. doi: 10.1021/ja0174940. [DOI] [PubMed] [Google Scholar]
- 10.O'Shea EK, Rutkowski R, Kim PS. Evidence that the leucine zipper is a coiled coil. Science. 1989;243:538–542. doi: 10.1126/science.2911757. [DOI] [PubMed] [Google Scholar]
- 11.O'Shea EK, Klemm JD, Kim PS, Alber T. X-Ray structure of the GCN4 leucine zipper, a two-stranded, parallel coiled coil. Science. 1991;254:539–544. doi: 10.1126/science.1948029. [DOI] [PubMed] [Google Scholar]
- 12.Gonzalez L, Brown RA, Richardson D, Alber T. Crystal structures of a single coiled-coil peptide in two oligomeric states reveal the basis for structural polymorphism. Nat. Struct. Biol. 1996;3:1002–1010. doi: 10.1038/nsb1296-1002. [DOI] [PubMed] [Google Scholar]
- 13.Gonzalez L, Woolfson DN, Alber T. Buried polar residues and structural specificity in the GCN4 leucine zipper. Nat. Struct. Biol. 1996;3:1011–1018. doi: 10.1038/nsb1296-1011. [DOI] [PubMed] [Google Scholar]
- 14.Akey DL, Malashkevich VN, Kim PS. Buried polar residues in coiled-coil interfaces. Biochemistry. 2001;40:6352–6360. doi: 10.1021/bi002829w. [DOI] [PubMed] [Google Scholar]
- 15.Knappenberger JA, Smith JE, Thorpe SH, Zitzewitz JA, Matthews CR. A buried polar residue in the hydrophobic interface of the coiled-coil peptide, GCN4-p1, plays a thermodynamic, not a kinetic role in folding. J. Mol. Biol. 2002;321:1–6. doi: 10.1016/s0022-2836(02)00592-2. [DOI] [PubMed] [Google Scholar]
- 16.Ciani B, Bjelic S, Honnappa S, Jawhari H, Jaussi R, Payapilly A, Jowitt T, Steinmetz MO, Kammerer RA. Molecular basis of coiled-coil oligomerization-state specificity. Proc. Natl. Acad. Sci. USA. 2010;107:19850–19855. doi: 10.1073/pnas.1008502107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yadav MK, Leman LJ, Price DJ, Brooks CL, Stout CD, Ghadiri MR. Coiled coils at the edge of configurational heterogeneity: Structural analyses of parallel and antiparallel homotetrameric coiled coils reveal configurational sensitivity to a single solvent-exposed amino acid substitution. Biochemistry. 2006;45:4463–4473. doi: 10.1021/bi060092q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Su L, Cukier RI. Hamiltonian replica exchange method studies of a leucine zipper dimer. J. Phys. Chem. B. 2009;113:9595–9605. doi: 10.1021/jp900309q. [DOI] [PubMed] [Google Scholar]
- 19.Cukier RI. A hamiltonian replica exchange method for building protein-protein interfaces applied to a leucine zipper. J. Chem. Phys. 2011;134:045104. doi: 10.1063/1.3548074. [DOI] [PubMed] [Google Scholar]
- 20.Gee J, Shell MS. Two-dimensional replica exchange approach for peptide-peptide interactions. J. Chem. Phys. 2011;134:064112. doi: 10.1063/1.3551576. [DOI] [PubMed] [Google Scholar]
- 21.Ramos J, Lazaridis T. Energetic determinants of oligomeric state specificity in coiled coils. J. Am. Chem. Soc. 2006;128:15499–15510. doi: 10.1021/ja0655284. [DOI] [PubMed] [Google Scholar]
- 22.Missimer JH, Steinmetz MO, Jahnke W, Winkler FK, van Gunsteren WF, Daura X. Molecular-dynamics simulations of C- and N-terminal peptide derivatives of GCN4-p1 in aqueous solution. Chem. Biodivers. 2005;2:1086–1104. doi: 10.1002/cbdv.200590078. [DOI] [PubMed] [Google Scholar]
- 23.Lee H, Larson RG. Prediction of the stability of coiled coils using molecular dynamics simulations. Mol. Simulat. 2007;33:463–473. [Google Scholar]
- 24.Price JL, Horne WS, Gellman SH. Structural consequences of β-amino acid preorganization in a self-assembling α/β-peptide: Fundamental studies of foldameric helix bundles. J. Am. Chem. Soc. 2010;132:12378–12387. doi: 10.1021/ja103543s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Collaborative Computational Project Number 4. The CCP4 suite: Programs for protein crystallography. Acta Crystallogr., Sect D: Biol. Crystallogr. 1994;50:760–763. doi: 10.1107/S0907444994003112. [DOI] [PubMed] [Google Scholar]
- 26.Murshudov GN, Vagin AA, Dodson EJ. Refinement of macromolecular structures by the maximum-likelihood method. Acta Crystallogr., Sect D: Biol. Crystallogr. 1997;53:240–255. doi: 10.1107/S0907444996012255. [DOI] [PubMed] [Google Scholar]
- 27.Emsley P, Cowtan K. Coot: Model-building tools for molecular graphics. Acta Crystallogr., Sect D: Biol. Crystallogr. 2004;60:2126–2132. doi: 10.1107/S0907444904019158. [DOI] [PubMed] [Google Scholar]
- 28.Langer G, Cohen SX, Lamzin VS, Perrakis A. Automated macromolecular model building for X-ray crystallography using ARP/wARP version 7. Nat. Protoc. 2008;3:1171–1179. doi: 10.1038/nprot.2008.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Adams PD, Afonine PV, Bunkoczi G, Chen VB, Davis IW, Echols N, Headd JJ, Hung LW, Kapral GJ, Grosse-Kunstleve RW, McCoy AJ, Moriarty NW, Oeffner R, Read RJ, Richardson DC, Richardson JS, Terwilliger TC, Zwart PH. PHENIX: A comprehensive Python-based system for macromolecular structure solution. Acta Crystallogr., Sect D: Biol. Crystallogr. 2010;66:213–221. doi: 10.1107/S0907444909052925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Strelkov SV, Burkhard P. Analysis of α-helical coiled coils with the program TWISTER reveals a structural mechanism for stutter compensation. J. Struct. Biol. 2002;137:54–64. doi: 10.1006/jsbi.2002.4454. [DOI] [PubMed] [Google Scholar]
- 31.Dundas J, Ouyang Z, Tseng J, Binkowski A, Turpaz Y, Liang J. CASTp: Computed atlas of surface topography of proteins with structural and topographical mapping of functionally annotated residues. Nucleic Acids Res. 2006;34:W116–W118. doi: 10.1093/nar/gkl282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Krissinel E, Henrick K. Inference of macromolecular assemblies from crystalline state. J. Mol. Biol. 2007;372:774–797. doi: 10.1016/j.jmb.2007.05.022. [DOI] [PubMed] [Google Scholar]
- 33.Gill SC, Vonhippel PH. Calculation of protein extinction coefficients from amino-acid sequence data. Anal. Biochem. 1989;182:319–326. doi: 10.1016/0003-2697(89)90602-7. [DOI] [PubMed] [Google Scholar]
- 34.Becktel WJ, Schellman JA. Protein stability curves. Biopolymers. 1987;26:1859–1877. doi: 10.1002/bip.360261104. [DOI] [PubMed] [Google Scholar]
- 35.Shortle D, Meeker AK, Freire E. Stability mutants of staphylococcal nuclease: Large compensating enthalpy entropy changes for the reversible denaturation reaction. Biochemistry. 1988;27:4761–4768. doi: 10.1021/bi00413a027. [DOI] [PubMed] [Google Scholar]
- 36.Betz S, Fairman R, Oneil K, Lear J, Degrado W. Design of 2-stranded and 3-stranded coiled-coil peptides. Phil. TransRSoc. Lond. B. 1995;348:81–88. doi: 10.1098/rstb.1995.0048. [DOI] [PubMed] [Google Scholar]
- 37.Laue TM, Shah BD, Ridgeway TM, Pelletier SL. Computer-aided interpretation of analytical sedimentation data for proteins. In: Harding SE, Rowe AJ, Horton JC, editors. Analytical Ultracentrifugation in Biochemistry and Polymer Science. Cambridge, UK: The Royal Society of Chemistry; 1992. pp. 90–146. [Google Scholar]
- 38.Perkins SJ. Protein volumes and hydration effects. EurJBiochem. 1986;157:169–180. doi: 10.1111/j.1432-1033.1986.tb09653.x. [DOI] [PubMed] [Google Scholar]
- 39.Durchschlag H, Zipper P. Calculation of the partial volume of organic compounds and polymers. Prog. Colloid Polym. Sci. 1994;94:20–39. [Google Scholar]
- 40.Prakash V, Timasheff SN. The calculation of partial specific volumes of proteins in 8 M urea solution. Anal. Biochem. 1981;117:330–335. doi: 10.1016/0003-2697(81)90788-0. [DOI] [PubMed] [Google Scholar]
- 41.Laue TM. Sedimentation equilibrium as thermodynamic tool. Methods Enzymol. 1995;259:427–452. doi: 10.1016/0076-6879(95)59055-2. [DOI] [PubMed] [Google Scholar]
- 42.Hukushima K, Nemoto K. Exchange monte carlo method and application to spin glass simulations. J. Phys. Soc. Jpn. 1996;65:1604–1608. [Google Scholar]
- 43.Hansmann U. Parallel tempering algorithm for conformational studies of biological macromolecules. Chem. Phys. Lett. 1997;281:140–150. [Google Scholar]
- 44.Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 45.Friedrichs MS, Eastman P, Vaidyanathan V, Houston M, Legrand S, Beberg AL, Ensign DL, Bruns CM, Pande VS. Accelerating molecular dynamic simulation on graphics processing units. J. Comput. Chem. 2009;30:864–872. doi: 10.1002/jcc.21209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Eastman P, Pande V. OpenMM: A hardware-independent framework for molecular simulations. Comput. Sci. Eng. 2010;12:34–39. doi: 10.1109/MCSE.2010.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Eastman P, Pande VS. Efficient nonbonded interactions for molecular dynamics on a graphics processing unit. J. Comput. Chem. 2010;31:1268–1272. doi: 10.1002/jcc.21413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Eastman P, Pande VS. CCMA: A robust, parallelizable constraint method for molecular simulations. J. Chem. Theory. Comput. 2010;6:434–437. doi: 10.1021/ct900463w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chodera JD, Shirts MR. Replica exchange and expanded ensemble simulations as Gibbs sampling: Simple improvements for enhanced mixing. J. Chem. Phys. 2011;135:194110. doi: 10.1063/1.3660669. [DOI] [PubMed] [Google Scholar]
- 50.Garcia AE, Sanbonmatsu KY. Alpha-helical stabilization by side chain shielding of backbone hydrogen bonds. Proc. Natl. Acad. Sci. USA. 2002;99:2782–2787. doi: 10.1073/pnas.042496899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shirts MR, Chodera JD. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008;129:124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. The weighted histogram analysis method for free-energy calculations on biomolecules I: The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 53.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Onufriev A, Bashford D, Case DA. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 55.Schaefer M, Bartels C, Karplus M. Solution conformations and thermodynamics of structured peptides: Molecular dynamics simulation with an implicit solvation model. J. Mol. Biol. 1998;284:835–848. doi: 10.1006/jmbi.1998.2172. [DOI] [PubMed] [Google Scholar]
- 56.Case DA, Darden TA, Cheatham ITE, Simmerling CL, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, Roberts B, Wang B, Hayik S, Roitberg A, Seabra G, Kolossvary I, Wong KF, Paesani F, Vanicek X, Liu J, Wu X, Brozell S, Steinbrecher T, Gohlke H, Cai Q, Ye X, Wang J, Hsieh MJ, Cui G, Roe DR, Mathews DH, Seetin MG, Sagui C, Babin V, Luchko T, Gusarov S, Kovalenko A, Kollman PA. AMBER. 11 ed. San Francisco: University of California; 2010. [Google Scholar]
- 57.Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of nalkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 58.The PyMOL Molecular Graphics System Version 1.5.0.4. Schrodinger, LLC; [Google Scholar]
- 59.Crick FHC. The fourier transform of a coiled-coil. Acta Crystallogr. 1953;6:685–689. [Google Scholar]
- 60.Dragan AI, Privalov PL. Unfolding of a leucine zipper is not a simple two-state transition. J. Mol. Biol. 2002;321:891–908. doi: 10.1016/s0022-2836(02)00699-x. [DOI] [PubMed] [Google Scholar]
- 61.Harbury PB, Kim PS, Alber T. Crystal structure of an isoleucine-zipper trimer. Nature. 1994;371:80–83. doi: 10.1038/371080a0. [DOI] [PubMed] [Google Scholar]
- 62.Sindhikara DJ, Emerson DJ, Roitberg AE. Exchange often and properly in replica exchange molecular dynamics. J. Chem. Theory. Comput. 2010;6:2804–2808. doi: 10.1021/ct100281c. [DOI] [PubMed] [Google Scholar]
- 63.Earl DJ, Deem MW. Parallel tempering: Theory, applications, and new perspectives. Phys. Chem. Chem. Phys. 2005;7:3910–3916. doi: 10.1039/b509983h. [DOI] [PubMed] [Google Scholar]
- 64.Trebst S, Troyer M, Hansmann UH. Optimized parallel tempering simulations of proteins. J. Chem. Phys. 2006;124:174903. doi: 10.1063/1.2186639. [DOI] [PubMed] [Google Scholar]
- 65.Nadler W, Hansmann U. Optimizing replica exchange moves for molecular dynamics. Phys. Rev. E. 2007;76 doi: 10.1103/PhysRevE.76.057102. [DOI] [PubMed] [Google Scholar]
- 66.Zheng W, Andrec M, Gallicchio E, Levy RM. Simulating replica exchange simulations of protein folding with a kinetic network model. Proc. Natl. Acad. Sci. USA. 2007;104:15340–15345. doi: 10.1073/pnas.0704418104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Pitera JW, Swope W. Understanding folding and design: Replica-exchange simulations of "Trp-cage" miniproteins. Proc. Natl. Acad. Sci. USA. 2003;100:7587–7592. doi: 10.1073/pnas.1330954100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Nymeyer H, Garcia AE. Simulation of the folding equilibrium of alpha-helical peptides: A comparison of the generalized born approximation with explicit solvent. Proc. Natl. Acad. Sci. USA. 2003;100:13934–13939. doi: 10.1073/pnas.2232868100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Jas GS, Kuczera K. Equilibrium structure and folding of a helix-forming peptide: Circular dichroism measurements and replica-exchange molecular dynamics simulations. Biophys. J. 2004;87:3786–3798. doi: 10.1529/biophysj.104.045419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Yeh IC, Lee MS, Olson MA. Calculation of protein heat capacity from replica-exchange molecular dynamics simulations with different implicit solvent models. J. Phys. Chem. B. 2008;112:15064–15073. doi: 10.1021/jp802469g. [DOI] [PubMed] [Google Scholar]
- 71.Zhou HX, Dill KA. Stabilization of proteins in confined spaces. Biochemistry. 2001;40:11289–11293. doi: 10.1021/bi0155504. [DOI] [PubMed] [Google Scholar]
- 72.Zhou HX, Rivas GN, Minton AP. Macromolecular crowding and confinement: Biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Drees BL, Grotkopp EK, Nelson HCM. The GCN4 leucine zipper can functionally substitute for the heat shock transcription factor's trimerization domain. J. Mol. Biol. 1997;273:61–74. doi: 10.1006/jmbi.1997.1283. [DOI] [PubMed] [Google Scholar]
- 74.Woolfson DN, Alber T. Predicting oligomerization states of coiled coils. Protein Sci. 1995;4:1596–1607. doi: 10.1002/pro.5560040818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Fletcher JM, Boyle AL, Bruning M, Bartlett GJ, Vincent TL, Zaccai NR, Armstrong CT, Bromley EHC, Booth PJ, Brady RL, Thomson AR, Woolfson DN. A basis set of de novo coiled-coil peptide oligomers for rational protein design and synthetic biology. ACS Synth. Biol. 2012;1:240–250. doi: 10.1021/sb300028q. [DOI] [PubMed] [Google Scholar]
- 76.Testa OD, Moutevelis E, Woolfson DN. CC+: A relational database of coiled-coil structures. Nucleic Acids Res. 2009;37:D315–D322. doi: 10.1093/nar/gkn675. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.