Thermodynamic dissection of estrogen receptor promoter interactions reveals that steroid receptors differentially partition their self-association and promoter binding energetics

Abstract

Steroid receptors define a family of ligand-activated transcription factors. Recent work has demonstrated that the receptors regulate distinct but overlapping gene networks, yet the mechanisms by which they do so remain unclear. We previously determined the microscopic binding energetics for progesterone receptor (PR) isoform assembly at promoters containing multiple response elements. We found that the two isoforms (PR-A and PR-B) share nearly identical dimerization and intrinsic DNA binding free energies, but maintain large differences in cooperative free energy. Moreover, cooperativity can be modulated by monovalent ion binding and promoter layout, suggesting that differences in cooperativity might control isoform-specific promoter occupancy and thus receptor function. To determine whether cooperative binding energetics are common to other members of the steroid receptor family, we dissected the thermodynamics of estrogen receptor-α (ER-α):promoter interactions. We find that the ER-α intrinsic DNA binding free energy is identical to that of the PR isoforms. This was expected, noting that receptor DNA binding domains are highly conserved. Unexpectedly, ER-α generates negligible cooperativity – orders of magnitude less than predicted based on our studies of the PR isoforms. However, analysis of the cooperativity term suggests that it reflects a balance between highly favorable cooperative stabilization and unfavorable promoter bending. Moreover, ER-α cooperative free energy is compensated for by a large increase in dimerization free energy. Collectively, the results demonstrate that steroid receptors differentially partition not only cooperative energetics, but also dimerization energetics. We speculate that this ability serves as a framework for regulating receptor-specific promoter occupancy and thus receptor-specific gene regulation.

The estrogen receptor (ER) is a member of the steroid receptor family of ligand-activated transcription factors (1). Other members include the androgen receptor (AR), glucocorticoid receptor (GR), mineralocorticoid receptor (MR) and progesterone receptor (PR). ER exists naturally as two isoforms (ER-α and ER-β), as does PR (PR-A and PR-B). Shown in Figure 1A is a schematic of ER-α, showing the modular structure common to all the receptors. Centrally located is the highly conserved DNA binding domain (DBD). C-terminal to the DBD is a moderately conserved hormone-binding domain (HBD) thought to be the primary interface for receptor dimerization. Transcriptional activation functions (AFs) are located within the HBD and N-terminal to the DBD.

Figure 1.

Estrogen receptor-α domain structure and promoter assembly states. (A) Schematic of ER-α primary sequence. Functional domains as labeled: DBD, DNA binding domain; LBD, ligand binding domain; AF, activation functions are present in both the N-terminus and LBD. (B) Schematic describing the dimer binding pathway for ER-α assembling onto the ERE₂ promoter. The circle represents an ER-α monomer. Squares represent ER-α dimers either free in solution (k_di) or bound to an ERE (k_int). Binding at both promoter sites can be accompanied by intersite cooperative interactions (k_c). Events potentially associated with cooperativity are illustrated through protein-protein contacts and bending of promoter DNA. The arrow on the promoter indicates transcriptional start site. (C) Sequence of the ERE₂ promoter in the vicinity of the two binding sites, ERE 1 and ERE 2. Underlined sequences indicate the half-sites of each palindromic response element.

Biochemical evidence suggests that all steroid receptors follow a similar mode of action. Ligand-bound receptors dimerize in solution; bind to palindromic response elements typically located upstream of the transcriptional start site; and recruit coactivator proteins to initiate transcription. Although this model provides a strong qualitative framework for explaining steroid receptor function, it nonetheless remains incomplete. For example, due to the highly conserved DBD, steroid receptors bind to identical or nearly identical response elements in vitro. Yet in vivo the proteins regulate distinct but overlapping gene networks (2–4). The molecular basis by which this occurs is unknown. A focus of our research is to determine the quantitative mechanisms responsible for receptor-specific gene regulation – how do homologous transcription factors regulate different subsets of genes?

To address this problem, we are dissecting the energetics of receptor-promoter interactions and correlating the results to functional outcomes. Shown in Figure 1B are the microstate energetic terms associated with receptor assembly at a simple two-site promoter. As already noted, receptors are thought to dimerize in the absence of DNA (k_di) and then bind as pre-formed dimers to their response elements (k_int). Binding to promoters containing multiple response elements may or may not be coupled to intersite cooperativity (k_c). Each of these parameters represents a discrete microscopic interaction and thus has a clear molecular interpretation. By contrast, the more traditionally measured apparent binding constant, K_app, represents an irreducible composite of some or all of these terms and therefore offers little mechanistic insight.

We previously determined the microscopic interaction parameters for PR-A and PR-B binding to the promoter layout in Figure 1B, containing two progesterone response elements (PRE₂) (5, 6). We found that although both isoforms have similar apparent promoter binding affinities, PR-B exhibits an overall increased affinity, largely via an approximately 100-fold enhancement in cooperativity (k_c). Interestingly, this difference correlated with the stronger transcriptional activity of PR-B compared to PR-A at this promoter. However, it also raised the question of how PR-A could possibly assemble at promoters when in the presence of PR-B, given the latter’s more favorable binding energetics. Simulations revealed that simply increasing PR-A cooperativity or decreasing PR-B cooperativity allowed preferential binding of PR-A. We subsequently discovered that differences in promoter binding site layout could indeed increase PR-A cooperativity (7). Likewise, PR-B cooperative interactions could be selectively decreased via an allosteric linkage to monovalent cation binding (8). Combined with our observation that cooperativity was necessary for efficient coactivator recruitment and therefore transcriptional activation (9), these results suggested a fundamental role for cooperative binding energetics in isoform-specific gene regulation.

As a step toward addressing whether cooperative binding energetics are common to different receptors as well as different isoforms, we dissected the energetics of ER-α:promoter interactions. ER-α is generally a strong transcriptional activator relative to ER-β, much like PR-B is to PR-A (10, 11). We therefore hypothesized that ER-α, like PR-B, might exhibit the common attribute of strong cooperativity (k_c) on a promoter analogous to that used in our previous work with the PR isoforms. This promoter (ERE₂) is identical in sequence to the previously described PRE₂ promoter, with the exception that two estrogen response elements derived from the vitellogenin promoter replace the PRE sequences (ERE₂; Figure 1C). Surprisingly, we found that ER-α exhibits negligible cooperativity – orders of magnitude less than predicted based on our studies of PR-B. This observation raised the question of how ER-α generates full promoter occupancy and thus maximal function on multisite promoters. We found that the weak cooperative free energy of ER-α is compensated for by a corresponding increase in dimerization free energy relative to PR-B. Thus, homologous receptors differentially partition their promoter binding energetics via compensating processes.

However, these results do not imply that ER-α is a noncooperative binding protein. Analysis of the molecular contributions to the k_c term reveals that the observed weak cooperativity of ER-α reflects a balance of favorable cooperative stabilization (likely via protein-protein contacts) offset by unfavorable DNA bending. Thus ER-α, like the PR isoforms, may also be able to modulate cooperative assembly as a function of promoter layout (and possibly solution conditions). We speculate that the ability of receptors to differentially partition both cooperative and dimerization energetics serves as a mechanism for generating receptor-specific gene regulation.

MATERIALS AND METHODS

Expression and purification of full-length, human ER-α

A baculovirus vector containing human ER-α (amino acids 1–595) fused to an N-terminal hexa-histadine tag (His-ER-α) was generated in-house. An expression vector containing human ER-α fused to an N-terminal FLAG tag (FLAG-ER-α) was donated by Dr. Lee Kraus (Cornell University). Both constructs were expressed in baculovirus-infected Sf9 cells using a multiplicity of infection of 1. Cells were treated with 1 μM 17β-estradiol (E2) twenty-four hours post-infection and harvested twenty-four hours later.

All purification steps were carried out at 4°C and in the presence of 10 μM E2. Cells containing His-ER-α were Dounce homogenized in a buffer containing 20 mM Tris or AMPSO, pH 8.7 at 4°C, 500 mM NaCl, 10% glycerol, 10 mM β-ME, 10 μM E2, 30 mM imidazole and protease inhibitors (Complete, EDTA-free, Roche). Following centrifugation at 100,000 × g for 70 min, the supernatant containing His-ER-α was incubated for one hour with Ni-NTA Agarose (Qiagen). The resin was then washed with lysis buffer and eluted using the same buffer now containing 250 mM imidazole. The eluted receptor was chromatographed on a Sephacryl S-300 size exclusion column (GE Healthcare) equilibrated in 20 mM Tris or AMPSO, pH 8.7 at 4°C, 500 mM NaCl, 10% glycerol, 10 mM β-ME, and 10 μM E2. Fractions containing His-ER-α were aliquoted, flash frozen and stored in liquid nitrogen. His-ER-α concentration was determined using a calculated extinction coefficient of 69,510 mol⁻¹ cm⁻¹ (12).

Cells containing FLAG-ER-α were treated as described for His-ER-α, using a buffer containing 20 mM Tris, pH 8.7 at 4°C, 500 mM NaCl, 10% glycerol, 10 mM β-ME, 10 μM E2 and protease inhibitors. FLAG-ER-α was partially purified from the supernatant using Anti-FLAG M2 Affinity Gel (Sigma). The resin was washed with lysis buffer and the receptor was eluted using 0.3 mg/ml FLAG peptide (Sigma). FLAG-ER-α was then chromatographed on a Sephacryl S-300 size exclusion column as described for His-ER-α. Due to the lower yield of FLAG-ER-α, receptor fractions were pooled, dialyzed into the chromatography buffer containing 100 mM NaCl, and concentrated using Q-Sepharose resin. The receptor was eluted using 500 mM NaCl, aliquoted and flash frozen in liquid nitrogen. FLAG-ER-α concentration was determined using a calculated extinction coefficient of 64,010 mol⁻¹ cm⁻¹ (12).

Sedimentation velocity

Sedimentation velocity experiments were carried out using a Beckman XL-A analytical ultracentrifuge equipped with absorbance optics, using two-sector Epon centerpieces and an An-50 rotor. ER-α (His or FLAG-tagged) was dialyzed into 20 mM HEPES, pH 8.0 at 4 °C, 2.5 mM MgCl₂, 1.0 mM CaCl₂, 0.5 mM DTT, 10 μM E2 and NaCl concentrations from ranging 100 mM to 1M. Other than steroid type, these conditions were identical to our previous work on the PR isoforms. Different buffers (e.g. Tris versus HEPES) did not affect ER-α sedimentation properties. The receptor was sedimented at concentrations ranging from 0.2 to 2 μM, at 50,000 rpm and 4°C. Samples were monitored at 230 nm and scans were collected as quickly as the instrument would allow.

Sedimentation coefficient (s) distributions were calculated using the program Sedfit (13) and corrected to standard conditions (water at 20°C) using standard methods (14). A frictional coefficient (f) was calculated using the Svedberg equation:

$$s=\frac{M(1-\overline{v}·\rho )}{N_A·f}$$ (1)

where M is the calculated ER-α molecular weight, v̄ is the partial specific volume (15), ρ is the solvent density (16), and N_A is Avogadro’s number.

Sedimentation equilibrium

Sedimentation equilibrium experiments were carried out under identical buffer conditions as the velocity experiments. His-ER-α at 0.5, 1.0 and 2.0 μM was sedimented in a six-channel Epon centerpiece and at a rotor speed of 10,800 rpm. This data was analyzed by nonlinear least-squares as implemented in NONLIN (17), in order to resolve the reduced molecular mass (σ), using the equation

$$Y_r=\delta +\alpha exp[\sigma \left(\frac{r^2-r_0^2}{2}\right)]$$ (2)

where Y_r is the absorbance at radius r, δ is the baseline offset, and α is the absorbance at the reference radius, r₀. The reduced molecular mass, σ, is defined as

$$\sigma =\frac{M(1-\overline{v}\rho ){\omega }^2}{RT}$$ (3)

where M is the weight-average molecular mass of a single, ideal species, v̄ is the partial specific volume, ρ is the solvent density as calculated on the basis of the buffer composition and temperature (16), ω is the angular velocity, R is the gas constant and T is the temperature in Kelvin.

DNA preparation for DNase I footprinting

A plasmid containing two palindromic estrogen response elements (ERE₂) derived from the vitellogenin promoter was donated by Dr. Kathryn Horwitz (University of Colorado Anschutz Medical Campus) (18, 19). Both EREs, spaced 25 base pairs apart, contain the sequence AGGTCACAGTGACCT. A mutant template that eliminates binding to site 1 (ERE_1-) was created in-house, using the sequence AAATCACAGTGATTT. Each promoter fragment was excised from the parent plasmid using Nae I and Hind III digestion. The fragments (1.3 kb) were gel purified and ³²P-end labeled on the sense strand with a Klenow (Invitrogen) fill-in reaction. Other than response element sequence, the ERE₂ and ERE_1- templates are identical to the PRE₂ and PRE_1- constructs used in our previous work.

Individual-site binding experiments

Quantitative DNase I footprint titrations were carried out as described by Ackers and co-workers (20, 21) with slight modifications (22). Briefly, reactions were carried out in an assay buffer containing 20 mM HEPES, pH 8.0, 100 mM NaCl, 1 mM DTT, 1 mM CaCl₂, 2.5 mM MgCl₂, 10 μM E2, 100 μg/mL BSA and 2 μg/mL salmon sperm DNA. Other than BSA and salmon sperm DNA, this buffer is identical to the 100 mM NaCl buffer used in the sedimentation experiments. Footprint titrations were also carried out for PR-B under identical conditions using a PRE₂ and PRE_1- promoter, and substituting E2 with progesterone. Finally, noting that PR-B cooperativity is eliminated in the presence of KCl, we carried out control ER-α footprint titrations using 100 mM KCl rather than NaCl. No differences were observed (data not shown).

Each reaction contained 20,000 cpm of labeled ERE₂ or ERE_1- promoter sequence. The concentration of DNA in the reactions (maximally 60 pM) was kept well below the intrinsic binding affinity of ER-α to allow the assumption [ER-α_free] ~ [ER-α_total]. ER-α was added to each reaction to cover four orders of magnitude, ranging from tens of picomolar to sub-micromolar. Reactions were allowed to equilibrate at 4°C for 45 minutes to two hours prior to adding DNase I. The DNase concentration approximated “single hit kinetics” so as to not perturb the reaction equilibrium (20). Digested fragments were electrophoresed using 6% acrylamide-urea gels. The gels were visualized using phosphorimaging, and individual-site binding isotherms were calculated as described previously (21) using ImageQuant.

Resolution of microscopic interaction free energies

Footprint titrations resolve the fractional occupancy of receptor binding at each site. The statistical thermodynamic expressions that describe the individual-site binding isotherms are constructed by summing the probabilities of each microscopic species that contributes to binding at each site. A detailed approach for creating each mathematical formulation has been presented elsewhere (23). Briefly summarized, the probability (f_s) of each microscopic species is defined as:

$$f_s=\frac{e^{(-\mathrm{\Delta }{G}_s/RT)}{[x]}^j}{{\sum }_{s=1}^j{e}^{(-\mathrm{\Delta }{G}_s/RT)}{[x]}^j}$$ (4)

where ΔG_s is the free energy of configuration s relative to the reference state, x is the ER-α monomer concentration (calculated from an assumed dimerization constant, k_di) and j is the stoichiometry of ER-α monomer bound to an ERE. R is the gas constant, and T is the temperature in Kelvin. The relationship between each free energy change and its association constant is defined via the standard expression ΔG_i = −RT ln k_i

The microstates and free energy terms associated with ER-α binding to the ERE₂ promoter (Figure 1B) are shown in Table 1. Using this model, the fractional saturation (Ȳ) of dimer binding to site 1 of the ERE₂ promoter is the sum of the probabilities for the isolated dimer binding event at that site (species 2) and the cooperative binding reaction with the adjacently bound dimer 2 (species 4). Expressed in units of free monomer concentration (as determined from the estimated dimerization constant), the expression for fractional saturation is:

$${\overline{Y}}_{{\mathit{ERE}}_2}=\frac{k_{di}{k}_{int}{x}^2+k_{di}^2{k}_{int}^2{k}_c{x}^4}{1+2k_{di}{k}_{int}{x}^2+k_{di}^2{k}_{int}^2{k}_c{x}^4}$$ (5)

where k_di and x are as defined above, k_int is the intrinsic binding affinity for an ER-α dimer binding to an ERE, and k_c represents the intersite cooperativity contribution. Since the sequence of site 2 of the ERE₂ is identical to site 1, the equation also describes binding to the second site. Finally, assembly of an ER-α dimer onto the ERE_1- promoter, where the mutated site 1 no longer binds ER, is expressed as:

$${\overline{Y}}_{{\mathit{ERE}}_{1-}}=\frac{k_{di}{k}_{int}{x}^2}{1+k_{di}{k}_{int}{x}^2}$$ (6)

where x is the concentration of ER-α in monomer units. The microscopic binding constants, k_int and k_c, were resolved by simultaneously fitting the individual-site isotherms from the ERE₂ and ERE_1- promoters as a function of fixed dimerization constant, k_di, using the program Scientist (Micromath, Inc.).

Table 1.

Species distributions, binding constants and free energy changes for ER-α dimer assembly onto the ERE₂ promoter

Species Number	Species Schematic	Microscopic constant	Free Energy Contributiona
1		--	reference state
2		kint	ΔGint
3		kint	ΔGint
4		kint 2 · kc	2·ΔGint + ΔGc

^aThe free energy change is related to each microscopic association constant through the relationship ΔG_i = −RTlnk_i, where R is the gas constant and T is temperature in Kelvin.

In addition to analyzing the fractional occupancy at the two ER-α binding sites, the receptor-induced hypersensitive region that appears between the two binding sites of the ERE₂ was quantified and interpreted as reporting on the fully ligated state (Table 1, species 4). The expression describing the hypersensitivity was therefore modeled as:

$${\overline{Y}}_{\mathit{Hyper}}=\frac{k_{di}^2{k}_{int}^2{k}_c{x}^4}{1+2k_{di}{k}_{int}{x}^2+k_{di}^2{k}_{int}^2{k}_c{x}^4}$$ (7)

The hypersensitivity data were globally fit with the ERE_1- isotherms using Equation 6 to resolve the intrinsic binding and cooperativity parameters (24, 25).

Finally, because protein interactions at each binding site do not completely protect from DNase activity, all binding and hypersensitivity isotherms were treated as transition curves fit to upper (m) and lower (b) endpoints using the equation:

$${\overline{Y}}_{\mathit{app}}=b+(m-b)\overline{Y}$$ (8)

To estimate the error of the resolved parameters, and to compare parameters between different fits, Monte Carlo simulations (26) were carried out using Scientist. The experimentally determined values for k_int and k_c from each analysis and their respective model were used to simulate new data sets. Gaussian error equivalent to the standard deviation associated with the global fit was added to each data set. The new data sets were then globally analyzed, resolving new k_i values. This process was carried out for fifty iterations, and the resolved parameters from each iteration were binned as a histogram distribution. For error that was Gaussian distributed, the 68% confidence intervals were calculated using standard approaches (27). For skewed distributions, 68% confidence intervals were calculated by integrating each distribution to determine the 68% area about the median.

RESULTS

Full-length, human ER-α was expressed in baculovirus-infected Sf9 cells as an N-terminal, hexa-histidine-tagged construct. The receptor was purified to homogeneity as judged by SDS-PAGE (Figure 2A); average yield was 2 mg/L of cell culture. To confirm that we purified full-length ER-α, we carried out MALDI-TOF mass spectrometry on intact and trypsin-digested receptor. Analysis of the undigested protein resulted in a mass of 71 kDa, in good agreement with the calculated molecular weight of 70.5 kDa. Analysis of the trypsin digested peptides resolved fragment masses with the highest probability of corresponding to residues 9–581 of ER-α. Finally, the presence of the N-terminal His-tag was confirmed by immunoblotting. In order to assess any influence of the hexa-histidine tag on ER-α function, we also purified to homogeneity FLAG-tagged ER-α (data not shown); average yield was 0.6 mg/L.

Figure 2.

Purification of full-length, human ER-α and analysis by sedimentation velocity. (A) ER-α (5 μg) purified from baculovirus-infected Sf9 cells, resolved by 4–12% gradient SDS-PAGE and Coomassie stained. Molecular weight markers are indicated to left. (B) Sedimentation velocity data of His-ER-α (0.5 μM) collected at 300 mM NaCl, pH 8.0, 4°C. Circles represent scans collected at 50,000 rpm, plotted as a function of time and radial position. Solid lines represent direct fitting to the Lamm equation as implemented in Sedfit. For clarity, only every sixth scan is shown. (C) The residuals associated with the fit to the data presented in Panel B. (D) Overlaid c(s) distributions determined for three concentrations of His-ER-α: 1.7 μM (dashed grey line), 1.0 μM (solid black line) and 0.3 μM (solid grey line).

Sedimentation studies reveal that ER-α is a structurally homogeneous dimer

Sedimentation velocity was carried out to determine the hydrodynamic and self-association properties of His-tagged and FLAG-tagged ER-α. Each protein was sedimented at concentrations ranging from 0.2 to 2.0 μM, and at NaCl concentrations ranging from 0.1 to 1 M. We were unable sediment either protein at NaCl concentrations below 100 mM NaCl due to receptor insolubility.

Shown in Figure 2B are representative boundary absorbances of His-ER-α sedimented at 300 mM NaCl. Shown in Figure 2C are the corresponding sedimentation coefficient distributions (13) determined at three protein concentrations (0.3, 1.0 and 1.7 μM). Regardless of concentration, the receptor sediments as a single species with a buffer and temperature corrected sedimentation coefficient (s_20,w) of 5.7 s. c(M) analysis of the 5.7 s peak resolved a molecular weight of 124 kDa, close to the predicted molecular weight of a His-ER-α dimer (141,079 Da).

Experiments were also performed with FLAG-ER-α, resolving an s_20,w of 5.7 s and a molecular weight of 134 kDa (data not shown). This result is again comparable to a calculated molecular weight of 134,422 kDa, indicating that the N-terminal tags do not influence ER-α hydrodynamic properties. These results were independent of NaCl concentration, indicating that both proteins exist as single, non-dissociating species with a molecular weight consistent with dimer. Finally, noting that the receptors sedimented as a dimer even at the lowest protein concentration analyzed (0.2 μM or the limit of detection by absorbance optics), and that sedimentation techniques are sensitive enough to detect 10% monomer, the upper limit for the dimerization dissociation constant must be 20 nM or −9.9 kcal/mol.

In order to more rigorously determine the assembly state of His-ER-α, we carried out sedimentation equilibrium studies as a function of protein concentration and under identical buffer conditions as the sedimentation velocity experiments. Empirical studies revealed that after twenty hours, ER-α samples at concentrations greater than1 μM underwent irreversible aggregation regardless of buffer conditions. We were therefore only able to collect useful data at 0.5 μM His-ER-α. As shown in Figure 3, the data were fit to a single-species model, resolving a molecular weight of 138,586 ± 9,800 Da. This estimate is in excellent agreement with the calculated molecular weight of the His-ER-α dimer. The close agreement between the velocity and equilibrium experiments lends high confidence in interpreting the subsequent promoter binding studies.

Figure 3.

Sedimentation equilibrium analysis of His-ER-α at 300 mM NaCl, pH 8.0 and 4°C, plotted as r²/2. (A) Initial ER-α loading concentration was 0.5 μM. Circles represent absorbance at 10,800 rpm. Solid line represents best fit using a single species model. Standard deviation of the fit was 0.0054 absorbance units. (B) Residuals of fit using single species model.

Hydrodynamic properties for His-ER-α were calculated from the experimentally estimated s_20,w and a calculated dimer molecular weight. The frictional coefficient for the dimer was 1.15 × 10⁻⁷ g/s and the Stokes radius was 61 Å. Comparing the frictional coefficient of the dimer to that of a compact sphere of the same molecular weight resulted in a frictional ratio of 1.55, indicating significant hydrodynamic asymmetry. For example, modeling the dimer as a hydrated prolate ellipsoid yielded a major:minor axial ratio of 10:1. These results are summarized in Table 2.

Table 2.

Hydrodynamic properties of ER-α determined by analytical ultracentrifugation at pH 8.0, 300 mM NaCl and 4 °C

s20,w	5.7
f (g/s)	1.15 × 10−7
f/f0	1.55
Stokes radius (Å)	61
axial ratio	10:1
Mw (Da)a	125,402
Mw (Da)b	138,586 ± 9,800

^aEstimated by a c(M) analysis as implemented in Sedfit.

^bResolved molecular weight from sedimentation equilibrium.

ER-α dimers assemble at a two-site promoter with negligible cooperativity

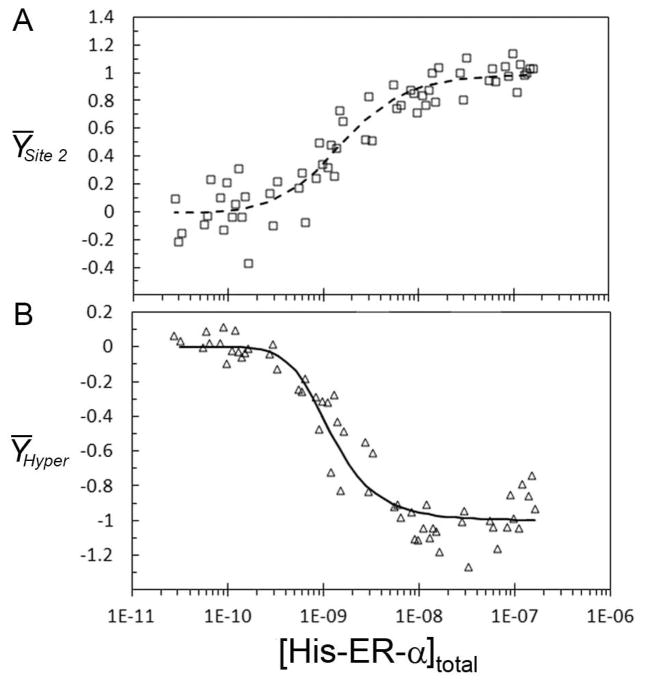
Quantitative DNase footprint titrations were used to resolve the microscopic affinities associated with ER-α dimer assembly at the ERE₂ promoter (Figure 1B). Shown in Figure 4A is a representative footprint titration collected at 100 mM NaCl. Independent dideoxy sequencing confirms that the observed protection sites correspond to the two ERE sites. We also observe significant receptor-induced DNase hypersensitivity immediately adjacent to each palindrome (thin arrows). This is seen for both the ERE₂ and ERE_1- promoter (not shown) and is attributed to previously observed ER-α induced DNA bending (28). A more dramatic hypersensitive region, located between the two bindings sites (thick arrow) and observed only on the ERE₂ promoter, is discussed later in the text.

Figure 4.

Quantitative DNase footprint titrations and individual-site binding isotherms determined from global analysis of the ERE_1- and ERE₂ promoters. (A) Representative DNase footprint titration of an ERE₂ promoter carried out in 100 mM NaCl. ER-α concentration increases from left to right. Schematic of ERE₂ structure shown to the right. Arrows at left highlight hypersensitive sites associated with ERE₂ and ERE_1- promoters (thin arrows), and site seen only with ERE₂ promoter (thick arrow). (B) Solid red circles represent binding to site 1 and open red circles represent binding to site 2 of the ERE₂ promoter (three independent footprint titrations); open blue squares represent binding to the ERE_1- promoter (three independent footprint titrations). Red and blue lines represent best fit from global analysis of nine isotherms. Binding energetics for each site of the ERE₂ promoter are identical, therefore the lines for each site overlay. Lines represent best fit assuming a dimerization dissociation constant of 1 nM; however, a visually identical result is obtained regardless of assumed k_di.

The individual-site isotherms generated from the ERE₂ template are shown in Figure 4B. An isotherm generated from the ERE_1- promoter containing only a single site is also shown. Typically, the isotherms are globally fit to Equations 5–6 in order to resolve the intrinsic binding affinity (k_int) and cooperativity (k_c) using an independently determined dimerization constant as a fixed parameter. However, because ER-α dimerization energetics are too strong to measure quantitatively, we globally fit the footprinting data as a function of fixed dimerization values ranging from 1 fM to 1 mM (Figures 5A and 5B). It is evident that both binding parameters are sensitive to the assumed dimerization constant, particularly the intrinsic binding affinity, k_int. However, since the sedimentation studies demonstrate that the dimerization dissociation constant is 20 nM or less, all values greater than 20 nM can be eliminated (shaded area). Over this smaller range, cooperativity (k_c) remains negligible, varying from 0.65 to maximally 2.0. The intrinsic dimer affinity is slightly more dependent upon the assumed dimerization constant, yet when expressed as a dissociation constant it still remains constrained within a ten-fold range of 0.1 to 1.0 nM.

Figure 5.

Resolved ER-α binding parameters and associated error surface determined as a function of dimerization constant. (A) Resolved intrinsic binding affinity, k_int, versus dimerization constant, k_di. Both parameters are plotted as dissociation constants in molar units. Error determined by Monte Carlo analysis. (B) Resolved cooperativity, k_c, versus dimerization constant, k_di. Error determined by Monte Carlo analysis. (C) Standard deviation of global fit plotted as a function of assumed k_di. Shaded area represents binding parameters eliminated from consideration as a result of the sedimentation studies.

As noted, we can only place an upper limit on the ER-α dimerization constant. However, the strong affinity observed here is entirely consistent with previous biochemical and fluorescence studies, which placed ER-α dimerization in the low nanomolar range (29, 30). Shown in Figure 5C is the error surface associated with fitting the footprint titration data as a function of k_di. It is evident that there is a minimum in the error surface at an assumed k_di of 1 nM. The error associated with this value is not statistically improved relative to any other k_di as judged by an F-statistic (31). However, simulated binding isotherms using a 1 nM dimerization constant; a comparable level of experimental error; and fit using the same range of dimerization constants generated an error surface and minimum identical to that shown in Figure 5C. For purposes of subsequent analysis and interpretation, we therefore report the k_int and k_c terms based on an assumed k_di of 1 nM. The resolved interaction energetics determined from this value are summarized in Table 3.

Table 3.

Resolved free energies (kcal/mol) from the analysis of individual site binding isotherms for ER-α and PR-B, including the hypersensitivity data for ER-α^a

	ΔGdi	ΔGint	ΔGc	Standard Deviation of fit
His-ER-αb	−11.4	−11.7 ± 0.2	−0.18 (0 to −0.5)	0.073
His-ER-αc	−11.4	−11.8 ± 0.3	−0.71 (−0.5 to −0.9)	0.071
His-ER-αd	−12.0 ± 1.2	−11.5 ± 0.3	−0.68 ± 0.3	0.077
PR-B	−6.8 ± 0.5e	−11.1 ± 0.2f	−2.3 ± 0.4f	0.045

^aAn assumed k_di of 1 nM was used for all ER-α analyses.

^bResolved free energies from global analysis of individual site binding isotherms.

^cResolved free energies from global analysis of ERE_1- and hypersensitivity data.

^dResolved free energies from global analysis of ERE_1-, ERE₂ and hypersensitivity data; errors as reported in Scientist.

^eMeasured independently using sedimentation equilibrium (33); error estimates from NONLIN.

^fError represents 68% confidence intervals as reported in the program Scientist.

DISCUSSION

Cooperative binding energetics of ER-α

The studies presented here are the first to analyze the energetics of ER-α: promoter assembly using highly purified, full-length receptor. With regard to self-association energetics, the sedimentation data indicates that ER-α is entirely dimeric to concentrations as low as 0.2 μM. We were unable to assess ER-α assembly state at protein concentrations significantly below micromolar due to the limits of absorbance optics; however, the minimum in the error surface associated with a 1nM k_di agrees well with previous estimates. With regard to ER-α hydrodynamic properties, the strong asymmetry observed by sedimentation velocity (f/f₀ = 1.55) is consistent with biochemical work indicating that the N-terminal region of ER-α is natively unfolded (32). The hydrodynamic results are also consistent with the asymmetry observed in our previous work on the two PR isoforms (33, 34).

In contrast to dimerization, there are significant discrepancies in the literature as to the extent of ER-α cooperativity. Early studies alternatively reported either strong or non-cooperative interactions (35, 36). Our own work indicates that ER-α binds the ERE₂ promoter with little to no cooperativity. Assuming a 1nM dissociation constant, we resolve a k_c term of 1.4, which translates to a ΔG_c of −0.18 kcal/mol. However, as seen in Figure 4A, receptor binding to the ERE₂ promoter is coincident with the appearance of a region of strong DNase hypersensitivity located between the two binding sites. Although not always the case, such hypersensitivity frequently arises from protein-induced distortion of the DNA. Furthermore, this intersite hypersensitivity is not observed on the ERE_1- promoter. This implies that the distortion or bending is likely coupled to cooperative interactions between adjacently bound ER-α dimers. Because the experimentally measured cooperativity was negligible, we hypothesized that the microscopic k_c term is composed of two components – an energetically favorable cooperative interaction (likely via protein-protein contacts) almost entirely offset by an energetic penalty associated with DNA bending. A prediction of this hypothesis is that the hypersensitive region seen in Figure 4A must therefore be reporting only on the fully-ligated promoter state (Table 1, species 4). Consequently, an analysis of the hypersensitive region globally fit with the ERE_1- binding isotherm (Equations 6–7) should resolve the same values of k_int and k_c as determined from the global analysis of the ERE₂ and ERE_1- binding isotherms.

Shown in Figure 6 are the ERE_1- and hypersensitivity isotherms and the corresponding global fit. It is evident that the data are well described by the same model used to fit the ERE_1- and ERE₂ data. Moreover, the analysis resolved similar parameter values as determined from the global fit of the ERE_1- and ERE₂ data (see Table 3). In order to determine whether the resolved parameters from each fit were also statistically identical, we carried out a comparative Monte Carlo analysis. Shown in Figure 7 are the predicted values for k_int and k_c from the ERE_1- and ERE₂ global fit, overlaid with those predicted from the ERE_1- and hypersensitivity fit. There is clear overlap, and the parameters from each fit are statistically identical (Table 3). Noting this, we globally fit the ERE_1- and ERE₂ and hypersensitivity isotherms, allowing all binding parameters (k_di, k_int and k_c) to float. As shown in Table 3, it is possible to resolve all three parameters. Moreover, the k_di term translates to a dissociation constant of 0.35 nM (68% confidence intervals of 0.1 to 1.2 nM), in statistical agreement with our earlier assumption of 1 nM.

Figure 6.

The distinctive hypersensitive region between the binding sites shown in Figure 4A was quantified and fit globally with the binding data from the ERE_1- promoter to resolve k_c from the hypersensitivity. (A) Open squares represent the data from three ERE_1- footprint titrations. The line through the data represents the best fit from the global analysis with the hypersensitivity data. (B) Open triangles represent the quantification of the hypersensitive region. The line represents the best fit through the data from the global analysis. Data were arbitrarily rescaled from 0 to −1 after fitting to make the distinction between the decreasing band intensity of the footprint titrations and the increasing band intensity associated with the hypersensitive site.

Figure 7.

Comparative Monte Carlo analysis of errors associated with global analyses of ERE₂ and ERE_1- isotherms versus hypersensitive region and ERE_1- isotherm. (A) Overlaid histograms reporting the error distribution of k_int from the ERE₂ and ERE_1- (black bars) and hypersensitivity (grey bars). (B) Overlaid histograms reporting the error distribution of k_c from the ERE₂ and ERE_1- (black bars) and hypersensitivity (grey bars). Solid and dashed horizontal bars represent 68% confidence limits for ERE₂/ERE_1- and ERE_1-/hypersensitivity binding parameters, respectively.

The results seen here also allow insight into the molecular contributions to cooperativity. For example, the maximum amount of cooperativity observed for DNA binding proteins is rarely greater than −4 kcal/mol. This is likely so because values greater than this generate an asymptotic limit of isotherm steepness (37). Assuming that the entire sequence of twenty-five basepairs between the two EREs is bent, and using the resolved −0.18 kcal/mol for cooperativity, this results in a maximal penalty of +3.8 kcal/mol for DNA bending. Using the approach of Crothers (38), this penalty corresponds to an ER-α-induced bend angle of 87°.

Noting differences in receptor purity, solution conditions and experimental approach, some caution should be observed in comparing the current results to previous work. However, it is tempting to speculate that the earlier contradictory results concerning ER-α cooperativity arose due to varying contributions of DNA bending versus strong cooperativity. This interpretation is consistent with biochemical studies indicating that ER-α cooperativity is a function of response element number, spacing, and flanking sequence (39). Combining the observations from the literature with the results presented here, we expect that manipulation of the spacing of the two ERE’s within the ERE₂ promoter should allow both the k_c term and hypersensitivity to be modulated significantly.

Homologous receptors bind an identical promoter layout using differential energetics

We originally hypothesized that since ER-α and PR-B were both strong transcriptional activators, ER-α and PR-B should generate strong cooperativity. In order to directly compare ER-α binding energetics with those of PR-B, we carried out matched footprint titration experiments using the PRE₂ and PRE_1- promoters and highly purified PR-B. The resultant binding isotherms are shown in Figure 8, and the resolved energetics are summarized in Table 3. For comparative purposes, the predicted isotherms for ER-α binding are overlaid. Comparison of the parameters for PR-B to those for ER-α shows considerable differences. For example, dimerization energetics vary by 4.6 kcal/mol or nearly 4,000-fold, and cooperativity varies by 2.1 kcal/mol or nearly fifty-fold. By contrast, the intrinsic DNA binding energetics are essentially identical – this latter result is not unexpected noting that the tertiary structure of the two DNA binding domains is highly conserved (40, 41). Regardless, the results demonstrate that contrary to our expectations, these two strong transcriptional activators do not share the common attribute of strong cooperativity (or of weak dimerization). Thus, ER-α and PR-B differentially partition their binding energetics.

Figure 8.

Individual-site binding isotherms for PR-B assembly at the PRE₂ promoter. Solid red circles represent binding to site 1 and open red circles represent binding to site 2 the PRE₂ promoter. Open blue squares represent data from the PRE_1- promoter. Lines through the data represent best fit from the global analysis. PRE₂, solid red line; PRE_1-, dashed blue line. Binding energetics for each site of the PRE₂ promoter are identical, therefore the lines for each site overlay. For comparative purposes, the isotherms determined from analysis of the ER-α footprint titration data are overlaid. ERE₂, solid black line; ERE_1-, dashed black line.

When plotted in units of total receptor concentration (Figure 8), the ER-α and PR-B binding isotherms appear to have little in common. This is a direct consequence of the large differences in ER-α and PR-B binding energetics. However, a very different picture emerges if the results are analyzed in units of dimer concentration as calculated from the respective dimerization constants. Shown in Figure 9A are the probability distributions for each microstate associated with PR-B binding to the PRE₂ promoter. Shown in Figure 9B is an analogous plot for ER-α. Regardless of dimer concentration, there are still large differences in the probability of PR-B and ER-α free dimers, unligated DNA, and the singly ligated promoter state. However, the probability of the fully ligated microstate -- that is, the transcriptionally active microstate – is largely identical for both receptors. For example, even though PR-B maintains stronger cooperativity that ER-α (as evidenced by the steep transition for the PR-B fully ligated state), the receptors reach a 50% probability of full-ligation at 0.3 and 0.1 nM dimer, respectively. Thus, despite the fact that the two receptors maintain large differences in interaction energetics, the final result is that the probability of generating the fully ligated, functionally active binding species is nearly the same. This is so because the weak cooperative interactions of ER-α are compensated for by strong dimerization energetics, and weak dimerization energetics of PR-B are compensated for by strong cooperativity. Thus two homologous receptors differentially distribute their microstate energetics to achieve the same result. Finally, we note that saturation of the respective promoters occurs at concentrations of receptor typically thought to exist intracellularly (42).

Figure 9.

Predicted ligation states for PR-B and ER-α assembly at respective two-site promoters. (A) PR-B:PRE₂ probabilities as determined from the experimentally determined interaction energetics. (B) Same as (A) but ER-α:ERE₂. Unligated HRE₂ promoter is represented by the dashed black lines, singly ligated promoter by the solid black lines and the fully ligated HRE₂ by the red dotted lines. The proportion of dimer in solution is represented by the open-dashed black lines.

Why should these receptors assemble onto an identical promoter layout with such large variability in energetics? We speculate that differences in microstate energetics allow for differential gene regulation. We have already noted that differences in cooperativity for the two PR isoforms may potentially generate isoform-specific promoter occupancy (6, 8, 9). Modulation of dimerization energetics may be an additional mechanism by which receptors achieve preferential promoter binding, particularly in the presence of other competing steroid receptors. For example, promoter layouts containing an abundance of palindromic binding sites will favor receptor dimer binding over monomer binding, whereas promoter layouts containing an excess of imperfect palindromes or half-sites (4) should allow for preferential monomer binding. Of course, since ER-α and PR-B recognize slightly different DNA sequences, a mechanism for differential binding is unnecessary. However, ER and PR exist naturally as multiple isoforms, and each pair of isoforms regulates distinct but overlapping gene networks (2, 4). Moreover, the PR isoforms likely compete with GR, MR and AR for promoter binding. A dissection of the promoter binding energetics of the remaining steroid receptors should reveal whether differential binding energetics is common to the entire steroid receptor family. If so, it may eventually be possible to design synthetic promoter sequences capable of receptor-specific gene regulation.

Abbreviations

PR-A

progesterone receptor A-isoform

PR-B

progesterone receptor B- isoform

ER-α

estrogen receptor α-isoform

AR

androgen receptor

GR

glucocorticoid receptor

MR

mineralocorticoid receptor

DBD

DNA-binding domain

HBD

hormone-binding domain

AF

activation function

E2

17β-estradiol

DTT

dithiothreitol

β-ME

2-mercaptoethanol

ERE

estrogen response element

PRE

progesterone response element