Landmark Prediction of Long Term Survival Incorporating Short Term Event Time Information

Summary

In recent years, a wide range of markers have become available as potential tools to predict risk or progression of disease. In addition to such biological and genetic markers, short term outcome information may be useful in predicting long term disease outcomes. When such information is available, it would be desirable to combine this along with predictive markers to improve the prediction of long term survival. Most existing methods for incorporating censored short term event information in predicting long term survival focus on modeling the disease process and are derived under restrictive parametric models in a multi-state survival setting. When such model assumptions fail to hold, the resulting prediction of long term outcomes may be invalid or inaccurate. When there is only a single discrete baseline covariate, a fully non-parametric estimation procedure to incorporate short term event time information has been previously proposed. However, such an approach is not feasible for settings with one or more continuous covariates due to the curse of dimensionality. In this paper, we propose to incorporate short term event time information along with multiple covariates collected up to a landmark point via a flexible varying-coefficient model. To evaluate and compare the prediction performance of the resulting landmark prediction rule, we use robust non-parametric procedures which do not require the correct specification of the proposed varying coefficient model. Simulation studies suggest that the proposed procedures perform well in finite samples. We illustrate them here using a dataset of post-dialysis patients with end-stage renal disease.

1 Introduction

In the quest to provide accurate prognosis of disease for patients it has become evident that a wide range of biological and genetic markers hold great potential in improving prediction. The prediction potential of these markers has led to a more personalized approach to individual patient care (Bauer et al., 2007; Wilson et al., 1998; Folsom et al., 2006). Incorporating short term outcomes in addition to these markers may further improve prediction accuracy. For example, the extent to which change in oncological status after surgery can predict long term survival for breast cancer patients was examined in Hatteville et al. (2002). Additionally, treatment response in breast cancer patients may provide useful information for prediction of future events (Osborne, 1998). Hirschtick et al. (1995) demonstrated an association between occurrence of bacterial pneumonia and death among HIV-positive patients. Recently, the association between acute graft versus host disease and survival of acute leukemia patients following bone marrow or stem cell transplantation was investigated in Cortese & Andersen (2010) and Lee et al. (2002). Among end-stage renal disease patients, the relationship between an early hospitalization and risk of death has been examined by Collins et al. (2009) and USRDS (2010).

In the aforementioned examples, the long term outcome of interest is often time to a terminal event e.g. death and the short term outcome is often time to a non-terminal event. This setting is referred to as a semi-competing risk setting since the occurrence of the terminal event would censor the non-terminal event but not vice versa. Throughout, we let T and T denote event times for the short term and long term events, respectively. Most existing methods for analyzing semi-competing risk data focus on estimation of the cause-specific hazard functions and/or the joint distribution of events under semi-parametric models (Fine et al., 2001; Siannis et al., 2007; Jiang et al., 2005). The joint distribution estimators can potentially be used to make predictions about T given information on T. Methods developed specifically to incorporate T information and baseline predictors for the prediction of T have concentrated primarily on semi-parametric models in a multi-state framework (Putter et al., 2006; Kay, 1986; Klein et al., 1994; Datta et al., 2000; Hatteville et al., 2002; Cortese & Andersen, 2010). For example, Klein et al. (1994) use a standard Cox regression analysis to incorporate information on whether or not the intermediate event has occurred by a certain time. Hatteville et al. (2002) extend this method to include non-proportional hazards and propose estimation procedures. Recently, Van Houwelingen & Putter (2008) proposed a landmark prediction procedure to incorporate the status of the short term event by a landmark point t₀.

These methods provide useful tools to leverage information about T to improve the prediction of T. However, these simple semi-parametric models may not capture the relationship among the two outcomes and the covariates in practice. As an example, T may be highly associated with unknown subtypes of disease and the effect of observed covariates on T may vary with the disease subtype. Commonly used proportional hazards models may be inadequate for data from such a mixture of populations. When there is only a single discrete baseline covariate, a fully non-parametric procedure was proposed in Parast et al. (2011) to estimate the conditional distribution of the residual life from a landmark time t₀, T − t₀, given both T and the covariate among subjects who survive past t₀. However, such an approach is not feasible in settings with one or more continuous covariates due to the curse of dimensionality (Robins & Ritov, 1997). To overcome such limitations, we extend the landmark Cox model of Van Houwelingen & Putter (2008) and propose a flexible varying-coefficient working model to incorporate T information along with a vector of covariates that may consist of information collected up to t₀. The varying-coefficient model can potentially approximate the underlying disease process better compared to commonly used semi-parametric models. Landmarking along with an inverse probability weighting (IPW) approach (Rotnitzky & Robins, 2005; Robins & Rotnitzky, 1992) enables us to overcome both non-informative dropout and informative censoring issues for T due to competing risks. In contrast to Parast et al. (2011), our proposed approach can also incorporate longitudinal predictor information collected up to t₀, such as repeated biomarker measurements and the frequency of complications or adverse events up to t₀.

An important follow up step in developing methods for risk prediction is to objectively assess its predictive performance. Due to the complexity of the disease process as mentioned above, it is important to estimate the prediction accuracy measures non-parametrically without requiring that the fitted statistical models hold. To evaluate the performance of the proposed landmark prediction rule, we make inference about the accuracy measures using robust non-parametric procedures. We provide inference procedures for comparing prediction rules and resampling based procedures for interval estimation. Results from our simulation studies suggest that our proposed procedures work well in finite samples and the flexibility of our varying coefficient model could lead to a substantial gain in accuracy compared to a landmark Cox model based approach. For illustration, we apply our procedures to a dataset of post-dialysis patients with end-stage renal disease and develop a landmark risk model for kidney transplant free survival incorporating time to first hospitalization as well as several available predictors.

2 Estimation

2·1 Notations and Settings

We consider the semi-competing risk setting where T is a terminal event and can only be censored by the administrative censoring, C, not T, while T may be censored by both T and C. For example, T may represent time to a nonfatal stroke or hospitalization and T may represent time to death. Considering the potential difference in the underlying disease process, patients who experience the short term outcome may have substantially different clinical outcomes from the general patient population. Therefore, it may be important to incorporate information on the short term outcome in the prediction of a long term outcome. In this paper, we focus on predicting the risk of T ≤ t₀ + τ among subjects whose T is greater than a pre-defined landmark point t₀ for any given τ. We denote this subset of subjects as Ω_T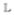>t0 = {T > t₀}. For example, if t₀ is a 1 year check-up appointment from the time of surgery and T is death, we are interested in predicting future mortality among patients who have survived at least 1 year after surgery. Our goal is two-fold: 1) to accurately assess the probability of survival to time t₀ + τ among Ω_T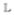>t0 using information on T and a vector of covariates Z and 2) to quantify how much prediction accuracy was improved by incorporating T information compared to using only covariates Z. When short term outcome information is used, it is essential that the prediction only use information on T up to the landmark point t₀. Note that though we condition on patients surviving up to t₀, these patients may still experience both T and T after t₀.

Our potential data for analysis is composed of n independent and identically distributed random vectors {D_i = (X_i, δ_i, X_i, δ_i, 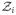)′, i = 1, …, n}, where X = min(T, C), X = min(T, C), δ = I(T ≤ C), δ = I(T ≤ C), and 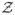indicates all available collected covariate information up to t₀. We let Z represent the vector version of 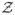. It is important to note that X_i is not always observable due to competing risks, however, given our interest in the subset, Ω_T>t0, the information concerning X_i required for our proposed estimation procedure is always observable. For details see Section 2·3. We assume that C is independent of (T, T, Z) with a survival function G(·) and P(X > t₀ + τ, X > t₀)P(T ≤ t₀) > 0. Without specifying the true model for the conditional survival, such an independent censoring assumption is often required to enable valid estimation of the prediction performance measures (defined in Section 2·4) due to the curse of dimensionality (Robins & Ritov, 1997). When censoring does depend on Z, one may relax such assumptions by imposing a semi-parametric model on C given Z, see Section 6.

2·2 Landmark Risk Prediction for the Subpopulation Ω_T>t0

2·2.1 Landmark Prediction with Z only

For comparison, we are first interested in developing landmark prediction rules based on Z only, which would enable us to assess the incremental value of T in prediction. To estimate $P_{t_0,\tau }^{(1)}(z)=P(T_{\mathbb{L}}\le t_0+\tau \mid T_{\mathbb{L}}>t_0,\mathbf{Z}=\mathbf{z})$, we consider a working time-specific generalized linear model (GLM)

$$P_{t_0,\tau }^{(1)}(\mathbf{Z})=g({\phi }_{t_0}^{\top }\mathbf{Z}),$$ (2·1)

where g is a known, strictly increasing link function and φ_t0 is a vector of unknown regression coefficients. Model (2·1) allows the effect of Z to vary over t₀ which is attractive in settings where markers predictive of short term risk may not be predictive of long term risk. In the presence of censoring, φ_t0 may be estimated by modifying the IPW estimator proposed in Uno et al. (2007) to incorporate landmarking. Specifically, we estimate φ_t0 as φ̂_t0, the solution to:

$$\sum _i{\widehat{W}}_{\mathbb{L}i}{\mathbf{Z}}_i[I(X_{\mathbb{L}i}\le t_0+\tau )-g({\phi }_{t_0}^{\top }{\mathbf{Z}}_i)]=0,$$ (2·2)

where

$${\widehat{W}}_{\mathbb{L}i}=\frac{I(t_0<X_{\mathbb{L}i}\le t_0+\tau ){\delta }_{\mathbb{L}i}}{\widehat{G}(X_{\mathbb{L}i})}+\frac{I(X_{\mathbb{L}i}>t_0+\tau )}{\widehat{G}(t_0+\tau )},$$

and Ĝ(·) is the Kaplan-Meier estimator of G(·). Note that Ŵ_i = 0 for all subjects with X_i > t₀. By using this weight, we essentially use the subgroup with X > t₀ as an unbiased random sample for the subpopulation Ω_T>t0 since P(T ≤ t₀ + τ | X > t₀) = P(T ≤ t₀ + τ | T > t₀) under independent censoring.

2·3 Landmark Prediction with Z and T

We now consider developing landmark prediction rules to estimate the probability that T ≤ t₀ + τ given Z and the information on T up to t₀ for subjects in Ω_T>t0,

$$\begin{array}{l}{P}_{t_0,\tau }^{(2)}(T_{\mathbb{S}},\mathbf{Z})=P(T_{\mathbb{L}}\le t_0+\tau \mid T_{\mathbb{L}}>t_0,min(T_{\mathbb{S}},t_0),I(T_{\mathbb{S}}\le t_0),\mathbf{Z})\\ =P_{t_0,\tau ,T_{\mathbb{S}},\mathbf{Z}}I(T_{\mathbb{S}}\le t_0)+P_{t_0,\tau ,\mathbf{Z}}I(T_{\mathbb{S}}>t_0)\end{array}$$

where

$$P_{t_0,\tau ,t_s,\mathbf{z}}=P(T_{\mathbb{L}}\le t_0+\tau \mid T_{\mathbb{L}}>t_0,T_{\mathbb{S}}=T_s,\mathbf{Z}=\mathbf{z})\text{if}{T}_{\mathbb{S}}=t_s\le t_0$$ (2·3)

$$P_{t_0,\tau ,\mathbf{z}}=\text{P}(T_{\mathbb{L}}\le t_0+\tau \mid T_{\mathbb{L}}>t_0,T_{\mathbb{S}}>t_0,\mathbf{Z}=\mathbf{z})\text{if}{T}_{\mathbb{S}}>t_0$$ (2·4)

as in Parast et al. (2011). The quantity P_t0,τ,ts,z pertains to subjects with T ≤ t₀ while P_t0,τ,z pertains to those with T > t₀. The conditional risk P_t0,τ,Z can also be approximated via a time-specific GLM similar to (2·1), $P_{t_0,\tau ,\mathbf{Z}}=g({\mathit{\beta }}_{t_0}^{\top }\mathbf{Z})$, and the unknown model parameter β_t0 can be estimated as β̂_t0, the solution to:

$$\widehat{\mathbf{S}}(\mathit{\beta })\equiv \sum _{i}I(T_{\mathbb{S}i}>t_0){\widehat{W}}_{\mathbb{L}i}{\mathbf{Z}}_i[I(X_{\mathbb{L}i}\le t_0+\tau )-g({\mathit{\beta }}_{t_0}^{\top }{\mathbf{Z}}_i)]=0$$ (2·5)

Here, we now use the subgroup with {X > t₀, T > t₀} as an unbiased random sample for the subpopulation {T > t₀, T > t₀} since P(T ≤ t₀ + τ, | X > t₀, X > t₀) = P(T ≤ t₀ + τ, | T > t₀, T > t₀) under independent censoring. Now, to approximate P_t0,τ,tsz, we consider a varying coefficient model (Hastie & Tibshirani, 1993; Fan & Zhang, 1999; Fan & Zhang, 2008):

$$P_{t_0,\tau ,t_s,\mathbf{Z}}=g({\mathit{\beta }}_{t_s}^{\top }\mathbf{Z})t_s\le t_0$$ (2·6)

where g is a known, strictly increasing link function and β_ts is vector of unknown functions of t_s. This model allows the effect of Z on the risk to vary over the short term outcome. To estimate β_ts in the presence of censoring, we propose to obtain β̂_ts as the solution to the following IPW kernel smoothed estimating equation:

$${\widehat{\mathbf{S}}}_{t_s}(\mathit{\beta })\equiv \sum _{i}I(T_{\mathbb{S}i}\le t_0){\widehat{W}}_{\mathbb{L}i}{\mathbf{Z}}_i{K}_h\{\psi (T_{\mathbb{S}i})-\psi (t_s)\}[I(X_{\mathbb{L}i}\le t_0+\tau )-g({\mathit{\beta }}_{t_s}^{\top }{\mathbf{Z}}_i)]=0$$ (2·7)

where K_h(x) = h⁻¹K(x/h), K(·) is a known smooth symmetric kernel density function with a bounded support, ψ: [0, ∞) → (−∞, ∞) is a given transformation function and the bandwidth h > 0 is assumed to be O(n^−v), for 1/5 < v < 1/2. To potentially improve estimation one can implement an appropriate transformation ψ(·) such as log(·)(Wand et al., 1991; Park et al., 1997). Combining β̂_T and β̂_t0, we can now estimate $P_{t_0,\tau }^{(2)}(T_{\mathbb{S}},\mathbf{Z})$ as

$${\widehat{P}}_{t_0,\tau }^{(2)}(T_{\mathbb{S}},\mathbf{Z})=g({\widehat{\mathit{\beta }}}_{T_{\mathbb{S}}}^{\top }\mathbf{Z})I(T_{\mathbb{S}}\le t_0)+g({\widehat{\mathit{\beta }}}_{t_0}^{\top }\mathbf{Z})I(T_{\mathbb{S}}>t_0).$$

Note that the observed data have sufficient information on T and T for the estimation of (2·3) and (2·4). The conditional risk (2·3) only involves the subgroup with T ≤ t₀ < T and since X_i > t₀ implies C_i > t₀, when X_i > t₀ and X_i ≤ t₀, then T_i = X_i and I(T_i ≤ t₀) is observable. The probability in (2·4) involves the subgroup with min(T, T) > t₀ and can be obtained based on the subset of patients with min(X, X) > t₀ which is always observable.

It is known that the choice of the smoothing parameter h when estimating β_ts is critical as in any non-parametric functional estimation problem. To obtain an appropriate h we use a standard K-fold cross-validation procedure to obtain h_opt, the minimizer of an appropriately weighted mean squared error estimate. It is common practice to undersmooth, due to the difficulty in estimating the bias, and obtain an estimator whose variance dominates bias. For example, to obtain the final bandwidth for the estimation of β_ts, one can choose h = h_optn^−c₀, for some c₀ ∈ (0, 3/10). Estimation is then performed over a region of t_s defined as [ψ⁻¹(ρ_l + h), ψ⁻¹(ρ_r − h)] where (ρ_l, ρ_r) is a subset of ψ(t_s). In all numerical examples, (ρ_l, ρ_r) is taken to be the (0.02, 0.98) percentiles of the observed X values.

2·4 Information gained by incorporating short-term outcome

To investigate the incremental value in predicting I(T ≤ t₀ + τ) gained from incorporating the short-term outcome T information, we compare the predicted individual risk for subjects using (T, Z) with that using Z alone. A wide range of accuracy measures have been proposed in the literature to quantify and compare the predictive performance of risk models. Interesting discussions on this topic can be found in Heagerty & Zheng (2005), Cook (2007), Gerds et al. (2008), Pencina et al. (2008), Kerr & Pepe (2011). For illustration purposes, we focus on two commonly used measures, the Brier score (Brier, 1950; Gerds & Schumacher, 2006; Lawless & Yuan, 2010) and the area under the Receiver Operating Characteristic (ROC) (AUC) curve (Swets & Pickett, 1982; Heagerty & Zheng, 2005). The Brier score and the AUC of a risk function p(T, Z) in the context of landmark prediction can be defined as BS_t0,τ= E{[I(T_i ≤ t₀ + τ) − p(T_i, Z_i)]²|T_i > t₀} and AUC_t0,τ = P{p(T_i, Z_i) > p(T_j, Z_j) | t₀ < T_i ≤ t₀ + τ, T_j > t₀ + τ}. Similar to Gerds & Schumacher (2006), Uno et al. (2007) and Parast et al. (2011), for each prediction model, these measures can be estimated empirically using an IPW approach. Specifically, if the jth model estimates the conditional risk for the ith subject as ${\widehat{P}}_i^{(j)}$, then

$${\widehat{\text{BS}}}_{t_0,\tau }^{(j)}=\frac{{\sum }_i{\widehat{W}}_{\mathbb{L}i}{\{I(t_0<X_{\mathbb{L}i}\le t_0+\tau )-{\widehat{P}}_i^{(j)}\}}^2}{{\sum }_i{\widehat{W}}_{\mathbb{L}i}I(X_{\mathbb{L}i}>t_0)}$$ (2·8)

$${\widehat{\text{AUC}}}_{t_0,\tau }^{(j)}=\frac{{\sum }_{i:X_{\mathbb{L}i}\le t_0+\tau }{\sum }_{j:X_{\mathbb{L}j}>t_0+\tau }I({\widehat{P}}_i^{(j)}>{\widehat{P}}_j^{(j)}){\widehat{W}}_{\mathbb{L}i}{\widehat{W}}_{\mathbb{L}j}}{{\sum }_{i:X_{\mathbb{L}i}\le t_0+\tau }{\sum }_{j:X_{\mathbb{L}j}>t_0+\tau }{\widehat{W}}_{\mathbb{L}i}{\widehat{W}}_{\mathbb{L}j}}.$$ (2·9)

consistently estimate BS_t0,τ and AUC_t0,τ for the corresponding risk model, respectively. Based on P̂⁽²⁾(T_i, Z_i) and P̂⁽¹⁾(Z_i), the incremental value of T can be quantified by ${\widehat{\text{BS}}}_{t_0,\tau }^{(1)}-{\widehat{\text{BS}}}_{t_0,\tau }^{(2)}$ and ${\widehat{\text{AUC}}}_{t_0,\tau }^{(2)}-{\widehat{\text{AUC}}}_{t_0,\tau }^{(1)}$. In addition, one may quantify the incremental value of T by the additional proportion of variation explained by model (2) relative to model (1), defined as ${\text{IPEV}}_{2/1}=1-{\widehat{\text{BS}}}_{t_0,\tau }^{(2)}/{\widehat{\text{BS}}}_{t_0,\tau }^{(1)}$. When the sample size is not large, it is important to correct for over-fitting bias via procedures such as cross-validation.

3 Inference

To make inference about β_ts, it can be shown using the weak convergence of $n^{\frac{1}{2}}\{\widehat{G}(t)-G(t)\}$ to a zero-mean Gaussian process (Kalbfleisch & Prentice, 2002), that the uncertainty of Ĝ(·) in Ŵ_i is of order $n^{-\frac{1}{2}}$, which is negligible compared to the standard non-parametric rate of {(nh)⁻¹ log(n)}^1/2. Therefore, the proposed estimator is asymptotically equivalent to the estimator obtained by replacing Ŵ_i with W_i. Using similar arguments as given by Bickel & Rosenblatt (1973), Dabrowska (1989) and Cai et al. (2010), one can show that β̂_ts → β_ts in probability as n → ∞ regardless of whether (2·6) is correctly specified, where β_ts is the unique solution to the estimating equation, $E[{\mathbf{Z}}_i\{I(T_{\mathbb{L}i}\le t_0+\tau )-g({\mathit{\beta }}_{t_s}^{\top }{\mathbf{Z}}_i)\}\mid T_{\mathbb{L}i}>t_0,T_{\mathbb{S}i}=t_s]=0$. In addition, one can show that for any given t_s ≤ t₀ and h = O_p(n^−v) with v ∈ (1/5, 1/2), $\widehat{\mathbf{B}}(t_s)={(nh)}^{\frac{1}{2}}({\widehat{\mathit{\beta }}}_{t_s}-{\mathit{\beta }}_{t_s})={(nh)}^{-\frac{1}{2}}{\sum }_{i=1}^n{K}_h\{\psi (T_{\mathbb{S}i})-\psi (t_s)\}\xi ({\mathbf{D}}_i)+o_p\{{(nh)}^{-\frac{1}{2}}\}$ for some fixed function ξ. Thus, it follows from similar arguments as given in Bickel & Rosenblatt (1973) that ${sup}_{t_s\le t_0}\mid \widehat{\mathbf{B}}(t_s)\mid =O_p\{{(nh)}^{-\frac{1}{2}}log{(n)}^{\frac{1}{2}}\}$ and B̂(t_s) converges in distribution to a zero-mean normal random variable for any given t_s.

To construct a confidence interval (CI) for β_ts in practice, we employ a perturbation-resampling method (Park & Wei, 2003; Cai et al., 2005; Tian et al., 2007) to approximate the distributions of the proposed estimators. Let { ${\mathbf{V}}^{(b)}={(V_1^{(b)},\dots ,V_n^{(b)})}^{\top },b=1,\dots B$} be n × B independent copies of a positive random variable V from a known distribution with mean and variance equal to one. Then one may obtain perturbed estimates of β_ts, ${\widehat{\mathit{\beta }}}_{t_s}^{(b)}$, either as the solution to

$${\widehat{\mathbf{S}}}_{t_s}^{(b)}(\mathit{\beta })\equiv \sum _{i}I(T_{\mathbb{S}i}\le t_0){\widehat{W}}_{\mathbb{L}i}^{(b)}{K}_h\{\psi (T_{\mathbb{S}i})-\psi (t_s)\}{\mathbf{Z}}_i[I(X_{\mathbb{L}i}\le t_0+\tau )-g({\mathit{\beta }}^{\top }{\mathbf{Z}}_i)]V_i^{(b)}=0$$

or explicitly as ${\widehat{\mathit{\beta }}}_{t_s}^{(b)}={\widehat{\mathit{\beta }}}_{t_s}+{\widehat{\mathbb{A}}}_{t_s}({\widehat{\mathit{\beta }}}_{t_s}){\widehat{\mathbf{S}}}_{t_s}^{(b)}({\widehat{\mathit{\beta }}}_{t_s})$, where 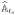(β) = −∂Ŝ_ts(β)/∂β,

$${\widehat{W}}_{\mathbb{L}i}^{(b)}=\frac{I(t_0<X_{\mathbb{L}i}\le t_0+\tau ){\delta }_{\mathbb{L}i}}{{\widehat{G}}^{(b)}(X_{\mathbb{L}i})}+\frac{I(X_{\mathbb{L}i}>t_0+\tau )}{{\widehat{G}}^{(b)}(t_0+\tau )}$$

and Ĝ^(b) is the Kaplan-Meier estimator of G(·) with weights $V_i^{(b)}$. Note that, although the variation in Ĝ is negligible asymptotically for assessing the variation of β̂_ts, we find that accounting for this variation provides a better approximation in finite samples and thus perturb Ĝ with Ĝ^(b) to obtain ${\widehat{\mathit{\beta }}}_{t_s}^{(b)}$. The variance of β̂_ts, ${\widehat{\sigma }}_{{\mathit{\beta }}_{t_s}}^2$, can be estimated as the empirical variance of { ${\widehat{\mathit{\beta }}}_{t_s}^{(b)},b=1,\dots ,B$}. Such a perturbation procedure also enables us to construct 100(1 − α)% simultaneous confidence bands for {β_ts, 0 < t_s0< t_s ≤ t₀} based on {β̂_ts ± ζ_ασ̂_βts}, where ζ_α is the upper 100(1 − α)th percentile of { ${sup}_{t_{s_0}<t_s<t_0}\mid {\widehat{\mathit{\beta }}}_{t_s}^{(b)}-{\widehat{\mathit{\beta }}}_{t_s}\mid /{\widehat{\sigma }}_{{\mathit{\beta }}_{t_s}},b=1,\dots ,B$} and t_s0 is selected such that P(T < t_s0) > 0.

For {β̂_t0, φ̂_t0}, it can be shown using similar arguments as given by Uno et al. (2007) and Parast & Cai (2010) that they converge in probability to {β_t0, φ_t0}, the respective solutions to $E[{\mathbf{Z}}_i\{I(T_{\mathbb{L}i}\le t_0+\tau )-g({\mathit{\beta }}_{t_0}^{\top }\mathbf{Z})\}\mid T_{\mathbb{L}i}>t_0,T_{\mathbb{S}i}>t_0]=0$ and $E[{\mathbf{Z}}_i\{I(T_{\mathbb{L}i}\le t_0+\tau )-g({\phi }_{t_0}^{\top }{\mathbf{Z}}_i)\}\mid T_{\mathbb{L}i}>t_0]=0$. Further more, { $\sqrt{n}({\widehat{\mathit{\beta }}}_{t_0}-{\mathit{\beta }}_{t_0}),\sqrt{n}({\widehat{\phi }}_{t_0}-{\phi }_{t_0})$} converges jointly in distribution to a multivariate normal. Similar perturbation procedures can be used to construct CIs for β_t0 and φ_t0. For the accuracy measure estimates, it is not difficult to justify their root-n consistency and normality using the uniform consistency of the risk estimates and functional central limit theorem Pollard (1990) along with modifications of the arguments given in Zheng et al. (2008). We note that although β̂_ts is estimated at a slower non-parametric rate, the estimated overall accuracy parameters remain the standard parametric rate of root-n since they are essentially integrated over the distribution of T. To overcome the bias and variance trade-off, we choose to under smooth with h = O(n^−v) and v ∈ (1/4, 1/2). The CIs for the Brier score and AUC can be constructed by perturbing (2·8) and (2·9) along with all the estimated model parameters and Ĝ. For all estimators with standard convergence rate of root-n, the variation due to Ĝ is no longer negligible and hence it is important to use the perturbed censoring weight ${\widehat{W}}_{\mathbb{L}i}^{(b)}$ to account for the sampling variations.

4 Simulations

We conducted simulation studies to examine the finite-sample properties of the proposed estimation procedures. For simplicity, we consider a single continuous covariate Z generated from a Normal(0,4) distribution and the survival times T and T from the model:

$$\begin{array}{ll}{T}_{\mathbb{S}}\hfill & =exp(-\eta Z_i+{\epsilon }_1)\hfill \\ T_{\mathbb{L}}\hfill & =exp(-\eta [Z_{i}log(T_{\mathbb{S}})-log(T_{\mathbb{S}})+Z_i]+{\epsilon }_2)\hfill \end{array}\text{where}\begin{array}{ll}{\epsilon }_1\hfill & ~N({\mu }_1,{\sigma }_1^2)\hfill \\ {\epsilon }_2\hfill & ~N({\mu }_2,{\sigma }_2^2)\hfill \end{array}$$ (4·1)

and η, μ₁, μ₂, ${\sigma }_1^2$, and ${\sigma }_2^2$ were chosen in order to produce (i) a low-event rate setting and (ii) a moderate-event rate setting. In each setting, we considered a sample size of n=2,000 and 5,000. Throughout, the results are summarized based on 1000 simulated data sets for each setting. For illustration, we chose t₀ to be year 2 and τ to be 8 years. Therefore, among patients who have not experienced the long-term event by year 2, T > 2, we wish to estimate their probability of experiencing the long term event before year 10. Throughout all of the numerical examples, we let g be the logit link function. For the estimation of P̂_t0,τ,ts,z using (2·7), we let K(·) be the gaussian kernel and ψ(x) = log(x). The smoothing parameter h was obtained using the 3-fold cross-validation scheme and c₀ = 1/10 and hence h = O(n^−0.3). The standard error (SE) estimates were obtained based on B = 500 perturbations each.

In setting (i), the low event rate setting, the survival times were generated from (4·1) with η = 0.4, μ₁ = 1.8, μ₂ = 3.3, ${\sigma }_1^2=1.0$ , and ${\sigma }_2^2=1.2$. Under these conditions, P(T ≤ t₀ | T > t₀) = 0.20 and P(T > t₀) = 0.98 and P(T ≤ t₀ + τ |T > t₀) = 0.13. We consider the case when C was generated from a Weibull distribution with shape = 1.6 and scale = 20. With this censoring pattern, 30% of observations are censored for T, 80% are censored for T and P(T ≤ t₀, δ = 1 | X > t₀) = 0.18 and P(X > t₀) = 0.96 and P(T ≤ t₀ + τ, δ = 1|X > t₀) = 0.11. Estimates of β_ts in P_t0,τ,ts,z for t₀ = 2 and τ = 8 and n = 2, 000 and 5, 000 are shown for multiple values of t_s in Table 1(i). Values of t_s in the table were chosen as the 20^th, 40^th, 60^th, and 80^th percentiles of T < t₀. The SEs estimated from the perturbation resampling method are close to the empirical SEs with higher SEs in the case of a lower sample size as expected. In addition, the SEs for both intercept and slope estimates tend to be higher for smaller values of t_s possibly due to smoothing when there are fewer events in this time period as is typically seen in non-parametric estimation. All estimates have slight but negligible bias and the empirical coverage levels are close to their nominal level.

Table 1.

Bias estimates for β̂_ts with corresponding averages of the SE estimates from the perturbation-resampling method (ASE), empirical SEs (ESE), and empirical 95% coverage levels (Coverage) from setting (i), the low event rate setting and (ii), the moderate event rate setting. Values of t_s were chosen as the 20^th, 40^th, 60^th, and 80^th percentiles of T ≤ t₀. All entries are multiplied by 100.

(i) low event rate setting
n=2000
	Intercept				Slope
ts	t0.20	t0.40	t0.60	t0.80	t0.20	t0.40	t0.60	t0.80
Bias	5.6	3.2	1.8	0.7	−2.0	−0.1	1.7	3.6
ASE	39.8	33.3	29.0	26.8	14.5	13.2	12.6	12.6
ESE	41.6	35.2	29.8	26.7	15.5	14.7	13.3	12.6
Coverage	93.6	93.5	94.3	94.5	93.8	92.7	92.5	93.4
n=5000
	Intercept				Slope
ts	t0.20	t0.40	t0.60	t0.80	t0.20	t0.40	t0.60	t0.80
Bias	1.9	0.8	0.8	−0.2	−0.7	0.8	1.8	3.5
ASE	33.7	27.4	23.0	20.2	11.8	10.5	9.8	9.5
ESE	35.4	28.3	22.6	20.2	12.6	10.9	9.8	10.0
Coverage	93.9	94.0	95.6	94.5	92.9	93.1	94.4	91.1
(ii) moderate event rate setting
n=2000
	Intercept				Slope
ts	t0.20	t0.40	t0.60	t0.80	t0.20	t0.40	t0.60	t0.80
Bias	−26.3	−2.8	3.5	5.3	10.2	2.1	−0.3	−3.4
ASE	84.7	50.4	31.6	21.2	29.0	19.2	18.1	19.4
ESE	92.2	53.4	31.9	21.7	31.9	20.3	18.4	21.1
Coverage	93.3	95.0	95.1	94.7	92.7	94.6	94.7	93.8
n=5000
	Intercept				Slope
ts	t0.20	t0.40	t0.60	t0.80	t0.20	t0.40	t0.60	t0.80
Bias	−3.5	−3.1	4.2	5.7	−1.0	2.3	−0.2	−3.6
ASE	51.6	31.1	19.6	13.3	17.7	12.0	11.3	12.2
ESE	52.0	33.5	20.4	13.4	18.2	12.5	11.9	12.5
Coverage	95.8	94.0	93.3	93.4	94.7	93.5	94.3	95.0

In setting (ii), the moderate event rate setting, the survival times were generated from (4·1) with η = 0.7, μ₁ = 1.2, μ₂ = 2.3, ${\sigma }_1^2=1.0$, σ₁₂ = 0.5, and ${\sigma }_2^2=1.3$. Under these conditions, P(T ≤ t₀ | T > t₀) = 0.35 and P(T > t₀) = 0.95 and P(T ≤ t₀ + τ |T > t₀) = 0.23. We again consider the case when C was generated from a Weibull distribution with shape = 1.6 and scale = 20. With this censoring pattern, 25% of observations are censored for T, 70% are censored for T and P(T ≤ t₀, δ = 1 | X > t₀) = 0.35 and P(X > t₀) = 0.92 and P(T ≤ t₀ + τ, δ = 1|X > t₀) = 0.21. We again consider estimation of β_ts in P_t0,τ,ts,z and results are shown in Table 1(ii). The SEs estimated from the perturbation resampling method are again close to the empirical SEs with lower SEs in this event rate setting as compared to the lower event rate setting. Similar to the results in setting (i), SEs tend to by higher for smaller values of t_s. All estimates have slight bias, however the empirical coverage levels are close to their nominal level. In both the low and moderate event rate setting, the procedures appear to perform well though care should be taken when there are very few events in a specific time interval as this could lead to some unstable estimates.

In both settings we examined the value of using the additional short-term outcome information in ${\widehat{P}}_{t_0,\tau }^{(2)}(T_{\mathbb{S}},Z)$ using the procedures discussed in Section 2·4. Here we use a 3-fold cross-validation procedure to correct for over-fitting bias. Brier score and AUC estimates are shown in Tables 2 and 3. In the low event rate setting, the proportion of explained variation in predicting long-term t₀ + τ survival increased by 0.077 when n=2,000 and by 0.086 when n=5,000 after incorporating short-term outcome information compared to using Z information only. In the moderate event rate setting, the proportion of explained variation in predicting long-term t₀ + τ survival increased by 0.306 when n=2,000 and by 0.317 when n=5,000 after incorporating short-term outcome information compared to using Z information only. In the low event rate setting, including the short-term outcome information results in a 0.011 increase in AUC when n=2,000 and a 0.013 increase in AUC when n=5,000 compared to using Z information only. In the moderate event rate setting, including the short-term outcome information results in a 0.060 increase in AUC when n=2,000 and a 0.062 increase in AUC when n=5,000 compared to using Z information only. The SEs estimated from the perturbation resampling method are close to the empirical SEs with smaller SEs in the higher sample size setting as expected. Empirical coverage levels are close to their nominal level.

Table 2.

Average apparent and cross-validated (CV) estimates for the Brier score using T, Z information ( ${\text{BS}}_{t_0,\tau }^{(2)}$) and Z information only ( ${\text{BS}}_{t_0,\tau }^{(1)}$), and the increase in proportion of explained variation(IPEV) with corresponding empirical SEs (ESE), average of the SE estimates from the perturbation-resampling method (ASE) for the apparent estimates and empirical coverage levels (Cvg) from setting (i), the low event rate setting and (ii), the moderate event rate setting. All entries are multiplied by 100.

(i) low event rate setting
	n=2000
	Apparent			CV (3-fold)
	Average	ESE	ASE	Average	ESE	Cvg
${\text{BS}}_{t_0,\tau }^{(2)}$	7.6	0.4	0.5	7.9	0.4	95.6
${\text{BS}}_{t_0,\tau }^{(1)}$	8.5	0.4	0.5	8.6	0.5	95.2
IPEV2/1	10.7	2.4	2.8	7.7	2.8	90.3
	n=5000
	Apparent			CV (3-fold)
	Average	ESE	ASE	Average	ESE	Cvg
${\text{BS}}_{t_0,\tau }^{(2)}$	7.7	0.3	0.3	7.8	0.3	95.5
${\text{BS}}_{t_0,\tau }^{(1)}$	8.5	0.3	0.3	8.6	0.3	93.7
IPEV2/1	10.4	1.5	1.7	8.6	1.6	95.3
	(ii) moderate event rate setting
	n=2000
	Apparent			CV (3-fold)
	Average	ESE	ASE	Average	ESE	Cvg
${\text{BS}}_{t_0,\tau }^{(2)}$	9.6	0.4	0.5	10.2	0.5	89.8
${\text{BS}}_{t_0,\tau }^{(1)}$	14.6	0.5	0.5	14.7	0.5	94.9
IPEV2/1	33.9	2.7	2.9	30.6	2.8	92.2
	n=5000
	Apparent			CV (3-fold)
	Average	ESE	ASE	Average	ESE	Cvg
${\text{BS}}_{t_0,\tau }^{(2)}$	9.8	0.3	0.3	10.0	0.3	93.0
${\text{BS}}_{t_0,\tau }^{(1)}$	14.6	0.3	0.3	14.6	0.3	94.9
IPEV2/1	32.9	1.7	1.8	31.7	1.8	94.6

Table 3.

Average apparent and cross-validated (CV) estimates for the AUC using T, Z information ( ${\text{AUC}}_{t_0,\tau }^{(2)}$) and Z information only ( ${\text{AUC}}_{t_0,\tau }^{(1)}$) with corresponding empirical SEs (ESE), average of the SE estimates from the perturbation-resampling method (ASE) for the apparent estimates and empirical coverage levels (Cvg) from setting (i), the low event rate setting and (ii), the moderate event rate setting. All entries are multiplied by 100.

(i) low event rate setting
	n=2000
	Apparent			CV (3-fold)
	Average	ESE	ASE	Average	ESE	Cvg
${\text{AUC}}_{t_0,\tau }^{(2)}$	90.0	0.9	1.0	89.3	1.0	91.5
${\text{AUC}}_{t_0,\tau }^{(1)}$	88.2	1.0	1.0	88.2	1.0	93.8
	n=5000
	Apparent			CV (3-fold)
	Average	ESE	ASE	Average	ESE	Cvg
${\text{AUC}}_{t_0,\tau }^{(2)}$	90.0	0.6	0.6	89.6	0.6	93.8
${\text{AUC}}_{t_0,\tau }^{(1)}$	88.3	0.6	0.6	88.3	0.6	94.7
(ii) moderate event rate setting
	n=2000
	Apparent			CV (3-fold)
	Average	ESE	ASE	Average	ESE	Cvg
${\text{AUC}}_{t_0,\tau }^{(2)}$	92.0	0.7	0.8	91.2	0.8	92.6
${\text{AUC}}_{t_0,\tau }^{(1)}$	85.2	1.0	1.0	85.2	1.0	95.2
	n=5000
	Apparent			CV (3-fold)
	Average	ESE	ASE	Average	ESE	Cvg
${\text{AUC}}_{t_0,\tau }^{(2)}$	91.8	0.4	0.5	91.5	0.5	94.0
${\text{AUC}}_{t_0,\tau }^{(1)}$	85.3	0.6	0.6	85.3	0.6	95.9

Additionally, we also consider the prediction accuracy of risk estimates based on a landmark Cox model as previously proposed in the literature (Van Houwelingen & Putter, 2008; Cortese & Andersen, 2010). Such a model would involve fitting a conditional proportional hazards working model for the residual life among Ω_T>t0 using baseline covariates along with a variable indicating whether the short term event had occurred by the landmark time. We denote the resulting risk estimate as ${\widehat{P}}_{t_0,\tau }^{(\text{cox})}(T_{\mathbb{S}},{\mathbf{Z}}_i)$. To evaluate the prediction rule resulting from this landmark Cox model approach, the corresponding Brier Score and AUC may be estimated by replacing ${\widehat{P}}_{t_0,\tau }^{(2)}(T_{\mathbb{S}i},{\mathbf{Z}}_i)$ in (2·8) and (2·9) with ${\widehat{P}}_{t_0,\tau }^{(\text{cox})}(T_{\mathbb{S}},{\mathbf{Z}}_i)$ to obtain ${\widehat{\text{BS}}}_{t_0,\tau }^{(2)(\text{cox})}$ and ${\widehat{\text{AUC}}}_{t_0,\tau }^{(2)(\text{cox})}$, respectively. Simulations results comparing the accuracy estimates from the proposed model to those from the landmark Cox model are shown in Table 4. In the low event rate setting, the proportion of explained variation in predicting long-term t₀ + τ survival increased by 0.063 and the AUC is 0.017 higher when n=5,000 when using the proposed approach to incorporate short-term outcome information compared to the landmark Cox model approach. In the moderate event rate setting, we observe a substantial increase in accuracy. When n = 5000, the proposed approach yields an increase in AUC of 0.057 and a 26% improvement in the proportion of variation explained.

Table 4.

Average cross-validated estimates using T and Z information using the proposed procedure ( ${\text{BS}}_{t_0,\tau }^{(2)},{\text{AUC}}_{t_0,\tau }^{(2)}$) compared to using the landmark Cox model ( ${\text{BS}}_{t_0,\tau }^{(2)(\text{cox})},{\text{AUC}}_{t_0,\tau }^{(2)(\text{cox})}$) (with corresponding SE estimates). All entries are multiplied by 100.

(a) Brier score
	${\text{BS}}_{t_0,\tau }^{(2)}$	${\text{BS}}_{t_0,\tau }^{(2)(\text{cox})}$	IPEV2/cox
(i) low event rate
n=2000	79.2 (0.42)	83.9 (0.45)	5.3 (7.6)
n=5000	78.2 (0.27)	83.6 (0.29)	63.4 (4.8)
(ii) moderate event rate
n=2000	10.2 (0.44)	13.5 (0.50)	24.6 (4.5)
n=5000	10.0 (0.28)	13.5 (0.32)	25.9 (2.7)
(b) AUC
	${\text{AUC}}_{t_0,\tau }^{(2)}$	${\text{AUC}}_{t_0,\tau }^{(2)(\text{cox})}$	${\text{AUC}}_{t_0,\tau }^{(2)}{-\text{AUC}}_{t_0,\tau }^{(2)(\text{cox})}$
(i) low event rate
n=2000	89.3 (0.93)	87.9 (1.01)	1.4 (1.54)
n=5000	89.6 (0.58)	87.9 (0.65)	1.7 (0.93)
(ii) moderate event rate
n=2000	91.2 (0.69)	85.8 (0.95)	5.4 (1.22)
n=5000	91.5 (0.44)	85.8 (0.64)	5.7 (0.79)

5 Example

To illustrate our proposed procedures, we use a dataset of patients with end-stage renal disease (ESRD) who had initiated maintenance peritoneal or hemodialysis from the United States Renal Data System (USRDS) (USRDS, 2010). The USRDS consists of a total of 463,240 patients from 18 regional areas who initiated dialysis between 2000 and 2004. Our analysis focused on the subset of patients from one network consisting of six-states in the New England area without a previous kidney transplant. This subset consisted of 9,785 patients with individual information on time to death or kidney transplant, time to first hospitalization, and several baseline covariates measured at initiation of dialysis. Total time at risk was measured from the earliest outpatient date after initiation of dialysis until censoring at transplantation, death, loss to follow-up, or December 31, 2005. Time until first hospitalization was measured from the earliest outpatient date after initiation of dialysis to the first hospitalization date, when available.

We define T as time to first hospitalization and T as time to death or kidney transplant. Early hospitalizations are frequent in patients with ESRD and are associated with higher morbidity and risk of death (USRDS, 2007; Collins et al., 2009). Previous work has examined the incremental value of incorporating hospitalization time in predicting residual life in this dataset in the presence of a single discrete marker, erythropoietin use (Parast et al., 2011). While this marker is useful, it would be of great clinical interest to be able to incorporate information on the other clinical variables available. For our analyses, we include the following baseline covariates measured at initiation of dialysis based on results from a multivariate analysis: age, albumin, erythropoietin use, serum creatinine, and prior history of heart failure (HF), arrhythmia, chronic obstructive pulmonary disease (COPD), and cancer. There is an abundance of clinical literature examining associations of these demographic and clinical predictors with all-cause or cause-specific hospitalization and mortality (Sands et al., 2006; Barrett et al., 1997; Murphy & Parfrey, 2000). In addition, some patients are hospitalized multiple times prior to t₀, which might indicate poor prognosis and hence a higher risk of death. Using our procedure, we are able to incorporate such information into prediction by adding the frequency of hospitalizations before t₀ as a covariate.

There were a total of 5,480 first hospitalizations, 5,448 deaths, 111 transplantations and the 18 month hospitalization rate was about 0.57; the 18 month death or transplant rate was about 0.40. For illustration, we chose t₀ to be 6 months and τ to be 1 year. Among the 7,679 patients who survived past 6 months, 37% were hospitalized within 6 months of initiating dialysis and 63% did not have a hospitalization before 6 months. We aim to make a prediction concerning 1-year survival among those who survived 6 months using the proposed procedures incorporating information on time of first hospitalization (T) and frequency of hospitalizations between baseline and t₀ as well as multiple baseline covariates. For example, the probability of interest, P_t0,τ,ts,z, for a patient with T = t_s = 24 days is displayed Figure 1.

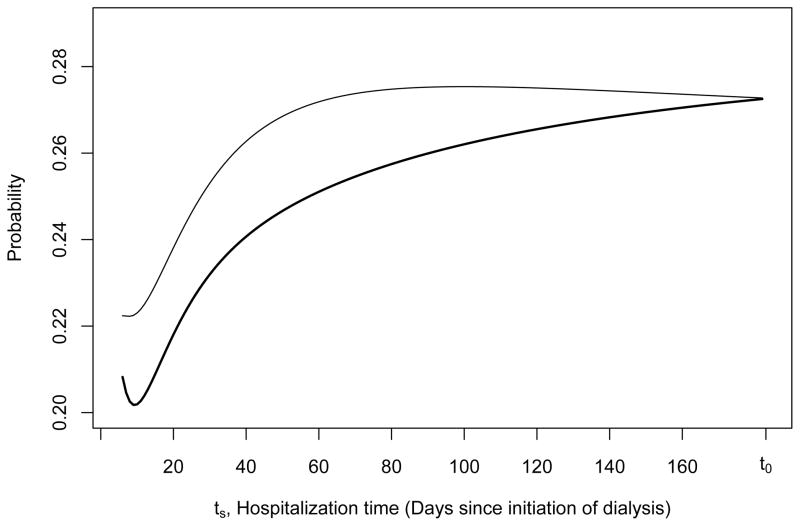
Figure 1.

Given patient i is hospitalized 24 days after initiation of dialysis, T_i = t_s = 24, but survives past 6 months, P_t0,τ,ts,Zi is the probability of death within the shaded region when t₀ = 6 months and τ = 1 year.

Estimates of β_ts are shown in Table 5 with corresponding SE estimates from the perturbation-resampling method. Figure 2 displays the estimates ${\widehat{P}}_{t_0,\tau }^{(2)}(t_s,\mathbf{z})={\widehat{P}}_{t_0,\tau ,t_s,\mathbf{z}}=\widehat{P}(T_{\mathbb{L}}\le t_0+\tau \mid T_{\mathbb{L}}>t_0,T_{\mathbb{S}}=t_s,\mathbf{Z}=\mathbf{z})=g({\widehat{\mathit{\beta }}}_{t_s}^{\top }\mathbf{z})$ over a range of t_s for two sets of patients with T = t_s ≤ t₀ who differ only by history of HF. Both patients were hospitalized once before t₀ and have the following same baseline covariate values: age = 76, albumin = 3.2, using erythropoietin, serum creatinine = 6.5, no prior history of arrhythmia, COPD, or cancer. However, one patient has prior history of HF (solid black thin line) while the other has no prior history of HF (solid black thick line). Using baseline covariate information only, ${\widehat{P}}_{t_0,\tau }^{(1)}(\mathbf{z})$, the predicted risk of having an event between 6 months and 1.5 years is equal to 0.21 for the patient with prior history of HF and 0.18 for the patient without prior history of HF regardless of hospitalization time. Note that ${\widehat{P}}_{t_0,\tau }^{(1)}(\mathbf{z})$ is the predicted risk for all patients who survived past 6 months whereas P̂_t0,τ,ts,z is for patients who survived past 6 months and were hospitalized before 6 months. Given that a hospitalization did not occur before 6 months, ${\widehat{P}}_{t_0,\tau }^{(2)}(t_s,\mathbf{z})={\widehat{P}}_{t_0,\tau ,\mathbf{z}}=0.16$ and 0.14 for the patient with and without prior history of HF, respectively. These results are consistent with the clinical literature which shows a clear association between morbidity upon initiation of dialysis, particularly cardiovascular conditions, and higher risk of hospitalization and death in end-stage renal disease patients (USRDS, 2010; Foley et al., 1997; Saravanan & Davidson, 2010; Cheung et al., 2004). Sudden cardiac death is the most common form of death in dialysis patients and it is has been argued that early referral of patients with co-morbid conditions would lead to planned transition from stage 4 chronic kidney disease to end-stage renal disease, perhaps reducing morbidity and mortality in the first year of dialysis treatment (Collins et al., 2009; Herzog et al., 2008). In addition, we note a peak at 60 days since initiation of dialysis which could potentially be explained by the tendency for patients to change dialysis modality within the first 90 days of dialysis treatment (Dalrymple et al., 2010).

Table 5.

Estimates of β_ts = (β₀, β_albumin, β_{epo use}, β_{serum creatinine}, β_{PHx HF}, β_{PHx arrhythmia}, β_{PHx COPD}, β_{PHx cancer}, β_age, β_hosp)^⊤ with corresponding SE estimates from the perturbation-resampling method (SE) when t₀ = 6 months and τ = 1 year in a dataset of end-stage renal disease patients. Values of t_s were chosen as the 20th, 40th, 60th, and 80th percentiles of T ≤ t₀. Note that PHx = “prior history of”, HF = heat failure, COPD = chronic obstructive pulmonary disease, epo = erythropoietin, hosp = number of hospitalizations before 6 months.

ts	t0.20		t0.40		t0.60		t0.80
	Estimate	SE	Estimate	SE	Estimate	SE	Estimate	SE
β0	−2.17	0.99	−2.22	0.81	−2.86	0.78	−3.14	0.87
βalbumin	−0.27	0.13	−0.29	0.10	−0.22	0.10	−0.15	0.10
βepo use	−0.21	0.15	−0.07	0.12	−0.07	0.12	−0.12	0.13
βserum creatinine	−0.04	0.03	−0.03	0.02	−0.02	0.02	−0.01	0.02
βPHx HF	0.13	0.15	0.11	0.12	0.11	0.12	0.06	0.12
βPHx arrhythmia	0.18	0.20	0.34	0.17	0.46	0.17	0.55	0.18
βPHx COPD	0.46	0.22	0.32	0.17	0.27	0.16	0.30	0.17
βPHx cancer	0.15	0.23	0.04	0.19	0.10	0.18	0.21	0.19
βage	0.03	0.01	0.03	0.01	0.03	0.01	0.03	0.01
βhosp	0.20	0.06	0.24	0.05	0.27	0.06	0.27	0.06

Figure 2.

For t₀ = 6 months (183 days) and τ = 1 year, estimates of P̂_t0,τ,ts,z = P̂(T ≤ t₀ + τ | T > t₀, T = t_s, Z = z) over time for two patients with T = t_s ≤ t₀ who differ only by history of HF are shown. Both patients were hospitalized one time and have the following baseline covariate values: age = 76, albumin = 3.2, using erythropoietin, serum creatinine = 6.5, no prior history of arrhythmia, chronic obstructive pulmonary disease, or cancer, but one patient has prior history of HF (solid black thin line) while the other has no prior history of HF (solid black thick line). Note that using baseline covariate information only, P̂(T ≤ t₀ + τ | T > t₀, Z = z) is equal to 0.21 and 0.18 for the patient with prior history of HF and for the patient without prior history of heat failure, respectively.

Brier score estimates with corresponding values of the increase in explained variation and AUC estimates are shown in Table 6. Incorporating intermediate hospitalization information leads to an improvement in accuracy with ${\text{BS}}_{t_0,\tau }^{(1)}-{\text{BS}}_{t_0,\tau }^{(2)}$ estimated as 0.005 (95% C.I. [0.0020, 0.0072]), IPEV_2/1 estimated as 0.026 (95% CI: [0.012, 0.041]), and increase in AUC by 0.051 (95% CI: [0.034, 0.068]). This indicates a significant gain in predictive ability after incorporating short-term outcome information. We note that in many clinical applications, the increment in AUC due to the inclusion of new novel biomarkers is often as little as ~ 0.01 (e.g. Wang et al., 2006).

Table 6.

Apparent and cross-validated (CV) estimates and corresponding SEs from the perturbation-resampling method (SE) for Brier score and AUC using hospitalization time and baseline marker information ( ${\text{BS}}_{t_0,\tau }^{(2)},{\text{AUC}}_{t_0,\tau }^{(2)}$), marker information only ( ${\text{BS}}_{t_0,\tau }^{(1)},{\text{AUC}}_{t_0,\tau }^{(1)}$) and the increase in proportion of explained variation(IPEV) using the ESRD patient dataset with t₀ = 6 months and τ = 1 year. All entries are multiplied by 100.

Brier Score
	Apparent	CV (3-fold)	SE
${\text{BS}}_{t_0,\tau }^{(2)}$	16.5	17.0	0.3
${\text{BS}}_{t_0,\tau }^{(1)}$	17.3	17.4	0.3
IPEV2/1	4.4	2.6	3
	95% C.I. for ${\text{BS}}_{t_0,\tau }^{(1)}-{\text{BS}}_{t_0,\tau }^{(2)}=(0.20,0.72)$
AUC
	Apparent	CV (3-fold)	SE
${\text{AUC}}_{t_0,\tau }^{(2)}$	67.0	65.2	0.9
${\text{AUC}}_{t_0,\tau }^{(1)}$	60.6	60.1	0.9
	95% C.I. for ${\text{AUC}}_{t_0,\tau }^{(2)}-{\text{AUC}}_{t_0,\tau }^{(1)}=(3.4,6.8)$

As previously mentioned, Parast et al. (2011) proposed non-parametric procedures to estimate predicted probability and evaluate the incremental value of including short term event information when there is only a single discrete covariate available. Using these procedures, there was an increase in predictive ability after incorporating hospitalization time in addition to the single discrete marker used for illustration, erythropoietin use. Since a significant advantage of the procedure proposed in this paper is the ability to accommodate one or more continuous covariates including time-varying covariate information collected up to t₀, it would be of interest to quantify how much the proposed procedure gained over the Parast et al. (2011) procedure in terms of prediction accuracy. In Parast et al. (2011), a prediction rule which incorporates both intermediate hospitalization information and erythropoietin use resulted in a Brier score estimate of 0.1741 with an SE of 0.0025 and an AUC of 0.6111 with an SE of 0.0080. Compared to these results, our procedure which incorporates the frequency of hospitalizations before t₀ and all the aforementioned baseline covariates leads to an improvement in prediction accuracy as demonstrated by a reduction in the Brier score of 0.0046 (95% CI: [−0.0129,0.0038 ]) and an increase in AUC of 0.0410 (95% CI: [0.0169,0.0652]).

6 Discussion

In this paper, we propose a flexible varying-coefficient model to incorporate short term event time information up to a landmark point along with baseline covariates for the prediction of long term survival. In addition, we use robust non-parametric procedures to make inference about the resulting accuracy measures and the difference in the accuracy measures between various prediction rules without requiring the correct specification of the proposed model. One may expect that including the short term event information could significantly improve the prediction accuracy when the short term event is highly correlated with the long term event of interest. Though we assumed independent censoring, the proposed procedure could accommodate marker dependent censoring by replacing Ĝ in Ŵ_i with Ĝ_z obtained as the Kaplan Meier estimator of P(C > t | Z = z) for the subgroup with Z_i = z. It is important to note that under model mis-specification β_ts may not necessarily reflect the effect of Z on T among the subgroup in Ω_t0,ts = {T > t₀, T = t_s}. However, it would still reflect the relative importance of Z in terms of prediction for subjects with different values of t_s. Especially when the model is approximately true, one may follow the same arguments as given in Eguchi and Copas (2002) that β_ts could be interpreted as the best linear combination of Z in predicting I(T ≤ t₀ + τ) among the subgroup Ω_t0,ts.

Though we present cross-validated estimates of the proposed accuracy measures, in an effort to reduce bias from potential over-fitting, it is often appealing to validate the performance of a risk prediction model in a population independent of the study population. We additionally acquired patient information from another region of the USRDS, specifically New York state and assessed the accuracy of our proposed risk score in this dataset. All accuracy measures were estimated assuming that β_ts, β_t0, and φ_t0 were fixed and known i.e. equal to β̂_ts, β̂_t0, and φ̂_t0, estimated previously in the first region of New England states. The accuracy measures from this separate validation set are similar in magnitude to those of the cross-validated accuracy measures in the original dataset and the proposed procedure performs well in both regions. For example, after incorporating hospitalization information, the AUC increased by 0.034 (95% CI: 0.026, 0.043) indicating a gain in predictive ability.

When a single discrete marker is available for prediction, one may consider a non-parametric approach as in Parast et al. (2011). When there are few markers available, one may extend this method using multi-dimensional smoothing. However, a large sample size would be required for even two-dimensional smoothing in the presence of censoring (Dabrowska, 1987). This lack of power would be even more pronounced here due to the reduced effective sample size as the analysis is restricted to patients who survive to t₀. While more parametric methods can certainly be considered, risk estimates from some model-based procedures may have poor accuracy if the model assumptions fail to hold. The proposed varying coefficient landmark prediction modeling framework also enables use to incorporate longitudinally measured covariates easily. This differs from the standard Cox model with time-varying covariates in that we do not use covariate information at time t to infer about hazard rate at t, but allow for a prediction of future events occurring long after t. We also note that our proposed method holds for any choice of t₀ and τ. In practice, one may consider the proposed estimator across a range of t₀ and τ as a basis for selecting an appropriate time point such that the prediction model is most accurate.

Throughout this paper we have assumed that the covariates and short term event time are measured without error. In practice, this may not be a valid assumption and if it is violated, this procedure may lead to biased estimates for the regression parameters. One may consider extensions to this procedure using measurement error models proposed in the literature (Carroll et al., 2006) to handle such situations. However, the added complexity and issues resulting from model mis-specification should be carefully considered. On the other hand, our proposed model can also be viewed as a working model aimed to approximate the underlying data generating process and to obtain the best prediction rule with the given marker values potentially measured with error. Future research on accounting for measurement error to improve prediction performance is warranted.

All analyses were performed in R. Code for implementing the proposed procedures is available upon request.