Poisson-Boltzmann Calculations: van der Waals or Molecular Surface?

Abstract

The Poisson-Boltzmann equation is widely used for modeling the electrostatics of biomolecules, but the calculation results are sensitive to the choice of the boundary between the low solute dielectric and the high solvent dielectric. The default choice for the dielectric boundary has been the molecular surface, but the use of the van der Waals surface has also been advocated. Here we review recent studies in which the two choices are tested against experimental results and explicit-solvent calculations. The assignment of the solvent high dielectric constant to interstitial voids in the solute is often used as a criticism against the van der Waals surface. However, this assignment may not be as unrealistic as previously thought, since hydrogen exchange and other NMR experiments have firmly established that all interior parts of proteins are transiently accessible to the solvent.

1 Introduction

Electrostatics plays important roles in biomolecular interactions, such as between proteins, ligands, and nucleic acids [1–3]. Stability, specificity, and rates can all be tuned by charge mutations. The development of reliable and fast methods for computing electrostatic free energies has attracted great attention in the past several decades. The Poisson–Boltzmann (PB) equation has emerged as one of the most widely used method for modeling biomolecular electrostatics. Advances and biophysical applications of the PB model can be found in many recent reviews [4–10]. One particular aspect of the PB model is that calculation results are very sensitive to the specification of the boundary between the low dielectric solute and the high dielectric solvent [11–19]. What is the proper dielectric boundary in PB calculations is still an open question. The present review focuses on recent studies addressing this question.

2 Solvation energy

The energy of a biomolecule (or a biomolecular complex) in an aqueous environment can be decomposed into an internal component and a solvation component. The solvation energy is determined by the interactions of the solute molecule and the solvent molecules (water, ions, and other species). Operationally the solvation energy is the free energy of transferring the solute molecule from a reference medium to the aqueous environment. Solvation energy can be calculated by a variety of methods, from the very time-consuming quantum mechanical approaches to simple Coulomb’s law [20, 21]. Broadly speaking there are two types of solvation models: explicit solvent and implicit solvent. The explicit models represent the solvent in molecular and atomic details, and therefore require extensive computational sampling and provide a physically more sound description. In contrast, implicit solvent models represent the solvent as a dielectric continuum; the calculation is more efficient and the results are usually more intuitive to interpret.

3 Poisson-Boltzmann equation

The most popular implicit solvation model is based on the PB. It is a second-order elliptic partial differential equation describing the electrostatic potential around a fixed charge distribution in an ionic solution. The full, nonlinear PB equation in a solution containing a 1:1 salt takes the form

$$\nabla ·\epsilon (\mathbf{r})\nabla \varphi (\mathbf{r})=({\epsilon }_{\mathrm{s}}{k}_{\mathrm{B}}T/e){\kappa }^{2}S(\mathbf{r})\text{sinh}[e\varphi (\mathbf{r})/k_{\mathrm{B}}T]-4\pi \rho (\mathbf{r})$$

where ϕ(r) is the electrostatic potential at position r; ε(r) denotes the dielectric constant, with value ε_p in the solute dielectric and ε_s in the solvent dielectric; κ is the Debye-Hückel screening parameter dependent on the ionic strength of solution; S(r) is a “masking” function with value 1 in the region accessible to the ions in the solvent and value 0 elsewhere; e is the protonic charge; k_B is Boltzmann’s constant; T is the absolute temperature; and ρ(r) is the solute charge density. Expanding sinh[eϕ(r)/k_BT] ≡ sinhϕ̃(r) to the lowest order results in the linearized PB equation:

$$\nabla ·\epsilon (\mathbf{r})\nabla \varphi (\mathbf{r})={\epsilon }_{\mathrm{s}}{\kappa }^{2}S(\mathbf{r})\varphi (\mathbf{r})-4\pi \rho (\mathbf{r})$$

The electrostatic free energy of the system is [22]

$$G_{\text{el}}={\displaystyle \int }{d}^3\mathbf{r}\{\frac{1}{2}\rho (\mathbf{r})\varphi (\mathbf{r})+\frac{{\epsilon }_{\mathrm{s}}{(k_{\mathrm{B}}T\kappa /e)}^2}{4\pi }S(\mathbf{r})[1+\frac{1}{2}\mathrm{\varphi ̃}(\mathbf{r})\text{sinh}\mathrm{\varphi ̃}(\mathbf{r})-\text{cosh}\mathrm{\varphi ̃}(\mathbf{r})\left]\right\}$$

The term in brackets disappears for the linearized PB equation.

The dielectric constant of proteins and other biomolecules is generally thought to be between 2 and 4. In comparison, water has a high dielectric constant ~ 80. The solute charge distribution is typically represented by a set of discrete partial charges (e.g., one at each atomic center). The most widely used PB solver, APBS [23], uses an iterative finite-difference approach. The basic idea is to represent all the position-dependent functions [ε(r), S(r), ρ(r), and ϕ(r)] on a cubic lattice and approximate the gradient operations in the PB equation by finite difference. To reduce numerical errors, the PB equation is usually solved twice, once for the regular ε(r) S(r) assignment and once with ε(r) set to ε_p everywhere and with S(r) set to 0 everywhere. The latter situation represents the reference medium. The difference in electrostatic free energy between the two calculations is the solvation energy:

$$\mathrm{\Delta }{G}_{\text{solv}}=G_{\text{el}}-G_{\text{el}}{|}_{\stackrel{\epsilon (\mathbf{r})={\epsilon }_{\mathrm{p}}}{S(\mathbf{r})=0}}$$

For proteins, ΔG_solv is usually dominated by favorable interactions of the atomic charges with the high-dielectric solvent and thus negative in sign; the magnitudes of ΔG_solv are typically several thousand kcal/mol [19].

It is worth mentioning that more recently the generalized Born (GB) model has been developed as a fast substitute of the PB model [10, 24–28], especially for use in implicit-solvent molecular dynamics simulations. The GB model is usually benchmarked or even parameterized against the PB model.

4 Dielectric boundary: van der Waals versus molecular surface

As noted above, the calculated solvation energy is sensitive to the choice of the dielectric boundary. The sensitivity is little blunted by dielectric smoothing (whereby grid points on the boundary are assigned dielectric values intermediate between ε_p and ε_s), which is often introduced for numerical stability.¹ Making the solute charges closer to the solvent dielectric, e.g., by reducing the atomic radii, will make the solute-solvent interactions more favorable and hence ΔG_solv more negative. Even a 0.1% change in ΔG_solv amounts to several kcal/mol, which would be comparable in magnitude to binding free energy and other quantities of interest. Thus uncertainty in the choice of the dielectric boundary could bring significant uncertainty in calculation results in PB applications.

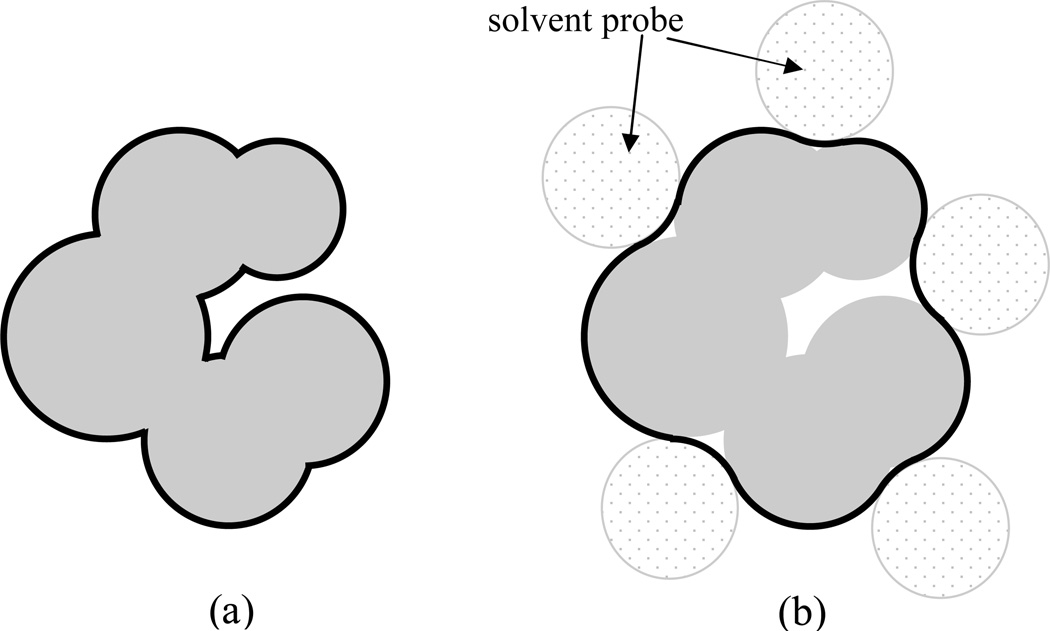
By far the most widely used choice for the dielectric boundary is the molecular surface (MS). This surface was first introduced by Richards [29], defined as the boundary between the region inaccessible to a spherical probe and that accessible to it, and hence also more specifically known as the solvent-exclusion surface (Fig. 1). Although Richards introduced MS as a geometric descriptor of protein structures, it was appealing to the early developers of PB solvers [1, 2] as the choice of the dielectric boundary. That sentiment continues to this day. Because of its easier implementation, the van der Waals (vdW) surface was occasionally used but was considered as an inferior substitute for the molecular surface [11, 26]. A usual criticism of vdW is that it leaves numerous interstitial voids, which are too small for discrete water molecules to occupy but nevertheless would be assigned the solvent high dielectric constant, a situation viewed by many as undesirable [11, 25, 30].

Figure 1.

Definitions of (a) the van der Waals surface and (b) the molecular surface. In this two-dimensional illustration, the van der Waals spheres of the atoms are represented by gray disks. In (a), the exposed boundaries of the van der Waals spheres, shown in dark, constitute the van der Waals surface. In (b), a spherical probe is rolled around the solute molecule. In addition to the van der Waals spheres, small crevices inaccessible to the probe are now part of the solute region. The boundary of this inaccessible region, shown in dark, is the molecular surface. Taken from Tjong and Zhou [19].

In addition to MS and vdW, other dielectric boundaries have been implemented in PB (and GB) calculations, including Gaussian surface [26, 28, 31], spline surface [32], and geometric flow surface [21]. The latter surfaces are often parameterized against MS- or vdW-based PB results.

5 Test against experimental data

Against the popular sentiment for MS, our group has advocated the use of vdW as the dielectric boundary [12–16, 18]. This position was based on comparing PB results against experimental results on protein folding and binding stability and protein association rates.

Qualitatively, solute charges are less accessible to the solvent in the MS protocol (with a 1.4-Å probe radius) than in the vdW protocol. Accordingly the desolvation cost of charged groups and the protein charges overall upon folding or binding is higher in the MS protocol than in the vdW protocol. Indeed, the desolvation cost of protein charges calculated according to the MS protocol is so high as to make the net electrostatic contribution ΔG_el generally unfavorable to protein folding and binding stability [33, 34]. Similarly, MS-based PB results showed that a majority of salt bridges were electrostatically destabilizing to protein folding [35]. However, we found that vdW-based PB results, with lower desolvation cost, led to the opposite conclusion [12–16].

There is no known experimental method that directly gives the net electrostatic contribution (ΔG_el) to folding or binding stability. However, one may surmise that, when charged residues, e.g., those forming a salt bridge in the folded or bound state, the dominant effect on stability is electrostatic. We thus compared PB results for ΔΔG_el directly against experimental results for the changes in folding or binding free energy by charge mutations [12–16]. Either MS or vdW was used as the dielectric boundary and other parameters (AMBER charges [36]; Bondi radii [37]; ε_p = 4) were kept the same. Consistently the vdW-based PB results were in better agreement with the experimental results.² The effects of ionic strength predicted by the vdW and MS protocols were essentially identical, depriving a potential source of experimental data for discriminating the two protocols.

Concomitant with the higher desolvation cost of the MS protocol, the interactions between charged residues upon folding or binding are also stronger, since they are less screened by the solvent than in the vdW protocol. The charge-charge interaction energy can be measured by a double-mutant cycle (to the extent that non-electrostatic effects of the two residues are either additive or insignificant). For several salt bridges formed upon folding or binding, the vdW-based results are in good agreement with the experimental data, whereas the MS-based results overestimated the charge-charge interaction energies [12–14].

These results led us to conclude that the MS protocol tends to overestimate the desolvation cost as well as the strength of charge-charge interactions. This conclusion appears to be consistent with the work of Gilson and co-workers [38, 39] on predictions of pK_a shifts. pK_a shifts can be determined from the desolvation cost and charge-charge interactions of titratable groups. Gilson and co-workers found that MS-based PB calculations tended to over-predict pK_a shifts, an indication of overestimation of desolvation cost and charge-charge interactions. As a remedy, they proposed using an ε_p of 20 to reduce desolvation cost and weaken charge-charge interactions. This remedy is now commonly used in predictions of pK_a shifts, but not often used for other purposes. We found that, for pK_a shifts and mutational effects on binding stability [14, 15], this remedy, by reducing desolvation cost and weakening charge-charge interactions, shifts the MS-based PB results toward the vdW-based results. We also note that MS-based PB calculations by Caflisch and Karplus [40] indicated a well-formed double salt bridge on the surface of barnase to be unstable, leading the authors to suggest overestimation of desolvation cost.

In contrast to the situation with folding and binding stability, the total electrostatic contribution to protein-protein association rates can be teased out, at least in the diffusion-limited regime. The association rate constant can be calculated as [18]

$$k_{\mathrm{a}}=k_{\mathrm{a}0}{e}^{-\mathrm{\Delta }{G}_{\text{el}}^{*}/k_{\mathrm{B}}T}$$

where k_a0 is the “basal” rate constant for reaching by random diffusion a transient complex, where the two subunits have near-native separation and orientation but have yet to form the short-range specific interactions of the native complex; and $\mathrm{\Delta }{G}_{\text{el}}^{*}$ is the electrostatic interaction energy of the transient complex. The basal rate constant is of the order of 10⁵ M⁻¹s⁻¹, but observed association rate constants can reach 10¹⁰ M⁻¹s⁻¹, due to long-range electrostatic attraction [41]. With the vdW protocol, we obtain negative values for $\mathrm{\Delta }{G}_{\text{el}}^{*}$ and thus electrostatic rate enhancement in such cases. Indeed, our calculations have been able to quantitatively reproduce experimental data for the association rates of a large number of protein complexes [18, 42–44]. However, when the MS protocol was used, $\mathrm{\Delta }{G}_{\text{el}}^{*}$ (like the counterpart ΔG_el for binding stability; see above) switched sign to become positive, resulted in electrostatic rate retardation instead of electrostatic rate enhancement [18]. This MS-based prediction is impossible to explain associate rate constants in the 10⁷ to 10¹⁰ M⁻¹s⁻¹ range, which are observed on many protein complexes [41].

As noted above, a usual criticism of vdW is that it would assign the solvent high dielectric constant to the interstitial voids in the solute. That would be unrealistic if the protein structure were static. Of course all protein molecules are dynamic. It is now known from NMR experiments that even deeply buried water molecules in proteins can exchange with bulk water on sub-millisecond timescales [45]. At a minimum, these observations indicate that parts of the proteins not solvent-accessible in their static X-ray structures must be accessible to the internal water molecules during their exchange with bulk water. That should not be a surprise, since hydrogen exchange experiments have long established that all backbone amides, exposed or buried, are accessible to solvent [46].

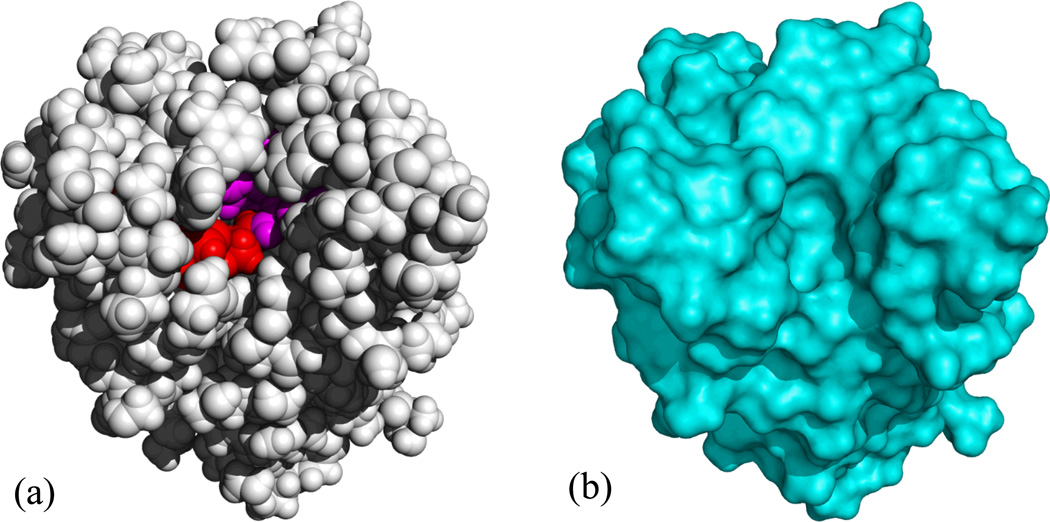
Transient solvent access to “buried” groups may be essential for biological functions, as is the case for acetylxylan esterase. As shown in Fig. 2, this enzyme has a deep tunnel leading to the catalytic triad [47]. Obviously the tunnel and the catalytic triad are accessible to water and the substrate. However, in the static X-ray structure, they are inaccessible to the 1.4-Å probe used to define the MS [19]. This example illustrates the artificial nature of using a spherical probe on a static structure to define the solute-solvent boundary. We suggest that, considering the inevitable transient solvent access to the internal regions of proteins, assigning the solvent high dielectric constant to interstitial voids in the solute according to the vdW protocol may not be as unrealistic as others have previously thought.

Figure 2.

Representations of acetylxylan esterase by (a) van der Waals surface and (b) molecular surface. In (a) the catalytic triad is shown in red, and other residues lining the tunnel are shown in purple. Taken from Tjong and Zhou [19].

6 Test against explicit-solvent computational results

The two choices, MS and vdW, of the solute-solvent dielectric boundary have been evaluated against solvation free energies obtained from explicit-solvent molecular dynamics (MD) simulations [11, 30, 48–50].³ Below we critically assess these studies.

On the outset, we should point out that, while all other PB parameters (atomic charges and dielectric constants) can be unequivocally obtained from the corresponding explicit-solvent simulations, there is ambiguity in choosing a set of atomic radii that faithfully model the explicit-solvent system and are not adjusted for the purpose of reproducing MD results. This ambiguity complicates the evaluation of the choice between MS and vdW, since MS-based PB results can be reproduced by vdW-based PB results by increasing the atomic radii and vice versa [11, 19]. The amount of radius adjustment required to match MS-based and vdW-based PB results generally increases with increasing solute size [19].

Nina et al. [11] were the first to benchmark PB results for biomolecules, in their case the 20 types of amino acids, against solvation free energies obtained from explicit-solvent MD simulations. They determined atomic radii according to the solvent charge radial distribution functions (followed by slight adjustments). The vdW-based PB results were able to reproduce the MD results well. By reducing the atomic radii by 2%, MS-based PB results could also reproduce the MD results. When standard CHARMM PARAM22 atomic radii [51] were used instead, PB results were in poor agreement with MD results.

Lee and Olson [48] extended the study of Nina et al. [11] to the solvation free energies of two proteins (villin headpiece and protein L) in various fixed conformations. Consistent with Nina et al. [11], PB results using PARM22 atomic radii, with either the vdW or MS dielectric boundary, had large deviations from the MD results. The deviations were reduced significantly for vdW-based PB results using the solvent distribution-based radii of Nina et al. However, when adjustments were made to the PARM22 atomic radii, the MS protocol outperformed the vdW protocol. It seems likely that the vdW-based PB results could be improved if adjustments were made to the solvent distribution-based radii, but Lee and Olson did not pursue such adjustments.

Swanson et al. [30] used the explicit-solvent potential of mean force (PMF) between H_δ and N_ε atoms of two N_δ-protonated histidines to evaluate PB protocols. The explicit-solvent PMF is oscillatory, with minima at 2 and 4.8 Å of H_δ-N_ε separation and maxima at 3.2 and 5.8 Å. MS-based PB calculations produced a maximum ~3.2 Å whereas PB calculations based on a spline surface (similar to vdW) did not. The production of the maximum was taken as strong support for the MS protocol. However, further analysis suggests that the maximum at 3.2 Å in the explicit-solvent PMF has a different origin than the maximum in the MS-based PB calculations. The maximum in the MS-based PB calculations comes about because at the 3.2-Å separation a 1.4-Å probe cannot be placed between the H_δ and N_ε atoms; therefore there is a significant desolvation cost (relative to the situation where the two histidines are infinitely apart).⁴ Hence the maximum in the MS-based PB calculations is completely electrostatic in origin. However, the oscillatory shape of the explicit-solvent PMF is common for the pair distribution functions of small solute molecules with hard-core repulsion by solvent molecules; an extreme example is the pair distribution function of a hard-sphere liquid. In that case minima in the PMF arise when an integral number of solvent spheres can exactly fit between the two solute spheres, and maxima arise when the two solute spheres are further separated by half the diameter of a solvent sphere, creating an inaccessible empty space. The maxima and minima are traced to the entropy of arranging the solvent spheres around the two solute spheres. The oscillatory shape and the spacing between the minima and maxima of the PMF of the two histidines suggest a similar explanation. It is likely that a similar oscillatory shape will be obtained in explicit-solvent simulations where the partial charges on the two histidines are all set to zero. For such neutralized histidines, all PB calculations would produce a zero PMF at any separation. In short, whether the first maximum in the explicit-solvent PMF of the two histidines can be used as strong support for the MS protocol is debatable.

Aguilar et al. [49] recently compared PB results against the electrostatic free energies for four conformations of an 10-alanine peptide obtained by Roe et al. [52] from explicit-solvent MD simulations. Aguilar et al. found MS-based PB results to agree best with the MD results when the probe radius was 1.4 Å for one conformation of the peptide and was 2.0 Å for the other conformations, but did not specify what atomic radii were used. As alluded to above, atomic radii optimized for MS-based PB results will not be optimal for vdW-based PB results.

Salari and Chong [50] recently compared PB and explicit-solvent MD simulation results for the electrostatic solvation energies of 14 salt bridges across protein-protein interfaces. The PB calculations used the OPLS/AA-L atomic radii [53] (same as in the explicit-solvent simulations). vdW-based PB results reproduced the MD results both in the bound and unbound states without systematic errors, whereas MS-based PB results systematically underestimated the magnitudes of the MD results, although the latter errors canceled to a large extent when the difference between the two states was taken.

7 Concluding remarks

For a given set of atomic radii, PB results are sensitive to whether the solute-solvent dielectric boundary is specified as the molecular or the van der Waals surface. The vdW-based protocol, by assigning the solvent high dielectric constant to interstitial voids in the solute, may provide a way to model transient solvent access to solute interior regions. Purported support of the MS protocol by explicit-solvent MD simulation studies seems disputable. Given the empirical nature of the PB equation, the debate over which surface provides a better dielectric boundary will likely continue.

One possible outcome is that the difference between the MS and vdW protocols would be narrowed, when explicit water molecules in the first hydration shell are included in PB calculations. Intuitively one expects that incorporating information from explicit-solvent simulations would generally improve continuum electrostatic calculations. A number of recent studies [54–56] have shown that this is indeed a promising direction. Hybrid explicit-implicit modeling will likely be a fertile ground for further investigations.