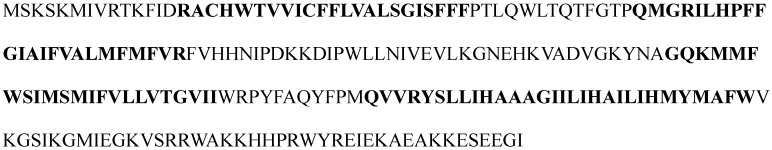A Simple Method for Predicting Transmembrane Proteins Based on Wavelet Transform

Abstract

The increasing protein sequences from the genome project require theoretical methods to predict transmembrane helical segments (TMHs). So far, several prediction methods have been reported, but there are some deficiencies in prediction accuracy and adaptability in these methods. In this paper, a method based on discrete wavelet transform (DWT) has been developed to predict the number and location of TMHs in membrane proteins. PDB coded as 1KQG is chosen as an example to describe the prediction process by this method. 80 proteins with known 3D structure from Mptopo database are chosen at random as data sets (including 325 TMHs) and 80 sequences are divided into 13 groups according to their function and type. TMHs prediction is carried out for each group of membrane protein sequences and obtain satisfactory result. To verify the feasibility of this method, 80 membrane protein sequences are treated as test sets, 308 TMHs can be predicted and the prediction accuracy is 96.3%. Compared with the main prediction results of seven popular prediction methods, the obtained results indicate that the proposed method in this paper has higher prediction accuracy.

Introduction

With the accomplishment of human genome project (HGP), post-genome era has come with the main character functional genomics and proteomics. Along with the HGP, a new subject—bioinformatics has developed. However the obtained massive biological data which is still in the rapid increase and the complexity of the life essence challenged young bioinformatics, so bioinformatics needs constant innovation and development in various aspects of technical means, methods and correlative field.

The study of structure and function of membrane protein is one important subject in bioinformatics. The knowledge of the function of membrane protein itself has been expanded enormously and deeply, and the more study of it can be used as a breakthrough of studying protein structure and function and the genetic information in DNA sequence. In order to explore the relationship between membrane protein structure and function, understand various work mechanism in membrane protein life activities, bioinformatics methods and techniques of developing the study of membrane protein are needed.

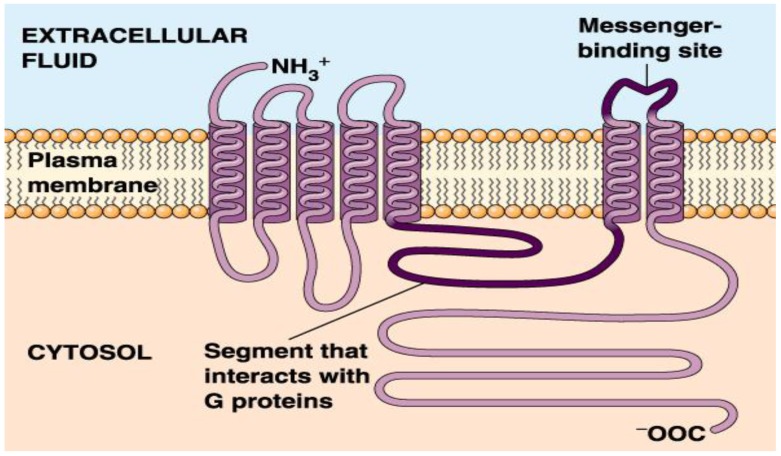
In the genome data, a large portion (about 20%-30%) of proteins in a genome encodes membrane protein ^1-4, the proportion of such shows the importance of membrane protein in biology. Membrane protein, especially transmembrane proteinin has very important function in organism, such as photosynthesis, respiration, neural signaling, immune response, nutrient absorption and so on, and it is also the important drug target. Of the drug target known and being researched is about 70% of the membrane protein ⁵. For example, G protein-coupled receptors (GPCRs) is a kind of transmembrane protein receptors with one article of peptide chains and seven transmembrane helical segments (TMHs), as shown in Figure 1 below. It is a kind of very important molecular receptors and the biggest transmembrane protein family in the eukaryotes ⁶. GPCRs has the largest gene families coding in animal genome. The known 1% of the fruit flies genes and more than 5% of the nematode gene are responsible for coding GPCRs, and more than 1% of the gene in human genome is used to encode more than 1000 GPCRs ⁷.

Figure 1.

Schematic drawing of a G protein-coupled receptor structure.

The dysfunction of GPCRs can lead to many diseases, such as Alzheimer's disease, parkinsonism syndrome, dwarfism, achromat, retinitis pigmentosa and asthma, etc. Through regulation GPCRs' signal transduction can treat depression, schizophrenia, insomnia, high blood pressure, kidney function decline, cerebrovascular disease, etc. Most of the drugs, through targeting effect on GPCRs, achieve remedial effect. Currently in the small molecule drugs market of the world, more than a third of the drug's effect targets are GPCRs ^{8, 9}. More than 50% of the prescription drugs take effect through GPCRs ¹⁰. In addition to GPCRs, there are some other important transmembrane protein family, including ion channels, actin and some of the proteins related to biological energy, for example, those proteins related to electronic transport system ¹¹.

The hydrophobic nature of membrane proteins makes it form a stable natural conformation together with biological membrane, which goes against measuring its three-dimensional (3D) structure by using X-ray crystal diffraction method and nuclear magnetic resonance (NMR) technology. Among about 56000 kinds of protein data bank (PDB), less than 1% of the protein of known structure are membrane proteins ^12,13. Until now, what we know about 3D structure of membrane proteins with high-resolution are a few, such as bacteriorhodopsin (bR), photosynthetic reaction center, cytochrome C oxidase, etc. This shows that there is a big gap between the number of the known membrane protein sequence and the known membrane protein structure, which greatly restricted the deep research of the function of membrane protein. With functional genomics and proteomics research developing, the launch of the analysis of membrane protein sequence increase rapidly, urgently needing the effective, high accuracy of the algorithm to predict the membrane protein TMHs and transmembrane direction to guide the research of membrane protein; On the other hand, through the comparison of the prediction accuracy of different algorithms, the hidden biological significance can be revealed, so as to guide the membrane protein biological experiment. Therefore, the membrane protein structure prediction, especially the prediction of transmembrane helical segments in membrane proteins has caused strong interest of the researchers.

So far many transmembrane helical segments (TMHs) predicting algorithms for membrane proteins have been proposed. In 1982 Kyte and Doolittle firstly suggested a hydrophobicity analysis method of membrane protein sequences ¹⁴. Thereafter von Heijne put forward the well-known "positive-inside rule" to guide prediction in 1986 ¹⁵. SOSUI ¹⁶, PRED-TMR ¹⁷ were based on the foregoing two methods. In recent years, some statistical methods have been developed that like DAS ¹⁸, TMAP ¹⁹, neural networks PHDhtm ^{20, 21}, TMHMM ^{1, 22} and HMMTOP ^{23, 24} based on hidden Markov model, MEMSAT-SVM prediction method based on support vector machine ^{25, 26}. Wavelet transform was first introduced into bioinformatics research in 1996 ²⁷ and raised extensive attention immediately ^28-37. Liò et al ²⁹ proposed a non-parametric method based on a wavelet data-dependent threshold technique for change-point analysis which was applied to predict TMHs in membrane proteins. Continuous wavelet transform (CWT) for predicting the number and location of helices in membrane proteins is presented by Qiu et al ³¹. Pashou et al ³² applied a dynamic programming algorithm on wavelet-denoised 'hydropathy' signals to determine membrane spanning segments.

In this paper, we make full use of the hydrophobicity of amino acids and multiresolution feature of discrete wavelet transform (DWT) to decompose the amino acids of TM proteins into a series of structures in different layers, then predicting the location of TMHs according to the information of the amino acids sequence in different scales. 80 proteins with known 3D structure are chosen at random as data sets. Firstly, cross-validation method is introduced and five commonly used hydrophobic parameters are used to predict the position and number of TMHs based on two different levels in order to find the best hydrophobic parameters, offer help for further membrane protein work and reduce the blindness of choosing hydrophobic parameters. Results show that the best membrane proteins TMHs is achieved when choosing FP and KD hydrophobic parameters. Secondly, take one membrane protein sequence as an example to bat around and do comparison combined with the prediction results by the other seven methods in order to confirm the effectiveness of WavePrd method. The above 80 membrane proteins are divided into 13 groups according to their function and type. The prediction of TMHs of the 13 groups by using KD hydrophobicity parameters is satisfying. 308 TMHs of 80 proteins (including 325 TMHs) can be predicted and the prediction accuracy is 96.3%. The prediction accuracy of rate of amino acid residues reaches 83.5%. Compared with the main prediction results of seven popular prediction methods, DAS ¹⁸, HMMTOP2.0 ^{23, 24}, PHDhtm ^{20, 21}, PRED-TMR2 ¹⁷, SOSUI ¹⁶, TMAP ¹⁹, TMHMM2.0^{1, 22}, the obtained results indicate that the proposed method in this paper has higher prediction accuracy.

Materials and Methods

Materials

The test dataset is retrieved from the latest MPtopo database ³⁸, which collects a set of membrane protein structure data identified by crystallography or other experimental technologies such that they can be treated as reliable samples. One group of test data sets that contain total 80 protein sequences with known 3D structure including 325 TMHS and 19396 amino acid residues. The data can be obtained from http://blanco.biomol.uci.edu/mptopo. According to the function and type of membrane proteins, we divided 80 membrane proteins sequences into 13 groups, which are shown in Table 1.

Table 1.

Membrane protein families used in our predictions.

Family name	PDB code
ABC transporters	1jsq	1l7vA	1pf4
Bacteriorhodopsin	1ap9
Channel proteins	1fqyA	1fx8A	1msl	1mxm	1oedA	1oedB
	1oedC	1oedE	1p7b	1rc2A	1rhzA	1rhzB
Cytochrome bc1 complexes	1bgyE	1bgyJ	1bgyK
Cytochrome b6f complexes	1um3A	1um3B	1um3D	1um3F	1um3G	1um3H
Cytochrome c oxidases	1ehkA	1ehkB	1ehkC	1occA	1occB	1occC
	1occD	1occG	1occI	1occJ	1occK	1occL
	1occM	1qleA	1qleB	1qleC	1qleD
Glycophorin	1afoA
Light-harvesting complexes	1kzuA	1lghA
Photosynthetic reaction centers	1eysH	1eysL	1eysM	1prcH	1prcL	1prcM
	2rcrL	2rcrM
Photosystems	1jboA	1jboB	1jboF	1jboI	1jboJ	1jboK
	1jboL	1jboM
Respiratory proteins	1a91C	1fftA	1fftB	1fftC	1fumC	1kqgB
	1kqgC	1lovD	1nekC	1nekD	1okcA	1q16C
	1qlaC
Rhodopsins	1f88	1h2sB	1h68A
Translocation proteins	1pw4A	1s7b	2cpb

Methods

As is known to all, the feature of protein structure is the balance between hydrophobic and hydrophilic and the structure stability depends heavily on molecules' hydrophobic effects ^39-41. The determination of hydrophobic value of amino acid is mainly calculated according to distribution coefficient in which various amino acid is in organic solvent and water. Due to the different laboratory test equipment, experimental conditions, organic solvents and calculation methods, hydrophobicity values obtained are also of considerable gap. So when we map the amino acid sequence of protein onto a sequence of hydrophobicity, we need to optimize a variety of different hydrophobic parameters. Here, we list five commonly used hydrophobic parameter values, as is shown in Table 2. 80 membrane protein sequence data set are used to verify their actual effect one by one, so as to find out the best hydrophobic parameters, offer help for further research work of membrane protein and reduce blindness of the selection of hydrophobic parameters.

Table 2.

Five different hydrophobicity values.

Amino acids	FPa	KDb	PPc	EId	JTTe
A	0.62	1.80	0.324	0.62	0.595
C	0.29	2.50	0.184	0.29	0.205
D	-1.05	-3.50	-1.877	-0.90	-1.276
E	-0.87	-3.50	-2.033	-0.74	-1.291
F	1.19	2.80	0.804	1.19	1.467
G	0.48	-0.40	0.147	0.48	0.065
H	-0.40	-3.20	-0.930	0.30	-0.387
I	1.38	4.50	0.734	1.38	1.888
K	-1.35	-3.90	-2.230	-1.50	-1.245
L	1.06	3.80	0.612	1.06	1.234
M	0.64	1.90	0.407	0.64	0.626
N	-0.85	-3.50	-0.944	-0.78	-0.870
P	0.12	-1.60	-0.516	0.12	-0.746
Q	-0.78	-3.50	-1.300	-0.85	-0.995
R	-1.37	-4.50	-2.085	-2.53	-1.073
S	-0.18	-0.80	-0.216	-0.18	-0.247
T	-0.05	-0.70	-0.129	-0.05	-0.154
V	1.08	4.20	0.563	1.08	1.280
W	0.81	-0.90	0.582	0.81	0.891
Y	0.26	-1.30	0.073	0.26	0.034

^aFauchere and Pliska ⁴² (1983). ^bKyte and Doolittle ¹⁴ (1982). ^cPasquier et al. ¹⁷ (1999). ^dEisenberg et al. ⁴³ (1984). ^eBoyd et al. ⁴⁴ (1998).

Method of wavelet analysis

The wavelet transform (WT) is relatively analysis methods with the changeable time-frequency window, which has very good localization properties in the time and frequency intra-areas. The discrete wavelet transform (DWT) decomposes a function into its wavelet coefficients. From a computational point of view, it proceeds by recursively applying two convolution functions, known as quadrature mirror filters, each producing an output stream that is half length of the original input, until the resolution level zero is reached. Mallat brought out the most important concept multiresolution analysis (MRA) in a discrete wavelet theory as well as fast algorithm of orthonormal wavelet tranform—Mallat algorithm⁴⁵.

Let φ(x) be a scaling function which satisfies the following two-scale equation:

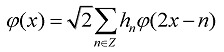(1)

Where Z is a set of integers, and the coefficients {h_n, n ∈ Z} denote a low-pass filter (H). The wavelet function ψ(x) can be constructed using the scaling functionφ(x) as

(2)

where the coefficients {g_n, n ∈ Z} denote a high-pass filter (G).

Assume that the shifted scaling function {φ(x-k), k ∈ Z} and the shifted wavelet functions {ψ (x-k), k ∈ Z} are orthonormal, respectively. Let {c_l⁰} denote a sequence of hydrophobicity values, and we define a linear combination f(x) of the sequence with scaling functions {φ(x-k), k ∈ Z}:

(3)

According to a wavelet theory, we have another expansion of f(x):

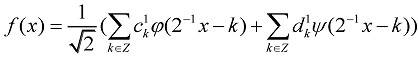(4)

From Eqs (3) and (4) and using orthonormality of the scaling and wavelet functions, we can decompose the sequence {c_l⁰} into low frequency and high frequency components.

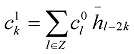(5)

and

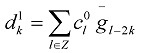(6)

Repeatedly application of this decomposition, we can deduce

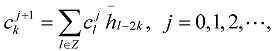(7)

And

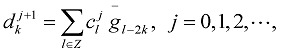(8)

Conversely, we can derive a reconstruction formula form Eqs (3) and (4):

(9)

Above-mentioned formulas can refer to the literature of Mallat ⁴⁵.

In Eqs. (7) and (8), the sequences {c_k^j+1} and {d_k^j+1} mean low and high frequencies. In this paper, only the first formula Eq. (9) is used because as far as most of the protein hydrophobicity signals are concerned, low frequency domain is especially important and it can reflect the general characteristics of signals. However the high frequency domain is always connected with noise and disturbance, so the basic features of signals will be reserved when the high frequency domain is discarded by putting {d_k^j+1} =0. Using Eq. (9), we reconstruct a new sequence 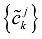only from {c_k^j+1}, that is, we utilize low-pass filtering of wavelet transform. In wavelet analysis, the low frequency can be easily obtained from a raw function by the decomposition and reconstruction formula. So high frequency domain is deleted and low frequency region is left for reconstructing wavelet because we only study the general features of protein sequences. In the results, we obtain precise filtering signals that can help us to find the actual location and number of TMHs in the protein sequences.

In order to predict TMHs of membrane protein sequence, with the condition of selecting the suitable wavelet basis functions, the best scale level and threshold are particularly important. Here cross-validation method is introduced, that is, m sequences of are selected at random as training set from n membrane protein sequences, the remaining n-m sequences are treated as test set, generating a set of samples. According to this step multiple sample sets can be generated to optimize threshold. The threshold here is determined by the maximum average prediction accuracy of training set. Using this threshold, we are able to predict TMHs among membrane protein sequences from test set. Then we experiment at five different scale levels utilizing Mallat algorithm using cross-validation method.

Its realization procedure is as follows:

Step 1 According to their own hydrophobic amino acid value, map 80 amino acid sequence of membrane protein into a sequence of hydrophobicity value.

Step 2 Six-fold cross-validation method is introduced, namely, 50 sequences are chosen at random as the training set from 80 sequences, the rest 30 sequences as test set, generating a set of samples, according to this step, six groups of random samples are generated altogether.

Step 3 According to the data of training set, analyze and determine wavelet function.

Step 4 Decompose the original signal into low frequency domain and high frequency domain by using the Eqs. (7) and (8), then reconstruct wavelet to restore the original signal by using the Eqs. (9). Putting d_k^j+1=0, reconstruct a new sequence 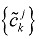by using {c_k^j+1}.

Step 5 In order to achieve higher prediction accuracy, according to the average length and inherent characteristics of biochemistry of each TMH, the post-treatment can be generalized in the following steps:Step 5.1 Discard those predicted TMHs that have less than 7 amino acid residues.

Step 5.2 If the predicted TMHs is between 30 and 50 residues, which means the TMHs is too long and is not factual, then the TMHs is expanded 10 amino acid residues from the two sides respectively and further we cut this TMHs into two equal parts to seek for potential TMHs.

Step 5.3 If the length of the predicted TMHs is greater than 50 residues, then the TMHs is cut into three equal parts using the same method above.

Step 6 According to step 3 to 5, learn samples of the training set, and finally determine the optimal wavelet basis, scale level and optimal threshold value.

Step 7 Get prediction result by predicting samples of the test set, and do statistics and analysis of the precision of prediction compared with experimental data.

For convenience, our prediction method is called WavePrd. We have implemented it in MATLAB 7.1 in windows XP running on a PC with system configuration Intel Pentium(R) Dual-Core processor (2.60 GHz) with 4 GB of RAM.

Selection of evaluation index

In order to test the accuracy of prediction methods, we study TM proteins from two aspects—TMHs and amino acid residues ³³.

Because of the restriction of experimental condition and other extra conditions, we believe that the predicted TMHs are regarded as correct when over half of the predicted TMHs coincide with the observed TMHs. From the view of statistics, the average length of TMHs is 20 a.a. In our approach, we decide that predicted TMHs are correct when at least 9 continuous residues are contained in the observed TMHs. There are two important evaluation indexes: (1) Prediction accuracy of TMHs ²³: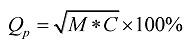, here M=Ncor/Nobs (Ncor stands for the number of correctly predicted TMHs, Nobs stands for the number of observed TMHs), M can be regard as a measure index of sensitivity; C=Ncor/Nprd (Nprd stands for the total number of predicted TMHs), C is regarded as a measure index of specificity. (2) Prediction accuracy of residues is another evaluation index. The calculation fomula is FAAcor=(NAAcor/NAAall) × 100%, where NAAcor is the number of correctly predicted TMHs residues and NAAall is the total residues.

Results and Discussion

Through the analysis of the sample data of the training set, combined with a wavelet function main properties and five commonly used hydrophobic parameters characteristics, we choose Daubechies (dbN) wavelet and discrete Meyer wavelet (dmey) as mother wavelets. Using DWT low-pass filtering in the spatial frequency domain, according to the above steps in the part of method of wavelet anaysis, we analyze sample data and determine db10 and dmey as the optimal wavelet bases.

In the execution of wavelet transform under the trend of low frequency, we do verification at five different scale levels. From j=1 to 5, we found that, when scale level is 1, 2, 3, the filtering effect is not apparent, and when scale level is 5, excessive filter appear, which lose much useful information about the original sequences. Only when scale level is 4, the filtering effect is moderate and signal peak can basically show the true TMHs, getting satisfactory results. So through the analysis of the sample data of the training set, according to the five kinds of hydrophobic parameters, we choose j=4 as the optimal scale level.

For FP hydrophobic parameter sequences, through the analysis of the data of the training set, we determine db10 as the optimal wavelet basis and get the corresponding optimal threshold at the scale level j=4. From six-fold cross-validation results (see Table 3), threshold 0.422 appeared five times, and the corresponding prediction accuracy is higher, getting maximum average prediction accuracy of the membrane protein TMHs is 96.1%, with the largest average prediction accuracy of residue is 79.1%.

Table 3.

Prediction accuracy for each group of training set and test set of FP hydrophobic parameters.

Set number	Qp %		FAAcor %
	Training set	Testing set
1	96.7 (0.422)	94.7	81.1
2	96.1 (0.422)	93.8	81.6
3	96.3 (0.422)	97.1	79.7
4	95.6 (0.433)	95.4	82.9
5	95.1 (0.422)	97.3	75.6
6	96.2 (0.422)	95.1	77.6

For sequence of KD hydrophobic parameters, we determined db10 as the optimal wavelet basis. At scale level j=4, data of each group of training set obtained the corresponding optimal threshold. In six-fold cross-validation result (see Table 4), threshold 0.888 appeared twice, threshold 0.836 appeared three times. In the test set, through the comparative analysis, we use the threshold 0.836, get maximum average prediction accuracy of the membrane protein TMHs being 95.8%, maximum average prediction accuracy of residue being 83.1%.

Table 4.

Prediction accuracy for each group of training set and test set of KD hydrophobic parameters.

Set number	Qp %		FAAcor %
	Training set	Testing set
1	95.4 (0.888)	93.0	85.3
2	95.6 (0.773)	94.1	86.5
3	95.5 (0.836)	95.8	81.5
4	95.9 (0.888)	94.9	84.6
5	94.6 (0.836)	96.7	82.3
6	95.5 (0.836)	94.9	85.6

For sequence of PP hydrophobic parameters, we determined dmey as the optimal wavelet basis. At scale level j=4, data of each group of training set obtained the corresponding optimal threshold. In six-fold cross-validation result (see Table 5), threshold 0.050 appeared twice. In the test set, we use the threshold 0.050, get maximum average prediction accuracy of the membrane protein TMHs being 93.3%, maximum average prediction accuracy of residue being 80.8%.

Table 5.

Prediction accuracy for each group of training set and test set of PP hydrophobic parameters.

Set number	Qp %		FAAcor %
	Training set	Testing set
1	96.2 (0.022)	90.2	77.8
2	94.7 (-0.074)	89.5	67.3
3	95.8 (0.017)	90.8	81.0
4	94.5 (0.050)	92.0	81.8
5	93.9 (0.081)	93.2	73.9
6	93.4 (0.050)	94.5	79.8

For sequence of EI hydrophobic parameters, we determined db10 as the optimal wavelet basis. At scale level j=4, data of each group of training set obtained the corresponding optimal threshold. In six-fold cross-validation result (see Table 6), threshold 0.384 appeared three times. In the test set, we use the threshold 0.384, get maximum average prediction accuracy of the membrane protein TMHs being 93.0%, maximum average prediction accuracy of residue being 73.9%.

Table 6.

Prediction accuracy for each group of training set and test set of EI hydrophobic parameters.

Set number	Qp %		FAAcor %
	Training set	Testing set
1	94.0 (0.414)	92.0	78.5
2	94.9 (0.384)	92.8	76.2
3	95.9 (0.384)	92.8	74.0
4	93.6 (0.436)	93.2	81.3
5	92.8 (0.384)	93.4	71.4
6	93.4 (0.413)	91.9	76.6

For sequence of JTT hydrophobic parameters, we determined db10 as the optimal wavelet basis. At scale level j=4, data of each group of training set obtained the corresponding optimal threshold. In six-fold cross-validation result (see Table 7), threshold 0.411 appeared twice, threshold 0.409 appeared twice too. In the test set, through the comparative analysis, we use the threshold 0.411, get maximum average prediction accuracy of the membrane protein TMHs being 94.7%, maximum average prediction accuracy of residue being 82.0%.

Table 7.

Prediction accuracy for each group of training set and test set of JTT hydrophobic parameters.

Set number	Qp %		FAAcor %
	Training set	Testing set
1	95.4 (0.446)	92.2	86.6
2	95.8 (0.411)	94.0	83.5
3	95.8 (0.411)	95.4	80.5
4	94.8 (0.409)	94.6	82.8
5	94.6 (0.412)	96.7	80.0
6	94.6 (0.409)	93.0	81.1

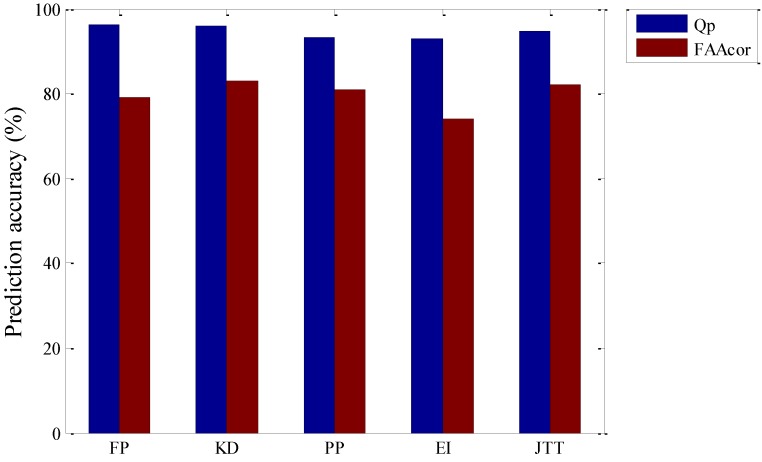
For these hydrophobic sequences mapped by the five commonly used hydrophobic parameters, through six-fold cross-validation method, we utilize the low-pass component of DWT and get different prediction accuracy of membrane protein TMHs and residue one by one, with the main results being shown in Figure 2.

Figure 2.

Prediction accuracy for test set of five kinds of hydrophobic parameters.

From Figure 2, prediction accuracy of the membrane protein TMHs by using FP hydrophobic parameters is the highest, which is 96.1%, but the prediction accuracy of residue is 79.1%. The second highest to predict residue is by using KD hydrophobic parameters, which is 83.1% and prediction accuracy of the membrane protein TMHs is also high, which only differ 0.3% compared with the prediction by FP hydrophobic parameters, that is, 95.8%. The third one is JTT hydrophobic parameters, with the prediction accuracy of the membrane protein TMHs and residue being 94.7% and 82.0% respectively. Lastly, prediction accuracy of the membrane protein TMHs and residue by EI hydrophobic parameters is the lowest, being 93.0% and 73.9% respectively. Through comparison, we think that choosing FP hydrophobic parameters is the best to only predict TMHs. While KD hydrophobic parameters is the best when combined with the prediction accuracy of residues.

We pick PDB ID 1KQG from MPtopo database as an example and choose KD hydrophobic parameters to describe this method to predict the number and position of membrane protein TMHs. Also we predict 13 groups of membrane protein sequence TMHs by using KD hydrophobicity scale values.

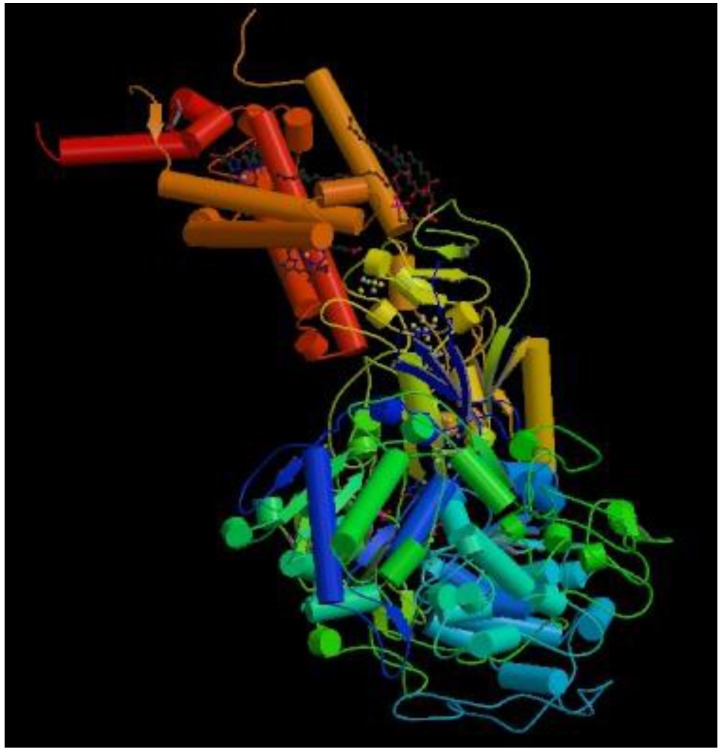
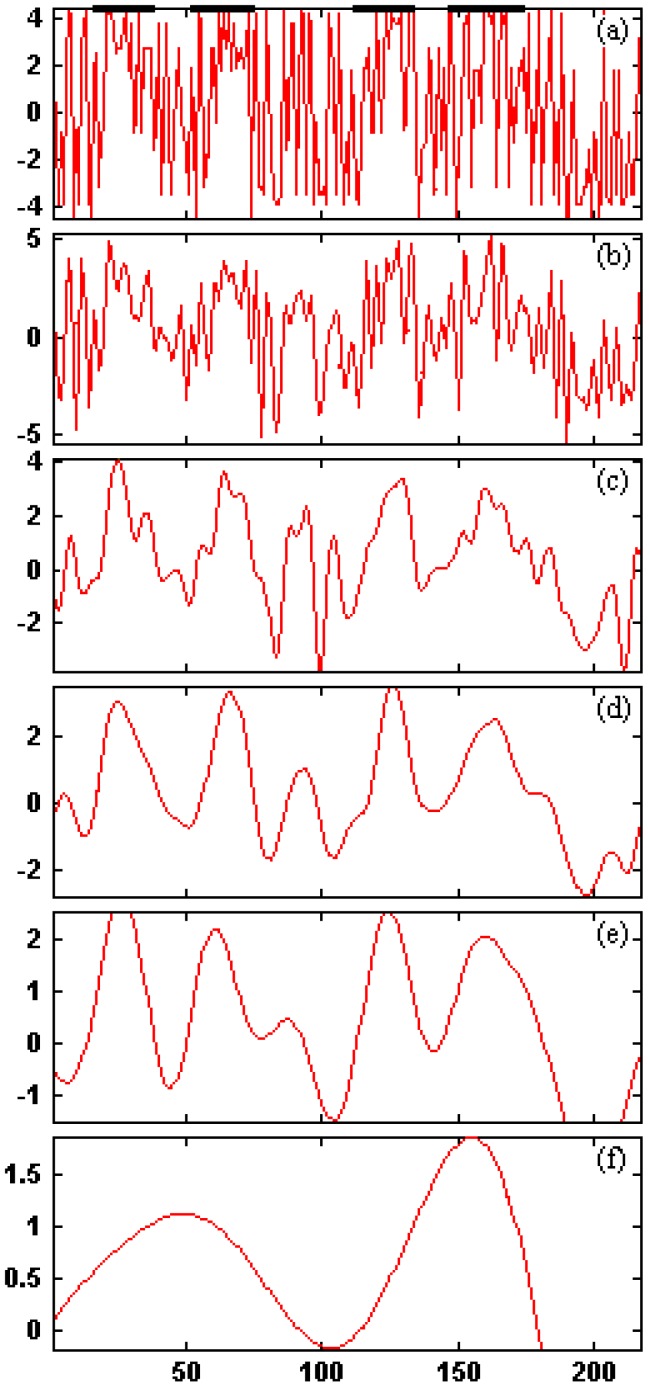
The 3D structure of protein 1KQG is measured by X-ray diffraction method, which is shown in Figure 3 ⁴⁶. It consists of three subunits, each subunit being transmembrane protein. Transmembrane segments traverse fat double as α helix. Here we mainly analyze transmembrane protein of γ subunit, which is four-transmembrane protein including 217 amino acid residues, as is shown in Figure 4.

Figure 3.

The three-dimensional structure of protein 1KQG.

Figure 4.

Linear sequence of the 1KQG protein and the parts of bold-face denote the real TMHs.

By using db10 wavelet basis, its original hydrophobic plots and reconstructed wavelet image at five different scale level is shown in Figure 5. We know that the signal peak after wavelet filter is corresponding to the real TMHs, each summit corresponding to the core of TMH. Through the above method, we can get a group of predicted TMHs. It can be seen that at the scale level 4, according to the wavelet filtering graph for the hydrophobicity sequence of 1KQG protein the predicted TMHs are correspondent well with the real TMHs. The selection of level 4 is based on our comparisons of wavelet filtering at each scale level. The effects of filtering at scale level 1, 2 and 3 are not apparent but the hydrophobicity signals are excessively filtered at scale level 5, which further results in the loss of much information about the original sequences. The TMHs prediction accuracy reaches 100% and the amino acid residues prediction accuracy reaches 98.8% at the scale level 4 with optimal threshold 0.836. The contrast data in Table 8 show above result more clearly. And amino acid sequence of membrane proteins 1KQG was prediced by the method DAS ¹⁸, HMMTOP2.0 ^{23, 24}, PHDhtm ^{20, 21}, PRED-TMR2 ¹⁷, SOSUI ¹⁶, TMAP ¹⁹, TMHMM2.0 ^{1, 22}. The result is shown in Table 8. From the Table 8, we can see the four TMHs of membrane proteins 1KQG were correspondence of TMHs we have predicted, i.e. All TMHs of membrane proteins have been predicted by WavePrd. One more TMHs was predicted by DAS; Three TMHs were predicted by PHDhtm and the third TMHs has 64 residues, i.e. the third and the fourth TMH were predicted together and result in big error. Good result has been achieved by other methods, yet TMHs and residues prediction accuracy are the highest by WavePrd.

Figure 5.

The hydrophobicity signal plot and low frequencies at five different scale levels for 1KQG protein. (a) j=0; (b) j=1; (c) j=2; (d) j=3; (e) j=4; (f) j=5.

Table 8.

Location of TMHs of the sequence of 1KQG (top row), WavePrd prediction and results from other currently used prediction methods.

	TM1	TM2		TM3	TM4
Observed	15-37	51-74		112-134	146-175
WavePrd	17-36	53-70		116-134	149-176
DAS	18-39	57-75	90-92	118-136	149-175
HMMTOP2.0	20-38	55-73		116-135	152-176
PHDhtm	18-45	55-76		117-180
PRED-TMR2	19-37	55-73		115-135	156-176
SOSUI	18-40	55-77		115-137	150-172
TMAP	14-42	51-78		112-134	148-172
TMHMM2.0	21-40	55-77		117-139	154-176

According to the function and classification of membrane proteins, we divided 80 membrane proteins sequences into 13 groups, which was shown in Table 9. Mentioned above, the choosing of threshold was ascertained by the maximal and average prediction accuracy given by test data. For every group of membrane proteins, at the scale level 4, we tried to choose a proper threshold to raise prediction accuracy. Prediction accuracy in each protein family by using threshold 0.836 is shown in Table 9. As is mentioned above, threshold 0.836 is determined by cross-validation and is the optimal threshold obtained from the training set samples. Membrane proteins of the same family are homologous, so the optimal threshold of each group of membrane proteins may be different. The values of parenthesis in Table 9 are the optimal threshold used in prediction.

Table 9.

Prediction accuracy of TMHs in each protein family based on different thresholds.

Family name	Prediction accuracy %
	Qp a	FAAcora	Qp b	FAAcorb
ABC transporters	95.3 (0.836)	74.8	100 (0.566)	75.6
Bacteriorhodopsin	100 (0.836)	70.7	100 (0.885)	71.3
Channel proteins	91.4 (0.836)	81.1	91.4 (0.847)	81.3
Cytochrome bc1 complexes	86.6 (0.836)	66.7	86.6 (0.765)	68.9
Cytochrome b6f complexes	95.7 (0.836)	82.5	95.7 (0.891)	82.6
Cytochrome c oxidases	99.2 (0.836)	93.7	99.2 (0.836)	93.7
Glycophorin	100 (0.836)	91.3	100 (0.668)	92.0
Light-harvesting complexes	100 (0.836)	93.9	100 (0.915)	97.9
Photosynthetic reaction centers	98.4 (0.836)	90.6	98.4 (0.866)	91.2
Photosystems	97.0 (0.836)	82.6	97.0 (0.836)	82.6
Respiratory proteins Rhodopsins	93.7 (0.836) 100 (0.836)	91.6 79.5	93.7 (0.836) 100 (0.885)	91.6 79.9
Translocation proteins	97.0 (0.836)	88.1	97.0 (0.868)	88.5
Average	96.5	83.6	96.8	84.4

^aThe average prediction accuracy of every group of membrane proteins with the threshold 0.836. ^bWith the different threshold for every group of membrane proteins , the prediction accuracy will be raised.

From Table 9, we can see that to choose different threshold for every group of membrane proteins can raise the prediction accuracy of TMHs and residues. With the threshold 0.566, the prediction accuracy of TMHs of ABC transporters is from 95.3% to 100%; With the threshold 0.915, the prediction accuracy of residues of light-harvesting complexes is from 93.9% to 97.9%. From another angle, we can see the TMHs and residues average prediction accuracy of the five groups of membrane proteins are the best, which are cytochrome C oxidases, glycophorin, light-harvesting complexes, respiratory proteins and photosynthetic reaction centers. For the thirteen groups of membrane proteins data, with the threshold 0.836, the maximal and average prediction accuracy of membrane proteins TMHs is 96.5% and that of residues is 83.6%. But by choosing different threshold for every group of membrane proteins of data base, the average prediction accuracy of TMHs and residues is the highest, which are 96.8% and 84.4%.

To access the effect of the method, 80 membrane proteins with known 3D structure are selected as test sets to be predicted by WavePrd, including 325 TMHs, 19396 amino acid residues altogether. Through analysis, we choose db10 as the optimal wavelet basis. The total number of predicted TMHs is 315 at the scale level 4 with optimal threshold 0.836, among which 308 TMHs are identical to real TMHs. The average prediction accuracy of TMHs is 96.3% and that of residues is 83.5%. The total residues of TMHs is 6580, among which 5495 are predicted rightly. The number of false positive segments is 7 and the number of false negative segments is 17. These results are better than that obtained by using other wavelets or levels. We predict 80 set of membrane proteins by 7 methods—DAS ¹⁸, HMMTOP2.0 ^{23, 24}, PHDhtm ^{20, 21}, PRED-TMR2 ¹⁷, SOSUI ¹⁶, TMAP ¹⁹, TMHMM2.0 ^{1, 22} and the prediction result can be found in Table 10.

Table 10.

Main results of eight prediction methods.

Method	Nobs	Nprd	Ncor	Qp %	M	C	FP	FN	FAAcor %
WavePrd	325	315	308	96.3	94.8	97.8	7	17	83.5
DAS	325	357	308	90.4	94.8	86.3	49	17	77.6
HMMTOP2	325	321	308	95.4	94.8	96.0	13	17	84.3
PHDhtm	325	286	269	88.3	82.8	94.1	17	56	72.5
PRED-TMR2	325	285	279	91.7	85.9	97.9	6	46	76.8
SOSUI	325	297	288	92.7	88.6	97.0	9	37	78.9
TMAP	325	299	291	93.4	89.5	97.3	8	34	81.7
TMHMM2.0	325	307	299	94.7	92.0	97.4	8	26	84.6

Nobs, Nprd and Ncor are the number of observed, predicted and correctly predicted TMHs, respectively. Qp stands for prediction accuracy of TMHs, M and C stand for the measure indexes of sensitivity and specificity. FP and FN are the number of wrongly predicted TMHs and the number of not-predicted TMHs, respectively. FAAcor is the prediction accuracy of residues.

From Table 10, the prediction accuracy of TMHs by WavePrd is the highest, which is 96.3%. The next highest prediction method which is based on hidden Markov model are HMMTOP2.0, TMHMM2.0, with prediction accuracy being 95.4% and 94.7% respectively. The prediction accuracy of PHDhtm method based on neural network is the lowest, which is only 88.3%, short of 8.0% compared with WavePrd method. The highest prediction method of residue is TMHMM2.0 and HMMTOP2.0 methods, which is 84.6% and 84.3% respectively. The second highest prediction method of residue is WavePrd method, with the prediction accuracy being 83.5%. The above eight methods do prediction according to single sequence information. These comparisons indicate that our method is more accurate and effective in predicting the TMHs number and location of membrane proteins, which provide important information for research of membrane protein structure and function.

Conclusion

With the advancement of high-throughput sequencing technology and the practice of sequencing model organisms' genomes, more and more DNA and protein sequences are swarming into biological sequence databases with an unprecedented rate. How to mine valuable information efficiently from mass biological sequences is crucial to the research of bioinformatics as well as to many significant fields of functional genomics. The study of the structure and function of TM proteins is increasingly emphasized since TM proteins play an extraordinarily important role in the life activity of the cells, such as signal transduction, immune response and membrane transport. However, the structural determination of proteins needs a considerable number of purified proteins and it is a hard task because the peptide chains of the TM proteins span a lipid bilayer and sometimes transverse membrane many times ⁴⁷. Because transmembrane helix combine closely with membrane, first of all, the membrane must be disintegrated by eradicator to separate TM proteins. Then, the TM protein can be purified and made crystal. This is not only difficult in technique, but is also expensive. Thus, the high-resolution 3D structural determination and analysis of TM proteins cannot answer the need of the research for TM protein functions. The computer prediction and analysis of the TMHs is able to provide much important information to disclose the relationship between the structure and function of TM proteins.

We make use of multiresolution analysis theory to decompose the original signals into low frequency and high frequency domains in amino acid hydrophobicity scale format. In wavelet analysis, the low frequency can be easily obtained from a raw function by the decomposition and reconstruction formula. So high frequency domain is deleted and low frequency region is left for reconstructing wavelet because we only study the general features of protein sequences. In the results, we obtain precise filtering signals that can help us to find the actual location of TMHs in the protein sequences. The post-treatment of the filtering signals through reconstructing is very important in order to reach a high accuracy when we predict TMHs of protein sequences. 80 membrane proteins with known 3D structure are selected as test sets to be predicted by WavePrd. Firstly, six-fold cross-validation method is introduced and five commonly used hydrophobic parameters are used to predict the position and number of TMHs based on two different levels in order to find the best hydrophobic parameters, offer help for further membrane protein work and reduce the blindness of choosing hydrophobic parameters. Results show that the best membrane proteins TMHs is achieved when choosing FP and KD hydrophobic parameters. Secondly, take one membrane protein sequence as an example to bat around and do comparison combined with the prediction results by the other seven methods in order to confirm the effectiveness of WavePrd method. A group of TMHs are predicted for 13 groups of membrane protein sequences by using KD hydrophobic parameters. At last, in order to prove the feasibility of the method, 80 membrane proteins are selected as test sets. Compared with the main prediction results of seven popular prediction methods, the obtained results indicate that WavePrd method proposed in this paper has higher prediction accuracy.

Although the proposed method has the characteristics of simplicity, visual process, and high accuracy, through the analysis of the predicted results of data set, we found that compared with the actual structure of membrane protein, there still exist some differences in the position and number of the predicted TMHs. They are as follows: too much prediction, that is the position and number of the predicted TMHs and the actual structure is not completely corresponding; less prediction, i.e. we haven't predicted all the position and number of the actual structure of TMHs. This is because: (1) While doing wavelet transform, we just map the amino acid sequence of membrane protein into hydrophobic value sequence. Although hydrophobic effect is the most important factor to determine the stability of protein structure, it is not the only factor. In addition to hydrophobic effect, there are hydrogen bond, ionic bond and van der Waals force and disulfide bond of peptide chain, etc; (2) The volume of protein molecules, electric charge and many kinds of factors all have the regulation effects on the protein structure and stability; (3) According to the signal peptide hypothesis, the signal peptide can form TMHs in protein synthesis, auxiliary peptide chain across the endoplasmic reticulum (ER) membrane, so in forecasting TMHs, it is very normal that signal peptide is contained. In addition, because hydrophobicity is the main sequence characteristic of transmembrane helices, and there are likely to be long hydrophobic sequence in the hydrophobic core of water-soluble globular protein, which also can produce false positive results. In view of many kinds of factors, we think while we predict the position and number of membrane protein TMHs by mapping the amino acid sequence into hydrophobic value sequence, the deviation within the scope is allowed. If the above many factors are considered, the prediction accuracy can be improved. In this paper, we only predict the location and number of TMHs of membrane protein without considering the orientation of N-terminus of membrane protein. If we consider the physicochemical property of membrane protein and analyze membrane protein sequence by combining and altering "positive-inside-rule" in particular, we can better solve the above problems, which is our next research direction.