Logic reversibility and thermodynamic irreversibility demonstrated by DNAzyme-based Toffoli and Fredkin logic gates

Abstract

The Toffoli and Fredkin gates were suggested as a means to exhibit logic reversibility and thereby reduce energy dissipation associated with logic operations in dense computing circuits. We present a construction of the logically reversible Toffoli and Fredkin gates by implementing a library of predesigned Mg²⁺-dependent DNAzymes and their respective substrates. Although the logical reversibility, for which each set of inputs uniquely correlates to a set of outputs, is demonstrated, the systems manifest thermodynamic irreversibility originating from two quite distinct and nonrelated phenomena. (i) The physical readout of the gates is by fluorescence that depletes the population of the final state of the machine. This irreversible, heat-releasing process is needed for the generation of the output. (ii) The DNAzyme-powered logic gates are made to operate at a finite rate by invoking downhill energy-releasing processes. Even though the three bits of Toffoli’s and Fredkin’s logically reversible gates manifest thermodynamic irreversibility, we suggest that these gates could have important practical implication in future nanomedicine.

Energy dissipation associated with logic operations represents a fundamental limitation for the generation of future dense computing circuitries (1, 2). Theoretical studies have indicated that any logic operation that is irreversible leads to the generation of heat, at least kTln2, as a result of a loss of a bit (k is Boltzmann’s constant; T is the ambient temperature). Familiar binary logic gates, such as AND or OR, are logically irreversible because there are four possible distinct inputs and only two distinct outputs. As a result, there is no possibility of recovering the input from the known outputs. Logical irreversibility is therefore widespread in computing circuits. The resulting losses are nowadays below the actual heat generation in real machines, but as circuits become even denser such losses will become more of a problem. Several methods were presented to overcome logical irreversibility. One approach (3) suggested the addition of a history tape that records erased data to the routine write–read–erase function of an irreversible Turing machine. By this method, the information kept in the history tape can reverse the machine to its original state. This concept was exemplified using the polymerase-induced replication of DNA and reverse process (3, 4). Alternatively, the development of a logically reversible gate has attracted theoretical and experimental interest. Reversible logic gates are defined as systems in which each possible set of inputs maps into a unique pattern of outputs; such systems do not lead to the generation of heat (5, 6). Two universal reversible logic gates—the Toffoli gate (7) and the Fredkin gate (8)—have been suggested to implement logically reversible operations. The Toffoli gate is a three-bit gate that inverts the state of a target bit conditioned on the state of two control bits, whereas the Fredkin gate is a three-bit gate that swaps the last two bits conditioned on the state of the control bit. In these two gates, any set of inputs is processed and results as a unique pattern of outputs. These gates are therefore logically reversible.

Recent research efforts implementing molecular and supramolecular systems that perform a reversible (not universal) logic operation were reported (9, 10). Other approaches including NMR (11), linear optical lattices (12), ion trap systems (13), and superconducting circuits (14, 15) were also used to assemble the Toffoli/Fredkin gates. Additionally, DNA-based logic gates revealing chemical reversibility were recently reported (16). These logic gates consist of an equilibrated mixture of structures that respond to changes in the concentrations of inputs.

Computing with DNA attracts substantial research efforts because of the possibility to exploit the structural (base sequence) and functional (reactivity) properties of nucleic acids (17–19) for the “logical” control of biological processes. Different logic gates, cascaded logic gates, and logic circuitries were demonstrated with nucleic acids (20–25). Also, different computing paradigms with DNA were reported, including the “tile” approach (26), catalytic strand displacement cascades (23, 27, 28), and enzyme-guided finite automata on DNA scaffolds (29, 30). Recently, we introduced catalytic nucleic acids as functional units that perform a universal set of logic gates, and the systems were implemented to activate logic-gate cascades, fan-out gates, and field-programmable logic circuitries (31). Here we demonstrate the use of the Mg²⁺-dependent DNAzyme (32) as a functional unit for the construction of the logically reversible Toffoli and Fredkin gates. These systems follow the fundamental definition of logical reversibility, in which the relation between the set of inputs and outputs is one to one. However, we emphasize that the systems are thermodynamically irreversible. This originates from two nonrelated fundamental limitations: (i) the readout of the inputs in the form of any physical signal is an unavoidable energy-releasing process and (ii) the activity of DNAzyme leads to the cleavage of a chemical bond, thus generating nucleic acids fragments as outputs. This reaction is energetically downhill and represents an energy-releasing process. These two features introduce the thermodynamic irreversibility that precludes the reversing of the outputs to the inputs.

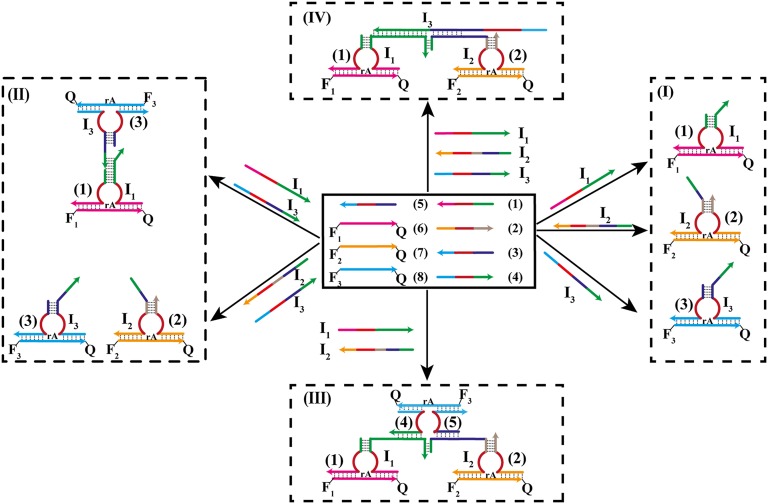
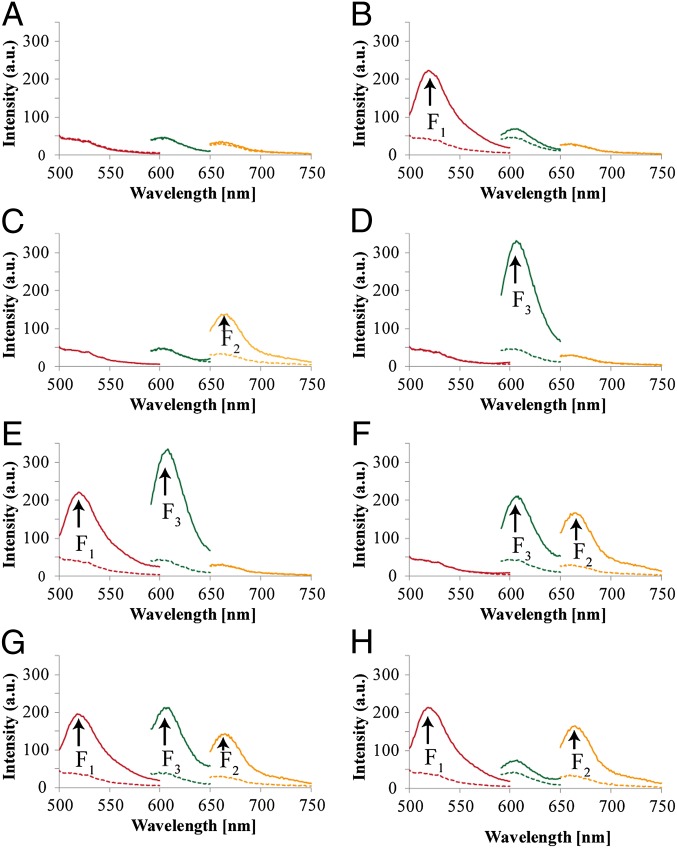
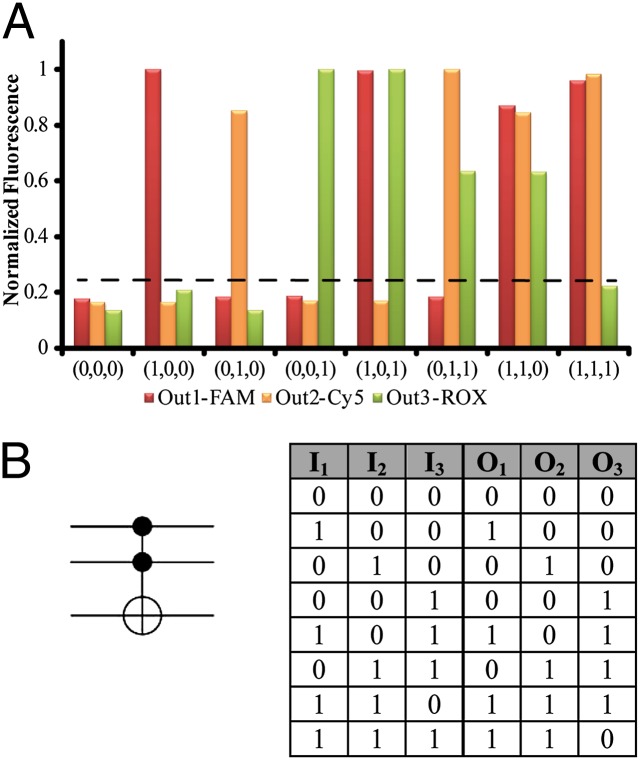
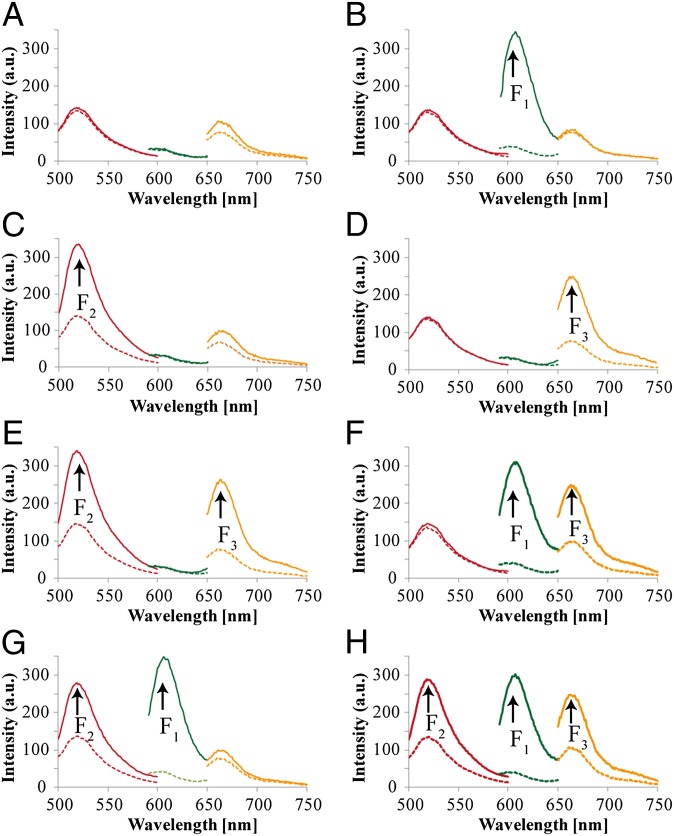
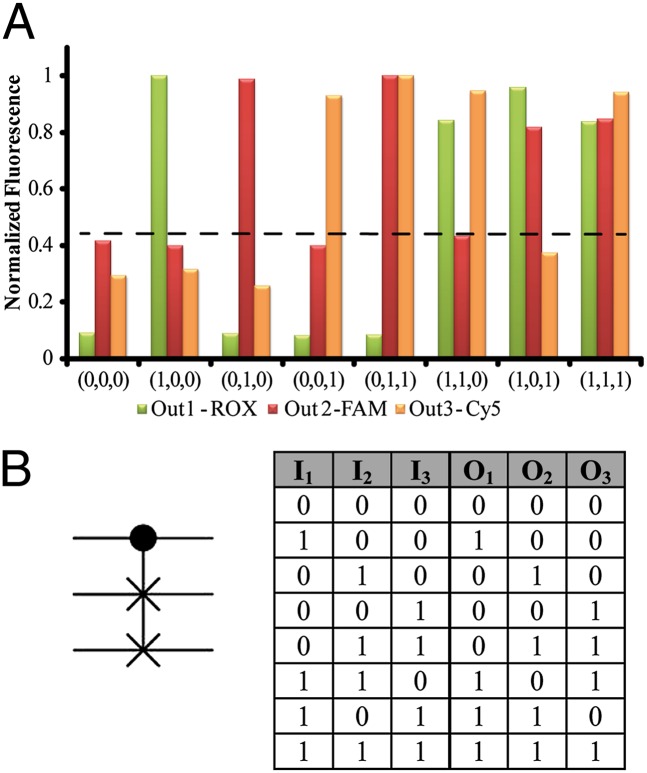
Fig. 1 depicts the construction of the Toffoli gate. In the development of the system, we make use of three principles. (i) The DNAzyme can be cleaved into subunits, and the subunits may assemble into active DNAzyme structures using cooperative hybridization processes with auxiliary nucleic acid strands. (ii) The stabilities of the resulting DNAzyme structures are controlled by the stabilizing energy contributed by the different duplexes in the systems. In the presence of auxiliary nucleic acids, strand-displacement reactions leading to new structures of enhanced stability prevail. (iii) The Mg²⁺-dependent DNAzyme cleaves a ribonucleobase-containing substrate. Upon labeling the 3′ and 5′ ends of the substrate with a fluorophore/quencher pair, the fluorescence of the fluorophore is quenched. The DNAzyme-catalyzed cleavage of the substrate leads, however, to the fragmentation of the substrate and this triggers-on the fluorescence. The system consists of a library of five nucleic acid strands 1–5, that correspond each to a subunit of a Mg²⁺-dependent DNAzyme. Also, the substrates 6, 7, and 8, each labeled with a different fluorophore/quencher pair, are included in the library. The library by itself cannot spontaneously form any active DNAzyme structure because either the complementary DNAzyme unit is absent in the library or the stability of two subunits is too low to organize the active DNAzyme structure. The nucleic-acid strands I₁, I₂, and I₃ act as inputs for the gates. The inputs’ nano-engineered sequences correspond to the respective subunits of the DNAzyme or reveal complementarity that introduces cooperative interactions with two of the subunits. The interaction of the library with any of the inputs I₁, I₂, or I₃ (100, 010, or 001) yields the Mg²⁺-dependent DNAzyme structure shown in Fig. 1, I, giving rise to the output fluorescence of F₁, F₂, or F₃, respectively. Fig. 2 shows fluorescence intensities before and after the addition of one of the inputs to the system. Thus, a low background fluorescence signal is generated in the absence of any input (000) (Fig. 2A). However, high-fluorescence signals of F₁, F₂, or F₃ are observed in the presence of input I₁ (100) (Fig. 2B), input I₂ (010) (Fig. 2C), or input I₃ (001) (Fig. 2D), respectively. The interaction of the library with two inputs, I₁ + I₃ (101) or I₂ + I₃ (011), yields stable DNAzyme structures, as shown in Fig. 1, II. In the case of I₁ + I₃, I₃ includes a tether that cooperatively hybridizes with a single-strand domain of the tether associated with I₁. As a result, a bidentate DNAzyme structure consisting of subunits I₁/(1) and I₃/(3) that is cooperatively stabilized by substrates 6 and 8 is formed. This structure leads to the cleavage of 6 and 8, along with the fluorescence of F₁ and F₃, output (101). The reaction of the library with the inputs I₂ + I₃ (011) yields the assembly of the two Mg²⁺-dependent DNAzyme structures I₂/(2) and I₃/(3), consequently leading to the fluorescence of F₂ and F₃ output (011). The most interesting logic operation occurs upon the interaction of the library with I₁ + I₂ (110), as shown in Fig. 1, III. Under these conditions, the most stable structure consists of three DNAzyme units in which the DNAzyme subunits (4)/(5) are stabilized in an active structure through hybridization to the tethers of I₁ and I₂. As a result, substrates 6, 7, and 8 are cleaved, giving rise to the fluorescence of F₁, F₂, and F₃ outputs (111). Namely, the input (110) is inverted into the output (111). The interaction of the library in the presence of all three inputs, I₁ + I₂ + I₃ (111), yields the structure shown in Fig. 1, IV. In this case, I₃ displaces the DNAzyme subunits (4) and (5) because of a higher number of base-paired hybridization. Accordingly, this strand displacement results in the formation of two DNAzyme structures consisting of the subunits I₁/(1) and I₂/(2), which leads to the fluorescence F₁ and F₂, output (110). Consequently, this state inverts the input from (111) to the output (110). Fig. 2 depicts the fluorescence outputs for the set of inputs shown in Fig. 1 II–IV. Indeed, the set of inputs I₁ + I₃ leads to the fluorescence of F₁ and F₃, whereas the set of inputs I₂ + I₃ yield the fluorescence of F₂ and F₃ (Fig. 2 E and F, respectively). Fig. 2G shows that the set of the two inputs I₁ + I₂ leads to the fluorescence of F₁, F₂, and F₃. However, the set of three inputs I₁ + I₂ + I₃ yields the fluorescence of F₁ and F₂ only (Fig. 2H). Fig. 3A shows the fluorescence intensities in the form of bars. The truth-table corresponding to the Toffoli gate is presented in Fig. 3B. Note that each set of inputs results in a distinct and unique pattern of outputs, as requested for a reversible logic circuit. (For further details about the formation of the DNAzyme structures see Fig. S1 and accompanying discussion.)

Fig. 1.

The activation of the Toffoli gate by a set of Mg²⁺-dependent DNAzyme subunits and their respective substrates. (I) Inputs 100, 010, and 001 along with the respective outputs 100, 010, and 001. (II) Inputs 101 and 011 along with the respective outputs 101 and 011. (III) Input 110 and the respective output 111. (IV) Input 111 and the respective output 110. Arrows on the DNA stands indicate on their directionality 5′→3′.

Fig. 2.

Output fluorescence intensities corresponding to the Toffoli gate using the following inputs: (A) 000, (B) 100, (C) 010, (D) 001, (E) 101, (F) 011, (G) 110, and (H) 111. Dashed lines correspond to the background fluorescence intensities before the addition of the respective inputs. Fluorescence spectra were recorded after a fixed time interval of 2 h.

Fig. 3.

(A) Fluorescence intensities using different inputs, in the form of a bar presentation. Dashed line represents the threshold fluorescence for defining the “0” or “1” outputs. (B) The representing symbol of the Toffoli gate and the resulting truth-table correspond to the order of input sets described in Fig. 1.

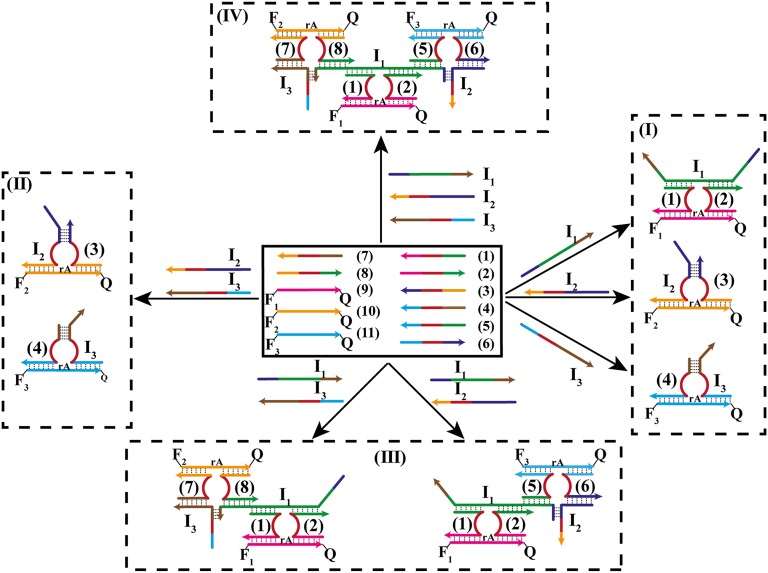
Fig. 4 depicts the construction of the reversible Fredkin gate. We implement the same paradigm, as for the Toffoli gate, and use the input-guide assembly of Mg²⁺-dependent DNAzyme to construct the gate. The library consists of nucleic acids 1–8 and substrates 9, 10, and 11, each functionalized with a fluorophore quencher pair F₁/Q, F₂/Q, and F₃/Q, respectively. The nucleic-acid strands 1–8 include all sequences corresponding to subunits of the Mg²⁺-dependent DNAzyme. However, they differ in tether units that provide recognition sites for the input-guided assembly of the respective DNAzyme and their binding to the specific substrates. Reaction of the library with any of the inputs I₁, I₂, or I₃ leads to the assembly of the DNAzyme structures I₁/(1)/(2), I₂/(3), or I₃/(4) that cleave the associated substrates 9, 10, and 11, respectively, Fig. 4, I. Consequently, the set of inputs (100), (010), and (001) yields the outputs F₁, F₂, and F₃, (100), (010), and (001). Fig. 5 shows that, indeed, I₁, I₂, or I₃ selectively activate the fluorescence of F₁, F₂, or F₃ (Fig. 5 B, C, and D, respectively). Treatment of the library with inputs I₂ + I₃ (011) guides the assembly of the DNAzyme structures I₂/(3) and I₃/(4) with the respective substrates 10 and 11, giving rise to the fluorescence of F₂ and F₃, output (011) (Figs. 4, II and 5E), demonstrating that, indeed, only the fluorescence of F₂ and F₃ is triggered on. Subjecting the library to inputs I₁ + I₂ (110) or I₁ + I₃ (101) results in the cooperatively, input stabilized DNAzymes I₁/I₂/(1)/(2)/(5)/(6) or of the I₁/I₃/(1)/(2)/(7)/(8) DNAzymes that bind the substrates 9 and 11 or 9 and 10, respectively (Fig. 4, III). Fig. 5 F and G show that the set of inputs I₁ + I₂ (110) yields the fluorescence of F₁ and F₃, output (101), whereas the set of inputs I₁ + I₃ (101) generates the fluorescence F₁, F₂ output (110). Fig. 4, IV depicts the energetically favored DNAzyme assembly upon interaction of the library with I₁ + I₂ + I₃. The inputs cooperatively stabilize the three DNAzymes (1)/(2), (5)/(6), and (7)/(8), leading to the cleavage of all three substrates 9, 10, and 11 and to the generation of the fluorescence of F₁, F₂, and F₃. Fig. 5H demonstrates the set of inputs I₁ + I₂ + I₃ (111) that generate the fluorescence of all three fluorophores, output (111). Fig. 6A presents the fluorescence intensities in the form of bars. Fig. 6B summarizes the truth-table corresponding to the Fredkin gate. Evidently, each of the sets of inputs results into a distinct pattern of outputs as required from a reversible gate. (For further details about the formation of the DNAzyme structures see Fig. S2 and accompanying discussion.)

Fig. 4.

The activation of the Fredkin gate by a set of Mg²⁺-dependent DNAzyme subunits and their respective substrates. (I) Inputs 100, 010, and 001 along with the respective outputs 100, 010, and 001. (II) Input 011 and the respective output 011. (III) Inputs 110 and 101 along with the respective outputs 101 and 110. (IV) Input 111 and the respective output 111. Arrows on the DNA stands indicate on their directionality 5′→3′.

Fig. 5.

Output fluorescence intensities corresponding to the Fredkin gate using the following inputs: (A) 000, (B) 100, (C) 010, (D) 001, (E) 011, (F) 110, (G) 101, and (H) 111. Dashed lines correspond to the background fluorescence intensities before the addition of the respective inputs. Fluorescence spectra were recorded after a fixed time interval of 2 h.

Fig. 6.

(A) Fluorescence intensities using different inputs in the form of a bar presentation. Dashed line represents the threshold fluorescence for defining the “0” or “1” outputs. (B) The representing symbol of the Fredkin gate and resulting truth-table corresponding to the order of input sets described in Fig. 4.

The interest of the present systems relies on the logical reversibility of the gates, which is achieved by the explicit definition of the set of inputs and the readout of the respective outputs. Nonetheless, the systems demonstrate thermodynamic irreversibility, and we can trace two sources for the irreversibility. First, the set of reactions in the present systems are energetically downhill; as a result, the logic process cannot be reversed. This difficulty may be resolved, however, by designing reversible and slow chemical transformations that could reverse the direction at any stage. This irreversibility resulting from operation at a finite rate could therefore be reduced or ideally altogether eliminated. There is, however, second source for thermodynamic irreversibility. The readout of the output is made in an inherently irreversible way, both because the fluorescence is emitted in all spatial directions and because the fluorescence is, as always, downshifted in energy (Fig. 2) compared with the excited fluorophore. This is an inherent thermodynamic cost of the computation. This cost is unavoidable and its minimal value is, as discussed early on by von Neumann (33), the cost of identification of a quantum state, kTln2. Here it is the cost of identification that the fluorophore is excited.

In conclusion, the present study has introduced the application of catalytic nucleic acids, Mg²⁺-dependent DNAzymes, as functional units for the construction of the universal and reversible Toffoli and Fredkin gates. That is, the set of inputs is explicitly coded by the resulting outputs. The versatility in the design of the substrates of the DNAzymes (31) and the variety of fluorophores that can be implemented as optical labels of the substrates pave the way to construct cascaded Toffoli or Fredkin gates. Furthermore, the availability of other DNAzymes and particularly pH-controlled DNAzymes enables the design of pH-switchable field-programmable DNAzyme networks comprising reversible gates (34). In fact, in a preliminary report the polymerase-stimulated replication of DNA has been suggested to design the Fredkin gate using electrophoresis as readout signal (35). This approach is, however, very limited compared with the DNAzyme subunits approach because it relies on a common enzyme (polymerase) that prohibits effective cascading of gates. We believe that reversible logic gates might find important applications in future nanomedicine. For example, microRNAs (miRNAs) act as posttranscriptional regulators that bind to mRNA and result in translational repression or gene silencing. Aberrant expression of miRNAs was found to cause different diseases, such as cancer (36, 37). By implementing the Toffoli gate–type logic system, one might suggest a means for the selective silencing of one harmful miRNA by the resulting DNA outputs, generated by the gate. For instance, the set of all three miRNA inputs (I₁ + I₂ + I₃) may generate the outputs O₁ and O₂, which will cooperatively bind and silence the harmful miRNA. In contrast, in the presence of only one of the miRNA inputs or inputs I₁ + I_3, or inputs I₂ + I₃, no combination of the outputs O₁ and O₂ is formed and, thus, the miRNA is not being silenced. Interestingly, the set of miRNA inputs I₁ + I₂ yields all three outputs (O₁, O₂, and O₃). Nonetheless, these three outputs are designed to form an inter-output, cooperatively stabilized structure that lack binding affinity, and thus no silencing effect to the harmful miRNA.

Materials and Methods

Materials.

Phosphate buffer, NaCl, and Mg(NO₃)₂were purchased from Sigma-Aldrich. DNA oligonucleotides were HPLC-purified and purchased from Integrated DNA Technologies Inc. Ultrapure water from a NANOpure Diamond (Barnstead) source was used in all of the experiments.

Instrumentation.

Light emission measurements were performed using a Cary Eclipse Fluorometer (Varian Inc). The excitation of FAM, ROX, and Cy5 were performed at 480 nm, 570 nm, and 630 nm, respectively.

DNA Oligonucleotides.

All DNA sequences were designed to minimize undesired cross-hybridization using NUPACK (http://www.nupack.org/) (38). The sequences shown in Table 1 and Table 2 were used for the Toffoli and the Fredkin gates, respectively.

Table 1.

Nucleic acid sequences used to construct the Toffoli gate

Entry	Sequence 5′→3′
(1)	AACTCACTGTGAACATACGGCACCCATGTTATCCTA
(2)	TTCTACACAGCGATCTAGACTATAGCTTAGACGT
(3)	CCTGCTACTAGTCACAGCACCCATGTACAGTCA
(4)	TAGTAGCAGGAGGAGAAGCACCCATGTACAGTCA
(5)	GTCATTCAGCGATCTTCTCTCGCAAGTTTGGTATT
(6)	FAM /TAGGATATrAGGAGTACT/BHQ
(7)	Cy5/AATGTAATrAGGTGTAGAA/IABkRQ
(8)	ROX /TGACTGTTrAGGAATGAC/BHQ
I1	AGTACTCAGCGATCCGTATGTTCACAGTGAGTTACGATAGATAAATACCAAACTTGCGAGCCTCCTGTAGATGCATTCACCTCTAC
I2	GTAGAGGTGAATGCATCTACGCTACTAGTCACAGATGTCTAAGCTATAGTCTAGCACCCATGTTTACATT
I3	GTCATTCAGCGATCTGTGACTAGTAGCAGGAGGCTCGCAAGTTTGGTATTTATCTATCGT

Table 2.

Nucleic acid sequences used to construct the Fredkin gate

Entry	Sequence 5′→3′
(1)	TCCTAGTACCTGCTTTGCACCCATGTACAGTCA
(2)	GTCATTCAGCGATCAAACGAAGTACTGTATC
(3)	AGTACTCAGCGATCCGTATGTTCACAG
(4)	ACGTCTAAGCTATAGCACCCATGTTTACATT
(5)	GCATGATCGTATCGCTTGCACCCATGTTTACATT
(6)	TTCTACACAGCGATCAAGAGTCTCAGAGTCTCAG
(7)	GTACAATCGTACATCCAAGCACCCATGTTATCCTA
(8)	AGTACTCAGCGATCTTGCATGAGCATGAGGGC
(9)	ROX /TGACTGTTrAGGAATGAC/BHQ
(10)	FAM /TAGGATATrAGGAGTACT/BHQ
(11)	Cy5/AATGTAATrAGGTGTAGAA/IABkRQ
I1	CCGTATGTTCACAGGCATTCACCCGATACGATCATGCGATACAGTACTTCGGCAGGTACTAGGACTCATGCTCATGGTCAGTCAACGTCTAAGCTATAG
I2	CTGAGACTCTGAGACTGGTGAATGCCTGTGAACATACGGCACCCATGTTATCCTA
I3	TTCTACACAGCGATCTATAGCTTAGACGTTGACTGACGATGTACGATTGTAC

Sample Preparation.

All reactions were performed in phosphate buffer (50 mM, 500 mM NaCl) at a final DNA concentration of 1 µM and 50 mM of Mg(NO₃)₂. The samples, without the inputs, were heated to 95 °C for 5 min, then cooled to 37 °C for the Toffoli system and 25 °C for the Fredkin system. Fluorescence spectra of all three fluorophores were recorded for each one of the states before adding the inputs and after 2 h. It should be noted that the Fredkin gate was operated at 25 °C and the Toffoli gate was activated at 37 °C. This difference is due to partial interfering hybridizations of the components in the Toffoli gate that led to relatively high background signals. By elevating the temperature to 37 °C, the respective interfering hybrids are separated; all other structures presented in Fig. 1 are in an intact configuration. The fluorescence intensities of the different systems were recorded after 2 h of operation of the DNAzyme constructs. This time interval was selected as it yields a true, “1”, output value that is, at least 2.5-fold higher than the background fluorescence intensities, corresponding to “0” output.

Polyacrylamide-Gel Electrophoresis (PAGE).

The gels consisted of 10% (wt/vol) polyacrylamide (acrylamide/bis-acrylamide, 29:1) in a Tris-borate-EDTA buffer solution that included Tris base (89 mM, pH 7.9), boric acid (89 mM), and EDTA (EDTA, 2 mM). A portion (2 μL) of each of the reaction mixtures was mixed with the loading dye and loaded onto the gel. The gels were run on a Hoefer SE 600 electrophoresis unit at 10 °C (150V, constant voltage) for 8 h in 0.5× Tris-borate-EDTA buffer. After electrophoresis, the gels were stained with SYBR Gold nucleic acid gel stain (Invitrogen) and imaged.