High-Gradient Nanomagnets on Cantilevers for Sensitive Detection of Nuclear Magnetic Resonance

Abstract

Detection of magnetic resonance as a force between a magnetic tip and nuclear spins has previously been shown to enable sub-10 nm resolution ¹H imaging. Maximizing the spin force in such a magnetic resonance force microscopy (MRFM) experiment demands a high field gradient. In order to study a wide range of samples, it is equally desirable to locate the magnetic tip on the force sensor. Here we report the development of attonewton-sensitivity cantilevers with high gradient cobalt nanomagnet tips. The damage layer thickness and saturation magnetization of the magnetic material were characterized by X-ray photoelectron spectroscopy and superconducting quantum interference device magnetometry. The coercive field and saturation magnetization of an individual tip were quantified in situ using frequency-shift cantilever magnetometry. Measurements of cantilever dissipation versus magnetic field and tip-sample separation were conducted. MRFM signals from protons in a polystyrene film were studied versus rf irradiation frequency and tip-sample separation, and from this data the tip field and tip-field gradient were evaluated. Magnetic tip performance was assessed by numerically modeling the frequency dependence of the magnetic resonance signal. We observed a tip-field gradient $\partial B_z^{\mathrm{tip}}∕\partial z$ estimated to be between 4.4 and 5.4 MT m⁻¹, which is comparable to the gradient used in recent 4 nm resolution ¹H imaging experiments and larger by nearly an order of magnitude than the gradient achieved in prior magnet-on-cantilever MRFM experiments.

The 4 to 10 nm resolution demonstrated by Degen et al.¹ in their proton-imaging magnetic resonance force microscopy^2–7 (MRFM) experiment is competitive with the 3 to 8 nm resolution achieved by cryo-electron tomography (cryo-ET) applied to single copies of biomacromolecules^8–11 and approaches the 2 nm resolution often achieved by cryo-electron microscopy (cryo-EM) applied to multiple copies of disordered asymmetric complexes. Given the established importance of cryo-ET and cryo-EM, this resolution comparison suggests that MRFM has an important and complementary role to play in the determination of the structure of single copies of biomacromolecules, biomacromolecular complexes, and other organic nanostructures.

In the most sensitive MRFM experiments to date, signal has been detected as a force variance generated by interactions between the magnetic field gradient produced by a nanomagnet and magnetic dipole fluctuations in a small ensemble of nuclear spins. An attonewton-sensitivity cantilever is used as the force sensor to detect this interaction. In this limit where the force variance is measured, for a given cantilever sensitivity and imaging resolution, the signal acquisition time is dependent on the magnetic tip-field gradient such that the acquisition time is proportional to the inverse of the field gradient to the fourth power.¹² To achieve high-sensitivity MRFM detection it is thus critical to use a high gradient magnetic tip.

In the three-dimensional MRFM imaging experiment of Ref. 1, a magnetic tip with a field gradient of 4.2 MT m⁻¹ was achieved by fabricating a 200 nm diameter Fe₇₀Co₃₀ pillar on a flat surface.¹³ The resultant high-resolution imaging experiments were conducted after affixing an individual tobacco mosaic virus to the leading edge of a high-compliance silicon cantilever. Though this work had unprecedented NMR imaging resolution, few biological samples are as robust as the tobacco mosaic virus and the “sample-on-cantilever” nature of the experiment precluded the use of cryopreservation techniques.

Switching instead to the “magnet-on-cantilever” geometry would enable the study of a broad range of samples. Delicate biological samples that need to be embedded in a thin film of water and flash frozen to preserve their native structure^8–10,14,15 could be prepared for MRFM using standard methods. Since MRFM can be used to noninvasively reconstruct three-dimensional images, working organic semiconductor devices could also be studied. For both of these applications, and many others, having the sample off of the cantilever is essential.

Positioning the magnet on the cantilever dictates that high-gradient magnets must be fabricated directly on high-compliance cantilevers. Magnet-on-cantilever detection of electron spin resonance (ESR)^16–21 and nuclear magnetic resonance (NMR)^22,23 has been observed in prior MRFM experiments; however, the tips were prepared by ion beam milling and the achievable magnetic field gradients were limited by ion damage. In practice these tips produced a gradient nearly an order of magnitude smaller than that achieved by Degen and co-workers. Thus nearly 10⁴ longer imaging times would be required to achieve the 4 to 10 nm resolution of Ref. 1 using the best ion-beam milled tip demonstrated to date.

To avoid ion beam damage, Hickman et al. batch-fabricated attonewton-sensitivity cantilevers with integrated 100 nm diameter nickel tips patterned by electron-beam (e-beam) lithography.²⁴ While these cantilevers were successfully used to detect ESR, the yield was very low and electron energy loss spectroscopy indicated that a significant percentage of the nickel was magnetically inactive, presumably as a result of processing damage. Moreover, the observed dependence of the signal on magnetic field agreed poorly with simulations, indicating that the tips were not behaving as a uniformly magnetized rod. To improve the yield, decrease processing-induced damage, and retain the critical ability to use high-resolution e-beam lithography to define the magnets, Longenecker and co-workers²⁵ recently introduced a combined batch/serial process for fabricating magnet-tipped attonewton-sensitivity cantilevers. Magnets were defined on a silicon-on-insulator wafer using e-beam lithography and liftoff. The wafer was then processed en batch to yield nanomagnet tips protruding from the leading edge of suspended micron-scale silicon chips, which were attached serially to the ends of attonewton-sensitivity silicon cantilevers using focused ion beam (FIB) milling and attachment. While this approach produced well-magnetized tips in high yield, magnetic resonance studies were not conducted.

Here we report magnet-on-cantilever detection of NMR using an attonewton-sensitivity cantilever with an integrated cobalt nanomagnet tip. Our tip's magnetic field gradient exceeds previous gradients produced by magnets on cantilevers by at least a factor of eight.^{18,19,21,23,26} Remarkably, the tip gradient is comparable to the tip employed in the high-resolution imaging experiment of Ref. 1. Our results thus demonstrate the potential for achieving 4 to 10 nm resolution proton magnetic resonance imaging with reasonable three-dimensional acquisition times for a wide range of thin-film organic samples.

In the subsequent sections of this paper we detail the fabrication, characterization, and implementation of these high-gradient tips in an NMR-MRFM experiment. To fabricate the e-beam-defined cobalt tips in high yield, the nickel-tip process of Ref. 25 was revised to avoid high-temperature processing steps. The resulting cobalt-tipped attonewton-sensitivity cantilevers were used to detect stochastic proton magnetization from a polystyrene film spun-cast over a microwire.²⁷ Artifact-free detection of NMR in this magnet-on-cantilever experiment required substantial modification of the spin-modulation protocols of Refs. 23 and 1. The spin signal was studied as a function of rf irradiation frequency at multiple tip-sample separations. By modeling this data numerically, the tip field and tip-field gradient were determined. The magnetic integrity of the tip at the nanoscale was assessed by comparing the spin signal to simulations carried out using different damage models. Measurements of force noise as a function of tip-sample separation over a copper microwire and over silicon indicate a larger-than-expected surface noise;²⁴ we suggest methods for mitigating this surface noise in future experiments.

Results

The experiment is sketched in Figure 1. The magnetic resonance force microscope used here has been described in detail elsewhere.^1,27 Cobalt-tipped cantilevers (Figure 2) were prepared as described in the Methods section. The cantilever used in these experiments had a resonance frequency f_c = 6644 Hz, an intrinsic quality factor Q = 8.4 × 10⁴ in vacuum, and a spring constant k = 1.0mNm⁻¹.

Figure 1.

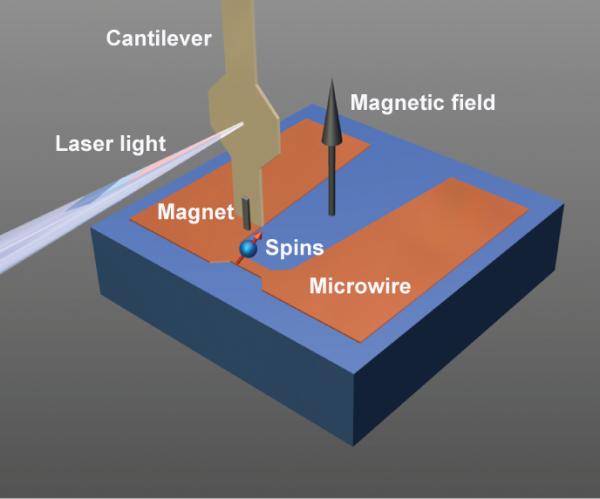
Schematic of the experiment. A cobalt magnet with cross section 225×79 nm² was extended past the leading edge of an attonewton-sensitivity cantilever. The cantilever was centered over a 1 μm-wide microwire coated with 40 nm of polystyrene. An external 2.63T magnetic field was applied in the direction of the long axis of the cantilever as shown. A laser interferometer was centered on a 30 μm-wide pad to measure cantilever vibrations.

Figure 2.

Scanning electron microscope images of the magnet-tipped cantilever used in the MRFM experiment. (a) Top-view image of the magnet-tipped chip attached to an underlying cantilever by ion-assisted platinum deposition; three rectangular platinum patches can be seen on the top side of the chip. The cobalt magnet is seen to overhang a 3 μm long finger at the leading edge of the chip. Scale bar = 5 μm. (b) Angled image of the overhanging cobalt nanomagnet, acquired before it was attached to a cantilever. The magnet was 225 ± 15 nm wide, 1494 ± 15 nm long, and 79 ± 4 nm thick. There was a 4 nm titanium layer under the magnet to promote adhesion to the silicon substrate, as well as an 8 nm platinum capping layer to mitigate oxidation. Scale bar = 200 nm. (c) Top-view image of a custom-fabricated 200 μm long cantilever drawn from the same batch as the cantilever used in this experiment. Scale bar = 20 μm.

The magnetic integrity of the tips was examined using a combination of characterization techniques. X-ray photoelectron spectroscopy (XPS), in conjunction with argon ion milling, was used to measure the elemental composition versus depth in 80 – 100 nm thick cobalt films prepared on silicon substrates. All films had a 4 nm titanium adhesion underlayer, and some films were capped with an 8 nm thick protective platinum coating. To estimate the damage incurred by subsequent processing, films were compared with and without exposure to elevated temperatures; baked films were coated with (poly)methylmethacrylate (PMMA) resist and heated at 115°C for 40 min (the PMMA was removed using solvent prior to XPS analysis). Unbaked films without protective platinum coatings measured oxygen within the first 3 nm of the cobalt layers; baking the material caused an additional 2–5 nm of oxidation for a total oxidation depth of 5–8 nm (Supporting Information, Figure S2). The platinum capping layer successfully eliminated the surface oxidation in both unbaked and baked films (Supporting Information, Figure S3). Superconducting quantum interference device (SQUID) magnetometry indicated that platinum-capped cobalt films exhibited saturation magnetizations close to the theoretical saturated magnetic moment for cobalt of 1.8 T (Supporting Information, Figure S5).

The magnetic integrity of the individual cobalt nanomagnet at the cantilever leading edge (Figure 2(b)) was verified in situ prior to MRFM measurements using frequency-shift cantilever magnetometry. The observed cantilever frequency shift Δf was converted to an equivalent magnet induced spring constant shift using k_m = 2kΔf/f_c. The resulting data between −5.0 T to −0.05 T and 0.05 T to 5.0 T were fit to^28,29

$$k_{\mathrm{m}}\left(B\right)={\mu }_{\mathrm{sat}}{\left(\frac{\alpha }{l}\right)}^2\frac{B\Delta B}{B+\Delta B}+c\mid B\mid ,$$ (1)

with B = μ₀H the applied magnetic field, α = 1.377 a constant for the fundamental cantilever mode, l = 200 μm the cantilever length, and μ_sat the saturated magnetic moment. Here ΔB = μ₀μ_satΔN/V is the shape-anisotropy field, with V the tip volume and ΔN = N_t – N_l the difference in demagnetization factor along the cantilever's thickness and length, respectively. The last term in eq 1 approximately accounts for the field-dependent spring constant shift of the bare cantilever at high field.^29,30 The measured magnetic moment was converted to saturation magnetization using μ₀M_sat = μ₀μ_sat/V with V = 225 nm × 1494 nm × 79 nm.

The measured k_m(B) data shown in Figure 3 was well described by eq 1. The observed ΔN = 0.56 ± 0.01 was in reasonable agreement with 0.50 expected for a high-aspect-ratio prolate ellipsoid. The observed saturation magnetization μ₀M_sat = 1.91 ± 0.03 T agreed well with 1.80 T expected for cobalt. Here we report the standard error in μ₀M_sat as an indication of the goodness of fit; the true error in μ₀M_sat is dominated by the uncertainly in k_m, which we caution could be 40% or larger. Taken together with the XPS and SQUID data on large-area thin films, these findings strongly support the conclusion that the tip exhibits a saturation magnetization close to the expected value for a fully intact cobalt nanomagnet.

Figure 3.

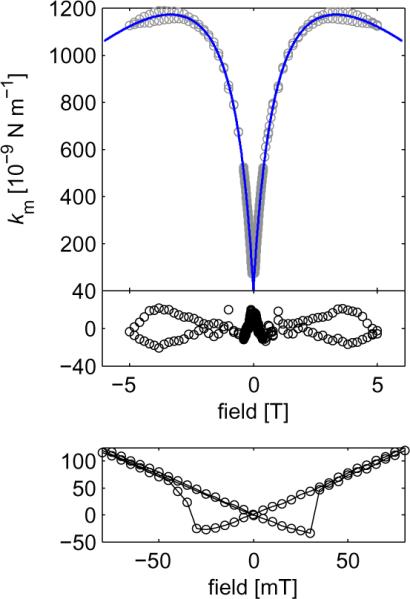
A frequency-shift cantilever magnetometry study of the cobalt nanomagnet used in this experiment. The external field was swept from +5 to −5 T and then back from −5 to +5 T. Upper: Magnetic spring constant shift k_m versus field (open circles) and a best fit to eq 1 (solid line). Middle: Fit residuals. Lower: Magnified view of the spring-constant hysteresis observed at low field.

To detect nuclear magnetic resonance, the magnet-tipped cantilever was centered over the microwire and brought into close proximity with the polystyrene film coating the microwire surface (Figure 1). The amplitude and frequency of the rf delivered to the microwire were modulated to induce cyclic inversions of the proton spins. To avoid spurious signal, a new spin modulation protocol COZMIC (COmpensated Zero Mean Inversion Cycles) was implemented, as described in the Methods section. A spin variance signal was inferred by subtracting in-phase and out-of-phase force fluctuations acting on the cantilever.

In Figure 4 we display measured spin variance signal ${\sigma }_{\mathrm{spin}}^2$ (open circles) as a function of the rf center frequency f_rf at five tip-sample separations h ranging from 42.3 nm to 13.1 nm. We observe that for each tip-sample separation the low-frequency edge of the signal is constant at a frequency of 112 MHz, whereas the high-frequency edges increase in rf frequency as the tip is brought closer to the sample. Both of these observations are well-understood. The spin variance signal arises from protons in the sample that meet the resonance condition f_rf = (γ_p/2π)|B^ext + B^tip(r)|, with γ_p/2π = 42.56 MHz/T the gyromagnetic ratio for protons, B^ext the applied magnetic field, and B^tip(r) the magnetic field generated by the cobalt nanomagnet at location r. The low-frequency edge of each signal shown in Figure 4 arises from spins far away from the tip where the magnetic field contribution from the tip is nearly zero. For |B^ext| = 2.63 T, such “bulk” spins should meet the magnetic resonance condition at a frequency f_l = 2.63 T × 42.56 MHz/T = 112 MHz, as we observed. The high-frequency edge of the signal arises from spins close to the cantilever experiencing an additional magnetic field from the cobalt nanomagnet. Due to the cobalt tip's field gradient, the field experienced by the spins at the surface increases as the tip-sample separation is reduced.

Figure 4.

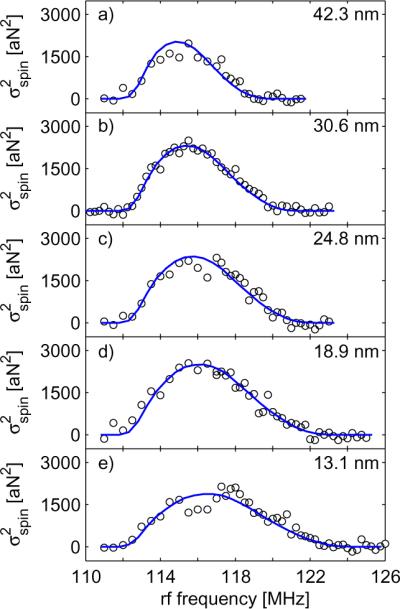
Magnetic resonance signal of protons in a 40 nm thick polystyrene film. The experimental spin variance signal ${\sigma }_{\mathrm{spin}}^2$ (open circles) was obtained by measuring the spin-induced force fluctuations experienced by a cobalt nanomagnet affixed to an attonewton-sensitivity cantilever that was brought into close proximity with the film. Signal was obtained at tip-sample separations of (a) 42.3 nm, (b) 30.6 nm, (c) 24.8 nm, (d) 18.9 nm, and (e) 13.1 nm. The static field was 2.63 T and the peak-to-peak rf frequency deviation Δf_FM was 2 MHz. Simulated spin variance signals (blue lines) were calculated at each tip-sample separation assuming a rectangular cuboid magnet with an extraneous spacing of 51 nm (Method 1).

The tip field and vertical tip-field gradient of the cobalt nanomagnet were estimated as a function of tip-sample separation by matching the shape of the experimental data in Figure 4(a–e) to simulated spin variances. In the simulations, the sample was assumed to be a 40 nm thick polystyrene film and the magnet had dimensions identical to the magnet shown in Figure 2(b). Details of the simulation parameters are provided in the Supporting Information.

Agreement between the simulations and the experimental data was obtained after considering several tip models. When simulations were conducted for a fully saturated cobalt nanomagnet, the tip field was overestimated by more than a factor of two (Supporting Information, Figure S6). Thus, damage models had to be considered. Magnet parameters using two models were optimized to match the shape of the spin variance signal and accurately estimate the tip field. In the first model (Method 1), the magnet was assumed to have a magnetic spacing that was 51 nm larger than the measured tip-sample separation. The spin variance signals calculated using this extraneous spacing of 51 nm are overlayed with the experimental data in Figure 4 as the blue lines. Using Method 1, the nanomagnet's tip field $B_z^{\mathrm{tip}}$ was calculated as a function of tip-sample separation (Figure 5; blue dot-dashed line) and numerical differentiation was used to calculate the tip-field gradient $\partial B_z^{\mathrm{tip}}∕\partial z$ (Figure 5; green dashed line). From the tip-field gradient plot in Figure 5, we can see that at the smallest tip-sample separation of 13.1 nm the vertical tip-field gradient was calculated to be 4.4 MT m⁻¹ for spins directly below the cobalt nanomagnet. In the second damage model (Method 2), the extraneous spacing was set to zero but the saturated magnetic moment for the nanomagnet was reduced from 1.8 T to 0.69 T. Method 2 provided a quality of fit that was almost as good as for Method 1. Using Method 2, the vertical tip-field gradient was estimated as 5.4 MT m⁻¹ for a tip-sample separation of 13.1 nm.

Figure 5.

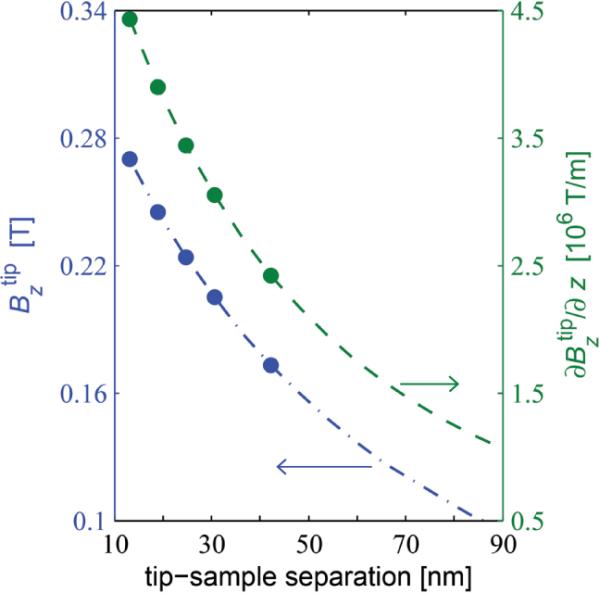
The tip field $B_z^{\mathrm{tip}}$ (left axis; blue) and tip-field gradient $\partial B_z^{\mathrm{tip}}∕\partial z$ (right axis; green) of the cobalt nanomagnet. As shown in Figure 4, a damage model for a tip with an extraneous spacing of 51 nm was used to calculate spin variance signal as a function of rf frequency. This model was used to determine $B_z^{\text{tip}}$ as a function of tip-sample separation (blue dot-dashed line) by calculating the difference between the high-frequency and low-frequency edges of the simulated signal at 15 different spacings. The five calculated tip fields that correspond to the tip-sample separations in Figure 4 are shown as blue filled circles. The tip-field gradient for the cobalt nanomagnet at the same 15 tip-sample separations (green dashed line) was determined by numerically differentiating the tip fields.

A comparison of the results obtained using Method 1 and Method 2 indicates to us that a number of tip damage scenarios could reproduce the data within experimental error but estimate some-what different tip-field gradients. As a check, we thus also tested a model-free method (Method 3) for estimating the tip field and tip-field gradient as follows. The downward-sloping peak data in each curve was fit to a line and the frequency f_h of the high-frequency edge was obtained from the x-intercept of the line. The z-component of the tip field was calculated as $B_z^{\mathrm{tip}}=(f_{\mathrm{h}}-f_{\mathrm{l}})∕({\gamma }_{\mathrm{p}}∕2\pi )$. The tip-field gradient was obtained by computing the derivative of the tip field data numerically; computing the tip-field gradient using the h = 13.1 nm and 18.9 nm data points gave the estimate $\partial B_z^{\mathrm{tip}}∕\partial z=5.1\mathrm{MT}{\mathrm{m}}^{-1}$. Because of the curvature of the slope of the simulated signal, we expect Method 3 to underestimate the tip field.

The friction coefficient Γ experienced by the magnet-tipped cantilever was studied over both the (polystyrene-coated) copper microwire and the (polystyrene-coated) silicon substrate at tip-sample separations ranging from 5 to 300 nm. Measurements were conducted at 2.63 T and at zero field over both surfaces. The corresponding spectral density of force fluctuations at the cantilever frequency was calculated from the measured friction coefficient using S_δF = 4k_BT Γ with k_B Boltzmann's constant and T = 5.5 K the temperature. The resulting data are displayed in Figure 6. For comparison, the cantilever's calculated internal friction coefficient is also shown; the cantilever's intrinsic properties were used to calculate that Γ = k/(2πf_cQ) = 2.85 × 10⁻¹³ Ns/m and that the associated thermally-limited force noise spectral density was 9.3 aN Hz^−1/2. The dissipation over the silicon substrate remained close to the thermal limit until a separation of approximately 100 nm. In contrast, the dissipation over the microwire became surface limited at tip-sample separations below 280 nm. The dissipation over both locations was essentially independent of applied magnetic field.

Figure 6.

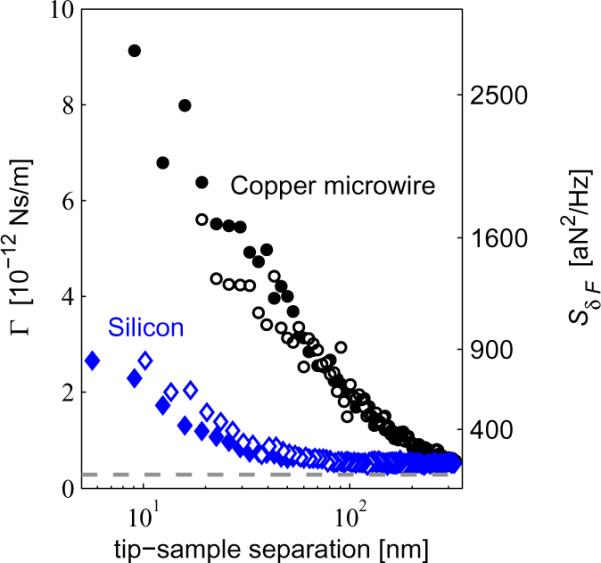
Cantilever dissipation G (left axis) versus tip-sample separation, and the corresponding spectral density of force fluctuations S_δF at T = 5.5K (right axis). Dissipation is shown for the tip centered over the copper microwire (black circles) and over the silicon substrate (blue diamonds). Measurements were conducted at B^ext = 2.63 T (closed circles and diamonds) and at zero field (open circles and diamonds). The dotted gray line is the cantilever's internal dissipation, calculated from the cantilever f_c, k, and Q measured far away from the surface.

Larger-than-expected cantilever frequency fluctuations were also observed over both the silicon substrate and the copper microwire (Supporting Information, Figure S7). Over silicon, the spectral density of cantilever frequency fluctuations S_δfc shows a low-frequency 1/f tail indicative of dielectric fluctuations in silicon or polystyrene.^31,32 The S_δfc over the microwire, in contrast, shows large spikes that suggest noise arising from mechanical vibrations.³³

Discussion

The data presented in Figure 4 and Figure 5 are the main results of this work. We demonstrated the successful detection of spin variance signal from protons in a magnet-on-cantilever MRFM experiment and found a vertical tip-field gradient on the order of 5 MT m⁻¹.

Method 1 and Method 2 (described in the Results section) provide relevant lower and upper bounds for the vertical tip-field gradient of the cobalt nanomagnet. In Method 1 the damage is modeled for the worst-case scenario in which all damage is concentrated at the magnet-sample interface. This extraneous spacing effectively increases the tip-sample separation and would most strongly reduce the tip-field gradient experienced by spins closest to the magnet's physical leading edge. Alternately, the damage is spread evenly throughout the entire magnet in Method 2, which allows for the retention of interactions between sample spins and magnetic material as close as the measured tip-sample separation of 13.1 nm. For a tip-sample separation of 13.1 nm, Method 1 and Method 2 were used to calculate vertical tip-field gradients of 4.4 MT m⁻¹ and 5.4 MT m⁻¹, respectively. As expected, the gradient estimated using Method 1 is the lower value.

To understand which, if either, of these simulated models correctly predicts the damage that led to the experimentally observed reduction in the tip field, we characterized the integrity of the cobalt material using XPS depth profiling, SQUID magnetometry, and in situ cantilever magnetometry. Results indicated that unprotected cobalt surfaces oxidized to a thickness of less than 10 nm, and that the rest of the cobalt remained fully intact. A simulation-free method for estimating the tip-field gradient was also used to compare to the results of Method 1 and Method 2; this method estimated that $\partial B_z^{\mathrm{tip}}∕\partial z\ge 5.1\mathrm{MT}{\mathrm{m}}^{-1}$. The gradient predicted by Method 1 is thus lower than expected, and the assumption in Method 2 that the damage is uniformly spread through the nanomagnet is in stark contrast with the less than 10 nm of damage expected based on the characterization measurements. Based on these findings, both of our simulation methods are likely oversimplifications of the true damage scenario. The simulation results taken together with the cobalt material characterization indicate that the discrepancy between the expected and observed tip fields may be due to a combination of (1) oxidation of all unprotected cobalt surfaces to a depth of 10 nm, (2) surface roughness on the magnet leading edge and sample film, and (3) a protrusion of the titanium underlayer past the cobalt leading edge.

While the nanomagnet's gradient is outstanding, the dissipation experienced by the magnet-tipped cantilever is disappointingly high, particularly near the microwire. At tip-sample separations of h ≤ 20 nm, the intrinsic force sensitivity of 9 aN Hz^−1/2 degraded to 40 aN Hz^−1/2 over the polymer-coated microwire and to 20 aN Hz^−1/2 over the polymer-coated silicon substrate. This behavior is in striking contrast with Hickman et al., whose cantilever with a similarly sized nickel tip maintained a force sensitivity of 10 aN Hz^−1/2 down to h ≤ 3 nm over a gold-coated polymer film.²⁴ Comparing the two experiments is instructive. In the Hickman et al. experiment, Γ was measured at zero field over a gold-coated polystyrene film spun on top of an ac-coupled gold halfwave microwave resonator, and the tip potential was adjusted to minimize Γ. Here, in contrast, the tip was brought over a dc-coupled copper microwire at high magnetic field, the sample covering the microwire was not metal coated, and it was not possible to adjust the tip potential to null the contact potential difference between the tip and the substrate.

There are two general dissipation mechanisms to consider: (1) tip magnetization coupling to fluctuating magnetic field gradients in the substrate, equivalent via the fluctuation-dissipation theorem to eddy current damping,^17,34,35 and (2) tip charge coupling to fluctuating electric field gradients in the substrate.^36–39 One might expect the eddy current damping to be stronger in a high external field where the tip is fully magnetized, whereas we instead observed Γ to be largely field independent. However, SQUID measurements revealed the magnetic film to have significant remanence (Supporting Information, Figure S5), which would lead to eddy current damping even at zero field. Now consider damping arising from fluctuating electric field gradients. There are certainly stray electrostatic fields between the tip and substrate at small separations due to both differences in the overall work functions and work function inhomogeneities. Previous room-temperature dissipation measurements^6,36,37 have shown sizeable differences between dissipation over metal layers and over polymer films due to electrostatic/dielectric effects; these same effects may be partly responsible for the roughly four times difference between the dissipation on and off the microwire. Still, since both the silicon and the microwire were covered with the same polymer, we suspect that the dominant dissipation source was magnetic.

For a tip-sample separation of 13.1 nm and under the signal averaging conditions of Ref. 1, our magnet-tipped cantilevers are projected to achieve a resolution of 5 to 10 nm. Assuming that we are dominated by eddy current damping, a simple solution to improve the dissipation and further enhance the achievable resolution could be to increase the sample thickness or introduce a dielectric spacer between the microwire and the sample.

Conclusion

In summary, we have produced magnet-tipped attonewton-sensitivity cantilevers and have used them to detect nuclear magnetic resonance with ≤ 500 μ_p sensitivity. The tip-field gradient of 4.4 to 5.4 MT m⁻¹ observed here is comparable to the 4.2 MT m⁻¹ field gradient produced by the Fe₇₀Co₃₀ pillar in the sample-on-cantilever experiment of Ref. 1 and is 8 to 10 times larger than the best tip gradient demonstrated to date in a magnet-on-cantilever MRFM experiment.¹⁸

That such a large gradient can be achieved in a magnet-on-cantilever MRFM experiment is an exciting advance. It should enable the characterization of as-fabricated semiconductor devices, for example, where Stark shifts of magnetic resonance transitions^40–42 allow the measurement of internal electric fields in semiconductor devices containing quadrupolar nuclei.^43–45 We moreover anticipate that moving the sample off-cantilever will allow the full battery of cryo-EM sample preparation techniques^14,15 to be applied in an MRFM experiment to prepare fragile biomolecules, macromolecular complexes, and thin sections of biological material. In contrast with cryo-EM, MRFM can accommodate micron-thick samples, and image contrast can be achieved by isotopic labeling, which is non-perturbative. MRFM's present resolution of 4 to 10 nm is competitive with what has been demonstrated in cryo-ET studies of subcellular structures,⁴⁶ organelles,⁴⁷ neuronal synapses,⁴⁸ and viral synapses⁴⁹ where studying a single copy of the structure is essential. When multiple precisely identical copies of a highly symmetric and large macromolecule or macromolecular complex are available, cryo-EM with single particle analysis can achieve near-atomic resolution. Frustratingly, broad classes of trafficking agents such as exosomes⁵⁰ and membrane proteins remain difficult to study by cryo-EM because the associated macromolecules or macromolecular complexes are disordered, have molecular weights less than 100 kDa,⁵¹ or simply do not retain their native structure in aqueous solution. With only slightly improved resolution, we anticipate that the type of magnet-on-tip magnetic resonance force microscope demonstrated here can begin to contribute to our understanding of such important biological nanostructures.

Methods

Measurements were conducted in high vacuum (P < 10⁻⁶ mbar) with the temperature maintained at T = 5.5 K. In all experiments reported here, both the sample and the cantilever were electrically grounded. In the following paragraphs we summarize the procedures used to produce the magnet-tipped cantilevers and study their tip magnetization in situ using frequency-shift cantilever magnetometry. We also summarize the protocols used to prepare the sample, detect nuclear magnetic resonance, and study cantilever dissipation.

Cantilever fabrication

Cantilevers were fabricated from single-crystal silicon-on-insulator (SOI) wafers as described by Jenkins et al.⁵² and Hickman et al.²⁴ The silicon orientation was ⟨100⟩, the device silicon thickness was 340 nm, the device silicon resistivity was 14 to 22 Ω cm, and the buried oxide thickness was 400 nm. The resulting cantilevers were 4 μm wide, 200 μm long, and had a 30 μm-wide reflective pad centered 70 μm from the leading edge (Figure 2(c)). Separately, cobalt nanomagnets were fabricated on silicon chips prepared from identical SOI wafers. The original protocol for the fabrication of nickel-tipped chips is described in Ref. 25; here an overview of the process is provided and required modifications to enable compatibility with cobalt nanomagnets are detailed. Etch slits were defined in the SOI wafer's device layer and the resulting chips were released using a buffered-oxide etch prior to deposition of the nanomagnets. The magnets were defined using e-beam lithography in bilayer (poly)methylmethacrylate (PMMA) resist and deposited by e-beam evaporation. The nanomagnets were prepared by depositing a titanium adhesion layer (4.0 ± 0.2 nm thick; deposited at 1.5 Å/sec), cobalt (79.2 ± 4.7 nm; 2.9 Å/sec), and a platinum capping layer (8.0 ± 0.5 nm; 1.2 Å/sec). Relative metal thicknesses were measured during deposition by a quartz crystal microbalance and the combined thickness of the Ti/Co/Pt film was measured after fabrication by atomic force microscopy (AFM). Silicon under the leading 300 nm of the magnets was removed by patterning U-shaped holes^24,25 in a layer of 700 nm thick, M_w = 4.95 × 10⁵ PMMA resist immediately in front of the magnet and isotropically etching the silicon using a sulfur hexafluoride and oxygen (SF₆:O₂) plasma. In order to prevent oxidation of the cobalt magnets, it was critical to bake the PMMA at only 115°C. Scanning electron microscope (SEM) images of the magnet-tipped chip and overhanging magnet are shown in Figure 2(a) and Figure 2(b), respectively. An FEI Strata 400 STEM dual focused ion beam (FIB) system was used to serially attach the magnet-tipped chips to cantilevers.²⁵ Compared to our prior work, the shape of the chips has been improved to facilitate their attachment to the cantilever (see Supporting Information, Figure S1). Magnet-tipped cantilevers were prepared at Cornell University four weeks before they were transferred to the MRFM apparatus at IBM Almaden Research Center. They were exposed to ambient air for approximately five days, were stored under nitrogen for three days, and were otherwise stored under a vacuum of 10⁻⁴ mbar.

Cantilever characterization

A representative cantilever is shown in the SEM image in Figure 2(c). The magnet-tipped cantilever used in this study had a resonance frequency f_c = 6644 Hz, an intrinsic quality factor Q = 8.4 × 10⁴ in vacuum, and a spring constant k = 1.0 mN m⁻¹. Cantilever displacement was monitored with a low-power⁵³ temperature-tuned⁵⁴ fiber optic interferometer (λ = 1550 nm, P ~ 25 nW). The interferometer output was sent to a field programmable gate array (FPGA) which was used to either control the cantilever Q via negative feedback⁵⁵ or self-oscillate the cantilever to a set amplitude via positive feedback.⁵⁶ The output of the FPGA drove a piezeoelectric disk at the base of the cantilever holder. The cantilever spring constant was determined from the mean square displacement of the undriven cantilever at a temperature T = 5.5 K;⁵⁷ a correction factor was used to account for the distance from the reflective pad to the end of the cantilever. Based on the ±15 μm uncertainty in the position of the laser, we estimate that the error in k could be as large as ±40%. To study cantilever dissipation, the cantilever ringdown time τ was measured and a cantilever quality factor and dissipation constant calculated using Q = τπ f_c and Γ = k/(2π f_cQ), respectively. The cantilever amplitude was set to 15 nm when measuring dissipation during approach. To study cantilever frequency noise, the instantaneous frequency of the self-oscillated cantilever was determined by fitting short 4 ms segments of the digitized cantilever oscillation to a sine wave; the power spectral density of cantilever frequency fluctuations was computed from the resulting frequency versus time data. For these studies a cantilever peak-to-peak amplitude of 60 nm was chosen because it approximated the ideal amplitude for detecting a single spin at a tip-sample separation of 23 nm in a force-gradient experiment, assuming a spherical tip radius of 41 nm.⁶ To determine the location of the sample surface, the tip-sample separation h was decreased until a dc deflection of the cantilever was observed. The displacement per volt of the vertical piezoelectric actuator was calibrated via fiber optic interferometry and the distance above this “touch point” was computed from the piezo voltage taking into account this (temperature-dependent) piezo calibration. The estimated error in h is ±3 nm.

Magnetic material characterization

The integrity of the cantilever's cobalt nanomagnet was analyzed in situ using frequency-shift cantilever magnetometry.^{24,25,28–30} The cantilever was mechanically driven into self-oscillation and the cantilever frequency was monitored as the field was swept from +5 to −5T and then back from −5 to +5T. Methods used to prepare and analyze magnetic thin-film samples using superconducting quantum interference device magnetometry and X-ray photoelectron spectroscopy are detailed in the Supporting Information.

Sample and microwire preparation

A lithographically-defined copper microwire was used to generate magnetic radiofrequency fields.^1,27 The microwire was prepared on a silicon substrate as described in Ref. 27, but with the magnetic pillar omitted. The sample consisted of a thin film of polystyrene prepared from solution via spin coating. Polystyrene powder (Pressure Chemical, M_w = 2.0 × 10⁵, M_w/M_n = 1.06) was dissolved into toluene to a final concentration of 0.3 weight percent and the resulting solution was spun onto a 4 mm × 4 mm silicon-plus-microwire substrate rotating at 6000 rpm. The high rotation speed and low viscosity resulted in a reasonably uniform film in spite of edge effects and the substrate's topographic features. The film's solvent was removed via air drying. Using FIB milling and SEM, the final film thickness was estimated to be 40 nm.

Spin detection protocol

Statistical fluctuations in proton magnetization were observed following the general approach of Degen et al.⁵⁸ Cyclic inversions of the sample magnetization were induced by triangle-wave rf sweeps with peak-to-peak FM deviation Δf_FM = 2MHz. The resulting cantilever motion was detected with a two-channel lock-in amplifier. The strength of the applied rf field was B₁ ≅ 5 mT. The proton magnetization fluctuated with a correlation time of τ_m = 100 to 150 ms; to accurately capture the induced cantilever position fluctuations, the cantilever response time was adjusted via feedback to be approximately 15 ms. The lock-in outputs were converted to units of force and a spin signal was computed from the variance of the outputs using ${\sigma }_{\mathrm{spin}}^2={\sigma }_x^2-{\sigma }_y^2$, where ${\sigma }_x^2$ and ${\sigma }_y^2$ represent the variances of the in-phase and quadrature lock-in signals, respectively. For most data points in Figure 4, the spin variance signal was computed from 12.5 minutes of lock-in data per rf frequency step. For the 117 to 126 MHz data at the three smallest tip-sample separations, h ≤ 25 nm, the spin variance signal was computed from 16.7 minutes of lock-in data per rf frequency step.

In prior sample-on-cantilever experiments,¹ optimized spin inversions were obtained using rf that was both frequency modulated (swept unidirectionally twice per cantilever cycle) and amplitude modulated (ramped to zero when the rf frequency was maximally off resonance). In our magnet-on-cantilever experiment, however, we found that this modulation scheme caused a parametric amplification of thermomechanical noise in one lock-in channel, yielding a false spin signal. This false variance imbalance was eliminated by operating the rf continuously and using triangle-wave frequency modulation. The triangle-wave frequency modulation, however, produced a spurious oscillation of the cantilever which in practice exhibited variations that obscured the spin signal.

Using our detection protocol COZMIC, we solved this problem by adding a small amount of amplitude modulation back into the rf so as to just cancel any spurious cantilever excitation caused by the frequency modulation (FM). This cancellation was accomplished by measuring the mean cantilever amplitude with the lock-in amplifier and applying a sinusoidal amplitude modulation (AM) to exactly cancel the mean cantilever excitation. The frequency-modulated rf waveform was multiplied by 1 + Acos (2π f_ct) + Bsin (2π f_ct), where A and B are small numbers that control the amplitude compensation. The in-phase and quadrature lock-in outputs X and Y were measured for two trials of amplitude compensation and a complex-number transfer function computed from χ ≈ (ΔX + iΔY)/(ΔA + iΔB). Knowing the transfer function, one can precisely predict how much amplitude modulation to apply to cancel the mean signal. After every 50 s of MRFM data collection and every time the cantilever was moved to a new location, we (1) measured the cantilever frequency, (2) computed a triangle FM waveform using the old values of A and B for AM compensation, (3) remeasured the lock-in mean for 5 s to determine the average X and Y, (4) calculated new values for A and B using the transfer function and the measured values for X and Y, (5) updated the triangle FM waveform using the new A and B values, (6) measured the mean lock-in outputs for 5 s and calculated an updated transfer function for future use, (7) measured the MRFM signal for 50 s, and (8) repeated. This compensation scheme worked precisely and automatically.