Quantum and classical dynamics simulations of ATP hydrolysis in solution

Abstract

ATP hydrolysis is a key reaction in living cells that drives many cellular processes. The reaction, which involves gamma phosphate cleavage from ATP, converting it to ADP, has been suggested to occur via an associative or dissociative mechanism dependent upon the surrounding environment. Prior quantum chemical studies suffered from short simulation timescales failing to capture free energy contributions due to relaxation of the surrounding aqueous environment. We have developed a highly parallelized QM/MM implementation in the NAMD and OpenAtom simulation packages, using the dual grid, dual length scale method for combined plane-wave and Eular exponential spline-based QM/MM simulations. This approach, using message-driven parallel quantum and classical dynamics, permits sufficient timescale simulations for quantum chemical events such as ATP hydrolysis, and is found to accurately and reliably include the free energy contributions of solvent relaxation to hydrolysis. In this paper we describe the application of the dual grid, dual length plane-wave-based QM/MM method to study both the associative and dissociative mechanisms of ATP hydrolysis, accounting for the free energy contribution from solvent relaxation, as well as for the key role of Mg²⁺ in the reaction.

1 Introduction

Hydrolysis of adenosine-5’-triphosphate, ATP, is a fundamental reaction in living cells responsible for driving many cellular processes. ATP, shown in Figure 1, is the most prevalent nucleotide derivative found at millimolar concentration in human cells and is a derivative of the nucleic acid adenine that has been triply phosphorylated at the 5’ position. A basic component of cellular metabolism and energy storage, ATP hydrolysis drives a diverse range of principal cellular processes such as ion gradient formation by ATP synthase,^1–4 membrane transport by ABC transporters,⁵ muscle contraction involving myosin,⁶ protein folding by chaperones,⁷ transport through kinases and dynein,⁶ phosphorylation,^8–10 and DNA repair or replication and translation.^11,12

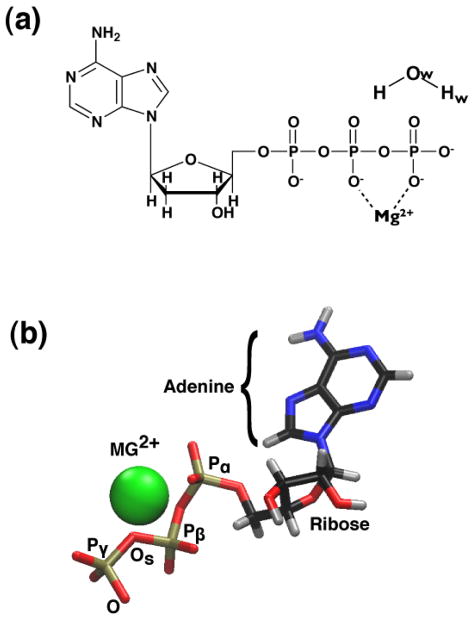
Figure 1.

(a) Adenosine-5’-phosphate (ATP) as found in its deprotonated form in aqueous solution. Magnesium and a water molecule are included for reference. (b) Structure of ATP. Extended conformation in aqueous solvent of the system before hydrolysis. Mg⁺² is shown chelated by P_α and P_γ.

ATP hydrolysis traditionally involves cleavage of the diphosphate anhydride bond between the β- and γ-phosphates, which breaks the terminal P_γ–O_s σ-bond. More rarely occurs cleavage of the α- and β-phosphates. Cleavage of the terminal P_γ–O_s bond has been proposed to release considerable energy due to the expected strong electrostatic repulsion between products.¹³ Other effects, like changes in resonance, protonation and solvation, as well as entropic effects, have been suggested to also contribute to the exothermicity of the reaction. Furthermore, while the importance of the surrounding environment has been illustrated by investigations of pH, salt composition, and solvent hydrophobicity effects on hydrolysis,^14–17 simulations of ATP hydrolysis thus far failed to capture the relaxation dynamics of solvent and its role in catalysis.

Knowledge of the conformational distribution and protonation state of ATP in water is crucial to models of ATP hydrolysis. The conformation of ATP in aqueous solution has previously been shown with reasonably high confidence to be linear with an anti-configuration.^18,19 Under neutral conditions with Mg²⁺ present, the triphosphate tail is fully deprotonated. While numerous X-ray structures for ATP salts have been reported,^20–24 to date the ATP•Mg²⁺ complex has not been crystalized due to spontaneous ATP hydrolysis that occurs during attempts to crystalize it.²⁵ While Na₂(ATP) crystals and Mg₂P₂O₇ hexahydrate salts 25 give clues to the binding configuration of Mg²⁺ and ATP with its four deprotonated oxygens, no study has yet provided an explicit structure or binding configuration.

Traditional ATP hydrolysis may be considered to occur via one of two mechanisms that lie at the two extremes of a continuum of possible mechanisms. At one extreme is the dissociative mechanism;²⁶ at the other is the associative mechanism.^10,27,28 The key difference between the mechanisms is the order of hydrolysis. In the dissociative mechanism, P_γ dissociates from ATP prior to nucleophilic attack by O_w of a lytic water; in the associative mechanism, a lytic water first associates with the γ -phosphate’s terminal oxygen, O_γ, and subsequent attack by O_w occurs before complete dissociation of P_γ.^26,28

Past attempts to simulate ATP hydrolysis encompass a wide range of approaches, including semi-empirical, molecular orbital based, Gaussian-centered atomic-orbital based (GCAO) and plane-wave Car-Parinello based quantum chemistry calculations.^29–33 These calculations ranged from gas-phase models of pyrophosphate to super-molecule representations of myosin’s active site,³⁴ as well as to a QM/MM treatment of ATP hydrolysis in the active sites of ATP synthase^3,4 and PcrA helicase.¹¹ Of these studies, those employing the simplest models^29–32 suggest that the thermodynamic energy difference between ATP•Mg²⁺ and ADP•P_i•Mg⁺² is marginal and fluctu-ates around a value close to zero. The results imply that the P_γ -O_s bond contains minimal internal bond energy. For the activation barrier, gas-phase GCAO calculations reported a 13.5 kcal/mol barrier for a simple pyrophosphate dianion model and formation of ${\text{PO}}_3^{-}$³¹ via a dissociative mechanism. This activation barrier is notably lower than the one determined in more extended QM and QM/MM calculations of enzyme active sites. However, it must be noted that upon inclusion of solvent and Mg²⁺ with ATP in a Car-Parinello plane-wave based study, an activation barrier of 35 kcal/mol was found for the dissociative reaction pathway. Akola et al. also found the dissociative reaction pathway more favorable than the associative reaction in aqueous solvent. It should be noted that 10 kcal/mol of the reported 35 kcal/mol activation barrier in the dissociative reaction pathway was attributed to insufficient solvation and equilibration of ${\text{PO}}_3^{-}$, ³³ but unfortunately this attribution was not computationally confirmed.

In this article, we describe the hydrolysis of ATP in aqueous solution via quantum mechanical/molecular mechanical (QM/MM) simulations using classical and density functional theory (DFT) based quantum dynamics. Of principle interest is the reaction mechanism of ATP hydrolysis in water. We will examine both associative and dissociative hypotheses and compare the results to previous purely quantum chemical studies. It is expected that extended equilibration and relaxation of the model system before, during and after the hydrolysis reaction will yield lower free energy activation barriers than previous studies of ATP hydrolysis in water. Of additional interest is the conformational distribution of ATP in an aqueous solution in comparison to the conformational distribution of ATP in an enzyme active site. Finally, we will examine the role of Mg²⁺ and its contributions to hydrolysis.

2 Methods

Simulation Model

The model systems used in the current study consisted of a cubic box including adenosine-triphosphate (ATP) complexed to a Mg²⁺ cation surrounded by solvent molecules and counter-ions. The deprotonated ATP, with a net charge of -2, was in complex with the Mg²⁺ cation and surrounded by solvated counter-ions. Solvation of the model was accomplished by embedding the ATP•Mg²⁺ complex in a 45 × 40 × 40 ų cube of ≈1800 water molecules. The QM subsystem was assigned to include the ATP•Mg²⁺ complex and 124 surrounding water molecules. The system was then energy minimized and subsequently equilibrated using classical molecular dynamics. Conformational analysis³⁵ was applied to the resulting trajectory and the system with the highest populated conformation of ATP was selected for subsequent QM/MM simulations.

Simulation Method

MD simulations were conducted using NAMD 2.8³⁶ with the CHARMM27 force field^37,38 and CMAP correction.³⁹ The equations of motion were integrated using a 0.5-fs time step, with all interactions calculated every 0.5 fs, including long-range electrostatic interactions, which were obtained using the particle mesh Ewald (PME) method with pencil decomposition. The PME grid density was never less than 1/ų and periodic boundary conditions were applied. Short-range, nonbonded interactions were calculated using a distance cut-off of 12 Å. Each system was minimized and equilibrated in the NpT ensemble (T =300 K, p=1 atm) using the following protocol: water and ions were equilibrated for 500 ps, keeping the ATP•Mg²⁺ complex’s atoms restrained; all restraints were then removed and the system equilibrated for 3 ns.

QM/MM simulations were performed using a dual grid, dual length scale method for plane-wave-based QM/MM simulations from Yarne et al.,⁴⁰ as implemented previously ^41–43 and now in the NAMD 2.8 simulation package. Electrostatic embedding, which reconciles electrostatic interactions between the MM and QM sub-systems, is accomplished through a cardinal B-spline-based formalism that explicitly introduces two length scales into the plane-wave based generalized-gradient-approximated-density-functional-theory (GGA-DFT) electronic structure calculation. One length scale, the shorter one, corresponds to the QM sub-system and the other, the longer one, to the MM system. Thus, two independent plane-wave cutoffs, one for each length scale, should be evaluated efficiently with a smooth, differentiable, rapidly convergent expression. Further detail can be found in prior publications.^40–45 The dual grid method scales as N log N where N is the number of atoms in the full system and the size of the QM sub-system remains constant. This electrostatic embedding method also relieves the need of ad hoc electrostatic potential fitting schemes that use point-charges to represent MM atoms in QM sub-system Coulombic calculations, as found in many other QM/MM methods. The resulting method elegantly links MM and QM sub-systems through their respective reciprocal space representation, conveniently taking advantage of the 3D FFTs necessary in PME for MD and in G-space transformations for QM.

QM Sub-system

The QM sub-system was treated using the plane-wave Car-Parinello molecular dynamics (CPMD) method based on density functional theory (DFT), as implemented in Open Atom.⁴⁶ Results were obtained within the generalized gradient approximation of DFT at the BLYP^47,48 level with an empirical dispersion correction⁴⁹ to yield appropriate water density and minimize over-structuring.^50–54 Troullier-Martins norm-conserving atomic pseudopotentials^55,56 were used with a plane-wave (pw) basis set truncated at 120 Ry for the density and a single k-point. A semi-core, nonlinear core corrected pseudopotential was used to describe Mg²⁺. The effective cutoff for the larger electrostatically embeddeded MM-grid during QM/MM calculations was 20 Ry. A fictitious electron mass of 400 amu with a CP dynamics timestep of 0.072 fs was used, keeping the electronic solution closer to Born-Oppenheimer energies and minimizing effects from dynamics.

Changes in the free energy, ΔF, of the simulated system were calculated by integration of the mean averaged force, <f_t >, along the reaction coordinate, ξ

$$\mathrm{\Delta }F(\xi )=-{\int }_{{\xi }_o}^{\xi }d{\xi }^{\prime }{f}_t({\xi }^{\prime })$$ (1)

where f_t (ξ) is generated by the constraining forces that impose a particular reaction coordinate, ξ, upon a selected set of collective variables or degrees of freedom in the system.

Reaction Coordinate Treatment

Unfortunately, atomic simulations are typically too short to capture the chemical dynamics of transition events like barrier crossings during bond formation and cleavage. To deal with this shortcoming, reaction coordinates are imposed that constrain the degrees of freedom in a molecule to a range. Within this range, the dynamics of orthogonal degrees of freedom may be sampled and molecular properties such as the potential energy may be calculated. Sampling at positions along the reaction coordinate provides a potential of mean force and, when taken together for all positions along the reaction coordinate, constitutes a mean path relating dynamics and energy along the selected coordinate.

A committor distribution would best help determine the optimal reaction coordinates for the the associative and dissociative reactions; however, the large system size of the QM subsystem and associated overhead renders determination of an accurate committor distribution a significant challenge. In lieu of empirically established reaction coordinates, the involved degrees of freedom were selected following previous investigations.³³

To model the associative reaction of ATP, we employ as the reaction coordinate the interatomic distance between P_γ and O_w which describes the approach of the lytic water and the resulting proton-transfer. The proton transfer from the lytic water to O_γ is unrestrained. This simple linear reaction coordinate models the hydrolysis as a classic SN² associative reaction, leaving the remainder of the system free to evolve on the energetic surface and imposing a minimal bias upon the system.

In the case of the dissociative reaction, we choose stretching of the P_γ –O_s–P_β anhydride bridge as the reaction coordinate corresponding to the interatomic distance seperating γ- and β-phosphorous atoms; approach of the lytic water and transfer of the proton are unrestrained. Similar to the reaction coordinate for the associative reaction, a simple linear coordinate for bond cleavage during hydrolysis was chosen. This reaction coordinate models the hydrolysis as an SN¹ dissociative process while imposing a minimal bias along a single degree of freedom that permits the remainder of the QM subsystem to evolve and independently sample the potential energy surface. The key difference between associative and dissociative hydrolysis processes lies in whether the reaction is an associative SN² or dissociative SN¹ process. The selected, minimally biasing reaction coordinates represent a least intrusive approach that allows one to drive sampling along the SN¹ and SN² reactions in efforts to construct potentials of mean force.

Cluster Analysis

Cluster analysis of QM/MM and QM-only trajectories were performed using the g_cluster module of GROMACS 4.5⁵⁷ with the Gromos clustering method⁵⁸ involving a RMSD similarity measure. RMSD values were calculated for the oxygen atoms of the five waters solvating the γ-phosphate and phospho-ether linking the γ and β-phosphates. Initial superpositioning for the RMSD calculations was performed using the heavy atom coordinates of ATP or ADP in the transition or ADP states, respectively, to measure intra-molecular reorganization. For the purpose of cluster analysis, QM-only calculations, as previously performed³³ were replicated and utilized in comparison to QM/MM calculations. Cutoffs were chosen based on the distribution of pairwise frame-frame RMSDs for each selection.

Computational Resources

Computations were performed on 48 AMD Opteron 6174 2.2 GHz processors with 240 Gb shared-memory. The resulting performance was predominately QM-computation time, with an average 3.2 iterations or steps per second, for ≈420 QM atoms and 5400 MD atoms. For comparison purposes, benchmarks of the QM/MM simulation were also performed on 2000 cores of a Cray XT5 possessing six-core AMD Opterons and 16 Gb memory per node, with an InfiBand network bandwidth of 240 Gb/s. Resulting performance was ≈ 0.95 steps per second, with further scaling to an increased number of processors still possible, as suggested by QM-only simulations that successfully scaled to 4000 cores. Overall computational speed is dependent upon performance of the QM calculation, and not the QM/MM interface. Processor load measurements of QM and MD portions of the calculation attribute an average of 98 CPU cycles to QM-based work for every 1 CPU cycle of MD-based work. This measurement indicates over 98% of the calculation time is expended during the QM calculation. Load-balancing may be improved by further software development to increase parallelism and provide better load-balancing schemes.

3 Results and Analysis

Results from QM/MM simulations of ATP hydrolysis, comparing the associative and dissociative mechanisms in aqueous solution, reveal that calculated electronic energies combined with simulated relaxation of water molecules surrounding the hydrolyzing ATP are in satisfactory agreement with abinitio energies of reaction profiles. In water, the dissociative mechanism is found to be energetically more favorable than the associative mechanism. The associative and dissociative mechanisms are discussed below.

Associative Mechanism

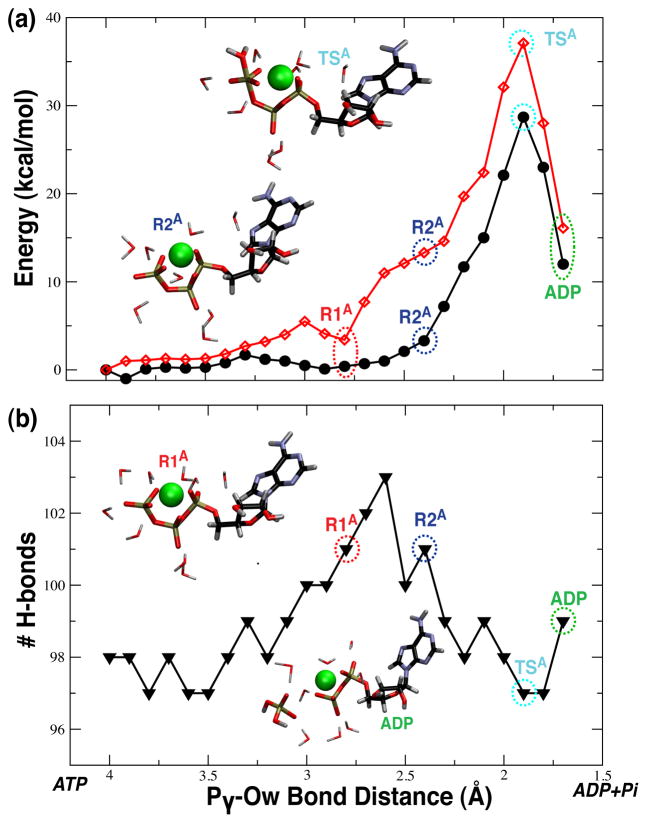
In the associative reaction, the P_γ –O_w distance is the natural reaction coordinate to represent nucleophilic attack of P_γ by the O_w atom of a nearby lytic water and the resulting cleavage of the terminal phosphate. Beginning at an interatomic distance of 4.0 Å, the distance between P_γ and O_w is systematically reduced to reveal the concomitant increase of both potential and free energy. As shown in Figure 2, energy increase peaks at a value of 26.7 kcal/mol for the potential energy and 36.2 kcal/mol for the free energy, at an interatomic P_γ –O_w distance of 1.9 Å. At this distance the resulting O– P_γ –O angle, presented in Figure 3, is approximately 118.0° indicating the γ-phosphate possesses the geometry of the expected pentacovalent transition state structure (structure TS^A) .^59,60 Progression along the reaction coordinate, further reducing the P_γ –O_w bond distance, reveals a sudden increase in the P_γ –O_s distance, the latter rapidly changing from 1.9 Å to more than 3.0 Å as the system relaxes to the ADP state. Overall the reaction is endothermic, with an increase of 11.0 kcal/mol in the potential energy. Inclusion of the free energy contributions after sufficient equilibration of the system increases the endothermic difference to 16.1 kcal/mol.

Figure 2.

Reaction energies for the associative mechanism. (a) Electronic (black circles) and free (red open diamonds) energies of the ATP•Mg²⁺ complex. (b) Number of hydrogen bonds (black triangles) formed with the ATP•Mg²⁺ complex as a function of the reaction coordinate, the P_γ –O_w bond distance.

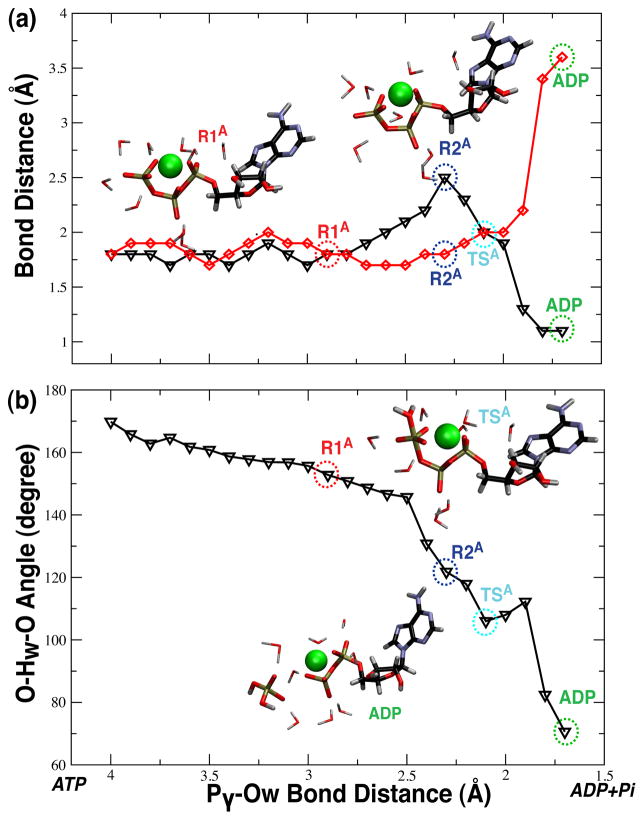
Figure 3.

Key structural features of the associative mechanism. (a) Bond distances of the Oγ–H_w bond (black triangles) and of the P_γ –O_s bond (red diamonds) as the P_γ –O_w distance (reaction coordinate) decreases. (b) O–H_w– O_w angle (black triangles) as a function of decreasing P_γ –O_w bond distance.

Structural changes during the associative reaction, interestingly, involve more than just a linear nucleophilic attack by O_w on P_γ and subsequent dissociation of the P_γ –O_s bond. As previously observed,³³ a hydrogen bond is initially formed between a hydrogen atom, H_w, of the lytic water and one of the unsataturated oxygen atoms, O, of the γ-phosphate (see structure R1^A). This hydrogen bond then grows stronger, decreasing the O–O_w distance and drawing the lytic water closer to the phosphate. As the lytic water is drawn closer, it slowly rotates as evidenced by the O–H_w–O_w angle change from 170°, when the P_γ –O_w distance is 4.0 Å, to 100°, when the P_γ –O_w distance is 2.2 Å (structure R2^A). The rotation then suddenly reverses, raising the O–H_w–O_w angle to 110° at the transition state for proton transfer of H_w from O_w to an unsaturated oxygen atom of P_γ and formation of the pentacovalent transition state structure (structure TS^D). The angle then quickly relaxes to 90°. Rotation of the lytic water is associated with reorganization of the surrounding solvent shell about P_γ and appears responsible for the notable increase in the free energy between the structures at R1^A and R2^A while the potential energy only marginally increases. Following the transition state, at a P_γ –O_s distance of 1.9 Å, the cleaved P_γ –O_s bond quickly increases and dissociates to a distance of over 3.0 Å, suggesting hydrolysis of the terminal γ-phosphate from ATP to be complete.

Solvent relaxation during associative mechanism

Prior work³³ suggested that sufficient relaxation of the surrounding solvent during the associative hydrolysis reaction decreases the observed difference in the values for free and potential energies. This suggestion is indeed supported in the present study, and with the increased sampling made possible by our QM/MM approach, free and potential energies in the pre- and post-hydrolysis states are indeed closer in value than seen in Akola et al.³³ In contrast, as the P_γ –O_w distance decreases with approach of the lytic water, potential and free energies diverge, as previously reported.³³ This divergence is of interest, as a difference between potential and free energies (by as much as 10 kcal/mol) is concurrent with rotation of the lytic water. However this energetic difference decreases to ≈5 kcal/mol at the transition state, TS^A (see Figure 2). Immediately following hydrolysis, the difference between free and potential energies decreases further. This behavior should be due to increased entropic contributions stemming from approach of the lytic water, specifically from rotation of the lytic water during its subsequent attack. It is notable that during the lytic water molecule’s rotation and associated increase in free energy, the number of hydrogen-bonds in the solvent shells momentarily increases as water molecules trade bonded partners during the conformational reorganization. Following the reorganization, the hydrogen-bonds are restored such that the structures of R1^A and R2^A (see Figure 3) experience an equivalent number, but quantitatively different, set of hydrogen-bonds. Possessing a large degree of conformational variability, the lytic water’s rotation and attack may require in future studies even further sampling than possible in the present study to adequately capture the lytic water’s free energy contributions as it approaches ATP.

Dissociative Mechanism

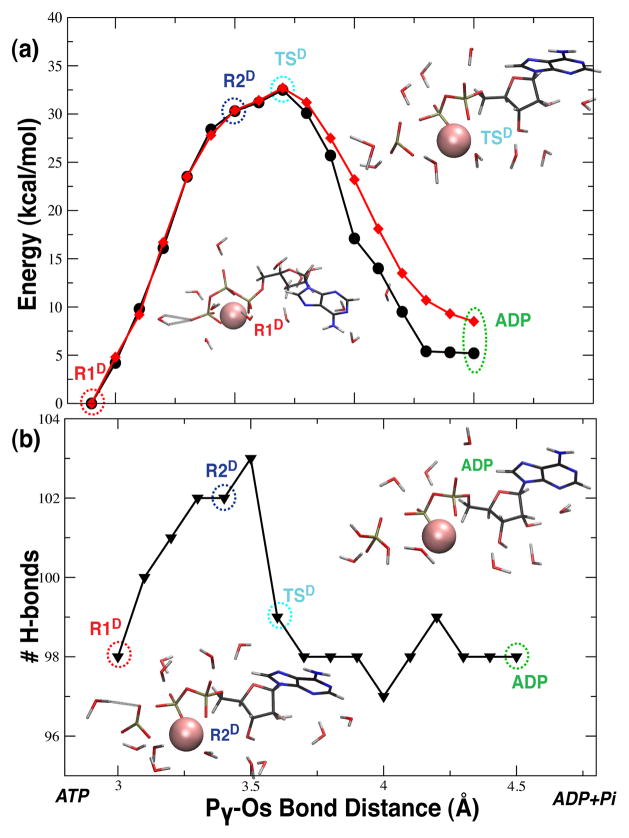
In modeling of the dissociative reaction the interatomic distance seperating P_βand P_γ was constrained as a reaction coordinate corresponding to cleavage of the P_β O_s– P_γ anhydride bridge and separation of the terminal γ-phosphate from ATP. Energetics are presented in Figure 4. Unlike the reaction energy profile for the associative mechanism, the potential and free energy value from the reactant (structure R1^D) to the transition state (structure TS^D) are close in value. A significant difference between potential and free energy is observed after the transition state, as the system energetically relaxes to the ADP state.

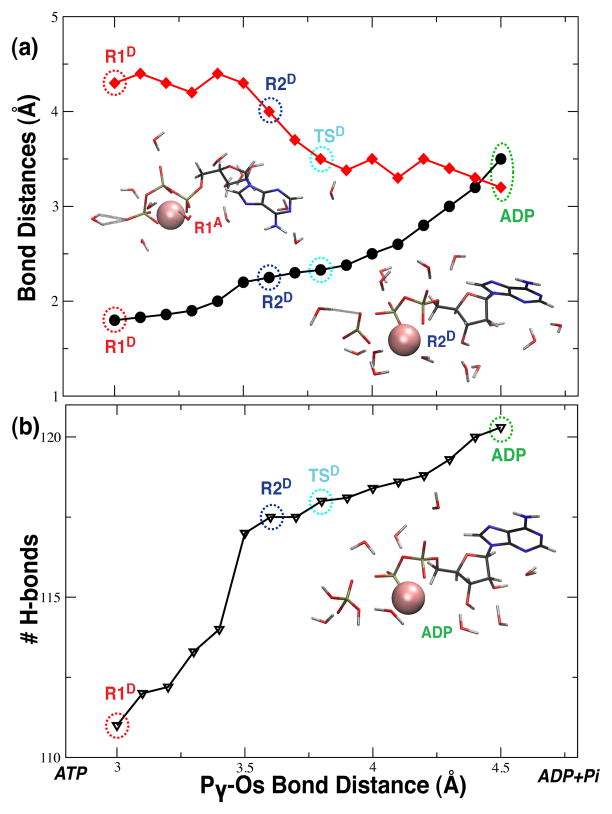
Figure 4.

Reaction energies for the dissociative mechanism. (a) Electronic (black circles) and free (red diamonds) energies of the ATP•Mg²⁺ complex. (b) Number of hydrogen bonds (black circles) formed with the ATP•Mg²⁺ complex as a function of the reaction coordinate, the P_γ –O_s bond distance.

On the potential energy surface, lacking free energy contributions, the reaction is endothermic with a ΔE of 6.0 kcal/mol and an activation barrier, ΔE^‡, of 33.4 kcal/mol. Inclusion of free energy contributions increases the calculated endothermicity to a ΔE of 10.1 kcal/mol; however, potential and free energy values are found to be close in values at the transition state (structure TS^D).

Structural changes along the reaction coordinate, shown in Figure 5, reveal how the terminal phosphate becomes cleaved³³ and how a subsequent nucleophlic attack by a water molecule yields ADP and ${\text{H}}_2{\text{PO}}_4^{-}$. Beginning from the reactant, R1^D, a lytic water molecule hydrogen-bonds one of the unsaturated oxygens of the terminal P_γ. The P_β–O_s– P_γ bridge elongates then asymmetrically as the P_γ –O_s bond stretches from 1.8 Å to 3.5 Å to form the planar ${\text{PO}}_3^{-}$ intermediate which is partially stabilized by the hydrogen bonds of the lytic water molecule and nearby solvent (structure R2^D). Late in this transition, at a P_γ –O_s distance of 3.5 Å, the lytic water rotates such that its O_w atom approaches P_γ, decreasing the interatomic distance by 1 Å (structure TS^D). Subsequently, formation of the new bond between O_w and P_γ stabilizes energetically the ${\text{PO}}_3^{-}$ intermediate, that is initially high in energy. As indicated by the barrier, labeled TS^D on the potential energy surface shown in Figure 4, breaking of the P_γ –O_s bond occurs at a distance of approximately 2.2 Å, after which point the O– P_γ –O angle begins to evolve from a value of ≈148° towards a value of 120°, corresponding to the planar geometry of solvated ${\text{PO}}_3^{-}$. The resulting planar geometry indicates cleavage of the terminal phosphate from ATP and completed formation of the planar ${\text{PO}}_3^{-}$ intermediate. The lytic water and ${\text{PO}}_3^{-}$ intermediate then bring about spontaneous formation of ${\text{HPO}}_4^{2-}$ and a proton which, through the Grotthuss mechanism, circuitously reduces one of the unsaturated oxygens of ${\text{HPO}}_4^{2-}$ to yield ${\text{H}}_2{\text{PO}}_4^{-}$ and ADP.

Figure 5.

Key structural features of the associative mechanism. (a) Bond distances of the P_γ –O_s bond (black circles) and a P_γ –O_w interatomic distance (red diamonds) as the P_γ –O_s distance (reaction coordinate) increases. (b) O– P_γ –O angle (black circles) as a function of increasing P_γ – O_s bond distance.

Role of Mg

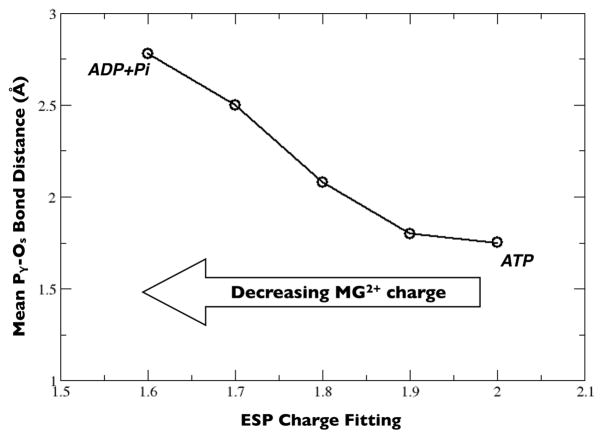
The well known role of Mg²⁺ in ATP hydrolysis is to accelerate the reaction rate.^14,15 Binding of Mg²⁺ to ATP forms a bidentate chelate, the ATP•Mg²⁺ complex; chelation of Mg²⁺ to ATP has been suggested to generate torsional strain in the anhydride P_γ –O_s–P_β bridge. 21,31 However, in the present study, evaluation of the mean forces and dihedral energies of the P_γ –O_s–P_β bridge with and without Mg²⁺ reveal only minor differences. This result suggests bidentate chelation of Mg²⁺ induces at best minimal torsional strain and is not a likely source of magnesium’s catalytic effect in ATP hydrolysis. In contrast, electrostatic potential (ESP) charge fitting of the ATP•Mg²⁺ complex suggests electronic stabilization by Mg²⁺ leads to lengthening of the P_γ – O_s bond as shown in Figure 6. As the cationic charge of the chelated Mg2+ decreases, it shares a larger percentage of the electron-density of the ATP•Mg²⁺ complex. Decrease of the net partial charge of Mg²⁺ results in increased fluctuation of the P_γ – O_s bond length. The calculations also show a lengthening of the mean P_γ – O_s bond distance with decreasing Mg2+ charge as it occurs also in the dissociative mechanism. As Mg²⁺ draws closer to ATP and assumes a greater portion of the electron density, which decreases its own net partial charge, the mean P_γ – O_s bond becomes longer and the bond length experiences increased fluctuations.

Figure 6.

Influence of Mg²⁺ partial charge (from electrostatic potential (ESP) fitting) on mean P_γ – O_s bond length.

Solvent relaxation

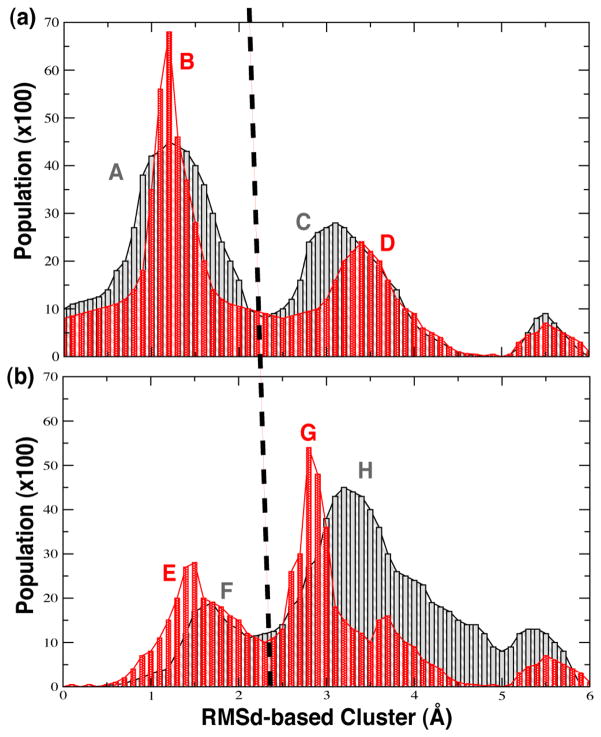
Prior work³³ suggested that sufficient relaxation of solvent surrounding the hydrolysis reaction reduces differences in free and potential energies. A similar observation is made in the present study, utilizing ≈416 QM atoms within 5400 MM atoms, compared to ≈ 200 QM atoms in Akola et al.³³ The increased size of the QM region, as well as the included MM buffer of water atoms, permits improved relaxation of the surrounding water molecules. Additionally, in the present study longer simulation times help provide increased sampling with ≈20 windows of 10 ps each, compared to ≈12 windows of 1 ps each in Akola et al.³³ The associated increase in simulation time provides an order of magnitude in increased sampling. Quantitative comparison of the degree of sampling for QM-only and QM/MM dynamics was performed through conformational clustering analysis using an RMSD based similarity measure.⁶¹ The resulting comparison reveals a notable difference between the extent of conformational sampling in QM/MM and simple QM-only calculations. The water molecules of the first solvent shell surrounding P_γ were clustered based on RMSD to determine the extent to which QM/MM and QM-only calculations differed in their conformational sampling and demonstrate the degree of solvent relaxation present following the dissociative reaction. Conformational analysis of dynamics at TS^D (Figure 7(a)) shows QM-only calculations (peak A) sample a narrower range of conformations than do QM/MM calculations (peak B). Even when the solvating water molecules of the TS^D state transiently occupy positions more similar to those around the structure of ADP (peaks C and D), a lower degree of sampling by QM-only dynamics is observed. More importantly, conformational analysis of the ADP state and of the associated change relative to the TS^D state, reflects the extent of simulated solvent relaxation following hydrolysis. In the QM/MM case, a significant conformational shift is found upon analysis of the ADP state, which shows a decrease of water molecules at positions corresponding to the TS^D state (peak F) and an increase in conformations corresponding to the ADP state (peak H). The solvating water molecules at P_γ reorganize following hydrolysis resulting in the growth of peak C into peak H, and the decay of peak A to peak F. In other words, after hydrolysis, water molecules formerly found at positions near P_γ in the TS^D state reorganize to positions that are on average 3.0 Å or more away and are found solvating the cleaved phosphate of the ADP state. In comparison, QM-only dynamics of the ADP state exhibits again a more narrowly sampled distribution of conformations (peak G) in the ADP state than does QM/MM dynamics (peak H). Additionally, compared to QM/MM, QM-only dynamics of the ADP state retains a higher number of waters molecules in conformations more similar to the TS^D state (peaks F and E), suggesting incomplete relaxation of the solvent in QM-only dynamics. Finally, as postulated in Akola et al.,³³ closer free and potential energies are observed in the pre- and post-hydrolysis states with improved sampling and solvent relaxation made possible by the parallel QM/MM dynamics.

Figure 7.

Conformational distributions from RMSD-based clustering analysis. QM-only results shown in red; QM/MM results shown in gray/black. (a) Results from dynamics at the TS^D state. (b) Results from dynamics at the ADP state. Peaks A, B, E and F correspond to TS^D conformations; peaks C, D, G and H correspond to ADP conformations.

4 Discussion and Concluding Remarks

Experimental measurement of ATP hydrolysis in aqueous solution and in enzyme active sites yields signficantly differing reaction free energies. In solution, the ΔG for hydrolysis ranges from −5 to −10 kcal/mol,^13–15 but in enzymes the reported calorimetric difference is only 1 to 2 kcal. This difference in ΔG values is suggested to result from ATP solvation since the aqueous solvation shell of ATP differs strongly between pure solution and the enzyme active site. The present study describes QM/MM simulations of ATP hydrolysis in solvent and compares two mechanisms of hydrolysis, the associative and the dissociative mechanism. In addition the conformational dynamics of ATP in aqueous solution is analyzed and a dominant conformation established. Finally the role of Mg²⁺ in the hydrolysis reaction is discussed. Results are compared to those reported in Akola et al.³³

Comparison of the associative and dissociative mechanisms reveal the latter to have a lower activation barrier and earlier transition state crossing than the associative mechanism in our description. In contrast to earlier work³³ that noted difficulties in acquiring free energy values due to insufficient solvent relaxation, the present study sampled the relaxing solvent more thoroughly and found the free and potential energies closer in value. In the current study the dissociative mechanism possesses a planar ${\text{PO}}_3^{-}$ intermediate stabilized by hydrogen-bonds and an electronic activation barrier of 33 kcal/mol, consistent with previous work.³³ However, in Akola et al.,³³ inclusion of free energy contributions yielded a near 15.0 kcal/mol difference between the potential and free energies of the ADP state. In the current study the potential and free energies of the ADP state from the dissociative mechanism are within 5 kcal/mol of one another. In fact, throughout the post-transition state dynamics leading to the ADP state, the potential and free energies do not diverge by more than 7.1 kcal/mol. Divergence prior to the transition state is less than 1.0 kcal/mol. This increased stabilization of the free energy is attributed to increased solvation and relaxation of the solvent along the reaction coordinate for dissociation of the planar ${\text{PO}}_3^{-}$ intermediate and it’s subsequent relaxation via the Grotthuss mechanism to ${\text{H}}_2{\text{PO}}_4^{-}$. In contrast to the dissociative mechanism, similar differences between the current and previous³³ work are seen for the potential and free energy surfaces of the associative mechanism. A late associative transition state is computed with geometries and energies similar to those reported by Akola et al.³³ This late transition state possesses an activation barrier of 28.5 kcal/mol on the potential energy surface. However on the free energy surface the activation barrier is nearly 40 kcal/mol in the prior³³ study, while the current study shows a free energy barrier of 36.2 kcal/mol, close in value to potential energies. As in the case of the dissociative mechanism, the improved free energy results are attributed to an improved description of solvent relaxation along the reaction coordinate.

The role of Mg²⁺ and its contribution to the hydrolysis reaction have also been examined. Both the prior³³ and the present study find that Mg²⁺ does not induce catalysis through strain of the phosphate backbone of ATP, in particular the coordination geometry of Mg²⁺ remains unchanged over the course of the reaction. In addition, the electronic properties of Mg²⁺, e.g., its charges, were found to vary throughout the reaction, suggesting stretching of the P_γ –O_s bond is directly compensated by electrostatic stabilization due to Mg²⁺. In the vibrational environment of an enzyme, as generated by the protein’s normal modes, fluctuations that drive Mg²⁺ closer to O_γ could conceivably weaken the P_γ –O_s bond by electronic stabilization of the P_γ –O_γ bond through the chelated O_γ –Mg²⁺ bond. In summary, the entropic and electronic contributions of Mg²⁺ are key in the catalysis of ATP hydrolysis in aqueous solution.

Our study has demonstrated that the dual grid, dual length scale method for hybrid QM/MM simulations accurately and reliably models structures, energetics and dynamics of ATP hydrolysis in aqueous solution. Previous approaches utilized quantum calculations of methyl-triphosphate as a model of ATP; the present study simulates a complete ATP molecule using density functional theory. In addition, in contrast to previous studies,³³ the QM/MM method of the present study permits extensive relaxation and equilibration of ATP and solvent along the hydrolysis reaction pathway. Parallelization of the QM/MM method in NAMD³⁶ and OpenAtom⁴⁶ facilitated rapid completion of the simulation through large-scale parallel runs, alleviating technical problems that have plagued previous efforts.³³ Finally, quantum dynamics simulation of an unrestrained reaction path for ATP hydrolysis both in solution and in the active site of enzymes, in the past, has presented a significant challenge due to large simulation size, memory demands and limited parallelization. The parallel dual grid, dual length scale QM/MM method should overcome the stated challenges and should permit unrestrained reaction simulations of ATP hydrolysis both in solution and within the catalytic sites of enzymes.

Future modeling of biochemical reactions stand to benefit signifcantly from load-balanced, scalable CPMD-based QM/MM simulations made possible by our new approach. Traditionally, QM/MM simulations have been hampered by poor scalability and limited load-balancing. In the approach of the present study, the implemented QM/MM method is built upon the Charm++ infrastructure to provide on-the-fly load-balancing that maximizes CPU utilization to accelerate QM/MM simulations’ time and efficiency. As QM/MM modeling of biochemical reactions approaches maturity, and key scientific problems like enzymatic catalysis and protein design begin to significantly benefit from QM/MM investigations, efficient, scalable QM/MM methods will be of increased importance and interest to the computational community.