Electrostatic Origin of the Catalytic Effect of a Supramolecular Host Catalyst

Abstract

The development of enzyme mimetic catalysts as well as the analysis of the catalytic effects of such catalysts has been a major challenge for synthetic chemists. One of the impressive examples of artificial catalysts has been the development of a highly charged host compound that provides a significant acceleration to the hydrolysis of orthoformates and other systems. However, the origin of the catalytic effect has not been quantified and its origin remains somewhat unclear. The understanding of the corresponding supramolecular catalysis has thus become a major challenge, both in terms of computational modeling and in terms of the analysis of the corresponding acid catalyzed reaction. Here we present a computer simulation study and kinetic analyses that reproduces the experimentally observed catalytic effect, establishing that this effect is due to electrostatic stabilization of the positively charged transition state (relative to the uncharged bound complex). Our study illustrates the crucial need for careful analysis of the complex kinetic of the catalytic effect and the host system, as well as the need for computational modeling in analyzing the catalytic effect and in the potential design of better catalysts. Finally, our finding of the large stabilization of the bound H₃O⁺ points out the very low “local pH” inside the host system even when the solvent is kept at a high pH.

I. Introduction

One of the long-standing challenges for synthetic chemists has been the construction of effective enzyme mimetic catalysts (e.g., refs ^1–4). The developments of such catalysts should help both in establishing what are the key catalytic factors and in providing practical directions for new biologically inspired catalysts.

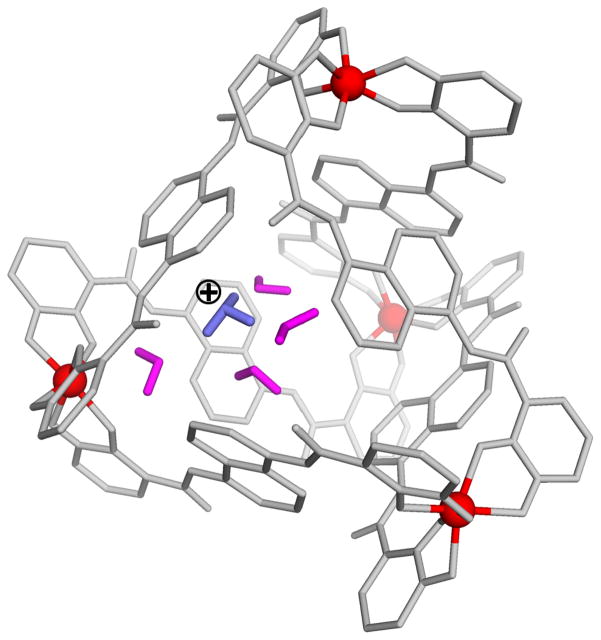
In many cases the catalytic power of biomimetic systems has not been so impressive, when taking into account the correct reference reaction in water (frequently the assessment of the catalytic effect involves incorrect treatment of the relevant reference reaction as discussed in the analysis of related cases of enzymatic reactions (see ref. 5). In other cases the design has not been focused on the most important catalytic factors. For example, placing the focus on the general base in trypsin inspired models (e.g., ref. 2) has helped in optimizing the well understood proximity factor (see ref. 5) but overlooked the key role of the oxyanion hole. Thus it has been very encouraging to see the recent construction of supramolecular host complexes with effective catalytic activity.^{6, 7} That is, the host complex (which is described in Fig. 1 and defines here as 1) that was developed by Raymond’s group (e.g., ref. 8) has been used, in collaboration with Bergman’s group, to catalyze the hydrolysis of orthoformates with a significant rate acceleration.^{6, 7} However, the nature of the catalytic effect has not been quantified and its origin remains somewhat unclear. Thus we have here both a fundamental problem and a truly challenging benchmark for modeling studies.

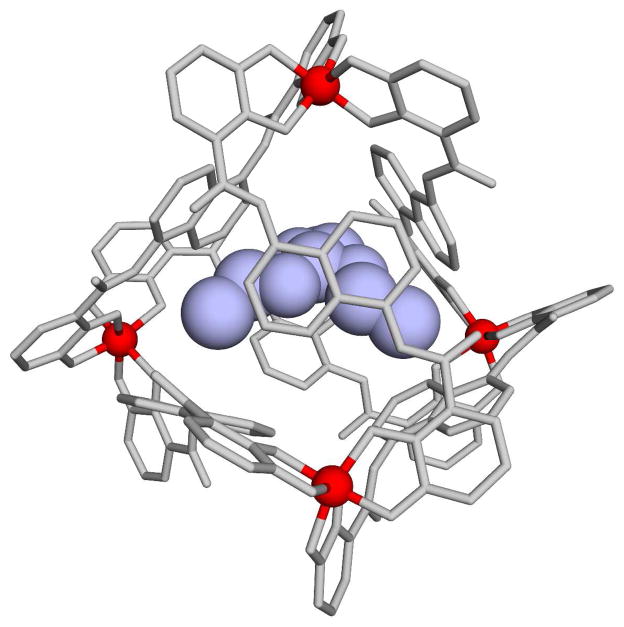
Figure 1.

The supramolecular assemblies of the complex Ga₄L₆, where L is N,N′-bis(2,3-dihydroxybenzoyl)-1,5-diaminonaphthalene. The Ga(III) ions are shown in pink color. These components self-assemble in solution to form tetrahedral clusters with chiral metal ions at the vertices and bridging ligands spanning each edge.

We would like to clarify that although it has been suggested that the catalysis of 1 may be associated with electrostatic effects, the actual analysis of the catalytic effect has not be formulated in terms of well-defined energy contributions (nor was it discussed in relationship to consistent analysis of such effects in enzyme catalysis).⁵ In fact, as is the case with enzymes, it is hard to see any clear way to quantify the origin of the catalytic effect without reproducing this effect by reliable computational tool. Thus for example, previous attempts to study related problems, such as the catalytic effect of β-cyclodextrin catalysis, involved qualitative and sometimes problematic arguments and arguably only the EVB computational study of Luzhkov and Åqvist ⁹ was able to quantify this effect and to relate it to electrostatic stabilization.

In the case of 1 we have a much larger catalytic effect than in the case of β-cyclodextrin and a major challenge, since even if it is all due to electrostatic factors, we are dealing with an extremely large charge distribution, where the corresponding energetics is notoriously hard to model. Unfortunately we have here also additional major complications with regards to the correct kinetic scheme and the meaning of the apparent k_cat, since it is not clear from the available experiments if (for example) the proton moves to 1 before or after the substrate binding (see below). In fact, as will be demonstrated in this work the analyses of the sequence of reaction steps and the observed saturation trend is as challenging as reproducing the catalytic effect and probably cannot be accomplished with calculating the energetics of some key intermediates.

The present work focused on the reproduction of the catalytic effect of 1 using the EVB model and a careful electrostatic treatment. This results in what is clearly the first quantitative study, with stable and conclusive findings for the catalytic hydrolysis of orthoformates. It is established that the catalytic effect of 1 is due to electrostatic stabilization of the positively charged transition states. This finding should provide a useful guide for designing artificial catalysis and the option of screening different possible designs. We also provide an illustration of the crucial need of computer simulations in analyzing the effects of artificial catalysts.

II. Background

As will be shown below the analyses of the catalytic reaction studied here is far more complex than previously assumed. Thus we must start by defining the problem that we intend to explore. More specifically, in order to evaluate catalytic effect we need to have a clear idea about the free energy barrier and overall mechanism of the reference solution reaction. Furthermore, we also need to have a clear formulation of the steps of the catalyzed reaction. Now, the formate hydrolysis reactions considered here (see Fig. 2) belong to a class of reaction that has been studied by physical organic chemists for a very long time (e.g., see review in ref. 10). However despite very extensive mechanistic studies (e.g., ref. 10) it has been very rare to find estimates of the actual activation barriers of the different steps. On some level it seems to us that this reflects the early doubt in the validity of transition state theory and the assumption that the preexponential factor in the rate expression cannot be approximately constant. Realizing this issue quiet early we have invested a major effort in quantifying reference solution reactions (e.g., refs ^11–13, see also a review in ref. 5). Our insistence on this issue stems from the fact that it is basically impossible to analyze catalytic effect in a clear logical way without characterizing the activation barriers in the reference solution reaction. A simple example is the common omission of the step of cage formation in comparing reactions in enzymes and solution. Overlooking the cage effect (that corresponds roughly a 55 M concentration ^{5, 14}) leads typically to a significant overestimate of the actual catalytic effect (see discussion of the case of Kemp eliminase ¹⁵).

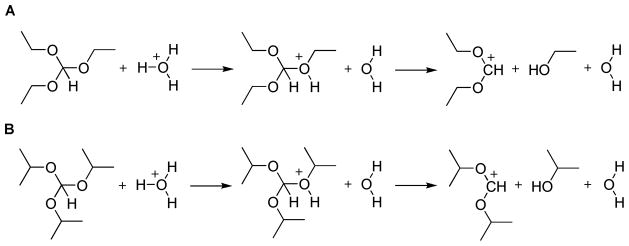
Figure 2.

The formate hydrolysis reaction.

Now even the careful mechanistic studies of the systems considered here (e.g., refs ^{7, 16, 17}) have not resulted in clear and well-defined estimates of the elementary activation barriers. For example, the diagrams given in refs ^{16, 18} do not correspond to the actual elementary chemical steps, or to explicit free energy values, making it rather hard to focus on the origin of the catalytic effect (see below). Thus we had attempted here to provide a detailed analysis of the energetics of the relevant reactions.

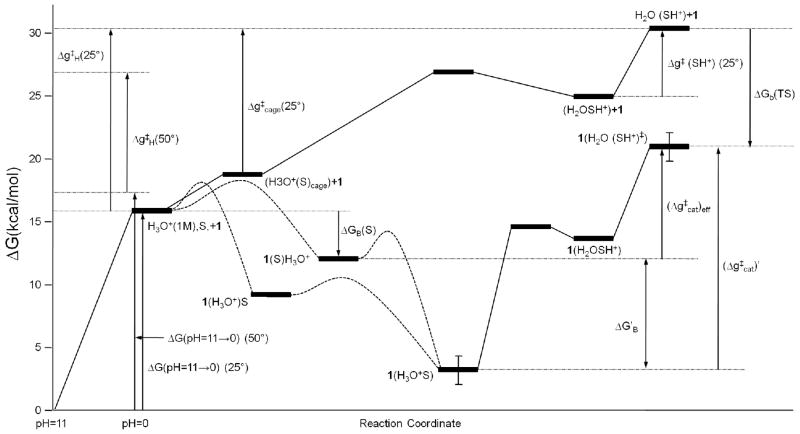
Our guide for analyzing the energetics of the reference reaction is provided in Fig. 3, which has some common elements with our early analysis of specific acid catalysis.^{13, 14} The energy considerations used in generating the figure start from the observed rate constant at the specified pH, where it is concluded from mechanistic studies (e.g., ref. 17) and from series of early studies ¹⁰ that the apparent rate constant can be written as

Figure 3.

A consensus energy diagram for the energetics of the orthoformates catalysis in water and in 1. S and SH⁺ designate the substrate and the transition state, respectively. The figure reflects the complex combination of careful analysis of the available experimental information about the reference reaction (see section II) and the calculated energetics of different states during the catalyzed reaction. Here in contrast to the case with enzymes the effective k_cat is not determined by the difference between the TS energy and the lowest energy in the reactant state but by the free energy difference between the TS and the bound uncharged substrate (see SI for the relevant analysis).

$${\text{k}}_{\text{app}}={\text{k}}_{\text{H}}[{\text{H}}^{+}]$$ (1)

Moving to standard conditions and to pH=0 leaves us with k_H for the reaction with 1M of H₃O⁺. Therefore k_H corresponds to the rate constant for moving one protonated water and the substrate in a molar volume to the same solvent cage, a proton transfer to the substrate and finally the reaction of the protonated substrate.

The activation free energies that correspond to Eq. 1 can be written

$$\mathrm{\Delta }{g}_{\mathit{app}}^{\ne }(pH)=2.3RT(pH-0)+\mathrm{\Delta }{g}_H^{\ne }$$ (2)

where $\mathrm{\Delta }{g}_H^{\ne }$ corresponds to k_H.

We can also write

$$\mathrm{\Delta }{g}_H^{\ne }=\mathrm{\Delta }{G}_{\mathit{cage}}+\mathrm{\Delta }{G}_{PT}(\mathit{cage})+\mathrm{\Delta }{g}_{{SH}^{+}}^{\ne }=\mathrm{\Delta }{G}_{\mathit{cage}}+\mathrm{\Delta }{g}_{\mathit{cage}}^{\ne }$$ (3)

where ΔG_PT (cage) is the free energy of proton transfer in the solvent cage, S is the substrate, SH⁺ is the protonated substrate and $\mathrm{\Delta }{g}_{{SH}^{+}}^{\ne }$ is the activation barrier of the reaction of SH⁺. The value of ΔG_PT (cage) can be estimated as about 4.8, assuming a pK_a of approximately −5.2¹⁰ for ethyl orthoformate (also known as triethyl orthoformate) and a pKa of about −1.7 for H₃O⁺. With an estimate of $\mathrm{\Delta }{g}_H^{\ne }=14\text{kcal}/\text{mol}$ (using k_H of about 700 s⁻¹ from ref. 19 and ΔG_cage=2.3 kcal/mol (e.g., ref. 14), we obtain $\mathrm{\Delta }{g}_{{SH}^{+}}^{\ne }=6.9\text{kcal}/\text{mol}$ at 25°C.

Alternatively, we can evaluate directly the free energy of moving a proton from a protonated water at pH=11 to the substrate and then the reaction of the protonated substrate. In this way we have

$$\begin{array}{l}\mathrm{\Delta }{g}_{\mathit{app}}^{\ne }=\mathrm{\Delta }{G}_{PT}(pH)+\mathrm{\Delta }{g}_{{SH}^{+}}^{\ne }\\ \mathrm{\Delta }{G}_{PT}=2.3\text{RT}(\text{pH}-{\text{pK}}_{\text{a}})\end{array}$$ (4)

For example, considering the triethyl orthoformates we have from ref. 7 k_app=k_uncat =1.44·10⁻⁵ s⁻¹ at 50° C and pH=11. This gives $\mathrm{\Delta }{g}_{\mathit{app}}^{\ne }=26.1\text{kcal}/\text{mol}$. We also have ΔG_PT (pH = 11)=26.1 kcal/mol for an estimate of pKa =−5.2 and thus $\mathrm{\Delta }{g}_{{SH}^{+}}^{\ne }$ is close to zero. Here there are several possibilities; one is that the observed pH dependence at pH =11 does not give us the exact k_H, perhaps due to some alternatively reactions (e.g., hydrolysis catalyzed by OH⁻). It is also possible that we have a significant temperature dependence of the activation barrier. These issues should be resolved by exploring the reaction at a wider pH range and different temperatures. Our main point is that the analysis of the reference reaction is quite complex and that more unique conclusions require probably careful ab initio calculations (as we have done in many cases (e.g., refs ^{15, 20}) and a more systematic experimental analysis which is focused on activation free energies and not as had been customary on just kinetic results. Fortunately, at this stage we are interested in the catalytic effect, which is easier to evaluate than the exact $\mathrm{\Delta }{g}_{{SH}^{+}}^{\ne }$, as we are looking at the change in this barrier rather than its absolute value.

At any rate, our task is to determine the catalytic effect. Usually, this can be done by comparing $\mathrm{\Delta }{g}_{\mathit{cage}}^{\ne }$ and $\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }$ but in the present case the molecular meaning of $\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }$ is far from trivial since it is not clear a priori what is the state that is equivalent to ES (see Fig. 3). In fact, the situation is much more complex than what has been envisioned by the kinetic studies of the catalyzed reaction and the nature of the limiting cases requires reliable computational studies. The complex kinetics that corresponds to Fig. 3 is explored in the SI. Basically, as found in the SI, the effective k_cat [(k_cat)_eff] at the range of high pH is determined by the difference between the free energy of the (1(H₂O(SH⁺)) transition state (TS) and the free energy of the 1(S) ground state. This point is supported qualitatively by noting that if we have a bound S (saturation by S) then the kinetics of a subsequent binding of H₃O⁺ and a reaction would follows $k_{\mathit{cat}}^{\prime }/K_M^{\prime }$ which corresponds to ${\left(\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }\right)}_{\mathit{eff}}$. Furthermore, to be more confident about the kinetics (whose complex features led to some difficulties in the SI of ref. 7) we will focus mainly on the numerical solution of the kinetic equation of Eq. S1 and use the analytical solution only as a general guide.

With the above rather complex analysis we conclude that the evaluation of the catalytic effect can be done by following the thermodynamic cycles of Fig. S1 (A and B) and Eq. S15 that lead to

$${\left(\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }\right)}_{\mathit{eff}}-\mathrm{\Delta }{g}_{H^{+}}^{\ne }\cong \mathrm{\Delta }{G}_{\mathit{sol}}{(TS)}^1+\mathrm{\Delta }\mathrm{\Delta }G(H_{2}O)-\mathrm{\Delta }{G}_{\mathit{sol}}{(TS)}^w+\mathrm{\Delta }{G}_{\mathit{sol}}{(S)}^w-{\mathrm{\Delta }{G}_{\mathit{sol}}(S)}^1$$ (5)

where ΔG_sol(TS)¹ and ΔG_sol(TS)^w are the solvation energies of the TS in 1 and in water, while ΔΔG(H₂O) is the change is free energy upon moving the internal water molecule from 1 to the bulk aqueous solution.

We must note that ${\left(\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }\right)}_{\mathit{eff}}$ is not equal to $\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }$ and that this make the analysis of the catalytic effect significantly different than what has been assumed in previous studies.

III. Methods

Our simulation strategy is based on the EVB approach and on an adiabatic charging procedure. The EVB has been described extensively in previous works (e.g., refs ^{14, 21, 22}). Briefly, this method describes the reacting system in terms of diabatic states (see Fig. 4 for the present reactions) which include the interaction with the environment, and then mixed these states and evaluate the free energy of the resulting adiabatic ground state by a specialized free energy perturbation (FEP) umbrella sampling (FEP/US) approach.^{14, 23}

Figure 4.

The EVB states used in modeling the reaction steps in the hydrolysis of triethyl orthoformate (A) and triisopropyl orthoformate (B).

The EVB calculations were carried out by the MOLARIS simulation program ^{24, 25} using the ENZYMIX force field. The EVB activation barriers were calculated from the free energy profiles obtained by the above FEP/US. In addition we spent our main effort on calculating the solvation free energies of the EVB transition states (as well as other states) using and adiabatic charging FEP calculations (e.g., ref. 26). The simulation systems were solvated by the surface constrained all atom solvent (SCAAS) model,²⁵ using a water sphere of 18 Å radius, centered on the substrate and surrounded by a 2 Å grid of Langevin dipoles and then by a bulk solvent, while long-range electrostatic effects were treated by the local reaction field (LRF) method.²⁵ Additional validation studies were also done with a sphere of 22 Å radius. The FEP mapping was evaluated by 21 frames of 5 ps each for moving along the reaction coordinate using SCAAS model. All the simulations were done at 300 K with a time step of 1 fs. In order to obtain reliable results the simulations were repeated eight times with different initial conditions (obtained from arbitrary points of the relaxation trajectory).

The starting X-ray geometry of the host complex 1 was taken from the Cambridge Crystallographic Data Centre (CCDC ID: 100947).^{27, 28} The crystal ligands were replaced with the reacting fragments within the host complex 1. The crystal waters were removed during the system preparation and new water molecules were added by MOLARIS software package.^{24, 25}

The construction of the EVB surfaces of the reference solution reactions focused on the energy and charges of the corresponding TSs. The charges were determined by performing ab initio calculations on the reactant, product and transition states, and using the Merz-Kollman scheme to obtain the EVB effective charges. The substrate geometries were first optimized using the MPW1PW91 theory level and the 6-31+G* basis set, using by the Gaussian03 package (Revision E.01)²⁹. The solvent effect was treated implicitly and calculated at MPW1PW91/6-311++G** level by performing the single point calculations on the optimized structures using the COSMO continuum model.^{30, 31} The resulting ab initio RS, TS and PS charges are given in Fig. S2. In addition to the effective charges we used the EVB parameters, which are given in Table S1. These parameters reflect standard EVB parameters plus a calibration on the observed activation barrier of the reference reaction.

The Ga(III) metal – ligand interactions were parameterized using the cationic dummy atom approach, where ligands octahedrally coordinated to the metal.^{32, 33} The van der Waals parameters for the interaction of the dummy atoms with metal were tuned based on the calculations of the solvation free energy using an adiabatic charging FEP procedure^{14, 26} in MOLARIS simulation program.^{24, 25} The van der Waals parameters used in simulations are given in Table S1.

Since the present work involves a major challenge in terms of treating electrostatic effects, we emphasized two aspects that are not always considered in the EVB studies. First we included a polarizable EVB treatment; the use of polarizable force field has been introduced by us in 1976 ³⁴ and have been used by used frequently.³⁵ The MOLARIS polarizable model which has been described elsewhere (e.g., ref. 25) uses our non-iterative approach (see ref. 25), which allows extremely effective evaluation of the effect of the induce dipoles. Our polarizable model has also been used in different EVB studies (e.g., refs ^{36, 37}) but in the present case it has been really crucial. Furthermore, since we are dealing with a very highly charged system we also include explicit counter ions, using 12 K⁺ potassium ions to balance the −12 overall charge of the complex in the simulation volume which corresponded roughly to a molar volume. The counter ions were restrained with a weak constraint of 0.03 kcal/mol/A² to the substrate charge centers.

IV. Results and discussion

The host complex system 1 of Fig. 1 is a highly charged system, where the evaluation of the energy of an internal group is a major challenge. Thus we started by a validation procedure of evaluating the pK_a shift of the N,N,N′,N′-tetraethyl-1,2-diaminoethane. The results of the simulations with several models are describes in Table 1. Remarkably, only the complete model with polarizable force field and counter ions could reproduce the observed pK_a shift. It would be useful to see if other simulations packages or simulation methods and boundary conditions will be able to overcome the above challenge.

Table 1.

The calculated and observed $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol}}^{w\to \mathbf{1}}$ for systems explored in this work using three different approaches.^a,^b

Energies	pKaobs	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},\mathit{obs}}^{w\to \mathbf{1}}$	no ions	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol},\mathit{calc}}^{w\to \mathbf{1}}$ no induced	induced and ions
System
N,N,N′,N′-tetraethyl-1,2-diaminoethane
water	10.8	−4.8	5.7	12.1	−3.8
complex	14.3
TS of triethyl orthoformate
water	no exp.	-	−1.8	4.2	−8.7
complex
TS of triisopropyl orthoformate
water	no exp.	-	2.3	3.4	−7.7
complex

^aEnergies in kcal/mol.

^bThe calculated $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol}}^{w\to \mathbf{1}}$ reflects an average over eight conformations (forward and backward) obtained by starting the solvation energy calculations from equally spaced points along the relaxation trajectory. The table also provides the stabilization of the TSs of the reactions studied here. The error range of the calculations is about 2 kcal/mol as judged from the variation of the results obtained by simulations with different starting points.

Next we moved to the challenge of evaluating the actual catalytic effect, starting by considering the catalysis of the orthoformate systems by 1. As outlined in the method section, we calibrated the EVB on the reference solution reaction (see parameters in the SI). We then used the same parameters without any change to evaluate the reaction in 1 and in particular ΔΔG_sol(S ⇒ (SH⁺)^≠). The results of the simulations of the triethyl and triisopropyl orthoformates are summarized in Table 2 and as seen from the table we have a significant error limit reflecting the extremely large charge of the system and the variation in the results for different substrate orientations. Since the deviation between the calculated results of the two substrates are larger than the observed difference in rate constants, we used the average to obtain the “consensus” results for othroformates and give the corresponding results in Fig. 3. As seen from the table and the figure we obtained extremely large stabilization of the complex with the protonated water molecule and also a significant TS stabilization. The calculated ${\left(\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }\right)}_{\mathit{eff}}-\mathrm{\Delta }{g}_{H^{+}}^{\ne }$ is about −6 kcal/mol which is in the right range, where the actual comparison of the calculated and observed results will be discussed below.

Table 2.

The average calculated free energies of key states.^a

Energies	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol}}^{w\to \mathbf{1}}\left(S\right)$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol}}^{w\to \mathbf{1}}\left(H_3{O}^{+}S\right)$	$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{sol}}^{w\to \mathbf{1}}\left(H_{2}O{\left({SH}^{+}\right)}^{\ne }\right)$	${\left(\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }\right)}_{\mathit{eff}}-\mathrm{\Delta }{g}_{H^{+}}^{\ne }$
System
H3O+	−10.0	-	-	-
triethyl orthoformate	-	−14.0 ± 3	−8.0 ± 3	−5.0± 3
triisopropyl orthoformate	-	−9.0 ± 3	−10.0 ± 3	−7.0± 3

^aEnergies in kcal/mol.

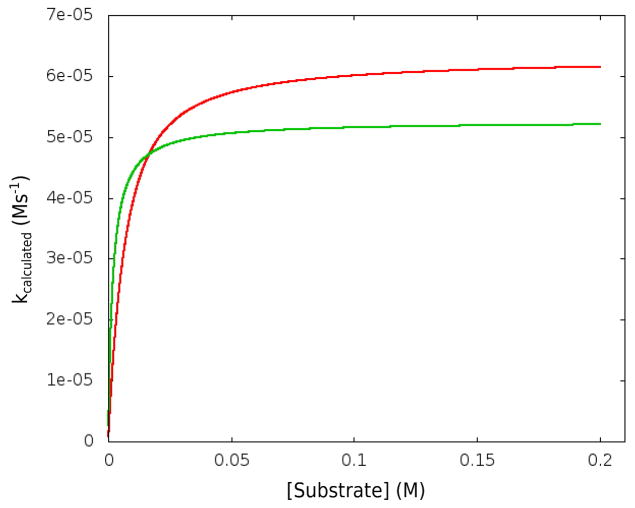
Now, although the calculated TS stabilization might involve some overestimate, it is due entirely to the electrostatic stabilization of the positively charged TS. Of course, at this point one should be concern with the comparison to the calculated and observed rates, rather than just our estimate of the catalytic effect. To do so we took the kinetic parameters obtained from the free energy calculations (see Table S2) and then used them in evaluating numerically the kinetics of the system (integrating Eq. S1). The corresponding calculated results are given in Figs 5 and 6, which depict, respectively, the calculated dependence of the rate constant on the substrate concentration and pH (at 50 C). The saturation point in Fig. 5 corresponds to (k_cat)_eff 6·10⁻⁵ s⁻¹, whereas the reported k_cat is about 8·10⁻³ s⁻¹ and 4·10⁻³ s⁻¹ for triethyl orthoformate and triisopropyl orthoformate, respectively. The value of the calculated rates at saturation is clearly in the observed range, considering the 2 kcal/mol error range of the calculations, as well as the fact that our estimate of the activation barrier of the reference reaction in water is significantly higher that the estimate from the observed uncatalyzed reaction. The pH dependence is also in a reasonable agreement, noting however, that in contrast to the assumption of ref. 7 (which seems to have some typographical problems) we predict a point where the pH dependence will start to reflect a complex competition between the binding of the proton and the binding of the substrate. This behavior is due to the very strong predicted binding of the H₃O⁺(S) to 1. Of course, the strong binding reflects a very negative energy of (1(H₃O⁺(S)) relative to the separate H₃O⁺ and 1(S) which is not obvious intuitively, but the corresponding results appeared to be relatively stable to the simulations conditions (see also section V).

Figure 5.

The calculated dependence (red and green for numerical and analytical, respectively) of the rate constant on the substrate concentration at 50°C.

Figure 6.

The calculated pH dependence obtained with the set used for 5 at 50°C.

Interestingly the calculated ${\left(\mathrm{\Delta }{g}_{\mathit{cat}}^{\ne }\right)}_{\mathit{eff}}$ is around 9 kcal/mol (from our free energy diagram at Fig. 3) as compared to 7.0 kcal/mol deduced from the simulated kinetics. Now, if we like to examine the consistency between our calculations and the observed catalytic effect we have to consider the fact that the rate obtained at 50 ° C from $\mathrm{\Delta }{g}_{H^{+}}^{\ne }$ used in our diagram (about 14 kcal/mol) underestimates the observed uncatalyzed rate, giving a rate constant of 2·10⁻⁹ s⁻¹ instead of around 4·10⁻⁶ s⁻¹ (see section II). However, the catalytic effect is still at the right range. Note that despite the fact that the kinetics in 1 is far more complex than previously envisioned, we have captured the trend in the catalytic effect.

We also like to point out that the effective activation barriers are quite different than that deduced by the simple use of transition state theory with the observed rate constant at pH=11. Of course, the work of moving the catalytic H₃O⁺ to the substrate cage, or at least to a molar volume, can be considered as a part of the activation barrier, but this makes it harder to reach a clear molecular picture.

V. Concluding Remarks

The host guest catalysis system developed by Raymond and Bergman⁷ groups have generated great excitement (e.g., ref. 3), highlighting the potential of artificial catalysis. However, the origin of the observed effect has not been elucidated and the corresponding ability to predict the catalytic activity has not been developed.

The present work used the EVB and FEP methods and demonstrated the ability to reproduce the observed catalytic effect of a very highly charged host complex. The corresponding calculation has captured the compensation of different electrostatic effects (induced dipoles, solvent and ions), which combined together to reproduce the electrostatic stabilization of the TS (relative to the uncharged bound substrate) and the corresponding effective dielectric.

Our ability to explore the individual steps of the catalytic process demonstrated that we are dealing here with a more complex kinetics than what have been envisioned previously. In particular the competition between the substrate binding and the proton binding as well as the binding of the proton to the protonated substrate leads to an effective k_cat [(k_cat)_eff], which is very different than the regular k_cat in enzymatic reactions. In fact, the complex catalytic effect is expressed in the large (k_cat)_eff but the actual TS stabilization in 1 is not an enzyme like effect. That is, it appears that the electrostatic stabilization of the actual protonated reactant state (1(H₃O⁺S)) is larger than that of the TS (1(H₂OSH⁺). However, the special kinetics (see Fig. 3 and its kinetic analysis in the SI) lead to an effective k_cat which is indeed larger than the rate constant of the catalyzed reaction.

It is quiet significant that the catalytic effect has been found to be due entirely to the change in the electrostatic contributions to the activation free energy. Here again the effect can be classified as electrostatic preorganization effect.^{5, 12} Thus we have an additional support to the idea that the most important catalytic effect in enzyme like system is electrostatic TS stabilization.^{5, 12}

We also like to point out on the remarkably strong binding of the H₃O⁺ ion obtained in the present calculations. This results were unexpected since it is hard to provide to H₃O⁺ more solvation than in water,³⁸ but the calculations seem to be stable enough to be meaningful. In fact, we found that once we uncharged the complex the binding energy becomes positive and larger than 10 kcal/mol. Thus all the negative binding of the H₃O⁺ is due to the highly negative charge of the complex. Overall, our study indicates that, in contrast to the regular situation (where the polarization of water molecules compensate for large electrostatic effects,³⁹ between ion pairs) the internal water molecules in 1 are polarized in the direction of the field from the four external charge centers (see Fig. 7). It is true that in regular cases of interaction between ions the compensating effect comes from the water around the ions and not the from the water between the ions (see Fig. 2 in ref. 40) but in 1 we have a clear stabilizing contributions from the internal water, as is shown in Table S3. Thus the internal water molecules actually increase the solvation of the of H₃O⁺ ion in the (1[H₃O⁺S]) system. Here it is important to note that due to the special kinetics at high pH, the trend in our calculated catalytic effect will not change even if we have a significant overestimate of the binding of the protonated H₃O⁺. Thus, if the results for the binding of H₃O⁺ are in the right range we have here a remarkable case of a low “local pH” which should have interesting consequences.

Figure 7.

The orientation of the water molecules inside complex 1 with H₃O⁺.

At this point it is interesting to note that, as in the case of enzymes (and even more so in the present case), it is hard to determine experimentally the origin of the catalytic effect. In fact, it has been thought in some cases (e.g., ref. 41) that the catalytic effect is not due to electrostatic effect, based on the observed salt effect. However, as is the case with enzymes, salt effects do not change substantially electrostatic catalysis in internal sites. It has also been suggested ⁴¹ that the catalytic effect involves large entropic effects due to the substrate structural preorganization. However, as was shown in the examination of related proposals of solute entropies contributions to enzyme catalysis (e.g., refs ^{5, 42}), conformational entropy contributions are small. The observed entropic difference between the catalyzed and uncatalyzed reaction is most probably due to the entropic contribution to the electrostatic free energy (reflecting the solvent reorganization). An instructive similar example has been found in the analysis of the peptide bond formation by the ribosome.⁴³ Of course, it will be interesting to reproduce the observed entropic effect by our restraint release approach ^{42, 44} but this is out of the scope of the present work. At any rate, our main point here is that it is absolutely crucial to use computational approaches in determining the origin of catalytic effects, but only method that can determine to overall observed effect (without any special parameterization) should be used in such analysis.

We also like to point out that the influential idea that enzyme mimetic host systems largely work by shape complimentarily of rigid cavities (e.g., ref. 45), has similar difficulties as the idea that enzymes work by shape complimentarily. The only place where the shape enters is in restricting substrates whose size are too large. The rigid shape is important, but only in terms of its electrostatic preorganization effect,¹² which has not been widely recognized as a key catalytic factor by the biomimetic community. As found in this work and in our studies of enzymes (e.g., ref. 5), what counts is the electrostatic preorganization of the active site. Here it is important to realize that we are dealing with more than a semantic issue. That is, understanding the key catalytic factors should serve as a major guide in designing different systems and for refining existing systems, as well as for modifying the activity of a given catalyst.