Kalman Filter Techniques for Accelerated Cartesian Dynamic Cardiac Imaging

Abstract

In dynamic MRI, spatial and temporal parallel imaging can be exploited to reduce scan time. Real-time reconstruction enables immediate visualization during the scan. Commonly used view-sharing techniques suffer from limited temporal resolution, and many of the more advanced reconstruction methods are either retrospective, time-consuming, or both. A Kalman filter model capable of real-time reconstruction can be used to increase the spatial and temporal resolution in dynamic MRI reconstruction. The original study describing the use of the Kalman filter in dynamic MRI was limited to non-Cartesian trajectories, because of a limitation intrinsic to the dynamic model used in that study. Here the limitation is overcome and the model is applied to the more commonly used Cartesian trajectory with fast reconstruction. Furthermore, a combination of the Kalman filter model with Cartesian parallel imaging is presented to further increase the spatial and temporal resolution and SNR. Simulations and experiments were conducted to demonstrate that the Kalman filter model can increase the temporal resolution of the image series compared with view sharing techniques and decrease the spatial aliasing compared with TGRAPPA. The method requires relatively little computation, and thus is suitable for real-time reconstruction.

INTRODUCTION

Dynamic magnetic resonance imaging (MRI), which acquires a series of MR images to capture evolving physiological phenomena, is becoming more popular in many clinical applications including real-time cardiac function imaging, myocardial perfusion imaging, dynamic MRA and functional MRI. Short scan time is typically needed to reduce motion artifacts in dynamic imaging. One important method to reduce scan time is to exploit the redundancy in the acquired data and/or the raw images so that less k-space data are required for a given spatial and temporal resolution. Parallel imaging techniques, such as SMASH (1), SENSE (2) and GRAPPA (3), have been demonstrated to effectively reduce scan time without degrading image quality. These techniques take advantage of the spatial redundancy of the image with multiple receiver coils to reduce the amount of k-space data required. Similarly, in most dynamic image series, temporal redundancy can be also exploited, since the images are highly correlated. Various view-sharing techniques have been developed to make use of the temporal redundancy to reduce the number of k-space phase-encoding lines acquired for each image. These include the commonly used sliding window, which fills the unacquired k-space data with the previously acquired time-adjacent k-space data, and SLAM (4), which fills the unacquired k-space data by interpolating from neighboring frames. These techniques are the principal methods used clinically due to their simplicity and robustness, despite the fact that they can only increase the apparent temporal resolution and may introduce temporal blurring and ghost artifacts to the dynamic image series.

Instead of exploiting the redundancy in the time domain, other techniques apply a 1D Fourier transform along the time direction to explore the redundancy in the frequency domain and then use advanced reconstruction methods to recover the image series. These techniques include UNFOLD (5), kt-BLAST (6) and kt-FOCUSS (7), and they show advantages over the view sharing techniques in reducing aliasing and temporal blurring. Another category includes many reduced FOV (rFOV) methods (8–10), which take advantage of the fact that some parts in the FOV are relatively static in a dynamic image series so that the number of required k-space lines to update an individual image can be reduced. One representative method called Noquist (10) can effectively reconstruct the image series without residual artifacts from undersampled k-space data by decomposing the image and the corresponding Fourier transform matrix into dynamic and static parts and solving the resulting inverse problem with greatly reduced degrees of freedom, because the static part of the image series stays the same throughout the image series and requires much less data to reconstruct. However, these two types of methods often use retrospective reconstruction, which inhibits their adoption in many clinical applications in which real-time reconstruction is required, such as real-time catheter tracking and cardiac stress function studies. Furthermore, these techniques are not always robust; for example, in real-time cardiac imaging, the effectiveness of these methods can be impaired by respiratory motion during free breathing (11).

Recent techniques based on compressed sensing, including the aforementioned kt-FOCUSS and temporally constrained reconstruction methods (12), which exploit sparsity in the time and/or frequency domain, have gained attention. However, a major disadvantage of these methods is the long reconstruction time due to the iterative reconstruction, so that physicians cannot get the reconstructed images for rapid feedback during the scan. Furthermore, the nonlinear characteristics of these techniques make it difficult to predict and evaluate the noise in the images compared with linear methods.

The Kalman filter, a widely used method in many engineering fields including real-time object tracking, can also exploit the temporal redundancy in a time series by describing the dynamic problem with a time-evolving state model and rapidly estimating the current state using a real-time linear filtering process. Therefore, it is plausible to use this method in dynamic MRI for real-time imaging and real-time reconstruction. The original adoption of Kalman filter in dynamic MRI was proposed by Sümbül et al. (13–14). However, this method was confined to non-Cartesian k-space trajectories because of a limitation intrinsic to the model used in that study. In this paper we adapt the Kalman filter model to make it available for the more widely used Cartesian trajectory.

Spatial and temporal redundancy can be exploited in combination to more effectively reduce the scan time. Previous spatiotemporal acceleration approaches include TSENSE (15) and TGRAPPA (16), which mainly rely on spatial parallelism but improve the results with the temporal information; kt-SENSE (6), which is an expansion of kt-BLAST that incorporates coil sensitivity into the model; and PINOT (17), which combines the SPACE-RIP parallel imaging method (18) and the Noquist method. In this paper we also combine the Kalman filter model with spatial parallel techniques. If reliable coil sensitivity maps can be acquired, they can simply incorporate them into the model as in kt-SENSE and non-Cartesian Kalman filter combined with SENSE (13); however, since accurate coil sensitivity maps in many dynamic problems are difficult to achieve, we also developed a method that combines the Kalman filter with TGRAPPA to avoid the coil sensitivity estimation step.

In this paper, we will first introduce the implementation of the Kalman filter in Cartesian dynamic MRI, including the combination with parallel imaging techniques. Next, we focus on non-gated real-time cardiac imaging to study the performance of the Kalman filter model by both simulation and experiment. Finally, we will discuss our results and possible extensions.

THEORY

In general, a Kalman filter model is composed of a system model that describes the relationships among the time-evolving states and a measurement model that describes the measurement of the state at a given time. Usually the current measurement at a given time alone is not sufficient to obtain an accurate estimate of the current state. The key to the Kalman filter is to use all previous measurements and the relationship between states as described by the system model to estimate the current state. Furthermore, the estimation process is recursive, so there is no need to store past measurements for the purpose of computing present estimates. Thus, the process can be very fast and memory efficient. The general model of a Kalman filter is given as follows (19):

$$\begin{array}{l}{\underset{\_}{x}}_k={\mathrm{\Phi }}_{k-1}{\underset{\_}{x}}_{k-1}+{\underset{\_}{w}}_{k-1},{\underset{\_}{w}}_k~N(\underset{\_}{0},Q_k)\\ {\underset{\_}{z}}_k=H_k{\underset{\_}{x}}_k+{\underset{\_}{v}}_k,{\underset{\_}{v}}_k~N(\underset{\_}{0},R_k)\end{array}$$ [1]

where x_k is the system state in a vector form, Φ_k is the state transition matrix, w_k is the system noise vector assumed to have a zero-mean Gaussian distribution with covariance matrix Q_k, H_k and z_k are the measurement matrix and the corresponding measurement data, and v_k is the measurement noise also assumed to have a zero-mean Gaussian distribution with covariance matrix R_k. Given the appropriate initial conditions and assuming w_k and v_j are independent, we can get the state estimate x̂_k by a prediction-correction process described as

$$\begin{array}{l}{\underset{\_}{\widehat{x}}}_k^{-}={\mathrm{\Phi }}_{k-1}{\underset{\_}{\widehat{x}}}_{k-1}^{+}\\ {\underset{\_}{\widehat{x}}}_k^{+}={\underset{\_}{\widehat{x}}}_k^{-}+K_k[z_k-H_k{\underset{\_}{\widehat{x}}}_k^{-}]\end{array}$$ [2]

where the − and + refer to the predicted and corrected state estimates and K_k is the Kalman gain matrix calculated from H_k, Q_k, R_k and Φ_k (19). The general equations to calculate K_k are omitted here for brevity, as they will be discussed below in the Model Implementation section.

If we want to directly apply the Kalman filter model to a dynamic MRI application acquiring a 2D image series, the state to be estimated at each time point k is one individual image from the image series and the corresponding measurement is the acquired k-space data, where the measurement matrix is the 2D Fourier transform in matrix form. One major obstacle here is the size of the vectors and matrices. For an individual N by N image, the dimension of the state vector is N²*1 and the corresponding matrix is N²*N², which is generally too large to handle for a typical value of N. In Sümbül’s paper (13), a diagonalization assumption is made for Q_k, R_k and H_k^T H_k so that the prediction-correction process can be performed on a pixel-by-pixel basis to bypass the matrix multiplication and inversion steps in calculating K_k. The diagonalization of Q_k and R_k can still be applied for Cartesian trajectories, because Q_k reflects statistical properties of the dynamic image series that are independent from the data acquisition, and the diagonalization of R_k is intrinsic due to the whiteness of the measurement noise.

However, the diagonal simplification for H_k^T H_k is only possible for a non-Cartesian k-space trajectory such as a spiral trajectory. Assuming H_k is the undersampled 2D Fourier transform matrix connecting the image domain and the k-space domain with a matrix-vector multiplication, the off-diagonal terms of H_k^T H_k are determined by the aliasing pattern as displayed in the point spread function. For a spiral trajectory, the aliasing is diffuse and the side lobes of the point spread function are more evenly distributed; therefore, each single off-diagonal term is very small compared to the diagonal term and can be ignored without nullifying the model. However, for a Cartesian k-space trajectory, the aliasing pattern is generally very conspicuous as shown by separate peaks in the point spread function; therefore, the off-diagonal term of H_k^T H_k cannot be ignored. Without the diagonalization of H_k^T H_k, the direct implementation of the Kalman filter is impractical since the matrix calculation process can be extremely complicated and will greatly increase the reconstruction time. However, in an undersampled 2D Cartesian k-space measurement, undersampling usually only happens in the phase encoding direction and k-space is often fully sampled or even over sampled in the readout direction. Therefore, we can first apply a direct 1D Fourier transform along the readout direction and then use the Kalman filter for the reconstruction along the phase encoding direction for each readout pixel. By doing that, for the same N by N image, we now have N Kalman filter models which can be calculated in parallel and for each model, the dimension of the state vector becomes N and the matrix size becomes reasonable. Furthermore, since we have already transformed into the image domain along the readout direction before the Kalman filter model implementation, in many cases we need fewer than N Kalman filter models to cover the ROI along the readout direction, because portions of the object may not experience rapid motion. In this case, view-sharing techniques can be used for the remaining regions to further reduce the reconstruction time, as discussed below.

In the following paragraphs we will focus on a particular application: non-gated real-time imaging of cardiac function. We will describe a specific Kalman filter model and use this model to perform image reconstruction from undersampled data. Cardiac imaging has demanding requirements for a dynamic imaging method, because of the fast and complex motion of the heart combined with chest motion from breathing. First, we will introduce the implementation of the Kalman filter model and describe how to obtain the signal estimates. Then we will discuss several potential algorithms to simplify the model to reduce the reconstruction time. Finally we will discuss the combination of the Kalman filter with parallel imaging techniques.

Model Implementation

In a dynamic cardiac image series, the differences between two consecutive images are generally very small except for certain areas experiencing rapid changes; therefore, for simplicity, we can assume the state transition matrix is an identity matrix and the difference can be modeled as system noise having a zero-mean Gaussian distribution (13). In fact, the variance of this system noise can represent the degree of variation at each corresponding pixel as the absolute value of the image differences are generally larger in more dynamic areas and smaller in less dynamic areas.

Therefore, together with the 1D simplification, the Kalman filter model for real-time cardiac function imaging can be written as:

$$\begin{array}{l}{\underset{\_}{x}}_k={\underset{\_}{x}}_{k-1}+{\underset{\_}{w}}_{k-1},{\underset{\_}{w}}_k~N(\underset{\_}{0},Q_k)\\ {\underset{\_}{z}}_k=F_k{\underset{\_}{x}}_k+{\underset{\_}{v}}_k,{\underset{\_}{v}}_k~N(\underset{\_}{0},R_k)\end{array}$$ [3]

where x_k is simplified to be the image column vector assuming the row vector is along the readout direction for the 2D image, w_k is the system noise vector with covariance matrix Q_k, F_k is the 1D Fourier transform matrix, z_k is the corresponding k-space data column vector after the 1D Fourier transform along the readout direction, and v_k is the measurement noise with covariance matrix R_k. Given the initial estimate x̂₀ and the initial estimation error covariance matrix P₀, the subsequent estimation of x_k is given as:

$$\begin{array}{l}{\underset{\_}{\widehat{x}}}_k^{-}={\underset{\_}{\widehat{x}}}_{k-1}^{+}\\ {\underset{\_}{\widehat{x}}}_k^{+}={\underset{\_}{\widehat{x}}}_k^{-}+K_k[z_k-F_k{\underset{\_}{\widehat{x}}}_k^{-}]\\ P_k^{-}=P_{k-1}^{+}+Q_{k+1}\\ K_k=P_k^{-}{F_k}^T{[F_k{P}_k^{-}{F_k}^T+R_k]}^{-1}\\ P_k^{+}=[I-K_k{F}_k]P_k^{-}\end{array}$$ [4]

where P_k is the estimation error covariance matrix at each time step k and is a vital intermediate parameter to calculate the Kalman gain matrix K_k.

Parameter Estimation

From Equation [4] we can see that the parameters that need to be estimated include the system noise covariance matrix Q_k, the measurement noise covariance matrix R_k, the initial state estimate x̂₀ and the initial estimation error covariance matrix P₀.

First, we make an assumption that the distributions of the system noise vector w_k and the measurement noise vector v_k do not change during the scan, because the dynamic process (e.g., periodic cardiac motion) is stable from a statistical point of view. With this assumption, we have Q_k = Q and R_k = R. The estimation of Q and R are discussed below.

In Sümbül’s paper (13), as discussed before, Q was assumed to be a diagonal matrix to simplify the computation process. This assumption was also validated in the paper by determining that the cross-correlation terms of Q were very small, as shown in Fig. 1 of (13). The diagonal Q was then roughly estimated from a low spatial resolution training scan covering only the center of k-space or more precisely estimated from multiple training scans covering different portions of k-space in each scan.

In our model, the diagonal assumption of Q is not necessary from a computational point of view due to the 1D simplification; therefore, in theory it is possible to use a general covariance matrix Q in which the off-diagonal term can reflect the relationships among neighboring pixels to provide a better estimation of the image column vector x_k. However, in practice, it is difficult to estimate Q, since no prior information about the distribution of w_k is given and thus we must rely solely on the sample observations of w_k. From statistics, for an N-dimensional vector w_k, the number of observations should be much greater than N to provide a reliable estimate of its covariance matrix Q. For MRI, N is usually very large and hence the amount of training data needed would be even larger, which would result in an extremely long training scan. Furthermore, the error in the estimation of a general covariance matrix Q can sometimes cause divergence of the Kalman filter model. On the other hand, if we assume Q is a diagonal matrix and ignore the cross-correlation terms, the estimation of Q becomes a pixel-by-pixel problem; only the variance of w_k at each pixel needs to be estimated and the required sample observations can be greatly reduced. As compared with a potentially inaccurate general covariance matrix Q, a diagonal but more accurate Q is used in our model, and the accuracy of this simplification will be demonstrated in the simulation study described below.

To estimate the diagonal terms of Q, we use a low-resolution training scan that only acquires the center k-space lines. The fraction of the k-space lines acquired for the training is determined by the under sampling ratio in data acquisition so that the temporal resolution of the training images is the same as that of the actual images. Although the accuracy of the variance estimation can be impaired at sharp edges in the image with a low-resolution training scan due to blurring, we have found the error in pixel variance estimation to be acceptable, because the Kalman filter uses all previous measurements to arrive at the current estimate and thus exploits the overall redundancy of the k-space data.

An alternative way to estimate Q is to use multiple training scans to cover different parts of k-space, similar to the use of different spiral rings as introduced in (13). However, this requires multiple training scans and thus greatly increases the scan time. Furthermore, the effect of this more precise Q is not obvious in terms of the accuracy of the state vector estimate, which is our ultimate goal. Therefore, we prefer to use the low-resolution training scan to get Q. The accuracy of this approach will also be demonstrated in the simulation study described below.

In our estimation process, we use the differences between magnitude images rather than complex images to estimate the variance at each pixel. When using complex differences, differences in phase that result from off-resonance, motion or noise between consecutive training images can significantly increase the variance and thus make the estimate unreliable. This is especially true in regions where the image magnitude is small. The measurement noise can also affect the estimation of Q, but this can be corrected as described in the following paragraph.

To estimate R_k, we also use the diagonal and time-invariant assumptions, since the measurement noise can be regarded as independent white noise and does not change with time. Therefore, we have R_k =R = σ²I, where I is the identity matrix. It is necessary to mention that this noise is not the original 2D k-space measurement noise but the noise after a 1D Fourier transform along the readout direction; however, since the Fourier transform is an orthonormal transform, the whiteness of the noise is maintained. As discussed before, the estimation of Q is contaminated with measurement noise because the training data measurement is not noise-free and the noise is brought into the training images via the Fourier transform. Assuming the raw estimation of Q is given as Q_raw, we can derive that Q =Q _raw − 2cσ²I, where c is a constant determined by the normalization factor of the Fourier transform. To jointly correct for the contamination of measurement noise to get Q and estimate the noise level σ, we simply make the assumption that the minimum diagonal term of Q is close to zero, because there exists at least one pixel that stays almost the same during the dynamic process and consequently, the minimum diagonal term in Q_raw is due to the measurement noise. So we can get the estimate of σ and the corrected Q.

Finally, we need to initialize the model with the initial conditions of x̂₀ and its estimation error covariance matrix P₀. It is impossible to provide an accurate and alias-free initial image due to limited temporal and spatial resolution. The options are either the spatially-blurred image from the low-resolution training scan or the temporally-blurred image reconstructed using view sharing techniques. However, since the Kalman filter is a robust filter that can correct for the inaccuracy in the initial estimates with more and more measurements, the influence of the inaccuracy of the initial image will fade away; therefore, we choose an initial image with faster convergence. The performance of these two options are compared with the simulation study described in the following sections. Similarly, the inaccuracy in P₀ will also be corrected by the Kalman filter; therefore, we just empirically choose it to be Q multiplied by the undersampling ratio, because the estimation error of x̂₀ at one pixel is roughly proportional to the variance of that pixel and the undersampling factor.

Simplifications of the Kalman Filter Model

From Equation [4] we can see that the most time-consuming step is the calculation of the Kalman gain matrix K_k and the intermediate parameter P_k. However, as discussed before, the system noise covariance matrix Q and the measurement noise covariance matrix R are assumed to be time-invariant; therefore, the only matrix that changes from step to step involved in calculation of K_k and P_k is the measurement matrix F_k. If the k-space sampling pattern is periodic over the entire image series, the corresponding matrix F_k is also periodic. Because P₀ is a manually chosen parameter, the Kalman gain matrix K_k, as well as P_k, will gradually converge to a periodic steady state after several steps. After that, the update of K_k using Equation [4] can be replaced by using the pre-calculated periodic K_k. The reconstruction time can thus be greatly reduced. The convergence of K_k is demonstrated with the simulation study in the following sections.

In addition, as discussed before, we do not have to use the Kalman filter model for every phase encoding line. Each phase encoding line corresponds to one readout location after the 1D Fourier transform along the readout direction. If this phase encoding line is within a static or slowly-varying area, the simple view sharing methods are sufficient to reconstruct this line without aliasing, and thus the reconstruction time can be reduced. Instead of retrospectively selecting these areas, Q can provide this information, because in static or slowly varying areas the corresponding variance is very small compared to that in more dynamic areas. Specifically, we examine the variance vector Q_l that corresponds to each readout location and determine whether max(Q_l) < Q_mean/2, where Q_mean is the mean variance across the entire 2D image. If this is true, then we use a linearly interpolated view sharing method (SLAM) instead of the Kalman filter model. The effect of this simplification is examined in the simulation study below.

Multiple Coils

If multiple receiver coils are available, we can extend the Kalman filter model to incorporate the measurements from different coils by combining the Kalman filter with SENSE. If the coil sensitivity map is available, we can include the data from different coils, which results in the following model(13):

$$\begin{array}{ll}{\underset{\_}{x}}_k={\underset{\_}{x}}_{k-1}+{\underset{\_}{w}}_{k-1},\hfill & {\underset{\_}{w}}_k~N(\underset{\_}{0},Q_k)\hfill \\ \left[\begin{array}{c}{z}_{k1}\\ z_{k2}\\ ·\\ ·\\ z_{kn}\end{array}\right]=\left[\begin{array}{c}{F}_k{S}_{k1}\\ F_k{S}_{k2}\\ ·\\ ·\\ F_k{S}_{kn}\end{array}\right]{\underset{\_}{x}}_k+\left[\begin{array}{c}{v}_{k1}\\ v_{k2}\\ ·\\ ·\\ v_{kn}\end{array}\right],\hfill & {\underset{\_}{v}}_{ki}~N(\underset{\_}{0},R_{ki})\hfill \end{array}$$ [5]

where n is the number of receiver coils and S_kn is the coil sensitivity map. For generality, the coil sensitivity map is assumed to be time-variant, because in imaging during free breathing, the chest motion can cause the coil elements to move. To dynamically estimate the coil sensitivity map, we use the coil images reconstructed with view sharing techniques. Correct normalization of the coil sensitivity map is important to avoid divergence of the Kalman filter solution. The disadvantages of using this SENSE-based method include difficulty in accurately estimating the coil sensitivity map in dynamic imaging and greatly increased computation. The computation increases because the dimension of the measurement model is increased by n and the periodic property of the Kalman gain matrix K_k is lost, because the measurement matrix is no longer periodic due to non-periodic S_kn. Therefore, we also developed a method of combining the Kalman filter with GRAPPA to more effectively use the multi-coil measurements.

Compared with traditional GRAPPA, TGRAPPA is advantageous in dynamic cardiac imaging since no separate training step is required and the GRAPPA kernel is updated for every frame in the image series (16). In our model, first we use the updated GRAPPA kernel to fill all the missing k-space lines for each individual coil. We know that the filled k-space data is not accurate enough to generate an alias-free and high SNR image when the undersampling ratio is very high if we just do a Fourier transform and combine the coil images, as in TGRAPPA. However, we can still input this approximate k-space data into the modified Kalman filter model as follows:

$$\begin{array}{ll}{\underset{\_}{x}}_k={\underset{\_}{x}}_{k-1}+{\underset{\_}{w}}_{k-1},\hfill & {\underset{\_}{w}}_k~N(\underset{\_}{0},Q_k)\hfill \\ \left[\begin{array}{c}{\underset{\_}{z}}_k\\ {\underset{\_}{z}}_{k\_TG}\end{array}\right]=F{\underset{\_}{x}}_k+\left[\begin{array}{c}{\underset{\_}{v}}_k\\ {\underset{\_}{v}}_{k\_TG}\end{array}\right],\hfill & \left[\begin{array}{c}{\underset{\_}{v}}_k\\ {\underset{\_}{v}}_{k\_TG}\end{array}\right]~N(\underset{\_}{0},\left[\begin{array}{cc}{R}_k& 0\\ 0& R_{k\_TG}\end{array}\right])\hfill \end{array}$$ [6]

where z_k is the measured k-space data and z_{k _TG} is the unacquired k-space data estimated from z_k and the corresponding GRAPPA kernel; F, which replaces F_k in the original model, is now the fully sampled 1D Fourier transform matrix, since z_k and z_{k _TG} together cover all of k-space. It is worth mentioning that the measurement noise covariance matrix R_{k_TG} corresponding to z_{k _TG} is no longer determined by the actual k-space measurement noise since z_{k _TG} is not the measured k-space data. On the contrary, R_{k _TG} reflects the reliability of the filled k-space data using the GRAPPA kernel by considering the deviation of the filled k-space data from the “true” k-space data as noise. Similarly with R_k, for simplicity, R_{k _TG} is also assumed as white and time-invariant, given as R_{k _TG} = R_TG = p²σ²I, in which p describes the reliability of the filled data relative to the measurement noise. In fact, the off-diagonal terms of R_{k _TG} are not exactly zero as the missing k-space data points in one frame are generated using the same TGRAPPA kernel; the results might be more accurate with an approximate model to handle the noise related to TGRAPPA, but this is beyond the scope of this paper. Empirically, we have observed that p = 6r²/n, in which r is the undersampling ratio and n is the number of the coils. It is assumed that with a larger undersampling ratio, the standard deviation of the filled k-space data increases much faster and can be modeled with a square relationship. By this modified model, we can efficiently combine the spatial parallel information with the temporal model to give a better estimate of the dynamic image series. Also, with each coil, from Equation [4], the Kalman gain matrix K_k can still converge to save reconstruction time, since Q_k, R_k and R_{k_TG} are time-invariant and F is a constant.

METHODS

Simulations

To verify the basic concept of the Kalman filter model in dynamic MRI, we first did a numerical phantom study by constructing a dynamic image series containing three pairs of concentric circles with fixed radius, slowly oscillating radius and rapidly oscillating radius, respectively. To simulate the data acquisition process using a Cartesian trajectory, we calculated the instant image at a given time point and its Fourier transform and selected the corresponding k-space data of one phase encoding line assuming the actual measurement was done at that time point. The training data used for the Kalman filter model was simulated using the same method before the data acquisition. Then we reconstructed the simulated data set using sliding window, SLAM and the Kalman filter model with an acceleration factor of 2.

To study the effect of the Kalman filter model in reconstruction of undersampled data, we then conducted a series of more realistic simulations, where we reconstructed the image series after retrospectively throwing out a portion of the k-space data and then compared the reconstructed image series with the fully sampled data. The baseline image series were acquired using a balanced SSFP sequence in a real-time ungated cardiac MRI (CMR) study under both breath-hold and free-breathing situations. 2x TGRAPPA was used to increase the temporal resolution. A total of 80 frames covering approximately 9 heart cycles were generated. Then we did a Fourier transform for the baseline image series to get the fully sampled k-space data and manually undersampled that using a given sampling pattern with undersampling ratio 2 and/or 4. The training data for parameter estimation was also obtained from the fully-sampled k-space data of the first 40 frames by selecting the center ¼ of the k-space data.

To study the effect of Q in the Kalman filter model, in addition to the diagonalized Q estimated from the low-resolution training data, we also obtained a diagonalized Q and a non-diagonalized Q with fully-sampled training data in which no manual undersampling was performed. The performance of the Kalman filter model using these three Q s were compared by calculating the root mean square differences between the reconstructed image series and the baseline image series. Similarly, to study the effect of the initial image in the Kalman filter model, we used the spatially-blurred initial image and the temporally-blurred initial image and compared the root mean square differences.

In addition, to test the simplifications of the Kalman filter model, we implemented the original Kalman filter model without any simplifications, the Kalman filter model with the convergent simplification and the Kalman filter model with the convergent simplification and combined with SLAM. We compared their performances based on the root mean square differences.

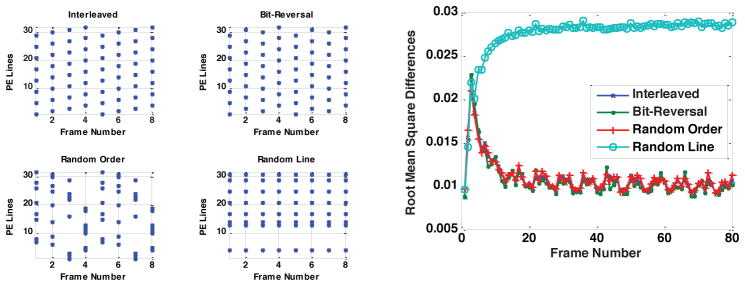
For these simulations, a periodic sampling pattern is required when evaluating the convergence of the Kalman filter. Therefore, we used four types of sampling patterns satisfying the periodic requirement and compared their performance. For types I–III, we first fixed the phase encoding line order for a fully-sampled data set and then select a subset of phase encodings corresponding to one frame based on the undersampling factor. The subsets selected for Type I were interleaved, those for type II were bit-reversed, and those for type III were random. For type IV, we generated a collection of random k-space lines based on the undersampling factor and repeated this collection for every frame.

Finally, to compare the Kalman filter method with other available real-time reconstruction methods represented by the view sharing techniques, we also implemented the sliding window method and SLAM. Furthermore, we used kt-FOCUSS as a representative of iterative reconstruction methods based on compressed sensing and compared it with the Kalman filter method with the same undersampling factor but a Gaussian random undersampling pattern. In addition to the root mean square differences between the reconstructed image series and the baseline image series, we also calculated the structural similarity index, which measures the similarity between two images based on human eye perception to better estimate the performance of each reconstruction method.

Experiments

The non-gated real-time cardiac imaging experiments were performed on a Siemens Avanto 1.5 T scanner (Erlangen, Germany) equipped with a 12-channel body coil array and a 32-channel body coil array. We used both coils in our experiments. A 2D Cartesian bSSFP sequence was used with sequence parameters as follows: TR = 2.14 ms, TE = 1.07 ms, FOV = 380–400 mm, slice thickness = 8 mm, flip angle = 46°, # PE lines = 128, # RO samples = 128, image matrix size = 128*128. A training scan of about 2.5 s was performed before the data acquisition to collect the center k-space lines. The total scan time was about 10 s. Both short axis and long axis views of the heart were imaged under breath held and free breathing conditions with acceleration factor 4. Array compression (20) was used for the primary coil data to simplify the calculation process for the large coil arrays. The data was then reconstructed using sliding window, SLAM, TGRAPPA, KF-SENSE and KF-TGRAPPA.

In order to independently assess the extent of spatial aliasing and to assess the image quality of rapid moving structures, two cardiologists (M.S. and C.M.K) graded the images for the severity of spatial aliasing and temporal blurring each on a 5-point scale. The ratings were then statistically analyzed with a two-tailed Wilcoxon test. For the spatial aliasing assessment a score of 1 corresponded to very severe aliasing precluding evaluation of myocardial function; 2 to severe aliasing but adequate to evaluate function; 3 to mild-moderate aliasing but not affecting region of interest; 4 to mild aliasing; and 5 to no aliasing. The perceived temporal blurring was graded as a score of 1 for virtually no temporal information; 2 for severe temporal blurring limiting ability to assess function; 3 for temporal blurring evident, but not affecting assessment of LV function; 4 for mild temporal blurring evident; and 5 for no temporal blurring. The image reviewers are both level III trained in CMR and have 6 and 20 years experience interpreting clinical CMR images.

A software implementation of the method is available at http://bme.virginia.edu/meyer/software/

RESULTS

Simulations

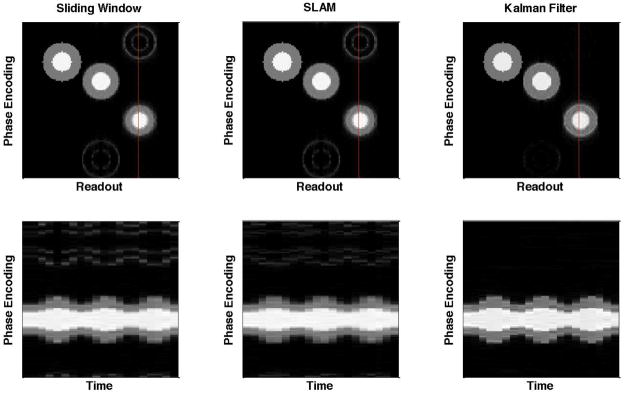
Figure 1 gives the results for the numerical phantom simulation in which the reconstructed images at one time point (top row) and the image intensities along one vertical line versus time (bottom row) using sliding window, SLAM and the Kalman filter model are shown. The three pairs of concentric circles, from left to right, are with fixed radius, slowly oscillating radius and rapidly oscillating radius, and the red lines indicate the image cross-section displayed in the bottom row. The ghost artifacts due to the change in radius are very obvious with the sliding window and SLAM methods, but are greatly reduced with the Kalman filter model. In addition, the temporal resolution with the Kalman filter is much higher than with the two view sharing methods, as can be seen in the images in the bottom row. Temporal blurring can be seen both by the smoothing of the peaks as a function of time and by spatial blurring vertically between the white center region (simulated left ventricle) and the gray outer region (simulated myocardium). This improved temporal resolution comes from the fact that the Kalman filter model can distinguish the more dynamic areas from the less dynamic areas and hence more effectively use the undersampled data to catch the movement in the more dynamic areas.

Figure 1.

Numerical phantom study. The reconstructed images (top row) and the image intensities along the red vertical line versus time (bottom row) using the sliding window, SLAM and Kalman filter methods. The three pairs of concentric circles are with fixed radius, slowly oscillating radius and rapidly oscillating radius (from left to right). The Kalman filter method substantially reduces aliasing and temporal blurring. The reduction in temporal blurring can be seen in the sharper temporal response and the reduced blurring of the boundaries between regions of the phantom.

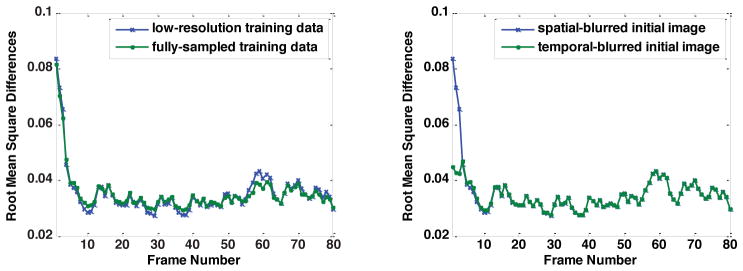
Figure 2 plots the root mean square differences between the reconstructed image series and the baseline image series using a diagonalized Q estimated from the low-resolution training data and from the fully-sampled training data (left) and using the spatially-blurred initial image and the temporally-blurred initial image. The reconstructed image series using a general Q estimated from the fully-sampled training data diverges, indicating the Kalman filter model fails with such an inaccurately estimated Q. The left side of Fig. 2 indicates that the result using the low-resolution training data is very similar to the fully-sampled training data or even performs better (lower root mean square differences) with certain frames. Therefore, this data indicates that it is unnecessary to use multiple scans for a more precise Q. The right side of Fig. 2 shows that the choice of initial image is not critical, because both initial images give the same results after approximately 10 frames. However, even though the root mean square differences are larger with the spatially blurred initial image in the beginning, they converge faster as the values drop faster compared with the temporal-blurred initial image. Therefore, we chose the spatially blurred initial image in our experiments.

Figure 2.

Root mean square differences of the Kalman filter model using different Q (left) and initial images (right).

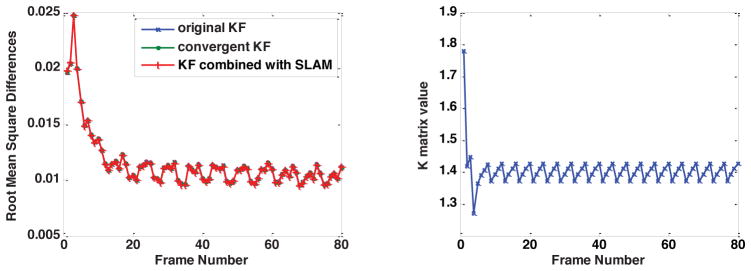
The left side of Fig. 3 shows the root mean square differences of the reconstructed image series and the baseline image series using the original Kalman filter model, the convergent Kalman filter model and the convergent Kalman filter model combined with SLAM. It indicates that the results using the original algorithm and the two simplified algorithms are almost identical, meaning the simplifications of the Kalman filter model do not harm the effectiveness of the model. The right side of Fig. 3 plots the value of K_k at a fixed location with the original Kalman filter model. The result conforms to our expectation as K_k approaches a periodic steady state with period 4, which is the undersampling ratio used in this simulation. Therefore, in practice we use the convergent Kalman filter model combined with SLAM to maximally reduce the reconstruction time.

Figure 3.

Left: Root mean square differences of the Kalman filter model using the original algorithm and the simplified algorithms. The simplified algorithms produce similar results. Right: Simulation demonstrating that K_k approaches a periodic steady state.

Figure 4 plots the 4 types of sampling patterns (left) and the resulting root mean square differences using these sampling patterns. There are no apparent differences among the first three types of the sampling patterns in terms of root mean square differences and they all perform better than the fourth type of the sampling pattern. This shows that a sampling pattern that covers the entire k-space in several frames is preferred. This is because the Kalman filter relies on all previous measurements to give an optimal estimate of the current state, so acquiring all of k-space provides comprehensive information to better estimate the current image, even though the k-space acquisition is completed over several frames.

Figure 4.

Root mean square differences of the Kalman filter model using different sampling patterns. The three sampling patterns that cover all of k-space in several frames result in similar error levels, and they each have substantially lower error than a random sampling pattern.

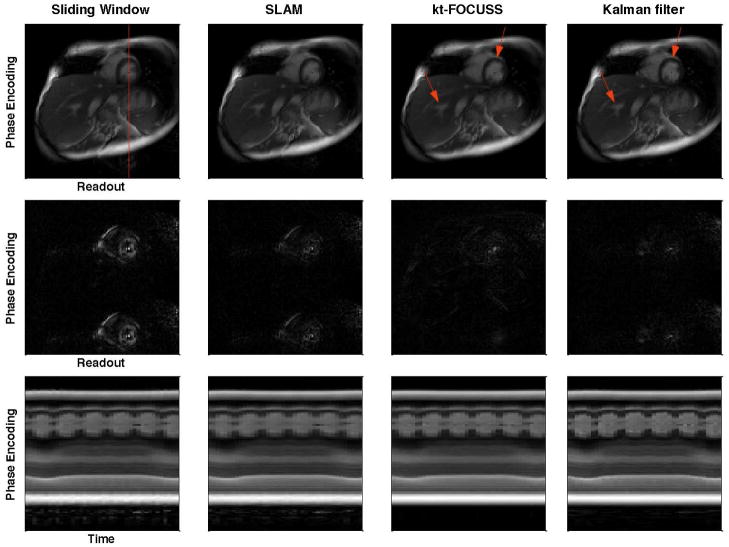
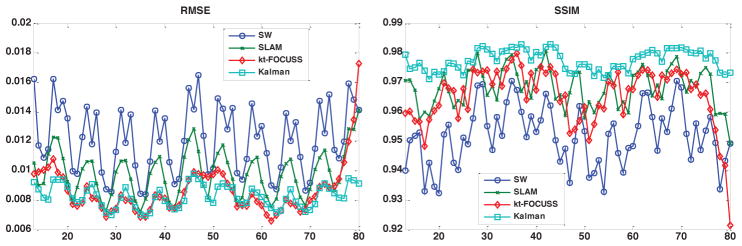
Figure 5 shows example images reconstructed using the sliding window, SLAM, kt-FOCUSS and the Kalman filter with undersampling ratio of 2 (top row), the corresponding difference images with the raw image (middle row) and the image intensities of one phase encoding line as indicated in the top left image across the entire image series (bottom row) in a single-coil simulation study with a free breathing short axis image series. The ghost artifacts due to motion are obvious in the sliding window and SLAM methods and are greatly alleviated with Kalman filter method. The aliasing pattern with kt-FOCUSS is different from the other methods due to the non-linearity of the reconstruction. In addition, some blurring occurs in free-breathing situations as illustrated by the arrows in Fig. 5. The images along the bottom row show that the Kalman filter provides the highest temporal resolution as the changes of the left ventricle radius are the sharpest. Figure 6 shows a plot of the root mean square error (RMSE) and the structural similarity index (SSIM) between the reconstructed image series and the raw image series in the same simulation study. The Kalman filter provides a lower RMSE and a higher SSIM compared with sliding window (SW) and SLAM in most of our simulation studies with undersampling ratios of 2 and 4, including the study shown in Fig. 5. As shown in Fig. 6, the decrease of RMSE and increase of SSIM are more obvious in frames when the cardiac motion is very fast, such as the end-systolic phase of the cardiac cycle. Comparing the Kalman filter with kt-FOCUSS, kt-FOCUSS yielded the lowest RMSE with most breath-held simulations; however, with free-breathing simulations, kt-FOCUSS sometimes had higher RMSE than the Kalman filter method.

Figure 5.

Images reconstructed using sliding window, SLAM, kt-FOCUSS and Kalman filter methods with undersampling factor of 2 (top row), the corresponding difference images with the raw image (middle row) and the image intensities along the red vertical line (top left image) as a function of time (bottom row). Aliasing and temporal blurring are lowest for the Kalman filter method.

Figure 6.

RMSE(left) and SSIM(right) between the reconstructed image series and the raw image series.

Experiments

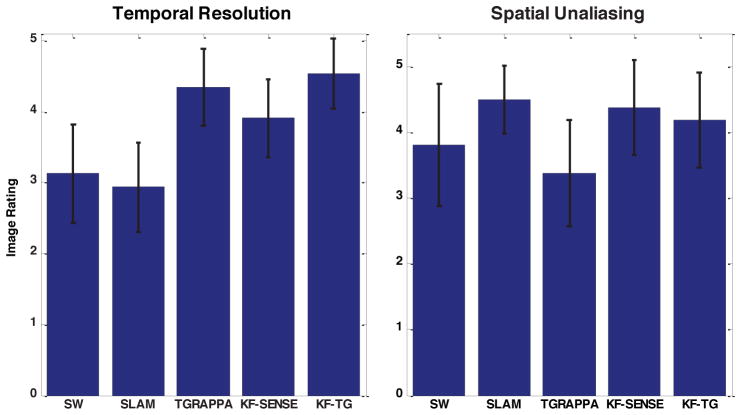
Figure 7 shows the results of the blind review for a total of 8 experiments including 4 short axis and 4 long axis experiments with acceleration factor 4. The visually assessed temporal resolution is improved with TGRAPPA, KF-SENSE and KF-TGRAPPA (KF-TG) compared with sliding window and SLAM and the improvement was statistically significant from the two-tailed Wilcoxon signed rank test (p<0.05 for SW vs. KF-SENSE, SW vs. KF-TG, SLAM vs. KF-SENSE, SLAM vs. KF-TG). For the degree of spatial aliasing, the ratings of KF-SENSE and KF-TGRAPPA were not statistically different from sliding window and SLAM, although KF-SENSE and SLAM were slightly better than SW and KF-TG. Comparing KF-TGRAPPA with TGRAPPA, there was significant reduction in spatial aliasing (p<0.05) and slightly better temporal resolution.

Figure 7.

Temporal resolution and spatial unaliasing ratings by two blinded expert readers.

DISCUSSION

We have developed a Kalman-filter-based image reconstruction method for real-time reconstruction of Cartesian dynamic image series and implemented it in a real-time CMR study. We combined the model with SENSE and TGRAPPA. The major advantages of this method include the capability for non-iterative real-time reconstruction and significantly improved temporal resolution. The capability for non-iterative real-time reconstruction lies in the fact that as long as the model is established, the Kalman filter can generate an optimal estimate of the current state given all previous measurements with a single prediction-correction process without iteration. The reconstruction in this study was performed offline using Matlab and has not yet been implemented on the scanner’s reconstruction computer. However, the computational load is relatively small and can be realized with moderate computing hardware. The offline reconstruction time for an entire image series (80 frames, 128*128) is about 4 seconds in Matlab using a laptop with a 2.2 Ghz CPU and without parallel computing. This corresponds to a computation time of 50 ms per temporal frame. Furthermore, as discussed previously, if the sampling pattern is periodic, the major computation, which is the calculation of the Kalman gain matrix K_k, can be performed before the data acquisition and thus the subsequent reconstruction requires only two matrix-vector multiplications and one vector-vector addition per readout pixel. In addition, the algorithm is easily parallelizable, because each readout pixel can be treated independently; thus, parallel computing can be easily implemented to reduce the reconstruction time.

The improvement in temporal resolution with this method is because the Kalman filter can capture rapid changes with limited measurements. For example, if the k-space measurements are under-sampled, the information is not enough to get an accurate current estimate from just that data; however, the relationship between the current and the past states represented by the state model can be exploited to benefit the current estimate. In this study, the pixels with lower variance rely more on past states by the prediction step; the pixels with larger variance rely more on the measurements by the correction step. Therefore, since the number of pixels with large variance is much smaller than the total number of pixels, the information contained in the k-space measurements is sufficient to provide an accurate current estimate.

Although in this paper we focused on the real-time cardiac study, this model is not limited to this application. In this application, we make a simple assumption to just copy the previous state to get the current state. For other applications, the model might need some modifications if we can get some information about the evolvement of the states. However, the framework to simplify the 2D problem to a 1D problem makes it easier to modify and implement a more complicated model such as the APMA model to more accurately describe the relationships among the states.

The combination with parallel imaging techniques can further reduce scan time and improve image quality, as demonstrated by KF-SENSE and KF-TGRAPPA. Both are suitable for real-time reconstruction, although KF-SENSE is more computationally demanding, resulting in longer image reconstruction times. The coil sensitivity estimation in KF-SENSE can be further explored to improve image quality. For KF-TGRAPPA, the error covariance of the filled k-space data in this paper is not an optimal choice but simply an empirical one. Therefore, further research is necessary to reduce the spatial aliasing by tuning this parameter.

Upon visual analysis, the improvement in temporal resolution is obvious with the Kalman filter; however, the cardiologists who scored the images were not bothered by some aliasing artifacts that were apparent in difference images in the simulation study, because they mainly focused on the cardiac region and the aliasing was relatively small in that region. There are some flickering artifacts with the Kalman filter model that lead to a lower rating in spatial unalising. Further study is needed to provide a more comprehensive understanding of the advantages and disadvantages of the Kalman filter model.

In conclusion, the Kalman filter method is a novel real-time reconstruction method in dynamic MRI that can improve the temporal resolution. The potential for real-time reconstruction may be valuable compared with retrospective and/or iterative reconstruction methods. The versatility of the model is also an advantage and is a promising topic for future study.

APPENDIX

Derivation of Q =Q_raw − 2cσ²I

The k-space data from the training scan z_t is contaminated with measurement noise n_t given as z_t =s_t + n_t and the covariance matrix Q_raw is estimated from the differences of two consecutive images i_i+1 − i_t in which i_t = F⁻¹ z_t+1. Therefore, we have

$$\begin{array}{l}{Q}_{\mathit{raw}}=\mathit{mean}[{(F^{-1}{z}_{t+1}-F^{-1}{z}_t)}^T(F^{-1}{z}_{t+1}-F^{-1}{z}_t)]\\ =\mathit{mean}[{(F^{-1}{s}_{t+1}-F^{-1}{s}_t)}^T(F^{-1}{s}_{t+1}-F^{-1}{s}_t)]+\mathit{mean}[{(s_{t+1}-s_t)}^T{(F^{-1})}^T{F}^{-1}(n_{t+1}-n_t)]+\mathit{mean}[{(n_{t+1}-n_t)}^T{(F^{-1})}^T{F}^{-1}(s_{t+1}-s_t)]+\mathit{mean}[{(F^{-1}{n}_{t+1}-F^{-1}{n}_t)}^T(F^{-1}{n}_{t+1}-F^{-1}{n}_t)]\\ =Q+\mathit{mean}[{(n_{t+1})}^T{(F^{-1})}^T{F}^{-1}{n}_{t+1}]+\mathit{mean}[{(n_t)}^T{(F^{-1})}^T{F}^{-1}{n}_t]\\ =Q+2c{\sigma }^{2}I\end{array}$$

in which the mean of the cross terms between s_t+1 − s_t and n_t+1 − n_t is zero due to the whiteness of the noise and c is a constant determined by the normalization factor of the Fourier transform matrix F.