The reaction mechanism of the enantioselective Tsuji allylation: inner-sphere and outer-sphere pathways, internal rearrangements, and asymmetric C–C bond formation

Abstract

We use first principles quantum mechanics (density functional theory) to report a detailed reaction mechanism of the asymmetric Tsuji allylation involving prochiral nucleophiles and non-prochiral allyl fragments, which is consistent with experimental findings. The observed enantioselectivity is best explained with an inner-sphere mechanism involving the formation of a 5-coordinate Pd species that undergoes a ligand rearrangement, which is selective with regard to the prochiral faces of the intermediate enolate. Subsequent reductive elimination generates the product and a Pd⁰ complex. The reductive elimination occurs via an unconventional seven-centered transition state that contrasts dramatically with the standard three-centered C–C reductive elimination mechanism. Although limitations in the present theory prevent the conclusive identification of the enantioselective step, we note that three different computational schemes using different levels of theory all find that inner-sphere pathways are lower in energy than outer-sphere pathways. This result qualitatively contrasts with established allylation reaction mechanisms involving prochiral nucleophiles and prochiral allyl fragments. Energetic profiles of all reaction pathways are presented in detail.

Introduction

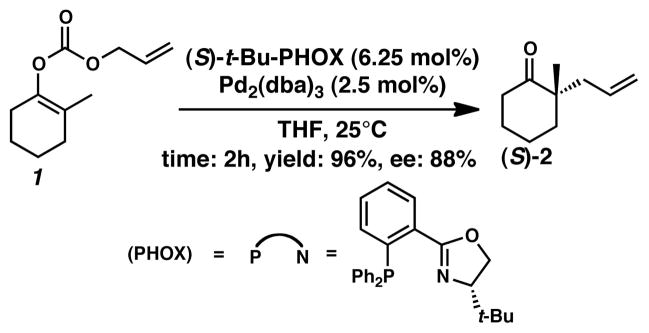
The importance of homogenous asymmetric catalysis increases as the world’s need for efficient access to enantioenriched molecules increases.^1–4 In particular, the synthesis of compounds containing enantioenriched quaternary stereocenters by catalytic methods remains a challenging problem. We recently reported a several related methods to prepare quaternary stereocenters of high ee^5–8 based on an enantioselective version of the Tsuji decarboxylation allylation reaction (Scheme 1).⁹ In a representative case, allyl enol carbonate 1 undergoes oxidative addition with a Pd⁰ complex and decarboxylation. (For a recent review on decarboxylative allylic alkylations and their asymmetric variants, see ref. 10.) The resulting Pd^II π-allyl complex then reacts with the in situ generated enolate forming α-allylated ketone 2. Before our work, the majority of asymmetric enolate allylations focused on reactions of prochiral allyl fragments with malonate nucleophiles,^11–13 or on prochiral ketones that had a single α-site or whose α-sites had large differences in acidity (e.g., Trost^12,14–17). Related to our work, Helmchen¹⁸ and Pfaltz⁴ also used malonates with similar catalyst ligands as we employed.

Scheme 1.

The enantioselective Tsuji allylation

Mechanistic studies of these prior asymmetric processes involving more stabilized enolates have established that they proceed via outer-sphere nucleophilic attacks.¹⁹ In more recent work, Trost has shown evidence that reactions of unstabilized enolates catalyzed by his bisphosphine ligands may proceed by either outer-sphere or inner-sphere mechanisms.^20–23 Lloyd-Jones and Norrby have suggested that hydrogen bonding interactions between the enolate and ligand backbone in Trost’s systems can lead to a subtle distinction where an inner-sphere reaction occurs with respect to the complex itself but not with respect to the metal center.²⁴ Insightful mechanistic studies investigating other allylation mechanisms must explicitly consider the feasibility of different modes of nucleophilic attack. Harder and more basic nucleophiles are known to attack at the metal center before C–C bond formation occurs in a number of processes.^25–29 A collaboration between our groups determined that the reaction we reported likely reacts via an inner-sphere mechanism that terminates with a non-traditional reductive elimination.³⁰ The present work reports considerably more detail on this mechanism.

Our original experimental study reported the formation of asymmetric quaternary stereocenters from unstabilized prochiral ketone enolate nucleophiles and allyl electrophiles.⁵ The 2-allyl-2-alkyl cyclohexanone products formed are distinct from the vast majority of asymmetric allylic alkylation products. In contrast to previous works that utilized prochiral electrophiles,^{4,9,12,14–16,18,19,31–35} we demonstrated enantioselective Tsuji allylation using non-prochiral electrophiles and prochiral ketone enolate nucleophiles. This permits the formation of quaternary centers from ketone enolates that have two similarly acidic sites alpha to the ketone. These desirable products are formed in high yields and high enantioselectivities. This process has found successful application in the total synthesis of many natural products to date,^36–45 as well as in the development of related enantioselective decarboxylative protonation^46,47 and sequential conjugate addition allylation reactions.⁴⁸ The standard ligand used in these transformations is (S)-t-Bu-phosphinooxazoline (PHOX)^49,50 (Scheme 1), which provided variants of ketone 2 with yields from 80 to 99% and ee’s ranging from 79 to 92%. Although this level of enantioselectivity is useful for many applications, ee’s consistently above 95% would make the process more appealing in industrial setting, and so we sought to understand the fine details of the reaction’s mechanism.

Well-established stereochemical probes involving cyclohexenyl electrophiles^26,27 were employed in attempts to determine the reaction mechanism. However, the extremely low yields, dr’s, and ee’s observed in all such attempts indicated that these cyclic substrates with our catalyst likely proceed by a substantially different mechanism from our standard high ee substrates. Extensive efforts to develop other experimental tests to elucidate this mechanism were not successful, thus we turned to quantum chemistry simulations to investigate the details of the mechanism.

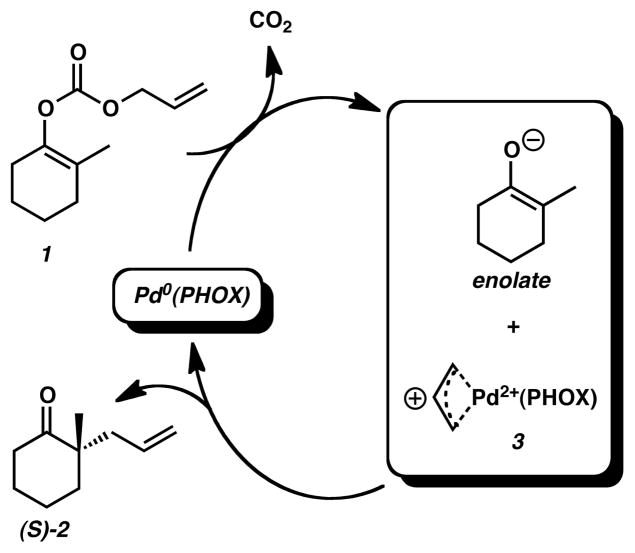
The observation that this reaction is effective using enol carbonates, silyl enol ethers, and π-keto allyl esters^5,6,51 indicated to us that they likely share a common intermediate. Because most substrates performed equally well in polar solvents such as THF and non-polar solvents such as benzene, the reaction mechanism appeared not strongly dependant on electrostatic solvation effects. However, we did find that a low solvent dielectric (in the 2–8 range) was important for obtaining high levels of enantioselectivity. Similar to other examples in the literature,^52–54 we obtained an X-ray crystal structure of a Pd(allyl)⁺PF₆⁻ complex, 3 (see Fig. 1), and found that it was a competent catalyst for reactions of silyl enol ethers, suggesting that it is an intermediate in the reaction. Two experiments within our group³⁰ suggested the reaction involved only one Pd(PHOX) complex: (1) experiments varying the ee of the catalyst from 0 to 100% showed no non-linear effects in the ee of the product formed, and (2) simple kinetic studies showed that the reaction was roughly zero-order in Pd(PHOX) and starting material.

Figure 1.

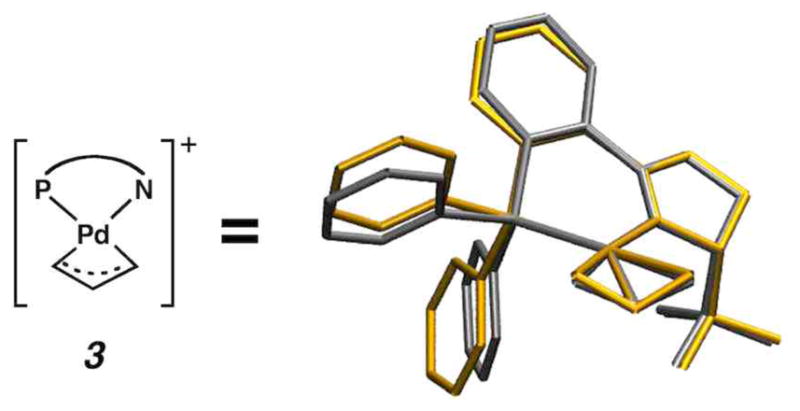
Superimposed calculated (yellow) and experimentally obtained solid-state (silver) structure for π-allyl complex 3. The experimental crystal structure was obtained using PF₆⁻ as the counter ion.

Given the current understanding of the Tsuji allylation mechanism and the information stated above, we investigated the enantioselective Tsuji allylation mechanism using first principles quantum mechanics including effects of solvation (in this study, the reaction was modeled in THF). Given the complexity of this mechanism, we focused on the steps following decarboxylation that begin with the association of the enolate and π-allyl complex 3 and report the reaction pathways leading to the enantioenriched product (S)-2. We also focused calculations using only the PHOX ligand. Our calculations identify an inner-sphere mechanism consistent with current experimental observations and shed light on the enantiodetermining step for this reaction. A key component to this mechanism is a pericyclic reductive rearrangement process that is distinct from the traditional three-centered process seen commonly in other C–C bond forming reactions mentioned previously. Based on the mechanism and the electronic structures of the intermediates and transition states, we suggest strategies for optimizing the catalyst and the reaction conditions for the process (Scheme 2).

Scheme 2.

The portion of the reaction mechanism studied in this work.

Computational Methods

Density functional theory (DFT) energy calculations, geometry optimizations, and vibrational frequencies were run using Jaguar version 7.0.⁵⁵ Reduced model systems for the PHOX backbone did not adequately describe steric effects, so all calculations involved the full PHOX ligand. Molecular geometries were obtained with the B3LYP hybrid exchange correlation functional,⁵⁶ which uses the Becke generalized gradient approximation⁵⁷ (GGA) in conjunction with a component of exact Hartree-Fock exchange (hybrid DFT) with the Lee, Yang, and Parr correlation functional.⁵⁸ This approach has been shown quite effective in elucidating important aspects of organometallic reaction mechanisms.^59–62

Preliminary geometry optimizations were run with a mixed-basis set approach, henceforth denoted as BS1. In this method, the Pd LACVP electronic core potential^63,64 (ECP) including 18 explicit electrons was used; the 6-31G* basis set was used on N, P, and the six atoms in the allyl- and enol- fragments; the MIDI! basis set⁶⁵ was used on all other atoms. Vibrational frequencies and their thermodynamic contributions from B3LYP/BS1 were negligibly different from values obtained using the same ECP and with the 6-31G** basis set on all other atoms (henceforth denoted as BS2). We report B3LYP/BS2 geometries.

The correct number of imaginary frequencies confirmed all stationary points. Starting from an optimized transition state, geometry optimizations starting from positions nudged along the imaginary vibrational mode confirmed that the transition states correctly linked stable intermediates along a mechanistic pathway. Thermodynamic energies were added to estimate the free energies and enthalpies at reaction temperature by calculating vibrational frequencies for all intermediates and transition states. Only the vibrational partition function was included for these energies to avoid uncertainties involving translations and rotations for species in aqueous solution. To eschew inconsistent thermal energies due to spuriously low vibrational frequencies, zero-point and thermal energies were calculated after substituting all vibrational frequencies < 50 cm⁻¹ with values of 50 cm⁻¹.

Single point energy calculations of triple-zeta quality (LACV3P, a decontracted version of LACVP, on Pd with 6-311G**++ on all other atoms, henceforth denoted as BS3) were calculated and compared to other single-point energies from the hybrid mPW1PW91⁶⁶ exchange correlation functional. Calculations include electronic relaxations due to THF solvation (basis set = (LACV3P**, 6-311G**), probe radius = 2.527Å, ε = 7.52) from single-point self-consistent Poisson-Boltzmann implicit solvation calculations.^67,68 Unless explicitly noted, all reported energies in the text are ΔG₂₉₈ values from B3LYP/BS3//B3LYP/BS2 calculations including solvation corrections. Lastly, single-point dispersion corrections intended to correct deficiencies in B3LYP when calculating non-bonding interactions were included with single point energy corrections using Grimme’s DFT-D3 method⁶⁹ as calculated with GAMESS-US.^70–72 Overall, assuming the appropriate physics of the chemical reactions is being modeled correctly, our calculations should be accurate to experiment within 2—3 kcal/mol for thermodynamic energies and 2—5 kcal/mol for barrier heights. Differences in barrier heights (which benefit from error cancellation) can be considered to be more accurate (to 1–2 kcal/mol). Molecular illustrations were made from VMD.⁷³

Results and Discussion

We calculate the reaction thermodynamics for enol-allyl carbonate 1 converting to (S)-2-allyl-2-methyl cyclohexanone, (S)-2, is exoergic by ΔG₂₉₈ = −36.6 kcal/mol in gas phase and −34.9 kcal/mol in THF. Of this energy, −15.2 kcal/mol comes from releasing CO₂. Experimental thermochemical reaction data is not available, however the gas phase value corresponds well with those calculated from additivity tables (−35 kcal).⁷⁴

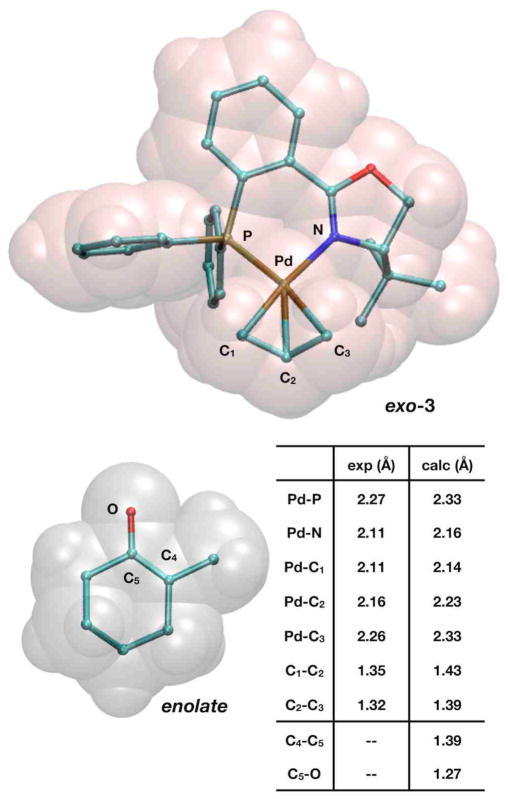
The experimental isolation of p-allyl complex 3·PF₆ (Figure 1) and its demonstration as a competent catalyst motivated us to start our mechanistic investigation at the point of an ion pair involving the cationic p-allyl intermediate and the enolate, 3·enolate. The crystal structure of 3·PF₆ contained a superposition of two conformers, exo-3 and endo-3, which we label according to Helmchen’s conventional notation specifying the orientation its allyl fragment with respect to the metal-center plane. The isolated product contained nearly equal amounts of endo-(49%) and exo-(51%) conformations, indicating both structures have essentially the same energy. The C-C-C angle of the allyl fragment (136.6°) in the crystal structure, however, is quite large and is most likely due to unresolvable superpositioning of the two structures. Our calculations on exo-3 and endo-3 calculations differ in energy by only 0.2 kcal/mol (ΔG₂₉₈ (exo-3) > ΔG₂₉₈ (endo-3)). As shown in Figure 1, the predicted structure is in very good agreement with experiment, non-CH bond distances have an RMSD of 0.03Å and bond angles are accurate within 2.1°. The error in bond angles reduces to 1.3° when omitting the C-C-C angle of the allyl fragment (calculated = 119.4°). Furthermore, the deviations due to phenyl groups projecting in different positions (Figure 1) are largely corrected when geometry optimizations take into account non-bonding interactions due to dispersion.⁷⁵ Despite the improved agreement in the calculated geometry with the crystal structure, the near-equivalent energies of exo-3 and endo-3 remain the same. Figure 2 displays interatomic bond distances for both exo-3 and then enolate molecule.

Figure 2.

Structural representations of exo-3 (a Pd²⁺ complex) and the enolate molecule and a table displaying relevant interatomic distances.

External nucleophilic attack product formation reactions

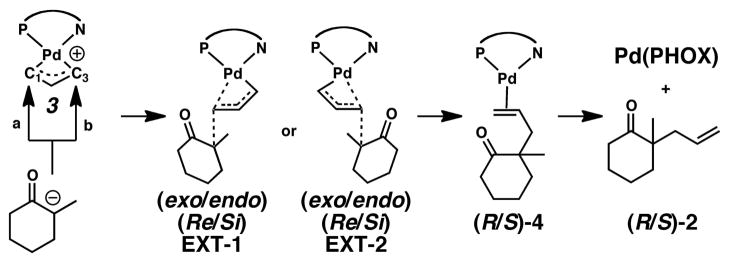
Note that throughout the text, figures, and schemes, we use the labeling notation of Prelog and Seebach,⁷⁶ where ‘Re’ denotes a pathway leading to an ‘R’ stereocenter, while ‘Si’ denotes a pathway leading to an ‘S’ stereocenter. As mentioned in the introduction, asymmetric allylation reactions using PHOX ligands are usually considered to proceed by an external nucleophilic attack as in Scheme 3. Here, the enolate can couple to intermediates (endo/exo)-3 producing the Pd⁰-bound complexes (R/S)-4, thereby forming products (R/S)-2.

Scheme 3.

Outer-sphere external nucleophilic attack processes considered in this work.

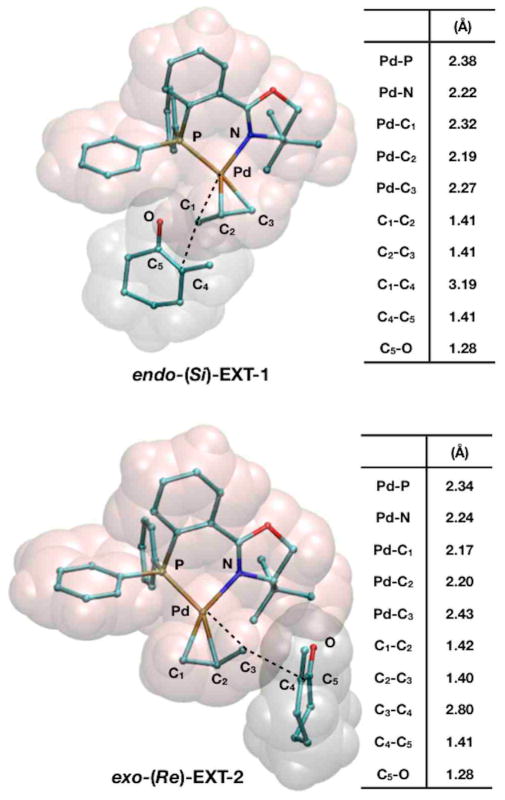
The allyl-coordinated complexes (endo/exo)-3 have two reactive carbons (C₁ or C₃) that may undergo nucleophilic attack. Attack at these carbons would result in one of eight different transition states: (endo/exo)-(Re/Si)-EXT-(1/2), and each would eventually form products (R/S)-2. The trans influence of phosphine leads to a longer Pd-C₃ bond than that for Pd-C₁. One might then expect that reactions trans to phosphine would be favored, calculated results indicate nucleophilic attacks at either C₁ or C₃ are almost equally favored. After identifying 6 of 8 of these transition states we found all have barriers within 1.3 kcal/mol with respect to each other, the two lowest transition states for their respective asymmetric products were endo-(Si)-EXT-1 and exo-(Re)-EXT-2. These transition states are only 0.7 kcal/mol different in energy, and are thus well within the accuracy of the computational methods employed.

Figure 3 shows structural details of the two lowest energy outer-sphere transition states, endo-(Si)-EXT-1 and exo-(Re)-EXT-2. Note that despite the differing modes of nucleophilic attack, both have similar energies and interatomic bond distances. All other non-reacting bonds remain essentially constant with respect to those in exo-3, though Pd–P and Pd–N bonds increase slightly now that the Pd^II center is undergoing a reduction to Pd⁰. The reacting bonds have intermediate bond lengths, where the breaking Pd–C bonds (R = 2.32Å and 2.43Å) are similar while the forming C–C bonds (R = 3.19Å and 2.80Å) are different due to the steric hindrance of the triphenylphosphine group when the enolate approaches trans to the nitrogen atom of the PHOX ligand.

Figure 3.

Representations of external nucleophilic transition states endo-(Si)-EXT-1 and exo-(Re)-EXT-2 and tables displaying relevant interatomic distances.

Endo-(Si)-EXT-1 and exo-(Re)-EXT-2 have barriers of 20.2 and 20.9 kcal/mol, respectively, with respect to the separated ion pair: exo-3 + enolate. Across all six characterized transition states, the barriers range from 20.2–21.5 kcal/mol. Control calculations using mPW1PW91 electronic energies result in slightly higher barriers ranging from 20.3–22.2 kcal/mol, but this shows the barriers are not simply an artifact of the B3LYP exchange correlation functional. Based on the proximity of the two electron-rich molecular fragments, we considered the possibility that non-bonding interactions would play a significant role in determining these overall barriers. Indeed, the non-bonding interactions due to dispersion lead to a dramatic reduction in these barriers so that they now range from 10.9–13.1 kcal/mol. This nearly 50% reduction in the activation barriers highlights the importance of dispersion in alkylation reaction mechanisms, though we note that the overall accuracy of dispersion-corrected DFT is not well-established for cases of asymmetric alkylation such as this.

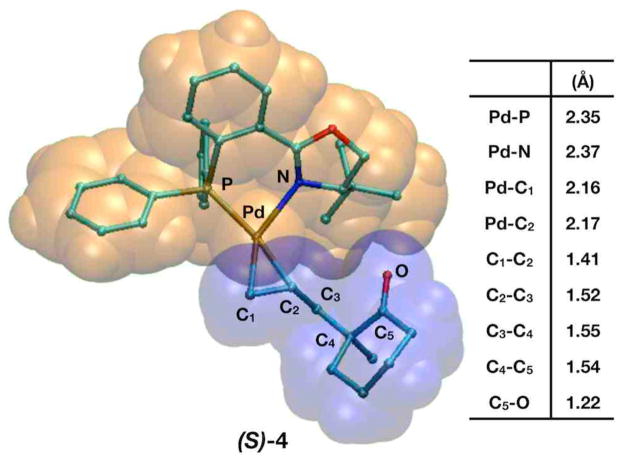
The experimental observation that (S)-2 predominates suggests the direct product of allylation should be the Pd•olefin complex (S)-4, whose geometry is presented in Figure 4. In this structure, the five carbons atoms C₁–C₅ and the carbonyl oxygen are connected sequentially and their bond lengths indicate a double bond between C₁ and C₂ (R = 1.40Å), three single bonds (R = 1.52–1.55Å), and a C–O double bond (R = 1.22Å) that is shorter than the C–O bond encountered in the enolate or the external nucleophilic transition states (R = ~1.28Å) now that the enolate fragment has an overall neutral charge. While the Pd–P bond length has remained largely constant throughout the mechanistic steps studied so far (R = 2.35Å), the Pd–N bond has lengthened (R = 2.40Å) now that the metal center has been reduced to Pd⁰ and in gas phase structure prefers linear coordination with phosphorus and the η-2 coordinated product.

Figure 4.

Representations of (S)-4 (a Pd⁰ complex) and a table consisting of relevant interatomic distances.

The overall energy of (S)-4 is −13.4 kcal/mol with respect to the solvated exo-3 and enolate species. Control calculations with mPW1PW91 find this structure is slightly more strongly bound (ΔG₂₉₈ = −17.6 kcal/mol) and the single point dispersion correction makes the overall energy approximately ~7 kcal/mol more exothermic (ΔG₂₉₈ = −20.9 kcal/mol). The η-2 bond strength in (S)-4 is challenging to ascertain since it is dependent on the calculation method employed. B3LYP calculations in solvent suggest it is only 2.8 kcal/mol, while control calculations with mPW1PW91 find it notably higher (8.7 kcal/mol). The difference between the B3LYP and mPW1PW91 calculations displays a significant degree of uncertainty comparing energies of Pd²⁺ and Pd⁰ complexes with different exchange correlation functionals. The single point dispersion correction to the B3LYP energy shows a substantially stronger η-2 bond (11.8 kcal/mol), suggesting dispersion forces play a significant role keeping Pd⁰ coordinatively saturated. Regardless of the methodology used in its energy calculation, (S)-4 is always the lowest energy intermediate on the reaction coordinate.

Inner-sphere rearrangements

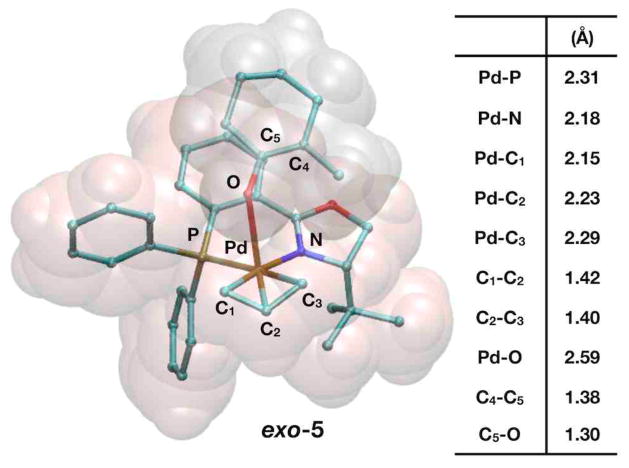
Up to this point, the reaction pathway for the enantioselective Tsuji allylation is unclear because none of the calculated external nucleophilic attack pathways can explain the experimentally observed ee’s. To investigate further, we sought pathways forming intermediates where C–C bond formation can easily occur and may be influenced by the stereocenter on the PHOX ligand. We considered the feasibility of a 5-coordinate complex resulting from the enolate binding to p-allyl complex exo-3 at an axial position. The structure for this complex is shown in Figure 5.

Figure 5.

Representations of 5-coordinate exo-5 (a Pd²⁺ complex) and a table displaying relevant interatomic distances.

We found several orientations that allow the enolate to bond axially with the exo-3 complex. The most stable intermediate, exo-5, has the enolate nestled within the PHOX ligand and anchored to the Pd with a longer than average bond length of 2.59Å. The longer bond length is characteristic of ligands axially coordinated to d⁸ transition metals. This Pd–O bond has little influence on the bonding of either the exo-3 fragment or the enolate as seen in a comparison of bond lengths with those in Figure 2. Other structures also had the enolate axially bound to Pd, but require the enolate to have less favorable steric interactions with the PHOX ligand. When the enolate is bound to endo-3, the energy of the structure is ~4 kcal/mol higher than when it is bound to exo-3. Thus, while exo-3 and endo-3 have effectively the same energy, axial coordination favors the exo form.

As with the energy of (S)-4, the energy of the Pd–O bond is highly dependant on the calculation scheme. Because exo-3 is a cation and the enolate is an anion, the separated ionic species are very unstable in vacuum, and bringing both species together results in an electronic energy gain of −72.9 kcal/mol. If zero point energies, thermal corrections, and entropic energy are added, the free energy released when bringing the two species together is less negative, −56.5 kcal/mol. Because the allylation reaction occurs in solution, the energy to form exo-5 should be referenced to the free energies in solution of the separately solvated exo-3 and enolate species. Under this model, solvated exo-5 is now unstable by +16.7 kcal/mol, though it is still ~3.5 kcal/mol lower in energy than the external attack transition states reported in the previous section. Control calculations with mPW1PW91 provide a value that is slightly less unstable, +14.0 kcal/mol. Finally, adding single point dispersion corrections to energies of solvated species causes exo-5 to be effectively isoenergetic (with exo-5 favored by merely −0.2 kcal/mol with respect to the solvated ions), and ~10 kcal/mol more stable than the external attack transition states. Note that in our previous communication on the Tsuji mechanism,³⁰ we reported only electronic energies with solvation corrections, while the present work shows that including the free energy penalty to form exo-5 essentially cancels out the energy gain captured by dispersion corrections, making exo-5 effectively isoenergetic with the separated ions in solution.

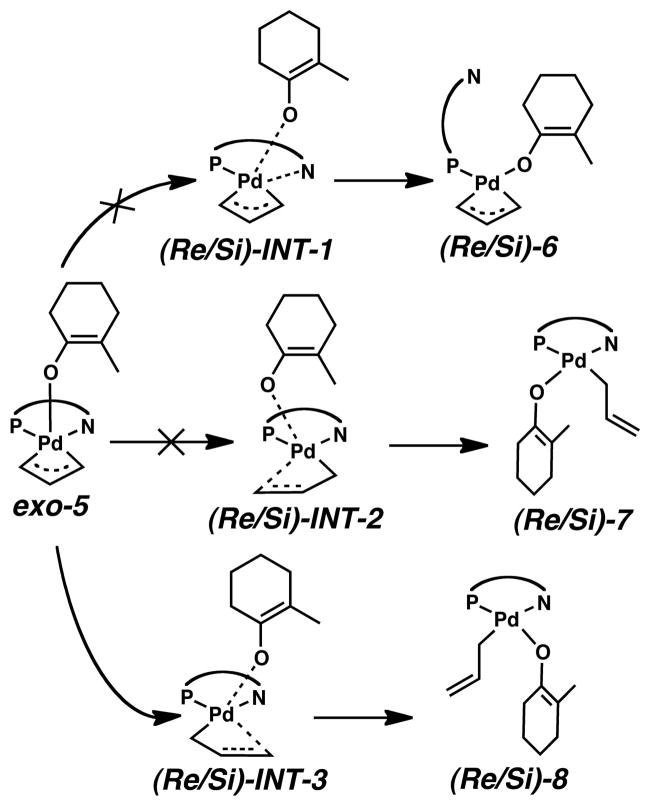
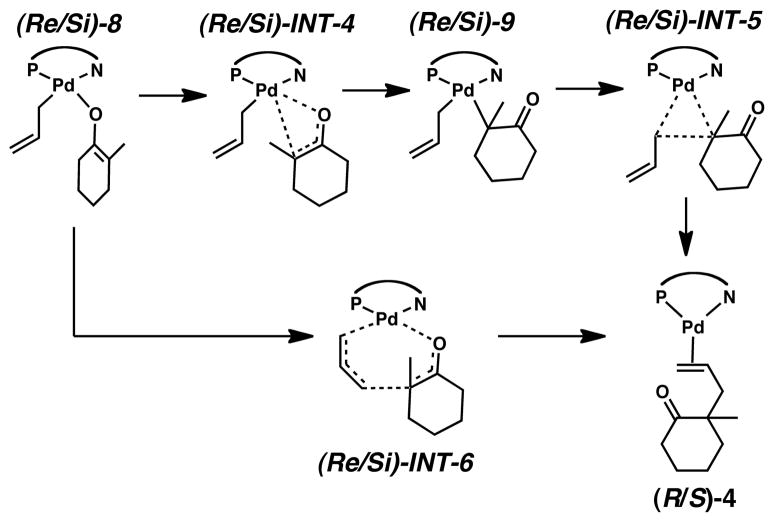
With routes to exo-5 established, we considered several internal rearrangements, shown in Scheme 4, that lead to 4-coordinate intermediates and can undergo reductive elimination to form Pd(0) olefin complex (S)-4. One possibility has the enolate O atom exchange into the binding site of the PHOX ligand N atom. Based on the long Pd–N bond in (S)-4, it seemed reasonable that the N atom donor from the PHOX ligand would be displaced more readily than the phosphorus donor.

Scheme 4.

Internal rearrangement mechanisms considered in this work.

The energies of (Si)-6 and (Re)-6, are +8.9 and +9.3 kcal/mol with respect to the separated ion pair in solution. The energies are similar to those obtained with mPW1PW91 control calculations (+8.6 and +9.2 kcal/mol, respectively), however dispersion energy corrections again greatly reduce this instability making the energies −0.2 and +0.6 kcal/mol, respectively. Thus, (Si)-6 and (Re)-6 are almost the same energy as the separated exo-3 and enolate ions, as well as exo-5. The transition states leading to these intermediates, (Si)-INT-1 and (Re)-INT-1 are +22.4 and +24.9 kcal/mol, values that are slightly higher than those for external nucleophilic attack. Even with mPW1PW91 and dispersion corrections, the barriers remain higher than expected racemizing processes. Breaking the Pd–N bond would seem to be unfavorable from an enantioinduction standpoint because that side of the PHOX ligand contains the stereocenter that makes the reaction enantioselective.

Another possibility involves the O atom of the enolate exchanging into the binding site of the C₁ atom of the allyl group. During this process the η-3 allyl fragment slips to become an η-1 bonded allyl group, which may be a more favorable position from which to facilitate C–C bond formation. However, the energies for the 4-coordinate species where the enolate becomes trans to the N, (Si)-7 and (Re)-7, as well as their corresponding transition states (Si)-INT-2 and (Re)-INT-2 are higher than the cases were the N atom of the PHOX ligand underwent substitution. Thus, we ruled out these as feasible enantioselective processes.

The last rearrangement we present was expected to be most favorable because 1) the PHOX ligand remains intact throughout the reaction and 2) that the trans-influence of the phosphino group should help activate the P–C₃ bond. Indeed, the 4-coordinate species (Si)-8 and (Re)-8 are more stable than those just mentioned. Again, B3LYP free energies with solvation show the complexes are less stable than the separated exo-3 and enolate ions at +5.7 and +5.9 kcal/mol, respectively. As with (Si)-7 and (Re)-7, mPW1PW91 single point electronic energies make these slightly higher, both are +6.7 kcal/mol. However, adding dispersion corrections now makes these intermediates −4.8 and −4.7 kcal/mol more stable than the separated ions. Unlike all of the other pathways from Scheme 4, this pathway has a significant thermodynamic driving force, and so we now focus our discussion on the transition states that lead to these intermediates, (Si)-INT-3 and (Re)-INT-3.

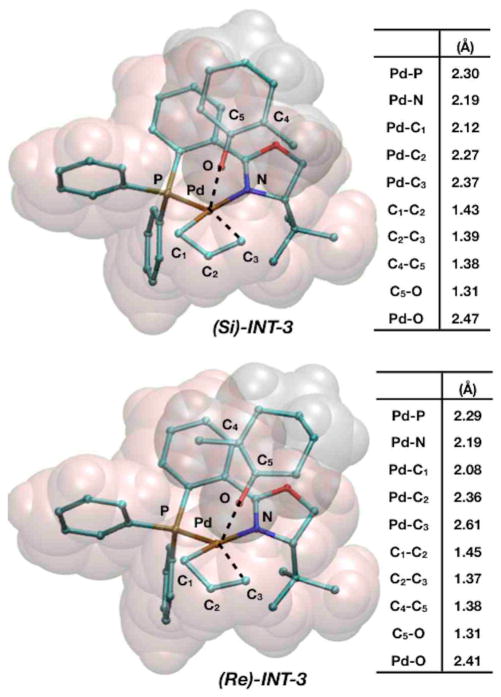
The geometries for these transition states are shown in Figure 6. Interestingly, this is the first transition state we have discussed that also shows promise regarding enantioselectivity. Almost all interatomic distances are similar between the two transition states are similar with the notable exception of the breaking Pd–C₃ bond, which is significantly longer in (Re)-INT-3 (R = 2.61Å) than it is in (Si)-INT-3 (R = 2.37Å). The orientation of the methyl group influences the transition state to be later along the reaction coordinate in (Re)-INT-3 than in (Si)-INT-3.

Figure 6.

Representations of transition states (Si)-INT-3 and (Re)-INT-3 and a table consisting of relevant interatomic distances.

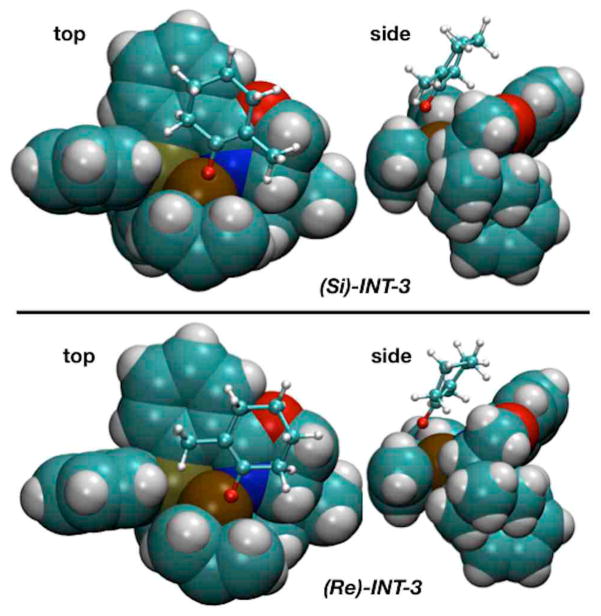
Figure 7 shows another perspective of these transition states, this time with the p-allyl Pd(PHOX) catalyst rendered with space-filling spheres while the enolate is rendered with a ball and stick model. The top view of (Re)-INT-3 (Figure 7a) shows the enolate’s methyl group quite near to a phenyl group of the PHOX ligand, while the top view of (Si)-INT-3 (Figure 7c) has the methyl group pointing away from the phenyl group and poised above the oxazoline ring of the PHOX ligand. Side views of these two transition states (Figures 7b and 7d) illustrate that the two faces of the enolate interact differently with the PHOX ligand.

Figure 7.

Top and side view representations for (Re)-INT-3 and (Si)-INT-3.

The observed ee’s for the enantioselective Tsuji allylation reaction are approximately 90%, corresponding to an (S):(R) product ratio of 95:5. A Boltzmann relation of this ratio in turn corresponds to a ΔΔG₂₉₈ between the enantiodetermining reaction barriers to be only ~1.8 kcal/mol. Given the standard expectation of B3LYP to yield accurate barrier heights within 3–5 kcal/mol, capturing this energy difference accurately with theoretical calculations is probably not possible. Nevertheless, B3LYP calculated barrier heights are in excellent agreement with this value, calculating the barrier for (Si)-INT-3 to be 1.0 kcal/mol lower than the barrier for (Re)-INT-3. Barriers using single point mPW1PW91 calculations serendipitously makes this difference 1.6 kcal/mol, while inclusion of dispersion energies causes the barrier for (Re)-INT-3 to be energetically lower than (Si)-INT-3 by 1.4 kcal/mol. Dispersion corrections seem to favor a pathway that would result in asymmetric (R)-4 products rather than the observed (S)-4 products, but we caution against over-interpretation of barrier heights differing in energy by <2 kcal/mol, which is within the expected accuracy for these calculation methods.

When considering absolute barrier heights, B3LYP calculates the barriers for (Si)-INT-3 and (Re)-INT-3 to be 18.4 and 19.4 kcal/mol, respectively. Both values are smaller than the lowest barrier for external nucleophilic attack by 0.8 kcal/mol. Absolute barriers from mPW1PW91 calculations are 16.5 and 18.1 kcal/mol, respectively, and these are now more than 2 kcal/mol lower than the lowest external nucleophilic attack barrier. Finally, adding dispersion corrections makes the barriers 5.3 and 3.9 kcal/mol, respectively, which are more than 5 kcal/mol lower than the lowest external nucleophilic attack barrier. Thus, while the three different calculation methods disagree within a range of less than 2 kcal/mol as to which enantiodetermining process is favored, the three different methods unanimously identify that the internal rearrangement mechanisms (Si)-INT-3 and (Re)-INT-3 are energetically lower than external nucleophilic attack processes. Therefore the internal pathways are most likely to explain this chemistry. NBO charges⁷⁷ between respective atoms on the enolate and the Pd center differ by only ~0.02 charge units indicating electronic substitutions will not significantly favor one reaction pathway over another. However, the structural interactions between the enolate and the PHOX ligands differ between the two transition states, thus the enantioselectivity must be due to steric interactions.

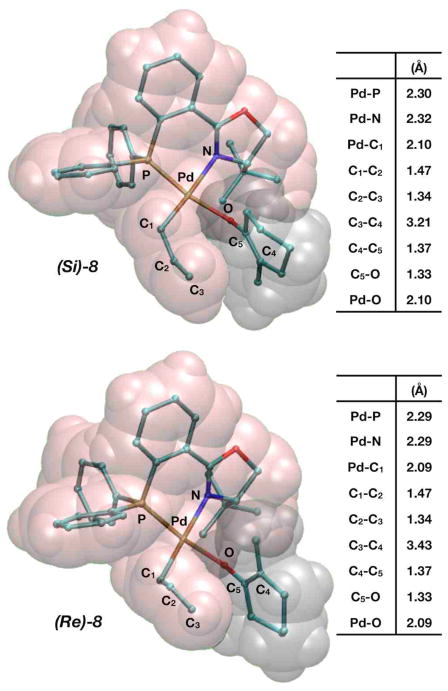
Figure 8 shows the geometric structures for the 4-coordinate species (Si)-8, however the relevant interatomic distances for (Re)-8 are the same. These geometries are consistent with expected structures from 4-coordinate Pd²⁺ complexes. The Pd–P bond remains the same length as was found in exo-3, however the Pd–N bond is lengthened due to the trans-influence of the C₁, which has now formed an η-1 bond. The Pd–C₃ bond in turn is completely dissociated, but the elongated C₁–C₂ and shortened C₂–C₃ bonds show the allyl fragment is no longer in resonance. One can visualize how the allyl and enolate ligands fit next to each other based on the space-filling models depicted in Figure 8.

Figure 8.

Representations of 4-coordinate (Si)-8 and (Re)-8 (Pd²⁺ complexes), formed after inner-sphere ligand rearrangement. The table displays relevant interatomic distances.

Rotational barriers of either the allyl fragment (about the Pd–C₁ bond) or the enolate fragment (about the Pd–O bond) within this complex are challenging to obtain with quantum mechanics since no chemical bonds are being created or destroyed. Nevertheless, knowing the barrier for the latter rotation is important to know since a free rotation would lead a racemic mixture of (Re/Si)-8, and would therefore render the potentially enantiodetermining barriers from the transition states (Re/Si)-INT-3 irrelevant to enantioselectivity. Determining such barriers would require dynamical simulations to ensure the potential energy surface was sufficiently sampled, and dispersion will most certainly play a critical role in these interactions as well. We have not yet calculated rotational barriers, however we note that the reverse barrier from (Si)-8 to exo-5 via (Si)-INT-3 is between 17–18 kcal/mol without dispersion corrections and ~10 kcal/mol when including the corrections. Overcoming that barrier would result in another opportunity for the reaction to proceed via (Re)-INT-3 instead of (Si)-INT-3 thereby leading to racemized products. Thus, these barriers are the upper limits of what subsequent barriers in the C–C bond forming steps would need to be in order to lead to asymmetric products.

From the 4-coordinate species, (Re/Si)-8, we then sought reaction pathways that would lead to asymmetric products (Scheme 5). Focusing first on a process leading to a traditional three-centered reductive elimination we characterized reaction pathways whereby the enolate’s carbonyl O atom would exchange with the tertiary a-C atom, (Re/Si)-INT-4. We could only characterize the (Re)-INT-4 transition state, however we see no reason why that barrier would not be a reasonable approximation for (Si)-INT-4 as well. Indeed, this barrier is quite high regardless of the method employed. Calculations using B3LYP with solvation resulted in a barrier of 28.0 kcal/mol, while those from mPW1PW91 calculations were very similar: 27.1 kcal/mol. These barriers were ~5 kcal/mol higher than the corresponding barriers for external nucleophilic attack. Dispersion energies made this barrier similar to external attack barriers (12.9 kcal/mol) and only a few kcal/mol higher than the reverse process back to exo-5.

Scheme 5.

Pathways for C–C bond formation considered in this work.

We also considered traditional 3-centered reductive elimination from the intermediates (Re/Si)-9. The energies of these intermediates were roughly the same as the 5-coordinate species exo-5, and B3LYP and mPW1PW91 calculations found the intermediates approximately +16 kcal/mol less stable than the separated intermediates exo-3 + enolate, however dispersion corrections made their stabilities about the same as the energies of exo-3 + enolate as well as exo-5. Notably, (Si)-9 is consistently >2 kcal/mol more stable than (Re)-9. However, the reductive elimination process (Si)-INT-5 has an extraordinarily high barrier: >45 kcal/mol regardless of calculation method.^†

Having ruled out 3-centered reductive elimination mechanisms, we considered different mechanisms analogous to those first reported by Echavarren and coworkers⁸⁰ coupling allyl fragments together at their terminal carbons, i.e., between C₃ on the allyl fragment and C₄ on the enolate. These mechanisms have also received consideration in other mechanistic studies.^81–85 As these reactions appear to be a hybrid of the Cope rearrangement and a cheletropic reaction, this process resembles a hybrid of a Claisen and reductive cheletropic rearrangement.⁸⁶ This process shown by (Re/Si)-INT-6 may also be considered as an intramolecular metalla-ene reaction leading to a palladacyclopropane complex, i.e. (R/S)-4.

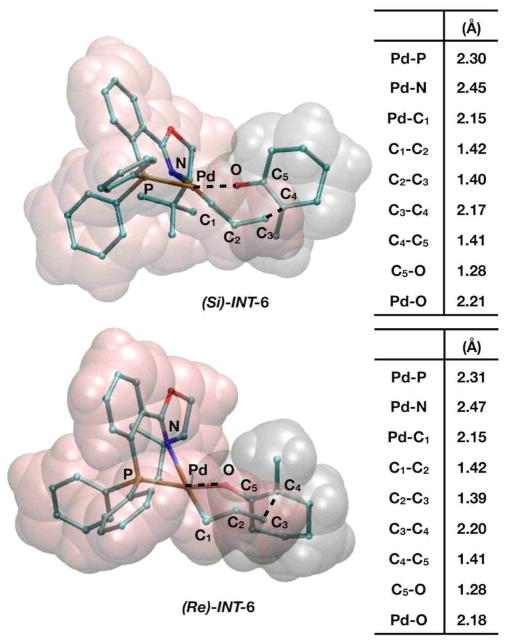
The transition states for these processes were (Re/Si)-INT-6 and each process considered a pericyclic reaction process where the allyl and enol fragments were aligned in a boat- and chair-like structure. Consistent with sterics for six-membered rings, as well as the work by Echavarren, the chair-like processes had the lowest energies. Figure 9 shows the geometric structure for (Si)-INT-6.

Figure 9.

Representations of the seven-membered reductive elimination processes (Si)-INT-6 and (Re)-INT-6. The tables display relevant interatomic distances.

In this process the Pd–P bond remained intact as it has throughout the entire mechanism, but the Pd–N, Pd–C₁, and Pd–O bonds are longer with respect to those seen in (Si)-8. In fact, the Pd–N bond in (Si)-INT-6 is slightly shorter than that found in the Pd⁰ complex (S)-4, indicating the occupation of anti-bonding orbitals during the reduction. The transition state has an intermediate C₃–C₄ distance of 2.17Å, and the bond distances about the Pd center indicate that bond formation and Pd²⁺ reduction to Pd⁰ is a concerted process. The geometry of the (Re)-INT-6 transition state is almost exactly the same as that for (Si)-INT-6, and interatomic distances vary by less than 0.03Å.

The energies of the boat- and chair-(Re/Si)-INT-6 transition states are likewise almost identical, thus it is unlikely these steps themselves would be enantiodetermining. The respective barriers for chair-(Si)-INT-6 and chair-(Re)-INT-6 were +16.9 and +16.8 kcal/mol using B3LYP with solvation, +16.9 and +17.1 kcal/mol with mPW1PW91 electronic energies, and dispersion corrections reduced the B3LYP barriers to +7.3 and +7.1 kcal/mol.

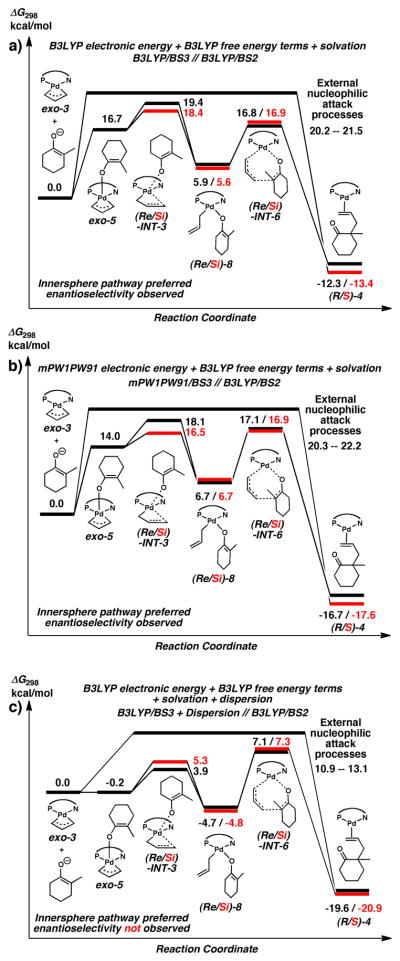
A partial picture of the enantioselective Tsuji allylation reaction is now complete. We refer the reader to Figure 10, which summarizes all key energies in the calculated mechanism. In calculations with B3LYP free energies with solvation (Figure 10a), combining exo-3 with the enolate is endothermic, and not a stable intermediate in THF solution. (Note that this energy does not include dispersion interactions, but those contributions are included in Figure 10c.) The calculated barriers suggest that internal rearrangement is an enantioselective process favoring the channel leading to (S)-2, the experimentally observed major product. Internal rearrangement, (Si)-INT-3, is 1.0 kcal/mol lower in energy than (Re)-INT-3, leading to a ΔΔG₂₉₈ value of 1.0 kcal/mol. If racemization of (Si)-8 to (Re)-8 does not occur, the high backward barrier back to exo-5 would mean all of the (Re/Si)-8 intermediates would react via (Re/Si)-INT-6 and the ratio of (S)-2 to (R)-2 would be 84:16. Since outer-sphere reaction barriers are higher, products arising from these pathways are unlikely.

Figure 10.

Mechanistic pathways summarizing three different calculation schemes used in this study. Numbers depict relative free energies (in kcal/mol) for relevant intermediates and transition states in the reaction mechanism. a) shows energies calculated from B3LYP/BS3//B3LYP/BS2 including single-point solvation corrections. b) shows the same energies as a) except with mPW1PW91/BS3 single-point electronic energies. c) shows the same energies as a) except including single-point dispersion energy corrections. See text for discussion.

In calculations similar to the previous case except using mPW1PW91 electronic energies (Figure 10b), forming exo-5 is still substantially endothermic. The calculated barriers still suggest that internal rearrangement is an enantioselective process favoring the channel leading to S-2, but (Si)-INT-3 is now 1.6 kcal/mol lower in energy than (Re)-INT-3, leading to a ΔΔG₂₉₈ value of 1.6 kcal/mol. The backward barrier to exo-5 is substantially lower in this calculation model, but because it is still lower than the (Re)-INT-3 barrier, all (Re/Si)-8 intermediates would react via (Re/Si)-INT-6 resulting in a (S)-2 to (R)-2 ratio of 94:6. Again, no products would arise from outer-sphere attack mechanisms. These results establish a measure of the uncertainties facing the DFT calculations without empirical dispersion corrections, and that a quantitatively similar perspective from theory is presented with two different DFT exchange correlation functionals.

In B3LYP free energy calculations with solvation and single-point dispersion corrections (Figure 10c), a substantially different picture is observed. Formation of exo-5 is now very slightly exothermic after changing the relative thermodynamics of single step by almost 17 kcal/mol. This suggests first that dispersion plays a significant role in this mechanism allowing the 5-coordinate exo-5 to act as a gateway to the inner-sphere processes. The (Re/Si)-INT-3 processes are affected differently by dispersion, however both are now substantially lower than the subsequent (Re/Si)-INT-6 processes. At face value, this causes (Re/Si)-INT-3 to not be an enantioselective process, and a roughly racemic mixture of (Re/Si)-8 would be expected during the reaction. We note however, that the current treatment of dispersion (based on empirically-based single point energy corrections) will likely bring with it greater uncertainties with energies requiring high precision (such as the barrier heights that determine the enantioselectivity of the reaction).

A natural question is which of the mechanistic profiles shown in Figure 10 is most accurately representing the true chemistry of this process. Since all of the geometries for these mechanisms were obtained using B3LYP optimizations without dispersion corrections, the values presented in Figure 10a will contain the most error cancellation. Thus, the ΔΔG₂₉₈ values for the enantioselective steps are the most meaningful when taken from Figure 10a. Indeed these results match well with experiment, while those in the control calculations shown in figure 10b serendipitously are in perfect agreement with experiment. In both cases, transition states (Re/Si)-INT-3 are enantiodetermining pathways, and these mechanisms predict the experimentally observed products. Figure 10c shows calculations involving dispersion corrections, which are undoubtedly important in this mechanism. Dispersion causes most inner-sphere intermediate energies to be shifted down by 10–15 kcal/mol. Due to this, the lower barriers seen here are probably more appropriate for modeling overall reaction kinetics, however as noted before, the precision of the enantioselective steps and their corresponding ΔΔG₂₉₈ values will not be as robust, since these calculations have not been taken at stationary points on DFT+dispersion potential energy surface. To alleviate this problem, a more rigorous calculation scheme involving geometries optimized with dispersion and/or solvation corrections at each iteration could be pursued, however the computational cost of such calculations outweighs the marginal gain over the data presented in Figure 10a. Instead, we use this ensemble of schemes to provide two general suggestions to improve the enantioselectivity of this reaction. First, chemical modifications to greater stabilize the (Si)-INT-3 transition state with respect to (Re)-INT-3 should improve enantioselectivities. Furthermore, modifications to make the intermediates (Re/Si)-8 as stable as possible will in turn ensure that those enantioselective products will rapidly convert to final products before reverse or racemizing reactions take place.

Conclusions

Based on our computational results, we propose a mechanistic model to describe the unique performance of the enantioselective Tsuji allylation reaction. The calculated pathways governing this process are presented in Figure 10. We note that enantioselectivity is only possible when the substrate undergoing allylation is a highly basic enolate nucleophile and/or susceptible to large non-bonding interactions due to dispersion such that it will form the exo-5 intermediate. We believe a competition between Re- and Si-pathways then ensues, and the most likely reaction step with enantiodetermining character is an internal rearrangement from the 5-coordinate exo-5 to the 4-coordinate (Si)-8 via the transition state (Si)-INT-3. Following this process, a non-traditional reductive elimination process occurs whereby C–C bond formation occurs at the 3 and 3′ positions of the allyl and enolate fragments.

Based on these results, we predict that this mechanism will be sensitive to by substitutions at the ortho-positions of the phenyl groups on the phosphine ligand to further obstruct the (Re)-INT-3 while leaving (Si)-INT-3 largely unaffected. Ideal-sized substitutions may enhance activity, though too large of a substitution runs the risk of interfering too much with the stability of exo-5, thus completely shutting down the inner-sphere pathways, leaving only outer-sphere pathways possible and leading to racemic products.⁸⁷ Once the enantioselective step has been optimized, the (Re/Si)-INT-6 barriers must be lower than the backward (Re/Si)-INT-3 barriers to maximize yields. Investigations with modified substrates and ligands are underway to further improve the performance of these catalysts.