Deformable registration of the inflated and deflated lung in cone-beam CT-guided thoracic surgery: Initial investigation of a combined model- and image-driven approach

Abstract

Purpose: Surgical resection is the preferred modality for curative treatment of early stage lung cancer, but localization of small tumors (<10 mm diameter) during surgery presents a major challenge that is likely to increase as more early-stage disease is detected incidentally and in low-dose CT screening. To overcome the difficulty of manual localization (fingers inserted through intercostal ports) and the cost, logistics, and morbidity of preoperative tagging (coil or dye placement under CT-fluoroscopy), the authors propose the use of intraoperative cone-beam CT (CBCT) and deformable image registration to guide targeting of small tumors in video-assisted thoracic surgery (VATS). A novel algorithm is reported for registration of the lung from its inflated state (prior to pleural breach) to the deflated state (during resection) to localize surgical targets and adjacent critical anatomy.

Methods: The registration approach geometrically resolves images of the inflated and deflated lung using a coarse model-driven stage followed by a finer image-driven stage. The model-driven stage uses image features derived from the lung surfaces and airways: triangular surface meshes are morphed to capture bulk motion; concurrently, the airways generate graph structures from which corresponding nodes are identified. Interpolation of the sparse motion fields computed from the bounding surface and interior airways provides a 3D motion field that coarsely registers the lung and initializes the subsequent image-driven stage. The image-driven stage employs an intensity-corrected, symmetric form of the Demons method. The algorithm was validated over 12 datasets, obtained from porcine specimen experiments emulating CBCT-guided VATS. Geometric accuracy was quantified in terms of target registration error (TRE) in anatomical targets throughout the lung, and normalized cross-correlation. Variations of the algorithm were investigated to study the behavior of the model- and image-driven stages by modifying individual algorithmic steps and examining the effect in comparison to the nominal process.

Results: The combined model- and image-driven registration process demonstrated accuracy consistent with the requirements of minimally invasive VATS in both target localization (∼3–5 mm within the target wedge) and critical structure avoidance (∼1–2 mm). The model-driven stage initialized the registration to within a median TRE of 1.9 mm (95% confidence interval (CI) maximum = 5.0 mm), while the subsequent image-driven stage yielded higher accuracy localization with 0.6 mm median TRE (95% CI maximum = 4.1 mm). The variations assessing the individual algorithmic steps elucidated the role of each step and in some cases identified opportunities for further simplification and improvement in computational speed.

Conclusions: The initial studies show the proposed registration method to successfully register CBCT images of the inflated and deflated lung. Accuracy appears sufficient to localize the target and adjacent critical anatomy within ∼1–2 mm and guide localization under conditions in which the target cannot be discerned directly in CBCT (e.g., subtle, nonsolid tumors). The ability to directly localize tumors in the operating room could provide a valuable addition to the VATS arsenal, obviate the cost, logistics, and morbidity of preoperative tagging, and improve patient safety. Future work includes in vivo testing, optimization of workflow, and integration with a CBCT image guidance system.

INTRODUCTION

Lung cancer accounts for over 200 000 new cases and 160 000 deaths in the USA each year, making it the most lethal malignancy for both genders.^{1, 2} Studies suggest that screening with low-dose CT can detect lung nodules at a smaller size (<10 mm diameter) and earlier stage than chest radiography,^{3, 4} and such early detection has been shown to decrease mortality.⁵ Of the three major treatment modalities (chemotherapy, surgery, and radiation therapy), surgical resection through thoracotomy is the preferred method of curative treatment of early stage lung cancer. A move to less invasive surgery via video-assisted thoracoscopy (VATS) over the last decade demonstrates equivalent outcome to open surgery, improved morbidity, faster recovery, and better preservation of normal lung function⁶ through lung-conserving approaches such as segmentectomy or wedge resection (cf. lobectomy). However, the minimally invasive approach, relying on palpation via a finger placed through the ∼1–2 cm wide intercostal ports into the pleural space, can face difficultly in confidently localizing small tumors (e.g., 3–10 mm in size), particularly lesions even a short distance from the pleura, as well as those that are subpalpable. A number of adjunctive techniques are used in current practice to address this issue—the most common involving tagging of the lung nodule via placement of a wire marker or dye.^{7, 8} Such localization is carried out preoperatively under CT fluoroscopy guidance, requiring coordination of two distinct invasive procedures (nodule tagging in interventional radiology and nodule resection in surgery) within a fairly short time. This approach increases the cost, risk, and complexity of care, and presents a considerable logistical burden.

Intraoperative imaging, specifically cone-beam CT (CBCT) acquired from a mobile C-arm, offers the potential to directly localize small malignancies during surgery. In addition to potentially obviating the cost and logistical burden of preoperative localization, intraoperative CBCT could facilitate safer surgery by visualizing also the critical structures surrounding the surgical target (e.g., pulmonary arteries, bronchial airways, etc.). CBCT has demonstrated sub-mm spatial resolution combined with soft-tissue visibility at low radiation dose (∼4.3 mGy per scan) in the thorax.^{9, 10} The potential benefits of intraoperative CBCT have been demonstrated in other applications (e.g., skull base and orthopaedic surgery) and motivated the development of advanced intraoperative image-guidance systems [Fig. 1a] to overcome the limitations inherent to navigation in preoperative image data alone. Application of this technology to high-precision thoracic surgery, however, meets an immediate challenge at

Figure 1.

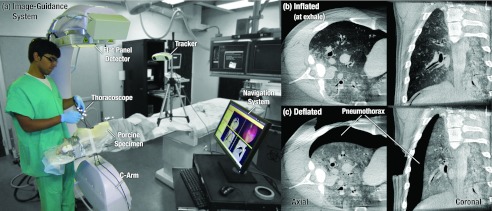
(a) Image-guidance system used during a thoracic surgery experiment performed on a fresh cadaveric porcine specimen. CBCT images illustrate the target lung in (b) inflated and (c) deflated states. Deflation of the lung imparts a large deformation in which the lung collapses from the chest wall toward the mediastinum, creating a pneumothorax between the lateral lung surface and two or more intercostal ports.

a key initial step of the operation during which the inflated lung (at inhale or exhale) is collapsed in a controlled manner to a fully deflated state, thus ensuring safe and stable surgical manipulation. The gross deformation induced by this process—as captured in Figs. 1b, 1c—creates a strong geometric disparity to preoperative imaging, thus preventing flow of valuable information to the intraoperative domain including the location of tumors within the target wedge, delineation of the target boundaries, the surgical plan, and adjacent critical anatomy such as major vessels and airways. To solve this previously unaddressed problem, we propose a novel solution using deformable registration of images acquired from intraoperative CBCT.¹³ For cases in which the tumor is difficult to visualize directly (e.g., a small, nonsolid mass), accurate registration would provide a valuable guide to localization within the target wedge, whereas for cases in which the tumor is readily visible in the deflated CBCT image, it would allow quick visualization and localization (rather than slice scrolling). Finally, a mathematical correlation of anatomy to the most up-to-date surgical scene allows advanced guidance techniques and more streamlined means of conveying information to the surgeon—e.g., augmentation of thoracoscopy with registered CBCT and planning data.

A considerable body of previous work in deformable image registration in thoracic contexts has focused primarily on geometrically resolving deformation of the lung during respiration,^{14, 15, 16, 17, 18} or on multimodal registration of images at same inflation (or deflation) states.^{19, 20} Adapting such techniques to the fully deflated lung (Fig. 1) is new territory. A similar problem of targeting needle brachytherapy procedures was addressed by Sadeghi Naini et al.,^{21, 22} where the displacement field obtained from the registration of inhale-exhale states in 4D CT was used to compute an extrapolation to the deflated state. This approach showed sub-mm accuracy in ex vivo specimens, where the lung motion continued along the respiration trajectory; an assumption that holds for cases in which the lung is drawn under negative pressure. The anatomical deformation in VATS is different in comparison, where the deflated lung collapses medially upon breach of the pleura, creating a large lateral pneumothorax (Fig. 1). Alternative methods have been investigated for registration under respiratory motion, taking advantage of anatomical landmarks and/or directly using image intensities to optimize various similarity metrics, such as those summarized and compared in the EMPIRE10 study.^{18, 23, 24, 25} Considering the magnitude of deformations involved in registering the inflated and deflated lung, a combined, sequential approach was employed in the proposed method: first, a robust model-driven method matching the lung surface and airway bronchial trees between inflated and deflated states to achieve a fairly coarse localization of the target wedge (∼3–5 mm required localization accuracy); then, an intensity-corrected variant of the Demons algorithm refining registration to ∼1–2 mm accuracy to localize both the tumor and surrounding critical anatomy. An initial implementation of the proposed approach was previously introduced,²⁶ focusing on an alternative method employing simple surface correspondence, manual airway matching, and a preliminary assessment of intensity correction to address partial volume effects, tested on a single dataset. The work detailed below reports a fully automated algorithm with an improved model-driven stage (surface mesh evolution instead of simple surface correspondence, and automated airway matching) and provides in-depth description of methods, preliminary analysis of overall performance in 12 datasets, and analysis of individual algorithmic steps.

METHODS

Figure 2 summarizes the proposed deformable registration algorithm, composed of two major stages: a model-driven stage based on image features, followed by an image-driven stage based on image intensities and gradients. In the work described below, we consider two CBCT images as input, an image of the inflated lung acquired immediately prior to pleural breach (taken as the moving image, I₀) and an image of the deflated lung acquired following pleural breach and collapse (deflation) of the lung within the thoracic cavity (taken as the target fixed image, I₁). Registration of preoperative CT to intraoperative CBCT is not considered in the current work, mainly to focus on the deformations due to deflation, although the ability to register CT and CBCT (despite image intensity differences) has been demonstrated previously in head and neck contexts.²⁷ CT-to-CBCT registration allows alignment of preoperative image and planning data (e.g., segmentation of the target and critical anatomy) with the initial intraoperative CBCT image (I₀). By extension to the methods proposed below, one could also envision registration of the preoperative CT (inflated lung) directly to the intraoperative CBCT of the deflated lung (I₁), as discussed in Sec. 4. A summary of notation associated with the images and model structures at each step in the algorithm is provided in Table 1.

Figure 2.

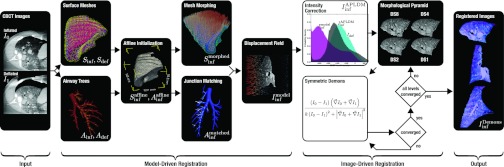
Overview of the proposed algorithm for deformable registration of the inflated and deflated lung. The two main stages of the method are: (1) a coarse model-driven registration using surface and airway structures; followed by (2) a fine image-driven registration using an intensity-corrected Demons algorithm. The hybrid model- and image-driven approach was hypothesized to give robust, adaptable registration with geometric accuracy suitable either for coarse localization of the target wedge (with model-driven stage only) and/or localization of the target nodule and adjacent critical anatomy (with model- and image-driven stages).

Table 1.

Summary of notation.

	Step	Symbol	Definition
	Input images	I0	Inflated lung image (“moving” image)
		I1	Deflated lung image (“fixed” image)
Model-driven	Model structures	Sinf	Inflated lung surface (triangular mesh) defined in I0
		Sdef	Deflated lung surface (triangular mesh) defined in I1
		Iinf	Region of inflated lung image (I0) interior to Sinf
		Idef	Region of deflated lung image (I1) interior to Sdef
		Ainf	Inflated lung airway tree defined in Iinf
		Adef	Deflated lung airway tree defined in Idef
	Affine initialization	$S_{\inf }^{\mathrm{affine}}$	Inflated lung surface (Sinf) following affine registration to Sdef
		$A_{\inf }^{\mathrm{affine}}$	Inflated lung airway tree (Ainf) following affine registration
	Surface morphing	$S_{\inf }^{\mathrm{morphed}}$	Inflated lung surface ($S_{\inf }^{\mathrm{affine}}$) following meshmorphing onto Sdef
	Airway matching	$A_{\inf }^{\mathrm{matched}}$	Inflated lung airway tree ($A_{\inf }^{\mathrm{affine}}$) following node matchingto Adef
	Voxelwise displacement	$I_{\inf }^{\mathrm{model}}$	Output of the model-driven stage: coarse registration of Iinf to Idef
Image-driven	Intensity correction	$I_{\inf }^{\mathrm{APLDM}}$	Inflated lung image (Iinf or $I_{\inf }^{\mathrm{model}}$) following APLDM intensity correction
	Morphological pyramid	DS8	Downsampled image (8 × 8 × 8voxel binning)
		DS4	Downsampled image (4 × 4 × 4 voxel binning)
		DS2	Downsampled image (2 × 2 × 2 voxel binning)
		DS1	Fully sampled image (1 × 1 × 1 voxel binning)
	Demons registration	$I_{\inf }^{\mathrm{Demons}}$	Output of the image-driven stage: fine registration of Iinf to Idef

Model-driven registration of the inflated and deflated lung

Segmentation of model structures

The first step in the model-driven stage is to identify the structures that drive coarse registration, viz., the lung surface and the bronchial airway tree—the former bounding the motion field to the region of interest and the latter providing a feature-rich description of motion interior to that boundary. As the main focus of the current work is the registration problem (not the segmentation problem), in this context the segmented structures are regarded as input to the algorithm. Exploiting the high image gradients at tissue-air boundaries, semiautomated region-growing methods demonstrated reasonable performance for initial investigation of the model-driven approach; however, more advanced segmentation methods^{28, 29, 30} exist and will be investigated in future work, as discussed in Sec. 4. For the surfaces, ∼10 “seeds” were manually placed, distributed throughout the structure of interest, and “grown” using a semiautomatic edge-constrained active contours algorithm.³¹ The airways, on the other hand, required only a single seed placement and exploited the tubular structure in segmentation.³² The resulting segmentations were subsequently filtered in an automated manner to identify and extract the largest connected component, fill holes in segmentations, and to smooth with a median kernel of 1 mm radius.

The segmentation results in two lung surfaces (S_inf and S_def) and two airway trees (A_inf and A_def). An important aspect of the use of surfaces is to define the region of interest over which the registration will operate—i.e., the volume interior to the lung parenchyma but excluding the surrounding ribs, diaphragm, etc. As in Table 1, the regions of I₀ and I₁ interior to the S_inf and S_def surfaces, respectively, are referred to as I_inf and I_def. This absolves complexities associated with deformation of the ribs, intercostal tissue excision, etc. and is consistent with the goal of the registration—i.e., to guide the surgeon with respect to targets and critical structures internal to the lung.

Affine initialization using airways and surface bounding boxes

Affine registration of I₀ and I₁ is composed of rigid alignment of airways and scaling of surfaces. The rigid component is obtained by aligning the airway trees using a regular step gradient descent optimization of mean square error and is performed primarily to account for patient displacement that may have occurred between the two scans. The scaling component on the other hand is obtained using surfaces via matching the corners of their axis-aligned bounding boxes. The combined affine transform is given by

$${\vec{D}}_{\mathrm{affine}}=\left[\begin{array}{cccc}\hfill s_x·n_x& \hfill o_x& \hfill a_x& p_x\\ \hfill n_y& \hfill s_y·o_y& \hfill a_y& p_y\\ \hfill n_z& \hfill o_z& \hfill s_z·a_z& p_z\\ \hfill 0& \hfill 0& \hfill 0& 1\end{array}\right],$$ (1)

where orthonormal vectors n, o, a denote rotation, p_x,y,z denote translation, and s_{x, y, z} are the scaling of each dimension. In experiments reported below, the rigid registration was small (no gross displacement of the subject between scans), and the main scaling factor was in the anteroposterior (s_y) direction associated with collapse of the lung medially toward the mediastinum. Scaling to match the corners exactly was observed to introduce gross errors in certain datasets due to imprecise assumption of the underlying structure, whereas moving the corners halfway toward the target corners of the bounding box provided a simple initialization to match extrema at the apex and lower lobes and improved runtime of the subsequent stage. The affine registration matches the overall scale of the volume of interest in I_inf and I_def, but does not account for complex changes in shape—e.g., concavities in the lung surface associated with the ribs and diaphragm.

Morphing the lung surface mesh

The affine-registered surfaces $S_{\inf }^{\mathrm{affine}}$ and S_def are used to generate triangular, quad-edge surface meshes using the marching cubes algorithm. The meshes are then decimated in a manner that preserves their topology to yield 500 vertices (∼1000 facets). Finally, Delaunay conformity is enforced to ensure coherent orientation and an even distribution of the triangles across the lung surface (Fig. 3).³³ The inflated surface mesh (denoted $S_{\inf }^{\mathrm{affine}}$ as the underlying segmentation) is morphed onto the deflated mesh (similarly denoted S_def) in an iterative fashion, where motion at each step is given by the displacement,

$$\begin{array}{ccc}& & {\vec{D}}_{v\left(t\right)}=\partial S_{\inf }^{\mathrm{affine}}/\partial t=-\left(v\left(t\right)-x_{\mathrm{def}}\right)·{\vec{\mathrm{N}}}_{v\left(t\right)},\hfill \\ & & \mathrm{such}\mathrm{that}|{\vec{d}}_{v\left(t\right)}|<\alpha ·{\overline{e}}_{v\left(t\right)}.\hfill \end{array}$$ (2)

At each step ∂t of the iterative process, each vertex v of the moving mesh ($S_{\inf }^{\mathrm{affine}}$) is displaced in proportion to the distance to the closest point x_def on the target mesh (S_def) along the direction of its current normal $\vec{\mathrm{N}}$. The displacement at each iteration is upper-bounded by a fraction α = 0.1 of the average edge length $\overline{e}$ at the current vertex and is regularized through smoothing of facet normals. A small step size provides smoother convergence at the cost of increased number of iterations, where the number of iterations depends both on ∂t and the average distance that needs to be traversed. For the collapsed lung (displacement ∼1–10 cm) a step size ∂t = 0.01 with 200 iterations was found to give fairly smooth, stable convergence. Additional steps were implemented to maintain physical/topological properties of the surface under deformation. The solution by Zaharescu et al.³⁴ was used to detect and resolve self-intersecting triangles through adaptive remeshing, optimize vertex valences (which for certain cases may result in loss of vertices), and apply Laplacian smoothing after each iteration.

Figure 3.

Triangulated surface meshes generated from (a) the inflated lung image I_inf (surface denoted S_inf) and (b) the deflated lung image I_def (surface denoted S_def), with corners of the axis-aligned bounding boxes highlighted.

Identifying and matching the bronchial airway trees

While the surface mesh registration governs the boundaries and bulk motion of the lung, the airways provide insight into the motion of inner structures. The unique tree structure of the airway allows identification of strong correspondences (viz., junction points at each airway bifurcation) and yields a sparse set of matched points throughout the lung interior. The process begins with the airway trees segmented as described in Sec. 2A1, yielding A_inf and A_def, which differ not only in shape (due to lung collapse) but also in extent (due to quality of the segmentation—typically fewer branch generations segmented in A_inf). Coincident to surfaces, the same affine registration is applied to A_inf to obtain $A_{\inf }^{\mathrm{affine}}$. The midline is extracted from each tree using iterative erosion of the airway segmentation until a single voxel-thick “skeleton” remains.³⁵ Next, the voxels of each skeleton are traversed, the branches are tagged, and the traversal distance is recorded for each branch.³⁶ A graph representation of the airway tree is thereby formed that is undirected, acyclic, and weighted (viz., using branch lengths as weights). For each tree, junction points are simply defined as nodes with three neighboring branches as illustrated in Fig. 4, resulting in 29 ± 9 junctions for $A_{\inf }^{\mathrm{affine}}$ and 41 ± 7 for A_def for the 12 datasets used.

Figure 4.

Airway trees and corresponding nodes. (a) Surface renderings showing overlay of the bronchial airways $A_{\inf }^{\mathrm{affine}}$ and A_def. (b) The resulting graph structure highlights the extracted midline, the nodes identified at each junction point, and the nodes for which correspondence was identified between the $A_{\inf }^{\mathrm{affine}}$ and A_def trees.

The correspondence of junction points is then established by solving the subgraph isomorphism problem, using the VF2 algorithm.³⁷ A subgraph in this context is a connected subset of junctions in the moving graph, whereas the isomorphism is defined according to whether or not it is contained within the fixed graph. The solution space is further constrained by ensuring difference in matching edge (branch) lengths to be no more than 2 mm and that matched node positions are within 2 cm of each other (following affine initialization). To improve robustness against segmentation errors and potential missing nodes, the isomorphism test was executed in a combinatorial optimization framework wherein combinations of subgraphs are generated from $A_{\inf }^{\mathrm{affine}}$ and tested against A_def. The nodes are scored heuristically based on the number of mappings to which they contributed, and the chosen mapping is that with the highest total score. As a result of this automated process, 17 ± 6 corresponding junctions were identified, as shown in Fig. 4.

Interpolating the sparse motion model to the voxel-grid

The model-driven registration yields a sparse motion field from the surface-to-surface mesh morphing (Sec. 2A3) and the airway-to-airway junction matching (Sec. 2A4). The former captures the boundaries and bulk motion, while the latter provides some sampling of interior motion. The surface models yield the vector field ${\vec{D}}_{\mathrm{surface}}$ connecting the vertices from $S_{\inf }^{\mathrm{affine}}$ to $S_{\inf }^{\mathrm{morphed}}$, and the airway models yield the vector field ${\vec{D}}_{\mathrm{airway}}$ connecting corresponding nodes from $A_{\inf }^{\mathrm{affine}}$ to $A_{\inf }^{\mathrm{matched}}$. The sparse motion field is simply the union of correspondences ${\vec{D}}_{\mathrm{surface}}\cup {\vec{D}}_{\mathrm{airway}}$. This motion field needs to be spatially interpolated in order to estimate the motion at every voxel in I_inf and obtain the deformed image, $I_{\inf }^{\mathrm{model}}$. An inverse distance-weighting approach was employed, since such methods provide good local support (i.e., allow for local deformations), and are exact interpolators, such that the sampled values are not modified (i.e., airway junctions will exactly overlap after transformation). This approach also simplifies combined use of surface and airways points, since the less sampled airway points are naturally weighted to a greater degree due to their spatial distribution in comparison to the more highly sampled but densely populated surface points. A variant of Shepard's method³⁸ was used,

$${\vec{D}}_{\mathrm{model}}\left(x\right)=\frac{{\sum }_{i\in n\subseteq N}\left(\vec{d}\left(x_i\right){\left|x-x_i\right|}^{-p}\right)}{{\sum }_{i\in n\subseteq N}|x-x_i{|}^{-p}},$$ (3)

where ${\vec{D}}_{\mathrm{model}}\left(x\right)$ denotes the displacement vector at each physical voxel location x, and the summation provides inverse distance weighting over a neighborhood (n) of the total (N) correspondences x_i yielded by the models. The neighborhood n was selected to further localize the contribution of points affecting the motion field while also improving computation speed. For the experiments detailed below, only points within a 67 mm radius (i.e., 25% of the image diagonal) contribute to a voxel's displacement. The parameter p controls the falloff rate of interpolation, selected as inverse-square (p = 2) in all cases below. Both the neighborhood (n) and strength of falloff (p) are tunable parameters that depend on the extent of the lung, with the values chosen qualitatively from the experiments below and a more rigorous sensitivity analysis the subject of future work.

Image-driven registration of inflated and deflated lung

Following initialization by the model-driven stage in Fig. 2, the image-driven stage uses all of the image voxels and gradients in $I_{\inf }^{\mathrm{model}}$ and I_def (not just a sparse set of points) to drive deformation at an increased level of geometric accuracy. The combination was hypothesized to be robust (by virtue of coarse model-driven initialization) and accurate (via image-driven refinement). Building on the adaptability and accuracy demonstrated in other applications, we employed a variant of the symmetric Demons algorithm accommodating intensity variation between the moving and fixed images.

Intensity correction using a priori lung density modification

The Demons algorithm is not insensitive to mismatch in image intensities (i.e., voxel values) between the moving and fixed image, since the displacement calculation at each voxel is a function of signal difference as well as image gradients. Such intensity variations can occur due to a variety of factors—e.g., scanner calibration (accuracy in HU), x-ray scatter, beam energy (kVp), etc. Previous work demonstrated a Demons variant robust against intensity mismatch arising between CT and CBCT (or between CBCT acquisitions at different energy or scatter conditions) using an iterative intensity match (IIM) within the registration process.²⁷ For the lung, a significant change in intensity is anticipated due to a change in bulk density of the parenchyma as a result of deflation. The mean intensity of lung parenchyma was measured to be $\overline{I_{\inf }^{\mathrm{model}}}\cong -650$ HU, attributable to partial volume effect in which each voxel comprises ∼70% air (−1000 HU) and ∼30% soft-tissue (∼0–50 HU). Reduction in air volume as the lung deflates increases the bulk density, giving a measured increase in mean voxel intensity ($\overline{I_{\mathrm{def}}}\cong -350$ HU) with ∼10%–20% air retention. Further increase in intensity was observed due to edema (fluid buildup) in the specimen used in experiments below. Example images are shown in Fig. 5.

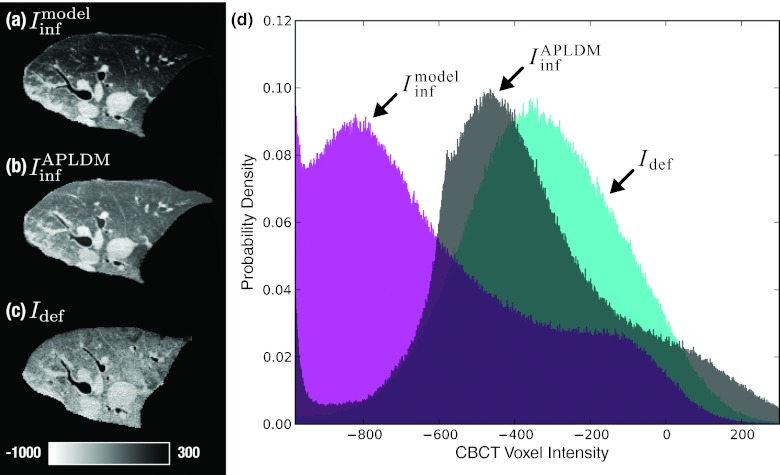
Figure 5.

Correction of CBCT image intensities using APLDM. Axial slices show (a) $I_{\inf }^{\mathrm{model}}$, (b) the intensity-corrected version of the moving image, $I_{\inf }^{\mathrm{APLDM}}$, and (c) the target image I_def. The mean intensity increase in (c) is due to expulsion of air upon deflation and buildup of fluid (edema) during intervention. (d) Normalized image histograms show the shift in voxel intensities for the APLDM-corrected image.

At least two approaches could be brought to bear on the intensity mismatch problem for Demons registration of the lung: the iterative intensity match (IIM) method²⁷ and the a priori lung density modification (APLDM) method.³⁹ The latter was chosen in the current implementation, since it addresses the problem explicitly in the lung context. The APLDM method first defines an “axis of deflation” [in this case, the left-right (medial-lateral) direction for a patient oriented in lateral decubitus and deflation of the lung toward the mediastinum] and corrects each voxel in the input moving image ($I_{\inf }^{\mathrm{model}}$) by the difference in mean values of $I_{\inf }^{\mathrm{model}}$ and I_def slice by slice along that axis,

$$\begin{array}{ccc}& & I_{\inf }^{\mathrm{APLDM}}\left(x\right)=I_{\inf }^{\mathrm{model}}\left(x\right)+\overline{I_{\inf }^{\mathrm{model}}\left(s\right)}-\overline{I_{\mathrm{def}}\left(s^{\prime }\right)},\hfill \\ & & \mathrm{such}\mathrm{that}x\in s,\hfill \end{array}$$ (4)

where each slice $s\in I_{\inf }^{\mathrm{model}}$ is linearly scaled to the corresponding slice s^′ ∈ I_def. Although originally developed to address intensity variation in the breathing (inhale-exhale) lung, APLDM was hypothesized to work well for the collapsed (inflated-deflated) lung as well, since motion (and the resulting intensity gradient) was also predominantly along one direction (namely, toward the mediastinum). Furthermore, the correction in Eq. 4 is fully automated using information derived in the preceding model-driven stage, which computes the bounding box scale needed to relate s to s^′, as well as the axis of deflation corresponding to the mean displacement (excluding rigid alignment). The algorithm was implemented in a manner that respects the mean displacement by reslicing the images along the inferred direction. Prior to application of the correction offset, recursive Gaussian smoothing (σ = 3) was applied along the same direction to eliminate potential discretization artifacts, and further analysis confirmed that the particular choice of σ (in the range 2–4) did not have significant effects on the final registration accuracy. The method was also anticipated to correct for the intensity variation due to edema, since both the deflation axis and the buildup of fluid were along the medial-lateral axis (i.e., the direction of gravity). As shown in Figs. 5a, 5b, 5c, the APLDM method demonstrated a reasonable match in overall intensity between $I_{\inf }^{\mathrm{APLDM}}$ and I_def, and the histograms of Fig. 5d capture the corresponding shift.

Multiscale Demons registration

The Demons algorithm forms the heart of the image-driven stage, implemented in a multiresolution morphological pyramid to improve robustness and convergence. The symmetric form of the algorithm⁴⁰ has been adapted to many applications, and has demonstrated accuracy at the level of the voxel size (∼0.5 mm) in CBCT-guided interventions.^{41, 42, 43} Use of the symmetric form was mainly motivated by its theoretically faster convergence rate over other forms, however alternative approaches have also been investigated, including the diffeomorphic Demons,⁴¹ and a mutual information minimizing b-spline registration.⁴⁴ The symmetric form was found to achieve comparable registration accuracies as the other algorithms, although a thorough comparison would involve further optimization of each of them, which is beyond the scope of this work.

At each iteration of the algorithm, the displacement for each voxel is computed from the difference and gradients in the moving image (I₀) and the fixed image (I₁), and the field obtained is regularized through Gaussian smoothing (σ = 1),

$${\vec{D}}_{\mathrm{Demons}}=\frac{2\left(I_0-I_1\right)\left(\vec{\nabla }{I}_0+\vec{\nabla }{I}_1\right)}{k{\left(I_0-I_1\right)}^2+{\left|\vec{\nabla }{I}_0+\vec{\nabla }{I}_1\right|}^2},$$ (5)

where k is a scale factor equal to the reciprocal of the squared voxel size (mm⁻²) at the current level of the morphological pyramid. For the full process illustrated in Fig. 2, the moving image I₀ in Eq. 5 is $I_{\inf }^{\mathrm{APLDM}}$—i.e., the inflated lung image following definition/extraction of S_inf, rigid/affine registration, coarse model-driven deformable registration of (S_inf, A_inf) to (S_def, A_def), and APLDM intensity correction. The fixed image I₁ is simply I_def, and the final image after applying ${\vec{D}}_{\mathrm{Demons}}$ is $I_{\inf }^{\mathrm{Demons}}$. The previously reported “smart” convergence criterion⁴⁵ was used to speed overall convergence by automatically advancing to the next level of the morphological pyramid when the change in motion vector fields falls below a specified threshold (viz., mean displacement field changing by less than 1/10th the voxel size in a given level of the pyramid). Various permutations of pyramid levels DS8, DS4, DS2, and DS1 (Sec. 3B4) were investigated, with nominal results reported below using a two-level pyramid (DS2-DS1).

Computational complexity and runtime performance

As with most applications designed for intraoperative use, shorter runtimes are desirable. Although the initial implementation focused more on achieving the desired levels of geometric accuracy, the algorithm was designed with the intention of respecting the time constraints of intraoperative workflow. The runtimes reported below were obtained from running the algorithm on an 8-core 64-bit workstation with 2 GHz Intel Xeon processors. Starting with the model-driven stage, the affine initialization takes ∼3 s. The mesh morphing algorithm that follows has a computational complexity of O(n log n) for calculating the distance-to-closest-point (v(t) − x_def) followed by O(n log³n) for maintaining topology. The choice for this method was in part motivated by its low complexity—much less than alternatives such as a finite element methods⁴⁶—and was found to converge in ∼50 s. The detection of airway branches and junctions was performed in ∼10 s. The combinatorial optimization aspect of matching junctions is costly in its current form, taking 50–80 s to span the search space and identify a mapping. The final step of model-driven stage (which interpolates the correspondences to the image grid) takes ∼30 s. For the image-driven stage, the APLDM intensity correction takes ∼8 s, while the Demons algorithm takes ∼3 min for registration of two 256³ volumes. In its current implementation, the Demons registration is the slowest step of the algorithm, however, parallel computation on GPU, exploiting the independent computation of forces per voxel has been shown to provide a significant speedup.⁴⁷

Experimentation in a porcine specimen

A freshly deceased (∼20–30 min) healthy porcine specimen was used to test and evaluate the deformable registration process in aligning CBCT images of the inflated lung (at exhale) to CBCT of the fully deflated/collapsed lung in a setup approximating VATS. The choice of a porcine model in these preliminary studies was motivated primarily by its size, which is representative of adult human lungs to be investigated in future work. The specimen was placed in left lateral decubitus (i.e., the right lung selected as target) as shown in Fig. 1, intubated using a cuffed endotracheal tube, with a manual pump maintaining positive pressure and/or a full range of respiratory motion.

The imaging system involved a prototype mobile C-arm with a flat-panel detector for intraoperative CBCT.^{9, 13, 48} Each scan was performed at 100 kVp, 230 mAs, and 200 projections over a ∼178^° semicircular orbit were acquired, comparable to the thoracic “soft-tissue” protocol as described by Schafer et al.⁹ and giving ∼4.3 mGy (dose to water at the center of a 32 cm cylindrical phantom). Projection data processing was described by Schmidgunst et al.,⁴⁹ and geometric calibration was performed as in Navab et al.⁵⁰ CBCT volumes were reconstructed using a variation of the filter backprojection algorithm,⁵¹ using a smooth reconstruction kernel and isotropic voxel size of 0.6 mm. A lateral truncation correction was applied based on projection domain extrapolation. There was no correction for x-ray scatter, beam hardening, or image lag artifacts. Approximate conversion of voxel values to HU used a simple manual selection of air and soft-tissue volumes to shift and scale from attenuation coefficient to HU in the range from −1000 to 50 HU, respectively.

CBCT images were acquired with the lungs in three states: (i) inflated to a state approximating full inspiration; (ii) inflated to a state approximating full exhalation; and (iii) deflated (collapsed medially toward the mediastinum) upon lateral breach of the intercostal muscles and pleura. The registration process was applied to images acquired in states (ii) and (iii) to evaluate registration accuracy between inflated (at exhale) and fully deflated states. Repeat testing was eventually confounded by collection of edemous fluid in the lungs after prolonged experimentation, causing a reduction in parenchymal tissue contrast and filling the airways with fluid in a manner not representative of the in vivo collapsed lung. Results presented below focus on the first set of experiments following first pleural breach and deflation. Subsequent scans resulted in a total of seven images of the right lung, with three acquired with the lung in an inflated state and four acquired at a deflated state. Reinflation of the lung between scans was achieved via intubation and a manual bellows pump. There was no need for resuturing between states. The lungs were variously manipulated between each scan by fingertip manipulation and/or thoracocscopy and are believed to represent realistic (and nonredundant) instantiations of inflated and deflated states. The quality of CBCT scans acquired later in the procedure was observed to suffer somewhat from increased buildup of edema and deformations induced by manual interaction with the lung. The seven images were cross-analyzed to yield a total of 12 image pairs—one for development and testing and eleven for repeatability.

Analysis of registration accuracy

The geometric accuracy of the registration process was quantitatively analyzed in terms of two metrics: target registration error (TRE) used to estimate the error in localizing distinct anatomical points in the lung; and normalized cross-correlation (NCC) between the deformed and fixed images. Image similarity metrics such as NCC provide rich quantitation and visualization of image alignment; however, recognizing potential shortfalls in such metrics (as discussed by Rohlfing et al.⁵² and highlighted below), TRE was also evaluated in (15–150) unambiguous anatomical point features distributed throughout the volume. Targets consisted of pointlike structures within the lung parenchyma, mostly airway and vessel bifurcations. Each point was localized by a single observer to ensure consistency in structure identification between the two images. Each point was selected once (with estimated accuracy of localization of ∼1 voxel, 0.6 mm), favoring a large population of targets selected throughout the lung volume over repeat localization of fewer target points. We recognize that target points associated with airway bifurcations tend to be close to airway junctions identified in A_inf and A_def of the model-driven registration process. However, physically identified “bifurcations” are distinct from mathematically identified “junctions”: the former refers to the most inferior aspect of tissue in a given bifurcation, and the latter is a centrally located point within the bifurcation on the centerline. Nonetheless, we sought to reduce possible bias associated with the proximity of such fiducials by rejecting target points identified within 2 mm of any junction point, yielding a total of 150 target points for the first dataset that better approximated ideal conditions. The resulting TRE values were fitted to χ² distributions in line with the expected theoretical distribution.⁵³ These fits were generated using maximum likelihood estimation, their goodness-of-fit was verified in terms of Pearson's χ² tests as well as the probability plot technique,⁵⁴ and were used to determine one-sided confidence bounds defining maximum errors with 95% confidence. For the remaining 11 sets, 15 target points were sampled from the 150 points in a manner providing uniform volumetric coverage of the lung. The results yielded a similar distribution in TRE as exhibited by the 150 points in the first image set as detailed below. A larger number of points would not likely have changed the results and is consistent with the number of targets analyzed in previous work.^{14, 15, 55} For these, distribution fitting was not feasible and the upper bound was instead approximated by the 95th percentile. Results are reported in terms of the median TRE value and the maximum upper bound defined with 95% confidence (denoted ${\mathrm{CI}}_{95}^{\mathrm{ub}}$).

NCC was computed as a similarity measure between the moving deformed and target fixed image:

$$\mathrm{NCC}=\frac{{\sum }_x\left(I_0\left(x\right)-\overline{I_0}\right)\left(I_1\left(x\right)-\overline{I_1}\right)}{\sqrt{{\sum }_x{\left(I_0\left(x\right)-\overline{I_0}\right)}^2{\sum }_x{\left(I_1\left(x\right)-\overline{I_1}\right)}^2}},$$ (6)

where I₀ is the output of the registration process (e.g., $I_{\inf }^{\mathrm{Demons}}$), and I₁ is the fixed image I_def. The metric was evaluated both globally using full images (e.g., I_inf and I_def) and also using a moving window (of size 7.5 cm³) to generate a local NCC image (LNCC) that quantifies local variations in image similarity. Similar to the TRE error analysis, two-sided confidence intervals were identified from maximum likelihood fits and approximated by a β distribution, which yielded good alignment with the observed values. Results are reported in terms of a NCC value computed over the full images as well as a 95% confidence interval (CI₉₅) obtained from the distribution exhibited by LNCC defined above.

Both TRE and NCC, along with qualitative visualization of the deformed images, were assessed at each step of the registration process in Fig. 2 to elucidate the behavior of the algorithm and to identify which processes (e.g., surface and/or airway deformation versus image-driven Demons registration in various steps of the pyramid) governed different aspects of the resulting deformation. Registration accuracy was assessed in six variations of the process illustrated in Fig. 2: (i) registration by the full model-driven + image-driven process in its presented form; (ii) registration using surfaces-only for the model-driven approach; (iii) registration using airways-only for the model-driven approach; (iv) registration without the APLDM intensity correction; (v) registration using various alternative (and fewer) levels for the morphological pyramid in the Demons algorithm; and (vi) registration using only the image-driven registration (without model-driven initialization).

RESULTS

Analysis of registration accuracy

The algorithm was applied to CBCT image pairs (I_inf, I_def) acquired at inflated and deflated (i.e., collapsed) states of the lung in the cadaveric porcine specimen. Segmentation of the lung surface was straightforward about the lateral aspects (chest wall) for both I_inf and I_def and could be delineated consistently by placement of seeds and region-growing, but the medial aspects proximal to the mediastinum were more challenging and required manual adjustment to ensure a consistent segmentation about soft-tissue boundaries. Segmentation of the airways performed well with a single seed, since airways appeared patent in CBCT images out to 3–4 generations of the bronchial tree, yielding 43 and 53 junctions prior to matching in I_inf and I_def, respectively.

As shown in Figs. 6a, 6b, starting with the model driven stage, the affine initialization roughly aligns the two surfaces, although complexities in surface shape and convexities are uncorrected. The surface morphing [Fig. 6c] accurately matched the surface irregularities, reducing the signed distance error from 1.5 ± 3.0 mm to 0.3 ± 1.4 mm, as illustrated in Fig. 6d.

Figure 6.

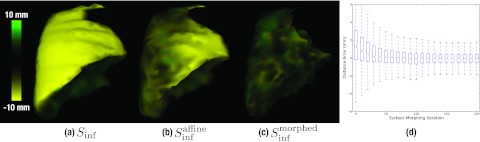
Signed distance errors between the target surface, S_def, and (a) the unregistered surface S_inf, (b) the affine-registered surface $S_{\inf }^{\mathrm{affine}}$, and (c) following surface morphing $S_{\inf }^{\mathrm{morphed}}$. The boxplot in (d) shows the distribution of signed distance error for all vertices over surface morphing iterations. For all boxplots herein, the horizontal line marks the median value, the upper and lower bound of the rectangle mark the third quartile range of the data, and the whiskers mark the full data range excluding outliers.

Figure 7 shows the deformed image obtained at key steps in the registration process. It should be noted that the algorithm does not actually deform the image at each step, but rather combines the individual transforms and composes a single displacement field to perform the deformation only once, thereby carrying out the entire registration in the physical coordinate system (as opposed to, for example, the sampled image grid with interpolations at each step). For qualitative visualization in Fig. 7, the displacement fields obtained at each step were used to deform I_inf and overlay the result on I_def. As evident in Fig. 7b, the affine initialization of the model-driven stage matches the volume extrema but without regard to underlying anatomy. Surface mesh morphing [Fig. 7c] brings the lung boundary in closer alignment, and the improvement can be visually appreciated for structures proximal to the surface; however, structures interior to the lung are subject to error. Alignment of airway junctions further aligns the interior structures of the lung as shown in Fig. 7d, especially evident in the reduced distance error of the airways. Note that the surfaces and airways are jointly interpolated in the algorithm, but are depicted serially in Fig. 7 for purposes of visualization. Following initialization by the model-driven process, the image-driven process improves registration further as shown for two levels of the Demons morphological pyramid—DS2 in Fig. 7e and the final step at full resolution (DS1) in Fig. 7f. As anticipated, the image-driven registration exhibits better alignment throughout the lung, including regions not represented by the surface and airway models.

Figure 7.

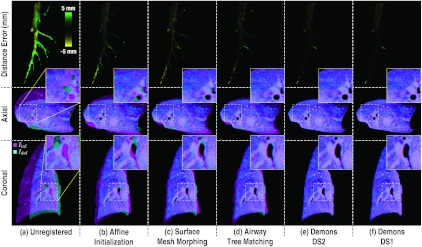
Registration performance at key steps in the algorithm. The top row shows the signed distance error in airway trees, A_inf and A_def. Axial and coronal slice overlays showing alignment of I_inf (magenta) and I_def (cyan) at each step of the algorithm. The zoomed inset in each case gives qualitative visualization of structure alignment.

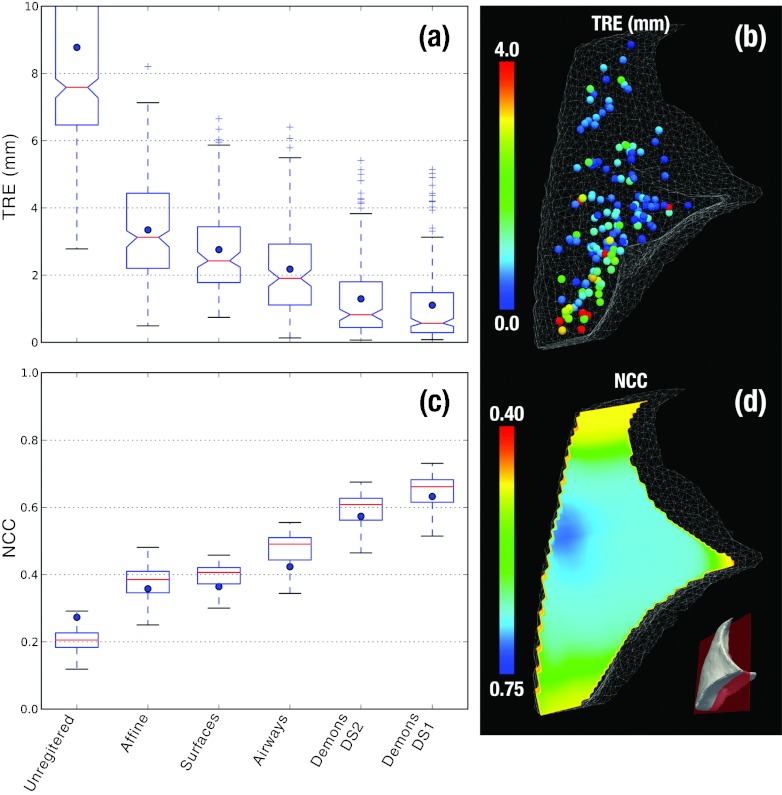
Figure 8 summarizes the quantitative analysis of geometric accuracy, showing TRE and NCC computed at each step of the algorithm illustrated in Fig. 7. The evolution in geometric accuracy demonstrates a monotonic reduction in registration error for both metrics. The unregistered images exhibit median TRE of 7.6 mm (<15.9 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and NCC of 0.27 (0.14–0.29 CI₉₅). The model-driven stage improves TRE to 1.9 mm (<5.0 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and NCC to 0.42 (0.30–0.52 CI₉₅). The image-driven stage using APLDM-corrected Demons improves the alignment further to TRE of 0.6 mm (<4.1 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and NCC of 0.63 (0.47–0.70 CI₉₅). Figure 8d shows the TRE to be in the range of ∼1–2 mm throughout the bulk of the lung, with a few points (red) exhibiting up to ∼3 mm misregistration in regions less well covered by the models and attributed primarily to weaker gradient information (very fine airway branches).

Figure 8.

TRE and NCC computed at key steps of the algorithm. (a) Distribution of TRE at each step in the algorithm, with blue dots marking the mean error. Outliers marked as “+” were measurements outside 1.5 × the standard deviation of the distributions. (b) 3D illustration of the 150 target points used in analysis of TRE, with the color bar conveying the final TRE. (c) Distribution of LNCC computed over a moving window over the images at each step of the algorithm. Blue dots mark the global NCC computed over the entire lung, and boxplots show median, quartile, and range of LNCC. (d) A coronal slice showing the final LNCC following model + image-driven registration.

The experiments were repeated for 11 additional datasets, and the results are summarized in Table 2. Note that the same algorithmic parameters were used in all trials (i.e., there was no parameter tuning), and following segmentation there was no manual interaction in the registration process. The combined model- and image-driven approach is seen to yield levels of geometric accuracy consistent with the surgical requirements for VATS specified above, where the model-driven stage providing coarse localization of the target wedge to ∼3–5 mm and the image-driven stage refining registration to ∼1–2 mm for precise localization of the target and critical anatomy.

Table 2.

Quantitative analysis of registration accuracy on 12 datasets.

	Unregistered			Model-driven			Image-driven
Set	Median TRE	TRE ${\mathrm{CI}}_{95}^{\mathrm{ub}}$	NCC	Median TRE	TRE ${\mathrm{CI}}_{95}^{\mathrm{ub}}$	NCC	Median TRE	TRE ${\mathrm{CI}}_{95}^{\mathrm{ub}}$	NCC
1–4	7.6	15.9	0.27	1.9	5	0.42	0.6	4.1	0.63
1–5	10.5	16.1	0.17	1.9	4.8	0.35	0.8	3.7	0.56
1–6	10.5	16.2	0.14	2.7	6.1	0.3	2.1	5.1	0.5
1–7	15.7	22.2	0.14	2.9	6.9	0.34	1.2	6.9	0.53
2–4	8.1	13.9	0.32	2.8	6.7	0.43	2.2	6.3	0.59
2–5	10	16.4	0.19	2.8	6.7	0.39	1.5	7.5	0.55
2–6	9.9	16.6	0.13	3.3	10.5	0.34	2.5	10.2	0.5
2–7	16.4	23.9	0.16	2.8	8.7	0.4	1.7	8.5	0.55
3–4	19.3	21.4	0.2	2.7	7.6	0.43	1.7	6.7	0.59
3–5	20.9	23.3	0.06	2.1	5.4	0.34	1.5	4.4	0.5
3–6	21.1	23.1	0.11	3.1	7.6	0.33	2.6	6.9	0.48
3–7	7.8	11	0.21	3.3	6.7	0.35	1.5	5.9	0.53
Total	9.7	21.8	0.18	2.3	6.8	0.37	1.2	6.2	0.54

Variations and possible simplifications

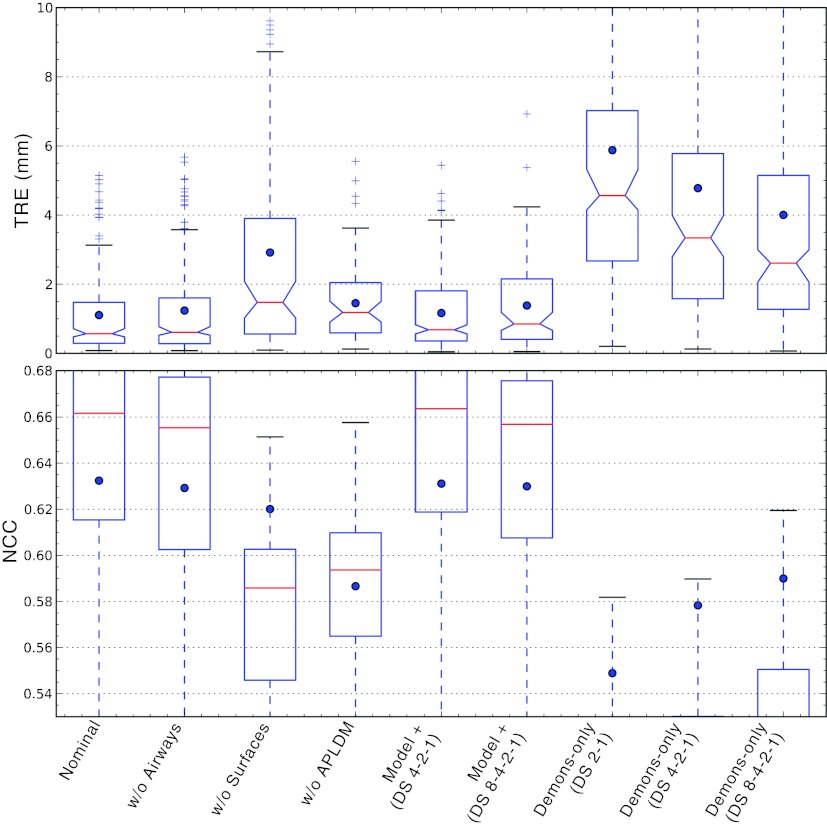
Specific variations of the algorithm were investigated to understand overall behavior by modifying (or knocking out) individual algorithmic steps and examining the effect on registration in comparison to the nominal (full) process in Fig. 2. In addition, this provided preliminary insight into possible simplifications that could reduce computational complexity. While the computational load is described in Sec. 2C for parts of the algorithm, a thorough evaluation of potential improvements in runtime would be premature for the initial implementation due to some manual steps (e.g., seed placement in segmentation) and areas for improvement and optimization in future work. The various scenarios are described below, and the resulting geometric accuracy for each is summarized in Fig. 9. Note that the Demons algorithm was applied on APLDM-corrected images, even for cases where other model information was not used, except for the explicitly noted variation that considered the effects of not using APLDM.

Figure 9.

Variations on the registration process detailed in Sec. 2B. (Top) TRE distributions with dots marking the mean, and (bottom) LNCC distributions computed from a moving window within the lung, with dots marking the global NCC computed over the entire lung.

Surfaces-only (w/o airways)

The surfaces-only scenario considers the case in which only lung surfaces are used in the model-driven stage, without use of the airway tree. The potential reduction in computational complexity comes primarily from avoiding the airway segmentation and junction correspondence steps. The TRE and NCC following the model-driven stage (using only the surfaces) were 2.4 mm (<5.6 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.41, respectively, compared to 1.9 mm (<5.0 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.42 for the full nominal approach. Using the surfaces-only result as initialization to the full image-driven stage yielded TRE of 0.6 mm (<4.5 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and NCC of 0.63 compared to 0.6 mm (<4.1 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.63. The lack of information on interior lung features is evident in the increase in TRE for the model-driven stage; however, the result following the image-driven stage is comparable to that of the nominal form and suggests that the Demons method is able to recover from the inferior initialization, likely due to the gradient-rich nature of the parenchyma.

Airways-only (w/o surfaces)

The airways-only scenario considers the case in which only the airway junctions are used in the model-driven stage. The potential simplification is the avoidance of bounding box scaling and surface morphing steps. Note, however, that although the surfaces are not used explicitly, they are indirectly made use of in extracting the ROI (i.e., excluding registration of the ribs, diaphragm, etc.) and in the subsequent image-driven stage, which operates only within the ROI. Eliminating the surface registration and relying only on the airways degraded TRE and NCC to 2.6 mm (<7.6 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.44, respectively, compared to 1.9 mm (<5.0 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.42 for the nominal model-driven approach. Although the median TRE is fairly low, there is a preponderance of outliers, associated primarily with a lack of registration in regions distal to the airways. The subsequent image-driven stage is less able to recover from the lack of initialization, yielding TRE and NCC of 1.5 mm (<10.3 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.62, respectively, compared to 0.6 mm (<4.1 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.63 for the nominal approach. A NCC value consistent with the nominal approach, despite degradation in TRE lead to an interesting finding: qualitative inspection of the resulting images appeared fairly well matched in many areas of the lung (even distal to the airways) but were geometrically erroneous. The image-driven stage matched gradients associated with air-tissue boundaries, but because the lung architecture is largely self-similar (analogous to a fractal), the method could not recover from poor initialization and was susceptible to incorrect matching—e.g., alignment of edges that did not correspond to the same anatomical structure.

Demons w/o APLDM correction

Failure to correct for the (+47%) increase in image intensity in the deflated lung degraded the TRE and NCC to 1.2 mm (<3.6 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.59, respectively, compared to 0.6 mm (<4.1 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.63 for the nominal approach. Unrealistic distortions of the lung architecture in the resulting deformed image were observed, similar to those previously reported in relation to Demons intensity correction applied to head and neck registration.²⁷

Demons with various morphological pyramids

A morphological pyramid is traditionally employed to avoid local minima, and when combined with a smart converge criterion,⁴⁵ can demonstrate faster overall convergence; hence, increasing the number of pyramid levels potentially offers an exponential reduction in computation time. Three variations in the morphological pyramid were tested, denoted (DS 2-1), (DS 4-2-1), and (DS 8-4-2-1). The first indicates the nominal pyramid of 2× 2×2 downsampling followed by registration at full-resolution. The second initializes with an additional 4×4× 4 downsampling level, and the third with yet another level at 8×8 ×8 downsampling. Somewhat counter to expectations, the inclusion of coarser levels in the pyramid had a negative effect on the TRE: (DS 2-1) giving 0.6 mm (<4.1 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$), (DS 4-2-1) giving 0.7 mm (<3.5 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$), and (DS 8-4-2-1) giving 0.9 mm (<3.9 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$), respectively. A similar trend was evident in the NCC, as a slight reduction in LNCC distributions. A close inspection of the error at each Demons iteration revealed that the more coarsely downsampled levels (DS4 and DS8) deteriorated the initialization provided by the model-driven stage, introducing an increase in TRE in early iterations (due to coarse voxelation) from which the algorithm was unable to completely recover. Moreover, the corresponding number of iterations determined by the smart convergence criterion was: 43-13 for (DS 2-1) giving 3.1 × 10⁸ voxel operations; 17-17-15 for (DS 4-2-1) giving 2.9 × 10⁸ voxel operations); and 9-10-20-15 for (DS 8-4-2-1) giving 3.0 × 10⁸ voxel operations. These results suggest that the deterioration of the initialization requires Demons to iterate more in order to satisfy the same convergence criterion, resulting in no significant gain in runtime for the longer pyramids.

Image-driven only

As a final variation on the method, images were registered using only the image-driven stage (i.e., APLDM-corrected Demons), omitting the model-driven initialization except to define the lung volume ROI over which the calculation is performed. The potential reduction in computational complexity comes from the avoidance of models, point correspondences, mesh evolution, etc. For the nominal morphological pyramid (DS 2-1), Demons alone performed poorly as anticipated, yielding TRE and NCC of 4.6 mm (<15.8 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.55, respectively, compared to 0.6 mm (<4.1 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and 0.63 for the full model-driven + image-driven approach. Alternative morphological pyramids were investigated to possibly absolve the lack of initialization, but performance was still inferior to the nominal method, as shown in Fig. 9: (DS 4-2-1) yielded TRE of 3.3 mm (<15.5 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and NCC of 0.58; and (DS 8-4-2-1) yielded TRE of 2.6 mm (<13.8 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) and NCC of 0.59. Unlike the previous case (Sec. 3B4), in which coarse pyramids were found to undo the initialization provided by the model, a pure image-driven approach benefited from coarser pyramids, but at a final level of performance inferior to the nominal approach and with a large number of outliers.

CONCLUSIONS

A deformable registration technique has been presented and evaluated as a means to facilitate intraoperative image-guidance in VATS resection of lung nodules. These initial studies demonstrate the technique to be capable of registering the inflated lung (at inhale or exhale) to the fully deflated state, thereby enabling the transfer of information such as preoperative surgical planning or segmented target and critical structures to the most up-to-date intraoperative context during tumor resection. In addition to potentially obviating the cost and logistical burden of preoperative localization, the method may facilitate safer surgery by visualizing also the critical structures surrounding the surgical target. The proposed method was shown to achieve the objectives in two levels of geometric accuracy via serialization of two distinct registration methods: the first employing lung surface and bronchial airway models for fast initialization of the registration process, and the second employing a variant of the Demons algorithm applied to intensity-corrected images for achieving a finer image-wide match. The inflated to deflated lung registration was tested in a freshly deceased porcine specimen, and the performance was assessed both quantitatively and qualitatively using TRE, NCC, and visualization of image overlays over 12 datasets. For the nominal approach, the model-driven stage provided nodule localization within the target wedge (to be resected) with median TRE of 1.9 mm (<5.0 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) (within the specified goal of 3–5 mm), while the subsequent image-driven stage yielded higher-precision localization of the target as well as registration of adjacent critical anatomy and landmarks identified in preoperative planning with median TRE of 0.6 mm (<4.1 mm ${\mathrm{CI}}_{95}^{\mathrm{ub}}$) (within the goal of 1–2 mm).

The algorithm was designed with the intention of respecting the time constraints of intraoperative workflow, although initial implementation focused more on achieving the desired levels of geometric accuracy. The sparse feature data used by the model-driven stage provided a relatively fast coarse initialization, and estimates of the computational complexity and approximate runtimes of key operations were summarized in Sec. 2C. Extensive analysis of each discrete step of the algorithm also offered some insight on opportunities for improving performance and simplifying the overall approach in some scenarios. For example, eliminating the use of airways is a possible option, since the surfaces-only model appeared to provide a sufficient initialization for Demons to achieve the specified level of registration accuracy by virtue of the gradient-rich nature of the parenchyma.

A number of limitations should be acknowledged with respect to this initial implementation, and future work is underway to improve the approach in anticipation of future translational studies: (1) better automation of workflow; (2) further optimization of computational performance; and (3) a more homogeneous and robust level of geometric accuracy throughout the lung region. Registration of CT to CBCT was not considered in current work but was previously investigated in other anatomical contexts.²⁷ The methodology described above is likely to be consistent with such a registration task, with image intensity mismatch between CT and CBCT handled either by the APLDM method employed above or the IIM method detailed in previous work.²⁷ This would allow registration of the preoperative CT to either an initial intraoperative CBCT (I₀) or perhaps directly to the intraoperative CBCT of the deflated lung. The segmentation methods used to define the lung surfaces and airways currently require manual placement of seeds, and although a number of automated methods have been developed for CT,^{28, 29, 30} none have been yet adapted for C-arm CBCT or the intraoperative workflow. One particular segmentation challenge is in obtaining an accurate boundary at the medial surface, and the sensitivity of registration accuracy to such segmentation errors is a subject of future work. Alternative methods for vector field interpolation will also be investigated, including advanced vector spline methods such as thin plate splines or compact support radial basis functions, which offer a higher degree of control over the resulting deformation and tend to exhibit better local support and increased robustness against errant vectors in noisy data. Support for weighting that favors the more easily segmented lateral surface and larger airways (and thereby penalizes points susceptible to segmentation error) could also be implemented to increase robustness.

Future work includes further testing and evaluation on datasets that better approximate surgical conditions and real pathology, including testing on live specimen with real and/or simulated lung nodules. Such work will benefit from semiautomatic target identification methods to further streamline error analysis and accuracy validation.⁵⁶ The additional trials will be enabled in part by integration of the model-driven and image-driven methods in an in-house image guidance system,¹¹ also facilitating workflow analysis and preclinical testing in CBCT guidance of thoracic surgery. Previous work in the context of spine and skull base surgery have demonstrated the utility of such application-specific modules for early translational research in seeing CBCT guidance from the laboratory to early clinical studies.^{9, 57, 58} In CBCT-guided surgery, such modules will encompass not only the deformable registration approach described above (possibly including simplified forms for scenarios appropriate to model-only and model + image-driven approaches) but also integration of the registered data with thoracoscopic video for accurate real-time overlay of registered planning data directly on the thoracoscopic scene.¹⁰