Stochastic model reduction using a modified Hill-type kinetic rate law

Abstract

In the present work, we address a major challenge facing the modeling of biochemical reaction networks: when using stochastic simulations, the computational load and number of unknown parameters may dramatically increase with system size and complexity. A proposed solution to this challenge is the reduction of models by utilizing nonlinear reaction rate laws in place of a complex multi-reaction mechanism. This type of model reduction in stochastic systems often fails when applied outside of the context in which it was initially conceived. We hypothesize that the use of nonlinear rate laws fails because a single reaction is inherently Poisson distributed and cannot match higher order statistics. In this study we explore the use of Hill-type rate laws as an approximation for gene regulation, specifically transcription repression. We matched output data for several simple gene networks to determine Hill-type parameters. We show that the models exhibit inaccuracies when placed into a simple feedback repression model. By adding an additional abstract reaction to the models we account for second-order statistics. This split Hill rate law matches higher order statistics and demonstrates that the new model is able to more accurately describe the mean protein output. Finally, the modified Hill model is shown to be modular and models retain accuracy when placed into a larger multi-gene network. The work as presented may be used in gene regulatory or cell-signaling networks, where multiple binding events can be captured by Hill kinetics. The added benefit of the proposed split-Hill kinetics is the improved accuracy in modeling stochastic effects. We demonstrate these benefits with a few specific reaction network examples

INTRODUCTION

Models of gene regulatory and cell signaling networks provide useful insight and quantitative understanding of the underlying dynamics of a system.^{1, 2} These models find applications in systems biology, in an effort to decipher the complexity of naturally occurring gene networks or other cellular pathways. The present work focuses on gene networks that use natural components, such as the lactose,^{3, 4} tryptophan,⁵ tetracylcin,^{6, 7} and arabinose⁸ operons. These models are also useful to synthetic biology where the goal is to design and construct new gene networks, such as repressilators,^{9, 10} AND-gates,¹¹ and toggle switches.^{12, 13}

The present work focuses on addressing a major challenge facing the simulation of gene networks using stochastic simulation techniques. These techniques have long been deemed necessary for modeling gene networks because of the presence of small numbers of reactants and products in select reactions. Such techniques include the stochastic simulation algorithm (SSA) and its derivatives.^{14, 15, 16, 17} The challenge with stochastic simulations is that the number of reactions and components necessarily becomes large with system complexity, dramatically increasing computational load. The number of unknown parameters that need to be fit to experimental data may also increase.

There are two ways to address this prohibitive computational burden. First, develop novel algorithms to speed up simulation for highly complex and stiff reaction networks with accuracy.¹⁸ Second, by reducing the reaction set through the elimination or replacement of subsets of reactions.¹⁹ Suites of such reduction techniques have been developed to dynamically speed up stochastic simulation,²⁰ and we hope our work can eventually become a standard part of any such collection.

The purpose of the work presented is to extend stochastic reduction methods with Hill-type kinetics, and to demonstrate the importance of higher-order statistics when utilizing complex reaction rate laws in stochastic simulation. The Hill-type reaction rate law is a natural choice as a transcription regulation rate law because it takes into account multibinding site mechanisms. The Hill law is already naively used as an approximation for gene network repression in stochastic models.⁹ Complex rate laws use a small number of parameters to replace multiple reactions, and thus are limited when attempting to capture biochemical network statistics accurately.

The use of the related Michaelis-Menten²¹ approximation has been explored for stochastic simulations²² with promising results, but requires complex steady-state assumptions.²³ The approximation may also not remain valid when the enzymatic reactions are placed within a larger network, a question of modularity.²³ The use of Hill-type rate laws poses an even greater difficulty as there is no mathematical derivation of this complex reaction rate.²⁴ Additionally, exact mathematical analysis is intractable as the chemical master equation is nonlinear.²⁵ Despite these challenges, we show computationally that splitting the Hill-type reaction into a small reaction network allows the incorporation of the complex reaction rate into gene network models without sacrificing accuracy or modularity.

The use of the Hill rate law for stochastic simulation was tested using a small gene regulatory model utilizing complex rate laws. The form and parameter values for this model were developed from a full elementary model previously fit to experimental data. In practice reduced models would be directly matched to experimental results. In this preliminary proof-of-concept study the mean protein output of stochastic simulations using the reduced Hill model and full elementary model is instead compared. This exclusively computational approach is used to more directly compare the accuracy of the different model constructions.

Three separate example networks are presented in order to determine the accuracy of both the Hill-type reaction rate and a newly introduced split-Hill counterpart matching higher-order statistics. In the first case, repression comes from an outside controllable source and steady-state protein output is used to determine suitable Hill parameters. In the second case, the repression protein is looped back to form a feedback repression loop in order to compare the accuracy of the Hill and split-Hill reaction rate laws. In the third case, two genes are linked into a larger network to form a bistable switch. The bistable switch results test modularity, the ability of gene models to maintain accuracy when placed in larger gene networks.

In each of the above example networks, four sample transcription models are simulated using the next-reaction Gillespie SSA. In simple systems a typical method of transcription repression is the binding of a repression factor onto one or several operator sites in the promoter region of a gene. Additionally, repressor proteins may be active in a monomer form or in a complex (e.g., an active dimer). The four models take into account the combinations of these two variables: (1) One operator with monomer binding (1M), (2) One operator with dimer binding (1D), (3) Two operators with monomer binding (2M), (4) Two operators with dimer binding (2D). These four example configurations aim to demonstrate the versatility of the Hill rate law in reducing even complex regulatory mechanisms.

BACKGROUND

The Hill-type rate law is a simple nonlinear function with versatile dynamics and is an important building block of transcription regulation models. The full models include all of the important biomolecular interactions, including transcription, translation, degradation and repression, and are comprised of reactions with elementary kinetics. The reduced models are generally identical to the full models except that transcription repression is described by the single, more complex, Hill-type reaction rate law:

$$a_{\text{Hill}}=\frac{a_{max}{\left[S\right]}^n}{{\left[S\right]}^n+K_m^n}or{a}_{\text{Hill}}=\frac{a_{max}{K}_m^n}{{\left[S\right]}^n+K_m^n}.$$ (1)

The first equation is a positive form (activation), the second is a negative form (repression). Here a_max is the maximum propensity for reaction, [S] is the amount of substrate (in molecules), K_m is the Michaelis constant describing the amount of [S] necessary to reduce the propensity to a_max/2, and n describes the shape of the function. The Hill model was first proposed in the early 1900s as a description of cooperative and multi-site binding in hemoglobin.²⁶ Many transcription regulation mechanisms involve multiple binding sites in the promoter region. The Hill rate law could potentially replace many of these complex regulation mechanisms in their entirety.

In Sec. 3 for Hill parameter matching the Hill coefficients are found by a simple linear regression. It is first assumed that the steady state reporter protein concentration (P) is proportional to the production rate of the Hill function representing transcription repression (a_Hill). When no repressor ([S] in Eq. 1) is present in the system the resulting output is called the basal protein concentration and basal production rate (P_b and a_{Hill, b}, respectively). By dividing the protein output and production rate by their basal counterparts one obtains the following equation:

$$\frac{a_{\text{Hill}}}{a_{\text{Hill},b}}=\frac{P}{P_b}=P^{*}=\frac{K_m^n}{K_m^n+\left[S\right]}.$$ (2)

Through simple mathematical manipulation the following equation is determined.

$$\log \frac{1-P^{*}}{P^{*}}=n·\log \left[S\right]-n·\log K_m.$$ (3)

Note that P* ranges from 0 to 1 in repression. A linear regression for log-distributed repression concentrations (log [S]) will thus produce a slope n and an intercept of −n · log K_m. In this way the parameters n and K_m are determined from the reporter protein concentration data in a simple gene repression network.

Full models: Gene network and kinetics

In the analysis of the sample models that follows refer to Table 1 for a list of reactions and kinetic constants. The 1M-model utilizes Reactions 1–12, the 1D-model utilizes Reactions 1–12 and 19–21, the 2M-model utilizes Reactions 1–18, and the 2D-model utilizes Reactions 1–21. The reaction rates presented here are used in producing all elementary model results. The network configuration and kinetic parameters used throughout the study are designed for stochastic simulation and matched to experimental data. The network represents the type of model that would be replaced by a reduced model with complex reaction rates. The network provides a test-of-concept in applying complex reaction rates to what can be considered an experimentally fitted, modular, stochastic model.

Table 1.

List of reactions utilized in full and reduced models. The abbreviations listed above are: RNAp = RNA polymerase, RNAp* = DNA bound RNA polymerase, mRNA = messenger RNA, rib = ribosomes, rib* = RNA bound ribosomes, X_a = active repressor. Γ_{(rate, step)} reaction events are described by a rate $\left(\frac{1}{s}\right)$ and a number of steps.

#	Reactions	k	#	Reactions	k
1	DNA + RNAp → DNA:RNAp	107$\frac{1}{M·s}$	13	DNA + Xa → DNAx2	108$\frac{1}{M·s}$
2	DNA:RNAp → DNA + RNAp	0.1 $\frac{1}{s}$	14	DNAx2 → DNA + Xa	0.01 $\frac{1}{s}$
3	DNA:RNAp → DNA + RNAp*	0.01 $\frac{1}{s}$	15	DNAx1 + Xa → DNAx12	108$\frac{1}{M·s}$
4	RNAp* → RNAp + mRNA	Γ(30 600)	16	DNAx12 → DNAx1 + Xa	0.01 $\frac{1}{s}$
5	mRNA + rib → mRNA:rib	105$\frac{1}{M·s}$	17	DNAx2 + Xa → DNAx12	108$\frac{1}{M·s}$
6	mRNA:rib → mRNA + rib	0 $\frac{1}{s}$	18	DNAx12 → DNAx2 + Xa	0.01 $\frac{1}{s}$
7	mRNA:rib → mRNA + rib*	33 $\frac{1}{s}$	19	2 · X → Xa	108$\frac{1}{M·s}$
8	rib* → rib + Product	Γ(33 200)	20	Xa → 2 · X	1 $\frac{1}{s}$
9	mRNA →	0.002 $\frac{1}{s}$	21	Xa → X	0.00116 $\frac{1}{s}$
10	Product →	0.000578 $\frac{1}{s}$	22	DNA + RNAp → DNA + RNAp*	kHill
11	DNA + Xa → DNAx1	108$\frac{1}{M·s}$	23	DNA → DNAx	k−
12	DNAx1 → DNA + Xa	0.01 $\frac{1}{s}$	24	DNAx → DNA	k+

In the base model only transcription, translation, and degradation reactions are used to build a straightforward model of protein synthesis. Reactions 1–4 represent transcription. Reactions 1 and 2 are RNA polymerase binding and unbinding events, respectively. Reaction 3 is initiation of transcription, and Reaction 4 is elongation and termination. It should be noted that elongation events are represented as Γ distributed events. The Γ-distribution is equivalent to a string of identical first order reactions (see Table 1), and models a protein or ribosome stepping along DNA or messenger RNA (mRNA).¹⁵ Translation takes on a similar form, Reactions 5 and 6 involve the binding and unbinding of ribosomes on a length of mRNA. Reactions 7 and 8 are the initiation and elongation/termination of translation. Two degradation reactions for mRNA (Reaction 9) and Products (Reaction 10) are also included in the base model.

The values for k₁–k₃ are approximated from equilibrium constants for the tetracycline and lactose operons.^{27, 28, 29, 30} The values for k₄ and n are from elongation approximations.³¹ The values for k₅–k₇ and k₉ are designed to produce approximately 20 production events during the lifetime of a single mRNA molecule. The value for k₈ is also from elongation approximations.³² The variable k₁₀ specifies a 20 min half-life.⁷ Reaction 10 can refer to an output protein or a repressor protein. For multiple products Reaction 10 represents multiple reactions.

To form the four sample models, additional reactions are then added to the base model. To take into account a single operator site Reactions 11 and 12 are added. To add a second operator site Reactions 13–18 are added. Finally to add dimerization Reactions 19–21 are added.

For the sample examples k₁₁, k₁₃, k₁₅, and k₁₇ are on the same order as RNA polymerase binding. Then, k₁₂, k₁₄, k₁₆, k₁₈ give relatively tight binding affinities. The constants k₁₉ and k₂₀ are adapted from data for tetracycline repressors (dimer active).³³ Finally, k₂₁ is simply two times the degradation rate of a protein monomer (X).

While the use of these specific kinetic constants limits the generality of the conclusions presented herein, the model was fit to experimental data and provides a good proof-of-concept. Additionally, the gene network described in Table 1 exhibits sufficiently interesting behavior to more generally suggest that when transcription repression diverges from a simple exponentially distributed reaction, matching higher-order statistics is necessary to guarantee accuracy.

Reduced models: Hill-type reaction rate law

The purpose of a reduced model is two-fold: it should reduce the number of reactions and/or simplify the reaction network, and it should maintain accuracy. The addition of repressor protein binding to operator sites (Reactions 11–21) creates a multisite binding system in which the more versatile Hill-type kinetics (Eq. 1) can be applied. Once reduced, all four models (1M, 1D, 2M, and 2D) have the same number of reactions, representing a severe reduction in the number of reactions. In all cases the transcription repression mechanism is replaced in its entirety by the Hill rate law. This is a common technique in both deterministic and stochastic simulations already,⁹ although naively applied in the case of stochastic simulation.

The fundamental difference between the elementary and reduced models is the replacement of Reactions 1–3 and Reactions 11–21 by Reaction 22. Here the kinetic rate, k_Hill, takes the form:

$$k_{\text{Hill}}=\frac{k_{base}{K}_m^n}{X_a^n+K_m^n}.$$ (4)

Thus three parameters: k_base (units of $\frac{1}{M·s}$ because the reaction is 2nd order), K_m (units of M), and n (unitless) are fit to the mean stochastic simulation results for the full elementary models. The remainder of each model is simply Reactions 4–10 condensing the repression function into strength (K_m) and shape (n) parameters.

Split Hill model theory

As will be shown the Hill-type kinetics are not readily applicable to stochastic simulations. Part of the problem is the inability for the Hill-type kinetics to capture the higher-order statistical properties found in the elementary model. Since the Hill rate law is replacing multiple elementary reactions by a single reaction rate the reaction events will often no longer be well described by an exponential distribution. This reduction results in a loss of accuracy in matching higher order moments when the Hill parameters are fit to mean results. The proposed solution is to split the Hill-kinetic model into multiple reactions. The additional degree of freedom will match higher-order statistical properties and allow the model to reclaim some of the loss of accuracy.

Reactions 23 and 24 are added to the system and they function as availability reactions for the DNA molecule described in Reaction 22. To implement these reactions a form for the rate laws (k⁻ and k⁺) need to be determined. Reactions 23 and 24 are both first order and thus the mathematics describing DNA availability can be determined exactly. By setting k_Hill to k_base the steady-state mean availability of the DNA is determined by

$$\frac{\partial ⟨\text{DNA}⟩}{\partial t}=0=-k^{-}⟨\text{DNA}⟩+k^{+}⟨{\text{DNA}}_x⟩,$$ (5)

where ⟨DNA_x⟩ is unavailable DNA and ⟨DNA_x⟩ = DNA_Total − ⟨DNA⟩. By manipulation the following equation is obtained.

$$\frac{{⟨\text{DNA}⟩}_{ss}}{{\text{DNA}}_{Total}}=\frac{k^{+}}{k^{+}+k^{-}}=\frac{1}{1+\left(\frac{k^{-}}{k^{+}}\right)}.$$ (6)

Note that what we have found is the percentage of DNA available at a given time.

To get the appropriate form the availability is matched to the Hill function. The following equation needs to be satisfied:

$$k_{base}{⟨\text{DNA}⟩}_{ss}=k_{\text{Hill}}{\text{DNA}}_{Total}.$$ (7)

Thus,

$$\frac{k_{base}}{1+\left(\frac{k^{-}}{k^{+}}\right)}=\frac{k_{base}}{1+{\left(\frac{X_a}{K_m}\right)}^n}.$$ (8)

This provides an additional degree of freedom (k⁺, a first-order reaction rate) and a form for k⁻ (also first-order),

$$k^{-}=k^{+}{\left(\frac{X_a}{K_m}\right)}^n.$$ (9)

This derivation relies on RNA polymerase concentration remaining relatively constant throughout the simulation.

The same k_base, K_m, and n fitted for the reduced model are used. Other forms for Eq. 9 are possible. For example, if k⁻ was the positive form of Eq. 1 and k⁺ was the negative form of Eq. 1, then Eq. 9 would remain valid. The chosen construction was used because if n = 1, splitting the Hill rate law should result in a first order reaction for k⁻ and zeroth order reaction for k⁺. This condition is desirable when reducing Michaelis-Menten like systems, and holds for Eq. 9. In this case the Split-Hill model is still conceptually simple and eliminates 2–11 reactions depending on the form of repression.

The non-Poisson behavior exhibited by added the availability reactions into the Hill network is due to a state of latency as DNA enters the off-state. In theory, as the k⁺ value goes to infinity the network will immediately reach steady state and the Poisson behavior is restored. Lower k⁺ values correspond to a higher period of latency and non-Poisson behavior.

It should be noted that additional splits could be applied to capture more information about the higher-order statistics. Such additional splits would increase accuracy in theory, especially for systems with very strong stochastic effects, but also complexity. Eventually, the number of parameters to be matched and size of the model will be equivalent to the elementary model. The give-and-take between complexity and accuracy would be interesting to observe in larger or more complex networks than were chosen for this study.

Bistable switch model

The final test of both the Hill-type kinetics and the split-Hill kinetics in a simple repressor system is the effect of these two methods on modularity. Modularity represents the universality of a model. A large complex model comprised of multiple smaller models should retain accuracy without altering the model parameters determined for the small models when isolated. A simple system for testing modularity is a dual-repressor bistable switch (Figure 4, inset). Two 2-operator dimer repressed genes (A and B) with kinetic constants identical to the 2D model are used. Gene A outputs a repressor monomer, X_B, that complexes and represses the function of gene B. Gene B acts similarly, producing a repressor monomer, X_A, the represses the function of gene A.

Figure 4.

Elementary (blue solid line), Hill (red circle-line), and split-Hill (green dashed line) models, mean product count versus time for gene A. The inset figure describes the reaction network. Each line represents an average over 10 000 trajectories.

In bistable switches there is often a signal that causes the network to switch states. In the sample model this is not the case. Instead the network is either dominated by gene A or gene B from the start, and the steady-state behavior is thus of little interest. Modularity is instead compared by observing how the models evolve early in the simulation.

RESULTS

Reduced Hill parameter fits and feedback results

In the reduced models it is necessary to fit the three parameters (k_base, K_m, and n) to data procured from full stochastic simulations. Only the steady state product output, for a range of repressor levels, is used to obtain the fit. This method is used because, while we are fitting to data from stochastic simulations, it would be desirable to fit the parameters to experimentally realizable data. Typically, the data available experimentally are the level of a output fluorescence protein. The parameters are fit using a simple linear regression based on Eq. 3. In these fits the maximum propensity is approximately equal to 0.00975 $\frac{1}{s}$ for all models. By dividing by the total RNA polymerase in the elementary model a k_base of 21 800 $\frac{1}{M·s}$ is found. The total number of RNAp molecules on average was chosen as 270 molecules, enough to saturate the system. The fits are provided in Figure 1.

Figure 1.

The Hill parameter fits for models 1M, 1D, 2M, and 2D. The parameters K_M and n are given in the plot along with R² values for quantitative comparison. The steady-state of the product from elementary stochastic simulations (blue dots), and the linear fit from Eq. 3 (red dashed line).In the figure, X refers to X_a (monomer).

In Figure 1, simulation results are shown from all four elementary models for various levels of repressor (X_a for monomer repression, X for dimer repression). By eliminating generation and degradation reactions the level of repressor is constant and a steady-state product concentration is found. This is approximately equivalent to determining a steady-state output when a known concentration of repressor protein is provided to a sample. The final Hill parameters are provided in the figure insets along with the R² values for the fits.

Once the Hill parameters are determined the reduced models are tested in feedback loop repression. Feedback loops are simulated using both elementary and reduced models. The mean product outputs are compared by relative root mean squared differences (rRMS). The variance-to-mean data (VMR) for the mRNA output is also provided for analysis. In stochastic systems reactions are assumed to be Poisson distributed events, so the time between reaction events is exponentially distributed. Poisson processes have the distinct feature of a variance-to-mean ratio of one. The VMR data give a rough metric for determining when repression diverges from a simple Poisson process, and thus when higher-order statistics become significant.

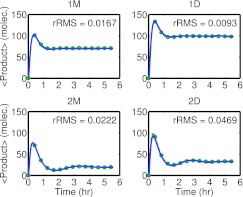
The mean product output for all four models is shown in Figure 2. In all four cases the transient behavior, specifically the overshoot of the steady-state early in the simulation, differs significantly. Quantitative comparisons are reported in Figure 2. For the 1M, 1D, 2M, 2D models the steady-state VMR for mRNA production for the full models are 0.983, 0.989, 1.247, 1.321. Thus the 2-operator models diverge significantly from simple Poisson processes. For the reduced models the VMRs are 0.918, 0.902, 0.992, 0.950, respectively. The reduced models tend to lie close to a VMR of one, and fail to capture the more complex behavior in the 2-operator system. By reducing mRNA production to a single reaction an implicit assumption was made that repression is an approximately Poisson distributed event. This naive application of Hill kinetics fails to accurately describe the behavior of the system.

Figure 2.

Models 1M, 1D, 2M, and 2D, mean product count versus time. Elementary (blue solid line) and reduced (red circle line) models. Each line represents an average over 10 000 trajectories. Elementary simulations used Hy3S, reduced simulation used a basic Gillespie next-reaction SSA. Relative root mean squared differences (rRMS) values are provided for comparison.

Split-Hill results

In the case of the split-Hill model the same four sample models (1M, 1D, 2M, and 2D) were simulated, and the product means were compared. In Figure 3 the mean output is plotted for both the elementary and split-Hill models. The constant k⁺ is adjusted to create the best quantitative fit to the elementary data. For the 1M model k⁺ = 0.0086  s⁻¹, for the 1D model k⁺ = 0.0075 s⁻¹, for the 2M model k⁺ = 0.000185 s⁻¹, and for the 2D model k⁺ = 0.00028 s⁻¹. Figure 3 also provides a quantitative comparison of the fits (as described by the rRMS). Across all models the fitted split-Hill model provides a more accurate representation of the full-model results.

Figure 3.

Models 1M, 1D, 2M, and 2D, mean product count versus time. Elementary (blue solid line) and split-Hill (green circle line) models. For the split-Hill model k⁺ = 0.0086 s⁻¹ (1M), 0.0075 s⁻¹ (1D), 0.000185 s⁻¹ (2M), and 0.00028 s⁻¹ (2D). Each line represents an average over 10 000 trajectories. Relative root mean squared differences (rRMS) values are provided for comparison.

For the 1M, 1D, 2M, 2D models the steady state VMRs for mRNA production for the split-Hill models are 0.997, 1.031, 1.380, 1.496, respectively (compared to 0.983, 0.989, 1.247, 1.321, from before). In the case of one-operator models (1M and 1D) the VMR of the split-Hill model matches well with the elementary case. In these cases the higher-order effects are primarily due to the DNA-promoter region going into a period a latency when bound by a repressor. For the one-operator models this effect is restored. In the cases of the two-operator repressors, the VMR is still significantly different, but now the reduced model shows a VMR greater than 1, and thus is able to capture non-Poisson behavior.

Bistable switch and modularity

Finally, the bistable switch model was simulated for the full model, the reduced Hill model, and the reduced split-Hill model. The three resulting trajectories for gene A through time are shown in Figure 4. Quantitatively, the rRMS for the Hill and split-Hill models are 0.0363 and 0.2425, respectively. The split-Hill model tends to conserve modularity more effectively than the Hill-model, presumably due to the more accurate matching of higher-order statistics.

DISCUSSION

The results provided herein attempt to quantify the affect of reducing a full elementary reaction network using complex reaction rate laws on both the accuracy and modularity of the model. Hill parameters were fit to mean output protein concentrations and four sample models were created. Simple feedback loop networks were compared to test accuracy and a bistable switch network was used to test modularity. Relative root mean squared differences analysis was used to quantify the accuracy of the simulation compared to the full elementary simulation results.

The Hill-type rate law was able to match the mean output protein results for the four systems with reasonable accuracy (see Figure 1). The single complex rate law was thus used to replace a number of elementary reactions. The four models were then reconfigured to form simple feedback loops. The mean output of the Hill models were compared to elementary reaction network results to assess accuracy of the Hill-models (see Figure 2). As was demonstrated the one-operator systems exhibited reasonable accuracy, but the two-operator models diverged significantly from the full-model results.

The VMR ratios indicate that the two-operator systems diverge from simple Poisson processes (VMR = 1) exhibited by the Hill models. The failure to match output dynamics using the Hill type kinetic rate law is due to the inability to accurately account for complex higher-order statistics observed in gene transcription.

The proposed solution is to split the Hill-reaction rate into several more abstract reactions in order to generate an additional degree of freedom. This additional kinetic constant (k⁺) can be fitted in such a way that the higher-order statistics are accounted for, and accuracy in the feedback loop is much improved (see Figure 3). The VMR, while not an exact match, indicates that the split-Hill model is able to exhibit the highly non-Poissonian behavior that is observed in these more complex gene repression schemes. Note that in Figure 2 the models with high rRMS values corresponded to lower k⁺ values in Figure 3. This intuitively makes sense because the poor fits were likely due to an inability to match higher-order statistics corresponding to a need for a higher latency period in the availability reactions.

The final observation was concerning modularity. The ability for a smaller kinetic model to be plugged into a large network without modification to its parameters is a trait that is highly desirable in gene models. The results from the bistable switch suggest that the effects of higher-order statistics can result in disproportionately inaccurate mean output results when present in a larger gene network. The split-Hill, with a better fit for higher-order statistics, appears to maintain a higher level of modularity.

The primary advantage of the models presented is their intuitive construction. The Hill-type reaction rate law is well classified and versatile. When necessary, higher-order statistics are then progressively folded into the system as new data are made available. The question of when it is appropriate to split the Hill model is still open considering the mathematical difficulties involved with stochastic simulation. At the moment the only way to implement the model as presented would be to fit the parameters to experimental data and then observe the fit. While the resulting network is more abstract than elementary models or the reduced Hill-model, the added versatility of the split-Hill model may allow for model reductions that can be widely applied, maintain accuracy, and are modular.

CONCLUSION

Working with sample models of small gene networks (1–2 genes) and borrowing kinetic parameters from previous studies we propose that: (1) It is possible to successfully implement Hill-type kinetics in stochastic simulations with some modification; (2) The reduced models are simpler and more intuitively constructed compared to de novo models currently in existence; (3) Unknown kinetic constants can be approximated from data analogous to experimentally obtainable data with current technology; (4) The final models maintain a level of modularity not found in models using traditional Hill-type kinetics.

Four single-gene feedback repressor models were produced: a single operator monomer-repressed model (1M), a single operator dimer-repressed model (1D), a double operator monomer-repressed model (2M), and a double operator dimer-repressed model (2D). It was shown that even in simple cases the reduced models using Hill-type kinetics to represent transcription repression could not accurately capture the transient results. By splitting the Hill model into three reactions an additional degree of freedom (k⁺) allows for the mean output to match almost exactly to the elementary model (Figure 3). This additional degree of freedom in the split-Hill model allows for the higher moments (such as the variance) to be fit better than in a traditional Hill-type kinetic model. The bistable switch results also suggest that such systems can have a higher degree of modularity compared to the reduced Hill-models.

The results as presented suggest that the split-Hill modification may allow for much simpler systems to accurately describe the mean output of gene networks. The advantage of the split-Hill model is its ability to retain the simplicity of the Hill-type kinetic rate law while accounting for the importance of higher-order statistics, in particular the variance, in a stochastic simulation. The model parameters are easily fit to accessible data, and what is provided is a method for intuitively matching the higher-order statistics. While it is not suggested that the split-Hill model is or should be used as a catch all for transcription regulation, it does indicate that even in simple systems the importance of matching higher-order statistics, when available, should not be underestimated.