Perspective: Alchemical free energy calculations for drug discovery

Abstract

Computational techniques see widespread use in pharmaceutical drug discovery, but typically prove unreliable in predicting trends in protein-ligand binding. Alchemical free energy calculations seek to change that by providing rigorous binding free energies from molecular simulations. Given adequate sampling and an accurate enough force field, these techniques yield accurate free energy estimates. Recent innovations in alchemical techniques have sparked a resurgence of interest in these calculations. Still, many obstacles stand in the way of their routine application in a drug discovery context, including the one we focus on here, sampling. Sampling of binding modes poses a particular challenge as binding modes are often separated by large energy barriers, leading to slow transitions. Binding modes are difficult to predict, and in some cases multiple binding modes may contribute to binding. In view of these hurdles, we present a framework for dealing carefully with uncertainty in binding mode or conformation in the context of free energy calculations. With careful sampling, free energy techniques show considerable promise for aiding drug discovery.

INTRODUCTION

Structure-based drug design seeks to predict binding

Structure-based drug design seeks to take an experimental structure of a drug target and identify or design a small molecule which binds to this macromolecular target in a desired way, modulating its function and thereby treating a target disease or condition.^{1, 2, 3} The goal is a process which begins with a structure and yields a good drug.^{2, 4} Unfortunately, every aspect of this process has proven challenging.

Currently, computational techniques are applied throughout the discovery process.^{3, 5, 6, 7, 8} Of particular interest here are the early to middle stages of the process, where one seeks to first identify an initial “hit”—a small molecule which binds to the target with sufficient affinity to be interesting—and then improve this molecule's properties, affinity, and specificity to the point where it is good candidate for further development as a drug.^{6, 7, 9} That is, we seek computational techniques which can be applied to hit identification (often called “virtual screening” as this is usually applied to screen libraries of compounds) and the lead optimization stage of drug discovery.

At the earliest stages of this process, large libraries of existing compounds are often considered,^{3, 10, 11, 12, 13} so computational techniques need to above all be fast, even if unreliable for many individual molecules.¹⁴ But once initial hits are identified, the goal changes from identifying which molecules bind, to making these initial hits bind better, otherwise improving their properties, or expanding chemical diversity.⁹ At this stage (lead optimization), accuracy is a much larger consideration than speed, as experiments now involve synthesis of new molecules and can be slow and expensive.^{3, 15} An accurate computational method could reduce the need for synthesis and experiment and accelerate the process.

Existing computational methods used in the pharmaceutical industry are mostly focused on the earliest stages of this process—library screening. These methods, including docking, chemoinformatics, and ligand-based methods, are highly approximate and often empirical. While they can be helpful for screening large libraries, their ability to predict binding strength is typically extremely poor.^{7, 10, 16, 17}

Free energy calculations could guide structure-based design

Free energy calculations based on molecular simulations show promise at providing higher accuracy for the lead optimization stage of discovery. These calculations yield binding free energy (or affinity) results which are correct given the force field (which provides the potential energy as a function of system configuration), at least in the limit of adequate sampling and simulation time.^{4, 18, 19, 20, 21, 22} Our focus is mainly on “alchemical” free energy calculations, which see the most use, and particularly on innovations that make these calculations appealing for drug discovery, as well as challenges that still stand in the way of their widespread use.

Binding free energy calculations yield either absolute free energies (measuring the free energy of binding of a single ligand to a single receptor), or, more commonly, relative free energies (comparing the binding of related ligands to a receptor or a single ligand to related receptors). Relative calculations are generally thought to be more efficient.^{4, 19, 20, 23} This is partly because practitioners hope for a cancellation of errors where, for example, inadequate sampling of receptor motions for one ligand would have similar effects on binding of another ligand, thus yielding minimal errors. While this cancellation is not guaranteed, it seems reasonable to us that for small ligand modifications, relative free energy calculations will indeed be more efficient. Also, accurate prediction of relative binding free energies would be well suited to applications in lead optimization, as noted above. For these reasons, we focus here on relative calculations.

Alchemical free energy calculations work by introducing a series of intermediate unphysical states spanning between the desired end states. For example, for relative calculations, binding free energies are compared by changing one ligand into another or turning off interactions of one ligand in a receptor while turning on interactions of another ligand in a receptor (Fig. 3). The intermediate states here are, roughly speaking, associated with fractional presence of each ligand, as discussed in more detail elsewhere.^{4, 18, 19, 20, 21}

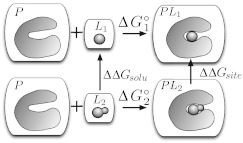
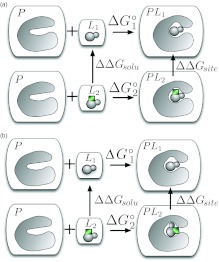
Figure 3.

Standard thermodynamic cycle for relative free energy calculations. P represents the protein (or receptor) and L the ligands. To compute the relative binding free energy of two ligands, L₁ and L₂, to the same protein, L₂ is mutated into L₁ in solution yielding ΔΔG_solv, and L₂ into L₁ in the binding site, yielding ΔΔG_site. The difference, ΔΔG_site − ΔΔG_solv, is related to the difference of $\Delta G_1^{\circ }$ and $\Delta G_2^{\circ }$. In the figure, each box denotes a separate solvated system which does not interact with the other boxes.

Alchemical free energy calculations are built on groundwork laid by Kirkwood²⁴ and Zwanzig,²⁵ among others. Kirkwood described a coupling parameter approach, where a parameter (λ) controls interaction strength between a molecule or particle and the remainder of the system, and described how this could be used to compute free energy differences using thermodynamic integration (TI). Zwanzig showed that a free energy difference between two states can be computed via an appropriate exponential average of energy differences over an ensemble of configurations.²⁵ The coupling parameter approach underlies all alchemical free energy simulations, and TI and the Zwanzig relation can be thought of as analysis techniques for these calculations.

Since these techniques predate molecular simulations, they were quickly applied in new ways in simulations. Many early applications focused on solvation free energies.^{26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38} Soon after the basic idea for relative binding free energy calculations was laid out,³⁹ the first applications to binding followed, in host-guest systems^{30, 40, 41} and proteins.^{35, 42, 43, 44, 45, 46, 47} Several early reviews provide useful perspective.^{48, 49}

Despite early enthusiasm for alchemical calculations, a number of key innovations were necessary to make them more robust. The development of “soft-core potentials”⁵⁰ or “separation-shifted scaling”⁵¹ led to much better convergence⁵² for transformations involving changes in the number of atoms or chemical structure, opening up new applications and improving performance. Rediscovered appreciation for the Bennett acceptance ratio approach⁵³ for computing free energies^{54, 55} yielded a much more efficient analysis tool than the Zwanzig relation, and the subsequent generalization into the multistage Bennett acceptance ratio took this still further.⁵⁶ Today, these improvements make solvation free energy calculations for small or at least fragment-like molecules essentially routine,^{57, 58} even for hundreds of molecules^{59, 60, 61, 62, 63} and binding free energy calculations are much more tractable.

Relative free energy calculations have seen some significant applications. The Jorgensen lab at Yale routinely applies MC-based alchemical free energy calculations to help guide optimization of lead candidates in an early-stage drug discovery setting.^{15, 64} Several other groups in academia have applied them in similar efforts.^{65, 66, 67} Industry has also found some use for these techniques,^{68, 69, 70} and several studies have argued that these methods are accurate enough to be used routinely in a drug discovery context.^{4, 71, 72, 73, 74} Several recent reviews cover foundations and highlights.^{4, 18, 19, 20, 75, 76}

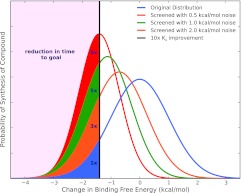
Robust free energy calculations could have a profound impact on the drug discovery process with a modest level of accuracy. To see this, consider a hypothetical discovery pipeline (following Ref. 4). A computational chemist participates in an existing drug discovery project which already has several hits which otherwise look promising but lack sufficient affinity. The computational chemist's job, each week, is to take a list of proposed compounds which could be made next and select the most promising for synthesis. For example, the medicinal chemistry team might propose 100 compounds and the computational chemist might need to select 10 for synthesis. Assume our goal is to gain a factor of 10 in binding affinity (or make the binding free energy better by ∼1.4 kcal/mol). What accuracy do we need to achieve to dramatically reduce the time or number of compounds that must be synthesized to reach this goal? It turns out that even a very modest level of accuracy can provide significant benefits for lead optimization (Fig. 1). To quantitatively analyze this, we assume our computational method yields correct affinity predictions with a given level of Gaussian random noise, and ask what level of noise we can tolerate. It turns out that the distribution of affinity changes seen in actual compounds proposed by medicinal chemists is very nearly Gaussian and centered at an affinity change of zero.⁷⁷ Thus, a rather simple statistical analysis is possible. Screening a fixed number of compounds will result in finding an increasing number of highly potent compounds as the method's noise goes down (Fig. 1). We can use this to reduce the number of molecules which must be synthesized. Assume we will actually screen up to 10 molecules each week, and ask how many total molecules must be screened to gain a factor of 10 in affinity after filtering by our computational method. With 0.5 kcal/mol of noise, the number screened is reduced by a factor of 8; with 1.0 kcal/mol of noise, a factor of 5, and with 2.0 kcal/mol of noise, a factor of 3 (see Ref. 4). Thus, a method which could screen ∼10–100 molecules per week with even 2 kcal/mol of noise would impact lead optimization by reducing the synthesis needed in a lead series by a factor of 3.

Figure 1.

The probability of synthesizing a compound with a particular binding free energy change. Filled regions indicate those compounds with at least a factor of 10 gain in binding affinity, and are labeled with the reduction in the number of compounds which would need to be synthesized (on average) to gain this factor of 10 in affinity. Blue is the approximate distribution observed experimentally for compounds proposed internally at Abbott; orange, green, and red are distributions generated by filtering molecules with a hypothetical computational method which gives correct free energy estimates with 2.0, 1.0, and 0.5 kcal/mol of noise, respectively. Figure adapted from Ref. 4.

In reality, binding affinity is just one consideration in lead optimization—improvements in affinity must be balanced against other factors such as solubility, bio-availability, stability, and so on.^{6, 7, 8} Still, accurate tools for affinity prediction will provide tremendous help. For example, ligand modifications made for solubility reasons must not ruin the binding affinity, so affinity prediction will be useful even while optimizing other factors.^{7, 20}

In summary, free energy calculations could dramatically aid structure-based drug design, one of our overarching goals. But a concrete and hopefully realistic near-term goal is to routinely exceed a 2 kcal/mol (root mean squared error) level of accuracy in computing relative binding free energies of related molecules. If possible with reasonable computational efficiency, this would yield real improvements in early-stage drug discovery.

Free energy calculations face serious challenges

Free energy calculations, while in principle rigorous, face three main challenges. One is simply a logistical challenge—these calculations remain difficult to set up, conduct, and analyze, and choices which may be relatively unimportant for other types of molecular simulations (such as the choice of thermostat, barostat, or even cutoff⁷⁸) can adversely affect accuracy. But beyond logistics, computed free energies can be in error because of limitations in the force field or due to inadequate sampling. In the limit of infinite sampling, most analysis approaches are guaranteed to yield correct free energies for the force field. But practical simulations may often fall short of this limit, and research on how much simulation is needed to reach this limit is ongoing.

Here, our interest is free energy techniques themselves—that is, obtaining correct results for the particular setup and choice of force field. So we focus primarily on limitations due to sampling, as new force field developments can generally easily be incorporated in free energy simulations. Evidence from solvation free energy studies suggests that current force fields actually may be good enough to reach the level of accuracy needed for relevance to pharmaceutical drug discovery, further justifying our focus on sampling.^{59, 60, 61, 62, 63, 79, 80, 81} It is certainly the case that force field limitations do exist,^{59, 62, 63, 82} but these are not our focus here. There are many different places where sampling can go wrong. We might have difficulty finding the relevant configurations of a system, or obtaining correct populations for these configurations. This could occur for the receptor, such as in the case of receptor conformational changes, or for the ligand (for ligand conformational changes or changes in binding mode).

Assessing the magnitude of the error introduced by sampling problems in relative free energy calculations can be difficult, but some compelling evidence shows these problems introduce significant errors. Since the sum of free energies around any thermodynamic cycle is by definition zero, cycle closure errors provide a lower bound on the amount of sampling error present in free energy calculations. In cycle closure analysis, the relative binding free energy of two ligands is computed by at least two different paths, forming a cycle. Cycle closure errors are reported relatively infrequently, but in cases where they have been reported, cycles may fail to close (indicating an error) by as much as several kcal/mol, far in excess of statistical error estimates,^{83, 84, 85, 86, 87} suggesting serious sampling problems. This may contribute to relative free energy calculations' reputation for unreliability, where performance can be good in some systems and terrible in others.

Some significant error in free energy calculations, then, originates with sampling problems. Considering a flexible ligand binding to a flexible receptor, our fundamental problem is that multiple states contribute to binding. These include multiple conformations of the receptor, multiple conformations of the ligand, and multiple orientations of the ligand,⁸⁸ as we discuss further in Sec. 1E. Adequate sampling means that our simulations have visited all of the relevant states in the correct proportions, and thus we can obtain correct free energies. Some or all of these states will be within the same local minima on the energy landscape, so interconversion between them will be relatively quick. But other states may be separated by substantial barriers. We will call these distinct metastable states separated by barriers “binding modes.” Different binding modes may differ in ligand orientation, ligand conformation, receptor (usually protein) structure, or even presence or absence of water molecules in the binding site region, for example.⁸⁸ Given this (broad) definition of a binding mode, then, typical sampling errors in free energy calculations originate from a failure to adequate sample relevant ligand-receptor binding modes.

Many sampling problems involve binding mode sampling challenges

This problem of binding mode sampling is particularly important for relative free energy calculations. Specifically, relative free energy calculations (as we discuss below) typically assume that two related inhibitors share a common binding mode or that any energy barriers between binding modes are small, so their different potential binding modes interconvert quickly. While this is sometimes the case, there are many cases where the binding mode is not shared or not known a priori and interconversion is slow, leading to the potential for serious errors, as we show in the examples that follow.

To be more specific, whenever the dominant ligand binding mode is not definitively known for the two ligands being compared, and shared by these two ligands, the thermodynamic cycle may not close, except in the limit of impractically long simulations. In this case, no accurate affinity prediction is possible. Computed relative free energies may be incorrect by an unknown amount which, as we highlight below, is related to the free energy of changing binding modes. Recall that by “binding mode” here we include ligand orientation and also ligand and receptor conformation.

Binding modes are difficult to predict

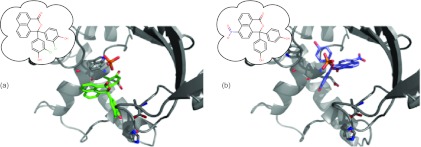
Both experimental and computational evidence suggests this binding mode problem poses a real challenge. In lead optimization, one typically starts from a known inhibitor of a protein (often with a known binding mode) and modifies it to attempt to improve binding.^{19, 70, 89} In cases where the ligand binding mode is maintained as functional groups are modified, conventional relative free energy calculations may often work well without any special treatment of alternate potential binding modes. However, small modifications to ligands do on occasion yield big differences in ligand binding orientation,^{65, 88, 90, 91, 92, 93, 94, 95, 96, 97} and there is currently no way to know when this will happen. For example, Stout et al. developed a series of thymidylate synthase (TS) inhibitors based on phenolphthalein and phthalein derivatives. They found that changing a five membered ring to a six membered ring dramatically altered the binding mode, then adding a nitro group (removing two chlorines) to the resulting compound introduced yet another unexpected binding mode (Fig. 2). These changes led to marked differences in affinity and specificity for the enzyme, and the authors highlighted how some other structures show multiple binding orientations for individual inhibitors. They speculate that many TS inhibitors actually have multiple binding orientations, with the affinity involving a combination of these.⁹¹ A variety of data suggests this same conclusion may hold true in a variety of other systems.^{20, 68, 88, 97, 98, 99, 100, 101, 102, 103} Going beyond ligand orientation, closely related ligands can bind with significantly different protein conformations. Protein conformational changes can be important, and even protein side chain differences in the binding site can be slow and, calculations indicate, thermodynamically significant.^{101, 103, 104, 105} Ligand modifications can also result in changes of binding mode by way of displacing water molecules.⁸⁷ So related ligands may have significantly different binding modes, in terms of binding orientation, protein conformation, or even binding site water occupancy.

Figure 2.

Thymidylate synthase inhibitors. (a) Initial binding mode. (b) Modified binding mode on addition of a nitro group and deletion of chlorines. (PDB codes 1TSL and 1TSM⁹¹).

The situation is even worse if we move beyond lead optimization and imagine using relative free energy calculations to screen binding of a small library of more dissimilar compounds. As structural dissimilarity grows, we can expect that alternate binding modes (in the form of alternate ligand orientations or conformations, or alternate protein structures) become increasingly likely. Furthermore, in screening a small library of compounds, there is no guarantee we know the bound structure of either ligand, let alone that they share a common binding mode.

Hence, the issues discussed here are likely to affect relative free energy calculations in a variety of different applications, even for drug-like ligands.

Computation provides some evidence concerning how much binding mode sampling problems can affect binding free energy estimates. Previously, we found that an alternate stable (and potentially reasonable) binding mode of phenol in a model binding site differed by 4.0 kcal/mol in free energy from the true binding mode, yet was predicted to be the dominant binding mode by some docking techniques.¹⁰⁶ Thus, mutating phenol into benzene in this binding mode, for example, would yield computed binding free energies erroneously favoring binding of benzene over phenol by 4 kcal/mol. Thus, appreciable errors are possible. Problems of similar magnitude were also observed in some relative free energy calculations—the ΔΔG between different small ligands in the polar lysozyme cavity varied by up to 4 kcal/mol depending on how the mutation was set up, for reasons that were attributed to sampling of binding modes.¹⁰³

These trends seem to hold true in pharmaceutically relevant binding sites. For thrombin inhibitors, addition of a methyl group yields a ring flip which alters the binding mode; without special care, free energy calculations miss this change in binding mode and yield errors around 1 kcal/mol in computed relative free energies.¹⁰⁵ Work on neutrophil elastase using end-point free energy calculations considered multiple binding modes and found one case where the relative free energy was clearly wrong due to two different kinetically distinct conformations of a ligand (by up to 1.6 kcal/mol). Obtaining correct binding free energies required including the free energy of flipping the relevant portion of the ligand.⁶⁵ Michel et al. used dual-topologies to compute the relative free energy between different potential binding modes of the same ligands,^{107, 108} highlighting the fact that adequate sampling over binding modes is not guaranteed, nor is the binding mode always obvious. Here, subtle differences in ligand composition could easily alter the binding mode,¹⁰⁷ and stable binding modes differed by 1 kcal/mol¹⁰⁷ to 7 kcal/mol.¹⁰⁸ One other study of particular interest highlighted multiple binding modes of catechol-O-methyltransferase inhibitors which had to be treated separately in relative calculations because of time scale issues.⁶⁸ Multiple distinct binding modes were seen and in one case differed by up to 1.5 kcal/mol. Other applications have highlighted similar issues.^{18, 109, 110, 111, 112} Water plays a thermodynamically significant role as well—slow water motions into and out of binding sites can yield errors in computed relative free energies in excess of 10 kcal/mol.⁸⁷ Thus, available computational data, though limited, suggest that issues relating to uncertain, incorrect, or changing ligand binding modes can introduce errors up to 7 kcal/mol in relative binding free energy calculations when these effects are ignored. Errors relating to binding mode may be a factor in both the overall unreliability of these calculations and in the cycle closure problems noted above.

Clearly, binding free energy calculations face very real sampling challenges. Modifying an existing ligand with a known binding mode, without taking into account the possibility of an important, slow change in binding mode, can lead to errors of several kcal/mol in relative free energy calculations. Uncertainty in ligand binding mode can introduce similar errors. We now discuss how typical relative free energy calculations are done, then highlight how binding mode changes can introduce these errors, and provide a general framework for handling multiple binding modes and changes in binding mode in the context of relative free energy calculations.

THEORY OF RELATIVE FREE ENERGY CALCULATIONS

Relative free energy calculations normally assume adequate sampling

Here, our interest is accurate calculations of relative binding free energies of different ligands to a receptor. We must assume, based on the analysis above, that their binding modes may not be completely known. As noted, the idea of “binding mode” here includes receptor conformation, as well as ligand position and orientation and ligand conformation.

Relative binding free energy calculations employ a thermodynamic cycle like that shown in Fig. 3. This cycle compares binding of ligands L₁ and L₂ to a single protein receptor, using an alchemical transformation of L₂ into L₁. The cycle involves turning L₂ into L₁ in solvent (or replacing L₂ with L₁), which yields ΔΔG_solv, and turning (or replacing) L₂ into L₁ in the receptor binding site, which yields ΔΔG_site. Since these compose two legs of a thermodynamic cycle as shown, we can then write $\Delta G_1^{\circ }-\Delta G_2^{\circ }=\Delta \Delta G_{site}-\Delta \Delta G_{solv}$, where $\Delta G_1^{\circ }$ is the standard binding free energy (also sometimes called the absolute binding free energy) for L₁ and $\Delta G_2^{\circ }$ is the corresponding quantity for L₂. Alternatively, ΔΔG_{1 → 2} = ΔΔG_site − ΔΔG_solv where ΔΔG_1→2 is the relative binding free energy.

This thermodynamic cycle is the standard approach for relative binding free energies, but its implementation can take several forms. Single topology relative free energy calculations actually involve directly changing L₂ into L₁, while dual topology relative free energy calculations involve turning off the interactions of one ligand in the binding site while turning on interactions of the other ligand in the binding site.¹¹³ This issue is discussed in more detail in the supplementary material;¹¹³ here we focus mainly on single topology calculations, though the same considerations apply to dual topology calculations.¹¹³

Alternate binding modes pose potential problems for relative binding free energy calculations

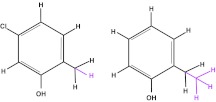
To understand the nature of challenges related to binding mode sampling in free energy calculations, consider the case where related ligands L₁ and L₂ both bind to a receptor (as in Fig. 4 for binding of 5-chloro-2-methylphenol vs. 2-ethylphenol). Assume L₁ has a known, single, dominant binding mode, but L₂ has two distinct potential binding modes, both of which are stable in MD simulations on time scales longer than our typical binding free energy calculations. This scenario is described in Fig. 5. In our example here, L₂ is a ligand which consists of L₁ plus an additional functional group (green rectangle). L₂ might share a binding mode with L₁ (Fig. 5a). But L₂ might alternatively have a modified binding mode (Fig. 5b).

Figure 4.

Relative free energy calculations might be done to compare binding of 5-chloro-2-methylphenol, left, with binding of 2-ethylphenol, right. Atoms which would be transformed into dummy atoms in a single topology calculation¹¹³ are shown in magenta and the scaffold is shown in black.

Figure 5.

Thermodynamic cycles for comparing binding of L₁ and L₂, where L₂ has two possible binding modes, as indicated by the positioning of the green rectangle. In (a), L₁ and L₂ share a common scaffold (gray spheres) which has the same binding mode in both ligands (as in Fig. 3). In (b), L₁ and L₂ share a common scaffold (gray spheres) which is actually rotated in binding of L₂ relative to L₁.

Both these cycles yield identical results only in the limit of adequate sampling. While adequate sampling may be straightforward in case Fig. 5a since the two ligands share the same binding mode, energy barriers mean it will be very challenging in Fig. 5b, which involves a change in binding mode. In this latter case, computed ΔΔG_1→2 will depend on the starting structure and be incorrect unless the simulations sample enough binding mode interconversion events.

To sum up, whenever different potential ligand binding modes are separated by large kinetic barriers, thermodynamic cycles of the sort in Fig. 5 are unlikely to close with normal simulation lengths due to convergence problems. This will be especially problematic whenever the binding mode of one (or more) of the potential ligands in the calculations is uncertain, or when their binding modes are different.

Longer simulations or separation of states can both solve convergence problems

Currently, there are two established approaches to solving these types of sampling problems. The most straightforward approach is simply to simulate longer until convergence is adequate; after all, both thermodynamic cycles yield correct free energies in the limit of infinite sampling. But this may not always be practical.¹¹⁴ Another approach involves separation of states (also called “integration over parts”¹¹⁵)—specifically, focusing sampling on individual regions of phase space likely to be important and treating kinetically distinct states separately.^{115, 116, 117, 118} For example, for proteins with multiple relevant conformations, one might consider each distinct stable conformation individually (such as in cases of different stable rotamers or isomers).^{104, 115, 116, 117, 119, 120, 121, 122, 123} For a ligand with multiple binding orientations, one might consider different orientations separately.^{65, 68, 106, 115, 116, 124} Here, we can think of each of these approaches as considering a different stable binding mode separately. In this scenario, the main advantage is that we only have to adequately sample each binding mode, not transitions between binding modes. The price we have to pay, however, is that we must obtain the relative free energies of the different binding modes. Still, in cases where transitions between binding modes are slow but transitions within binding modes are fast, this can dramatically improve convergence of free energy estimates.^{106, 124}

There is a simple general expression for relative free energies involving multiple binding modes

Separation of states approaches have a long history in free energy calculations, even predating simulations themselves.¹¹⁶ There have been a reasonable number of applications of these techniques to protein conformational changes, but relatively few to binding free energy calculations. And of these, most applications were in absolute free energy calculations,^{101, 103, 106, 124} with only very few to relative free energy calculations.^{68, 107}

Here, we are interested in a general approach to handle multiple binding modes within relative free energy calculations. In this approach, we pick a reference binding mode for the ligand which we will use for doing the actual binding calculation, from which we will obtain ΔΔG_{site, r}, the binding free energy in that particular mode. Additionally, we need ΔΔG_{Ln, i→r}, the free energies of taking each ligand L_n between binding mode number i and the reference binding mode r (“interconversion free energies” (IFE), in our terminology). Then we can write (motivated by Refs. ¹⁰⁶ and ¹²⁴; see the supplementary material¹¹³ for the derivation) the following general expression for the relative binding free energy:

$$\begin{array}{ccc}\hfill \Delta \Delta G_{1\to 2}& =& \Delta \Delta G_{site,r}-\Delta \Delta G_{solv}\hfill \\ & & -{\beta }^{-1}\ln \frac{\left[1+\sum _{\mathrm{modes}i\ne r}exp(-\beta \Delta G_{L1,i\to r})\right]}{\left[1+\sum _{\mathrm{modes}i\ne r}exp(-\beta \Delta G_{L2,i\to r})\right]}.\hfill \end{array}$$ (1)

Here the sum runs over different stable binding modes. Two important limiting cases of this expression are: (1) When all of the ΔG_{Ln, i→r} are large and positive (when all other binding modes except r are unfavorable), Eq. 1 reduces to ΔΔG_{1 → 2} = ΔΔG_{site, r} − ΔΔG_solv; and (2) When all other binding modes are equivalent to the reference binding mode (when all binding modes are equal), then all of the ΔG_{Ln, i→r} are zero and $\Delta \Delta G_{1\to 2}=\Delta \Delta G_{site,r}-\Delta \Delta G_{solv}-{\beta }^{-1}\ln \frac{N}{M}$ where N is the number of equivalent binding modes of L₁ and M is the number of equivalent binding modes of L₂. In the latter case, the term involving the logarithm essentially amounts to a ligand symmetry number correction analogous to those in Ref. 106.

This approach requires clear separation into multiple, non-overlapping binding modes. As we will discuss below, this is simple in the limit of extremely slow interconversions between binding modes, but when only a few transitions occur on simulation time scales, a clear definition of each binding mode is necessary.

Overall, this expression is a general one for handling multiple binding modes in the context of relative free energy calculations. Next, we consider several additional limiting cases.

In general, we may not know the binding mode of either ligand

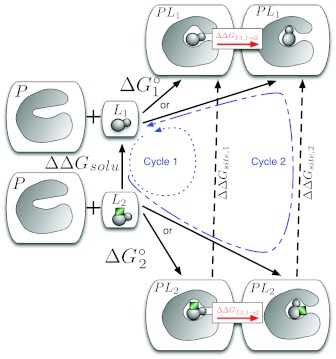
In the general case (Eq. 1) each ligand L₁ and L₂ may have multiple binding modes⁸⁸ or at least we may not know their dominant binding modes. To deal with this, we might dock each ligand into the binding site and run some short (i.e., nanosecond) MD simulations from several different starting poses.^{103, 106, 111} From these, we might identify stable states for each ligand which would be potential binding modes, but if time scales for interconversion are slow, we will have no data at this point about which binding modes are the most important to binding—we will simply know of a small set of stable binding modes of each ligand. Consider the case of two ligands, each with two possible binding modes (Fig. 6). Depending on how the calculations are set up, we can imagine two possible values for $\Delta G_1^{\circ }$—one going to binding mode 1 (left) of L₁ and one going to binding mode 2 (right) of L₁. Similarly, there are two possible values for $\Delta G_2^{\circ }$. The more negative of these free energies for each ligand will correspond to the more dominant binding mode,¹⁰⁶ and we do not know a priori which this will be. This is one of the things we would like to find out, in addition to ΔΔG_1→2.

Figure 6.

To correctly treat binding of L₁ and L₂ when both have multiple potential binding modes, we need a different approach depending on the preferred binding mode, as discussed in the text. Calculating ΔG_{L1, 1→2} and ΔG_{L2, 1→2} will tell us which binding modes are preferred, and we can combine this with Eq. 1 to get the correct binding free energy.

Assume that simulation time scales are short enough that the ligand does not switch between binding modes. Then, because each ligand has two possible binding modes, calculations will obtain one of the two different potential values for the free energy change in the binding site, ΔΔG_{site, 1} and ΔΔG_{site, 2}, depending on the choice of reference binding mode for the calculations.¹²⁵ In the limit where a single (common) binding mode dominates, the corresponding ΔΔG_{site, r} will yield the correct binding free energy, but we do not know which is correct at this point.

We note three limiting scenarios in this situation:

1. Both ligands prefer the left (#1) binding mode.

2. Both ligands prefer the right (#2) binding mode.

3. The ligands prefer different binding modes (assume L₁ prefers the left binding mode and L₂ prefers the right binding mode).

These three cases require slightly different approaches, but to distinguish between them, we need to know which binding mode of each ligand is preferred. This, as discussed in Sec. 2B, will require a separate calculation of ΔG_{L1, 1→2}, the free energy of taking L₁ from the left to the right binding mode, and ΔG_{L2, 1→2}, the corresponding free energy for L₂. Calculation of these may be challenging in its own right, though we provide some discussion below of how these may be obtained (Sec. 3). For now, assume we have obtained these IFEs, allowing us to distinguish between the scenarios noted above.

With these quantities in hand, we now consider our three scenarios:

1. Left binding mode: In this case, we follow the thermodynamic cycle labeled “Cycle 1” and ΔΔG_{1 → 2} = ΔΔG_{site, 1} − ΔΔG_solv.

2. Right binding mode: In this case, we follow the thermodynamic cycle labeled “Cycle 2” and ΔΔG_{1 → 2} = ΔΔG_{site, 2} − ΔΔG_solv.

3. Different binding modes: In this case, we obtain ΔΔG_{1 → 2} = ΔΔG_{site, 1} − ΔΔG_solv + ΔG_{L2, 1 → 2} or ΔΔG_{1 → 2} = ΔΔG_{site, 2} − ΔΔG_solv − ΔG_{L1, 1 → 2}. These are thermodynamically equivalent, though in practice they will have different convergence properties. These follow from Eq. 1 in the appropriate limits.¹²⁶

If the possibility of multiple binding modes is ignored, as in many relative calculations, then typically scenario 1 or scenario 2 will be assumed and no IFEs (ΔG_{L1, 1→2} and ΔG_{L2, 1→2}) are calculated. This introduces an error of ΔG_{L2, 1→2} (or ΔG_{L1, 1→2} depending on the cycle) when scenario 3 describes binding. As noted in the Introduction, these free energies can be large, up to 7 kcal/mol.

Lead optimization campaigns will in some cases begin with knowledge of the dominant binding mode of one of the ligands. But even if we know the binding mode of one ligand, we may not know the binding mode of the other. Thus we still need ΔG_{L1, 1→2}, as long as transitions between binding modes in the site are slow compared to simulation time scales.

The same framework applies when handling mutations to a common scaffold

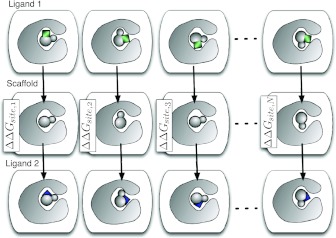
In general, one ligand may not be a subset of the other, so instead of directly mutating L₁ into L₂, the free energy calculation may need to pass through a common scaffold (as shown in the supplementary material,¹¹³ Fig. 1(b)). Additionally, we may need to consider even more potential binding modes—for example, for mutations of 5-chloro-2-methylphenol to catechol, we tried four potential binding modes (which differed substantially in free energy) since there are four ways to overlay it onto catechol while preserving the position of the hydroxyl.¹⁰⁶ To handle such cases, we introduce an additional intermediate state (Fig. 7) corresponding to the scaffold. Depending on whether these are single or dual topology calculations, specification of this scaffold may be explicit or implicit (supplementary material,¹¹³ Fig. 1).

Figure 7.

In the fully general case, each ligand (Ligand 1, Ligand 2) may have multiple potential binding modes, and one ligand may not be a subset of the other. In this case, for single topology calculations, we need to pass through an intermediate state or scaffold which is a common substructure of both ligands. Computing the relative free energy may require computing all of the ΔΔG_{site, 1}...ΔΔG_{site, N}, as well as the free energy of moving the scaffold between different scaffold binding modes. Here the different ligands are shown with colored additions representing functional groups; the common substructure is gray.

Figure 7 shows a variety of possible structures (which represent metastable states or potential binding modes) which may affect the relative binding free energy.¹²⁷ What exact information do we need to get the relative binding free energy in this case? Minimally, we require a path between every stable potential binding mode to every other stable potential binding mode. We have considerable flexibility in how these paths can be constructed, including:

1. Compute the free energy of altering the binding mode of the scaffold only, and all of the binding site free energies ΔΔG_{site, i}.

2. Compute the free energy of altering the binding mode of each ligand in its binding site between all binding modes, and only one ΔΔG_{site, i} avoiding the need for scaffold IFEs.

3. Compute the free energy of altering the binding mode of just one ligand in its binding site, and all of the binding site free energies ΔΔG_{site, i}.

As we will discuss below in Sec. 3, different approaches for computing the binding mode IFEs may give us reason to favor one of these scenarios over the others, but all of these yield the requisite information. Addition of some redundancy is advisable to allow computation of cycle closure errors as a test for convergence.

Assuming we have this information, we then use IFEs in combination with the other information available to identify which binding mode(s) are dominant and then construct a thermodynamic cycle such as Fig. 6 which includes our scaffold to get the correct relative free energy.

While our discussion here has focused on single topology calculations, similar issues face dual topology calculations as we note in the supplementary material.¹¹³

RECOMMENDED APPROACHES

For ligands with slow binding mode changes or unknown binding modes, efficient relative free energy calculations require the free energies of taking ligands between stable binding modes (the IFE) in the binding site. Otherwise, free energy calculations will need to be extremely long in order to achieve convergence. We envision several potential ways to obtain the IFE in the binding site (the free energies, ΔG_{Ln, i→r} (Eq. 1), to take each binding mode to the reference binding mode).

Two different types of IFEs would suffice. We could use IFEs of the scaffold (as in Fig. 7) or IFEs of actual ligands. Scaffold IFEs may be easier to obtain due to fewer steric hindrances (and in special cases such as a scaffold consisting of a symmetric ring, scaffold IFEs may be zero¹²⁸), though IFEs of a ligand can provide additional physical insight. These IFEs could be obtained a number of ways, including potential of mean force approaches, relative free energy calculations between different binding modes,^{65, 68, 107, 108} and even absolute binding free energy calculations to get relative free energies of binding modes.^{106, 124} Relative calculations between binding modes seem likely to work particularly well, and would probably best be implemented with a dual topology strategy, where the ligand is turned off in one binding mode while being turned on in another binding mode. Orientational restraints¹⁰⁶ could be used to ensure the two binding modes are well separated and the correct IFE is obtained, as in Rocklin et al.¹²⁹ Other potential strategies for computing IFEs include Markov state models,¹²⁴ metadynamics, and even the “deactivated morphing” approach.¹³⁰

We recommend one of two approaches to calculate the IFEs in a relatively general way, though more alternatives are becoming available:

1. Using absolute free energy calculations to compute the free energy to change the binding mode of the scaffold in the binding site. While this may seem overkill for a relative free energy calculation, there are two main benefits. First, it actually enables a set of relative free energy calculations to be used to obtain absolute binding free energies (by virtue of knowing the absolute binding free energy of our scaffold). Second, it scales extremely well with additional related ligands. Particularly, imagine instead of two related ligands we want to compare, we have 10 which share a common scaffold. We can compute absolute free energies of the scaffold binding modes just once, and use this one set of absolute binding free energy calculations to compute correct relative or absolute binding free energies of all 10 of our ligands. This is done simply by adding additional ligands (i.e., in Fig. 7) and connecting each ligand to the common scaffold.

2. Using relative free energy calculations combined with orientational restraints to calculate the free energy to change the binding mode of each ligand in the binding site. With a dual topology scheme, we can turn a ligand into dummy atoms in one binding mode while turning it on from dummy atoms in another, potentially using orientational restraints to ensure that no interconversion between binding modes happens during the calculations and thus obtaining a correct IFE.^{107, 108, 129}

Both of these approaches have the caveat that, as noted previously, treating different binding modes separately in the these calculations requires careful separation of kinetically distinct binding modes.^{106, 124} Consider a ligand L₁ which has two metastable binding modes A and B, and its transformation into L₂ which has the same two binding modes. When the barrier between A and B is large enough that no binding mode interconversion occurs, separation into distinct binding modes is trivial. And when rapid interconversion between A and B occurs, no separation is necessary. But in the intermediate regime, when just one or several transitions between A and B occur (but not enough to ensure convergence), the simulations either need be lengthened, or simulation data need to be sorted by binding mode and each binding mode analyzed separately.

A third approach is to use enhanced sampling techniques^{21, 131, 132} to sample all relevant binding modes easily within the context of a single free energy calculation, eliminating the need for IFEs. However, success with these techniques so far seems confined mainly to model binding sites.^{21, 105, 110, 128, 133}

Here, we focused on cases where likely possible binding modes can be discovered relatively easily, which is sometimes true but certainly will not always be the case. We have typically done this by docking ligands into binding sites, running molecular dynamics simulations beginning from a wide range of substantially different docking poses, and then clustering the resulting simulation snapshots to identify a variety of different binding modes which are well populated.^{101, 103, 106} In model sites we have studied, this has typically yielded a variety of plausible binding modes from which, using free energy calculations, we have often been able to identify the dominant binding modes.^{101, 103, 106} Others have had some success with a similar strategy.^{65, 124} However, in general the problem of identifying likely binding modes will be extremely challenging, especially in cases of dramatic receptor rearrangement on ligand binding, or where ligand modifications introduce unexpected and slow conformational rearrangement in the protein. In such cases, discovering candidate binding modes may be much more difficult. In principle the same considerations raised here still apply, but new approaches for binding mode exploration will likely be needed.

SUMMARY AND CONCLUSIONS

Relative free energy calculations are increasingly intriguing for structure based drug discovery, yet still notoriously unreliable. Major challenges include force fields and sampling, and here our focus is on sampling. Problems with binding mode sampling can pose significant challenges, and the straightforward approach of simply lengthening simulations until convergence is achieved may not be adequate. Relative free energy calculations, we argue, can benefit from separation of states approaches, where different stable binding modes are treated separately to enhance convergence. This is especially important whenever the binding mode of one or both ligands is not absolutely known (that is, in essentially all discovery applications) and whenever the ligands being compared do not share the same binding mode. If ligand binding mode interconversions are ignored, thermodynamic cycles used in relative free energy calculations often fail to close, resulting in errors in computed binding free energies of several kcal/mol. Using the framework here requires free energies to take each ligand between its different potential binding modes, or to take the scaffold (common substructure) between its potential binding modes. One route for obtaining these free energies is absolute binding free energy calculations.

In general, when binding mode sampling is ignored in relative free energy calculations and binding mode interconversions are slow, the error introduced is related to the free energy to take either ligand from the binding mode actually used in the calculations to the correct binding mode(s), and can in some cases be several kcal/mol.⁸⁸ It is difficult to say how often these effects will be important without more exhaustive computational or experimental study. As noted, at this point our data consist primarily of examples of unexpected binding modes and multiple relevant binding modes. But we suspect (probably conservatively) that at least 10% of cases will be affected by problems with binding mode sampling.

Historically, one argument in favor of relative free energy calculations over absolute binding free energy calculations is that the former are simpler and do not require turning the entire ligand into dummy atoms in the binding site. However, convergence of relative free energy calculations when ligand binding modes are uncertain (as in any predictive context) will likely require computing the free energy of taking the ligands or scaffold between different kinetically stable binding modes. One straightforward route to that information is provided by absolute binding free energy calculations, and another is to use dual topology relative free energy calculations to obtain the binding mode IFE for each ligand after a careful separation of binding modes.

In our view, the time is ripe for a careful examination of binding mode sampling issues, perhaps in model systems such as the lysozyme binding sites^{100, 101, 103, 105, 106, 128, 134, 135, 136, 137, 138, 139} and the cytochrome C cavities.^{109, 140, 141, 142} These are relatively simple binding sites which bind small, fragment-like ligands and yet are susceptible the binding mode sampling problems discussed here. Much of the work in these sites has been with absolute free energy calculations (with notable exceptions^{105, 109, 128}), but the available high quality data pave the way for a careful examination of relative free energy calculations in this context. These also should provide an excellent test case for new methodological innovations aimed at tackling binding mode sampling problems.^{105, 128}

Overall, we believe the literature and our analysis suggests ligand binding mode sampling presents serious challenges to relative free energy calculations. It is easy in practice to ignore these issues and plunge ahead with such calculations. But the data suggest this is unwise if these calculations are ever to be robust enough for routine application in a predictive setting such as drug discovery. The issue of orientational and binding mode sampling for ligands needs to receive much more attention in relative free energy calculations (as it is beginning to in absolute free energy calculations^{101, 103, 106, 124}). Hopefully, the separation of states approach we have highlighted will provide a route forward.

Already, a good number of free energy studies have achieved the level of accuracy needed to be helpful in drug discovery. If we can advance binding free energy techniques to where hydration free energy studies are today in terms of speed and accuracy, they will play a dramatically different role in the drug discovery process.