Abstract
Purpose: A novel technique for beam profiling of megavoltage photon beams was investigated for the first time by capturing images of the induced Čerenkov emission in water, as a potential surrogate for the imparted dose in irradiated media.
Methods: A high-sensitivity, intensified CCD camera (ICCD) was configured to acquire 2D projection images of Čerenkov emission from a 4 × 4 cm2 6 MV linear accelerator (LINAC) x-ray photon beam operating at a dose rate of 400 MU/min incident on a water tank with transparent walls. The ICCD acquisition was gated to the LINAC sync pulse to reduce background light artifacts, and the measurement quality was investigated by evaluating the signal to noise ratio and measurement repeatability as a function of delivered dose. Monte Carlo simulations were used to derive a calibration factor for differences between the optical images and deposited dose arising from the anisotropic angular dependence of Čerenkov emission. Finally, Čerenkov-based beam profiles were compared to a percent depth dose (PDD) and lateral dose profile at a depth of dmax from a reference dose distribution generated from the clinical Varian ECLIPSE treatment planning system (TPS).
Results: The signal to noise ratio was found to be 20 at a delivered dose of 66.6 cGy, and proportional to the square root of the delivered dose as expected from Poisson photon counting statistics. A 2.1% mean standard deviation and 5.6% maximum variation in successive measurements were observed, and the Monte Carlo derived calibration factor resulted in Čerenkov emission images which were directly correlated to deposited dose, with some spatial issues. The dose difference between the TPS and PDD predicted by Čerenkov measurements was within 20% in the buildup region with a distance to agreement (DTA) of 1.5–2 mm and ±3% at depths beyond dmax. In the lateral profile, the dose difference at the beam penumbra was within ±13% with a DTA of 0–2 mm, ±5% in the central beam region, and 2%–3% in the beam umbra.
Conclusions: The results from this initial study demonstrate the first documented use of Čerenkov emission imaging to profile x-ray photon LINAC beams in water. The proposed modality has several potential advantages over alternative methods, and upon future refinement may prove to be a robust and novel dosimetry method.
Keywords: cerenkov, dosimetry, quality assurance, photon beam
INTRODUCTION
Quality assurance (QA) of all clinical electron and photon linear accelerator (LINAC) beams is an important practice. The accurate calibration of each, by virtue of a direct measurement of dose, or dose rate, in water is typically performed using a point radiation detector mechanically raster-scanned through the phantom volume.1 Due to scanning time limitations, routinely only a subset of volumetric dose is directly measured as sparsely spaced 2D profiles and depth dose scans. Of the several available techniques, the most commonly used and widely accepted method relies on using ionization chamber-based systems in which the dose in the surrounding medium is assumed to scale with chamber ionization signal.2 With extensive research and development into necessary correction factors, these measurements are advantageous in that they are well understood, can be instantly readout, and are both accurate and precise. However, the relatively slow mechanical scanning makes a full 3D dose distribution measurement expensive in routine everyday clinical practice, and is not commonly performed after initial LINAC installation.
Gel dosimetry methods offer an alternative method well suited for large scale 3D profiling, but suffer from major limitations in that a dose-readout method is required, such as magnetic resonance imaging (MRI) or optical computed tomography, and the recorded dose distribution blurs with time due to postirradiation diffusion of ions.3, 4, 5 As beam delivery methods become more complex, it would be ideal to have QA processes that enable verification of more advanced radiosurgery or dynamic radiotherapy procedures. Therefore, there is great interest in a simple, yet accurate method of rapidly obtaining 2D and 3D beam profiles.
More recently, plastic scintillator dosimetry has been proposed as an optical method for beam profiling in which light generated in a scintillating fiber during LINAC irradiation is recorded and used to estimate dose at a given spatial location.6 This new technique has been extended to 2D planar measurements using a fiber-array, and is desirable for a number of reasons, including near-water equivalence, energy independence, reproducibility, and resistance to radiation damage.7, 8, 9 The scintillation method has also been used in imaging systems that capture projections of the scintillation light distribution in a liquid scintillating volume or horizontally placed plastic scintillating sheet.10, 11 One major challenge in the development of this technology has been the decoupling of the desired scintillation optical signal, and background signal or stem effect.12, 13 Parallel fiber, air-core fiber, spectral, and temporal methods have been used with varying degrees of success to remove this source of signal contamination which arises due to Čerenkov emission, a phenomenon which occurs when an energetic charged particle enters a dielectric medium with a velocity greater than the local speed of light.13, 14, 15, 16, 17
Although undesirable in scintillation dosimetry, Čerenkov emission has long been productively utilized in astronomy and high energy physics applications focused on the detection and identification of various particles’ trajectory, velocity, distribution, and type.18, 19, 20, 21, 22 Recently, Cherry et al. and others have explored the use of the Čerenkov effect in the context of medical research through Čerenkov luminescence imaging (CLI), a novel method for tracking β-emitting radionuclides in vivo.23, 24, 25, 26, 27 Due to the increased optical photon yield with increasing β particle energy, Axelsson et al. investigated Čerenkov emission spectroscopy (CES) from a LINAC during external beam radiotherapy (EBRT) for treatment monitoring.28, 29 Furthermore, a recent study by Jang et al. reported a fiber-optic system utilizing Čerenkov emission in the measurement of Bragg and spread-out Bragg peaks for proton beam dosimetry.30
In the present study, the feasibility of imaging the intrinsic Čerenkov emission induced by megavoltage x-ray photon beams to estimate dose deposition by secondary electrons in a water phantom is theoretically motivated and examined using simulations and experiments. A sensitive camera gated to the radiation beam pulse is used to suppress acquisition noise and ambient room lights which can contaminate the Čerenkov emission signal, and Monte Carlo simulations are used to properly correct for the camera's ability to capture the induced anisotropic light volume.31 Through imaging of this emission on the seconds timescale, calibrated 2D images directly correlated to a projection of the deposited dose summed in the viewing-direction relative to the camera are obtained. These 2D projections of Čerenkov emission could then be processed with tomographic and stereoscopic approaches to derive full 3D dose distributions on the order of minutes. As a proof of concept, the speed of acquisition, measurement variability, and accuracy of a single 2D projection of Čerenkov emission relative to a reference dose distribution for a 4 × 4 cm2 6 MV beam is examined.
THEORY
In contrast to fluorescence and scintillation which exhibit isotropic photon generation, optical photons generated via Čerenkov emission are released uniformly along a cone parallel to the axis of particle propagation with a half-angle known as the Čerenkov angle, given by
| (1) |
where n is the refractive index of the medium and β is the relativistic phase velocity, defined as
| (2) |
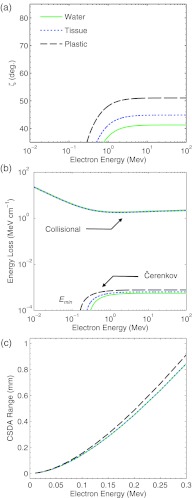
for a particle of energy E and rest mass mc2.32 Equation 1 is plotted in Fig. 1a for an electron traveling through water, tissue, and polystyrene plastic.33 The energy dependence of Eq. 1 is governed by Eq. 2, and rises sharply at a threshold energy given by
| (3) |
which approaches a constant angle in the limit that the phase velocity tends toward unity with increasing particle energy.
Figure 1.
In (a) the Čerenkov angle, ζ, (b) collisional and Čerenkov emission energy losses per unit path length, and (c) CSDA range for an electron traveling through water, tissue, and polystyrene plastic are plotted as a function of particle energy.
The number of Čerenkov photons emitted within the cone described by Eq. 1 in a given photon energy range [ε1, ε2] is given by the Frank-Tamm formula, which when combined with Eq. 2 and assuming a constant refractive index can be used to express the number of emitted photons per unit path length, , due to the Čerenkov effect as
| (4) |
where the fine structure constant α is approximately , and z is the particle charge.32 The emission spectrum is constant with respect to photon energy ε, and therefore the total energy loss per unit path length, , can be expressed as
| (5) |
where the mean emission photon energy is equated as . Equation 5 is plotted in Fig. 1b for an electron traveling through water, tissue, and polystyrene plastic in comparison to the National Institute of Standards and Technology (NIST) ESTAR values for the electron collisional stopping power, , in each material.34 In order to accurately model the amount of electron energy loss captured by a typical camera system, the optical photon energy range in Eq. 4 was constrained to 1.65–3.1 eV, corresponding to the visible wavelength region of 400–750 nm, although the energy loss at all electron energies simply scales as the difference of the square in the photon energy band bounds (i.e., ).
Similar to Eq. 1, the energy dependence of Eq. 4 is governed by Eq. 2 and rises sharply at the threshold energy given by Eq. 3, approaching a constant energy loss per unit path length in the limit that the phase velocity tends toward unity with increasing particle energy. Per Eq. 4, this constant energy loss per unit path length at electron energies above the threshold energy corresponds to a fixed number of emitted photons per unit path length, . Representative values for n, , Emin, and for water, tissue, and polystyrene plastic are listed in Table 1.
Table 1.
Relevant optical parameters of Čerenkov emission in water, tissue, and polystyrene plastic.
| Water | Tissue | Plastic | |
|---|---|---|---|
| Refractive index n | 1.33 | 1.411 | 1.59 |
| Emission angle (deg.) | 41.2 | 44.8 | 51.0 |
| Threshold energy Emin (keV) | 264.1 | 213.8 | 146.3 |
| Photon yield2 (photons cm−1) | 232 | 266 | 323 |
Tissue refractive index approximated from Ref. 33.
For an emission waveband of 400–750 nm and β = 1.
In the context of radiation therapy, the above is applicable to megavoltage x-ray photon beams, which irradiate a given volume liberating secondary electrons in the process. Assuming a volume of homogenous atomic composition and density irradiated by a monoenergetic beam perpendicularly incident on a medium in the z direction, the fluence of primary x-ray photons, ψ, penetrating to a certain distance, z, will follow an exponential distribution:
| (6) |
where ψo is the fluence at the surface and μ is the linear attenuation coefficient of the medium. The corresponding kinetic energy released per unit mass (KERMA) at any point within the medium that leads to the production of secondary electrons which deposit their energy locally through ionization events, Kc, can be expressed as
| (7) |
where μen is the mass energy absorption coefficient of the medium of density ρ, and ψ is as defined in Eq. 6. Although the collisional KERMA will decay exponentially per the x-ray photon fluence, for megavoltage beams the transfer of energy from the primary photons to electrons, and electrons to the medium will not occur at the same spatial location due to the nonzero propagation distance of the secondary electrons.1 Therefore, a buildup region will exist until a depth of z = dmax (defined as the maximum penetration distance of secondary electrons produced at the surface of the medium), after which the medium will be in transient charged particle equilibrium (TCPE) and the energy absorbed per unit mass of the medium (i.e., imparted dose) will be proportional to Kc, and can be expressed as
| (8) |
where Φ is the polyenergetic electron fluence spectrum and is the electron collisional stopping power.2 Similarly, the radiant energy, Q, and total number of optical photons, N, released per unit mass of the medium due to the Čerenkov effect can be expressed as
| (9) |
| (10) |
where and are given by Eqs. 4, 5. As can be seen in Fig. 1b, for all three materials, and are approximately proportional above the threshold energy given by Eq. 3, below which the two quantities become disproportionate. Therefore, in regions of TCPE where the relative spectrum of Φ is constant and when considering electron energies greater than Emin, the dose given by Eq. 8 and radiant energy release in the form of Čerenkov given by Eq. 9 at any location will be directly correlated, and the number of emitted Čerenkov photons given by Eq. 10 may serve as a surrogate to determine the corresponding dose deposition in the medium. However, in regions not satisfying the conditions for TCPE (i.e., the buildup and beam penumbra region or an air cavity), the spectral characteristics of Φ will vary and the above relationship will not be valid.
When considering the characteristics of the surrogate Čerenkov photons, N, there are several important considerations. Per Eq. 1 and given the distribution of scattered electron trajectories, the angular distribution of Čerenkov emission at any spatial location will be complex and anisotropic. Therefore, a phase function will exist at each point in the irradiated medium, which describes the number of Čerenkov photons emitted per unit solid angle dΩ.
Due to the complicated directional dependence of multiply scattered secondary electrons and therefore Čerenkov photons at any spatial location in the irradiated medium, P is difficult to determine analytically. Instead, Monte Carlo methods can be easily used to stochastically determine the phase function in the form of a five-dimensional (5D) histogram P(x, y, z, θ, ϕ) which describes the global emission characteristics in terms of spatial location (x, y, z) and polar and azimuthal angle (θ, ϕ), see Sec. 3C. Note, in this convention, for a photon emitted with a directional vector, , the polar angle is defined as cos θ = v3 and the azimuthal angle as where . However, prior to simulations several properties of P(x, y, z, θ, ϕ) can be determined by considering the radiation beam geometry and subsequent radiation interactions:
-
(1)
Due to the forward dominance of Compton scattering, the independence of Compton scattering with azimuthal angle relative to the incident direction of scattering x-ray photons, and the independence of the azimuthal angle of Čerenkov emission relative to the scattered electron direction, P(x, y, z, θ, ϕ) is expected to be independent of ϕ.
-
(2)
As a direct result of azimuthal symmetry, within the central beam region where TCPE exists, P(x, y, z, θ, ϕ) is expected to be independent of x and y.
-
(3)
The relative energy spectrum and angular distribution of the electron fluence at any spatial location satisfying TCPE is constant and instead scales in absolute magnitude by the incident x-ray photon fluence. Therefore, the relative change in P(x, y, z, θ, ϕ) is expected to be independent of z beyond dmax.
-
(4)
Given the previous statement, for a constant θ and ϕ, P(x, y, z, θ, ϕ) would be indicative of the deposited dose distribution all spatial locations (i.e., if the same solid angle of emission is captured at each point in the irradiated medium). However, for a conventional camera lens, differing values of θ and ϕ are captured from each point in an image and therefore a calibration factor is necessary (see Sec. 3D).
-
(5)
The nature of P(x, y, z, θ, ϕ) and therefore any derived calibration factor is dependent on the incident radiation direction (i.e., the correction factor can only be applied for a monodirectional radiation beam, not for multiple radiation beams with differing incident directions as in a typical IMRT plan).
-
(6)
A camera may only capture a 2D spatial projection of P(x, y, z, θ, ϕ), and therefore any captured image will represent a summation of the imparted dose in either the x or y or z direction. Computed tomography would then be necessary to resolve the third dimension.
-
(7)
Despite disproportionality for an electron at an energy below Emin, the continuous slowing down approximation (CSDA) range of electrons in this energy regime is expected to be less than 1 mm. Furthermore, the relative electron fluence energy spectrum below Emin is expected to be constant in regions of TCPE. Therefore, these low-energy electrons do not severely blur or shape the spatial dose distribution and are expected to be a scalar offset in the radiant energy loss due to Čerenkov emission relative to the imparted dose. NIST ESTAR values for the CSDA range of electrons in water, tissue, and tissue polystyrene plastic are shown in Fig. 1c.34
-
(8)
Although the above analysis is for a monoenergetic x-ray photon beam, the principles could be extended to a polyenergetic megavoltage x-ray photon beam.
MATERIALS AND METHODS
Experimental setup
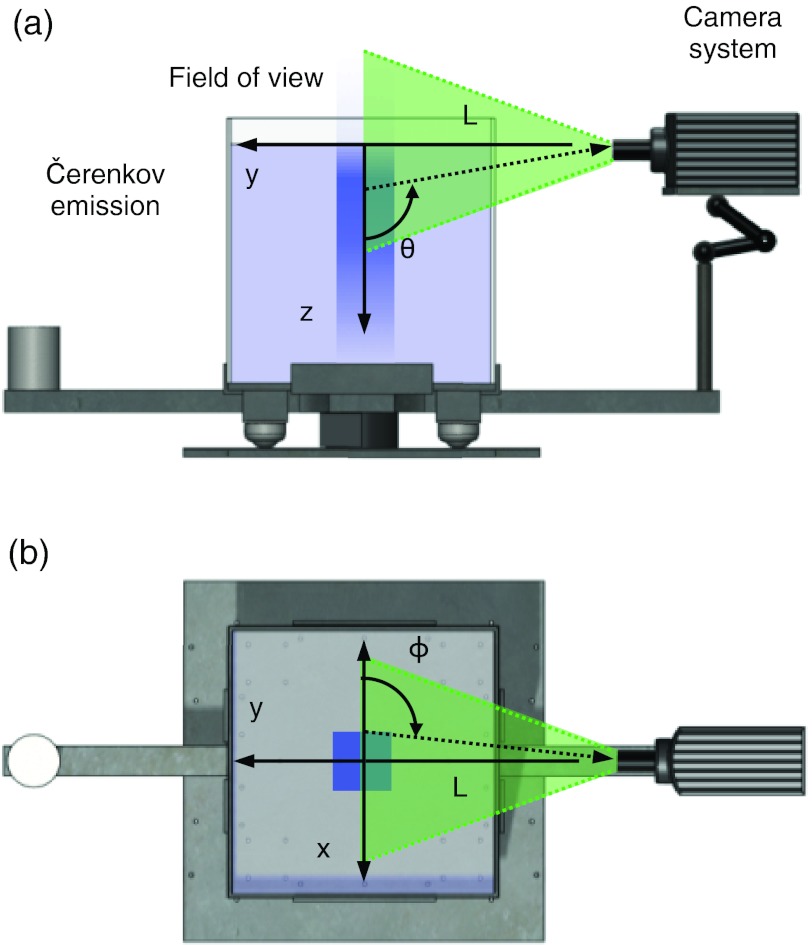
All experiments were performed using a 4 × 4 cm2 6 MV x-ray photon beam delivered from a clinical LINAC (Varian 2100 C, Varian Medical Systems, Palo Alto, CA) running at a dose rate of 400 MU/min. As shown in Fig. 2 the experimental setup was comprised of a tank and a peripherally placed camera normal to the central beam direction at a distance of L = 45 cm from the beam center. The camera was also placed in line with the water surface to avoid surface reflection artifacts. The 45.7 × 45.7 × 45.7 cm3 tank used was constructed of 5 mm thick glass walls and was chosen to be large enough to avoid boundary effects and to mimic the size of tanks used in commercial ionization chamber systems. For all experiments, the tank was filled with tap water to a source-surface distance (SSD) of 100 cm. The global coordinate axes and definitions for polar angle, θ and azimuthal angle, ϕ referenced throughout the text in both experiments and simulations are also shown in Fig. 2.
Figure 2.
A side view of the system is shown in (a) with the radiation beam vertically entering the tank and inducing Čerenkov light emission, which is captured by a camera placed at an imaging distance L = 45 cm from beam center. The definition of the polar angle of emission θ is shown with respect to the camera field of view. In (b) an aerial view of the system is shown, with the corresponding definition of the azimuthal angle of emission ϕ.
Images were acquired using a 1024 × 1024 pixel intensified-CCD (ICCD) system capable of gating on the nanosecond timescale (PI-MAX3: 1024i-Unigen2, Princeton Instruments, Acton, MA) cooled to −25 °C, and coupled to a 25 mm focusable double gauss lens with a 14.7° angular field of view (FOV) and F4 aperture (Edmund Optics, Barrington, NJ). The LIGHTFIELD (Princeton Instruments, Acton, MA) software package was used to control the ICCD system, and images were collected by running the ICCD in a gated mode in which the camera shutter was triggered externally by the 180 Hz LINAC sync pulse as described in a previous study (see Ref. 31). The number of CCD accumulations per readout frame was set to 60, resulting in a frame rate of 3 frames per second (FPS) for use in temporal median filtering of impulse noise due to stray radiation striking the camera components. In all measurements, the total exposure time was set to 10 s, corresponding to 30 total frames. Using the dose rate in conjunction with the output factor for a 4 × 4 cm2 6 MV beam, the total delivered dose per frame and per acquisition was 2.2 and 66.6 cGy, respectively. For all experiments, the image intensifier gain setting was set to 100/100× and ambient room lights were turned off to maximize the signal to background ratio.
Image processing
For the chosen experimental camera distance of L = 45 cm, the spatial resolution and FOV were calculated to be 0.25 mm and 25 × 25 cm2 by imaging a reference object of known dimensions. The resulting images were subject to a dark frame subtraction, cropped to a 10 × 10 cm FOV, processed for impulse noise removal using temporal median filtering on a pixel-by-pixel basis, and resized to a 1.0 mm dose grid using MATLAB 7.12.0 (The MathWorks Inc., Natick, MA). Temporal median filtering was chosen over spatial median filtering of a single image due to its increased performance over other spatial noise filtering techniques (see Ref. 35).
Monte Carlo simulations of Čerenkov emission angular distributions
Due to the specific angle of Čerenkov emission given by Eq. 1, and the tortuous path of propagating electrons, the distribution of Čerenkov photons emitted into any angle at any given spatial location inside the irradiated medium is extremely complex and anisotropic.
Therefore, in order to study this phenomenon, Monte Carlo simulations were performed using GAMOS, a software framework based upon on the validated GEANT4 toolkit.36, 37 The GAMOS interface was chosen for its ease of use and flexibility in creating GEANT4 simulations, and the GEANT4 architecture was chosen for its robust physics package and ability to model both radiation and light transport (see Ref. 38 for details on the GEANT4 implementation of the Čerenkov process). In all simulations, the origin was placed at the center of the beam at the water surface with the x axis lateral to the camera, the y axis parallel to the viewing direction of the camera, and the z axis positive with increasing depth downward from the origin into the water tank (see Fig. 2).
The standard GEANT4 electromagnetic physics package was used, and the electron step size in each simulation was limited to 100 μm. The refractive index and absorption length of water were interpolated to a 10 nm spectral resolution within the visible spectral range of 400–750 nm.39, 40 The refractive index of air and the water tank glass were assumed to be a constant 1.0 and 1.49, respectively, and the optical absorption of both was assumed negligible.
For each simulation, 9 × 107 histories were used and the simulation geometry was designed to mimic the dimensions and configuration of the experimental setup. To generate each particle history, a phase space file for a 4 × 4 cm2 6 MV beam applicable to a Varian 2100 C LINAC from the International Atomic Energy Agency (IAEA) phase space database was used. In addition, although not imaged experimentally, identical simulations were also performed using phase space files from the IAEA database for a 10 × 10 and 20 × 20 cm2 6 MV beam to explore the field size dependent characteristics of the induced Čerenkov emission.
As a result of some of the independent characteristics of P(x, y, z, θ, ϕ) outlined in Sec. 2, as well as computational constraints, the entire 5D phase function was not directly calculated. Instead, 2D histograms, P(θ, z) and P(x, ϕ) for the characteristics of Čerenkov emission as a function of depth, z, and polar angle, θ, independent of x and y location (i.e., summed in the x-y plane), as well as lateral displacement, x, and azimuthal angle, ϕ, independent of y and z location (i.e., summed in the y-z plane) were recorded. Both histograms were normalized to a summed value of 1, and generated using 1 mm spatial and 1° angular binning, where the range of z was set to 0–40 cm, x to −40 to 40 cm, θ to 0–180°, and ϕ to −180 to 180°.
Calibration factor determination
Due to the cone of acceptance for the conventional lens used in this study, Čerenkov photons emitted at each spatial location in the irradiated medium are captured at differing azimuthal and polar angles. Therefore, using the Monte Carlo derived angular emission distributions, the Čerenkov emission capture by the lens, P(θlens, z) and P(x, ϕlens) were calculated using bicubic interpolation, where the lens capture angles at each depth z and lateral location x were determined geometrically as
| (11) |
| (12) |
where L is the distance from the lens to beam center, and x and z are the lateral and vertical coordinates of the position in the irradiated medium being imaged (see Fig. 2). Note, in this formulation the lens diameter is ignored and the lens is approximated as a point detector.
When imaging isotropic light emission, the distortion due to the lens-viewing angles in Eqs. 11, 12 may be neglected, as the emission is independent of θ and ϕ. However, when imaging anisotropic light as in the case of Čerenkov emission, the above must be accounted for. Therefore, in order to calibrate the images of Čerenkov emission for the angular emission and camera lens capture dependence, calibration factors were derived from the Monte Carlo results as
| (13) |
| (14) |
which takes the ratio of integrated Čerenkov emission into all angles, expected to be a surrogate to deposited dose, to the emission capture by the camera lens at each spatial location in the image.
Image calibration
For the experimentally imaged 4 × 4 cm2 6 MV beam, a calibrated intensity image to correct for the lens collection of the anisotropic Čerenkov emission was calculated by applying the calibration factors calculated in Secs. III.C and III.D for the 4 × 4 cm2 field size to all pixels in the experimentally captured image as
| (15) |
where I(x, z) and I′(x, z) are the uncorrected and corrected Čerenkov emission intensity images, respectively. After calibration, I′(x, z) was normalized to a relative intensity of 100% on central axis at z = dmax.
Signal to noise ratio (S/N)
To evaluate the speed and signal quality of the proposed system, the S/N ratio was calculated as a function of delivered dose by comparing the ratio of the mean and standard deviation in pixel intensity inside a 25 × 4 pixel region of interest (ROI) laterally centered at a depth of z = dmax for the experimentally imaged 4 × 4 cm2 6 MV beam.
The ROI was chosen to be wider in the lateral direction as less deviation in actual dose and therefore captured intensity is expected in the lateral versus depth direction, and any interpixel fluctuations in intensity would be attributable to the system's signal collection ability. To assess image quality at delivered doses less than 66.6 cGy corresponding to the full 10 s acquisition, a reduced subset of the 30 total acquired frames was temporally median filtered before analyzing the mean and standard deviation pixel intensity of the ROI.
Measurement variability
To examine the variability of the system measurements, the calculated mean of the ROI described in Sec. 3F was compared in ten successive acquisitions to determine the intermeasurement standard deviation and maximum intensity difference.
Percent depth dose (PDD) and lateral dose profile comparison
To explore the accuracy of the technique, the calibrated spatial intensity distribution of the acquired image for a 4 × 4 cm2 6 MV beam derived from 30 temporally median filtered frames and a corresponding delivered dose of 66.6 cGy was compared to a reference dose distribution (see Sec. 3I). The difference between the reference dose distribution and calibrated Čerenkov emission image was evaluated as
| (16) |
where the PDD and lateral difference profiles were computed by evaluating δ(x, z) at x = 0 cm and z = dmax, respectively. Distance to agreement (DTA) measurements were computed for both profiles near the high dose gradients in the buildup and beam edge regions by determining the minimum spatial distance required for dose equivalence between D(x, z) and I′(x, z).
Reference dose distribution
Due to the need for an effective 2D dose projection and therefore a full 3D reference dose distribution, outputs from the Varian ECLIPSE treatment planning system (TPS) commissioned with experimentally derived dose measurements for the Varian 2100 C LINAC were used. A treatment plan comprised of a water volume and beam geometry commensurate with the experimental setup was used to generate results on a 1.0 mm dose grid for a 4 × 4 cm2 6 MV beam. The 2D dose projection, D(x, z), used in comparison to the Čerenkov emission image was approximated by linearly summing the distribution with respect to the y-direction, although the captured projection images are expected to be nonlinearly weighted per the lens depth of field (DOF). Similar to the normalization of the experimentally measured intensity image, the resulting dose projection was normalized to a relative dose of 100% on central axis at z = dmax.
RESULTS
Monte Carlo simulations of Čerenkov emission angular distributions
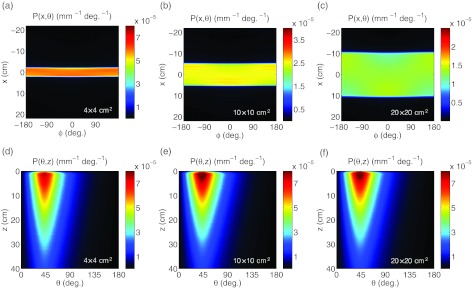
The 2D histograms of P(x, ϕ) for the 4 × 4, 10 × 10, and 20 × 20 cm2 6 MV beam are shown in Figs. 3a, 3b, 3c. The emission appears to be uniformly distributed over ϕ for all lateral values of x within the given beam field size and confirms the first and second statements in Sec. 2.
Figure 3.
In (a)–(c), the Monte Carlo derived histograms of Čerenkov emission, P(x, ϕ), for a 4 × 4, 10 × 10, and 20 × 20 cm2 6 MV beam. The histograms of Čerenkov emission, P(θ, z), for all three field sizes are shown in (d)–(f).
The 2D histograms of P(θ, z) for the same three beams are shown in Figs. 3d, 3e, 3f. As can be seen, the majority of the anisotropic Čerenkov emission is at an angle of θ ≅ 41°, consistent with Eq. 1 for emission in water from a Compton scattered electron at an angle of 0° relative to the incident x-ray photon. The emission at angles either larger or smaller than 41° (i.e., the Čerenkov angle of electrons traveling straightly downward at 0°) decreases rapidly at all depths.
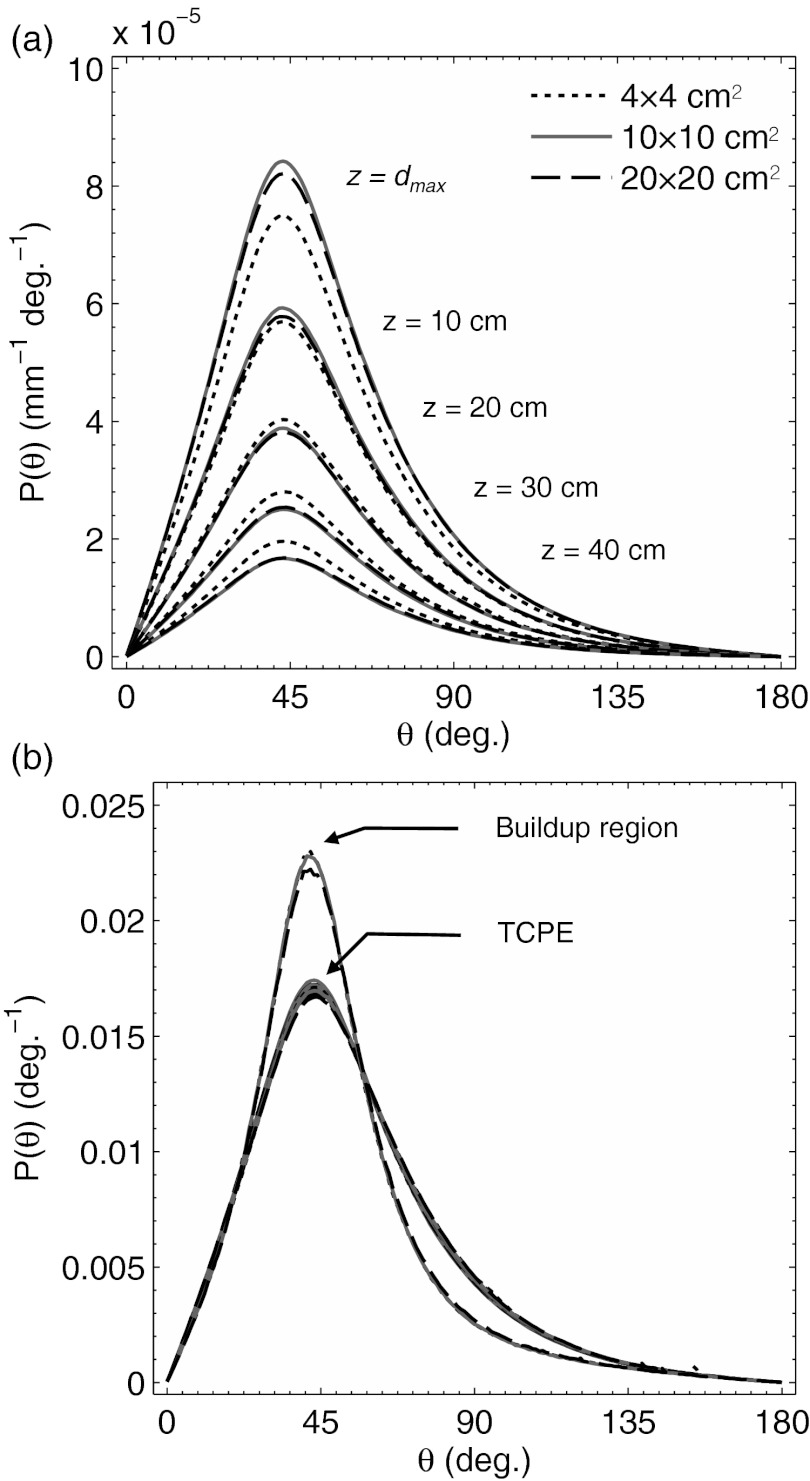
The polar angle phase function, P(θ), is plotted in Fig. 4a at z = dmax, and at depths of 10, 20, 30, and 40 cm for all three field sizes. As can be seen, the absolute magnitude of the phase function at all angles for each field size decreases exponentially with depth as specified in the third statement of Sec. 2, while the relative shape of the phase function remains constant. This is illustrated in Fig. 4b, where the phase functions from Fig. 4a are normalized to a cumulative value of 1 and plotted against a normalized phase function for emission in the buildup region at z = 0.2 cm. At depths beyond dmax where TCPE is satisfied, the normalized phase functions are consistent for all θ, irrespective of field size, in contrast to the buildup region, where the directional distribution of the electron fluence, Φ is more forward peaked at 0° [i.e., P(θ) appears more centrally peaked at the 41° Čerenkov angle].
Figure 4.
In (a) the Monte Carlo derived phase function, P(z, θ), for Čerenkov emission from a 4 × 4, 10 × 10, and 20 × 20 cm2 6 MV beam at depths of z = dmax, 10, 20, 30, and 40 cm. In (b) the normalized phase functions from (a) in comparison to the normalized phase function in the buildup region at z = 0.2 cm for all three field sizes is plotted.
Calibration factor determination
Although a directly proportional relationship should exist between the energy absorbed and released by the Čerenkov effect at points within a medium that satisfies the conditions for TCPE, as specified in the sixth consideration in Sec. 2 the complex anisotropic distribution of emitted photons at any spatial location will be sampled at differing polar, θ, and azimuthal, ϕ, angles, resulting in a distorted projection of the imparted dose distribution.
As a result, a conventional lens that effectively collects and samples emission from varying values of θ as a function of z will not perceive a relative depth emission profile proportional to the expected PDD. Due to the lens placement in line with the water surface to avoid surface reflection artifacts, at z = 0 cm the lens samples Čerenkov emission at θ = 90°, and at deeper depths the sampled value of θ increases per Eq. 12. Due to the negative gradient of emission as a function of increasing θ (see Fig. 4), the lens will capture an artificially lower amount of Čerenkov photons relative to dose at increasing depths. Similarly, the lens will sample ϕ = 90° from the center of the beam, and lower and high values of ϕ to the left and right of the central beam axis per Eq. 11, although due to the azimuthal symmetry of emission the laterally captured light is not distorted with respect to the dose distribution.
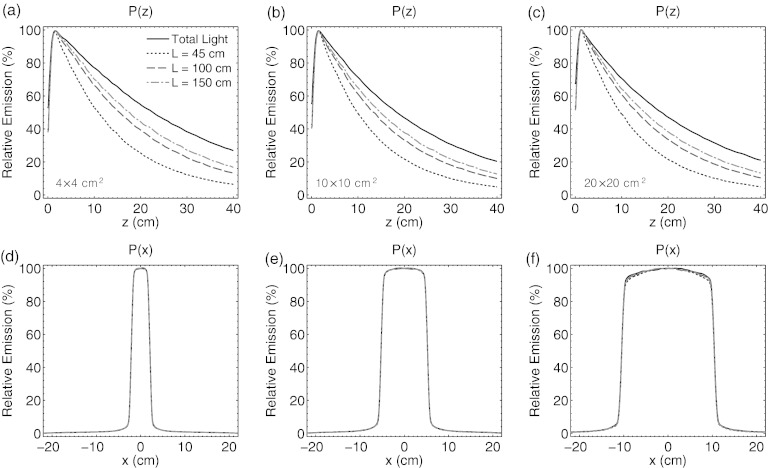
The results for the predicted collection of emission as a function of depth for the 4 × 4, 10 × 10, and 20 × 20 cm2 field sizes are shown for an imaging distance of L = 45 cm used in this study, as well as 100 and 150 cm in Figs. 5a, 5b, 5c. For all three of the simulated field sizes, the emission collected by a lens captures an emission profile that under-represents the total angularly integrated light emission profile. However, the difference between the two profiles is lessened at larger imaging distances due to a decrease in the spread of θ values sampled by the lens. All vertical profiles are normalized to a relative emission value of 100% at z = dmax.
Figure 5.
In (a)–(c) the Monte Carlo derived Čerenkov emission light profiles, P(θlens, z), as a function of depth for a 4 × 4, 10 × 10, and 20 × 20 cm2 6 MV beam at imaging distances of L = 45, 100, and 150 cm. In (d)–(f) lateral light profiles, P(x, ϕlens), for the same three field sizes and imaging distances. The solid lines denote the total light (i.e., angularly integrated emission profiles), expected to be a surrogate for the deposited dose in the medium.
Similar results for the collection of emission as a function of lateral location are shown in Figs. 5d, 5e, 5f for all field sizes at the same three imaging distances. However, in contrast to the vertical dependence of the polar angle of emission, the Čerenkov light captured by a lens for each field size at all three distances in the lateral direction is equivalent to the total integrated light emission. All lateral profiles are normalized to a relative emission value of 100% on central axis at x = 0 cm.
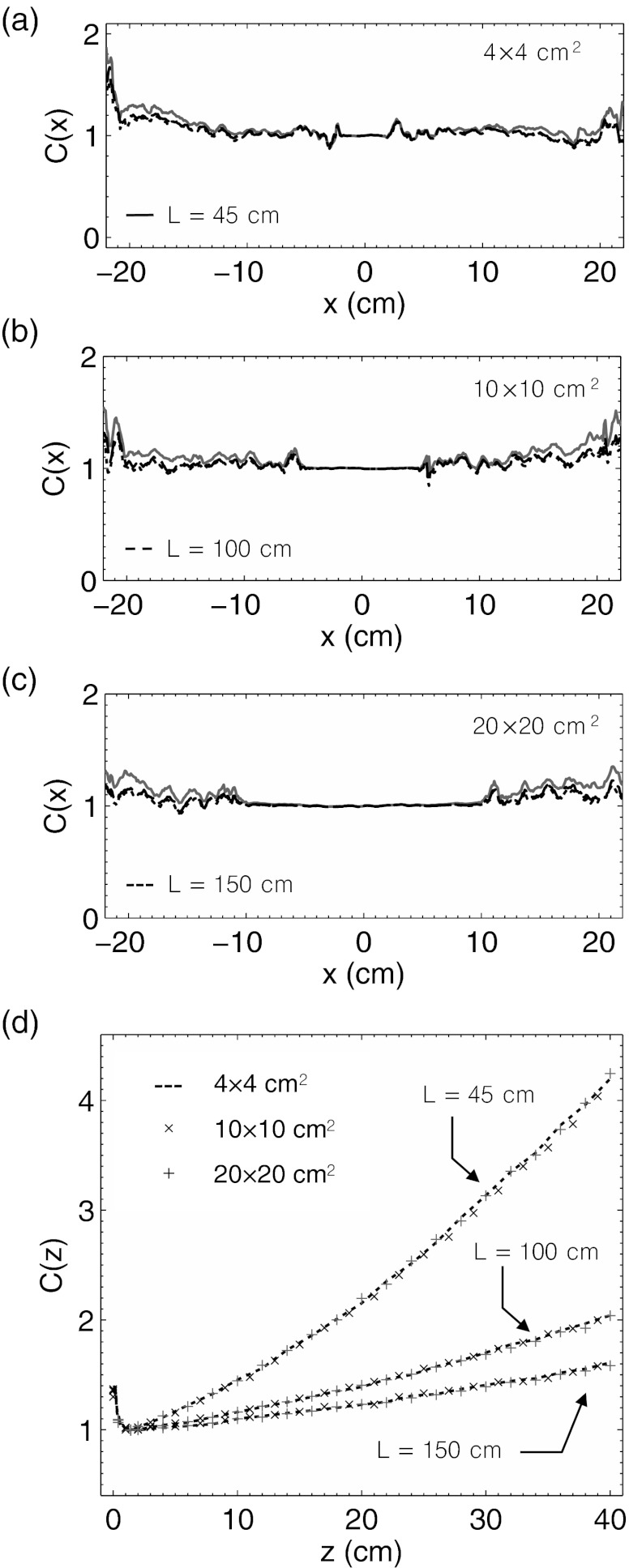
The lateral calibration factor, C(x), calculated from Eq. 13 is shown in Figs. 6a, 6b, 6c for the 4 × 4, 10 × 10, and 20 × 20 cm2 field sizes at imaging distances of L = 45, 100, and 150 cm. Due to the normalization of the relative emission profiles C(x) = 1 at x = 0 cm. However, within the entire central region of the beam (i.e., −10 to 10 cm for the 20 × 20 cm2 field size), C(x) is approximately equal to 1, indicating that no lateral calibration factor is necessary. Outside of the central beam region in the penumbra and umbra, the calibration factor shows only statistical noise features due to the low amount of Čerenkov emission present in the Monte Carlo calculated histogram P(x, ϕ).
Figure 6.
In (a)–(c) the horizontal calibration factor, C(x), is plotted for a 4 × 4, 10 × 10, and 20 × 20 cm2 6 MV beam at imaging distances of L = 45, 100, and 150 cm. In (b) the vertical calibration factor, C(z), for all three field sizes at each imaging distance is plotted.
The vertical calibration factor, C(z), calculated from Eq. 14 is shown in Fig. 6d. Due to normalization of the relative emission profiles, C(z) = 1 at dmax. In the buildup region, C(z) is nonlinear due to the failure of TCPE but follows a similar shape for all field sizes and imaging distances, approaching 1.5 at the surface. However, beyond dmax, the calibration factor appears approximately linear at all three imaging distances. Due to a different sampling of the polar angle phase function as a function of depth, C(z) increases at rates of roughly 0.083, 0.027, and 0.016 cm−1 at L = 45, 100, and 150 cm, respectively, indicating that less calibration is necessary at longer imaging distances. In addition, C(z) appears to be independent of field size at all three imaging distances.
Signal to noise ratio
The resulting Čerenkov emission images of a 4 × 4 cm2 6 MV beam after temporal median filtering of a various number of images are shown in Fig. 7. The images are shown at the native resolution of 0.25 mm per pixel prior to resizing to a 1.0 mm grid in order to better visualize the impulse noise.
Figure 7.
In (a)–(j) the full resolution captured images of a 10 × 10 cm2 FOV for a 4 × 4 cm2 6 MV beam after temporal median filtering of a various number of frames denoted by the numbers in the bottom right of each image. The scale bar in the bottom left of each image corresponds to 1 cm.
Initially, a high level of speckle noise is observed due to an inadequate number of frames for temporal median filtering. This can be attributed to energetic stray x-rays striking and saturating the CCD pixels. However, by accumulating successive images for temporal median filtering, the impulse noise is effectively suppressed. The efficacy of this noise removal technique increases with the number of available frames and therefore total delivered dose.
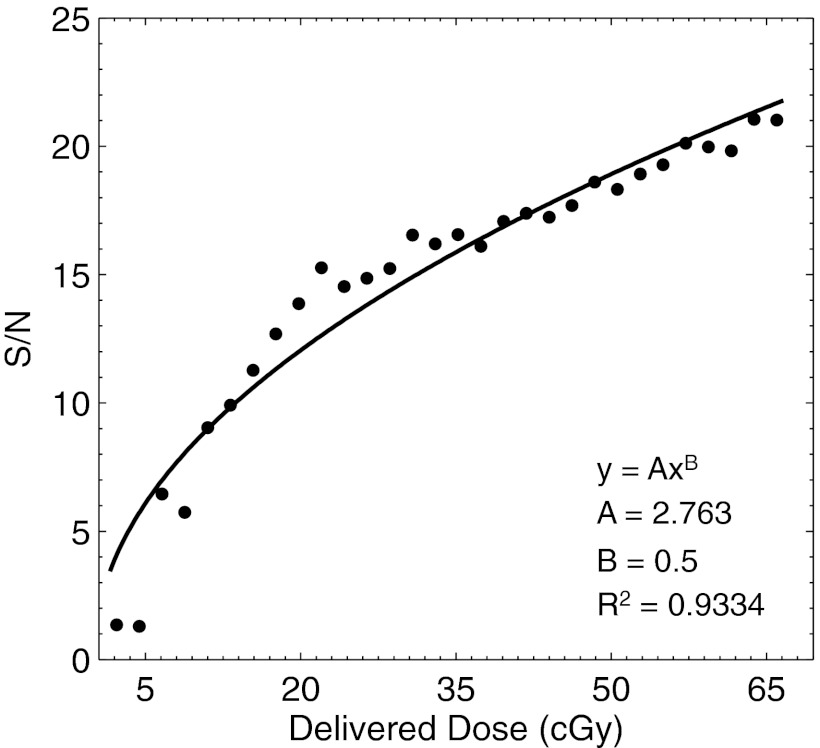
The result for the signal to noise ratio analysis of a 25 × 4 pixel ROI laterally centered at a depth of z = dmax is shown in Fig. 8. The resulting data points, calculated after temporal filtering of a variable number of frames corresponding to the plotted delivered dose indicate that the signal to noise ratio increases with delivered dose to a maximum of 20 at 66.6 cGy. The increases in signal to noise ratio are due both to removal of impulse noise due to stray radiation, and due to filtering of variation across individual pixels due to Poisson photon counting statistics. The latter is confirmed by fitting the data points to a power law, in which the exponent was assumed to be square root in nature. The first four data points appear below the signal to noise ratio regression, most likely due to inadequate removal of the stray impulse noise, after which the data points follow the expected square root trend.
Figure 8.
The signal to noise ratio as a function of delivered dose is plotted for a 4 × 4 cm2 6 MV beam. The corresponding coefficient values after regression to a square root power law are shown.
Measurement variability
The mean of the same ROI after temporal median filtering of 30 frames of 2.2 cGy each acquired over a total delivered dose of 66.6 cGy for ten successive measurements was found to be 302 counts. Given the calculated 2.2 cGy delivered dose per image frame, this corresponds to an approximate collection rate of 137 counts per cGy of delivered dose. This calculated rate is experiment-specific, and depends on several factors, including the camera to beam center distance, the chosen lens, beam size, dose rate, and energy, as well as the gain setting of the camera.
In addition, the standard deviation and maximum deviation of the ROI between all ten measurements was found to be 6.5 and 16.8 counts, respectively, indicating a 2.1 mean standard deviation 5.6% maximum variation in the recorded intensity between separate measurements. Although the fluctuation in the actual delivered dose of the LINAC is expected to be less than 1%, the observed variation is in agreement with the degree of interpixel fluctuation calculated in Sec IV.C, and therefore the magnitude of intermeasurement variability is limited by the signal to noise ratio of the captured images.
Percent depth and lateral dose profile comparison
Both calibration factors calculated in Sec. 3D were used in Eq. 15 to calibrate the experimentally captured image of Čerenkov emission for comparison to the reference dose distribution for the 4 × 4 cm2 6 MV beam. However, rather than propagating the statistical noise in the penumbra and umbra beam regions of the lateral calibration factor into the image calibration procedure, C(x) was assumed to be 1 for all values of x.
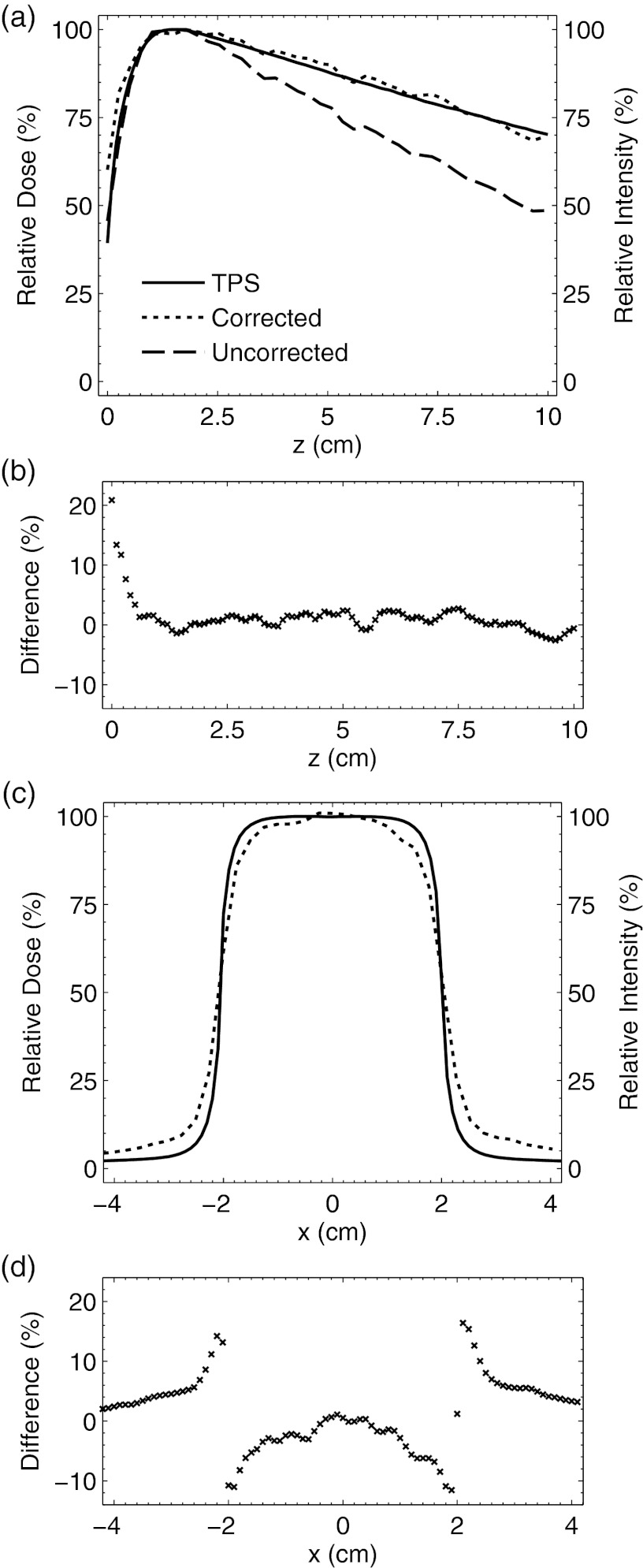
A vertical comparison of the captured light emission profile on central axis before and after calibration with respect to the PDD obtained from the TPS is shown in Fig. 9a. Before correction, the vertical light profile systematically underestimates the dose. However, after calibration the light emission profile follows the expected PDD to within ±3% at depths beyond dmax. In the buildup region, the observed dose difference is within 20% and the corresponding DTA was found to be 1.5–2 mm. The dose difference at all depths is shown in Fig. 9b.
Figure 9.
In (a) the PDD from the TPS and Čerenkov emission light profile before and after correction are plotted. The corresponding dose difference as a function of depth between the TPS and corrected signal is shown in (b). In (c) the lateral profile comparison between the TPS and corrected and uncorrected light profiles at a depth of dmax is shown. The corresponding dose difference is shown in (d).
The lateral comparison between the captured light and TPS at z = dmax is shown in Fig. 9c. Due to the fact that the lateral calibration factor was assumed to be 1 for all values of x, the uncorrected and corrected lateral emission profiles are equivalent. (i.e., effectively, no lateral calibration was applied). The corresponding dose difference at all lateral locations is shown in Fig. 9d. The light profile shows a decreased gradient at the beam edges resulting in a symmetric dose difference of ±13%, and overprediction of the dose in the umbra by 2%–3%. At the beam edges, the DTA is 0–2 mm, and in the beam interior the dose difference is 0%–5%.
DISCUSSION
The fundamental basis for the use of Čerenkov emission imaging as a means for relative dosimetry in LINAC beam profiling relies on considerations of electron energy losses per unit path length. At energies above the Čerenkov emission threshold (264 keV for water assuming a refractive index of 1.33), the absorbed energy due to secondary electrons is directly proportional to the energy radiated in the form of Čerenkov photons, which in turn may serve as a surrogate to indirectly determine the imparted dose distribution. However, with a visible waveband light yield of only 232 photons per cm for each secondary electron, the emission is extremely weak, but when captured by a highly sensitive camera the resulting images of Čerenkov emission may serve as a surrogate for a 2D projection of the deposited dose in the medium. In this study, we have demonstrated this concept for the first time and successfully modeled the experiments using Monte Carlo simulations for calibration purposes.
Simulations were performed to evaluate the angular characteristics of the emitted Čerenkov light for a 4 × 4, 10 × 10, and 20 × 20 cm2 6 MV beam, and from the results a vertical and lateral calibration factor were derived to correct for the anisotropic release of light within the irradiated medium. The lateral calibration factor was found to be insignificant within the central beam region and represented only statistical noise in the penumbra and umbra due to the low number of recorded Čerenkov photons outside of the primary beam. Similarly, the vertical calibration factor was found to be depth dependent and independent of field size. Although limited to the 6 MV beam energy in this study, the calibration procedure could be extended to additional energies. The exact form of the calibration factor would appropriately change based on the polar angle phase function of Čerenkov emission in regions of TCPE, which is expected to be energy dependent due to a change in the angular scattering angles for the various radiation interactions inside the medium.
The vertical calibration factor was evaluated at camera to beam center distances of 45, 100, and 150 cm and found to be dependent on the chosen imaging distance. As a result of the experiment geometry, the magnitude of the vertical calibration factor is reduced at larger distances due to a change in sampling of the Čerenkov emission polar angle phase function. For example, the rate of increase in the vertical calibration factor at depths beyond dmax at imaging distances of 45, 100, and 150 cm was found to be 0.083, 0.027, and 0.016 cm−1, respectively, and the calibration factor for each at a depth of 40 cm was 4.25, 2.04, and 1.61.
To validate the accuracy of the calibration factor for one field size at one of the imaging distances, a 2D dose distribution from the TPS was compared to a Čerenkov emission image of a 4 × 4 cm2 6 MV beam obtained at a distance of 45 cm. The accuracy of the method was determined by evaluating the dose difference in a lateral profile at z = dmax, as well as the PDD after vertical calibration to a depth of 10 cm. In the buildup region, the difference was within 20% with a corresponding DTA of 1.5–2 mm, and beyond dmax the difference in the PDD was within ±3%. In the lateral direction, the difference at the beam edges was ±13% and the DTA was 0–2 mm, while in the beam interior the difference was 0%–5%. Finally, outside of beam collimation the captured emission overestimated the expected dose by 2%–3%. Although the dose differences observed in this study are high with respect to a desired accuracy of 1%, precise measurement of dose in the buildup region and at the field edge near steep gradients is nontrivial even with traditional ionization chamber measurements due to their finite size.
The errors in the buildup region can be attributed to several factors. Although electrons propagating in the buildup region will generate Čerenkov photons, the analysis in Sec. 2 is restricted to regions satisfying the requirements for TCPE [i.e., in the buildup region the depth dependent correction factor, C(z), corrects the captured image to be indicative of the net energy loss due to the Čerenkov effect, which itself may not be proportional to the imparted dose]. For example, electron contamination at the surface results in a higher fluence of low energy electrons in the buildup region with energies below the threshold energy for Čerenkov emission, and therefore the expected scalar offset in energy emission relative to imparted dose is not valid in the absence of TCPE.41, 42 Furthermore, selection of the z = 0 cm pixel in the captured images is difficult to determine and only accurate to within approximately 1 mm due to the presence of a meniscus between the inner tank wall and irradiated water volume.
The observed dose difference in the beam umbra can also be attributed to several factors. Similar to the buildup region, in the beam umbra the lateral calibration factor is expected to correct the captured light to be indicative of the net energy loss due to the Čerenkov effect, which itself may not be proportional to the imparted dose due to the failure of TCPE. Given the increased fluence of low energy electrons in the beam umbra not leading to Čerenkov emission, the light profile is expected to underestimate the actual dose, although the results in this study show the opposite trend. The overestimation of dose in the beam umbra may instead be attributable to LINAC radiation leakage striking the phosphor of the ICCD. Unlike the high intensity speckle noise observed from energetic secondary particles directly striking the CCD (which was removed using temporal median filtering), counts originating due to stray radiation striking the phosphor would be lower in intensity and isotropically emitted toward the CCD, resulting in an artificially increased background intensity across the entire captured image. In future experiments, a second background image with the lens cap affixed will be used to estimate this background contamination, and a future experimental design will explore camera shielding to reduce both forms of noise and prevent radiation damage to the camera components. In addition, a second calibration factor will be explored to correct the captured images in regions of TCPE failure by considering the relative fluence of electrons below the threshold energy for Čerenkov emission at each spatial location in the irradiated medium.
Furthermore, the large errors in the lateral profile at the beam edges are a result of the conventional lens used in this study. The errors arise from the fact that the lens provides varying magnifications at different object distances, and therefore the captured images are nonorthographic and not adequate for direct comparison to the linearly summed reference dose distribution. In the measurements made in this study, the lateral beam width of the 4 × 4 cm2 field size will appear to increase at the edge of the beam closest to the lens, and decrease at the edge of the beam farthest from the lens, and only appear to be exactly 4 cm at the focal distance of the lens, despite the beam having a constant width of 4 cm. Therefore, when viewing 2D projections of the Čerenkov emission, the lateral profile will appear blurred and yield values higher than expected just outside of the beam edge, and lower than expected just inside of the beam edge. These predictions are consistent with the symmetric lateral errors observed in this study, and would be more significant when imaging larger field sizes. In future studies, this perspective error will be corrected by using a telecentric lens that provides a constant magnification at all object distances, or reduced by optimizing the imaging geometry with a conventional lens.
Despite these discrepancies, the results in this study serve as a proof of concept and will benefit from future research into additional correction factors. The Čerenkov emission imaging technique also has several advantages over current alternative dosimetry methods. For example, the proposed modality has increased speed and flexibility over conventional ionization chamber dosimetry systems, is completely noninvasive and water equivalent unlike plastic and liquid scintillation dosimetry, and does not require an external readout mechanism or suffer from time-sensitivity as in gel dosimetry. Although this study focused on capturing and comparing a single 2D projection, the concept could easily be extended to tomographic acquisitions, potentially yielding full 3D dose profiles. Based on the preliminary data in this study, full tomographic scans could be completed on the order of minutes depending on the desired number of projections and signal to noise ratio. A quick scan using 20 projections at a total frame acquisition time of 10 s with an expected signal to noise ratio of 20 could be completed in less than 4 min. A higher resolution scan using 90 projections and a frame exposure time of 20 s and a predicted signal to noise ratio of 32 (see Sec IV.C) could be completed in 30 min. The scan speed could be further improved by increasing the dose rate of the LINAC beyond the 400 MU/min used in this study, as the technique should be dose rate independent, and a higher dose rate would imply more primary particles per second and therefore more captured Čerenkov photons per second.
Paralleling gel dosimetry, the noninvasive nature of the proposed modality could also be extended to imaging from solid phantoms. Although this would compromise the water equivalent advantage of the method, solid phantoms composed of a tissue-equivalent plastic could be used to investigate dose deposition in more complex geometries without the previously mentioned disadvantages associated with gel dosimetry. Tissue-equivalent plastics would have an added benefit, as they would exhibit lower Čerenkov emission energy thresholds and therefore less emission to dose discrepancy at low electron energies (see Table 1). Imaging from complex solid phantoms, as well refinement of the Čerenkov emission imaging system will be investigated in future studies.
CONCLUSIONS
It has been shown for the first time that the intrinsic Čerenkov emission generated by energetic secondary electrons in media irradiated with a megavoltage x-ray photon LINAC beam can be imaged and used to spatially estimate the imparted dose distribution. Monte Carlo simulations were successfully used to characterize the angular characteristics of the induced Čerenkov emission and calibrate for the system's ability to image the anisotropic light distribution. With future system refinement, improved accuracy, and extension to tomographic acquisitions the proposed modality may become an important method for 3D beam profiling.
ACKNOWLEDGMENT
This work has been funded by National Institutes of Health (NIH) Grant Nos. RO1CA120368 and PO1CA084203.
References
- Podgorsak E. B., Radiation Oncology Physics: A Handbook for Teachers and Students (International Atomic Energy Agency, Vienna, 2005). [Google Scholar]
- Attix F. H., Introduction to Radiological Physics and Radiation Dosimetry (Wiley, New York, 1986). [Google Scholar]
- Fricke H. and Morse S., “The chemical action of roentgen rays on dilute ferrosulphate solutions as a measure of dose,” Am. J. Roentgenol. Radium Ther. 18, 430–432 (1927). [Google Scholar]
- Maryanski M. J., Schulz R. J., Ibbott G. S., Gatenby J. C., Xie J., Horton D., and Gore J. C., “Magnetic-resonance-imaging of radiation-dose distributions using a polymer-gel dosimeter,” Phys. Med. Biol. 39, 1437–1455 (1994). 10.1088/0031-9155/39/9/010 [DOI] [PubMed] [Google Scholar]
- Gore J. C., Ranade M., Maryanski M. J., and Schulz R. J., “Radiation dose distributions in three dimensions from tomographic optical density scanning of polymer gels: I. Development of an optical scanner,” Phys. Med. Biol. 41, 2695–2704 (1996). 10.1088/0031-9155/41/12/009 [DOI] [PubMed] [Google Scholar]
- Beddar A. S., “Plastic scintillation dosimetry and its application to radiotherapy,” Radiat. Meas. 41, S124–S133 (2006). 10.1016/j.radmeas.2007.01.002 [DOI] [Google Scholar]
- Beddar A. S., Mackie T. R., and Attix F. H., “Water-equivalent plastic scintillation detectors for high-energy beam dosimetry: I. Physical characteristics and theoretical consideration,” Phys. Med. Biol. 37, 1883–1900 (1992). 10.1088/0031-9155/37/10/006 [DOI] [PubMed] [Google Scholar]
- Beddar A. S., Mackie T. R., and Attix F. H., “Water-equivalent plastic scintillation detectors for high-energy beam dosimetry: II. Properties and measurements,” Phys. Med. Biol. 37, 1901–1913 (1992). 10.1088/0031-9155/37/10/007 [DOI] [PubMed] [Google Scholar]
- Guillot M., Beaulieu L., Archambault L., Beddar S., and Gingras L., “A new water-equivalent 2D plastic scintillation detectors array for the dosimetry of megavoltage energy photon beams in radiation therapy,” Med. Phys. 38, 6763–6774 (2011). 10.1118/1.3664007 [DOI] [PubMed] [Google Scholar]
- Collomb-Patton V., Boher P., Leroux T., Fontbonne J. M., Vela A., and Batalla A., “The DOSIMAP, a high spatial resolution tissue equivalent 2D dosimeter for LINAC QA and IMRT verification,” Med. Phys. 36, 317–328 (2009). 10.1118/1.3013703 [DOI] [PubMed] [Google Scholar]
- Ponisch F., Archambault L., Briere T. M., Sahoo N., Mohan R., Beddar S., and Gillin M. T., “Liquid scintillator for 2D dosimetry for high-energy photon beams,” Med. Phys. 36, 1478–1485 (2009). 10.1118/1.3106390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beddar A. S., Mackie T. R., and Attix F. H., “Cerenkov light generated in optical fibers and other light pipes irradiated by electron-beams,” Phys. Med. Bio. 37, 925–935 (1992). 10.1088/0031-9155/37/4/007 [DOI] [Google Scholar]
- Beddar A. S., Suchowerska N., and Law S. H., “Plastic scintillation dosimetry for radiation therapy: Minimizing capture of Cerenkov radiation noise,” Phys. Med. Biol. 49, 783–790 (2004). 10.1088/0031-9155/49/5/009 [DOI] [PubMed] [Google Scholar]
- Čerenkov P. A., “Visible light from pure liquids under the impact of γ-rays,” C. R. Acad. Sci. URSS 2, 451–457 (1934). [Google Scholar]
- Lambert J., Yin Y., McKenzie D. R., Law S., and Suchowerska N., “Cerenkov-free scintillation dosimetry in external beam radiotherapy with an air core light guide,” Phys. Med. Biol. 53, 3071–3080 (2008). 10.1088/0031-9155/53/11/021 [DOI] [PubMed] [Google Scholar]
- Frelin A. M., Fontbonne J. M., Ban G., Colin J., Labalme M., Batalla A., Isambert A., Vela A., and Leroux T., “Spectral discrimination of Cerenkov radiation in scintillating dosimeters,” Med. Phys. 32, 3000–3006 (2005). 10.1118/1.2008487 [DOI] [PubMed] [Google Scholar]
- Clift M. A., Johnston P. N., and Webb D. V., “A temporal method of avoiding the Cerenkov radiation generated in organic scintillator dosimeters by pulsed mega-voltage electron and photon beams,” Phys. Med. Biol. 47, 1421–1433 (2002). 10.1088/0031-9155/47/8/313 [DOI] [PubMed] [Google Scholar]
- Jelley J. V., Čerenkov Radiation, and its Applications (Pergamon, New York, 1958). [Google Scholar]
- Weekes T. C., Cawley M. F., Fegan D. J., Gibbs K. G., Hillas A. M., Kwok P. W., Lamb R. C., Lewis D. A., Macomb D., Porter N. A., Reynolds P. T., and Vacanti G., “Observation of TeV gamma-rays from the Crab-Nebula using the atmospheric Cerenkov imaging technique,” Astrophys. J. 342, 379–395 (1989). 10.1086/167599 [DOI] [Google Scholar]
- Andres E., Askebjer P., Bai X., Barouch G., Barwick S. W., Bay T. C., Becker K. H., Bergstrom L., Bertrand D., Bierenbaum D., Biron A., Booth J., Botner O., Bouchta A., Boyce M. M., Carius S., Chen A., Chirkin D., Conrad J., Cooley J., Costa C. G. S., Cowen D. F., Dailing J., Dalberg E., DeYoung T., Desiati P., Dewulf J. P., Doksus P., Edsjo J., Ekstrom P., Erlandsson B., Feser T., Gaug M., Goldschmidt A., Goobar A., Gray L., Haase H., Hallgren A., Halzen F., Hanson K., Hardtke R., He Y. D., Hellwig M., Heukenkamp H., Hill G. C., Hulth P. O., Hundertmark S., Jacobsen J., Kandhadai V., Karle A., Kim J., Koci B., Kopke L., Kowalski M., Leich H., Leuthold M., Lindal P., Liubarsky I., Loaiza P., Lowder D. M., Ludvig J., Madsen J., Marciniewski P., Matis H. S., Mihalyi A., Mikolajski T., Miller T. C., Minaeva Y., Miocinovic P., Mock P. C., Morse R., Neunhoffer T., Newcomer F. M., Niessen P., Nygren D. R., Ogelman H., de los Heros C. P., Porrata R., Price P. B., Rawlins K., Reed C., Rhode W., Richards A., Richter S., Martino J. R., Romenesko P., Ross D., Rubinstein H., Sander H. G., Scheider T., Schmidt T., Schneider D., Schneider E., Schwarz R., Silvestri A., Solarz M., Spiczak G. M., Spiering C., Starinsky N., Steele D., Steffen P., Stokstad R. G., Usechak N., Vander Donckt M., Walck C., Weinheimer C., Wiebusch C. H., Wischnewski R., Wissing H., Woschnagg K., Wu W., Yodh G., and Young S., “Observation of high-energy neutrinos using Cerenkov detectors embedded deep in Antarctic ice,” Nature (London) 410, 441–443 (2001). 10.1038/35068509 [DOI] [PubMed] [Google Scholar]
- Ypsilantis T. and Seguinot J., “Theory of ring imaging Cherenkov counters,” Nucl. Instrum. Methods Phys. Res. A 343, 30–51 (1994). 10.1016/0168-9002(94)90532-0 [DOI] [Google Scholar]
- Weekes T. C., Badran H., Biller S. D., Bond I., Bradbury S., Buckley J., Carter-Lewis D., Catanese M., Criswell S., Cui W., Dowkontt P., Duke C., Fegan D. J., Finley J., Fortson L., Gaidos J., Gillanders G. H., Grindlay J., Hall T. A., Harris K., Hillas A. M., Kaaret P., Kertzman M., Kieda D., Krennrich F., Lang M. J., LeBohec S., Lessard R., Lloyd-Evans J., Knapp J., McKernan B., McEnery J., Moriarty P., Muller D., Ogden P., Ong R., Petry D., Quinn J., Reay N. W., Reynolds P. T., Rose J., Salamon M., Sembroski G., Sidwell R., Slane P., Stanton N., Swordy S. P., Vassiliev V. V., and Wakely S. P., “VERITAS: The very energetic radiation imaging telescope array system,” Astropart. Phys. 17, 221–243 (2002). 10.1016/S0927-6505(01)00152-9 [DOI] [Google Scholar]
- Robertson R., Germanos M. S., Li C., Mitchell G. S., Cherry S. R., and Silva M. D., “Optical imaging of Cerenkov light generation from positron-emitting radiotracers,” Phys. Med. Biol. 54, N355–N365 (2009). 10.1088/0031-9155/54/16/N01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell G. S., Gill R. K., Boucher D. L., Li C., and Cherry S. R., “In vivo Cerenkov luminescence imaging: A new tool for molecular imaging,” Philos. Trans. R. Soc. London, Ser. A 369, 4605–4619 (2011). 10.1098/rsta.2011.0271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spinelli A. E., D’Ambrosio D., Calderan L., Marengo M., Sbarbati A., and Boschi F., “Cerenkov radiation allows in vivo optical imaging of positron emitting radiotracers,” Phys. Med. Biol. 55, 483–495 (2010). 10.1088/0031-9155/55/2/010 [DOI] [PubMed] [Google Scholar]
- Ruggiero A., Holland J. P., Lewis J. S., and Grimm J., “Cerenkov luminescence imaging of medical isotopes,” J. Nucl. Med. 51, 1123–1130 (2010). 10.2967/jnumed.110.076521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H. G., Ren G., Miao Z., Zhang X. F., Tang X. D., Han P. Z., Gambhir S. S., and Cheng Z., “Molecular optical imaging with radioactive probes,” PloS ONE 5, 27 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axelsson J., Davis S. C., Gladstone D. J., and Pogue B. W., “Cerenkov emission induced by external beam radiation stimulates molecular fluorescence,” Med. Phys. 38, 4127–4132 (2011). 10.1118/1.3592646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axelsson J., Glaser A. K., Gladstone D. J., and Pogue B. W., “Quantitative Cherenkov emission spectroscopy for tissue oxygenation assessment,” Opt. Express 20, 5133–5142 (2012). 10.1364/OE.20.005133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jang K. W., Yoo W. J., Shin S. H., Shin D., and Lee B., “Fiber-optic Cerenkov radiation sensor for proton therapy dosimetry,” Opt. Express 20, 13907–13914 (2012). 10.1364/OE.20.013907 [DOI] [PubMed] [Google Scholar]
- Glaser A. K., Zhang R., Davis S. C., Gladstone D. J., and Pogue B. W., “Time-gated Cherenkov emission spectroscopy from linear accelerator irradiation of tissue phantoms,” Opt. Lett. 37, 1193–1195 (2012). 10.1364/OL.37.001193 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank I. and Tamm I., “Coherent visible radiation of fast electrons passing through matter,” C. R. Acad. Sci. URSS 14, 109–114 (1937). [Google Scholar]
- Tearney G. J., Brezinski M. E., Southern J. F., Bouma B. E., Hee M. R., and Fujimoto J. G., “Determination of the refractive index of highly scattering human tissue by optical coherence tomography,” Opt. Lett. 20, 2258–2260 (1995). 10.1364/OL.20.002258 [DOI] [PubMed] [Google Scholar]
- Berger M. J., Coursey J. S., Zucker M. A., and Chang J., ESTAR, PSTAR, and ASTAR: Computer Programs for Calculating Stopping-Power and Range Tables for Electrons, Protons, and Helium Ions (version 1.2.3) (2005). [Online] Available: http://physics.nist.gov/Star. National Institute of Standards and Technology, Gaithersburg, MD.
- Archambault L., Briere T. M., and Beddar S., “Transient noise characterization and filtration in CCD cameras exposed to stray radiation from a medical linear accelerator,” Med. Phys. 35, 4342–4351 (2008). 10.1118/1.2975147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arce P., Mendes P. Rato, Bruyndock P., Canadas M., Perez J. M., and Sarasola I., Nuclear Science Symposium Conference Record (IEEE, Dresden, Germany, 2008), pp. 3162–3168. 10.1109/NSSMIC.2008.4775023 [DOI]
- Agostinelli S., Allison J., Amako K., Apostolakis J., Araujo H., Arce P., Asai M., Axen D., Banerjee S., Barrand G., Behner F., Bellagamba L., Boudreau J., Broglia L., Brunengo A., Burkhardt H., Chauvie S., Chuma J., Chytracek R., Cooperman G., Cosmo G., Degtyarenko P., Dell’Acqua A., Depaola G., Dietrich D., Enami R., Feliciello A., Ferguson C., Fesefeldt H., Folger G., Foppiano F., Forti A., Garelli S., Giani S., Giannitrapani R., Gibin D., Gómez Cadenas J. J., González I., Abril G. G., Greeniaus G., Greiner W., Grichine V., Grossheim A., Guatelli S., Gumplinger P., Hamatsu R., Hashimoto K., Hasui H., Heikkinen A., Howard A., Ivanchenko V., Johnson A., Jones F. W., Kallenbach J., Kanaya N., Kawabata M., Kawabata Y., Kawaguti M., Kelner S., Kent P., Kimura A., Kodama T., Kokoulin R., Kossov M., Kurashige H., Lamanna E., Lampén T., Lara V., Lefebure V., Lei F., Liendl M., Lockman W., Longo F., Magni S., Maire M., Medernach E., Minamimoto K., de Freitas P. M., Morita Y., Murakami K., Nagamatu M., Nartallo R., Nieminen P., Nishimura T., Ohtsubo K., Okamura M., O’Neale S., Oohata Y., Paech K., Perl J., Pfeiffer A., Pia M. G., Ranjard F., Rybin A., Sadilov S., Di Salvo E., Santin G., Sasaki T., Savvas N., Sawada Y., Scherer S., Sei S., Sirotenko V., Smith D., Starkov N., Stoecker H., Sulkimo J., Takahata M., Tanaka S., Tcherniaev E., Tehrani E. S., Tropeano M., Truscott P., Uno H., Urban L., Urban P., Verderi M., Walkden A., Wander W., Weber H., Wellisch J. P., Wenaus T., Williams D. C., Wright D., Yamada T., Yoshida H., and Zschiesche D., “Geant4: A simulation toolkit,” Nucl. Instrum. Methods Phys. Res. A 506, 250–303 (2003). 10.1016/S0168-9002(03)01368-8 [DOI] [Google Scholar]
- Geant4 Physics Reference Manual (CERN, Switzerland, 2010). [Google Scholar]
- Hale G. M. and Querry M. R., “Optical-constants of water in 200-nm to 200-μm wavelength region,” Appl. Opt. 12, 555–563 (1973). 10.1364/AO.12.000555 [DOI] [PubMed] [Google Scholar]
- Segelstein B. J., M.S. thesis, University of Missouri-Kansas City, 1981. [Google Scholar]
- Nilsson B., “Electron contamination from different materials in high energy photon beams,” Phys. Med. Biol. 30, 139–151 (1985). 10.1088/0031-9155/30/2/003 [DOI] [PubMed] [Google Scholar]
- Nilsson B. and Brahme A., “Absorbed dose from secondary electrons in high energy photon beams,” Phys. Med. Biol. 24, 901–912 (1979). 10.1088/0031-9155/24/5/003 [DOI] [PubMed] [Google Scholar]