A flexible-protein molecular docking study of the binding of ruthenium complex compounds to PIM1, GSK-3β, and CDK2/Cyclin A protein kinases

Abstract

We employ ensemble docking simulations to characterize the interactions of two enantiomeric forms of a Ru-complex compound (1-R and 1-S) with three protein kinases, namely PIM1, GSK-3β, and CDK2/cyclin A. We show that our ensemble docking computational protocol adequately models the structural features of these interactions and discriminates between competing conformational clusters of ligand-bound protein structures. Using the determined X-ray crystal structure of PIM1 complexed to the compound 1-R as a control, we discuss the importance of including the protein flexibility inherent in the ensemble docking protocol, for the accuracy of the structure prediction of the bound state. A comparison of our ensemble docking results suggests that PIM1 and GSK-3β bind the two enantiomers in similar fashion, through two primary binding modes: conformation I, which is very similar to the conformation presented in the existing PIM1/compound 1-R crystal structure; conformation II, which represents a 180° flip about an axis through the NH group of the pyridocarbazole moiety, relative to conformation I. In contrast, the binding of the enantiomers to CDK2 is found to have a different structural profile including a suggested bound conformation, which lacks the conserved hydrogen bond between the kinase and the ligand (i.e., ATP, staurosporine, Ru-complex compound). The top scoring conformation of the inhibitor bound to CDK2 is not present among the top-scoring conformations of the inhibitor bound to either PIM1 or GSK-3β and vice-versa. Collectively, our results help provide atomic-level insights into inhibitor selectivity among the three kinases.

Introduction

Protein kinases—one of the most important targets in the current cancer therapy—are the largest enzyme family involved in cell signal transduction [1, 2]. They are encoded by approximately 2 % of eukaryotic genes and more than 500 protein kinases have been identified based on human genome sequencing [3] and biochemical studies. Protein kinases catalyze the transfer of the γ-phosphate group from an ATP molecule to tyrosine, serine or threonine residues in proteins. This process plays an essential role in regulating many fundamental cellular processes [4]. Constitutive or inappropriate activation of protein kinases are seen in a variety of cancers and small molecule inhibitors are designed to target/inhibit kinase signaling in such scenarios [5]. Understanding the inhibition and phosphorylation of protein kinases is significant in guiding cancer therapy. The kinases studied in this work—GSK3-β, CDK2, and PIM1—are all well-established drug targets.

A pharmacophore model of the ATP-binding site of protein kinases [6] is depicted in Fig. 1. One way to inhibit abnormal kinase activity is to design small molecule inhibitors to bind into the ATP binding cleft, block ATP binding and therefore inhibit phosphorylation. The success of small-molecule ATP-competitive inhibitors such as imatinib (Gleevec) for the treatment of chronic myeloid leukemia (CML) and gastrointestinal stromal tumors (GIST) confirmed that this strategy is indeed effective [7]. In spite of the success of Gleevec, the design of ATP-competitive inhibitors that are selective (specific) for a particular kinase appears to be quite challenging due to the conserved nature of the protein structures.

Fig. 1.

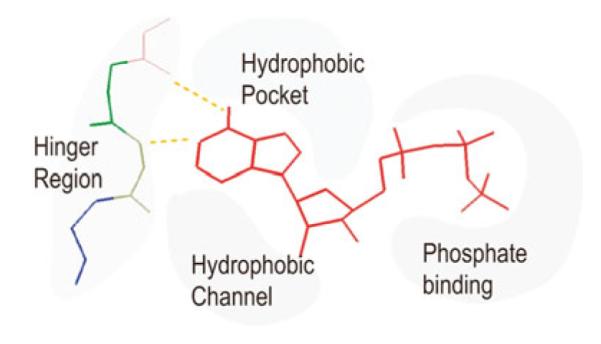
Pharmacophore model of the ATP-binding site of protein kinases. ATP is in red. Also depicted are the hydrophobic pocket, the hydrophobic channel, the hinge region, and the phosphate binding region

X-ray crystal structures for a range of kinases are available in the Protein Data Bank (PDB), providing a structural basis for understanding kinase inhibition and facilitating structure-guided design of kinase-specific inhibitors. The catalytic clefts of protein kinases usually include two hydrophobic pockets (Hyp1 and Hyc1), an adenine region, ‘sugar’ pocket and the phosphate groove (Fig. 1). The adenine region contains the two key hydrogen bonds formed by the interaction of the N-1 and N-6 amino groups of the adenine ring with the backbone NH and carbonyl groups of the adenine anchoring hinge region of the protein kinase. Many potent inhibitors use at least one of these hydrogen bonds. The hydrophobic pocket is not used by ATP, but is exploited in the design of most kinase inhibitors. It plays an important role in inhibitor selectivity, and its size is different in active and inactive kinase states. The hydrophobic channel opens to solvent and is not used by ATP and hence can be exploited in the design of inhibitors. The phosphate binding region offers little opportunity in terms of inhibitor binding affinity due to high solvent exposure. However, it can be utilized in improving selectivity.

As the overall protein fold is conserved in the kinase family, a major challenge is to understand the molecular basis for inhibitor sensitivity and to design small-molecule compounds that are highly selective (specific) for the targeted protein kinase. Progress towards the design of selective small-molecule kinase inhibitors based on the exploitation of distinct features presented by ATP-binding site has been reviewed recently [8, 9]. The vast majority of specific enzyme inhibitors are small organic molecules that gain their specificity by a combination of weak interactions, including hydrogen bonding, electrostatic contacts, and hydrophobic interactions. Recently, a novel strategy has been introduced for the design of small-molecule enzyme inhibitors by using substitutionally inert organometallic scaffolds [10, 11], based on the hypothesis that complementing organic elements with a metal center may provide new opportunities for building three-dimensional structures with unique and defined shapes. In particular, a class of half-sandwich ruthenium complex compounds based on the scaffold shown in Fig. 2 have been reported to show high affinities and promising selectivity profiles for protein kinases and lipid kinases [12–14].

Fig. 2.

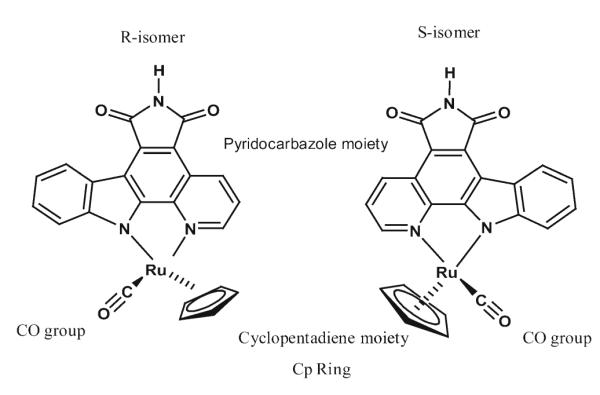
Chemical structure of ruthenium complex compound 1. Left R-enantiomer, right S-enantiomer

The new ruthenium complex compounds are designed to mimic the shape of staurosporine—a well-known protein kinase inhibitor—by replacing the indolocarbazole alkaloid scaffold with metal complexes in which the structural features of the indolocarbazole heterocycle is retained. The ruthenium metal center plays a structural role by organizing the organic ligands in three-dimensional space. As shown in Fig. 2, the coordination geometry around the ruthenium is pseudo-octahedral, formed by the pyridocarbazole ligand, the CO group oriented perpendicular to the pyridocarbazole plane, and the cyclopentadiene (Cp) moiety. The compound was designed to bind with the kinase by forming hydrogen bonds to the backbone residues at the hinge region of the kinases. However, unlike staurosporine, which is a nonspecific nanomolar inhibitor for most protein kinases, these ruthenium half-sandwich compounds show remarkable selectivity profiles. In particular, profiling the racemic mixture of (R/S)-1 against more than 50 protein kinases in vitro shows the high selectivity of this class of compounds for PIM1 (IC₅₀=3nM, 100 μm ATP) and GSK-3β (IC₅₀= 50nM, 100 μm ATP) [12]. Interestingly, the phylogenetically and structurally closely related cyclin-dependent kinases (CDKs) are not significantly inhibited, with IC₅₀=3μM (100 μm ATP) for the CDK2/cyclin A complex [12].

Sequence alignment analysis (Table 1) shows a high degree of conservation among the ATP binding pocket residues of the three kinases. Superposition of the kinase active sites using the α-carbon atoms of the residues around the ATP pocket also shows that the structure of the binding site is highly similar among the three kinases (Fig. 3). Despite these similarities, there are differences in specific amino acid positions (noted in Table 1 and labeled in Fig. 3), which possibly have a bearing on the differences in the binding interactions, and hence inhibitor selectivity.

Table 1.

Sequence alignment of residues around active site of the three protein kinases, PIM1, GSK3, and CDK2

Kinase	N-terminal lobe								Linker region				C-terminal lobe
PIM-1	L44	G45	S46	F49	V52	A65	I104	L120a	E121	R122	–	P123	E171	L174	I185a	D186
GSK-3β	I62	G63	N64	F67	V70	A83	V110	L132a	D133	Y134	V135	P136	Q185	L188	C199a	D200
CDK2	I10	G11	E12	Y15	V18	A31	V64	F80a	E81	F82	L83	H84	Q131	L134	A144a	D145

^aSignificantly different residues

Fig. 3.

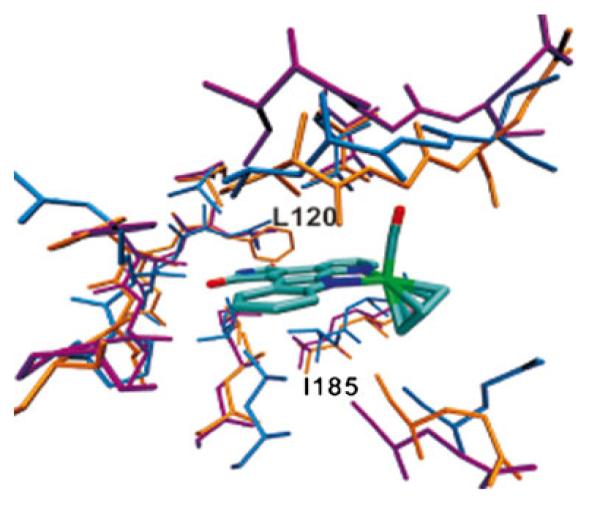
Structural alignment of the ATP binding pockets of three protein kinases, PIM1 (blue), GSK3 (purple), and CDK2/CYCLIN A (orange)

Although it is of great interest to understand the interaction of ruthenium compounds with the three protein kinases in atomic details, [15, 16] only one crystal structure, i.e., PIM1 bound with (R)-1, is currently available. It is not clear how the other enantiomer, (S)-1 is bound to PIM1. The bound conformations of both (R)-1 and (S)-1 are not known from experiments either. Thus, in this article, we modeled the interactions between the ruthenium scaffold and three protein kinases, PIM1, GSK-3β and CDK2/cyclin A, targeting the selectivity profile of the compound.

Molecular docking is used frequently to predict ligand binding in the absence of ligand-bound crystal structures and functional affinity data [17, 18]. While ligand flexibility is accounted for in most docking programs, many treat the protein as a rigid body. However, in practical scenarios in which the receptor structure is derived either from an experimentally determined structure of the apo-kinase or from a structure where the kinase is complexed with a different ligand, the rigid-receptor docking often fails to predict proper bound conformation. Hence, efforts have been made to account for protein flexibility [19, 20]. In this article, we applied the ensemble docking procedure to predict bound conformations of ruthenium compounds (R/S)-1 against the three protein kinases PIM1, GSK-3β and CDK2/cyclin A. As we describe in the following sections, our docking results reveal the protein–ligand interaction and suggest possible structural factors that may give rise to different binding affinities of the proteins.

Methods

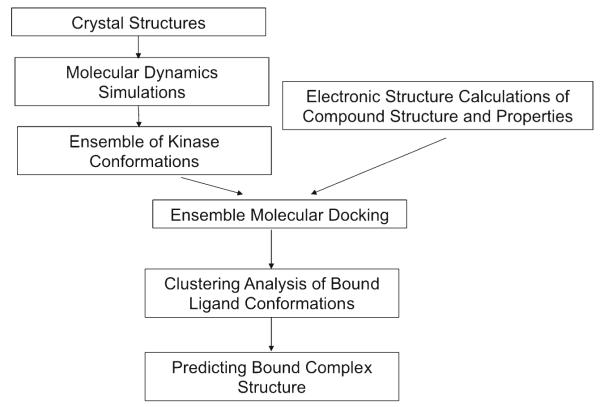
The flow chart in Fig. 4 depicts the ensemble docking protocol followed. To summarize, protein conformations are sampled with all-atom molecular dynamics (MD) simulations with explicit solvent. Charges and geometry of the ligands are calculated using electronic structure (ab-initio) methods. The ligands were then docked into each of the protein conformations using the docking program Auto-Dock3.0. The predicted bound conformations of ligand are subsequently clustered.

Fig. 4.

Flow chart of the ensemble docking method

Ab-Initio electronic-structure calculations of Ru-complex compounds

The geometries of both enantiomers of compound 1 were optimized using the Gaussian 98 [21] program at the density functional theory (DFT) level using the B3LYP functional as well as at the Hartree-Fock (HF) [21] level. For the hydrogen, carbon, oxygen and nitrogen, the 6-31 G* basis set was used, while for the Ru atom, the Los Alamos ECP (effective core potential) plus DZ (double zeta) basis set (LanL2DZ [22]) was used. The geometry optimization of the molecule returns the minimum-energy geometry of the molecule and the spatial electron-density map at 0 K. Following the procedure of Aiken et al. [23], the partial (Mulliken) charges on each atom were inferred from ab initio calculations, which are used to determine the molecular descriptors of the inhibitor compound and are used further in docking calculations. The minimum energy geometries obtained using HF and B3LYP methods agree closely with each other [root mean squared deviation (RMSD)=0.215 Å, see Fig. 5]; however, Mulliken partial charges differ for these two methods (see Table 2).

Fig. 5.

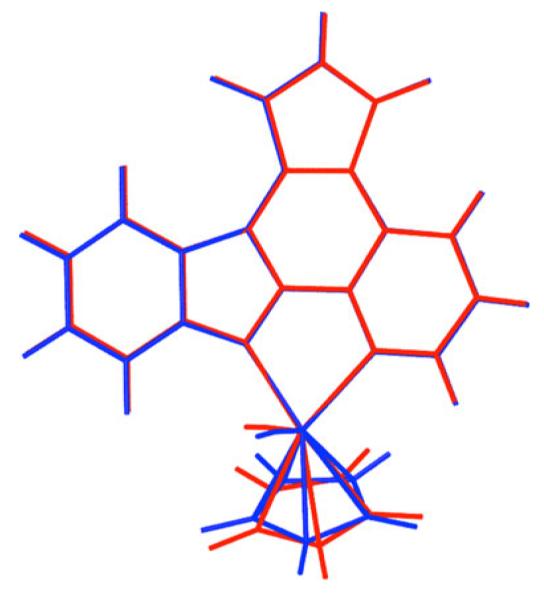
Overlay of the minimum energy geometry of the compound 1-R obtained using HF (red) and B3LYP (blue) methods. For both methods, the 6-31 G* basis set was used for the carbon, nitrogen, oxygen and hydrogen atoms, while the LanL2DZ basis set was used for the ruthenium atom. The root mean squared deviation (RMSD) between these two geometries is 0.215 Å

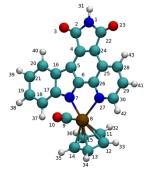
Table 2.

Mulliken charges computed for each atom of compound 1-R using HF and B3LYP methods. For both methods, the 6–31 G* basis set was used for carbon, nitrogen, oxygen and hydrogen atoms, while the LanL2DZ basis set was used for the ruthenium atom. The figure depicts the geometry of compound 1-R showing carbon atoms (cyan), oxygen (red), nitrogen (blue), ruthenium (brown) and hydrogen(white ). Indices used in the Table for each atom are also depicted

Index	Atom	HF	B3LYP	Atom Label
1	N	−0.94	−0.67
2	C	0.89	0.53
3	O	−0.56	−0.41
4	C	−0.13	−0.08
5	C	−0.03	0.08
6	C	0.34	0.24
7	N	−0.94	−0.64
8	Ru	0.54	0.20
9	C	0.41	0.26
10	O	−0.30	−0.26
11	C	−0.27	−0.13
12	C	−0.22	−0.18
13	C	−0.20	−0.12
14	C	−0.30	−0.19
15	C	−0.16	−0.10
16	C	−0.06	0.03
17	C	0.32	0.25
18	C	−0.26	−0.20
19	C	−0.19	−0.13
20	C	−0.17	−0.19
21	C	−0.25	−0.16
22	C	0.87	0.51
23	O	−0.59	−0.44
24	C	−0.21	−0.07
25	C	0.00	0.14
26	C	0.35	0.24
27	N	−0.78	−0.52
28	C	−0.10	−0.15
29	C	−0.30	−0.16
30	C	0.12	0.04
31	H	0.42	0.34
32	H	0.23	0.17
33	H	0.22	0.16
34	H	0.23	0.18
35	H	0.23	0.17
36	H	0.25	0.19
37	H	0.20	0.13
38	H	0.19	0.12
39	H	0.19	0.12
40	H	0.26	0.17
41	H	0.23	0.15
42	H	0.22	0.17
43	H	0.28	0.19

Even though a DFT level of theory is considered the appropriate because it includes electron correlation, which is critical in treating ruthenium interactions correctly, the HF level was included for comparison because the rest of the biomolecular interaction force-field was parameterized at that level, and the HF is the approach prescribed to parameterize new interactions. We note that the Ru is fully buried within the cp ring on one side and with the staurosporine group on the other and is not exposed to the solvent or the protein, and hence the partial charges derived at the HF level will still be accurate enough to model the protein–ligand interactions while maintaining compatibility with the rest of the biomolecular force-field (see below).

Protein conformation

The native and non-native protein conformations of PIM1 kinase were constructed based on two different crystallographic structures from the PDB: (1) the structure of the PIM1/(R)-1 bound complex (PDB ID: 2BZH), and (2) the structure of PIM1 bound to an ATP analog (PDB ID: 1YXT). For the GSK-3β and CDK2/cyclin A systems, conformations derived from crystal complex structures with the ATP analog (1I09 for GSK-3β and 1QMZ for CDK2/ cyclin A ) were employed in the docking simulations. Four apo-kinase conformations were generated based on these crystal structures, by removing ligands and adding hydrogen atoms and other missing residues using the CHARMM [24] biomolecular simulation package.

To generate an ensemble of conformations for each kinase, MD simulations for each protein kinase were performed with the respective crystal structures serving as the starting conformation. The proteins were solvated explicitly using the TIP3P model for water and neutralized by placing ions (sodium and chloride) at an ionic strength of 150 mM. The ions were placed at positions of electrostatic extrema predicted by mean-field Debye-Huckel calculations. The solvated models are energy minimized, heated to 300 K, and equilibrated at constant temperature and constant pressure (300 K and 1 atm) using the NAMD simulation package [25] in conjunction with the CHARMM27 force-field [26]. All our simulations were performed on a fully periodic system, and include long-range electrostatics using the particle mesh Ewald (PME) algorithm [27]. The extent of the equilibration phase was determined by tracking the plateau behavior of the RMSD of the protein backbone (C_αpositions) calculated with respect to the starting conformation. For each protein kinase system, 10 ns of dynamics runs were generated, from which we extracted 100 protein conformations at uniform intervals from the last 8 ns of the respective trajectories for use in our ensemble docking protocol. In order to make the comparison of different systems easier, all the protein conformations were aligned with respect to the PIM1 coordinates in 2BZH structure based on residues within 15 Å of the ATP binding site.

Docking protocol

The AutoDock3.0.5 program [28] was used for docking simulations. In silico or computational docking is used to generate a large set of conformations of the receptor-ligand complex and to rank them according to their stability; therefore, an essential component of docking is an algorithm for searching through conformational space. A well-appreciated fact regarding ligand–protein binding interactions is that both components flex and adjust to complement each other. As a result, it is necessary to include the flexibility for both receptor and ligand. Ligand flexibility is considered explicitly by AutoDock, while protein flexibility is considered implicitly in our MD simulations (described below). Another essential component of a docking program is a fast yet accurate method for scoring. In AutoDock, an approximate binding free energy based on the evaluation of a single structure is used as a scoring function, which assumes that the binding free energy can be estimated by a linear combination of pairwise terms: ΔG = ΔG_vdW + ΔG_hbond + ΔG_elec + ΔG_conform + ΔG_tor + ΔG_sol, where the first four terms are molecular mechanics terms, namely, dispersion/ repulsion, hydrogen bonding, electrostatics and deviations from the covalent geometry, the fifth term models the restriction of internal rotors, global rotation and translation, and the last term accounts for desolvation and the hydrophobic effect. Different methods implement different approximations for these terms. This class of scoring functions is of practical use for molecular docking and is computationally tractable. On the other hand, they have limitations in terms of the accuracy with which they represent the free energy of binding due to the various simplifying assumptions.

For each protein structure, the non-polar hydrogen atoms are merged to heavy atoms and Kollman charges and solvation parameters are then assigned to the protein atoms using AutoDockTool (ADT) [29]. Grid maps for each protein conformation of dimension 126×126×126 points with a grid spacing of 0.184 Å are constructed, encompassing the entire ATP binding site. The Lamarckian genetic algorithm (LGA) [28] is applied to explore the conformational space of the ligand using the scoring function. In each docking run, the initial population is set to 50 individuals, the maximum number of energy evaluations is set to 10⁸, and the generation of the GA run is set to 10,000; 30 GA runs are performed for each protein conformation. This choice for the set of run-parameters is adequate to achieve convergence of the docking results.

Ligand conformation clustering

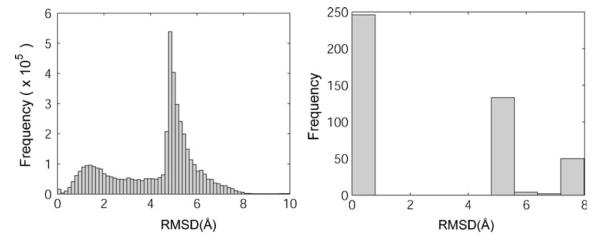
Ligand conformations were clustered using the hierarchical clustering algorithm in Matlab [30]. For each docking run, the RMSD value between each pair of all docking-generated ligand conformations (30 for single conformation docking with the crystal structure, and 3,000 for ensemble docking) were calculated and used as the distance matrix to build a hierarchical tree by progressively merging clusters using the unweighted average distance of each cluster. A cut-off RMSD value was then used to cluster ligand conformations based on the hierarchical tree. We used the pairwise RMSD distribution of docked conformation to determine the optimal radius [31]. The distribution of pairwise RMSD of all the docked conformations are depicted in Fig. 6. The minimum RMSD values after the first peak were chosen as the optimal clustering radius, namely, 2.0 Å for single conformation docking and 2.5 Å for ensemble docking. The conformations with the lowest docked energy in each cluster are reported as the predicted bound conformations for each system.

Fig. 6.

a,bPairwise RMSD distribution histogram of docked conformations for PIM1/(R)-1 system. a Single conformation docking, b ensemble docking

Results

Ensemble docking protocol takes into account protein flexibility and improves prediction of the bound complex structure

We are interested in predicting and comparing the interaction between the Ru-complex compound and three protein kinases, PIM1, GSK-3β and CDK2/cyclin A, to provide insight into the structural basis of the selectivity profile of the compound. Docking ligands to non-native protein conformations (apoprotein or protein complexed with other ligands) is still a challenging task. To account for protein flexibility, we used the ensemble docking protocol described in Fig. 4.

The protocol was first tested using the PIM1/(R)-1 system, where a crystal structure of the exact complex has been solved. To examine the reliability of different docking protocols, we performed two test cases to dock the (R)-1 compound to the PIM1 protein kinase. The first test was docking to the PIM1 structure (PDB ID: 2BZH) in which (R)-1 was co-crystallized. In the second test, the crystal structure of PIM1 (PDB ID: 1YXT) bound with an ATP analog was used instead. In each test, both the traditional docking protocol based on single protein structure and the ensemble-docking (using 100 conformations) protocol were applied to generate complex structures. The actual complex structure (2BZH) determined from crystallography serves as the “native” pose, or as a reference to evaluate the docking results.

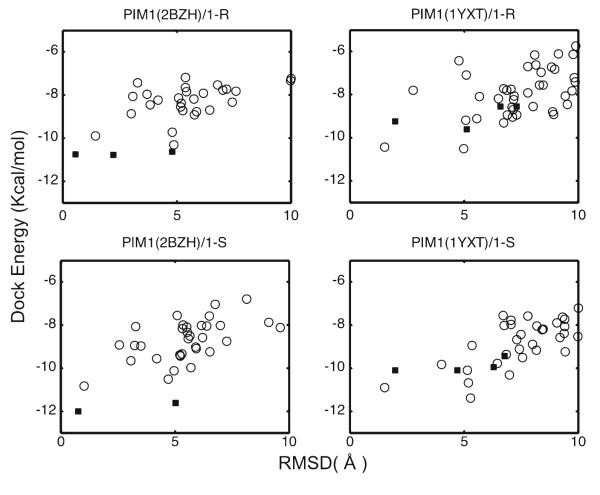
The results shown in Fig. 7 show that the predicted ligand-bound structures from single-conformation docking can be classified into several clusters with similar dockingenergies. When ensemble docking was used and the flexibility of the protein was thus accounted for, more complex conformations were generated and a better discrimination between the lowest (dock) energy conformations of different clusters was observed. Furthermore, conformations similar to the native pose emerge among the top clusters when ranked by dock energy.

Fig. 7.

RMSD relative to the reference structure versus the docked energy score for each predicted conformation of compounds (R/S)-1 to two PIM1 structures, i.e., the native structure of PIM1 bound to compound (R)-1 (PDB ID: 2BZH) and the non-native structure of PIM1 bound to an ATP analog (PDB ID:1YXT). ■ Single conformation docking results, ○ ensemble docking results

All predicted complex structures were superimposed on the native pose (2BZH), with the closest one from each docking task shown in Fig. 8. We also list the parameters of the critical hydrogen bond between the NH group of the inhibitor and the GLU121 of the protein in Table 3. When single-conformation docking was used in combination with the exact protein structure (2BZH), the results (blue structure) not surprisingly closely resemble the native pose present in the same crystal structure. However, when the approximate protein structure (1YXT) was used, the single-conformation docking failed to correctly present the critical hydrogen bond in the native pose. In contrast, when ensemble docking was applied on either the exact or the approximate protein structure, reasonable bound conformations (orange and pink structures) with the proper hydrogen bond and consistent with the native pose were among the sampled poses.

Fig. 8.

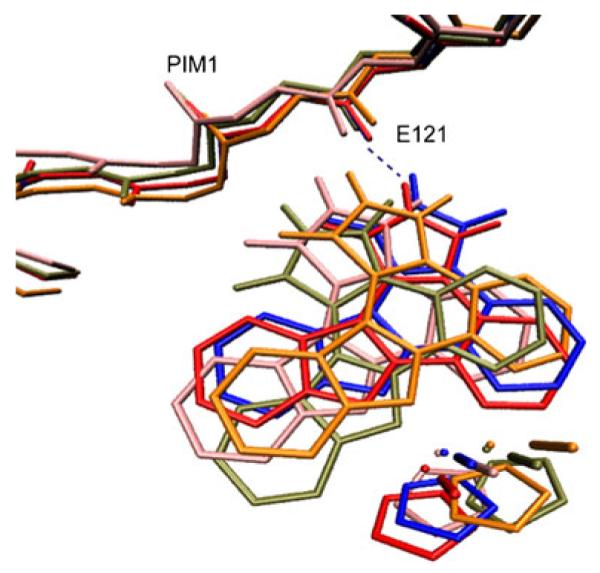
Predicted bound conformations of the inhibitor with the lowest RMSD to the reference structure from single conformation and ensemble conformation docking are aligned together with crystal structure. Blue Single conformation docking of compound (R)-1 to the native PIM1 structure (PDBID: 2BZH); orange ensemble conformation docking of compound (R)-1 to the PIM1 ensemble of structures based on native PIM1 structure; tan single conformation docking of compound (R)-1 to the non-native PIM1 structure (PDBID: 1YXT); pink ensemble conformation docking of compound (R)-1 to the ensemble of PIM1 structures based on non-native PIM1 structure; red crystal structures (PDB ID: 2BZH)

Table 3.

Parameters of the hydrogen bond between the NH group of compound 1-R and residue GLU121 in PIM1 for the complex conformations shown in Fig. 8

Structure	Distance (Å)	Angle (degrees)
Red (crystal structure)	2.0	151.02
Blue (native/single docking)	1.72	140.16
Orange (native/ensemble docking)	1.76	137.39
Tan (nonnative/single docking)	3.55	114.33
Pink (nonnative/ensemble docking)	1.65	135.03

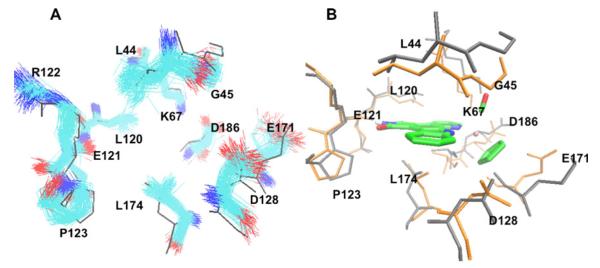
To show how the ensemble of conformations provides a more suitable ligand docking environment, the 100 conformations of the PIM1 ensemble corresponding to non-native structure (PDB ID: 1YXT) were aligned together (Fig. 9a). It is evident that the snapshots in our ensemble simulations sample kinase flexibility by exploring both backbone and side chain fluctuations around the crystallographic conformation used as the starting point for MD simulations. In Fig. 9b, the initial non-native PIM1 conformation (PDB ID: 1YXT), and the conformation, which binds the inhibitor with the lowest docking energy are aligned together, and key residues around the binding pocket are depicted. The comparison reveals the shifting of key residues, in particular GLU171, ASP128 and ASP186, from the initial non-native structure, and the rearrangement of the flexible Gly-rich loop (Gly45) to better position the CO group and the Cp ring.

Fig. 9.

Snapshots of PIM1 conformations generated from molecular dynamic (MD) simulations based on the non-native PIM1 structure (PDBID: 1YXT). Snapshots are aligned by overall RMSD, and colored by atom type. The black conformation is the crystallized non-native PIM1 conformation. b Protein conformation comparison between the non-native crystallized structure of PIM1 (PDBID: 1YXT, gray) and the predicted protein bound conformation with the lowest RMSD to the reference structure using the ensemble conformation docking corresponding to this non-native PIM1 system (orange)

As noted in Fig. 8, the non-native PIM1 structure fails to account for the conserved hydrogen bond between GLU121: O–(R)-1:H1, which is captured after the slight rearrangement of active-site residues using the ensemble docking protocol. Thus, the implicit protein flexibility in our protocol yields a better docked score for this conformation. Even though protein kinases are known to assume multiple conformational states in a rugged energy landscape [32], which are not exhaustively sampled in short MD simulations, we find that, by sampling the fluctuations of protein conformation around a given initial state of our control system, our ensemble protocol demonstrates clear improvement in the prediction of the ligand-bound structure of the complex.

Two dominant conformations are predicted for (R/S)-1 to bind with GSK-3β and PIM-1

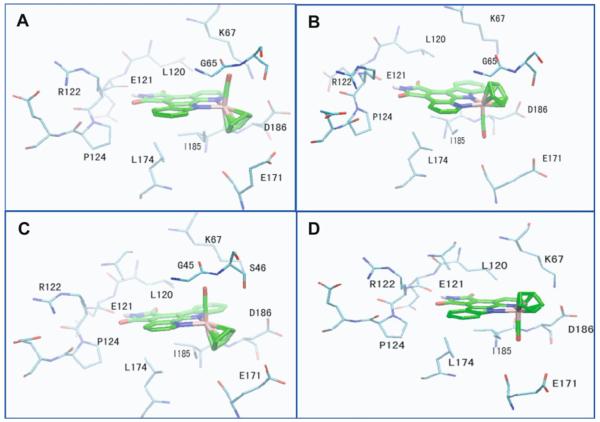
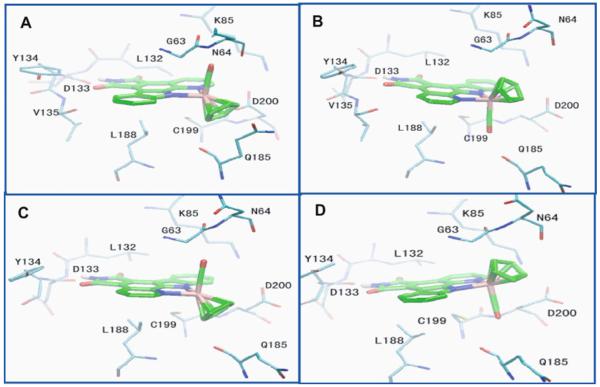
Figure 7 illustrates that, for both enantiomers, two conformations are predicted with relatively lower docking energies compared to other conformation, with RMSDs of 2 Å and 5 Å from the crystallized conformation, respectively. The two structures predicted for both enantiomers are depicted in Fig. 10. In all of the conformations, the pyridocarbazole moiety forms a hydrogen bond between the maleimide NH group and the backbone carbonyl oxygen atom of a residue within the hinge region (GLU121) of the kinase, which mimics the hydrogen-bonding pattern of the ATP as well as staurosporine with the kinase, and is present in the PIM1/ (R)-1 crystal structure. One of the two conformations, which we denote as conformation I (Fig. 10a,c), is very similar to the reference structure constructed from crystallography. In the second conformation, which we denote as conformation II, the CO and Cp groups occupy opposite (swapped) positions relative to conformation I. Thus the two conformations I and II are related by a 180° flip around an axis through the NH group of the pyridocarbazole moiety. The existence of conformation II as a stable structure has not been confirmed through crystallographic studies of the PIM1 kinase. However, this conformation is very close to a recent structure of compound (S)-2 bound to a lipid kinase (PI3Kγ) [14]. Hence, we propose conformation II as a competing alternative bound conformation for the inhibitor bound to the protein kinase. The same two conformations of compound (R/S)-1 also turn out to be the most dominant bound conformation with GSK-3β through ensemble docking as depicted in Fig. 11, making the binding characteristics of the (R/S)-1 Ru-compound with GSK-3β similar to those with PIM1.

Fig. 10.

d Top two ranks of conformations of compound (R/S)-1 bound to PIM1 predicted by ensemble docking. a, b Compound (R)-1. c, d Compound (S)-1. We denote the similar conformations in a and c as conformation I and those in b and d as conformation II

Fig. 11.

d Top two ranks of conformations of compound (R/S)-1 bound to GSK3-β predicted by ensemble docking. a, b Compound (R)-1. c, d Compound (S)-1. We denote the similar conformations in a and c as conformation I, and those in b and d as conformation II

A unique bound conformation of the ruthenium compound dominates its binding to CDK2

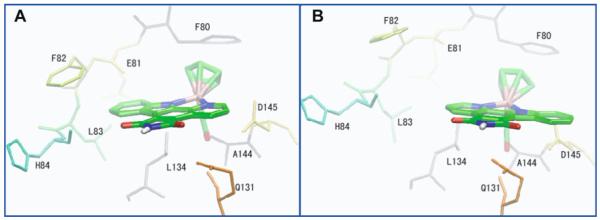
Our results for the bound conformations (R/S)-1 to CDK2/ cyclin A are in stark contrast to those for PIM1 and GSK-3β. The conformation close to the two conformations for PIM1 and GSK-3β are ranked lower [4th for (R)-1] or not present in our prediction [(S)-1]. The disfavorable two conformations are evidences for unfavorable binding of this compound to CDK2/cyclin A in the native conformation observed in PIM1 and GSK-3β. While conformations I and II are not favorable for CDK2, we found the top-ranked conformation for both enantiomers to be very similar, and this conformation is unique to CDK2, (i.e., not observed for PIM1 and GSK-3β). Figure 12 depicts the lowest-energy conformations predicted for CDK2/cyclin A. The lowest-rank conformations for both enantiomers are quite similar, showing strikingly that, instead of forming a hydrogen bond with the hinge region residue, the NH group of the pyridocarbazole moiety points outside the binding pocket. Moreover, the plane of the Cp ring stacks with the plane of the aromatic PHE80—the gate-keeper residue. The CO group orients into the small binding pocket formed by ALA144, ASP145, ASN132 and GLN131. In this conformation, even though the compounds appear to fit nicely within the CDK2 binding site, there is a distinct lack of a conserved hydrogen bond, which warrants further investigation and experimental validation of the structure of the inhibitor complexed to CDK2.

Fig. 12.

Top conformation predicted for both enantiomers bound to CDK2

Discussion

Based on in vitro protein kinase profiling results, it has been determined that the racemic mixture of ruthenium-based organometalic protein kinase inhibitor scaffold [compound (R/S)-1] prefers to inhibit PIM1, GSK-3β over CDK2/cyclin A, even though the active sites of the three kinases show high degree of sequence and structure similarity. Here, we found that ruthenium-based compounds bind in a similar fashion to PIM1 and GSK-3β but show a novel conformation with marked differences in binding to CDK2/cyclin A. Based on our structural analysis, we suggest the following explanations for this selectivity: (1) despite the extensive structure and sequence homology, CDK2 differs in the active site at the location of PHE80, which possibly stabilizes a novel bound conformation due to a stacking interaction with the Cp ring. This conformation also lacks the characteristic hydrogen bond between the inhibitor and linker region residue of the kinase and may cause a non-preference to the bound conformation. (2) Compared to PIM1 and GSK-3β, it is less preferable for CDK2/cyclin A to bind the inhibitor (especially the S-isomer) in a conformation that preserves the conserved hydrogen bond. By aligning the CDK2 structure to PIM1 and GSK-3β, we suggest that residue PHE80 might play a negative role in positioning the carboxyl group in the pyridocarbazole plane (Fig. 3). We therefore suggest examining the selectivity profile of a new compound 2 as shown in Fig. 13, which may help to further clarify the possible reason for the different binding of compound 1 with GSK-3β and CDK2.

Fig. 13.

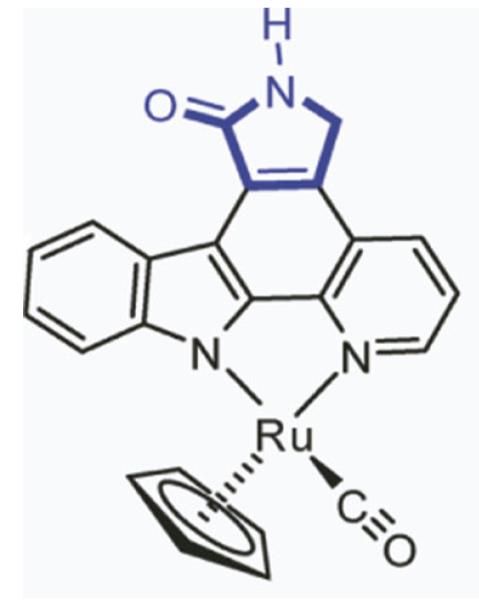
Structure of suggested new compound 2 proposed for further testing. This compound combines the structural features of compound 1 and the functionality of staurosporine

Using the existing crystal structure of PIM1/(R)-1 as a control test, we also have shown that by implicitly accounting for protein flexibility, the ensemble docking protocol is able to help refine the structural features as well as discriminate the docked energies associated with bound conformations of two enantiomeric forms of the inhibitor to the three kinases. The comparison of results from single point docking and ensemble docking demonstrate that the traditional docking method based on a single protein conformation is sensitive to the protein structure used. Although it generates good docking poses on the exact protein structure, the results become considerably worse on even a slightly different protein structure. The ensemble docking represents a significant improvement in this aspect, yielding consistent results regardless of the initial protein structure used. For the cases presented above, in which the native pose is unknown, the ensemble docking protocol is more robust and reliable in sampling the true complex structure.

In our ensemble docking analysis, we employ the lowest dock energy conformation to characterize the clusters, and show that, for PIM1 and GSK-3β, the ensemble docking protocol ranks the native-like conformations as one of the top clusters. Another popular choice for scoring the conformations is based on the frequency of an observed cluster [33]. In our case, we find that, based on the docking energy, many of the top-ranked clusters would also be identified by the high-frequency criterion. Hence, the two criteria tend to yield similar predictions for the top-ranked conformations.

In the ensemble docking protocol employed here, we do not consider the induced effect of the inhibitor to the protein conformation, i.e., our docking protocol only implicitly accounts for protein flexibility. Our assumption is that by sampling the protein kinase in and around its unbound (apo) state, the dynamics of the protein will account for the small induced effect and the bound conformations will select for those protein conformations resulting in lower dock scores. Thus for a good scoring function (with large correlation between experimental binding affinity and the computed docking score on an extensive test set of compounds), the ensemble docking is expected to yield conformations with the lowest binding affinities. We advocate that our ensemble docking approach is a good first step in cases where we have some knowledge of the protein structure (through experimental or modeling schemes), such as the prediction of the bound complex with a new inhibitor scaffold.

We also note the organometalic inhibitor compounds we have studied are very new, and fully flexible force-fields for these inhibitors are not yet available. Therefore, our focus in this article is on the structure prediction of the bound complex as opposed to the free energy of binding. Once the structural aspects are validated, our predictions are then logical candidates for a more rigorous evaluation using computationally intensive free energy protocols in fully atomistic systems [34–38].