Identifying contributors of two-person DNA mixtures by familial database search

Abstract

The role of familial database search as a crime-solving tool has been increasingly recognized by forensic scientists. As an enhancement to the existing familial search approach on single source cases, this article presents our current progress in exploring the potential use of familial search to mixture cases. A novel method was established to predict the outcome of the search, from which a simple strategy for determining an appropriate scale of investigation by the police force is developed. Illustrated by an example using Swedish data, our approach is shown to have the potential for assisting the police force to decide on the scale of investigation, thereby achieving desirable crime-solving rate with reasonable cost.

Introduction

When a crime is committed and a biological trace such as blood stain or semen is found at the crime scene or the body of the victim, forensic scientists can link the case to the arrested suspect through the matching of the trace evidence to the suspect, using DNA profiling. For cases in which no suspect can be identified based on non-DNA evidences such as fingerprints or witness reports, the police force may search a database of DNA profiles from previously convicted criminals or unsolved crime cases and open an investigation on individuals with perfectly matched profiles. Since 1995 when the first national DNA database came to operation, DNA database search has become an important crime-solving tool for suspect identification, benefit from the amassing of large offender DNA databases in many countries. For example, as of June 2011, the US Federal DNA database CODIS has assisted in over 141,300 investigations in the USA by more than 147,200 hits produced. The evaluation of the evidentiary value of perfect matches from DNA database search has been thoroughly discussed by Balding and Donnelly [1], Stockmarr [2], and Meester and Sjerps [3], among many others.

If no offender profile in the database perfectly matches the crime trace, an additional search can be performed, hoping that an individual in the database is a close relative of the perpetrator and can be identified through the search. The use of familial search on DNA database starts to become popular in recent years. As of May 2011, about 40 serious crimes has been solved with the aid of about 200 familial searches in the UK, showing that the familial database search has potential to be an effective forensic tool that can increase the number of suspects identified based on DNA evidences. Since many and even all individuals in the database may be qualified as the relative of the perpetrator, a scoring scheme is needed to rank the offender profiles, so that the police force can focus their investigation upon the top-listed candidates. A widely adopted familial search score is the likelihood ratio (LR) of the following hypotheses:

• H _p:   A relative of the individual is a contributor to the crime trace.

• H _d:   A relative of the individual is not a contributor to the crime trace.

The LR for various two-person relationships can be easily calculated using the formulae provided by Evett and Weir [4]. The performance of using LR scores for familial database searching has been evaluated in various articles [5–10]. Based on simulated and real DNA databases, the familial searches were demonstrated to be able to identify the first-order relative such as parent/child or full sibling of the perpetrator in the 100 top-listed candidates in over 70% of the cases, provided that the database really contains the profile of the relative.

In some typical crime cases such as murder cases or rape cases, the biological trace is often observed as a DNA mixture contributed by the victim and the perpetrator. Over the years, the evaluation of the DNA mixtures in probable cause cases has been studied extensively [11–14], and various formulae have been developed to handle situations when relatives are involved [15–17]. In two previous articles [18, 19], we have reported our progress on the attempt to apply database search on cases with DNA mixtures as part of the evidences and derived several formulae for evaluating the evidentiary values of “cold hits.” To go a further step, Chung et al. [20] has extended the familial database search method so as to handle mixture cases, and the performance is shown to be as good as in single source cases.

Based on the results of a familial search, the number of individuals to be further investigated may depend on the regional policy. For example, according to the California familial search policy, after the list of top-ranked candidates is produced, lineage DNA testing will be conducted on up to 168 candidates by using Y-STR typing [21]. In addition to familial search policy, the scale of the investigation will also vary based on practical considerations including the limitation of manpower, the resources of the police offices, and the scale of the crime severity. The main cost factor is in the need to investigate the background of each candidate so that irrelevant candidates can be eliminated as being the possible relative of the perpetrator. Investigating on thousands of candidates for every case is impractical as the law enforcement resources will be overwhelmed by the heavy case load. It would be more effective if a large number of candidates are investigated only for serious and high-profile criminal cases. It is therefore necessary to determine the scale of the investigation so that the effectiveness of the search can be guaranteed under reasonable cost. Ge et al. [10] had given some suggestions on the thresholds to the LR as well as the identity-by-state scores, with the aim of balancing the false-positive and false-negative rates. These thresholds, however, are specific to a particular database as they are determined based on a simulation study using Caucasian population data on the 13 CODIS STR loci. The primary aim of this work is to establish a general strategy on deciding the number of top-listed candidates to be investigated after the familial search, according to the statistical criteria on the true and false hit rates required by the police force.

This article is organized as follows: First, we describe the use of LR scores for producing a ranked list of candidates from familial search on DNA mixtures, on the basis of our previous work in Chung et al. [20]. We then establish an estimate of the true hit rate of the investigation on a specific number of top-listed candidates, from which a novel strategy is developed for determining an appropriate scale of the investigation. The performance of the familial search on DNA mixtures and the proposed strategy are demonstrated through an example using Swedish data. Finally, we conclude with a few remarks on the future direction of work.

Methods

Scoring scheme using likelihood ratio

Given a crime trace observed as a DNA mixture M contributed by the perpetrator and the victim, the familial search score for a particular individual j in the database D is defined as a LR of the following hypotheses:

• H _j:   The victim and a relative of individual j are contributors.

• H _d:   The victim and one unknown person are contributors.

Note that the prosecution hypothesis H _j here states that a relative of individual j, rather than the individual, is the contributor and therefore is not the same as the hypothesis formulated in Chung et al. [18] and Chung and Fung [19]. In general, a LR can be calculated for each of the possible genetic relationships for every member of the database. However, the familial search is practically used only for parent/child and sibling relationships because it would become less effective for other degrees of relatedness below sibling that share less genetic similarity.

At a particular locus l, denote M _l as the set of alleles present in the mixture and V _l and X _jl as the genotype of the victim and individual j, respectively, for j ∈ D and l = 1,...,L. Under linkage equilibrium assumption, Chung et al. [20] presented the following formula for calculating the LR of H _j versus H _d:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \label{eqn:lr} {\rm LR}_j=\prod\limits_{l=1}^{L}{\frac{P(M_l|V_l,X_{j\,l},H_j)}{P(M_l|V_l,H_{\rm R})}} $$\end{document} 1

where H _R is the hypothesis that the victim and a random person contribute to the mixture. The computation of P(M _l|V _l,X _jl,H _j) and P(M _l|V _l,H _R) is based on the Q-function presented in Hu and Fung [17] and Fung and Hu [22]:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{array}{lll} &&{\kern-6pt} P(M_l|V_l,X_{j\,l},H_j)\\ &&{\kern6pt}=k_0Q(2,U_l)+k_1\big(I_M(t_1)Q(1,U_l\setminus\{t_1\}) \\ &&{\kern138pt}+I_M(t_2)Q(1,U_l\setminus\{t_2\})\big) \\ &&{\kern18pt}+k_2I_M(t_1)I_M(t_2)Q(0,U_l\setminus\{t_1,t_2\}) \end{array}$$\end{document}

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ P(M_l|V_l,H_{\rm R})=Q(2,U_l) $$\end{document}

where t ₁ t ₂ is the genotype present in X _jl, U _l = M _l ∖ V _l is the set of alleles present in M _l but absent in V _l, and I _M(t) is the indicator function defined by I _M(t) = 1 if t ∈ M and 0 otherwise. The quantities (k ₀,2k ₁,k ₂) are the kinship coefficients for the relationship considered in H _j. In particular, (k ₀,2k ₁,k ₂) take the values of (0.25,0.5,0.25) for full siblings and (0,1,0) for parent/child relationship. Table 1 shows the computational formulae of Q(.,.) for a two-person mixture at a particular autosomal locus l with K alleles A ₁,A ₂,...,A _K and corresponding allele frequencies p ₁,p ₂,...,p _K \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$(\sum_{i=1}^{K}p_i=1)$\end{document}, under the assumption of Hardy–Weinberg equilibrium.

Table 1.

The calculating formulae of Q(j,B) for different combinations of mixture M _l and arbitrary set of alleles B at a particular autosomal locus l with alleles A ₁,A ₂,...,A _K and corresponding allele frequencies p ₁,p ₂,...,p _K, under the assumption of Hardy–Weinberg equilibrium

M l	B	Q(0,B)	Q(1,B)	Q(2,B)
A i	ϕ	1	p i	\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$p_i^2$\end{document}
A i,A j	ϕ	1	p i + p j	\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$(p_i+p_j)^2$\end{document}
	A i	0	p i	\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$p_i^2+2p_ip_j$\end{document}
	A j	0	p j	\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$p_j^2+2p_ip_j$\end{document}
A i,A j,A k	ϕ	1	p i + p j + p k	\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$(p_i+p_j+p_k)^2$\end{document}
	A i	0	p i	p i(p i + 2p j + 2p k)
	A j	0	p j	p j(p j + 2p i + 2p k)
	A k	0	p k	p k(p k + 2p i + 2p j)
	A i,A j	0	0	2p i p j
	A i,A k	0	0	2p i p k
	A j,A k	0	0	2p j p k
A i,A j,A k,A t	ϕ	1	p i + p j + p k + p t	\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$(p_i+p_j+p_k+p_t)^2$\end{document}
	A i	0	p i	p i(p i + 2p j + 2p k + 2p t)
	A j	0	p j	p j(p j + 2p i + 2p k + 2p t)
	A k	0	p k	p k(p k + 2p i + 2p j + 2p t)
	A l	0	p t	p t(p t + 2p i + 2p j + 2p k)
	A i,A j	0	0	2p i p j
	A i,A k	0	0	2p i p k
	A i,A t	0	0	2p i p t
	A j,A k	0	0	2p j p k
	A j,A t	0	0	2p j p t
	A k,A t	0	0	2p k p t

The indices i, j, k, and t are pairwise distinct

The individuals in the database are ranked in descending order by the LR scores, and the individuals with highest scores will be preliminarily identified as the suspects that need further investigations by the police force. In case when rare alleles are present in the unexplained profiles M _l ∖ V _l, the random match probability P(M _l|V _l,H _R) will become extremely small, and the unknown contributor’s relative will be assigned a large LR score so that the perpetrator will be more likely to be identified. Therefore, the performance of the familial search depends much on the observed mixture M = {M _l,l = 1,...,L} and the victim profile V = {V _l,l = 1,...,L}. To predict the performance of the search, Cowen and Thomson [8] suggested fitting the logistic regression model

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \label{eqn:logistic_model} {\rm logit}(P(\theta_k=1))=\alpha-\beta \log_{10}{P(M|V,H_{\rm R})} $$\end{document} 2

where θ _k is an binary response variable taking the value of 1 if the relative of the unknown contributor is located within the top k profiles and 0 otherwise. The model links the outcome of a particular search that limits the investigations to the k top-listed individuals to the random match probability P(M|V,H _R) and therefore can be used to predict the performance of the search given the observed DNA profiles (M,V). In particular, if the estimated probability P(θ _k = 1) is too small even for large k, the familial search may fail to provide effective assistant for identifying the suspect. This information can practically guide the police force to make decisions on whether it is worthwhile to open an investigation just based on the familial search results.

The use of logistic regression for evaluating the general performance of a familial database search will be demonstrated through an example. The logistic regression approach, however, uses only the random match probabilities but not the detail information provided in the DNA evidence for a particular case. For practical crime cases, it may be also necessary to determine the most appropriate scale of the crime investigation by fully utilizing the available DNA evidences. In the next section, we develop a novel strategy on deciding the number of individuals to be investigated after the familial search, based on an estimate of the hit rate of the crime investigation on a specific number of top-listed candidates.

Determining scale of crime investigation

Denote H _D as the hypothesis that the sibling of the contributor is in the database, i.e., H _D = ∪ _i ∈ D H _i. Under the assumption that the relative of someone in the database contributes to the mixture, the posterior probability that the contributor is the relative of individual j, given the mixture profile M, victim profile V and database profiles X _D = {X _jl,j ∈ D,l = 1,...,L} can be expressed as

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{array}{lll} \label{eqn:posterior} &&{\kern-6pt} P(H_j|M,V,\mathbf{X_{\rm D}},H_{\rm D})\\ &&{\kern6pt} =\frac{P(M|V,X_j,H_j)P(H_j|H_{\rm D})}{\sum_{i\in D}P(M|V,X_i,H_i)P(H_i|H_{\rm D})}. \end{array} $$\end{document} 3

whereeX _j = {X _jl,l = 1,...,L} for j ∈ D. The proof of Eq. 3 is given in the “Appendix.” Under most common scenarios, it is sensible to assume a uniform prior for H _i so that Eq. 3 becomes

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \label{eqn:posterior2} P(H_j|M,V,\mathbf{X_{\rm D}},H_{\rm D})=\frac{P(M|V,X_j,H_j)}{\sum_{i\in D}P(M|V,X_i,H_i)}. $$\end{document} 4

Alternatively, other priors can also be used if the police authority has acquired more information about the family status details of each individual in the database.

Without loss of generality, suppose that the database is sorted in descending order according to the posterior probabilities such that

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{array}{rll} P(H_1|M,V,\mathbf{X}_{\rm D},H_{\rm D})&\ge& P(H_2|M,V,\mathbf{X}_{\rm D},H_{\rm D})\\ &\ge& \cdots \ge P(H_n|M,V,\mathbf{X}_{\rm D},H_{\rm D}) \end{array}$$\end{document}

where n is the size of the database. For any integer 1 ≤ k ≤ n, the function defined by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \label{eqn:Hit_rate} q(k)=\sum\limits_{i=1}^{k}P(H_i|M,V,\mathbf{X_{\rm D}},H_{\rm D}) $$\end{document} 5

evaluates the probability that the relative of the contributor can be identified by investigating the top-k individuals with respect to their posterior probabilities, given that the relative is in the database. In other words, q(k) represents the hit rate of the crime investigation on k top-listed candidates, thereby providing a means for developing a practical crime investigation strategy under different criteria. For instance, a simple strategy is to investigate the top-k individuals in the database sorted with respect to their LRs or posterior probabilities, with k determined by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \label{eqn:kp0} k(p_0)= \min\{k>0:q(k)\ge p_0\} $$\end{document} 6

where p ₀ is the hit rate required by the police force.

Results

We illustrate here the performance of the familial search and the use of Eqs. 5 and 6. An offender database consisted of 50,000 unrelated DNA profiles is generated according to the Swedish allele frequencies given in Montelius et al. [23], at the 10 SGM Plus STR loci which are commonly used in European national DNA databases. The first 1,000 profiles in the database are used to represent the profiles of the relatives of the perpetrators in 1,000 different crime cases. For each of the first 1,000 profiles, a related profile (full sibling or parent/child) is generated to represent the unobserved profile of the unknown perpetrator in that particular case. The observed DNA mixtures are produced by mixing these relative profiles with independently generated victim profiles. For each case, a familial search is performed, and a list of 50,000 LR scores is calculated by using Eq. 1. The rank of the LR score of the true relative of the unknown contributor indicates at least how many top-listed individuals must be investigated in order to successfully identify the relative of the perpetrator. In general, such ranks recorded from the 1,000 cases can provide reasonable assessment of the effectiveness of the familial search. For example, there are 704 cases in which the true sibling of the unknown contributor is within the top 100 individuals in the database ranked by the LR scores, showing a chance of 70.4% that the sibling of the unknown contributor can be successfully identified if the 100 top-listed individuals are investigated, provided that the unknown contributor is a sibling of one of the individuals in the database. The chance of successful identification of the parent/child of the unknown contributor from the top 100 profiles is 88.0%. Table 2 and Fig. 1 shows the empirical probabilities of identifying the relative of the contributor using LR scores.

Table 2.

Empirical probabilities of identifying the parent/child and full sibling of the contributor in the top k profiles ranked by likelihood ratio scores

k	% of identification in top k profiles
	Parent–child	Full sibling
1	23.5	14.5
5	46.6	29.8
10	56.1	37.2
20	65.1	45.8
50	78.3	59.0
100	88.0	70.4

Fig. 1.

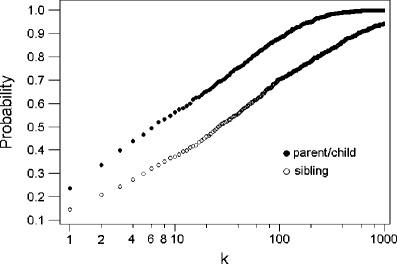
Empirical probability of identifying the parent/child and full sibling of the contributor in the top k profiles ranked by likelihood ratio scores in a one-unknown mixture case

Clearly as shown in Fig. 1, the empirical probabilities indicate a more effective search for the parent/child of the unknown contributor than the sibling. It is interesting to note that the empirical probabilities of successful identification are almost linearly related with logarithm of k, the number of top-listed individuals to be investigated. This suggests that enlarging the scale of the investigation will have little improvement to the performance of familial search if the original scale is already substantially large. In roughly 46% of the cases, the sibling of the unknown contributor can be found within the top 20 profiles, while in 56% of the cases, investigating the top 10 profiles is already enough for identifying the parent/child of the unknown contributor. Note that comparing to the other simulation results summarized in Chung et al. [20], the performance of the search here is slightly inferior as we use a larger database and less loci for profiling in this work. However, it is comparable to the result of Curran and Buckleton [7] in a single-source case which also use a system of 10 STR loci but a smaller database of about 24,000 profiles. Therefore, in cases with DNA mixture as part of the available clue, the familial DNA database search can be still applied for identifying the suspect, with the false hit rate as low as in single-source cases.

Following Cowen and Thomson [8], logistic regression models in the form of Eq. 2 are fitted to the data to estimate the dependence of the outcome with respect to the observed profiles (M,V). Table 3 listed the coefficients of the fitted models, with p values all smaller than 0.001. The performance of the search is strongly associated with the value of the random match probability. As shown in Fig. 2, the smaller the random match probability, the more likely the relative of the unknown contributor can be identified. In particular, if P(M|V,H _R) is less than 10^− 12, which is about the median of the random match probabilities from the simulated profiles, there will be a 41% chance to identify the sibling and a 63% chance to identify the parent/child within the top 10 profiles of the database. The performance would be worse if P(M|V,H _R) is as low as 10^− 9. The estimated probabilities of successfully identifying the parent/child and sibling are 24% and 17%, respectively. In such cases, an investigation on just 10 top-listed individuals from the familial search is definitely not enough.

Table 3.

Estimated parameters of the logistic regression models for the probability of identifying the relative of the contributor in the top k profiles

Relationship	k	Parameter estimate (SE)
		α	β
Parent/child	5	− 6.0635 (0.5733)	0.5114 (0.0492)
	10	− 6.1751 (0.5970)	0.5593 (0.0522)
	20	− 6.1630 (0.6355)	0.5969 (0.0565)
Full sibling	10	− 5.1906 (0.5513)	0.4014 (0.0468)
	50	− 4.7499 (0.5610)	0.4477 (0.0492)
	100	− 3.8619 (0.5926)	0.4173 (0.0528)

Fig. 2.

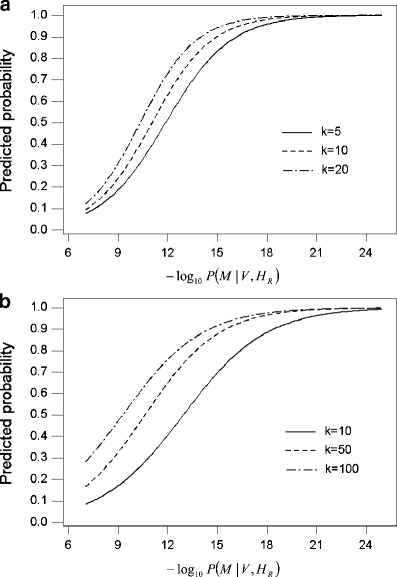
Predicted probability of identifying the a parent/child and b full sibling of the unknown contributor in the top k profiles

To determine an appropriate scale of the investigation, we can apply the proposed strategy. For illustrative purpose, we consider a search that aims at identifying the parent/child or the full sibling of the contributor from the database, though the basic principle can be applied to any kind of relationship. Figure 3 shows the average of the estimated hit rates evaluated by using the q(k) function in Eq. 5 and the empirical hit rates obtained as in Fig. 1. As can be seen, the average of the estimated hit rates are close to the empirical hit rates, suggesting reliable estimates of the hit rates by using q(k). The number of top-listed individuals that needs investigation can be determined by k(p ₀) defined in Eq. 6 for a particular required hit rate p ₀. The empirical distributions of k(p ₀) for various values of p ₀ are shown in Table 4. The distributions are all skewed toward the right as the averages are all greater than the medians. For the search that aims at identifying the parent/child of the contributor, large proportions of k(p ₀) are found to be less than 100 with respect to p ₀ ≤ 0.8. When the required hit rate p ₀ is as high as 0.9, there are still about 75% of the cases in which the values of k(p ₀) are less than 200, i.e., further investigations on less than 200 top-listed candidates will be suggested. Therefore, the investigation can be controlled under a reasonable scale even though a high hit rate is usually required.

Fig. 3.

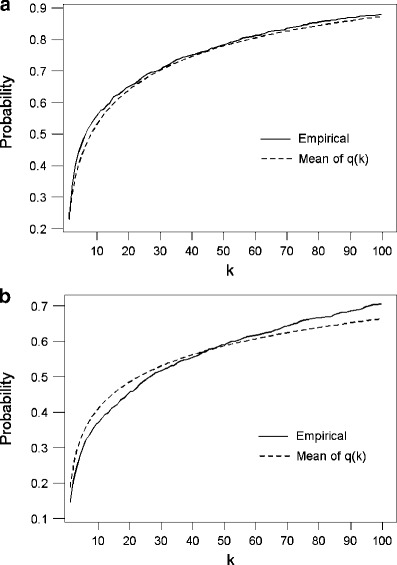
Probabilities of identifying the a parent/child and b full sibling of the unknown contributor in the top k profiles estimated using empirical hit rates (solid line) and the average of the q(k) function (dashed line)

Table 4.

Summary statistics of k(p ₀) from simulation results

p 0	Empirical probability	Average of k(p 0)	Percentiles of k(p 0) distribution
			10th	25th	Median	75th	90th
Parent/child
0.5	0.553	17.1	1	4	11	23	44
0.6	0.625	25.8	2	6	18	38	69
0.7	0.724	45.1	3	10	31	62	110
0.8	0.816	75.2	5	19	53	104	179
0.9	0.925	137	11	41	97	192	314
Full sibling
0.5	0.512	41.4	2	11	29	62	97
0.6	0.612	87.0	5	27	66	130	197
0.7	0.744	190	18	70	152	283	413
0.8	0.851	458	57	208	394	669	912
0.9	0.956	1,393	313	787	1,313	1,960	2,516

The empirical hit rates are the probabilities of identifying the parent/child and full sibling of the contributor within the top-k(p ₀) individuals

On the other hand, the values of k(p ₀) determined in searching for the full sibling of the contributor are relatively larger. If p ₀ = 0.9 is required, the values of k(p ₀) are greater than 1,000 in the majority of the cases, indicating that it may not be feasible to achieve such a high hit rate with limited law enforcement resources. The result is expected as the performance in searching for the full sibling should be inferior to the cases in searching for the parent/child. Nevertheless, lowering the requirement on the hit rate to p ₀ ≤ 0.7 can still reduce the values of k(p ₀) to less than 150 in about 50% of the cases, which are more feasible scales. Based on this information, the decision to open an investigation can be taken by the police force after thorough consideration on the crime severity and the law enforcement resources. It is remarkable to note that the empirical hit rates based on investigating the top-k(p ₀) individuals are all greater than the required hit rate p ₀, further justifying our approach in providing information for the police force to determine an appropriate scale of crime investigation based on the results from a familial database search.

Conclusion

This article illustrates how the traditional familial database search methods that were used only for single-source samples can be extended so as to handle mixture cases. An illustrative example using Swedish data is given. It is demonstrated that the familial search applied to two-person mixture cases can perform as good as in single-source cases by using the LR scoring scheme.

The results presented in previous section are based on the most common scenario when the mixed stain is originated from the victim whose DNA profile is available. For two-unknown mixture cases, the set of possible profiles for the unknown contributors will be less restrictive. As a result, the discriminatory power of the likelihood ratio score for database search in two-unknown mixture cases will become relatively lower, comparing to one-unknown mixture cases and single-source cases. To demonstrate this, consider the following hypotheses for a two-unknown mixture case:

• H _j:   A relative of individual j and an unrelated unknown person are contributors.

• H _d:   Two unrelated unknown persons are contributors.

and the corresponding LR can be calculated as

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\rm LR}_j=\prod\limits_{l=1}^{L}{\frac{P(M_l|X_{j\,l},H_j)}{P(M_l|H_{\rm R})}} $$\end{document}

where

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{array}{lll} P(M_l|X_{j\,l},H_j)&=&k_0Q(4,M_l)\\&&+k_1\big(I_M(t_1)Q(3,M_l\setminus\{t_1\})\\ &&\qquad\;+\; I_M(t_2)Q(3,M_l\setminus\{t_2\})\big) \\ && +k_2I_M(t_1)I_M(t_2)Q(2,M_l\setminus\{t_1,t_2\}), \end{array}$$\end{document}

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ P(M_l|H_{\rm R})=Q(4,M_l). $$\end{document}

Figure 4 shows the empirical search results on a two-unknown case using the same generated database. As expected, the performance is substantially inferior to the case in which the victim profile is available. There is only a 36% chance to identify the sibling and a 54% chance to identify the parent/child within the top 100 profiles of the database.

Fig. 4.

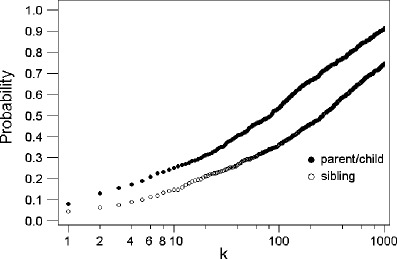
Empirical probability of identifying the parent/child and full sibling of the contributor in the top k profiles ranked by likelihood ratio scores in a two-unknown mixture case

In addition to the logistic regression approach that models the predicted hit rate as a function of the random match probability, we have derived a formula that can accurately estimate the hit rate for a specific case. Using this formula, a simple strategy is developed to determine the least number of individuals who should be included in the crime investigation, according to the desired hit rate required by the police force. It should be noted that the formula for estimating the hit rate, as well as the proposed strategy, is also applicable in single-source cases. As shown by the numerical example, the proposed strategy can provide useful information aiding the police force for deciding on the scale of investigation, thereby achieving desirable crime-solving rate with reasonable cost.

As commented by Chakraborty and Ge [24], it is necessary to point out that the familial DNA database search is an auxiliary tool for crime solving when there is no clue on the source of the crime trace, rather than playing a decisive role to bring the suspects identified through database search to trials. The evidentiary value of the cold hits from familial search should serve as supporting reference to aid the jury to make their decision, provided that a court case is raised after the investigation on the cold-hit suspects.

To clearly present our idea for the application of familial search to mixture cases, several key assumptions have been made in the works presented in this article. These include the linkage equilibrium that assumes independence of alleles across all loci and the Hardy–Weinberg equilibrium that assumes the independence between the two alleles of a genotype at a particular locus. The former is usually guaranteed by the proper choice of STR loci while the latter may fail to apply in case when the contributors of the mixture come from a small population or from different ethnic groups. Although it is not difficult to modify the formulae presented in earlier sections and Table 1 to handle allele dependence, the impact of the deviation from Hardy–Weinberg equilibrium to the performance of the familial search is yet to be studied. Besides, the presented method is based on the common scenario that there is only one perpetrator committing the crime and a two-person mixture is included as part of the DNA evidence. More general approach that considers multiple perpetrators as in group rape cases can make familial search a more useful crime-solving tool. Therefore, another possible direction for future work is to develop general methodologies that can handle the complication arises due to the presence of multiple perpetrators.

Appendix: Proof of Eq. 3

Under the assumption that the sibling of the contributor is someone in the database, the posterior probability of H _j given the DNA evidences M, V, X _D can be evaluated by using the Bayes’ rule:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\begin{array}{rll} &&{\kern-6pt} P(H_j|M,V,\mathbf{X_{\rm D}},H_{\rm D})\\ &&{\kern6pt}=\frac{P(M|V,\mathbf{X_{\rm D}},H_j,H_{\rm D})P(H_j|H_{\rm D})}{\sum_{i=1}^N P(M|V,\mathbf{X_{\rm D}},H_i,H_{\rm D})P(H_i|H_{\rm D})} \\ &&{\kern6pt}=\frac{P(M|V,\mathbf{X_{\rm D}},H_j)P(H_j|H_{\rm D})}{\sum_{i\in D} P(M|V,\mathbf{X_{\rm D}},H_i)P(H_i|H_{\rm D})} \end{array}$$\end{document}

where the equality results from the fact that H _i ∩ H _D = H _i for i ∈ D and P(H _i|H _D) = 0 for i ∉ D. When H _i holds true, the mixture M will depend only on V and X _i and is unrelated to the profiles of other individuals in the database. Substituting P(M|V,X _D,H _i) = P(M|V,X _i,H _i) into the above equation leads to Eq. 3.