Coupling-induced synchronization in multicellular circadian oscillators of mammals

Abstract

In mammals, circadian rhythms are controlled by the neurons located in the suprachiasmatic nucleus (SCN) of the hypothalamus. Each neuron in the SCN contains an autonomous molecular clock. The fundamental question is how the individual cellular oscillators, expressing a wide range of periods, interact and assemble to achieve phase synchronization. Most of the studies carried out so far emphasize the crucial role of the periodicity imposed by the light-dark cycle in neuronal synchronization. However, in natural conditions, the interaction between the SCN neurons is non-negligible and coupling between cells in the SCN is achieved partly by neurotransmitters. In this paper, we use a model of nonidentical, globally coupled cellular clocks considered as Goodwin oscillators. We mainly study the synchronization induced by coupling from an analytical way. Our results show that the role of the coupling is to enhance the synchronization to the external forcing. The conclusion of this paper can help us better understand the mechanism of circadian rhythm.

Introduction

Many organisms have endogenous circadian clocks that coordinate physiological and behavioral rhythms and synchronize the organisms to daily environmental cycles. In mammals, the circadian rhythms are controlled by a pacemaker located in the suprachiasmatic nucleus (SCN) of the hypothalamus (Reppert and Weaver 2002; Moore et al. 2002). The SCN is composed of 20,000 neurons arranged in a symmetric bilateral structure, including astrocytes and multiple neuropeptidergic classes of neurons. It has been shown that isolated single neurons are able to produce circadian oscillations, with periods ranging from 20 to 28 h (Welsh et al. 1995; Honma et al. 2004). Less well understood is how individual cells are assembled to create a whole tissue pacemaker that can govern behavioral and physiological rhythmicity. That is to say how these individual clocks achieve phase synchronization.

The rhythmicity of the SCN is a product of multiple individual cellular circadian oscillators that are coupled together in a tissue network. The core molecular regulatory mechanism underlying these oscillations of circadian clocks (e.g., Per1, Per2, Per3, Cry1, Cry2, Bmal1, Reverba, Clock, Rora) relies on a transcription-translation negative-feedback loop in which the protein products of circadian genes regulate their own transcription (Reppert and Weaver 2001). Because free-running periods of isolated neurons are broadly distributed, the self-sustained oscillations indicate that a coupling mechanism is operating among the neurons. The coupling between cells in the SCN is achieved partly by neurotransmitters which are released by each cell (Shirakawa et al. 2001; Hastings and Herzog 2004). The multiple synchronized single-cell circadian oscillators produce coordinated circadian outputs, which ultimately regulate overt rhythms.

Mathematical modeling can provide insights into potential mechanisms that lead to coordinated cellular oscillations (Benuskova and Kasabov 2008; Jiao and Wang 2006; Liu et al. 2010; Matsuura et al. 2008; Wang et al. 2011a, b). So far there have been a large number of studies on the cellular oscillators’ dynamics and synchronization which induce the circadian rhythm generated by the SCN (Aton et al. 2005; Maywood et al. 2006; Antle et al. 2003, 2007; Bush and Siegelman 2006; Rougemont and Naef 2006; Indic et al. 2007; To et al. 2007; Yamaguchi et al 2003; Liu and Reppert 2000). Among the previous studies, research works are mainly on either the models of the SCN cellular oscillators or the synchronization of the oscillators. In particular, To and his collaborators presented a multicellular molecular model of the mammalian circadian clock, which postulates that synchrony arises among circadian neurons because they release VIP rhythmically on a daily basis and in response to ambient light (To et al. 2007). However, their works are mainly based on numerical simulation with little theoretical analysis. In this paper, we aim to study analytically the synchronization of clocks coupled though neurotransmitter.

Specifically, in this paper we develop a model of nonidentical clocks coupled by neurotransmitter. Then we prove theoretically that the clocks can be synchronized by the neurotransmitter. At last we show the role of coupling in SCN from two aspects with the help of numerical simulation. On one hand, the coupling among neurons can synchronize circadian oscillators. On the other hand, considering environment cue of daily light-dark cycle, coupling can reduce the threshold of light strength for entrainment.

The model of coupled circadian oscillators

We model the circadian clocks at the basic genetic level by using a large ensemble of globally coupled nonidentical Goodwin oscillators. Each of the neurons, when uncoupled from the others, acts as an oscillator with an intrinsic period. A single cell or genetic oscillator model is described by a four-variable model based on the Goodwin oscillator (Goodwin 1965). In this model, a clock gene mRNA (X) produces a clock protein (Y) which, in turn, actives a transcriptional inhibitor (Z). The latter inhibits the transcription of the clock gene, closing a negative feedback loop. In both parts of the SCN, the neurotransmitter gammaaminobutyric acid(GABA) is released (Shirakawa et al. 2001). How neurotransmitters interfere with the clock is not completely clear. We introduce a global coupling term depending on the concentration of a synchronizing factor (a neurotransmitter) in the extracellular medium, and assume fast dynamics of the small neurotransmitter molecules in the extracellular medium. We assume that cells synthesize a neuropeptide neurotransmitter denoted by V which is induced by activation of the clock gene (X) (Gonze et al. 2005). The strong candidates regarding the VL cells and DM cells are respectively VIP and AVP. Here we adopt the model of an individual cell as follows (Gonze et al. 2005):

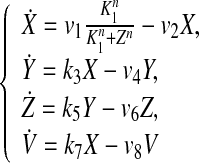1

where v₁, v₂, v₄, v₆, v₈, K₁, k₃, k₅, k₇ and n are all parameters.

The variable X represents mRNA concentration of a clock gene, per or cry; Y is the resulting protein, PER or CRY; Z is the active protein or the nuclear form of the protein (inhibitor); and V is the neurotransmitter. In this model, V can approximately be viewed as neurotransmitter’s production or its integrated effect although there are many steps in the life of a neuropeptide like VIP and AVP, such as mRNA’s production and its release process. In our previous work (Li et al. 2006), we gave the sufficient conditions for Hopf bifurcation of Eq. (1), showing that the single neuron is a self-sustained oscillator. Although V is induced by the product of X, such a regulation is approximately expressed by the concentration of X in the last equation of this model for the purpose of simplification.

For the complete model, we take N neuronal oscillators, each one of them described by four variables 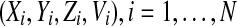, satisfying the above evolution equations. The global coupling dependents on the concentration of the synchronization factor(the neurotransmitter) in the extracellular medium. Under the fast transmission hypothesis, the extracellular concentration is assumed to equilibrate to the average cellular neurotransmitter concentration. This global variable is referred to as the mean field, denoted by ,

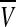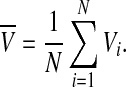Gonze et al. considered that the clock gene X_i was directly activated by the mean field 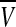(Gonze et al. 2005). This coupling mechanism is similar to the one suggested by Ullner et al. (2009). Under these conditions, the resulting model is

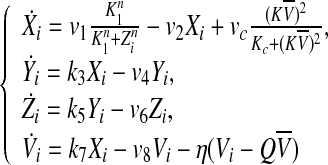2

In this case, the parameter Q describes the influx of external signaling molecule back into the cell (Jordi et al. 2004). The fact that the SCN is a relative small and highly dense area with short distances between the cells allows us to simplify the cell-to-cell communication by mean-field coupling. η measures the rate of neurotransmitter V_i in- and outflux extracellular medium. The coupling between the individual cell oscillators is determined by η, Q, v_c and K. For the convenience of analysis in the next section, we rewrite Eq. (2) as follows.

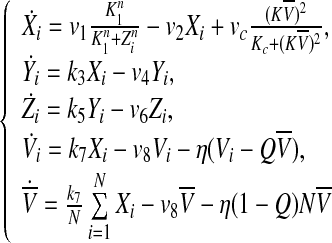3

Results

Synchronization of the circadian oscillators

Katriel G. have proved the synchronization of oscillators coupled through an environment (Katriel 2008). According to the conclusion of (Katriel 2008), if Eq. (1) has a stable periodic solution, that is to say, the single neuron, placed in the environment, performs periodic oscillations, and the solution of the linear system of Eq. (3) decays to 0 at an exponential rate as 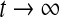, then a population of such neurons will synchronize. In the following, we analyze the convergency of the solution of the linear system of Eq. (3).

We assume that the system Eq. (1) has a stable periodic solution X(t), Y(t), Z(t), V(t). To obtain the stability of this solution as a synchronized oscillation of Eq. (3), we need to show that any solution of the following periodic linear system

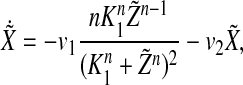4

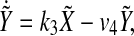5

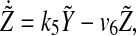6

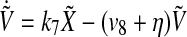7

decays to 0 at an exponential rate as 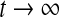. Let 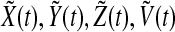be a solution of the system (4–7). Considering 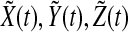and 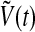are all concentrations, one has 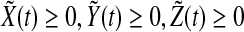and 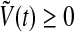for any t.

From Eq. (4), we get that

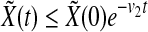8

so 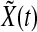decays exponentially.

Rewriting (5), we have

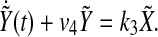9

Then 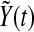can be written explicitly as

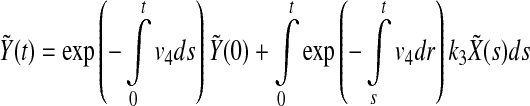Therefore, using Eq. (8) we have

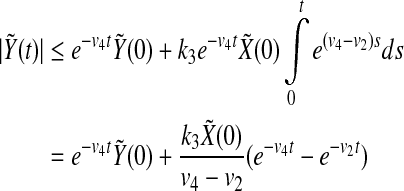which gives the exponential decay of 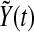. That is to say there exist m_y, k_y, so that

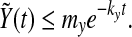10

Similarly, 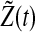and 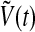also decays exponentially. Thus, according to the conclusion of (Katriel 2008), the oscillators can achieve synchronization with appropriate parameter values.

The role of coupling in SCN

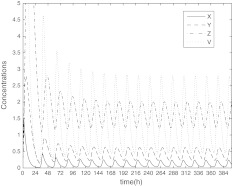
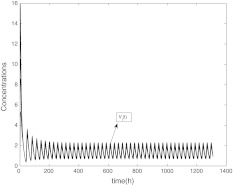
In this section, we will show the role of coupling in SCN from two aspects with the help of numerical simulation. The system of single neuron Eq. (1) has a stable periodic solution, just as Fig. 1 showing. The concentrations are expressed in nM, and the parameter values in the model are n = 10, v₁ = 0.7 nM/h, K₁ = 1 nM, v₂ = 0.18 nM/h, k₃ = 0.7 nM/h, v₄ = 0.18 nM/h, k₅ = 0.7 nM/h, v₆ = 0.18 nM/h, k₇ = 9 nM/h and v₈ = 0.7 nM/h.

Fig. 1.

The time evolution of X, Y, Z, V

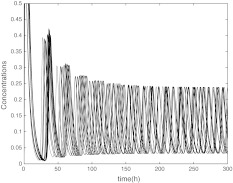
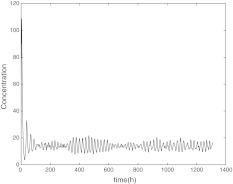
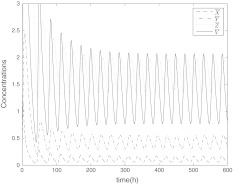
In the first place, the coupling can induce the synchronization of oscillators. We consider a small size of network with N = 10 neurons, though there are over thousands of neurons in the real SCNs. The concentrations are expressed in nM, and the parameter values in the model are n = 10, v₁ = 0.7 nM/h, K₁ = 1 nM, v₂ = 0.18 nM/h, k₃ = 0.7 nM/h, v₄ = 0.18 nM/h, k₅ = 0.7 nM/h, v₆ = 0.18 nM/h, k₇ = 9 nM/h, and v₈ = 0.7 nM/h. The mismatches are randomly distributed in ± 2% around the above values. Figure 2 gives the time evolution of mRNA (X_i) of the uncoupled oscillators. The other variables such as Y_i, Z_i and V_i are similar with X_i, which are not shown here. It is obvious that the self-sustained oscillators of neurons have different periods. In this situation, the extracellular concentration 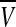is not periodic just as Fig. 3 showing. We also find that the system follows the same trajectories regardless of initial conditions (data are not shown).

Fig. 2.

The time evolution of 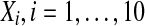, without coupling

Fig. 3.

The time evolution of 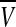without coupling

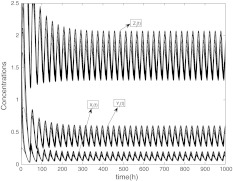
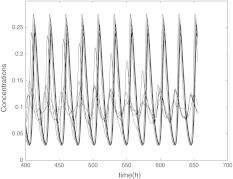
When the coupling strength is set appropriately, the oscillators achieve synchronization, as shown in Figs.  4, 5 and 6 which is not the complete synchronization but with a little difference between their amplitudes. In Figs.  4, 5 and 6, the parameter values express the coupling among the clocks are K_c = 1, K = 0.4, v_c = 0.04, Q = 0.9, η = 0.3. The period of the synchronized oscillators is longer than the single clocks. The initial values for each network neuron dose not affect the synchronization. From the mathematical viewpoint, complete synchronization can be reached only among identical oscillators. However, in our model the oscillators are nonidentical, which means that complete synchronization cannot be reached among these nonidentical oscillators and only the practical or phase synchronization can be expected, i.e. there are differences between their amplitudes.

Fig. 4.

The time evolution of X_i(t), Y_i(t), Z_i(t) for 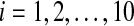with coupling

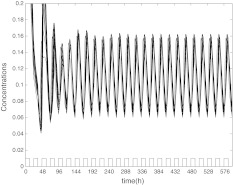
Fig. 5.

The time evolution of V_i(t) for 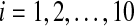with coupling

Fig. 6.

The average values of X_i, Y_i(t), Z_i(t) and V_i for 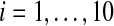with coupling

Besides intercellular coupling, in nature conditions, the circadian clock is subject to alternation of days and nights and in response to this cycling environment, phase-locks to the light-dark (LD) cycle, enabling the body to follow a 24 h rhythm. which is assumed to act independently from the negative feedback loop and is added as independent terms in the transcription rate of X. Light is incorporated through a periodic time-dependent function L(t), which can be realized in various forms. Here we use a square wave

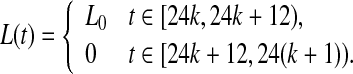and the signal oscillates between the values L(t) = 0 and L(t) = L₀ with a period 24 h.

With the help of numerical simulation, we find that intercellular coupling can reduce the threshold of light that makes the oscillators get phase synchronization with period of 24 h. Specially, Fig. 7 shows that the oscillators can not get synchronization when L₀ = 0.7 without coupling. These oscillators have different periods, which is consistent with the biological findings that isolated individual neurons are able to produce circadian oscillations, with periods ranging from 20 to 28 h (Welsh et al. 1995; Honma et al. 2004). Comparing with Figs.  7, 8 shows that the oscillators can achieve phase synchronization when L₀ = 0.7 with coupling and the values of coupling parameters are just the same as in Figs. 4, 5 and 6. These two figures display that the intercellular coupling is necessary for the oscillators to be entrained with period 24 h.

Fig. 7.

The time evolution of X_i(t) for 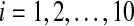without coupling when L₀ = 0.7

Fig. 8.

The time evolution of X_i(t) for 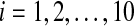with coupling when L₀ = 0.7, and the values of coupling parameters are the same as in Figs.  4, 5 and 6

Conclusion and discussion

Circadian rhythm mediated by SCN is an important phenomenon in mammals, and many theoretical and experimental works have been carried out to understand its mechanism. However, few works went further to study the synchronization mechanism in an analytical way. In this paper, we proposed a model for coupled neuronal oscillators by neurotransmitter. The model proposed here is a general model based on biological evidences, according to which we demonstrated the role of neurotransmitter. Other models or network configurations probably may also give the similar results. From the theoretical analysis in this article, we obtained the conclusion that one major effect of coupling among the neurons in SCN is to increase their synchronizability. With the help of numerical simulation, we show the role of intercellular coupling in two aspects. On one hand, the coupling can make the oscillators get synchronization. On the other hand, the coupling makes it more easy for the oscillators to be entrained with period 24 h. The results and analytical framework proposed here may provide insight to better understand the mechanism of circadian rhythm, and may also have implication for applications, such as designing interventions to treat circadian disorder.

Several aspects of the model are clearly oversimplifications of the known architecture of the SCN. For example, Although there are different transmitters in different parts of the SCN, such as VIP in VL and AVP in DM, we use the same differential equation to describe their dynamical behavior because they are both released rhythmically (Hamada et al. 2001). Actually, there are two basic cell types in different SCN regions, intrinsically rhythmic pacemakers and damped oscillators (Antle et al. 2003, 2007). However we consider only one type of self-oscillating neurons in this article. As mentioned in (Komin et al. 2011), the damped oscillators are more entrainable by the external forcing than the self-oscillating neurons with different periods. The results of this paper show that the coupling makes it more easy for the oscillators be entrained. The simplification may point to a underlying rule that the coupling among neurons perhaps probably makes the self-oscillating neurons damped firstly and then the damped oscillators are entrained more easily by LD cycle.

Actually, the structure of SCN i.e.intercellular connectivity is another factor affecting circadian rhythm. There have been some numerical works to study the effects of circadian oscillator network structure on circadian behavior (Vasalou 2009; Vasalou 2011; Kori 2012). In this article, we didn’t consider the structure of SCN. Under the fast transmission hypothesis, we simplify the cell-to-cell communication by mean-field coupling. In our later work, we will try to develop a multicellular SCN model based on the actual structure, in which the synchronization factor V may be a variational factor for different neuron in stead of the mean-field coupling for all neurons. Then the effects of SCN structure on circadian rhythm will be further studied theoretically.