Stochastic Simulation of Cardiac Ventricular Myocyte Calcium Dynamics and Waves

Abstract

A three dimensional model of calcium dynamics in the rat ventricular myocyte was developed to study the mechanism of calcium homeostasis and pathological calcium dynamics during calcium overload. The model contains 20,000 calcium release units (CRUs) each containing 49 ryanodine receptors. The model simulates calcium sparks with a realistic spontaneous calcium spark rate. It suggests that in addition to the calcium spark-based leak, there is an invisible calcium leak caused by the stochastic opening of a small number of ryanodine receptors in each CRU without triggering a calcium spark. The model also explores the mechanism of calcium wave propagation between release sites under the conditions of calcium overload.

I. Introduction

Calcium plays a crucial role in excitation-contraction coupling in cardiac myocytes as a signaling molecule connecting the depolarization of the cell to contraction of the myofilament. Central to this role is the “calcium release unit”. The calcium release unit consists of the t-tubule and the closely apposed junctional sarcoplasmic reticulum (JSR) that together define a small subspace called the dyad. In the dyad ryanodine receptors open in response to calcium to release calcium from the JSR in a process called calcium-induced calcium release. This release can either be triggered by opening of a closely apposed L-type calcium channel in the t-tubule or by the stochastic opening of a single ryanodine receptor. These stochastic openings have been recorded experimentally as calcium sparks [1].

Calcium sparks are considered to be the elementary events of excitation-contraction coupling. The calcium transient during an action potential is thought to be the summation of calcium sparks from many separate release units [1]. Another putative role of calcium sparks is to maintain calcium homeostasis of the myocyte through a mechanism known as “calcium leak”. Under pathological conditions, the SR calcium leak has been shown to increase and be associated with an increased potential for cardiac arrhythmias through the propagation of waves of elevated myoplasmic calcium.

Calcium is sequestered in the sarcoplasmic reticulum by the SR calcium-ATPase which consumes ATP to pump cytoplasmic calcium up a concentration gradient into the lumen of the SR. The diastolic calcium concentration in the sarcoplasmic reticulum, [Ca²⁺]_SR, is in the range of 0.7 to 1.0 mM. Under steady-state conditions during diastole, the activity of the SR calcium-ATPase is balanced by a calcium leak. The rate of loss of Ca²⁺ from the SR lumen can be measured experimentally when the SR calcium-ATPase is been disabled. The mechanism for this leak has been postulated to be mainly through calcium spark activity. In fact, an increase in spontaneous spark rate can be readily observed when the SR calcium concentration increases, as observed to result from calcium loading protocols, the spontaneous spark rate increases as well. However, calculations of the calcium released through calcium sparks does not account for enough calcium to explain the measured total leak. As a result, an “invisible leak” has been proposed to describe the calcium flux out of the SR that has not been directly measured using calcium indicator dyes [2-4].

In this computational modeling study, we have constructed a cardiac myocyte with the 20,000 stochastic calcium release units consistent with a rat ventricular myocyte. We use this model to explore the mechanism of the calcium leak out of the sarcoplasmic reticulum under different conditions and to characterize and suggest a mechanism for the invisible leak. We also explore how aberrations in normal calcium homeostasis can result in appropriate substrate for calcium arrhythmias.

II. MODELING METHODS

A. Model

A three-dimensional model of the cardiac myocyte has been constructed (Fig. 1). The geometry is idealized with the 20,000 release sites uniformly spaced at 2.0 μm in the longitudinal direction and 0.8 μm in the transverse directions (Fig. 1A & 1B). Each release site contains a dyadic subspace with 49 two-state ryanodine receptors that release calcium into the subspace (J_ryr) consistent with experimental estimates of ~30-300. The calcium diffuses into the myoplasm (J_efflux) from the subspace. The JSR is refilled from the network SR (J_refill). Each ryanodine receptor has an open and closed state with an opening rate that depends upon an increasing function of calcium in the subspace (Fig. 2A) as well as an increasing function of calcium in the JSR lumen (Fig. 2B). The ryanodine receptor dyadic and JSR lumen calcium sensitivities are based upon the experimental observations (Fig. 2) [6]. This combined with experimental estimated open and closed times contrained the parameters governing ryanodine receptor gating. Both opening and closing rates reflect cooperative gating of the ryanodine receptors based upon an energetic coupling formulation [7]. The coupling was set to achieve realistic spontaneous spark frequencies. Each release site also contains 7 six-state L-type calcium channels consisting of a one closed, one open, and two calcium inactivated and two voltage inactivated states.

Fig. 1.

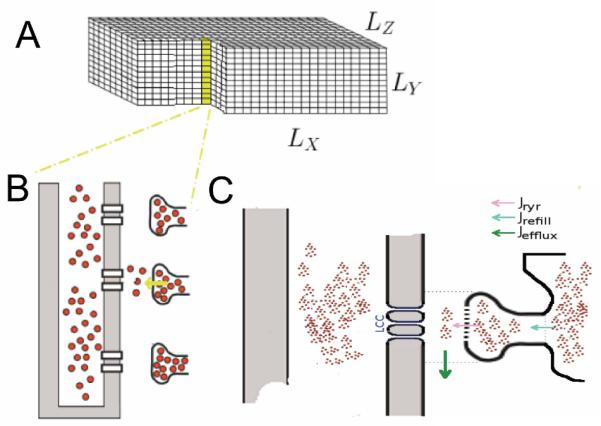
A. The rat ventricular myocyte is represented by a a rectangular grid with 100 μm × 20 μm × 18 μm. The size of each grid element is 200 nm × 200 nm × 200 nm. B. The release sites are arranged throughout the myocyte with a separation of 2 μm in the longitudinal direction and 0.8 μm in the transverse directions. C. A single release site in comprised of the dyadic space and junctional SR and associated channels and fluxes (through the ryanodine receptors, a JSR refilling flux and a subspace efflux to the myoplasm.

Fig. 2.

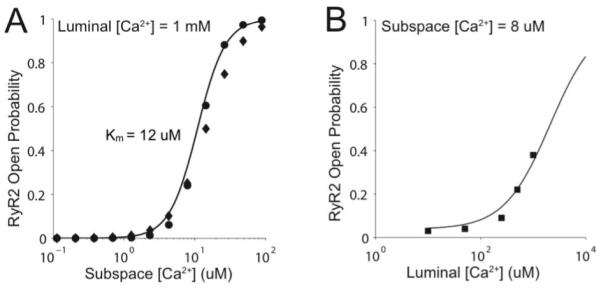
A. The ryanodine receptor open probability as a function of subspace calcium concentration. B. The ryanodine receptor open probability as a function of SR luminal calcium concentration. In both panels, the line is the model and the points are the experimental data from [2].

Calcium leaves the dyadic subspace to the adjacent myoplasm by diffusion.. Calcium refills the JSR by diffusion from the adjacent network sarcoplasmic reticulum. Calcium refills the network SR via the SR calcium-ATPase (J_serca) [8]. Calcium is extruded from the cell by the sodium-calcium exchanger and to a lesser degree by the sarcolemmal calcium-ATPase [9-10].

Calcium buffers are also included in the model: In the myoplasm troponin and calmodulin are modeled; in the dyadic subspace calmodulin is modeled; and in the JSR, calsequestrin is modeled. All buffers are modeled using the rapid buffering approximations [11].

The fluxes are as defined earlier with some modification [2,11]. Equations specifics and parameters can be shared upon request.

In the simulations, in order to compare the model results to experimental values, the binding of calcium to calcium indicator dyes such as Fluo-3 is simulated. Previous simulation studies have shown that calcium dynamics are not perturbed significantly at the indicator dye concentrations typically used (< 50 μM) [12]. For this reason, in the model, instead of including a set of partial differential equations for dye binding and diffusion, which would have increased computational expense, the rapid binding of calcium to dye was assumed to form an expression of the fraction of dye bound to calcium [11].

B. Numerical Methods

The efficient solution of the stochastic model required the development of the Ultrafast Monte Carlo Method. This method builds upon the matrix based methods developed by Smith and Williams for generalized Markov chain Monte Carlo simulation of ion channel gating [13]. This was further improved upon to increase computational efficiency and the result ported to run on GPU (Graphic Processing Unit) and is described elsewhere [14]. These algorithms result in a nearly 15,000 increase in computational efficiency.

The partial differential equations are solved using the explicit Euler method. A variable time step algorithm was used and a fixed spatial step of 200 nm. Release site are assumed to be in a 7 × 7 arrangement requiring approximately 210 nm [5]. It is assumed that a release site embedded in every 10^th grid element in the longitudinal direction and every 4^th grid element in the transverse directions consistent with experimental estimates of average release site separation [15]. As the time step required for the Monte Carlo simulation of channel gating is small, the Euler method does not impose any significant constraints on the time step.

C. Computer Infrastructure

The simulations were performed on a Aspen Systems GPU enabled workstation (Supermicron, Inc.) with two quad core E5640 Westmere CPUs, 24 GBytes memory and two Fermi C2050 GPU compute processors runnin Ubuntu Linux 9.04 with the code written in CUDA Fortran using the Portland Group 2010 compiler.

III. RESULTS AND DISCUSSION

The model has been developed to address two fundamental questions about calcium homeostasis in cardiac myocytes. The first question is what mechanisms account for the calcium leak out of the SR? The second question is how can aberrations in the SR calcium leak cause calcium waves?

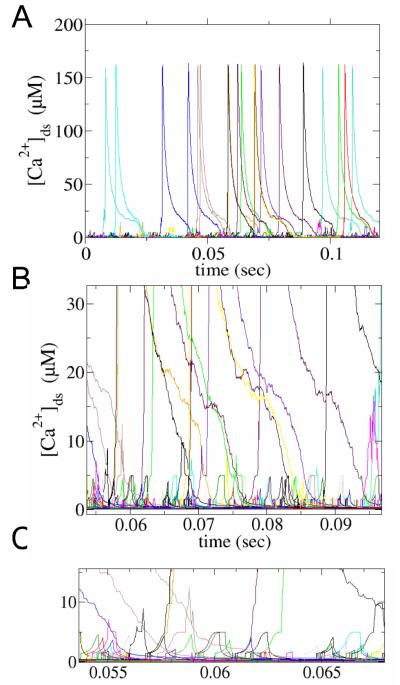
In a resting rat ventricular myocyte, calcium sparks are observed at a rate of 100-200 sparks/cell/s. In model simulations a similar rate of 150 sparks/cell/s was observed (Fig. 3A). During a calcium spark, the 49 ryanodine receptors in the calcium release unit open due to the regenerative nature of calcium-induced calcium release. The calcium flux through the clustered ryanodine receptors quickly declines as the JSR depletes. As the channels stochastically close, fewer channels reopen due to the lower JSR and subspace calcium levels. Once local calcium concentrations fall below a critical level stochastic attrition (facilitated by allosteric coupling) terminates the spark.

Fig. 3.

A. Spontaneous ryanodine receptor opening leads to calcium spark and non-spark openings both of which contribute to the SR calcium leak. B. A close-up of this activity. C. Further close-up demonstrating single ryanodine receptor openings in calcium blink sand sparks.

In addition to calcium sparks, there are smaller more frequent events (calcium quarks) that arise from the opening of one or a few ryanodine receptors. These can be seen more clearly in Fig. 3B. While their amplitude is small, they are numerous with approximately 3000 per cell per second yielding a ~20:1 ratio with respect to calcium sparks. The quarks observed in the model (Fig. 3C) are result of the opening of a one or a few channels (up to 5) that do not recruit additional ryanodine receptors to form a spark. As quarks are composed of channel opening events that result in a step increase in the subspace calcium concentration. The plateau, actually is not flat, but shows an increasing profile to reflect reduction in calcium efflux due to the rise in the bulk myoplasm outside the subspace. The novel distribution and character of the calcium release events generated by this model reflects our use of the most detailed and experimentally constrained description of calcium release in cardiac myocytes to date..

These calcium quarks contribute to non-spark or invisible calcium leak out of the SR. The reason they are invisible is that their amplitude and duration is below the detection threshold of current experimental methods. In these simulations of a rat ventricular myocyte, the invisible leak comprises ~10% of the SR calcium leak consistent with experimental estimates.

The model also allows spatial visualization of the stochastic calcium dynamics. Under normal conditions calcium sparks are observable as well as their diffusion into the different planes of focus. An advantage of the model is that it allows multiple focal planes to be observed simultaneously which is difficult in experiments.

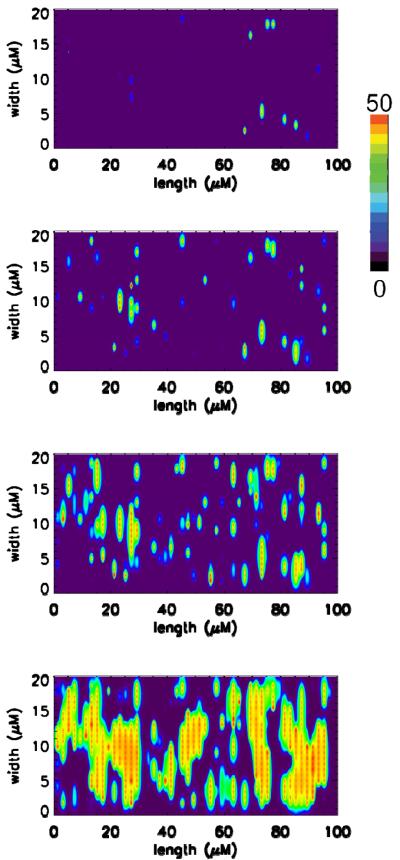
Under conditions of calcium overload, propagation of calcium release from one release site to the next can be observed in experiments using ventricular myocytes in the form of calcium waves. In the model calcium overload was simulated by increasing external calcium concentration (Fig. 4). Shown in each panel of Fig. 4 are the concentrations of calcium bound to the calcium indicator dye Fluo-3. Each row show the myocytes at different time points during the simulation with time progressing from top to bottom in increments of 75 ms. These simulations show that calcium release events can propagate from site to site through a fire-diffuse-fire mechanism i.e., calcium diffuses from one release event (spark) to adjacent sites where it can trigger calcium-induced calcium release from the adjacent site. In these simulations, propagation of calcium release between sites starts in the transverse direction (vertically in a panel or horizontally between panels) before proceeding in the longitudinal directions (horizontally in a panel). This is most likely results from the closer spacing of the release sites in the transverse direction compared to the longitudinal direction.

Fig. 4.

A. Spontaneous calcium release during calcium overload conditions (0.15 μM myoplasmic calcium and 1.5 mM network SR calcium). Shown are the concentration of calcium bound to Fluo-3 (Total Fluo-3 – 50 μM) for one focal plane of the simulated myocyte separated by 0.4 μm. The rows indicate different time of the simulation separated by 75 ms with time progressing from top to bottom.

IV. CONCLUSION

A three dimensional stochastic model of calcium dynamics in the rat ventricular myocyte was developed. Through a combination of improved algorithms and application of GPU technology the simulations were made tractable on relatively modest computer hardware.

The model demonstrates a mechanism of the SR calcium leak that consists of calcium sparks and an invisible leak that results from the stochastic opening of a small number of calcium channels. Spatial simulations support the hypothesis that calcium diffusion from calcium release sites to activate adjacent release sites is the primary mechanism for the generation of calcium wave under conditions of calcium overload.