Abstract
Purpose
To investigate the effect of standardized and study-specific human brain diffusion tensor templates on the accuracy of spatial normalization, without ignoring the important roles of data quality and registration algorithm effectiveness.
Materials and Methods
Two groups of diffusion tensor imaging (DTI) datasets, with and without visible artifacts, were normalized to two standardized diffusion tensor templates (IIT2, ICBM81) as well as study-specific templates, using three registration approaches. The accuracy of inter-subject spatial normalization was compared across templates, using the most effective registration technique for each template and group of data.
Results
It was demonstrated that, for DTI data with visible artifacts, the study-specific template resulted in significantly higher spatial normalization accuracy than standardized templates. However, for data without visible artifacts, the study-specific template and the standardized template of higher quality (IIT2) resulted in similar normalization accuracy.
Conclusion
For DTI data with visible artifacts, a carefully constructed study-specific template may achieve higher normalization accuracy than that of standardized templates. However, as DTI data quality improves, a high-quality standardized template may be more advantageous than a study-specific template, since in addition to high normalization accuracy, it provides a standard reference across studies, as well as automated localization/segmentation when accompanied by anatomical labels.
Keywords: DTI, spatial normalization, brain, template
INTRODUCTION
The potential of diffusion tensor imaging (1,2) (DTI) for detecting differences in brain tissue architecture and micro-structural integrity between healthy subjects and patients has been widely recognized (3–8). Several studies perform voxel-wise analysis to automatically investigate the whole brain for micro-structural differences across groups of subjects. This approach requires inter-subject spatial normalization of DTI data to minimize differences in brain positioning and structural features across subjects. Any remaining inter-subject DTI differences are then interpreted as differences in measured diffusion properties due to a disease process, normal development, or other factors (9). Thus, the accuracy of spatial normalization influences the accuracy of voxel-wise inter-group comparisons. The accuracy of spatial normalization depends on a) the quality of the available data, b) the effectiveness of the registration technique used, and c) the characteristics of the DTI brain template used as a reference (10). Different types of DTI templates have been developed to date (11). The present study focuses on the effect of DTI template selection on the accuracy of inter-subject spatial normalization, without however ignoring the important roles of data quality and registration algorithm effectiveness.
Human brain DTI templates can be divided into two categories: study-specific (11,12) and standardized (10,13–15). A study-specific DTI template is typically developed by averaging the data collected for the purposes of a particular study. The main advantage of a study-specific template is that, in theory, if carefully constructed (e.g. using an effective registration technique), it can be most representative of the characteristics of the data under investigation, thereby maximizing spatial normalization accuracy for that study (11). However, study-specific DTI templates are typically not coupled with a set of anatomical labels (atlas). Thus, registration to study-specific DTI templates does not directly accommodate automated segmentation of various white matter brain structures, or automated localization of detected brain changes. On the other hand, standardized DTI templates are developed by averaging data from a group of healthy subjects, independent of a specific clinical or research study. One advantage of a standardized template is that it may be part of an atlas (13,14), thereby allowing automated segmentation, localization, or seeding for tractography (16,17). Furthermore, a standardized template may be constructed from a larger number of subjects than those available in a specific study, and may therefore be characterized by lower noise levels than the study-specific template (18) (which is important for registration accuracy). However, care must be taken when using a standardized template, since a single such template is not representative of the brain of all human subjects (14).
It was recently demonstrated that carefully constructed study-specific DTI brain templates improve inter-subject spatial normalization compared to standardized templates (11). However, only one publicly available standardized template was evaluated, and only DTI data with visible magnetic susceptibility-induced artifacts was used. Standardized templates of higher quality are now publicly available (10,15), and DTI data acquisition techniques that substantially reduce or minimize susceptibility and other artifacts have been developed (19–23). Since the characteristics of the template and the quality of the data under study influence the accuracy of spatial normalization, the role of standardized and study-specific templates in inter-subject spatial normalization warrants further investigation. Therefore, the purpose of this study was to investigate the effect of standardized and study-specific human brain diffusion tensor templates on the accuracy of spatial normalization, considering DTI datasets with different levels of artifacts and different registration algorithms.
MATERIALS AND METHODS
DTI Data
Two groups of DTI data were used in this study. Written informed consent was provided by all participants according to procedures approved by the local institutional committees for the protection of human subjects. None of the datasets was included in the development of the standardized templates used in this study.
Group 1 consisted of data from 22 healthy human subjects (9 male, 32.3 ± 5.9 years of age, min age = 22 years, max age = 40 years) (13 female, 28.8 ± 4.6 years of age, min age = 22 years, max age = 36 years), obtained from the IXI brain database (24) (http://www.brain-development.org). DTI data in Group 1 was collected on a 3 Tesla (T) Philips MRI scanner (Best, Netherlands), using a single-shot echo-planar (EPI) DTI sequence with the following imaging parameters: TR = 12,000 ms, TE = 51 ms, field-of-view 224 mm × 224 mm, 2 mm slice thickness, 64 axial slices, 128 × 128 image matrix, b = 1,000 s/mm2 for 15 diffusion gradient directions, and parallel imaging with an acceleration factor of 2. Group 1 data was used to study the effect of standardized and study-specific DTI templates on the accuracy of spatial normalization of DTI data with visible artifacts.
Group 2 consisted of data from 22 healthy human subjects (9 male, 32.8 ± 5.8 years of age, min age = 20 years, max age = 40 years) (13 female, 28.8 ± 4.8 years of age, min age = 21 years, max age =36 years), collected on a 3 T General Electric MRI scanner (GE, Waukesha, WI) using Turboprop-DTI (25) and the following imaging parameters: TR = 5,800 ms, TE = 94 ms, 8 spin-echoes per TR, 5 k-space lines per spin-echo, 128 samples per line, 16 blades per image, field-of-view 24 cm × 24 cm, 3 mm slice thickness, 36 axial slices, 256 × 256 image matrix, b = 900 s/mm2 for 12 diffusion gradient directions (minimum energy scheme (26)), and two b = 0 s/mm2 image-volumes. The sex and age of the subjects was matched for Groups 1 and 2. Group 2 data was used to study the effect of standardized and study-specific DTI templates on the accuracy of spatial normalization of DTI data without visible artifacts.
Pre-processing
For each dataset of Group 1, diffusion-weighted (DW) and b = 0 s/mm2 image-volumes were co-registered using TORTOISE (27) to correct bulk motion and eddy-current distortions. A similar approach was followed for the data of Group 2 to correct bulk motion only, since eddy-current distortions are minimal in Turboprop-DTI (20). All corrected datasets from Groups 1 and 2 were then interpolated to cubic 1 mm3 voxels using trilinear interpolation. Finally, diffusion tensors were estimated for each dataset. Eigenvalues and eigenvectors were derived from the diffusion tensors, and maps of fractional anisotropy (FA) and trace of the diffusion tensor were generated (2).
DTI Registration
Three publicly available DTI registration techniques were used for registration of DTI data to the different templates: DTIGUI (28), MedINRIA (29), and DTITK (30). In DTIGUI, gray matter, white matter and cerebrospinal fluid are first segmented based on FA and trace maps, and the three tissue components are registered to the reference by a high-dimensional elastic registration method (31). The resulting deformation is then applied to the DTI data, and the tensors are reoriented (32). In contrast to DTIGUI, MedINRIA performs registration based on full tensor information, using a fast diffeomorphic demons algorithm (29). Also, the exact gradient of the registration objective function is calculated, and tensor reorientation with the finite-strain approach is incorporated and used as an additional constraint in the registration (33). DTITK is also tensor-based and performs piecewise affine registration with explicit optimization of tensor orientation. The finite-strain strategy is used for tensor reorientation during registration, while the preservation of principal direction approach is used for the final re-slicing (33). All registrations of DTI data to the standardized and study-specific templates were repeated with each of the three algorithms.
Diffusion Tensor Human Brain Templates
Two standardized brain templates were used in this work: the ICBM81 (13) and the IIT2mean (10). The ICBM81 template was constructed by averaging DTI data from 81 healthy subjects (18–59 years of age), collected on two 1.5 T MRI scanners using EPI-based DTI sequences with parallel imaging and an acceleration factor of 2. Affine registration was used for spatial normalization of the 81 datasets prior to averaging. The IIT2 template was constructed by averaging DTI data from 67 healthy subjects (20–40 years of age), collected on a 3 T MRI scanner using Turboprop-DTI (10). DTIGUI was used for spatial normalization of the 67 datasets prior to averaging. It was previously shown that the IIT2 template is characterized by higher image sharpness, provides the ability to distinguish smaller white matter fiber structures, has fewer image artifacts, and contains diffusion tensor information that is more representative of single-subject human brain data than ICBM81 (10,15). The ICBM81 and IIT2 templates were used in this study since they a) are publicly available, b) are in the same space (ICBM152), c) were constructed based on data with and without image artifacts d) from large numbers of subjects e) and age groups similar to those studied here, and f) contain full tensor information. Therefore, use of these two templates allowed tensor-based registration and minimized biases and nuisance factors in the comparison of spatial normalization accuracy achieved with standardized templates of different quality.
Study-specific templates were constructed for Group 1 and Group 2 data, using a population-based approach (34). For each group, the DTI data from a single subject was registered to the data from the remaining 21 subjects of the same group, using DTITK. The 21 transformations were then averaged, and the average transformation was applied to the data from the single subject. The same procedure was repeated for all subjects. The study-specific template of each group was then constructed by averaging the spatially transformed DTI data of the group.
Metrics of Inter-subject Spatial Normalization Accuracy
Group 1 and Group 2 DTI data were registered to the standardized and study-specific templates using all three registration techniques (Fig.1). In each case, white matter was identified through K-means clustering of the mean FA maps of the corresponding normalized data. K-means clustering was preferred instead of thresholding the mean FA maps, since no single FA threshold can segment WM similarly in data collected with drastically different DTI sequences. A number of metrics were used to assess the accuracy of spatial normalization achieved for each combination of: group of data, registration technique and template. These metrics have been described in detail previously and are simply listed here to avoid repetition. The average cross-correlation of FA values (corrFA) in white matter was estimated considering all possible pairs of subjects (10). The average Euclidean distance of tensors (DTED) for all possible pairs of subjects was estimated in each voxel (10). The average Euclidean distance of the deviatoric tensors (DVED) was also estimated (10). The average log-Euclidean tensor distance (LETD) for all possible pairs of subjects was estimated in each voxel (35). The average overlap of eigenvalues-eigenvectors between tensors (OVL) of all possible pairs of subjects was estimated in each voxel (10). The coherence of primary eigenvectors from co-registered tensors (COH) was estimated in each voxel (10). The 95% cone of uncertainty (36) (COU) and the total variance of the diffusion tensor (37) (TVDT) were estimated in each voxel considering co-registered tensors from all subjects. Maps of the average DTED, DVED and LETD, the average OVL, the COH, the COU and the TVDT were produced. Histograms of these quantities in white matter were also generated. Each histogram was normalized with the corresponding total number of white matter voxels.
Figure 1.
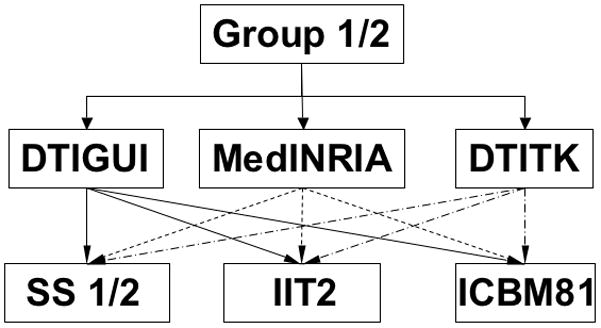
Outline of the spatial normalization process of Group 1 and Group 2 data to study-specific (SS), IIT2 and ICBM81 templates using DTIGUI (solid line), MedINRIA (dashed line) and DTITK (dash-dot line) registration techniques.
Comparison of Inter-Subject Spatial Normalization Accuracy Across Registration Techniques
For each combination of group of data and template (Fig.1), spatial normalization accuracy was first compared for different registration methods. For that purpose, the average corrFA in white matter was compared across registration techniques using analysis of variance (ANOVA) with Tukey’s honestly significant difference post hoc test accounting for multiple comparisons. Differences were considered significant at p<0.01. Also, for each combination of group of data and template, histograms of the metrics of spatial normalization accuracy listed in the previous section were compared across registration techniques. Based on the results of the above comparisons, the most effective registration technique for each combination of group of data and template was identified.
Comparison of Inter-Subject Spatial Normalization Accuracy Across Templates
For each group of data, spatial normalization accuracy was compared across templates using the preferred registration technique for each template. The average corrFA in white matter was compared across templates using ANOVA with Tukey’s honestly significant difference post hoc test accounting for multiple comparisons. Also, histograms of the metrics of spatial normalization accuracy were compared using the two-sample Kolmogorov-Smirnov (KS) test. Differences were considered significant at p<0.01. Furthermore, regions of interest (ROI) were selected in the following white matter structures based on the mean FA maps of the corresponding normalized datasets: 1) in relatively thin white matter structures where misregistration across subjects might have a substantial effect on metrics of spatial normalization accuracy: corticopontine tract (cpt), column of the fornix (fxc), medial lemniscus (ml), and cingulum (cg); 2) in relatively large structures where misregistration might have a relatively smaller effect on metrics of spatial normalization accuracy: splenium of the corpus callosum (scc), genu of the corpus callosum (gcc) and internal capsule (ic), in both hemispheres (Fig. 2). All ROIs were selected along the skeleton of white matter to avoid partial volume effects, and spanned three axial slices with 1mm slice thickness. The mean and standard deviation of metrics of spatial normalization accuracy were calculated in the ROIs. ANOVA with Tukey’s honestly significant difference post hoc test accounting for multiple comparisons was used to compare normalization accuracy in the selected ROIs across templates. Differences were considered significant at p<0.01.
Figure 2.
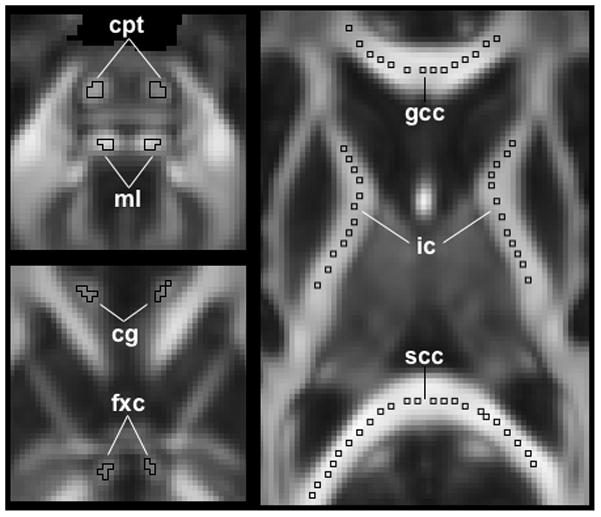
Location of selected regions of interest (ROIs). Top left: corticopontine tract (cpt) and medial lemniscus (ml); bottom left: cingulum (cg) and column of the fornix (fxc); right: genu of the corpus callosum (gcc), splenium of the corpus callosum (scc), and internal capsule (ic).
RESULTS
Group 1 data contained visible artifacts in the frontal and temporal lobes (Fig.3A) due to magnetic susceptibility variations. In contrast, Group 2 data did not contain visible artifacts (Fig.3B).
Figure 3.
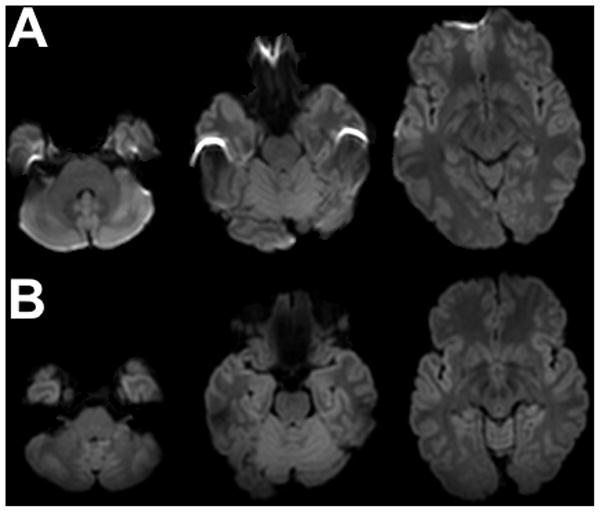
Typical examples of mean diffusion-weighted images from Group 1 (A) and Group 2 (B) data, after preprocessing.
Comparison of Inter-Subject Spatial Normalization Accuracy Across Registration Techniques
Tables 1 and 2 include the average corrFA values for registration of Group 1 and 2 data, respectively, to the standardized and study-specific templates using three registration techniques. DTIGUI resulted in the highest corrFA for registration of a) Group 1 data to the ICBM81 and IIT2 templates, and b) Group 2 data to the ICBM81 template. DTITK resulted in the highest corrFA for registration of a) Group 1 data to the study-specific template, and b) Group 2 data to the IIT2 and study-specific templates.
Table 1.
Values of average corrFA in white matter for registration of Group 1 data to the ICBM81, IIT2, and study-specific templates using three registration techniques (DTIGUI, MedINRIA, DTITK). The highest average corrFA for each template is shown in bold numbers.
| Template | Registration method | ANOVA P-value | Pairwise P-value | ||||
|---|---|---|---|---|---|---|---|
| aDTIGUI | bMedINRIA | cDTITK | a vs b | b vs c | a vs c | ||
| ICBM81 | 0.948±0.005 | 0.936±0.006 | 0.936±0.007 | <10−9 | <10−9 | 0.55 | <10−9 |
| IIT2 | 0.953±0.005 | 0.943±0.005 | 0.948±0.008 | <10−9 | <10−9 | <10−9 | <10−9 |
| Study-specific | 0.955±0.005 | 0.956±0.004 | 0.965±0.003 | <10−9 | 0.02 | <10−9 | <10−9 |
Table 2.
Values of average corrFA in white matter for registration of Group 2 data to the ICBM81, IIT2, and study-specific templates using three registration techniques (DTIGUI, MedINRIA, DTITK). The highest average corrFA for each template is shown in bold numbers.
| Template | Registration method | ANOVA P-value | Pairwise P-value | ||||
|---|---|---|---|---|---|---|---|
| aDTIGUI | bMedINRIA | cDTITK | a vs b | b vs c | a vs c | ||
| ICBM81 | 0.940±0.007 | 0.934±0.006 | 0.923±0.010 | <10−9 | <10−9 | <10−9 | <10−9 |
| IIT2 | 0.948±0.006 | 0.949±0.006 | 0.961±0.005 | <10−9 | 0.4 | <10−9 | <10−9 |
| Study-specific | 0.950±0.005 | 0.954±0.005 | 0.962±0.005 | <10−9 | <10−9 | <10−9 | <10−9 |
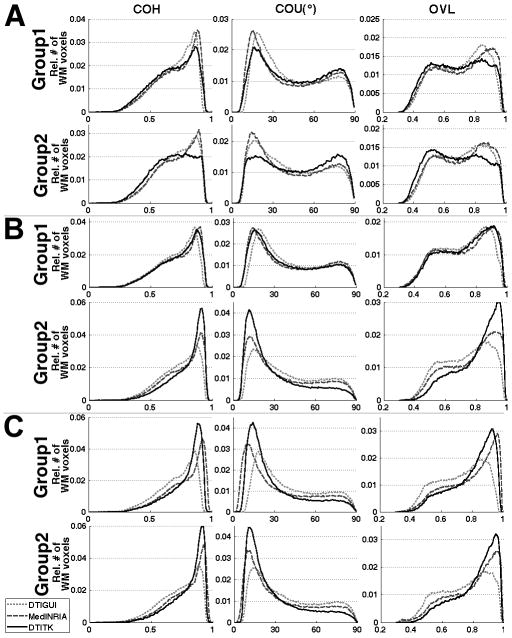
In histograms of the various spatial normalization accuracy metrics, MedINRIA was shown to be the preferred registration technique for registration of a) Group 1 data to all templates, and b) Group 2 data to the ICBM81 template, since it resulted in a higher percentage of white matter voxels with high COH, low COU and high OVL (Fig.4). DTITK was shown to be the preferred registration technique for registration of Group 2 data to the IIT2 and study-specific templates, since it resulted in a higher percentage of white matter voxels with high COH, low COU and high OVL (Fig.4). Histograms of the remaining spatial normalization accuracy metrics (average DTED, average DVED, average LETD, TVDT) provided the same results.
Figure 4.
Histograms of the relative number of white matter voxels at different values of COH, COU, and average OVL, for registration of Group 1 and Group 2 data to the ICBM81 (A), IIT2 (B) and study-specific (C) templates using DTIGUI (light grey curve), MedINRIA (dark grey curve) and DTITK (black curve).
The tests based on the average corrFA in white matter did not indicate the same preferred registration techniques for some combinations of data-groups and templates as the tests based on all other quantities. This was due to the fact that the average corrFA in white matter assesses spatial normalization accuracy for FA maps, while the rest of the quantities assess spatial normalization accuracy for other types of tensor-derived information, including the complete tensor. Since the average corrFA is based only on FA information, and the results from all other quantities were in agreement with each other, the registration method used for each combination of a group of data with a template in the rest of this work was decided according to the results for the average DTED, DVED, and LETD, the average OVL, the COH, the COU and the TVDT. Therefore, in the comparisons of spatial normalization accuracy across templates, MedINRIA was used for registration of Group 1 data to all templates, as well as for registration of Group 2 data to the ICBM81 template, and DTITK was used for registration of Group 2 data to the IIT2 and study-specific templates (Fig.4). Finally, as shown in the discussion section, the same conclusions about the effects of different templates on spatial normalization accuracy (main goal of this research) would be drawn if the decision for the preferred registration technique was made exclusively based on the average corrFA results.
Comparison of Inter-Subject Spatial Normalization Accuracy Across Templates
The average corrFA in white matter for registration of Group 1 data to the study-specific template (0.956±0.004) was significantly higher than that for registration to the IIT2 template (0.943±0.005) (p<10−9), which was significantly higher than that for the ICBM81 template (0.936±0.006) (p<10−9). The average corrFA values for registration of Group 2 data to the IIT2 (0.961±0.005) and study-specific templates (0.962±0.005) were similar (p=0.02), and significantly higher than that for registration to the ICBM81 template (0.934±0.006) (p<10−9).
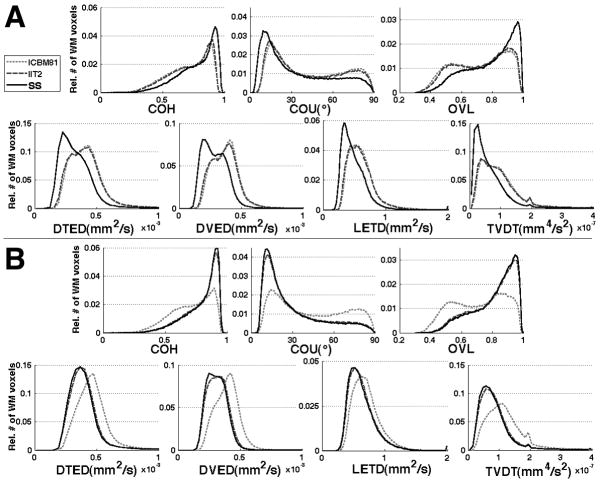
Histograms of the various spatial normalization accuracy metrics for Group 1 data showed that the study-specific template resulted in a higher percentage of white matter voxels with high COH, low COU, high OVL, low DTED, DVED, LETD and TVDT, compared to the IIT2 and ICBM81 templates (Fig.5A). The difference between the histograms corresponding to the study-specific template and those corresponding to the standardized templates was statistically significant according to the KS test (p<10−8). The difference between the histograms corresponding to the IIT2 and ICBM81 templates was small, but statistically significant according to the KS test (p<10−8). Histograms of the various spatial normalization accuracy metrics for Group 2 data showed that both the study-specific and IIT2 templates resulted in a higher percentage of white matter voxels with high COH, low COU, high OVL, low DTED, DVED, LETD and TVDT, compared to the ICBM81 template (Fig.5B). The difference between the study-specific or IIT2 histograms and those corresponding to the ICBM81 template was statistically significant according to the KS test (p<10−8). The difference between the study-specific and IIT2 histograms was small, but statistically significant according to the KS test (p<10−8). For both groups of data, the findings above were in agreement with the results observed in maps of the various metrics of spatial normalization accuracy (Fig.6).
Figure 5.
Histograms of the relative number of white matter voxels at different values of COH, COU, average OVL, average DTED, DVED and LETD, and TVDT, for registration of Group 1 (A) and Group 2 (B) data to ICBM81 (light grey curve), IIT2 (dark grey curve) and study-specific (SS, black curve) templates using the preferred registration method for each case.
Figure 6.
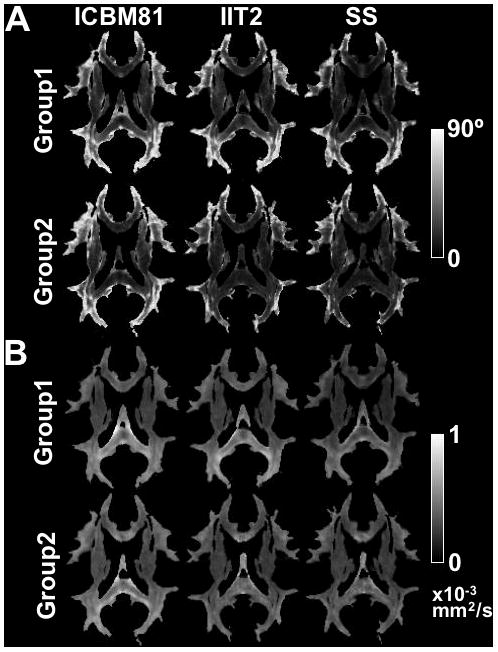
Maps of the COU (A) and average DVED (B) for Group 1 and Group 2 data registered to the ICBM81, IIT2 and study-specific (SS) templates using the preferred registration technique for each case.
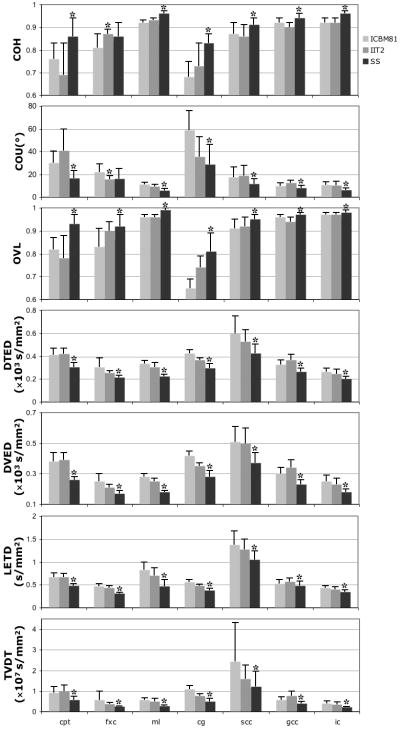
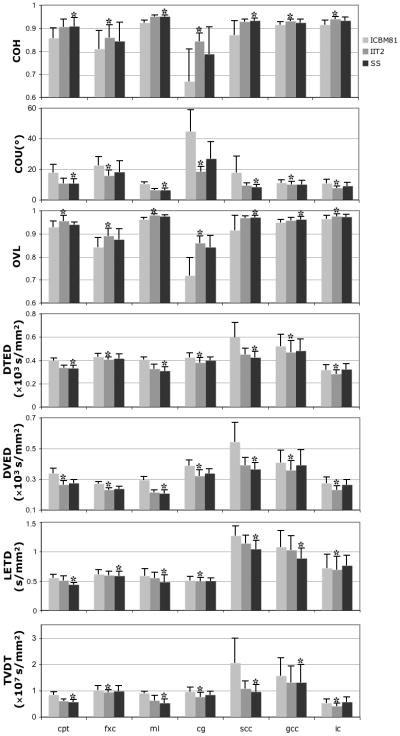
The results of ROI analysis were consistent with the above findings. More specifically, for Group 1 data, the study-specific template resulted in significantly higher COH, lower COU, higher OVL, lower DTED, DVED, LETD and TVDT, compared to the standardized templates, in almost all ROIs (Fig.7). For Group 2 data, both the study-specific and IIT2 templates resulted in significantly higher COH, lower COU, higher OVL, lower DTED, DVED, LETD and TVDT, compared to the ICBM81 template, in almost all ROIs (Fig.8).
Figure 7.
Means and standard deviations of the COH, COU, average OVL, average DTED, DVED and LETD, and TVDT in selected ROIs, for normalization of Group 1 data to the ICBM81, IIT2, and study-specific templates. For each ROI, the template with the best performance in each metric of spatial normalization accuracy is marked with an asterisk (*).
Figure 8.
Means and standard deviations of the COH, COU, average OVL, average DTED, DVED and LETD, and TVDT in selected ROIs, for normalization of Group 2 data to the ICBM81, IIT2, and study-specific templates. For each ROI, the template with the best performance in each metric of spatial normalization accuracy is marked with an asterisk (*).
DISCUSSION
The accuracy of inter-subject spatial normalization of DTI data depends on the quality of the available data, the effectiveness of the registration technique used, and the characteristics of the DTI brain template used as a reference (10). This work focused on the effect of DTI template selection on the accuracy of inter-subject spatial normalization, without however ignoring the important roles of data quality and registration algorithm effectiveness. In the following, we analyze the procedures and findings of this study and discuss the implications for DTI research.
Three different DTI registration techniques were first tested in this work for each combination of template and group of data. Several other DTI registration approaches have been published to date. However, the main goal of this study was not to compare the performance of all published DTI registration methods. That is beyond the scope of the present research (38). The purpose of using different registration techniques was to reduce any potential bias of the registration approach on the comparison of spatial normalization accuracy for different templates, by identifying a preferred method for each combination of template and data-group. The selected registration methods were appropriate and sufficient for the purposes of this work because they a) are robust, b) are freely available and widely used, c) allow deformations that substantially increase matching of anatomical features across subjects, d) cover a range of DTI registration approaches that perform at or near the highest level of published DTI registration algorithms (38). Therefore, we do not anticipate that use of a registration technique other than the three used here will alter the main conclusions of this work regarding the spatial normalization accuracy achieved with standardized and study-specific templates.
A number of standardized DTI templates have been developed to date (15). The IIT2 template was used here because it is a) the only standardized tensor template developed by nonlinearly normalizing and averaging a large number of datasets (i.e. 67) without visible artifacts (10), similar to Group 2 data, b) it was constructed based on subjects from the age-range of Groups 1 and 2, and c) it possesses characteristics that make it most representative of Group 2 data, among all standardized templates. The ICBM81 template was selected because a) it was developed based on a large number (i.e. 81) of EPI tensor datasets with typical visible artifacts, similar to Group 1 data, b) it included subjects from the age-range of the IIT2 template, as well as the age-range of Groups 1 and 2, and c) it is located in the same space as the IIT2 template (ICBM152). Several other templates have been built from EPI-based DTI data. However, some of these templates a) are not publicly available, b) are not in ICBM152 space, c) contain data from a single subject that may not be representative of the population in this study (39), d) were built using information from very different age-groups than those studied here (24), and others e) do not contain full tensor information (40). These factors may reduce spatial normalization accuracy, and those templates were therefore avoided. The selection of the IIT2 and ICBM81 standardized templates minimized nuisance factors and supported the objectives of this study.
A number of metrics was used to determine the registration technique that maximizes spatial normalization accuracy for each combination of template and data-group. Since each of these metrics is based on different portions of the information contained in the diffusion tensor, it is not guaranteed that the results from all metrics match. In fact, in the present work, the preferred registration technique resulting from the average corrFA values in white matter was not the same as that resulting from all other metrics, for some combinations of templates and data-groups. The final decision on the registration techniques used in the rest of this study was made based on the results from metrics other than the average corrFA, which were all in agreement. Nevertheless, using Tables 1, 2 and Figure 4, it can be seen that even if the preferred registration techniques were selected based exclusively on the average corrFA results, ignoring the other metrics, the same final conclusions would be reached about the spatial normalization accuracy achieved with different templates.
In this work, it was demonstrated that, for data with visible artifacts (Group 1), spatial normalization accuracy was significantly higher when using the study-specific template, compared to standardized templates (Table 1) (Fig.5–7). This finding was in agreement with the results of a recent study (11). The artifacts of Group 1 data were primarily caused by magnetic susceptibility variations in the frontal and temporal lobes, and consisted of signal loss or pileup and severe distortions (Fig.3). Since susceptibility-related effects in EPI-based acquisitions depend on subject-specific and scanner-specific factors, they are expressed differently in each dataset. As a result, the template that better represents the distinct features of a number of EPI-based DTI datasets is a template built from the data under investigation. Thus, for typical EPI-based DTI data a study-specific template results in higher spatial normalization accuracy than standardized templates.
It was also shown that for EPI-based DTI data with visible artifacts (Group 1) the IIT2 template resulted in similar or higher spatial normalization accuracy than the ICBM81 template (Fig.5,7) (Table 1), although the former was constructed from DTI data with no visible artifacts and the latter from EPI-based data with typical artifacts. One explanation for this finding may be that the artifacts in the data used to develop the ICBM81 template were not similar to those in the Group 1 data, and therefore the ICBM81 template did not have an advantage over the IIT2 template. A second factor that may have contributed to this finding is that, in brain regions free of artifacts, the diffusion tensor information contained in the IIT2 template is shown to be more representative of that of individual subjects from the 20–40 years age-range, than the information contained in the ICBM81 template (10).
For data without visible artifacts (Group 2), both the IIT2 and study-specific templates resulted in similar spatial normalization accuracy, significantly higher than that of the ICBM81 template (Table 2) (Fig.5,6,8). This was due to the fact that, for data without artifacts, both the IIT2 and study-specific templates are representative of the data under investigation, since there are no features in the data that are not contained in the two templates. Therefore, for DTI data without visible artifacts, the IIT2 template results in similar spatial normalization accuracy as the study-specific template. This has not been previously reported, since an earlier study on template selection used only EPI-DTI data with typical EPI artifacts (11).
Study-specific DTI templates of the human brain can be most representative of the data under study if carefully constructed using accurate registration algorithms based on full tensor information, unbiased template-building approaches, and large numbers of whole-brain datasets. One disadvantage of study-specific DTI templates is that they are typically not part of an atlas and therefore do not directly accommodate automated segmentation. Standardized DTI templates may be constructed from a larger number of subjects than those available in a specific study, and may therefore be characterized by lower noise levels than the study-specific template. In addition, a standardized DTI template provides a standard reference across studies, and may be part of an atlas, thereby allowing automated segmentation, localization, or seeding for tractography. However, this and other studies have shown that for data with visible artifacts, a carefully constructed study-specific template is more representative of the data under investigation than a standardized template, leading to higher spatial normalization accuracy. When using data without visible artifacts, a carefully constructed high-quality standardized template, provides similar spatial normalization accuracy to that of the corresponding study-specific template, as well as all other advantages of standardized templates mentioned above. Therefore, each DTI study must weigh the advantages and disadvantages of the two types of templates. Template selection depends on a number of factors, including the characteristics and quality of the data. As data quality continuously improves with the use of parallel imaging with high acceleration factors and other data acquisition techniques (19–23) high quality standardized templates become more advantageous for DTI research.
This study included healthy adult subjects and DTI templates constructed from data on healthy adults. DTI investigations of neonates, elderly subjects, or patients with various neurological disorders (excluding those with tumors and other large lesions in which registration to a template is problematic) require corresponding DTI templates (24, 38). It is expected that the conclusions from the comparison of standardized and study-specific templates discussed above also hold in studies of these populations, as long as the standardized templates used are generally representative of the population under investigation (i.e. are constructed using data from a cohort with generally similar characteristics as those of the cohort under study).
In conclusion, this work assessed the accuracy of inter-subject DTI spatial normalization for standardized and study-specific templates, using data with and without visible artifacts and different registration techniques. It was demonstrated that, for DTI data with visible artifacts, the study-specific template resulted in significantly higher spatial normalization accuracy than standardized templates. However, for data without visible artifacts, both the IIT2 and study-specific templates resulted in similar normalization accuracy. As the quality of DTI data improves with the use of advanced acquisition techniques, a high-quality standardized template may be more advantageous than a study-specific template, since in addition to high normalization accuracy, it provides a standard reference across studies, as well as automated localization/segmentation when accompanied by anatomical labels.
Acknowledgments
Grant Support:
NIBIB R21EB006525
NINDS R21NS076827
References
- 1.Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- 3.Bruno S, Cercignani M, Ron MA. White matter abnormalities in bipolar disorder: a voxel-based diffusion tensor imaging study. Bipolar Disorders. 2008;10:460–468. doi: 10.1111/j.1399-5618.2007.00552.x. [DOI] [PubMed] [Google Scholar]
- 4.Phan KL, Orlichenko A, Boyd E, et al. Preliminary evidence of white matter abnormality in the uncinate fasciculus in generalized social anxiety disorder. Biol Psychiatry. 2009;66:691–694. doi: 10.1016/j.biopsych.2009.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Werring DJ, Clark CA, Barker GJ, Thompson AJ, Miller DH. Diffusion tensor imaging of lesions and normal-appearing white matter in multiple sclerosis. Neurology. 1999;52:1626–1632. doi: 10.1212/wnl.52.8.1626. [DOI] [PubMed] [Google Scholar]
- 6.Rose SE, Janke AL, Chalk JB. Gray and white matter changes in Alzheimer’s disease: a diffusion tensor imaging study. J Magn Reson Imaging. 2008;27:20–26. doi: 10.1002/jmri.21231. [DOI] [PubMed] [Google Scholar]
- 7.Eriksson SH, Rugg-Gunn FJ, Symms MR, Barker GJ, Duncan JS. Diffusion tensor imaging in patients with epilepsy and malformations of cortical development. Brain. 2001;124(Pt. 3):617–626. doi: 10.1093/brain/124.3.617. [DOI] [PubMed] [Google Scholar]
- 8.Bendlin BB, Ries ML, Lazar M, et al. Longitudinal changes in patients with traumatic brain injury assessed with diffusion-tensor and volumetric imaging. Neuroimage. 2008;42:503–514. doi: 10.1016/j.neuroimage.2008.04.254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang H, Avants BB, Yushkevich PA, et al. High-Dimensional Spatial Normalization of Diffusion Tensor Images Improves the Detection of White Matter Differences: An Example Study Using Amyotrophic Lateral Sclerosis. IEEE Trans Med Imaging. 2007;26:1585–1597. doi: 10.1109/TMI.2007.906784. [DOI] [PubMed] [Google Scholar]
- 10.Zhang S, Peng H, Dawe JR, Arfanakis K. Enhanced ICBM Diffusion Tensor Template of the Human Brain. Neuroimage. 2011;54:974–984. doi: 10.1016/j.neuroimage.2010.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Van Hecke W, Leemans A, Sage CA, et al. The effect of template selection on diffusion tensor voxel-based analysis results. Neuroimage. 2011;55:566–573. doi: 10.1016/j.neuroimage.2010.12.005. [DOI] [PubMed] [Google Scholar]
- 12.Zhang H, Yushkevich PA, Rueckert D, Gee JC. Unbiased white matter atlas construction using diffusion tensor images. Med Image Comput Comput Assist Interv. 2007;10(Pt 2):211–218. doi: 10.1007/978-3-540-75759-7_26. [DOI] [PubMed] [Google Scholar]
- 13.Mori S, Oishi K, Jiang H, et al. Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. Neuroimage. 2008;40:570–582. doi: 10.1016/j.neuroimage.2007.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Oishi K, Mori S, Donohue PK, et al. Multi-contrast human neonatal brain atlas: application to normal neonate development analysis. Neuroimage. 2011;56:8–20. doi: 10.1016/j.neuroimage.2011.01.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Peng H, Orlichenko A, Dawe RJ, Agam G, Zhang S, Arfanakis K. Development of a human brain diffusion tensor template. Neuroimage. 2009;46:967–980. doi: 10.1016/j.neuroimage.2009.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lawes IN, Barrick TR, Murugam V, et al. Atlas-based segmentation of white matter tracts of the human brain using diffusion tensor tractography and comparison with classical dissection. Neuroimage. 2008;39:62–79. doi: 10.1016/j.neuroimage.2007.06.041. [DOI] [PubMed] [Google Scholar]
- 17.Zhang Y, Zhang J, Oishi K, et al. Atlas-guided tract reconstruction for automated and comprehensive examination of the white matter anatomy. Neuroimage. 2010;52:1289–1301. doi: 10.1016/j.neuroimage.2010.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang S, Carew JD, Arfanakis K. Variability of diffusion tensor characteristics in human brain templates: Effect of the number of subjects used for the development of the templates. Proceedings of the 18th Annual Meeting of ISMRM; Stockholm, Sweden. 2010. p. abstract 1637. [Google Scholar]
- 19.Blaimer M, Breuer F, Mueller M, Heidemann RM, Griswold MA, Jakob PM. SMASH, SENSE, PILS, GRAPPA: how to choose the optimal method. Top Magn Reson Imaging. 2004;15:223–236. doi: 10.1097/01.rmr.0000136558.09801.dd. [DOI] [PubMed] [Google Scholar]
- 20.Gui M, Peng H, Carew JD, Lesniak MS, Arfanakis K. A tractography comparison between turboprop and spin-echo echo-planar diffusion tensor imaging. Neuroimage. 2008;42:1451–1462. doi: 10.1016/j.neuroimage.2008.05.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Koch MA, Glauche V, Finsterbusch J, et al. Distortion-free diffusion tensor imaging of cranial nerves and of inferior temporal and orbitofrontal white matter. Neuroimage. 2002;17:497–506. doi: 10.1006/nimg.2002.1171. [DOI] [PubMed] [Google Scholar]
- 22.Liu C, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52:1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
- 23.Porter DA, Heidemann RM. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magn Reson Med. 2009;62:468–475. doi: 10.1002/mrm.22024. [DOI] [PubMed] [Google Scholar]
- 24.Zhang H, Yushkevich PA, Rueckert D, Gee JC. A Computational White Matter Atlas for Aging with Surface-Based Representation of Fasciculi. In: Fischer B, Dawant BM, Lorenz C, editors. Proceedings of International Workshop on Biomedical Image Registration; Berlin: Springer; 2010. pp. 83–90. [Google Scholar]
- 25.Pipe JG, Zwart N. Turboprop: improved PROPELLER imaging. Magn Reson Med. 2006;55:380–385. doi: 10.1002/mrm.20768. [DOI] [PubMed] [Google Scholar]
- 26.Hasan KM, Parker DL, Alexander AL. Comparison of gradient encoding schemes for diffusion-tensor MRI. J Magn Reson Imaging. 2001;13:769–780. doi: 10.1002/jmri.1107. [DOI] [PubMed] [Google Scholar]
- 27.Pierpaoli C, Walker L, Irfanoglu MO, et al. TORTOISE: an integrated software package for processing of diffusion MRI data. Proceedings of the 18th Annual Meeting of ISMRM; Stockholm, Sweden. 2010. p. abstract 1597. [Google Scholar]
- 28.Yang J, Shen D, Misra C, et al. Spatial normalization of diffusion tensor images based on anisotropic segmentation. SPIE Medical Imaging; San Diego. 2008. pp. 6914pp. 69140L.1–69140L.10. [Google Scholar]
- 29.Yeo BTT, Vercauteren T, Fillard P, et al. DT-REFinD: Diffusion Tensor Registration with Exact Finite-Strain Differential. IEEE Trans Med Imaging. 2009;28:1914–1928. doi: 10.1109/TMI.2009.2025654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhang H, Yushkevich PA, Alexander DC, Gee JC. Deformable registration of diffusion tensor MR images with explicit orientation optimization. Med Image Anal. 2006;10:764–785. doi: 10.1016/j.media.2006.06.004. [DOI] [PubMed] [Google Scholar]
- 31.Shen D, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Trans Med Imaging. 2002;21:1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- 32.Xu D, Mori S, Shen D, van Zijl PC, Davatzikos C. Spatial normalization of diffusion tensor fields. Magn Reson Med. 2003;50:175–182. doi: 10.1002/mrm.10489. [DOI] [PubMed] [Google Scholar]
- 33.Alexander DC, Pierpaoli C, Basser PJ, Gee JC. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans Med Imaging. 2001;20:1131–1139. doi: 10.1109/42.963816. [DOI] [PubMed] [Google Scholar]
- 34.Van Hecke W, Sijbers J, D’Agostino E, et al. On the construction of an inter-subject diffusion tensor magnetic resonance atlas of the healthy human brain. Neuroimage. 2008;43:69–80. doi: 10.1016/j.neuroimage.2008.07.006. [DOI] [PubMed] [Google Scholar]
- 35.Arsigny V, Fillard P, Pennec X, Ayache N. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magn Reson Med. 2006;56:411–421. doi: 10.1002/mrm.20965. [DOI] [PubMed] [Google Scholar]
- 36.Jones DK. Determining and visualizing uncertainty in estimates of fiber orientation from diffusion tensor MRI. Magn Reson Med. 2003;49:7–12. doi: 10.1002/mrm.10331. [DOI] [PubMed] [Google Scholar]
- 37.Papadakis NG, Xing D, Huang CL, Hall LD, Carpenter TA. A comparative study of acquisition schemes for diffusion tensor imaging using MRI. J Magn Reson. 1999;137:67–82. doi: 10.1006/jmre.1998.1673. [DOI] [PubMed] [Google Scholar]
- 38.Wang Y, Gupta A, Liu Z, et al. DTI registration in atlas based fiber analysis of infantile Krabbe disease. NeuroImage. 2011;55:1577–1586. doi: 10.1016/j.neuroimage.2011.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Oishi K, Faria A, Jiang H, et al. Atlas-based whole brain white matter analysis using large deformation diffeomorphic metric mapping: application to normal elderly and Alzheimer’s disease participants. Neuroimage. 2009;46:486–499. doi: 10.1016/j.neuroimage.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rohlfing T, Zahr NM, Sullivan EV, Pfefferbaum A. The SRI24 multichannel atlas of normal adult human brain structure. Hum Brain Mapp. 2010;31:798–819. doi: 10.1002/hbm.20906. [DOI] [PMC free article] [PubMed] [Google Scholar]