Mutation rate dynamics in a bacterial population reflect tension between adaptation and genetic load

Abstract

Mutations are the ultimate source of heritable variation for evolution. Understanding how mutation rates themselves evolve is thus essential for quantitatively understanding many evolutionary processes. According to theory, mutation rates should be minimized for well-adapted populations living in stable environments, whereas hypermutators may evolve if conditions change. However, the long-term fate of hypermutators is unknown. Using a phylogenomic approach, we found that an adapting Escherichia coli population that first evolved a mutT hypermutator phenotype was later invaded by two independent lineages with mutY mutations that reduced genome-wide mutation rates. Applying neutral theory to synonymous substitutions, we dated the emergence of these mutations and inferred that the mutT mutation increased the point-mutation rate by ∼150-fold, whereas the mutY mutations reduced the rate by ∼40–60%, with a corresponding decrease in the genetic load. Thus, the long-term fate of the hypermutators was governed by the selective advantage arising from a reduced mutation rate as the potential for further adaptation declined.

Mutations are the ultimate source of heritable variation for evolution. Therefore, understanding how selection can change mutation rates is crucial for quantitatively describing evolutionary processes (1). More mutations are deleterious than beneficial (2), and organisms from bacteria to eukaryotes encode proofreading and repair enzymes that reduce mutation rates (3). If selection for beneficial mutations is weak relative to selection against deleterious mutations, then the rate of adaptation in asexual populations is maximized at some intermediate mutation rate (4). However, when populations encounter new environments, selection for beneficial mutations can be strong (5), and much higher mutation rates may evolve. Indeed, surveys of laboratory populations of microbes (6–10), clinical isolates of bacterial pathogens (11, 12), and some types of eukaryotic tumors (13) have revealed a surprisingly high proportion of lineages that have evolved genetic defects in repair pathways. These hypermutators often have 10- to 100-fold increased mutation rates, and such elevated mutation rates can accelerate the progression of chronic diseases and the evolution of resistance to therapeutic agents.

Hypermutable mutants can become established in asexual populations while they adapt to changed environments owing to their higher per capita probability of discovering rare beneficial mutations compared with nonmutators (14–18). Although hypermutable genotypes should produce beneficial mutations at a higher rate than their less mutable counterparts, they do not necessarily increase the rate of adaptation to a corresponding, or even measurable, degree. In large asexual populations, the waiting time for new beneficial mutations to occur may be short relative to the time required for a mutant to increase from one individual to fixation in the population, assuming the beneficial mutant is not lost by random drift (19); as a consequence, the establishment of a hypermutator may have little effect on the population’s rate of fitness gain (6, 14, 20–22). The rate and effect size of beneficial mutations will also depend on how well adapted the population is to its current environment (20). Moreover, hypermutators are more likely to produce offspring with deleterious or lethal mutations. As a consequence of this tension between adaptation and genetic load, theory predicts that populations of hypermutators should re-evolve lower mutation rates after they have become well adapted to their current environment (23–25). However, genetic constraints might prevent this outcome (e.g., if repair genes have been deleted), and little is known about the long-term fates of hypermutator lineages in any setting. Here, by sequencing the genomes of Escherichia coli from a 20-year experiment, we were able to observe and quantitatively understand the rise and fall in mutation rates in an evolving asexual population.

For over 50,000 generations, 12 populations of E. coli have evolved in and adapted to a glucose-limited minimal medium with daily 1:100 dilutions and regrowth (26). A frozen “fossil record” of these populations has been archived at regular intervals, and the bacteria from these historical populations can be revived and analyzed at any time. We performed whole-genome resequencing to identify the base substitutions in the genomes of 22 evolved clones isolated at various times from one of the populations (Table S1), and we reconstructed their phylogenetic relationships from those mutations. It was reported previously that a hypermutator with a frame-shift mutation in the gene mutT became established in this population between 20,000 and 30,000 generations (27, 28). After the establishment of the hypermutator, we detected subsequent reductions in the mutation rate along two branches of the tree that partially compensated for the hypermutability, and these reductions were confirmed by performing fluctuation tests. Moreover, we identified the molecular–genetic basis for these changes, which were confirmed by inspection of the mutational spectra along the various lineages. Applying a maximum likelihood model, we then estimated the times of emergence of the different mutator alleles and their associated fitness effects.

Results and Discussion

Phylogenomic Analyses and Experimental Measurements of Mutation Rates.

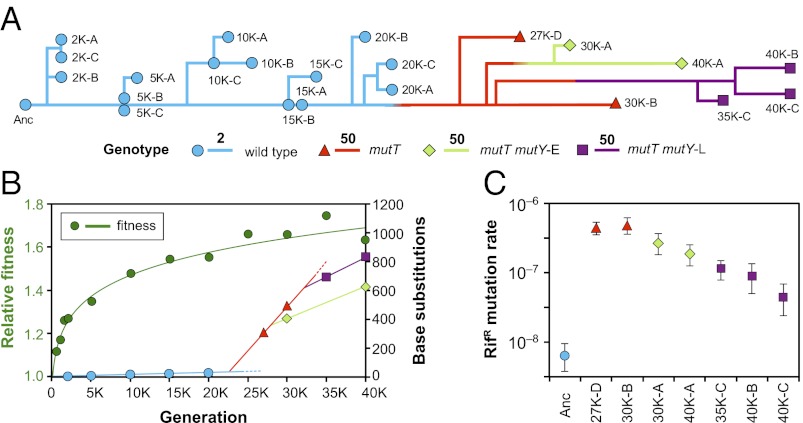
Phylogenetic analysis of the sequenced genomes revealed that the population had diverged into two deeply branched lineages by 30,000 generations and that each lineage persisted until at least 40,000 generations (Fig. 1A). Interestingly, clones that were sampled from both branches at later times accumulated mutations more slowly than did the earlier mutT isolates (Fig. 1B). The rate of accumulation of base substitutions was 62 per thousand generations using clones 27K-D and 30K-B that were sampled at 27,000 and 30,000 generations, respectively. For the later branches shown in green (clones 30K-A and 40K-A) and purple (clones 35K-C, 40K-B, and 40K-C), this rate had declined to 22 and 28 per thousand generations, respectively, which indicate reductions of ∼65% and ∼55%, respectively. However, the mutation in the mutT gene had not reverted to its ancestral state, even though that mutation was in a potentially mutable tract of five cytosines. Experimental measurements of mutation rates using Luria–Delbrück fluctuation tests also indicated substantial reductions in mutation rates along both evolutionary branches (Fig. 1C). In these tests, the two basal mutT clones (27K-D and 30K-B, sampled at 27,000 and 30,000 generations, respectively), on average, produced mutants resistant to the antibiotic rifampicin (Rif^R phenotype) at ∼73 times the rate of the ancestral strain. Mutation rates were significantly lower in later clones; the mutation rate to Rif^R of a 40,000-generation clone on the first branch (40K-A) was reduced by ∼60% compared with the early mutT clones, and rates in two 40,000-generation clones from the other branch (40K-B and 40K-C) were reduced by ∼80–90%.

Fig. 1.

Mutation rate dynamics in an experimental population of E. coli. (A) Phylogenomic tree reconstructed from point mutations in individual clones (designated by letters A to D) isolated at the indicated time points (e.g., 20,000 generations shown as 20K) and rooted at the ancestor. Branches are colored by the presence of ancestral (wild type) or evolved alleles in the mutT and mutY genes and scaled by the number of substitutions. Note the change in scale (bars of length 2 and 50) when the mutT genotype arose after 20,000 generations. (B) Trajectory of mean fitness measured in competition against the ancestral strain is shown in green; the trajectory was fit using log-transformed values of fitness and time (Materials and Methods). Other colored symbols show the total number of point mutations relative to the ancestor in sequenced genomes, with line segments indicating rates of mutation accumulation in each background. Dashed lines indicate apparent extinctions of the ancestral and mutT-only types at unknown times. (C) Rates of mutations conferring rifampicin resistance (Rif^R) in clones estimated from fluctuation tests. Mutation rates were highest in mutT genotypes and decreased in later clones with secondary mutY mutations. Error bars show 95% confidence intervals.

Identification of Antimutator Alleles and Mutational Spectra.

The MutT protein is a hydrolase that purges the cellular nucleotide pool of oxidized guanine nucleotides (8-oxo-dGTP), which can mis-pair with adenine and lead to A:T→C:G (adenine or thymine to cytosine or guanine) transversions after DNA replication. Loss-of-function mutations in mutY, which encodes a DNA repair glycosylase that excises mis-paired bases from DNA helices, also lead to elevated mutation rates on their own (29). However, mutY mutations have an antimutator effect in the context of a MutT defect because MutY mis-repairs 8-oxoG:A base pairs in DNA. The 60% reduction in overall mutation rates reported in mutT mutY double mutants compared with mutT single mutants (29) is similar to the rate changes we observed in both the phylogenomic analysis (Fig. 1B) and fluctuation tests (Fig. 1C). Indeed, genome resequencing showed that different mutY mutations had occurred along the two mutT branches sampled at 40,000 generations (Fig. 1A).

On one branch of the tree, a base substitution changed the amino acid at position 40 in MutY from leucine to tryptophan (L40W), whereas the other branch had a base substitution that introduced a premature termination codon at amino acid 164 (164-stop). We call the L40W allele mutY-E (for early) and the 164-stop mutY-L (for late) because they were first identified in clones sampled at 30,000 and 35,000 generations, respectively. A previous analysis of mixed-population sequencing data (28) found that the mutY-E allele was present in 65% (51–78%; 95% confidence limits) of the population at 30,000 generations and 39% (25–53%) at 40,000 generations. The mutY-L allele was not detected at 30,000 generations, but it constituted 69% (51–83%) of the population at 40,000 generations. The fact that the estimated frequencies for the two mutY alleles total slightly over 100% at 40,000 generations is a consequence of sampling variation at different genomic sites. In any case, these results show the power of combining mixed-population and clonal analyses for understanding the dynamics of genome evolution.

Changes in the mutational spectra along specific branches of the phylogenetic tree also support the hypothesis that the evolved mutY alleles caused the reductions in mutation rates. Mutations after the rise of the mutT hypermutator were highly skewed toward the A:T→C:G transversions typical of this defect (29). This same overall bias dominated along all of the later branches in the tree (Table 1), but the proportion of C:G→A:T substitutions increased from only 2/414 in the initial mutT genetic background to 38/274 in the mutT mutY-E lineage (one-tailed Fisher’s exact test, P = 4 × 10⁻¹⁴) and 24/319 in the mutT mutY-L lineage (P = 1.5 × 10⁻⁷). This secondary signature is characteristic of mutY defects (29). Thus, after the rise of a mutT hypermutator genotype, two distinct mutY alleles with reduced mutation rates independently evolved and invaded this E. coli population, driving the mutT-only lineage extinct (or at least to very low frequency).

Table 1.

Numbers and mutational spectra of base substitutions according to genetic background

Substitution	Ancestor	mutT	mutT mutY-E	mutT mutY-L
A:T→T:A	5 (1, 4, 0)	0	0	0
A:T→C:G	8 (1, 5, 2)	412 (48, 307, 57)	233 (32, 159, 42)	292 (41, 205, 46)
A:T→G:C	6 (0, 2, 4)	0	1 (0, 1, 0)	1 (0, 1, 0)
C:G→T:A	15 (0, 13, 2)	0	2 (1, 1, 0)	2 (1, 1, 0)
C:G→G:C	2 (0, 2, 0)	0	0	0
C:G→A:T	5 (0, 3, 2)	2 (0, 2, 0)	38 (13, 18, 7)	24 (6, 15, 3)
Total	41 (2, 29, 10)	414 (48, 309, 57)	274 (46, 179, 49)	319 (48, 222, 49)

Point mutations along all branches in the phylogenetic tree for each background (i.e., branches of the same color in Fig. 1A). Numbers in parentheses show the separate counts for synonymous, nonsynonymous, and noncoding mutations, respectively.

History of the Population and Mutation Rate Dynamics.

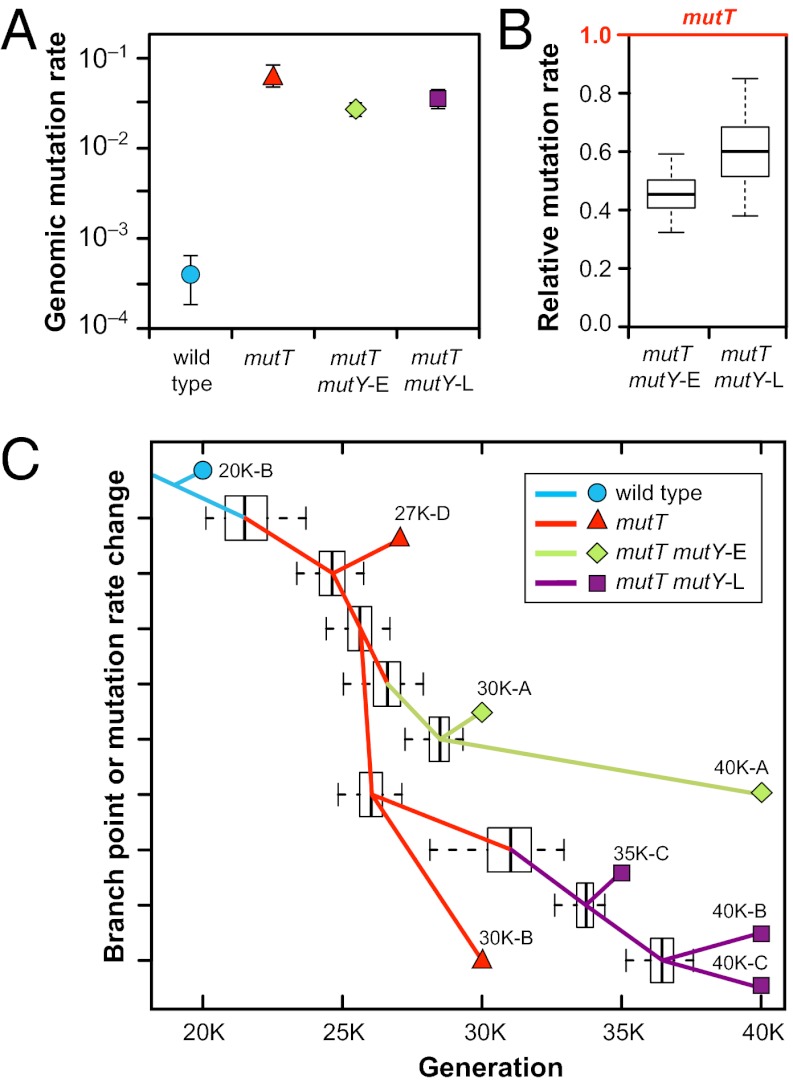
We then used only the synonymous mutations to reconstruct more precisely the history and mutation-rate dynamics in this population (Fig. S1). If one assumes that synonymous mutations are selectively neutral, then the expected number of such mutations in an evolved clone relative to its progenitor is equal to the product of the intrinsic substitution rate, the number of genomic sites at risk for synonymous mutations, and the number of elapsed generations (30, 31). Because we sequenced multiple genomes of clones with each mutator type isolated at different generations, we could use a maximum likelihood approach to estimate simultaneously the mutation rates in each genetic background, the times when each mutation that modified the mutation rate arose, and the times when the various branches diverged in the phylogeny (Tables S2 and S3). This analysis indicates an increase of ∼150-fold in the mutation rate in the mutT background relative to the ancestor (Fig. 2A), followed by secondary reductions of ∼56% and ∼36% in the mutT mutY-E and mutT mutY-L backgrounds, respectively (Fig. 2B and Table 2).

Fig. 2.

Maximum likelihood model of mutation rate dynamics fit to synonymous mutations. (A) Point mutation rate estimates, expressed on a genome-wide basis. The ancestral rate was derived from a previous analysis of nonmutator clones from eight experimental populations (31). Error bars are 95% confidence intervals. (B) Relative mutation rates for two mutY compensatory mutations inferred from the maximum likelihood model and expressed relative to the mutT-only rate. Box plots show the probability distribution of this parameter, where the box shows the upper and lower quartiles, the black line the median, and the whiskers the 95% confidence interval. (C) Timing of changes in mutation rates and phylogenetic branch points. Each box plot shows the probability distribution, in time, for a branch point or change in mutation rate (with quartiles, median, and confidence limits as above). The phylogeny is overlaid on the box plots.

Table 2.

Genomic mutation rates, times of origin for mutator lineages, and genetic loads

Background	μg	To	Ld
mutT	0.061 (0.049–0.088)	21,612 (20,136-23,846)	0.013 (0.011–0.019)
mutT mutY-E	0.027 (0.023–0.032)	26,769 (25,352-28,014)	0.0073 (0.0061–0.0085)
mutT mutY-L	0.039 (0.030–0.048)	30,821 (27,558-32,801)	0.0093 (0.0073–0.012)

Genome-wide point mutation rates, μ_g (generation⁻¹), for each mutator background were inferred from a five-rate model (Table S2) and used to calculate the times of origin, T_o (generations), for the mutators (Fig. 1A) and their genetic loads, L_d (generation⁻¹). All estimates are medians, with 95% confidence intervals shown in parentheses. The ancestor’s mutation rate was previously estimated as 0.00041 per generation based on the accumulation of synonymous substitutions in eight nonmutator lineages (31).

The mutation rates estimated from this analysis agree reasonably well with those based on the fluctuation tests (Fig. 1C). In general, we expect the rates inferred from the phylogenomic data to be more accurate because they encompass the entire genome across many thousands of generations. In contrast, the fluctuation tests focus on a single gene, and the spectrum of possible mutations that confer rifampicin resistance and how they interact with the mutational biases specific to each lineage are unknown. Also, the fluctuation tests were performed on individual clones, which could have acquired other rate-modifying mutations whose effects might not yet be evident in the mutation rates or spectra inferred from the phylogenomic analysis. For example, based on the fluctuation tests, clone 40K-C seems to have a lower mutation rate than clones 35K-C and 40K-B (Fig. 1C), even though all three clones lie on the mutY-L branch (Fig. 1A).

Inferring the Fitness Effects of the Antimutator Alleles.

Parallel evolution is a hallmark of adaptation, and so it is reasonable to infer that the two independent mutations in mutY achieved their high frequencies because they conferred an advantage. However, it is also possible that these mutY mutations were not adaptive, especially given the facts that (i) the mutT lineage had a greatly elevated mutation rate, (ii) the increased mutations caused by mutT hypermutators are A:T→C:G transversions, and (iii) both of the mutations in mutY were A:T→C:G transversions. We therefore sought to quantify the probability that the mutations in mutY could have arisen by chance alone, given the relevant parameters. There are 426 possible A:T→C:G substitutions in the mutY reading frame that would produce either nonsynonymous or nonsense mutations, and we made the conservative assumption that all of them would have led to a loss of function. Then, we used the mutT mutation rate and branching times inferred for the phylogenetic tree (Fig. 2C and Table 2) to estimate the probability of one of these mutations occurring on each relevant branch (i.e., after the mutT-only lineage split at ∼25,633 generations into the two lineages that independently acquired mutY mutations) as soon as, or sooner than, the mutations occurred. These probabilities are 1.3% and 5.7% for the mutY-E and mutY-L clades, respectively. The joint probability of these two events is <0.1%, and we therefore reject this nonadaptive explanation for the parallel evolution of reduced mutation rates. Of course, this calculation is specific to the mutY gene and the circumstances of this population (including branch lengths and mutation rate), and different calculations would be required to calculate the probability of parallel evolution by chance alone for unspecified sets of genes or under other circumstances (32, 33).

Using population–genetic theory, we can estimate the genetic load associated with an elevated mutation rate. Assuming that most nonsynonymous mutations are either neutral or deleterious, whereas most synonymous mutations are neutral, the fraction of nonsynonymous changes that are deleterious can be estimated from the ratio of the rates of nonsynonymous (dN) to synonymous (dS) substitutions. We observed a dN/dS ratio of ∼0.80 for all mutators, implying that ∼20% of all nonsynonymous mutations were deleterious. Confounding factors that can, in principle, alter the observed dN/dS ratio for other reasons include codon bias and selection, GC mutational skew, selection for higher GC content, and bottleneck effects. However, these factors had negligible effects in our study and left no signatures in the evolved genomes (SI Text). Given the estimated mutation rates, the calculated genetic load in the mutT background was 0.013 per generation, and this load was reduced to 0.0073 and 0.0093 with the addition of the mutY-E and mutY-L mutations, respectively (Table 2). These genetic load reductions imply positive selection coefficients of ∼0.57% and ∼0.37% for mutY-E and mutY-L, respectively. Selection can readily act on mutations with effects of this magnitude in the large population studied here (22, 26). Indeed, as the rate of fitness improvement decelerated late in the experiment (Fig. 1B), the fitness benefits of these reductions in genetic load were presumably among the highest that remained available to the evolving population, as evidenced by the simultaneous rise of the two mutY alleles.

We did not attempt to measure these selection coefficients directly for several reasons. First, it is difficult to measure very small selection coefficients, such as those estimated above. Second, it is challenging to produce the necessary isogenic strains in hypermutable backgrounds, owing to secondary mutations that would likely arise during strain construction. Third, the relevant selection coefficients here involve reductions in genetic load, which would require that competing populations achieve the equilibrium between the production of deleterious mutations and their removal by natural selection; but during that time interval, other beneficial mutations may arise that would confound measurements of the selection on the genetic load. It is conceivable that the mutY alleles, besides reducing the genetic load, might confer some additional, hypothetical benefit that accelerated their spread. However, the known function and mechanism of action of the MutY protein do not suggest an obvious advantage (34). In any case, a reduction in genetic load is expected for any mutations that compensate for hypermutators, whereas hypothetical effects of compensatory mutations on other aspects of fitness would depend on the particular genotype and environment.

Synthesis and Perspective.

Our results indicate that the tension between accelerating adaptive evolution and reducing genetic load depends on the fit between a population and its environment, with the relative importance of load reduction increasing as a population becomes well adapted to its circumstances. Many studies have documented the evolution of higher mutation rates as microbial populations adapt to changed environments (6, 8–12, 35). However, despite long-standing theoretical interest (23–25), the complementary prediction—that populations should evolve lower rates once they are adapted to their environments—has received only limited and indirect support (7, 20, 35–38). Some of the limitations of earlier studies include reliance on comparative data (36), lack of information on the genetic basis for mutation rate changes (37, 38), lack of quantification of effects on rates of sequence evolution (20, 37, 38), and the use of strains not well adapted to their environment (7, 37, 38). Moreover, reductions in mutation rates were observed surprisingly early in some studies (7, 37), and even in nonmutator backgrounds (38), and hence, these results could be seen as counterexamples to the prediction that increased mutation rates should evolve during adaptation to changed conditions, rather than as support for the hypothesis that rates decline when populations become well adapted to their environments.

In our view, the paucity of evidence for mutation rate reductions in evolving asexual populations lies not in flaws with the theory, but rather in the necessity for evolution to proceed in a test environment for a sufficiently long time that the scope for further adaptation is reduced to a level commensurate with the load of deleterious mutations. We realize that our experiment, which has run for over 20 years, represents a significant time commitment, but it is also a mere “blink of the eye” with respect to evolution.

Materials and Methods

Long-Term Evolution Experiment and Genome Sampling.

The focal population in this study is designated Ara–1. It is one of 12 E. coli B populations started from a common ancestor and propagated during a long-term evolution experiment (26). We sampled 16 evolved clones (Table S1), two each at generations 2,000 (2K-B and -C), 5,000 (5K-B and -C), 10,000 (10K-B and -C), 15,000 (15K-B and -C), 20,000 (20K-B and -C), 30,000 (30K-A and -B), and 40,000 (40K-B and -C) and one each at generations 27,000 (27K-D) and 35,000 (35K-C). We sequenced their genomes on the Illumina Genome Analyzer platform at the Centre National de Séquençage, Genoscope, with one lane of single-end 36-bp reads per genome. We also analyzed six previously sequenced genomes (27) from clones isolated at generations 2,000 (2K-A), 5,000 (5K-A), 10,000 (10K-A), 15,000 (15K-A), 20,000 (20K-A), and 40,000 (40K-A). Point mutations were identified by comparing sequence reads to the genome of the ancestral strain REL606 (39), using BRESEQ, a pipeline for analyzing resequenced microbial genomes (27, 31, 40).

Fluctuation Tests.

Fluctuation tests were performed in four blocks, and mutation rates and their respective confidence intervals were estimated by applying the Ma–Sandri–Sarkar Maximum Likelihood Estimation Method (41) as implemented in the Fluctuation Analysis Calculator (42). The first block included the ancestral strain only with 60 replicate cultures grown in DM500 (Davis Minimal medium supplemented with 500 μg/mL glucose); 48 cultures were plated on LB+Rifampicin(Rif) agar for mutant selection, and 12 were diluted and plated on LB agar to determine total cell counts. The second block included five evolved strains (30K-A and -B, 40K-A, -B, and -C) with 60 cultures of each grown in DM50 (DM with 50 μg/mL glucose); 48 cultures were plated on LB+Rif agar, and 12 were diluted and plated on LB agar. Most values shown in Fig. 1C are from this block. The third block included three evolved clones (27K-D, 30K-B, and 40K-B), as did the fourth block (30K-B, 35K-C, and 40K-B), with 66 replicate cultures of each strain grown in DM50; 54 cultures were plated on LB+Rif agar, and 12 were diluted and plated on LB agar. The values shown in Fig. 1C for the 27K-D and 35K-C clones are from these blocks, which were performed to confirm that their mutation rates were similar to other clones with the same mutator background; strains 30K-B and 40K-B were included as controls to facilitate comparisons with the other blocks. The estimated mutation rates were 3.7 × 10⁻⁷ (block 3) and 3.7 × 10⁻⁷ (block 4) for 30K-B, and 0.9 × 10⁻⁷ (block 3) and 1.1 × 10⁻⁷ (block 4) for 40K-B; neither difference was significant at the 0.05 level. The rate estimated for the 27K-D clone bearing the mutT allele differed significantly from the initially tested mutT clone 30K-B (P < 0.001), but the difference was only 1.3-fold and thus small compared with the difference between these mutT clones and the mutT mutY-L clone 40K-B (4.8- and 6.0-fold, respectively; each P < 0.001). Also, the mutation rate estimated for the 35K-C clone bearing the mutT mutY-L alleles was 1.1-fold higher than the rate for the 40K-B mutT mutY-L clone, a difference that was not significant (P = 0.30), whereas the rates for both of these mutT mutY-L clones differed significantly from the mutT-only 30K-B clone (by 3.4- and 3.2-fold, respectively; each P < 0.001). Thus, different clones with the same mutator genotype had similar or equal mutation rates.

Fitness Assays.

We estimated the mean fitness of population samples relative to the ancestor by performing competitions under the same conditions used during the evolution experiment, as described elsewhere (26). From these data, we calculated the net growth rates of each competitor, and we computed relative fitness as the ratio of the growth rate of the evolved population to that of the ancestor. The competitors were distinguished by using an arabinose-utilization marker that is neutral in these conditions. This procedure was performed with 20-fold replication for the ancestral clone and with 10-fold replication for evolved samples. Using the R package (43), a best-fit trajectory was obtained for the following model:

where W is mean fitness, a and b are model parameters, and t is time in generations. From these data, we estimated a = 0.101815 and b = 0.004284 per generation, with a correlation of 0.9898 between the predicted value and the mean of the measurements at the corresponding generation.

Phylogenetic Tree Reconstruction.

Our dataset was unusual because it included ancestral and derived genomes with known temporal relationships. Mutations were treated as discrete characters, and the phylogeny (Fig. 1A) was inferred by using maximum parsimony in Molecular Evolutionary Genetics Analysis version 4.0 (44). We represented the first half of the resulting tree relative to the line of descent leading from the ancestor to the late-generation clones (Fig. 1A). The rise of the mutT mutator dramatically changed the branch lengths after 20,000 generations, and so we adjusted the scale of genetic distances to the nonmutator and mutator backgrounds (Fig. 1A). For each evolved clone, we calculated its distance relative to the ancestor as the number of all point-mutation differences, and trend lines were fit separately for each background (Fig. 1B).

Estimating Genomic Mutation Rates and Times of Origin of Mutator Alleles.

We estimated the total genomic point-mutation rate per generation, μ, along three specific branches of the phylogenetic tree by using the genome sequences of pairs of evolved clones with each of the three mutator genotypes that were isolated from the population at different generations. We used the following equations:

and therefore

where T₁ and T₂ are the ages, in generations, of the two clones; t is the age of their most recent common ancestor; and n₁ and n₂ are the number of synonymous mutations specific to each clone. We applied this approach using only the A:T→C:G and C:G→A:T base substitutions because they were the classes of mutations clearly (and typically) affected by the mutT and mutY alleles (Table 1). From these data, we estimated the genomic point-mutation rates for the three evolved mutT mutY genetic backgrounds (Table 2). The results of this analysis would not be substantively affected by using all of the point mutations instead of only the two classes considered here. For the mutator backgrounds, there are a total of 142 synonymous mutations, and only two belong to the other four mutation classes combined (Table 1). With the penalty for additional parameters required to fit an extended model with one or more additional rates, the extended model would be no better than the model with only the two classes of mutation.

Using a Poisson framework, we can derive from that model a maximum likelihood estimate of the time of origin of the mutT allele. To do so, we added to the previous model a branch with n₀ mutations leading to the emergence of mutT at time x. The following equations were derived:

with P being the Poisson expectation, and:

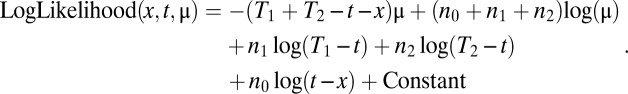This estimate can be easily optimized for all criteria. The maximum likelihood solution provides a mutation rate per generation, μ, similar to the previous estimate and indicates that the evolved mutT allele arose around generation 21,612 (Table 2).

However, this approach does not make full use of our data, nor does it allow estimation of the transition times to the mutY alleles. Therefore, we also used a Metropolis Hastings Monte Carlo Markov chain approach as follows. The topology of the phylogeny was estimated using the genome sequences as before, but the branch lengths and mutation rates were estimated by using the actual ages of the evolved clones sampled at 27K, 30K, 35K, and 40K generations. By using the numbers and types of synonymous mutations along all branches, we could estimate the likelihood of a particular combination of inner node ages, mutation rates, and transitions in mutation rates with a Poisson model. Three transition times were estimated including from the nonmutator to mutT, from mutT to mutT mutY-E, and from mutT to mutT mutY-L. We imposed a lower bound for the origin of the mutT allele at 20,000 generations based on the line of descent (Fig. 1A).

Depending on the model, we estimated two, three, or five mutation rates including the impact of the three mutator backgrounds on A:T→C:G and C:G→A:T mutations (Table S2). All other rates were set to zero because the mutations were observed rarely, if ever, on these backgrounds. Under the two-rate model, all three mutator backgrounds had the same A:T→C:G mutation rate and the two mutY alleles increased the C:G→A:T mutation rate from zero to the same new rate. In the three-rate model, the two mutY alleles were identical to one another but also differed from the mutT-only background in their A:T→C:G mutation rate. Finally, under the five-rate model, the two mutY alleles differed from one another in their A:T→C:G and C:G→A:T mutation rates. Along the Markov chain, a random set of up to 10 parameters was modified simultaneously with a Gaussian shift. Depending on the likelihood of the data with one set of parameters, a new set was either accepted (replacing the former one) or rejected using Metropolis Hastings criteria. The variance of the Gaussian distribution modifying the parameters was set such that the acceptance rate was ∼23%. After a burn-in period of 5 × 10⁶ sampling steps, the state of the Markov chain was recorded every 2,000th step for another 5 × 10⁶ samples. The distribution of these states was used to infer the distribution of the model parameters. Several initial conditions were used and convergence was achieved. Using the GC content of the genome and the number of synonymous sites for each type of mutation, we converted the substitution rates and types of mutation into genomic mutation rates for each genetic background (Table 2). Importantly, a comparison of the two- and three-rate models strongly supports different genomic rates for the mutT-only and the mutT mutY backgrounds (Table S2). The five-rate model suggests a difference between the mutT mutY-E and mutT mutY-L backgrounds (Fig. S2) but it did not provide a better fit than the three-rate model after imposing the penalty for additional parameters (Table S2). The fluctuation tests also showed different mutation rates for the mutT mutY-E and mutT mutY-L backgrounds (Fig. 1C), although that difference was in the opposite direction to the difference inferred from the phylogenomic analysis (Fig. S2).

To gain further insight into the possible differences between the mutT mutY-E and mutT mutY-L backgrounds, we applied the same two-, three-, and five-mutation-rate models to the set of all point mutations, including nonsynonymous and noncoding ones. On the one hand, we expect selection to have a much stronger impact on nonsynonymous and noncoding mutations than on synonymous mutations, and therefore pooling them to estimate mutation rates is problematic. On the other hand, we gain substantial statistical power by using all mutations because synonymous substitutions were only a small fraction of all point mutations (Table 1). When using all point mutations, the five-rate model gave a statistically better fit to the data than the best three-rate model, even with the penalty for additional parameters (Table S3). We therefore chose to use the five-rate model over the three-rate model, but we used the rates based on synonymous changes only to minimize the effect of selection on the estimation of mutation rates.

Estimating Genetic Load and Strength of Selection to Reduce Mutation Rates.

To estimate the fitness cost arising from deleterious mutations in the mutT background, we first calculated the number of nonsynonymous sites that experienced negative selection. If mutations at synonymous sites are neutral and mutations at nonsynonymous sites are either neutral or deleterious, then the fraction f_d of nonsynonymous sites where mutations are deleterious can be estimated from the ratio of synonymous to nonsynonymous mutations that accumulate along a branch relative to the numbers of sites at risk for those mutations. Let s and n be the numbers of synonymous and nonsynonymous mutations, respectively, observed along a branch of length T generations, and let S and N be the corresponding numbers of synonymous and nonsynonymous sites. Given the mutation rate μ per site per generation, then:

By substituting s/S for μT and rearranging terms, we obtain:

where K_a and K_s are the per-site rates for the accumulation of nonsynonymous and synonymous mutations, respectively. The genome-wide load L_d caused by deleterious point mutations is then calculated as:

where the mutation rate is estimated by the per-generation rate of accumulation of synonymous mutations. This load corresponds to the fraction of individuals lost each generation because they have acquired a deleterious mutation. This calculation may lead to a slight underestimate of the load if some deleterious mutations, not yet eliminated by selection, are included among the observed nonsynonymous mutations (n). Similarly, the load will be underestimated to the extent that some of the observed nonsynonymous mutations are beneficial. However, the number of beneficial mutations should be small because we are estimating the load only during the later generations of the long-term evolution experiment, after the rate of fitness improvement had greatly decelerated (Fig. 1B), indicating that beneficial mutations were fewer and of smaller effect than in the early generations of the experiment. In particular, we considered the mutations that had accumulated only in the mutT mutY backgrounds (using clones 30K-A, 35K-C, 40K-A, 40K-B, and 40K-C). These mutators produced a strongly biased spectrum of mutations, and therefore, we calculated K_a and K_s for the two types of mutation with sufficient numbers of synonymous changes (A:T→C:G and C:G→A:T). However, selection acting on the mutations should be independent of the mechanisms that produced them. Thus, we could infer selection against deleterious mutations using the mutT mutY clones and apply that information to the mutT background, while correcting for their different mutation rates and spectra. Taking into account the sum of branches for all mutT mutY clones, we found:

Using our previous estimates of the mutation rates for each background, we can then estimate the genetic load (Table 2) as follows: