Migration of cells in a social context

Abstract

In multicellular organisms and complex ecosystems, cells migrate in a social context. Whereas this is essential for the basic processes of life, the influence of neighboring cells on the individual remains poorly understood. Previous work on isolated cells has observed a stereotypical migratory behavior characterized by short-time directional persistence with long-time random movement. We discovered a much richer dynamic in the social context, with significant variations in directionality, displacement, and speed, which are all modulated by local cell density. We developed a mathematical model based on the experimentally identified “cellular traffic rules” and basic physics that revealed that these emergent behaviors are caused by the interplay of single-cell properties and intercellular interactions, the latter being dominated by a pseudopod formation bias mediated by secreted chemicals and pseudopod collapse following collisions. The model demonstrates how aspects of complex biology can be explained by simple rules of physics and constitutes a rapid test bed for future studies of collective migration of individual cells.

Collective migration, from migrating cells in tissue (1–3) to swarming insects (4) to flocks of birds (5) and pedestrians in heavy traffic (6), constitutes one of the most fascinating spectacles in nature. In addition to its aesthetic qualities, social cell migration is involved in embryonic development (7), wound healing (8), and immune response (9), and unregulated migration leads to disease, including cancer metastasis (10). Previous work on single-cell migration has focused on isolated (11–20) or strongly polarized and aligning (21, 22) cell types, mostly using population-averaged bulk assays (23) or simple observations in a social context (2, 3). However, strongly cross-correlated cell motion and collective substrate deformation has been found to arise in mechanically interlinked cells transmitting forces through both cell–cell linkages and the substrate (24–29). These studies revealed useful information on cell migration, but because in general the relevant interactions in a social context and their relative importance are not established, migratory behavior of cells in a social context remains as one of the major unresolved problems in biology (30). Furthermore, striking social effects such as highly sensitive collective responses in a number of sensing systems [e.g., quorum sensing (31, 32) and onset of collective behavior in Dictyostelium discoideum (33)] mediated by increased levels of cell-secreted signals in higher cell density indicate that mechanical links are not necessary for collective behavior. At the subcellular level, many types of nonswimming motile cells involved in multicellular biology [e.g., fibroblasts, Dictyostelium, and neutrophils (13, 14, 16–18)] have been found to transmit traction force to the substrate by intracellularly polymerizing their cytoskeletons in dynamically formed membrane protrusions known as pseudopodia. However, whether the social context changes this, mechanisms by which the social context manifests itself, and the implications of being close to neighboring cells all remain unexplored.

Here we shed light on these fundamental questions using a combination of high-throughput microfluidic cell culture (34) of 3T3 fibroblast cells expressing fluorescent fusion proteins, time-lapse microscopy with subcellular resolution, and physical modeling (SI Appendix, Materials and Methods and Model Details). Contrary to previous work (22, 24–26, 29), these cells form neither 2D sheets nor 3D structures, nor are they highly polarized, and their single-cell migratory behavior is established (13, 14, 16). The microfluidic cell culture platform hosts independent and isolated culture conditions in each of the isolated 96 polymethylsiloxane (PDMS) chambers (34-nL volume) that mimic physiological conditions more plausibly than traditional cell-culture environments in which concentrations of, for instance, secreted signaling molecules are diluted into large volumes of surrounding fluid. Using only freshly thawed cells, we cultured them at densities ranging from 15 to ∼100% confluence in up to 24 parallel chambers at a time; more than 8,000 cells were quantified, yielding hundreds of thousands of data points from a total of only five experimental runs. Experiments on any given density were repeated at least once on different chips, and we studied different densities in parallel on each chip (SI Appendix, Table S1). We replaced the chamber volume at time t = 0, sealed the chamber using the microfluidic membrane valves, and imaged the cells every 4–6 min for 5–6 h, focusing on a region of ∼500 μm × 700 μm in the center of the chamber to avoid edge effects, which contained a population consisting of between 36 and 246 cells [corresponding to an average minimum nucleus–nucleus distance in the range of approximately one to three cell diameters, which on average is 41.7 μm (SI Appendix, Fig. S12A)]. Using different fluorescent fusion proteins to image the nuclei (green) and cytosols (red) (Fig. 1A) coupled with high imaging resolution allowed us to track single-cell migration behavior and pseudopodia, producing a very comprehensive dataset; such detailed quantitative measurements of single-cell behavior are emerging as a strong tool for studying biological systems, as recently exemplified for cell cycle stability (35) and inflammatory signaling (36).

Fig. 1.

Trajectories of the cells generated during the first 200 min of an experiment. (A) Trajectories (yellow) displayed on top of the fluorescence image illustrating the different fusion proteins used for the cytosols (red) and nuclei (green). (B) Trajectories can be nominally straight, curve, or display little apparent directionality. The vectorial sum of the pseudopodia of the cell (marked by red in insets) predicts the observed movement, because each pseudopod applies nominally the same force (20).

Results

Quantitative Cell Migration Characteristics.

Our measurements reveal the migration characteristics of cells at different densities. Although all cells move (Fig. 1A and SI Appendix, Fig. S2 and Table S2 and Movie S1) with no preferred overall direction (SI Appendix, Fig. S3), we find large diversity with negligible cross-correlation in the migratory behavior of the cells at the same density (Figs. 1 and 2E and SI Appendix, Fig. S2): Some cells move along almost straight lines, other follow curved paths, and yet others traverse very short distances with little apparent directionality (Fig. 1B). This continuum of different migratory behaviors, which is very different from the stereotyped single-cell behavior found for isolated cells (11, 13, 14), suggests that there is a strong effect of the social context on the migration of the individual, even in the absence of cell–cell linkages (24–26). To fully understand this effect, including whether it is due to inherent cell–cell motility variations or is an emergent group property, we quantified all aspects of the migration using a number of cooperating statistical measures that together fully characterize the migration.

Fig. 2.

Experimental observations of cell migration and pseudopodia. (A) Single-cell speed distribution, with inset showing speed vs. time for four single cells. (B) Average single-cell speed distribution (blue; error bars indicate SD) is well fitted by a generalized extreme value (GEV) distribution characterized by the location parameter m, the scale parameter s, and the shape parameter ξ. (C) Population distribution of single-cell maximum path distance (MPD). (D) Chamber-average directional autocorrelation (blue circles) and fit (orange line). Also shown are single-cell autocorrelations from two sample cells moving nominally straight (lines). The SD of the distribution decays from ±0.20 min close to τ_lag = 0 to ± = 0.01 at τ_lag = 200 min (SI Appendix, Fig. S5). (E–H) Effect of density on collective cellular migration; dashed lines in F–H indicate results for isolated cells extracted from ref. 11 (compare with SI Appendix, Fig. S4). (E) Examples of trajectories (compare with SI Appendix, Fig. S2) and (F) the corresponding average directional autocorrelations that follow the same exponential decay (Inset). (G) Weight ϕ and persistence time τ_p from least squares fits of average directional autocorrelations to as a function of the average minimum nucleus-nucleus distance in the chamber showing that persistence time τ_p is not affected by the changing density whereas the weight factor ϕ decreases due to higher collision rate. (H) Location m, scale s, and shape ξ from least squares fits of average single-cell speed distributions to the GEV distribution remains constant across densities. (I) Time periods of contact for colliding cell pairs (combined for all densities) is heavily dominated by short times, and the distribution is independent of cell density (SI Appendix, Fig. S8A). Also shown are the actual trajectories of two colliding cells (blue and green), with red arrows indicating direction of motion. (J) Pseudopod formation angle Δα with the current direction of motion (pooled across densities) shows a clear a clear preference of pseudopod formation in the current direction of motion, although pseudopodia are observed to form at all angles. This distribution is independent of cell density (SI Appendix, Fig. S8C). (K) Position and angle of pseudopod formation Δθ in relation to the nearest neighbor cell. At time t = 0, the entire volume of the microfluidic chamber is replaced with fresh media, effectively removing any chemokine background and allowing new chemokine gradients to be established (see schematic to the right). The cells overwhelmingly move to the nearest neighbor during the first 20 min after media replacement but only mildly so (and only when the nearest neighbor is very close) after 60 min, indicating that secreted chemokines induce pseudopod formation (SI Appendix).

We first focus on an experiment at intermediate cell density to introduce our statistical measures and illustrate our key findings. The speed of the individual cell fluctuates substantially as a function of time (Fig. 2A Inset) with similar single-cell speed distributions (Fig. 2A), and the average single-cell distribution from one experiment displays a distinct non-Gaussian tail (Fig. 2B) that has previously been shown to be a general feature of non-sheet-forming motile cells (37). The existence of similar non-Gaussian single-cell speed distributions suggests by the central limit theorem that each cell does not have an inherent velocity scale, but rather that cell speed is a dependent variable. The simultaneous observations of fluctuating single-cell speed and cell velocity being a dependent variable is consistent with pseudopodia-driven motility (SI Appendix).

To quantify the variations in total space sampled by the individuals we introduce the “maximum path distance” (MPD), defined as the maximum distance between any two points on the trajectory of the individual cell. This measure, which is equivalent to the span dimension of polymer physics (38), displayed large variations across the population, with large and small MPD values corresponding to cells moving nominally straight and cells that displace themselves small distances, respectively (MPD is nontrivially related to variations in single-cell trajectory curvature).

The observed variations in trajectories could be caused by a relative lack of collisions; however, we observed cells moving nominally straight even though they were in direct contact with other cells, as well as cells without direct contact with other cells displaying little long-term directionality (Movie S1). This indicates that collisions are not solely responsible for the variations in migratory behavior, and so to further investigate this single-cell directionality, we compute the directional autocorrelation of the cellular trajectories using the unit vectors in the direction of instantaneous velocity (SI Appendix, Eq. S3 and Fig. 2D). This measure describes the average alignment of the direction of motion of the same cell over time and therefore measures the persistence of the direction of motion. Using the unit vectors in the direction of instantaneous velocity as opposed to the velocity vectors themselves removes any bias from the fluctuating speed and sets the range from 0 (no correlation) to 1 (complete correlation). The chamber-mean directional autocorrelation, which is representative of the majority of the cells (outliers only nominally affect the mean because the kurtosis is everywhere low; SI Appendix, Fig. S5), shows that the instantaneous step taken by each cell is positively correlated with the previous steps (Fig. 2D). The first sharp drop-off between the first and second time points occurs because changes in directionality are measured only every 4–6 min, and the rest of the data are well described by a decaying exponential . Here, the persistence time of directionality τ_p and the weight ϕ (varying from 0 to 1) describe, respectively, the time for the average cell to randomize its direction and the extent of directional motion in the chamber, with higher values of ϕ indicating a larger fraction of directionally persistent cells. For the present experiment we found ϕ = 0.46 and τ_p = 69 min.

Varying the cell density, we continue to observe straight-moving cells at all densities (Fig. 2E) even though each cell at intermediate and high densities experiences many collisions (and the ratio of cell surface area to total available chamber area is around 0.8 at all times; SI Appendix). The fraction of directionally persistent cells decreases at higher densities, but the persistence time of the individual cells remains essentially constant. This is illustrated by the decrease of the weight ϕ and the constancy of persistence time of directionality τ_p in Fig. 2 F and G. The average single-cell speed distribution is also independent of density, and this is well-fitted by generalized extreme value (GEV) distribution, which forms a natural parameterization (Fig. 2H; example fit shown in Fig. 2B). Both our measurements of speed distribution and the low-density limit of the directional autocorrelation agree with previous results for human fibroblasts (11) (the latter indicated by dashed lines in Fig. 2 F–H; compare with SI Appendix, Fig. S4). These findings indicate that the observed directionality does not depend on the fluctuating speed of the single cell, and the small variations in τ_p both within and across densities suggests that the directional persistence of motion, unlike cell speed and trajectory, is an inherent property of the cell’s motility apparatus (i.e., internal polarization). Furthermore, the convergence of all our statistical measures to the level of isolated cells at determines the critical density where the social context becomes important.

Pseudopod Formation and Lifetime Is Affected by Social Context.

We verified that the cell migration in the social context is also mediated by pseudopodia (Fig. 1B and Movie S2), and so to probe the origin of the diverse cellular migratory behavior we therefore next investigated their pseudopodia. Colliding pseudopodia of different cells transiently remain in contact before they collapse (39) in a process known as contact inhibition of locomotion (2) (Movie S3), which is presumably achieved by locally depolymerizing the actin cytoskeleton with associated cessation of the local force. The distribution of contact times is strongly dominated by short times and exhibits no dependence of density (Fig. 2I and SI Appendix, Fig. S8A). We found a distribution of pseudopod lifetimes with a mean of 11.8 min (SI Appendix, Fig. S6A), so the directional persistence of ∼50 min indicated by the autocorrelation analysis (Fig. 2 D and G) can only be maintained by the cells through ordered pseudopod formation. Further investigations indicated that pseudopod formation is dominated by independent biases by the current direction of motion (Fig. 2J) and chemicals (chemokine) secreted by the cells (Fig. 2K and SI Appendix, Table S2). Evidence of the former was found by computing the angle between the current cellular direction of motion and the position of pseudopod formation (Fig. 2J), which displayed a clear bias for the present direction of motion that is probably mediated by an internal polarization of key molecules (40), whereas evidence for the latter was found by studying the influence of neighbor cells in biasing pseudopod formation: Pseudopodia formed exclusively toward the nearest neighbor cell during the first 20 min after medium replacement (Fig. 2K Upper), but much less so when the analysis was redone starting 60 min after replacement (except when the neighbor is very close; Fig. 2K Lower). The effect was reproduced following additional media replacements in separate control experiments (SI Appendix, Fig. S9). Because these cells both posses chemotactic ability and furthermore are known to secrete some chemokines (SI Appendix), this effect is most likely caused by one or several secreted chemokine(s), as evidenced by the decrease of the response at later times except very close to neighbors and corroborated by the fact that most chemokine molecules have diffusivities on the order 10⁻¹⁰ m²· s⁻¹, which sets the time scale for chamber filling to ∼40 min. In other words, the secreted chemokines will have saturated the chamber by 40 min, effectively reducing chemokine gradient depths and the signal-to-noise ratio of chemokine receptor activity. Moreover, the constant base level of pseudopod formation observed in our investigation of directional bias (Fig. 2J) further illustrates the existence of an additional and independent pseudopod formation biasing system that on average is independent of the current direction of motion, and therefore is likely achieved by the chemokine bias. Although we did observe new pseudopods arising from splitting of existing pseudopodia, similar to the predominant origin of pseudopods observed in isolated cells (14), this was found to be secondary to the biased de novo formation of pseudopods just described (SI Appendix, Fig. S7). These observations indicate that the motile apparatus of the individual cell is centered around maintaining a certain direction through an internally controlled pseudopod formation bias (polarization), and that being in a social context introduces a second mechanism based on chemokine-mediated biasing, similar to findings in a previous report for Dictyostelium cells (41), as well as a higher frequency of pseudopod formation due to collisions.

Physical Model.

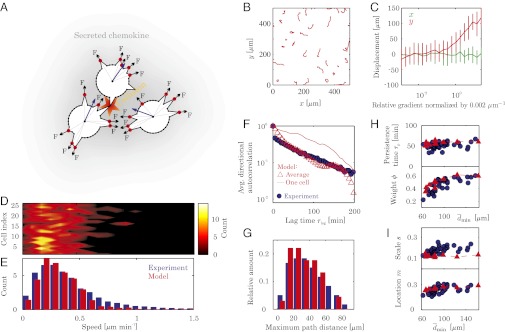
To investigate whether these observed traffic rules on the individual cell level indeed do cause the very varied collective motion we observed, we formulated an agent-based mathematical model using the simplest physically reasonable assumptions for the motion of the individual cell based on three types of input: (i) our own pseudopod observations, (ii) previous experimental studies on chemotaxis of isolated cells, and (iii) Newton’s second law of particle motion (SI Appendix, Model Details). This model, which can be considered an extension of the Vicsek model (21, 22, 42), exploits known cellular biophysics to simulate our experiments with a few hundred cells, a regime that is inaccessible to continuum modeling (43, 44). Model cells (Fig. 3A) dynamically form pseudopodia that each apply a force F_i of constant magnitude F_o radially away from the nucleus. In a time interval Δt the resultant force moves the cell a distance Δx, or equivalently imparts a velocity v = Δx/Δt given by

Fig. 3.

Model formulation and predictions (model, red; experiments, blue). Experimental data are the same as in Fig. 2. (A) Single cells move by dynamically and stochastically forming pseudopodia (red) while they secrete chemokine, with each pseudopod providing a force, and colliding pseudopodia collapse. (B) Example model trajectories. (C) Average displacement in a 300-min simulation for different relative gradients (the gradient is applied only in the y direction) illustrate that model cells reliably respond to gradients above 0.002 μm⋅m⁻¹, as experimentally observed by Melvin et al. (16). The simulation was repeated 20 times for a single cell at each gradient level and error bars indicate SD. (D) Single-cell speed distributions (compare with Fig. 2A). (E) Average single-cell speed distribution, showing excellent agreement with experiments. (F) Chamber-averaged directional autocorrelation and one single-cell autocorrelation from a cell moving nominally straight (compare with Fig. 2D; compare with SI Appendix, Fig. S5. (G) Population distribution of maximum path distance (blue, experiment; red, model). (H and I) Model results across densities with the latter expressed by the average minimum cell-cell distance (red, model; blue, experiment). (H) Weight ϕ and persistence time τ_p for the fit to . (I) Location parameter m and scale parameter s in fit of average speed distribution to a GEV distribution. The shape parameter ξ (SI Appendix, Fig. S11), describing the tail of the distribution, is not well captured by the model because it underpredicts this part of the speed distribution, as seen in E.

where γ is a friction coefficient assumed to be identical for all model cells. Pseudopod formation is biased by the current direction of motion and a spatiotemporal field of chemokine concentration secreted by all cells. We use biased stochastic pseudopod activation because of the large thermal fluctuations in the low concentrations of intra- and extracellular chemicals. Touching pseudopodia of colliding cells collapse, and their local forces stop because of contact inhibition of locomotion. We furthermore assume chemokine secretion is identical for all cells; that force, collision times, and chemokine response function is the same for all pseudopodia; and that this function is a Hill function of the local relative chemokine concentration (Fig. 3C). All model parameters are determined either directly from the data (such as Fig. 2 I and J) or from reported literature results, except for the cell friction coefficient γ, of which no reliable measurements exist. We determined γ from the ensemble average of velocity distribution data by fitting one simulation to one experiment; having determined this single parameter the model predicts all statistical aspects of the collective motion. This is shown below through a number of statistical tests. Although simpler theoretical models have been presented in the past with the objective of investigating certain traits of the collective migration phenomena (21, 22, 37, 42–45), none of these models is able to simultaneously account for a wide variety of the migration data such as ours, and our model thus provides one of the simplest ways of incorporating all of our observations in a physically transparent formulation.

Comparison with Experiments.

The model results are summarized in Fig. 3 and demonstrate quantitative agreement with the experiments in terms of single-cell speeds (Fig. 3 D and E), trajectories (Fig. 3 B and G), and directionality (Fig. 3F), thereby verifying our experimentally derived hypotheses of the role of the social interactions on motility (SI Appendix, Fig. S10 and Movie S4). The model quantitatively reproduces across cell densities—with a single value of γ—that the individual cells have the same nonnormal speed distribution (Fig. 3D) with an average that is similar to the experimental average (Fig. 3E); the exponentially decaying autocorrelation (Fig. 3F) including the changes in the weight factor ϕ, indicating the importance of the social interactions; and both the shape and range of the distribution of maximum path distances (Fig. 3G). The model also predicts the existence of cells moving along almost straight lines for the entire experiment (Fig. 3B) and the maximum path distance for these cells [largest single-cell measurements of maximum path distances are the same for model and experiment Fig. 3G)], but it does underpredict the ratio of these cells, as indicated by smaller tail of model predictions in Fig. 3G. In addition, the model value of γ = 39 kg⋅s⁻¹ is in fair agreement with an estimate of γ ≈ 29 kg⋅s⁻¹ extracted from ref. 20 but is roughly one order of magnitude greater than an estimate from endothelial cells and a Dictyostelium slug (46) (SI Appendix). Although the model captures many features of our single-cell microscopy data, it falls short of perfectly reproducing the tail of the speed distribution (Fig. 3 D and E and SI Appendix, Fig. S11), likely because of the assumption of identical and time-independent pseudopod forces (SI Appendix). The model furthermore also does not precisely capture the exact shape of the average directional autocorrelations (Fig. 3F), indicating that directional persistence is likely achieved through a more complex machinery than is assumed in the model.

Discussion

The agreement of model predictions with experimental data for all of the emergent properties presented in Fig. 3 suggests that the subprocesses included in the model govern the motility. We therefore arrive at the following explanations for our observations: The dynamically changing positions of pseudopodia cause large fluctuations in speed at all densities, whereas directional persistence is achieved primarily by the directional bias of pseudopod formation but heavily influenced by both collisions and the secreted chemokine. The cells at low density are effectively isolated as they rarely collide and the nominally isotropic chemokine field therefore has little influence on the positions of new pseudopodia, whereas high collision rates at high densities lead to constant randomization of pseudopodia positions and low ϕ. At any density, straight-moving cells execute this motile behavior because their lateral pseudopodia are more often suppressed by lateral collisions with other cells or abruptly changing, large chemokine gradients. Cells displaying little overall directionality constantly have their direction of motion cut off, leading to many collisions, whereas curling cells experience few collisions and/or a clear and slowly moving chemokine bias. The observed continuum of different trajectories is therefore a direct consequence of the fluctuating near-cell environment and is no more surprising than similar observations of very varied trajectories of many interacting bodies obeying Newtonian mechanics. The model thus provides a comprehensible description of social cell migration that captures all of the complexity formulated in terms of biophysically well-defined single-cell quantities and, furthermore, illustrates how very complex biological behavior emerges from simple interaction rules.

Contrary to several other cell types, such as keratocytes (22), 3T3 fibroblast cells do not exhibit large-scale multicellular organization such as flocking (21). Fibroblasts deviate from these flocking cell types by not having strong local alignment of the neighbors, which therefore must be considered critical in achieving flocking. We nonetheless hypothesize that the observed effects of the neighboring cells on single-cell migration is highly relevant at physiological conditions. Within a population, the high collision rate continuously randomizes the directionality of the individual cells, so that on average there will always be cells moving away from the population. In the presence of an external signal, some of these boundary cells will be correctly aligned with this signal and will reliably move up the gradient, with the directional persistence providing the initial stabilization of the movement away from the population. This mechanism provides a directionally isotropic and fast sensor of external signals for the population, even though the single-cell polarizations vary and single-cell realignment with the external signal would occur on the time scale of directional persistence (τ_p). Whereas this social effect is fundamentally different from flocking and other social effects such as quorum sensing, it is another example of how nature achieves group-level dynamics of ignorant individuals for biological function beyond the control of the individuals by simply modulating the signal at the level of the individual through increased cell density. This mechanism could be a general biological principle underlying emerging population behavior, yet the underpinnings, limits, and consequences remain to be investigated.

In summary, our investigations of social cell migration for thousands of cells at different densities have revealed a diverse migratory behavior that is largely controlled by the changing environment: Whereas the single cell tries to maintain its current direction of motion through preferentially forming pseudopodia in this direction, secreted chemokine-induced pseudopod formation along with collisions lead to pseudopod collapse, resulting in much more complex migratory behaviors than those reported for isolated cells, even in the absence of cell–cell variations. A simple model based on these observations quantitatively reproduces most migration behaviors across densities, including the existence of outliers, illustrating that these are the intercellular rules governing migration. In addition to their biological significance, our findings illustrate how complex biological behavior arises as a physical consequence of noisy single-cell behavior and interactions among the individuals, open a path for the derivation of continuum theory, and illustrate the importance of single-cell data in understanding such behavior.

Materials and Methods

Cell Line and Microfluidic Cell Culture Experiments.

We used newly thawed p65^−/− mouse fibroblast (3T3) cells expressing the cytosolic fluorescent fusion protein p65-DsRed under control of the endogenous mouse p65 promoter as well as the nuclear marker H2B-GFP driven by the human ubiquitin C promoter. Cells were seeded at densities from 4,000−40,000 cells cm⁻² (∼40—400 cells per chamber) into microfluidic chambers and the external conditions were set to standard culture conditions [5% (vol/vol) CO₂ and 37 °C external temperature] and maintained at this level. To conduct the experiments we replaced the chamber volume with fresh medium and sealed the chamber (the cells remained in the same media during the entire experiment; some cells were also exposed to TNF-α). The cells were imaged at a constant rate either every 4 or 6 min in both GFP and DsRed fluorescence channels during the entire experiment (5–6 h). Details are given in SI Appendix, Materials and Methods.

Automated Image Analysis.

Automated image analysis algorithms used to obtain cell trajectories and pseudopod statistics are detailed in SI Appendix, Materials and Methods.

Model.

Details of model development and implementation in MATLAB are given in SI Appendix, Model Details.