Conformal surface plasmons propagating on ultrathin and flexible films

Abstract

Surface plasmon polaritons (SPPs) are localized surface electromagnetic waves that propagate along the interface between a metal and a dielectric. Owing to their inherent subwavelength confinement, SPPs have a strong potential to become building blocks of a type of photonic circuitry built up on 2D metal surfaces; however, SPPs are difficult to control on curved surfaces conformably and flexibly to produce advanced functional devices. Here we propose the concept of conformal surface plasmons (CSPs), surface plasmon waves that can propagate on ultrathin and flexible films to long distances in a wide broadband range from microwave to mid-infrared frequencies. We present the experimental realization of these CSPs in the microwave regime on paper-like dielectric films with a thickness 600-fold smaller than the operating wavelength. The flexible paper-like films can be bent, folded, and even twisted to mold the flow of CSPs.

Surface plasmon polaritons (SPPs) are highly localized surface waves (1) that propagate along the interface between two materials whose real parts of electric permittivity have opposite signs, and decay exponentially in the transverse direction. At optical frequencies, metals behave like plasma with negative permittivity, and thus SPPs exist on metal–air interfaces (2, 3). Owing to their ability to confine light in a subwavelength scale with high intensity, SPPs can be used to overcome the diffraction limit, miniaturize photonic components, and build highly integrated optical components and circuits. Thus, they have found (or have potential) applications in biomedical sensing, near-field microscopy, optoelectronics, photovoltaics, and nanophotonics (4–11).

In the far-infrared, terahertz, and microwave frequency bands, metals behave akin to perfectly electrical conductors (PECs), and thus SPPs cannot be supported by a metal surface. Although some designs based on metal wires or strips are able to support surface leaky modes that have some degree of lateral confinement at terahertz frequencies (12, 13), the concept of plasmonic metamaterials has proven very useful in the production of highly confined surface electromagnetic (EM) waves at low frequencies (14–27). Early work in this area can be traced back to the 1950s and 1960s, when corrugated metal structures were used to generate surface EM waves at microwave frequencies (14, 15). Generally, plasmonic metamaterials consist of metal surfaces decorated with 1D arrays of subwavelength grooves, 2D arrays of subwavelength holes/dimples, or 3D metal wires in which a periodic array of radial grooves is drilled (16–26). Recently, an alternative “spoof” SPP structure using complementary split-ring resonators as the unit cell elements has been proposed theoretically (27). The surface EM modes decorated by all of these plasmonic metamaterials are called spoof SPPs, or designer SPPs, because their properties are very similar to those of SPPs at optical frequencies. An important advantage of this metamaterial approach is that the dispersion characteristics and spatial confinement of the spoof SPPs can be controlled simply by geometrical means. However, all of the aforementioned plasmonic metamaterials have a major limitation associated with their inherent 3D geometry.

For the production of advanced plasmonic functional devices, it is very important to realize surface EM waves that can be confined in the subwavelength scale and can propagate on flexible and curved surfaces. Electronic and photonic circuits, devices, and systems integrated on flexible, stretchable, and biocompatible curved substrates have numerous applications, including electronic eyeball cameras (28), personal health monitors and biomedical devices (29), deformable light-emitting displays (30), adaptive photonic systems (31), human body sensors (32), paper-like electronic displays (33), artificial skin sensors (34), and electronic vivo brain monitoring devices (35). More recently, nanoscale stencils fabricated on flexible and stretchable substrate have been used as plasmonic nanoantennas at infrared frequencies (36). Because flexible and stretchable photonic structures can be wrapped on curved surfaces and objects, they have advantages over devices integrated on traditional rigid wafer-based substrates.

For both SPPs and spoof SPPs, much of the research to date has concentrated on flat surfaces: SPPs on flat metal surfaces and spoof SPPs on flat virtual surfaces (i.e., flat metal surfaces plus periodic arrays of grooves or pits). At optical frequencies, it is difficult to make SPPs travel for long distances on curved metal surfaces because of radiation losses, particularly when the curvature radius is on the order of the SPP wavelength. At terahertz and microwave frequencies, it is even more difficult to make spoof SPPs propagate along curved surfaces, owing to the 3D character of the plasmonic metamaterials used up to now. Thus, the propagation of either SPPs or spoof SPPs on curved surfaces has not yet been realized.

Results and Discussions

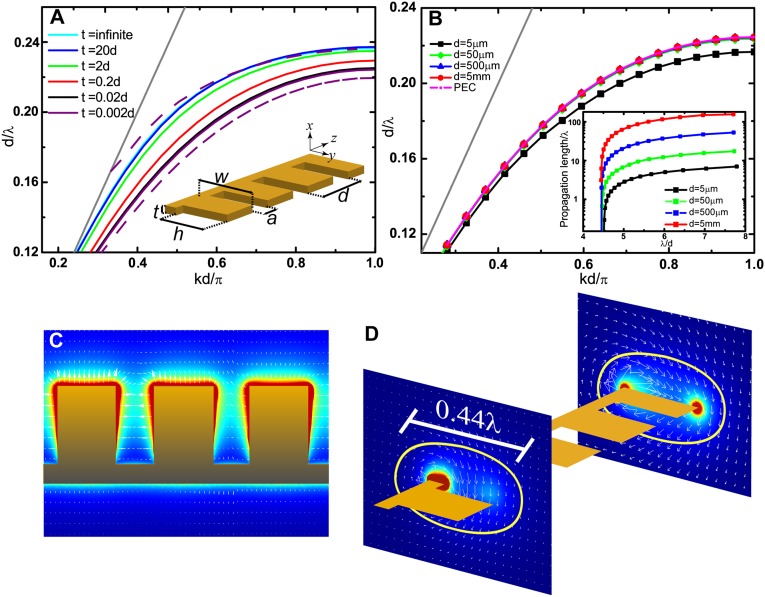
In this work, we propose the concept of conformal surface plasmons (CSPs), a type of surface EM wave that is supported by ultrathin films and whose propagation adapts to the curvature of the surface. These CSP modes are realized using nearly zero-thickness metal strips printed on flexible, ultrathin dielectric films. Our proposed plasmonic metamaterial that supports CSPs has a comb shape (Fig. 1A, Inset) and consists of a metal strip of thickness t and width W, in which a 1D periodic array of grooves of depth h is drilled. The period of the array is d, and the width of the groove is a. When the thickness t approaches infinity, the structure reduces to a 1D array of grooves (19). We analyzed the evolution of the dispersion relation of the surface EM waves supported by this structure with thickness t (Fig. 1A). We assumed that the metal behaves as a PEC, and thus that the results are scalable simply by modifying d, which is treated as the unit of length in our calculations. We used a finite element method (FEM) implemented in COMSOL Multiphysics to numerically calculate the dispersion curves of the TM-polarized waves propagating along the z-direction with momentum k.

Fig. 1.

Dispersion relationships and local field distributions of the comb-shaped CSP structures. (A) Normalized dispersion relations for the fundamental CSP mode as a function of thickness, t. (Inset) Geometric parameters of the structure, with W = d, a = 0.4d, and h = 0.8d fixed for all curves. The metal is modeled as a PEC. Continuous lines render the dispersion relations of single comb-shaped structures for different values of t, whereas the two dashed lines correspond to a double comb-shaped structure with t = 0.02d. (B) Variation of the dispersion relation with different values of d using copper optical constants and the same geometric parameters as in A for t = 0.02d. The PEC curve from A is also displayed for comparison purposes. (Inset) Propagation lengths normalized to the operating wavelength for the same values of d as in the main panel. (C) Amplitude (modulus) of the electric field evaluated at the yz plane that cuts the metal symmetrically, with the color scale ranging from red (highest amplitude) to dark blue (lowest amplitude). The white arrows depict the yz components of the electric field, showing its phase variation along the propagation direction. (D) Power flow contour plots evaluated at two transverse xy planes cutting the grooves (Left) and teeth (Right) of the comb-shaped structure. The color scale ranges from red (highest intensity) to dark blue (lowest intensity), and the white arrows depict the xy components of the magnetic field. The orange line denotes the modal size of the CSP mode, which represents 70% of the integrated energy flow. All geometric parameters in C and D correspond to those in B, with d = 5 mm and an operating wavelength of 30 mm.

All of the bands for different thicknesses (ranging from infinity to 0.002d) deviated significantly from the light line (gray curve in Fig. 1A), indicating that the corrugated metal plate supports the propagation of confined modes. The dispersion curves exhibited SPP-like behavior, presenting an asymptote controlled mainly by h and t. In contrast to the SPP modes at optical frequencies, in which this surface EM wave is built up as the result of the hybridization of a grazing photon with the collective plasma oscillations of the electrons, here the resonant mode of the cavities couples with the grazing photon. For a 1D array of grooves (infinite t), the initial cavity mode appears at frequency 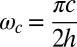, which then dictates the asymptote frequency of the corresponding surface EM mode. For this case, the electric field (E-field) points along the z-direction within the grooves, whereas the magnetic field (H-field) is directed along the x-direction. The important point to note is that when t is decreased to a finite value, the two cavity sides parallel to the yz plane are open, and thus the H-field remains unquantized in the x-direction. That is why the dispersion relation of the surface EM mode is insensitive to the thickness of the metal, in much the same way as domino plasmons (23, 37). Accordingly, there remains a surface EM mode supported by the structure in the limit of zero thickness. Because the dispersion relation of the mode remains unaltered, the subwavelength nature of its confinement is maintained when going from very large t to a nearly zero-thickness comb-shaped strip.

An important question concerns the frequency regimes in which these surface EM waves can operate. Fig. 1B shows the dispersion curves of the propagating EM modes for the same geometric parameters as in Fig. 1A with t = 0.02d but different values of d, ranging from 5 mm (to operate in the microwave regime) to 5 μm (to operate in the mid-infrared regime). To calculate these bands, in our numerical simulations we introduced the actual dielectric function of metal (copper in this case), as tabulated previously (38). The primary point to note is that the dispersion curves (d/λ) are not very sensitive to the frequency regime of operation, demonstrating that CSPs exist at microwave, terahertz, and mid-infrared frequencies. As expected, the corresponding propagation lengths (Fig. 1B, Inset) are much more sensitive to the frequency regime, because ohmic losses in the metal become more important with increasing frequency. Nevertheless, it is noteworthy that the propagation length of these CSP modes can be greatly enhanced through properly designed geometric parameters. Simply reducing h and/or increasing W will increase CSP propagation lengths by one order of magnitude compared with those shown in Fig. 1B, Inset.

CSPs are also supported by symmetric comb structures in which the two sides of the planar metal strip are symmetrically corrugated by two 1D arrays of grooves. Hybridization of the two CSP modes associated with these two combs leads to the emergence of two surface EM modes, as illustrated by their dispersion relations in Fig. 1A (dashed lines). As expected, this symmetrical combination leads to a confined mode with a lower frequency than that of the CSP mode of a single comb-shaped structure, whereas the antisymmetric mode is spectrally located at higher frequencies, closer to the light line. Owing to its higher confinement, the symmetric mode has a shorter propagation length (80λ for λ = d, with d = 5 mm) compared with its single comb counterpart (115λ for λ = d, with d = 5 mm) (Fig. 1B, Inset). However, on a positive note, it is much less sensitive to bending losses, which could be important when designing curved waveguides. The antisymmetric mode demonstrates the opposite behavior; although it is a very long-ranging CSP mode (propagation length, 440λ for λ = d, with d = 5 mm), its radiative losses are very large in curved geometries. Although symmetric comb structures could have some advantages over asymmetric comb structures in terms of smaller bending losses, single comb-shaped structures are superior because they are single-mode waveguides. For this reason, in what follows we concentrate on analyzing and testing the properties of asymmetric structures.

A key characteristic of the CSP modes is that they are confined at a very deep subwavelength scale in the three spatial dimensions. This property is illustrated in Fig. 1 C and D, which shows the E-field (vector field in white arrows and field amplitude in color scale) evaluated in a yz plane just above the structure (C) and the H vector field (white arrows) and flux intensity (color scale) calculated in two xy planes within the unit cell (D). In the latter panel, the closed orange curve denotes the area in which 70% of the flux energy of the propagating mode is contained. The EM field is highly localized within the comb-shaped metal structure, which has important implications for control in the propagation of CSP modes.

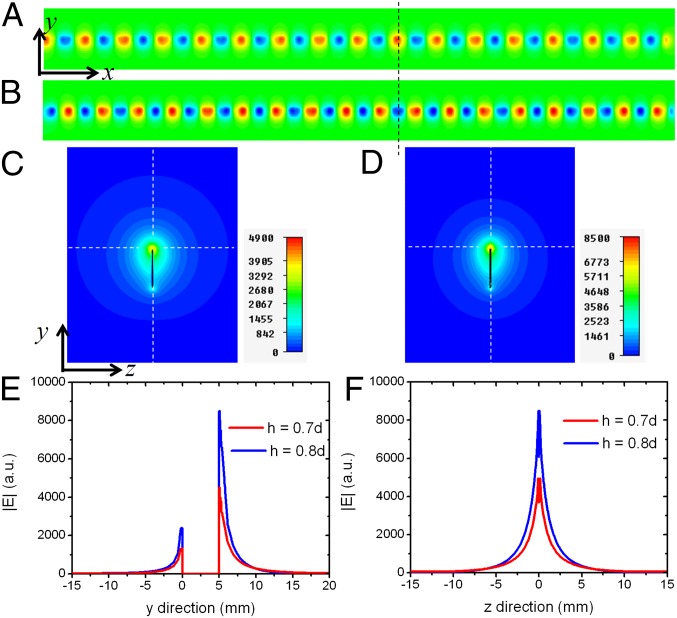
The dispersion relations and local fields shown in Fig. 1 demonstrate that the surface EM waves on corrugated ultrathin metal strips exhibit SPP-like behavior. This is further confirmed by an analysis of their field confinement and propagation lengths (see below). As discussed earlier, the characteristics of CSP propagation can be controlled by adjusting the strip width W and/or the groove depth h. By fixing W = d, a = 0.4d, and t = 0.0036d (with d = 5 mm as the periodicity), we now consider two ultrathin corrugated metal strips with different groove depths (h = 0.8d and h = 0.7d). From the dispersion relations (Fig. S1), we observe a decrease in asymptote frequency and an increase in deviation of the dispersion curve with respect of the light line as the groove depth increases. This implies a stronger field confinement, which is confirmed by full-wave numerical simulations. In the calculations that follow, we use the commercial software CST Microwave Studio. We set the boundary conditions as “open” to simulate the real space, and set the boundaries at large distances from the metal structure to avoid spurious reflections. Fig. 2 A and B illustrates the simulated electric fields (E_z components) evaluated at the top of two strips (16λ long, with λ as the wavelength) with different corrugations at 12 GHz. An electric monopole pointing to the y direction with unity current is used for excitation at the left edge. We see that the surface EM waves are tightly confined and propagate along the straight waveguide with very small losses.

Fig. 2.

Propagation of surface EM waves and field confinements on two ultrathin corrugated metal strips (W = d, t = 0.0036d, a = 0.4d, and d = 5 mm) with different groove depths (h = 0.8d and h = 0.7d). The operating frequency is 12 GHz (λ = 25 mm). An electric monopole pointing to the y direction with unit current is used for excitation at the left edge. (A and B) Simulated amplitudes of electric fields (|E|) on the two corrugated metal strips (A: h = 0.8d; B: h = 0.7d) over a length of 400 mm (16λ). (C and D) Field distributions on the cross-sections of the two corrugated metal strips (C: h = 0.8d; D: h = 0.7d) located 300 mm (12λ) away from the source (the dashed line in A and B). The black lines indicate the cross-sections of the two strips. The CSP modes are tightly confined to the corrugated strips with strong field enhancements. (E and F) Electric field distributions along the vertical cut (E) and horizontal cut (F), shown by the orthogonal dashed lines in C and D. The fields near the deeply corrugated strip (h = 0.8d) are much stronger and decay exponentially faster compared with those of the shallowly corrugated strip (h = 0.7d) along the two orthogonal directions.

The confinement details can be clearly seen from the distributions of electric field amplitudes (|E| = [|E_x|²+|E_y|²+|E_z|²]^1/2) in the cross-sections perpendicular to the strips (dashed line in Fig. 2 A and B), as illustrated in Fig. 2 C and D. We note that the deeper corrugated metal strip confines the CSP mode to a smaller region with more significant field enhancement (Fig. 2D). For quantitative descriptions, Fig. 2 E and F shows the field distributions along two lateral cuts (the white dashed lines in Fig. 2 C and D). Both fields clearly decay exponentially along the two orthogonally lateral (y and z) directions (although they are asymmetrical along the strip direction, owing to their geometric asymmetry), illustrating the typical features of SPP modes. As the groove depth h increases, confinement tightens and field enhancement increases, whereas propagation length diminishes. FEM calculations show that the propagation length of the CSP mode is significantly reduced with increasing h; for h = 0.7d, this length is 100 times the wavelength, compared with 67 times the wavelength for h = 0.8d. This trade-off is characteristic of CSP modes between localization and propagation loss, the same as for standard SPPs at optical frequencies.

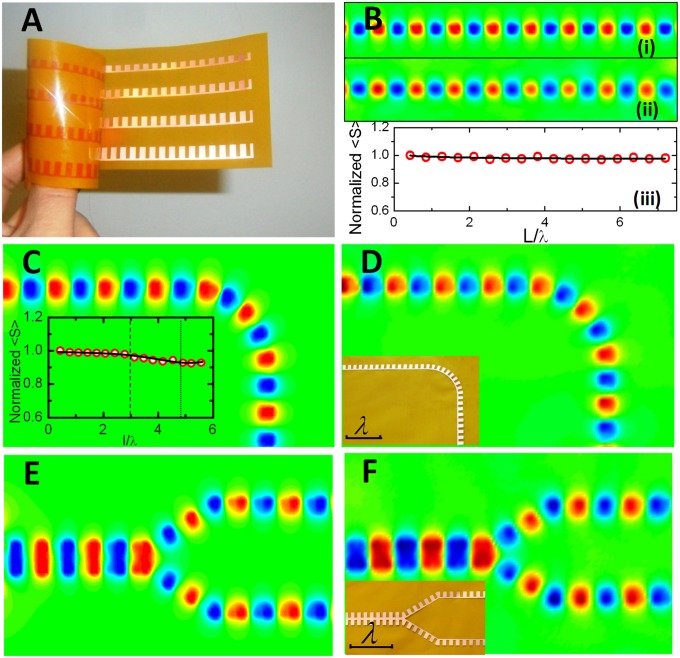
To realize the CSPs experimentally, we performed a series of experiments in the microwave regime by constructing comb-shaped corrugated metal strips with d = 5 mm. The corresponding plasmonic metamaterials were manufactured using the standard printed circuit board fabrication process on a three-layer flexible copper-clad laminate (FCCL), consisting of a single layer of polyimide and an electrolytic copper-clad sheet connected with the epoxy adhesive. The thicknesses of polymide, adhesive, and copper foil layers were 12.5, 13, and 18 μm (t = 0.0036d), respectively, and thus the total film thickness was 43.5 μm. The fabricated samples are ultrathin and flexible (Fig. 3A). They can be wrapped around curved surfaces, and thus are well suited for incorporation into arbitrarily curved surfaces to mold the flow of CSPs.

Fig. 3.

Simulation and measurement results of CSP waves on planar surfaces at 10 GHz. (A) Photograph of the nearly zero-thickness CSP structures on a flexible and ultrathin dielectric film, which can be wrapped on arbitrarily curved surfaces. The four CSP strips shown have groove depths h, from top to bottom, of 3, 4, 5, and 6 mm. Here a = 2 mm, d = 5 mm, t = 0.018 mm, and W = h + 1 mm. (B) Simulation (i) and measurement (ii) results of electric field (E_z) distributions along the ultrathin corrugated metal strip with groove depth h = 3 mm. (iii) Normalized time-averaged power densities (peak values) along an observation line (l) lying 1.5 mm above the corrugated edge. (C and D) Simulated (C) and measured (D) electric fields (E_z) of the 90^o bend. (C, Inset) Normalized time-averaged power densities (peak values) along a bending observation line (l) lying 1.5 mm above the corrugated edge, in which the region between two thin dashed lines is the bending path. (D, Inset) Photograph of an experimental sample, with a = 2 mm, d = 5 mm, h = 4 mm, W = 5 mm, and t = 0.018 mm. (E and F) Simulated (E) and measured (F) electric fields (E_z) of the 60^o Y-splitter. (F, Inset) Photograph of an experimental sample, with a = 2 mm, d = 5 mm, h = 4 mm, W = 5 mm, and t = 0.018 mm. In all cases, an electric monopole parallel to the plane was used to excite the CSP modes at the left edge.

The highly localized features of these surface EM modes precludes their characterization by traditional far-field technologies; thus, we used a near-field scanning system to map the localized fields along the structured metal films (Fig. S2). The experimental setup consisted of an Agilent N5230C vector network analyzer and two monopole antennas as the source and detector. The detector, controlled by two computer-controlled step motors, was fixed at 1.5 mm above the samples and moved to scan the perpendicular component of the E-field (Fig. S2B). The scanning step was 1 mm, to obtain high-resolution pictures. E-field magnitude and phase data were collected and recorded by the network analyzer.

We first conducted experiments on straightly planar structures with four different groove depths h and metal widths (h =3, 4, 5, and 6 mm and W = h+1 mm) and fixed a = 2 mm over flat, 300-mm-long FCCL strips (Fig. 3A). The operating frequency was fixed at 10 GHz. The full-wave simulation and measured electric fields (E_z components) for h =3 mm are shown in Fig. 3B, (i) and (ii), and other findings are shown in Fig. S3. These results demonstrate that the ultrathin comb-shaped metal strips can indeed confine surface EM waves in the lateral direction very efficiently while maintaining the intensities over distances much longer than the wavelength. To estimate the propagation loss of CSP modes quantitatively, we calculated the normalized time-averaged power density (i.e., the Poynting vector, <S> = 0.5Re[E×H*]) along an observation line lying 1.5 mm above the corrugated edge [Fig. 3B, (iii)]. For this particular set of geometric parameters, the propagation efficiency was as high as 98% after traveling over eight free-space wavelengths.

Our second set of experiments and numerical simulations tested how the propagation of CSP modes is affected by the presence of bends or splitters that imply a change of direction in the plane, with the groove depth fixed at h = 4 mm. Fig. 3 C and D shows numerically (C) and experimentally (D) that the CSP modes experienced little radiation loss after propagation through a 90° bend. Here the radius of curvature was equal to the operating wavelength of 30 mm. Fig. 3C, Inset shows the time-averaged power density <S> along a bending observation line that is always 1.5 mm above the bending corrugated edge, showing a radiation loss of <8% after propagation over a six-wavelength bending path. The propagation of the CSP modes was also very robust when the power intensity of a single surface EM wave on a corrugated metal strip was split into two arms separated by 60° (the so-called “Y-splitter”); the numerical simulation results in Fig. 3E and experimental results in Fig. 3E show an excellent match. Based on the normalized time-averaged power density <S> (Fig. S4A), we can estimate a radiation loss of <3.75% in each arm, demonstrating the potential of CSPs to build up planar devices in which surface EM waves are efficiently channeled at the very deep subwavelength scale.

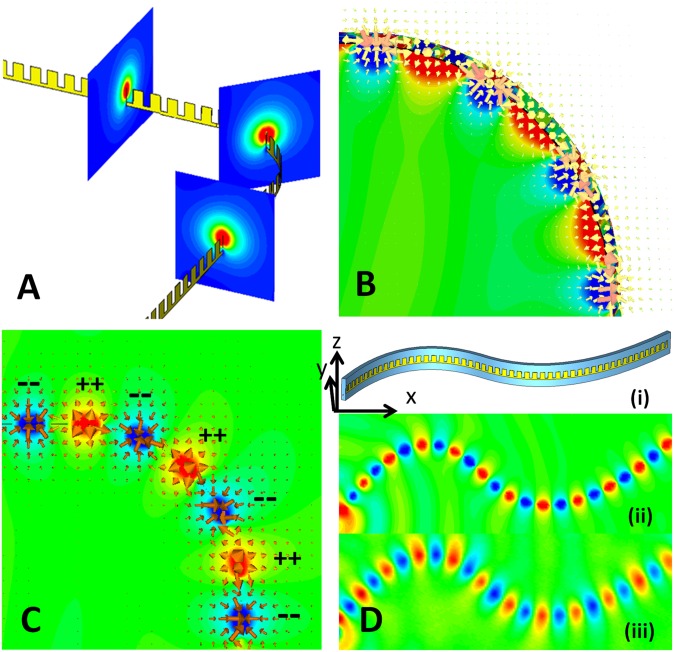
The flexibility and nearly zero thickness of the proposed FCCL films make it possible to realize CSPs on arbitrarily curved surfaces. The ultrathin films can be bent, folded, twisted, and wrapped on smooth and nonsmooth surfaces to control the propagation of CSPs. To reveal the physical origin of the CSP modes on curved surfaces, we first examined the propagation characteristics of these spoof SPP waves when the ultrathin corrugated metal strip (W = d, t = 0.0036d, h = 0.8d, a = 0.4d, and d = 5 mm) was bent vertically by 90° with a bending radius of 30 mm, the same as the operating wavelength. Fig. 4A shows the bending structure and numerical simulation results of power-density distributions on three vertical cross-sections before bending, at the bending center, and after bending. Three nearly identical patterns can be seen, implying that the bending loss is indeed very small (approximately 4%). Fig. 4B illustrates the detailed propagation of CSP modes across the bend in the 3D space, with arrows representing the vector E fields and color scales indicating the field amplitudes. A clear, very smooth transition of the E-field in both amplitude and polarization state is evident. Fig. 4C shows a top view of the vector E-field distribution, from which the generation of surface charges can be clearly seen. The collective oscillations of positive and negative surface charges across the bending surface result in the formation of CSP modes, in much the same way as SPPs at optical frequencies emerge from the collective excitation of electrons.

Fig. 4.

Simulation and measurement results of CSP waves on curved surfaces at 10 GHz. (A) An ultrathin corrugated metal strip (W = d, t = 0.0036d, h = 0.8d, a = 0.4d, and d = 5 mm) that is bent vertically by 90° with a bending radius of 30 mm, and numerical simulation results of power-density distributions on three different cross-sections before bending, at the bending center, and after bending. (B) 3D distribution of CSP modes across the bend, in which the arrows represent the vector E-fields and color scales indicate the field amplitudes. (C) Top view of the vector E-field distribution across the bend, clearly showing the generation of surface charges. (D) Simulation and experimental results of electric field distributions (E_z) on a vertically S-bending surface. (i) CSP structure on the S-bending surface. (ii) Simulation result. (iii) Experimental result. CSP waves creep through the bending surface smoothly. In both cases, an electric monopole pointing to the z direction is used for excitation at the left edge.

We next present the experimental results for CSP modes on several curved surfaces. In the examples that follow, we chose a strip of corrugated FCCL ultrathin film with geometrical parameters a = 0.4d, h = 0.8d, W = d, and d = 5 mm as the CSP carrier. Thus, the strip width was only 0.17λ at 10 GHz, the central frequency of the designed microwave band. The first example is a randomly fabricated curved surface (S bend) using a foam with a very low dielectric constant on which the comb-shaped metal strip was pasted [Fig. 4D, (i)]. For CSPs on curved surfaces, the fields were highly localized in two orthogonal directions, the direction perpendicular to the strip (i.e., the normal direction of the surface) and the direction parallel to the strip but perpendicular to the corrugated edge. We verified that the fields decay exponentially away from the interface in both directions (Fig. 2 E and F). Mapping near-field distributions along a curved surface is difficult, but we can measure the local fields along the corrugated edge of the CSP strip by cutting down the foam above the corrugated edge. The full-wave simulation and measurement results of electric fields (E_y components) at 10 GHz are shown in Fig. 4D, (ii) and (iii). Clearly, CSPs can propagate along the curved surface with very little loss. The time-averaged power density at the output side reached 95% of that at the input side after passing through eight wavelengths along the S-bending corrugated metal strip (Fig. S4B). Again, excellent agreement between the experimental and numerical results was seen.

The foregoing example clearly shows that CSP modes can creep efficiently on a smooth surface with the aid of the flexible FCCL film. The propagation of CSPs at sharp edges or corners is analyzed in Fig. S5. The simulation and measurement results demonstrate the excellent performance of CSPs when propagating through sharp edges as well; surface EM waves can creep through a 90° corner smoothly, with relatively little bending loss.

Their flexibility, nearly zero thickness, subwavelength width, and low loss propagation give our proposed structures much more freedom to control the propagation of surface EM waves on very thin metal films compared with previous plasmonic approaches. In the two examples discussed next, we controlled the CSP waves to propagate around a spiral route and a 3D helix route. The fabricated sample of the spiral structure along which the corrugated ultrathin FCCL strip was wrapped is shown in Fig. 5A. The minimum and maximum radii of the spiral were 20 mm and 40 mm, respectively. Numerical simulation (Fig. 5B) and experimental mapping (Fig. 5C) of the local electric fields (E_y components) at 11 GHz along the corrugated edge showed excellent agreement, demonstrating the excellent performance of CSP waves on the highly complex spiral surface. From the normalized time-averaged power density along a spiral observation line lying 1.5 mm above the corrugated edge (Fig. S4C), the power density was attenuated by 10% after propagation through the 9.5-wavelength spiral path. The comb-shaped metal strip also can be wrapped on a 3D dielectric cylinder to realize helix CSPs (Fig. 5D). In this case, the foam-dielectric cylinder had a radius of 15 mm, and the metallic CSP strip was wrapped spirally around it at a bevel angle of 10°. Fig. 5E illustrates the full-wave simulation results of near-field distributions at 11 GHz around the helix strip, which demonstrate that CSPs can creep along the helix path by maintaining a good modal shape with low bending loss. The time-averaged power density at the output end was up to 83% of that at the input end for CSP waves after passing through 12.5 wavelengths, including two cycles around the cylinder (Fig. S4D). Measuring the 3D field distributions is difficult using the experimental platform, however, and so we buried the cylinder wrapped with the helix CSP strip in the foam background, which allowed us to map the fringe and pillar regions of the strip. The near-field distribution measured on a plane lying 1.5 mm above the sample is shown in Fig. 5F. Note that the CSP waves on the output end were very well maintained compared with those on the input end after passing through the 3D helix path, indicating excellent performance. Additional simulation results demonstrate that the CSP waves can propagate smoothly along the helix strips wrapped on cylinders with various radii (Fig. S6).

Fig. 5.

Simulation and measurement results of CSP waves on a spiral surface and a 3D helical-shaped curved surface. (A) Fabricated sample of the spiral-shaped ultrathin CSP film with an initial curvature radius of 20 mm and a maximum curvature radius of 40 mm, in which a = 2 mm, d = 5 mm, h = 4 mm, w = 5 mm, and t = 0.018 mm. The CSP film is supported by a foam substrate with nearly unity dielectric constant. (B and C) Full-wave simulation (B) and experimental (C) results of electric field distributions (E_y) at 11 GHz on the plane lying 1.5 mm above the spiral sample. An electric monopole perpendicular to the foam surface (Fig. S2B) was used to excite the CSP modes at the inner edge. (D) Fabricated sample of the ultrathin CSP film that is wrapped on a foam cylinder spirally at a bevel angle of 10°. The foam cylinder had a radius of 15 mm and was buried in the foam background to allow measurement of the fringe and pillar regions of the CSP strip. An electric monopole parallel to the corrugated film was used to excite the CSP modes at the left edge. (E) Full-wave simulation results of electric field distributions (E_z) along the 3D helix path at 11 GHz. (F) Experimental results of electric field distributions at 11 GHz on the plane lying 1.5 mm above the top of the foam cylinder. Excellent performance of the CSP propagation is observed along the helical-shaped surface in both the simulation and the measurement results.

In summary, we have proposed the concept of CSPs and described the design, fabrication, and characterization of these surface EM waves on ultrathin and flexible dielectric films. Because of their very deep subwavelength confinement, CSPs are able to propagate along arbitrarily curved surfaces over long distances with very low absorption and radiation losses. We have demonstrated experimentally that these surface modes can be bent, folded, and even twisted to change their polarization state. The flexible, conformal, and ultrathin nature of the proposed metamaterial structures gives CSPs very promising applications in plasmonic devices, circuits, and systems in a wide broadband range, from microwave to mid-infrared frequencies.