On the Dielectric Boundary in Poisson-Boltzmann Calculations

Abstract

In applying the Poisson-Boltzmann (PB) equation for calculating the electrostatic free energies of solute molecules, an open question is how to specify the boundary between the low-dielectric solute and the high-dielectric solvent. Two common specifications of the dielectric boundary, as the molecular surface (MS) or the van der Waals (vdW) surface of the solute, give very different results for the electrostatic free energy of the solute. With the same atomic radii, the solute is more solvent-exposed in the vdW specification. One way to resolve the difference is to use different sets of atomic radii for the two surfaces. The radii for the vdW surface would be larger in order to compensate for the higher solvent exposure. Here we show that radius re-parameterization required for bringing MS-based and vdW-based PB results to agreement is solute-size dependent. The difference in atomic radii for individual amino acids as solutes is only 2–5% but increases to over 20% for proteins with ~200 residues. Therefore two sets of radii that yield identical MS-based and vdW-based PB results for small solutes will give very different PB results for large solutes. This finding raises issues about two common practices. The first is the use of atomic radii, which are parameterized against either experimental solvation data or data obtained from explicit-solvent simulations on small compounds, for PB calculations on proteins. The second is the parameterization of vdW-based generalized Born models against MS-based PB results.

I. Introduction

The Poisson-Boltzmann (PB) equation is widely used for modeling electrostatic effects and solvation of biomolecules.^1–30 The calculated electrostatic free energy of a solute molecule depends on the permanent partial charges on the atoms of the solute and the boundary of the low-dielectric solute and the high-dielectric solvent. Even when the radii of the atoms are given, there is still considerable freedom in specifying the dielectric boundary. In particular, two choices widely used in PB calculations are the van der Waals (vdW) surface and the molecular surface (MS) (see Figure 1). The vdW surface consists of the exposed surfaces of the spheres representing the solute atoms. The MS, introduced by Richards,³¹ relies on a spherical solvent probe. According to the MS, the atomic spheres and all crevices inaccessible to the solvent probe are all treated as part of the solute dielectric (the MS hence has also been referred to as the solvent-exclusion surface). The added crevices reduce the exposure of the solute charges to the solvent. Since solute charges have strong interactions with the solvent, the cumulative effects of the reduced solvent exposure of all the solute atoms can lead to a significant change in the electrostatic solvation energy. As a result, the electrostatic interaction free energy between an oppositely charged protein-protein pair or protein-RNA pair can change from negative to positive when the dielectric boundary is switched from vdW to MS.^{13, 20, 29, 30, 32} The electrostatic contribution of even a single mutation to the folding stability of a protein or the binding stability of a protein-protein or protein-RNA complex can be predicted very differently by the two choices of the dielectric boundary.^{8, 10, 13, 20, 32} One possible way to reconcile the differences in calculated electrostatic free energy is to use different sets of atomic radii for the two choices of the dielectric boundary.^{5, 26} Specifically, to compensate for the higher solvent exposure by the vdW specification, atomic radii would be increased relative to those in the MS specification. We carried out such radius re-parameterization and found that the changes in atomic radii are very dependent on the solute size. The difference in atomic radii for individual amino acids as solutes is only 2–5% but increases to over 20% for proteins with ~200 residues.

Figure 1.

Definitions of (a) the van der Waals surface and (b) the molecular surface. In this two-dimensional illustration, atoms are represented by gray disks. In (a), the exposed boundaries of the disks, shown in dark, constitute the van der Waals surface. In (b), a spherical solvent probe is rolled around the solute molecule. In addition to the van der Waals spheres, small crevices inaccessible to the solvent probe are now part of the solute region. The boundary of this filled-up solute region, shown in dark, is the molecular surface.

There is a widely held perception that, between vdW and MS, the latter is a better choice for the dielectric boundary, though a convincing argument has not been laid out. To the contrary, it has been shown that PB calculations with the vdW choice consistently give better agreement with experimental results for mutational effects on protein folding and binding stability^{8, 10, 13, 20, 32} and for electrostatic contributions to protein binding rates.^{29, 30} This paper does not aim to settle the difference between MS and vdW. Rather, the significance of our finding lies in its implications for two common practices in PB calculations. The first is parameterization of atomic radii using either experimental solvation data or explicit-solvent simulations, which are restricted to small solute molecules.^{19, 23, 26, 33, 34} Our finding would suggest that, on these solute molecules, the values of atomic radii obtained using either vdW or MS as the dielectric boundary differ very little (e.g., < 5%). However, when these radii are then used for PB calculations on proteins, the electrostatic solvation energies will be very different depending whether vdW or MS is specified as the dielectric boundary. The uncertainty on calculated solvation energies for proteins thus diminishes the value of experimental and explicit-solvent data on small solutes for parameterizing the PB model.

The second common practice occurs in developing generalized Born (GB) methods³⁵ as a fast substitute of the PB model. In some GB methods, the MS specification of the dielectric boundary is directly implemented and the GB results are benchmarked against MS-based PB results.^36–39 In many other GB methods,^40–46 the vdW specification of the dielectric boundary is implemented, and the resulting GB results are then benchmarked against the MS-based PB results through additional parameterization. Our finding suggests that the parameterization required for matching vdW-based GB and MS-based PB is protein dependent, and the use of a uniform set of parameterization introduces a new source of error for individual proteins.

II. Calculation Details

We carried out different sets of PB calculations over 55 test proteins. One set, used as the target, had MS as the dielectric boundary and Bondi radii⁴⁷ for the protein atoms. All the other sets had vdW as the dielectric boundary and the atomic radii increased by various percentages (denoted as %Δr) from the Bondi values. The aim of the variation in %Δr was to find the value which would lead to agreement in the electrostatic solvation energy, ΔG_solv, between the MS-based and vdW-based calculations for a particular protein. At the end, a collection of 55 “optimized” %Δr values was obtained for the test proteins.

The 55 test proteins have been used in our previous studies to find an empirical dependence of Δ G_solv on solute and solvent dielectric constants²¹ and to develop GB methods as substitutes of the linearized and full PB equation.^{48, 49} These proteins were collected from the Protein Data Bank (http://www.rcsb.org/pdb) using the following criteria: sequence identity less than 10%, resolution better than 1.0 Å, and number of residues less than 250. For protein structures without hydrogen atoms, hydrogen atoms were added with the LEAP module in the AMBER package,⁵⁰ then energy minimized in vacuum with heavy atoms fixed. The PDB code, total number of atoms (N_atom), net charge (Q) for each of the 55 test proteins are listed in Table I.

Table 1.

Number of atoms, net charge, and MS and vdW solvation energy (in kcal/mol) for 55 test proteins

PDB	Natom	Q	ΔGsolvMS	ΔGsolvvdW(0%Δr)
1a6m	2435	2	−1893.3	−2716.3
1aho	967	−2	−943.3	−1299.3
1byi	3383	−4	−2408.9	−3578.1
1c75	987	−4	−1094.4	−1398.5
1c7k	1929	−5	−1672.0	−2439.7
1cex	2867	1	−1863.7	−2873.1
1eb6	2572	−15	−4062.5	−5094.0
1ejg	678	0	−356.4	−574.7
1etl	145	0	−213.1	−288.2
1exr	2240	−25	−8081.8	−9253.6
1f94	982	1	−858.6	−1206.0
1f9y	2535	−5	−2018.1	−2915.9
1g4i	1842	−1	−1659.2	−2402.0
1g66	2794	−2	−1628.6	−2945.2
1gqv	2143	7	−1768.6	−2561.5
1hje	179	1	−221.7	−275.3
1iqz	1171	−17	−4149.4	−4598.3
1iua	1207	−1	−873.0	−1289.8
1j0p	1597	8	−2242.3	−2810.4
1k4i	3253	−6	−2696.4	−3888.8
1kth	894	0	−1104.7	−1454.4
1l9l	1230	11	−2684.4	−3084.0
1m1q	1265	−7	−1945.0	−2379.0
1nls	3564	−7	−2927.5	−4680.5
1nwz	1912	−6	−2015.0	−2728.9
1od3	1900	−3	−1307.3	−2026.4
1ok0	1076	−5	−1153.9	−1546.3
1p9g	529	4	−556.0	−745.6
1pq7	3065	4	−1484.9	−2574.2
1r6j	1230	0	−972.9	−1337.4
1ssx	2750	8	−1674.4	−2623.6
1tg0	1029	−12	−2815.9	−3191.5
1tqg	1660	−7	−2373.2	−2903.5
1tt8	2676	1	−1655.7	−2604.9
1u2h	1526	4	−1521.1	−2036.2
1ucs	997	0	−705.1	−1021.8
1ufy	1926	−3	−1679.0	−2293.7
1unq	1966	−3	−2635.0	−3410.4
1vb0	921	3	−794.7	−1107.3
1vbw	1058	8	−1476.3	−1805.0
1w0n	1756	−5	−1685.6	−2417.1
1wy3	560	1	−600.6	−768.9
1x6z	1741	0	−1511.5	−2153.4
1x8q	2815	−1	−2325.5	−3550.2
1xmk	1268	1	−1151.3	−1589.0
1yk4	770	−8	−1578.3	−1874.2
1zzk	1252	1	−1202.8	−1591.7
2a6z	3432	−3	−2363.5	−3636.6
2bf9	560	−2	−763.8	−911.8
2chh	1624	−3	−1523.6	−2128.3
2cws	3400	−3	−1936.4	−3208.1
2erl	573	−6	−983.5	−1167.2
2fdn	731	−8	−1410.3	−1702.1
2fwh	1830	−6	−1629.1	−2251.1
3lzt	1960	8	−1866.9	−2587.4

PB results for ΔG_solv were obtained by using the UHBD program.⁵¹ The dielectric boundary was chosen as MS or vdW by the presence or absence of the “nmap 1.4, nsph 500” option in the UHBD input file. By default dielectric smoothing was applied to both choices of the dielectric boundary. UHBD calculations on all the test proteins used a coarse grid with a 1.5-Å spacing followed by a fine grid with a 0.5-Å spacing. The dimensions of the coarse and fine grids were 160 × 160 × 160 and 200 × 200 × 200, respectively. The solute and solvent dielectric constants were set to 1 and 78.5, respectively. No salt was present in the solvent.

For investigating the dependence of optimized %Δr on solute size, we carried out corresponding PB calculations on individual amino acids as solutes. For each of the 20 types of amino acids, 10 conformations were randomly carved out of the 55 test proteins. The UHBD calculations were done on the individual amino acids, with a coarse grid with a 50 × 50 × 50 dimension and a 1.0-Å spacing followed by a fine grid with a 60 × 60 × 60 dimension and a 0.25-Å spacing. For each type of amino acid, the average of optimized %Δr values over the 10 conformations is reported. Results from averaging over 20 conformations for each amino acid were essentially unchanged.

Areas of the dielectric boundary according to the two choices were calculated. For vdW and MS, the respective programs used were Naccess v2.1.1 (http://www.bioinf.manchester.ac.uk/naccess/) with a probe radius of 0 and dms (http://www.cgl.ucsf.edu/chimera/docs/UsersGuide/midas/dms1.html) with a probe radius of 1.4 Å.

III. Results and Discussion

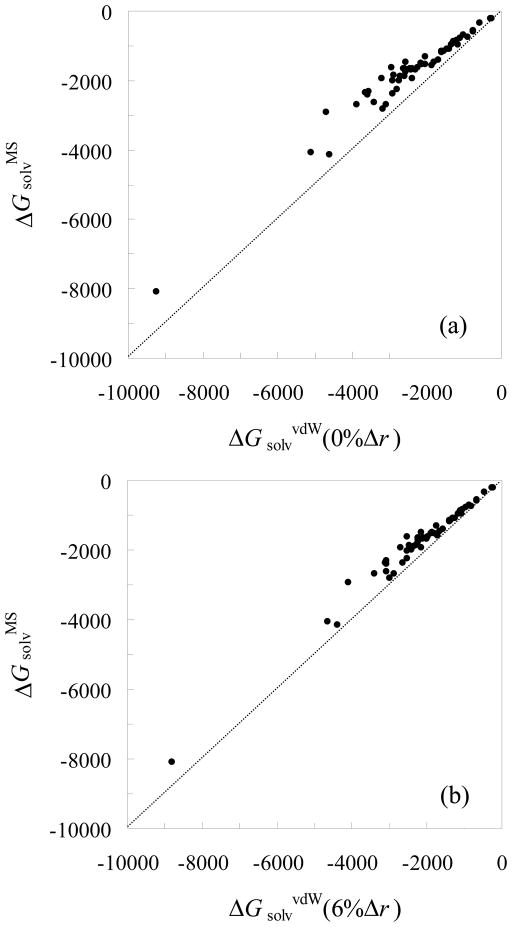
The electrostatic solvation energies of the 55 test proteins, calculated using Bondi radii and either the MS or vdW choice for the dielectric boundary, are listed in Table I and displayed in Figure 2a. It can be seen that the magnitudes of ΔG_solv are consistently larger with the vdW dielectric boundary, due to the resulting higher solvent exposure of solute charges. When the atomic radii are increased in vdW calculations, the magnitudes of ΔG_solv decrease and hence move toward those of the MS results. However, as Figure 2b shows, with a uniform increase of 6% in atomic radii, vdW results still consistently show larger magnitudes than the MS targets.

Figure 2.

Comparison of the electrostatic solvation energies of the 55 test proteins from MS-based and vdW-based PB calculations. For MS-based PB calculations, the Bondi radii are always used. (a) ΔG_solv^vdW calculated with Bondi radii. (b) ΔG_solv^vdW calculated with atomic radii increased by 6% from the Bondi values.

Figure 3 displays the optimized %Δr values for the 20 types of amino acids as solutes. The increases in atomic radii required to achieve consistency between vdW-based results for ΔG_solv and the MS-based target values are small, falling in the narrow range of 2% to 5%. The small changes in atomic radii are expected. With small solutes, all the atoms are well exposed to the solvent. Hence there are only limited chances that the MS will enclose small crevices outside the vdW surface. Interestingly, even within the narrow range of optimized %Δr values among the 20 types of amino acids, a positive correlation between optimized %Δr and N_atom is apparent. Linear regression analysis gave R² = 0.65.

Figure 3.

The percentage increase in atomic radii from the Bondi values required for ΔG_solv^vdW to match with ΔG_solv^MS for 20 types of amino acids as solutes.

On the 55 test proteins, the optimized %Δr values increase to at least 10%. As Figure 4a shows, there still seems to be a positive correlation between optimized %Δr and N_atom, but the data now exhibits much greater scatter. R² for linear correlation is now at 0.58. The variations in optimized %Δr within the 20 types of amino acids and within the 55 test proteins as well as between the two collections of solute molecules point to the accumulation of crevices that are outside the vdW surface but inside the MS as the major reason for the increase in optimized %Δr.

Figure 4.

(a) The percent increases in atomic radii, %Δr, for optimal agreement between ΔG_solv^vdW and ΔG_solv^MS on the 55 test proteins. (b) Percentage of difference in vdW surface area and MS area, 100(S^vdW – S^MS)/S^vdW, against the number of atom.

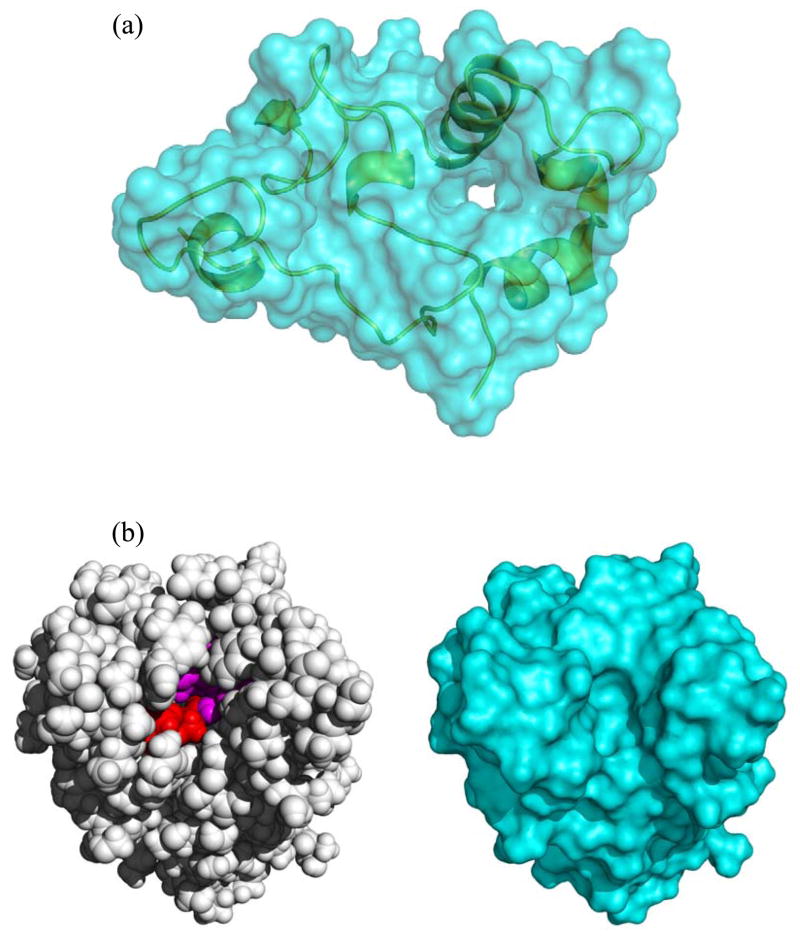
We examined the outliers in the correlation between optimized %Δr and N_atom. Some of the low-lying proteins, such as 2bf9, 1m1q, and 1j0p, in the optimized %Δr vs. N_atom plot were found to correspond to well-exposed structures (Figure 5a). For these proteins, the difference between the two types of solute surfaces are relatively small, and hence relatively small increases in atomic radii are required to bring vdW-based results for ΔG_solv into agreement with the MS-based target. One way of quantifying the differences between the two types of solute surfaces is by calculating the corresponding surfaces areas. Figure 4b displays %ΔS, the relative differences in MS area and vdW surface area, against N_atom. It can be seen that the low-lying proteins, 2bf9, 1m1q, and 1j0p, in the optimized %Δr vs. N_atom plot are also below the general trend in the %ΔS vs. N_atom plot. However, the correspondence between the two plots is far from being perfect. In particular, a low-lying protein, 1exr, in the %ΔS vs. N_atom plot actually occupies a position above the correlation trend line in the optimized %Δr vs. N_atom plot, and a high-lying protein, 1etl, in the optimized %Δr vs. N_atom plot does not take such a position in the %ΔS vs. N_atom plot.

Figure 5.

Comparison of van der Waals and molecular surfaces. (a) A well-exposed protein, 1m1q, which has the shape of a thin disk. The green ribbon representation of the protein is enclosed by the molecular surface in cyan; a hole appears near the center of the disk shape. (b) A protein, 1g66, with a deep channel. In the left panel, the van der Waals surface is presented, and residues lining the wall of the channel are displayed in red (for the catalytic triad) or purple. In the right panel, the molecular surface is presented. The active site now appears as an indent, but there is no channel penetrating into the center of the protein.

We suspected that the high-lying proteins in the optimized %Δr vs. N_atom plot correspond to structures with deep channels outside the vdW surface, which become enclosed in the MS and hence are treated as part of the solute dielectric in the MS-based PB calculations. This suspicion did not find support in 1etl, which is the smallest (with N_atom = 145) of the 55 test proteins but required a relatively large 17% increase in atomic radii to achieve a match between vdW-based and MS-based results for ΔG_solv. However, a deep channel in the structure of another high-lying protein, acetylxylan esterase with PDB code 1g66, was identified (Figure 5b). Part of the wall of this channel is lined by the catalytic triad; hence this channel is important for access by solvent as well as the substrate. The channel is inaccessible by the 1.4-Å spherical probe used to defined the MS. This example illustrates the artificial nature of using a spherical probe on a static structure to define the boundary between the solute and solvent. Proteins are dynamic, allowing for transient access of water molecules, as seen in NMR experiments⁵² and molecular dynamics simulations.⁵³ The transient excursions of water molecules into channels and interior positions are accounted for to some extent by choosing the vdW surface as the solute-solvent boundary, which perhaps partly explains the better performance of this choice in reproducing experimental results for electrostatic contributions to protein folding and binding.^{8, 10, 13, 20, 29, 30, 32}

We modeled the trend in the %ΔS vs. N_atom plot shown in Figure 4b as a power law,

$$\%\mathrm{\Delta }{S}_{\text{pred}}=\alpha {N_{\text{atom}}}^{\nu }.$$ (1)

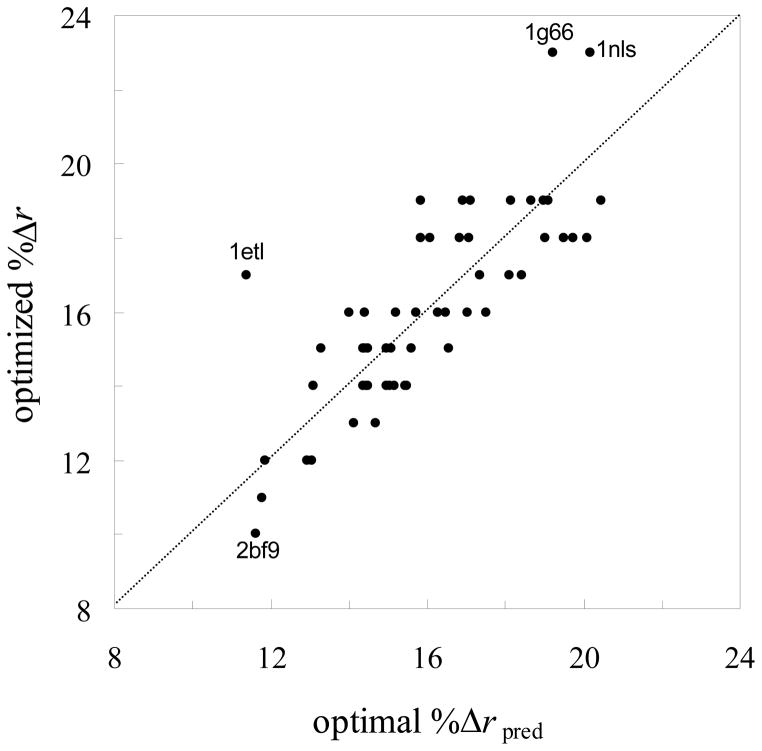
This function, with α = 13.8% and ν = 0.19, fitted the data with R² = 0.68. Given that the deviations from the trend of eq 1 could explain some of the outliers in Figure 4a, we included the ratio, (%ΔS)/(% ΔS_pred), as an independent variable along with N_atom in a multi-linear regression to model the variations of optimized %Δr among the 55 test proteins. The inclusion of the new variable led to a modest increase in R², from 0.58 to 0.65. As Figure 6 shows, there are substantial deviations between actual optimized %Δr values and those predicted from multi-linear regression, especially for 1etl, 2bf9, 1g66, and 1nls. The significant variations in optimized %Δr became apparent after we tested vdW-based and MS-based PB results on a large, diverse collection of proteins. So our study raises caution against using only a small number of test proteins to parameterize the PB model and draw conclusions.

Figure 6.

Comparison of actual optimized %Δr values against those predicted from a multi-linear relation.

Based on the efforts reported here, it seems unlikely that a simple way to predict optimized %Δr values can be found. The chance of bringing MS-based and vdW-based PB results into good agreement for a diverse set of proteins through radius re-parameterization is thus slim. This finding suggests that significant errors are introduced when vdW-based GB methods are parameterized to approximate MS-based PB results. It is interesting to note that, after parameterizing a vdW-based GB method against MS-based PB results for small compounds,⁴⁰ the deviations of this GB from the MS-based PB were found to increase with increasing sizes of test compounds.⁵⁴

The overall increase in optimized %Δr with increasing solute size also raises a cautionary note about the use of experimental and explicit-solvent data on small solutes for parameterizing the PB model. Very similar values of atomic radii will be obtained when MS-based and vdW-based PB calculations are benchmarked against the data on small solutes. However, when these radii are then used in respective PB calculations on proteins, the electrostatic solvation energies can differ significantly. Before the issue of the optimal choice for the dielectric boundary is settled, the value of small-solute data seems open to question. This applies not only to MS- and vdW-based PB calculations but also to alternative choices, such as spline-smoothed surfaces, of the dielectric boundary.^{5, 9, 14, 19, 26, 55–58} A fruitful approach to parameterizing the PB model is to use experimental data obtained on proteins.^{8, 10, 13, 20, 29, 30, 32}