Evolutionary and plastic rescue in multitrophic model communities

Abstract

Under changing environmental conditions, intraspecific variation can potentially rescue populations from extinction. There are two principal sources of variation that may ultimately lead to population rescue: genetic diversity and phenotypic plasticity. We compared the potential for evolutionary rescue (through genetic diversity) and plastic rescue (through phenotypic plasticity) by analysing their differential ability to produce dynamical stability and persistence in model food webs. We also evaluated how rescue is affected by the trophic location of variation. We tested the following hypotheses: (i) plastic communities are more likely to exhibit stability and persistence than communities in which genetic diversity provides the same range of traits. (ii) Variation at the lowest trophic level promotes stability and persistence more than variation at higher levels. (iii) Communities with variation at two levels have greater probabilities of stability and persistence than communities with variation at only one level. We found that (i) plasticity promotes stability and persistence more than genetic diversity; (ii) variation at the second highest trophic level promotes stability and persistence more than variation at the autotroph level; and (iii) more than variation at two trophic levels. Our study shows that proper evaluation of the rescue potential of intraspecific variation critically depends on its origin and trophic location.

1. Introduction

In the current period of unprecedented rapid global change, ecological communities are experiencing abrupt and sustained environmental stress. Many populations and species will be unable to cope ‘geographically’ with environmental change by adjusting their distributions and must rely on rapid phenotypic adaptation to be rescued from extinction [1,2]. Rescue by phenotypic adaptation occurs when the frequency of traits in a population changes in a way that increases the probability of population persistence. In nature, rapid phenotypic change can be based on two principal sources of trait variation: genetic diversity and phenotypic plasticity [3]. In the present theoretical study, we compare these two sources of intraspecific variability for their differential ability to preserve populations that face changing environmental conditions and interact with one another in food webs.

Theory predicts that rapid evolution can rescue populations that are threatened by significant and sustained environmental change [4]. In this evolutionary rescue scenario, natural selection changes allele frequencies in populations so that phenotypes are better adapted to novel conditions, thereby maintaining or restoring a positive population growth rate. Genetic diversity—the raw material for natural selection and, ultimately, evolutionary rescue—arises either from pre-existing variation or de novo mutations that occur during rescue. Evolution must be rapid because allele frequencies need to be readjusted before the expression of maladaptive alleles leads to the demise of the population. A recent experimental study using yeast showed that evolutionary rescue could be accomplished over as few as 25 generations [5,6].

The second source of intraspecific variation, adaptive phenotypic plasticity, leaves a population's genetic structure unchanged but allows the environment to influence the development of individuals' phenotypes [7,8]. Plasticity is found in many different ecosystems and at all trophic levels [9,10]. Theory predicts that plasticity can be an exceptionally effective way for populations to adapt to environmental stress [2] (reviewed in Tollrian & Harvell [11]). Plasticity can occur within a generation, whereas evolution is always transgenerational; therefore, plasticity will probably allow faster adaptations than genetic diversity [1]. In many cases, plasticity may be capable of providing most or all of the adaptive trait change required for populations to avoid extinction [2].

Our study of ‘rescue’ differs from previous research in two ways. First, many studies on rescue evaluate variability in the traits that explicitly determine an individual's fitness given a specific environmental stress [5,12–14]. However, in nature, environmental change may often produce several novel stressors, and only a small fraction of populations' variability will be pre-adapted to any of them [2]. Therefore, we decided to look at how variability, in general, increases the chance of rescue in the face of the general effects of environmental stress, which we believe are an increase in mortality and bottom-up effects of changes in carrying capacity. In particular, we focus on variability in a specific class of traits: those involved in defence against predation. Variation in defensive traits can occur prior to environmental change, and therefore may contain pre-adaptations that help populations persist following a change [15,16]. Defensive traits can mitigate mortality effects by reducing the impact of predation and, through costs, mitigate the bottom-up effects of nutrient enrichment. Furthermore, defensive traits occur at multiple levels and have been shown to have very different effects depending on their trophic location [15–17].

Second, we consider rescue in the framework of food web dynamics; that is, rather than focusing on the persistence of single, isolated populations or species, we evaluate the potential for rescue of ensembles of populations in specific model food web assemblages. While it is important to establish theoretical and empirical benchmark values of selection strength, critical population size, etc., that are necessary for single population rescue, we feel that our approach more realistically reflects the natural community context under which population rescue commonly happens in the wild. Previous studies have shown that within species diversity affects food web dynamics [18–20]; here, we examine how different sources of this horizontal diversity contribute to the persistence and rescue of whole communities.

We use two criteria to assess the likelihood of rescue: community persistence and dynamic stability. Persistence means that at least one phenotype/genotype from each trophic level maintains positive abundance over the period of model evaluation (i.e. the opposite of extinction). Persistence is in obvious ways related to evolutionary rescue: if, for instance, a community containing plasticity displays persistence over a wider range of parameter values than a community with genetic diversity, we would conclude that phenotypic plasticity enhances the likelihood of survival and that the potential for plastic community rescue is greater than that of evolutionary community rescue. Within the set of persistent dynamics, we use ‘dynamic stability’ as a secondary, more refined criterion for rescue potential. Dynamic stability refers to dynamics characterized by stable equilibria as opposed to intrinsically unstable dynamics characterized by regular or irregular population oscillations. We believe that the relative frequency of stable equilibria versus oscillations correlates with the likelihood of community rescue. Our major argument is that in natural settings, temporally stable populations tend to have less of an extinction risk than oscillating populations [21,22].

Both genetic diversity and phenotypic plasticity have been shown to increase the likelihood of persistence of trophic communities in theoretical and experimental systems. Most of the evidence derives from predator–prey studies in which prey express traits that provide different degrees of protection from predation. Trait variability arises either from the existence of several genotypes with different defence levels or from a plastic, inducible defence. Genetic diversity can increase population persistence if one or more of the phenotypes are well suited to the new environment [23] and/or if genotypes fluctuate asynchronously; the latter phenomenon is a form of compensatory dynamics known as cryptic dynamics [24,25]. Similarly, inducible defences can significantly enhance persistence and dynamic stability of small communities when subjected to nutrient and mortality stress [15,26,27]. The impact on community persistence seems to be greatest when plasticity is expressed at the autotroph level [17,28].

Although we are beginning to understand how genetic diversity and plasticity affect community persistence, we know little about their comparative effects and interaction. Studies comparing the effect of the two sources on communities have focused on variation at a single level in simple food chains and webs [29–31]. These studies have found that plasticity is more stabilizing than genetic diversity [30,31], that plasticity can increase the maximum mortality that predators can withstand [29] and that plasticity cannot produce all of the dynamics seen with genetic diversity [30]. Despite these findings, no studies have attempted to generalize how the trophic level of variation affects persistence and stability by comparing the two sources at multiple trophic levels.

In our study, we explored the potential for rescue in community models with alternative sources (genetic versus plastic) and different trophic locations (autotroph versus herbivore) of variability (figure 1). We specifically tested the following hypotheses: (i) plastic communities are more likely to exhibit stability and persistence than communities where genetic diversity provides the same range of traits. (ii) Variation at the lowest trophic level promotes stability and persistence more than variation at higher levels. (iii) Communities with variation (either of plastic or genetic origin) at two levels have greater likelihoods of stability and persistence than communities with variation at only one level.

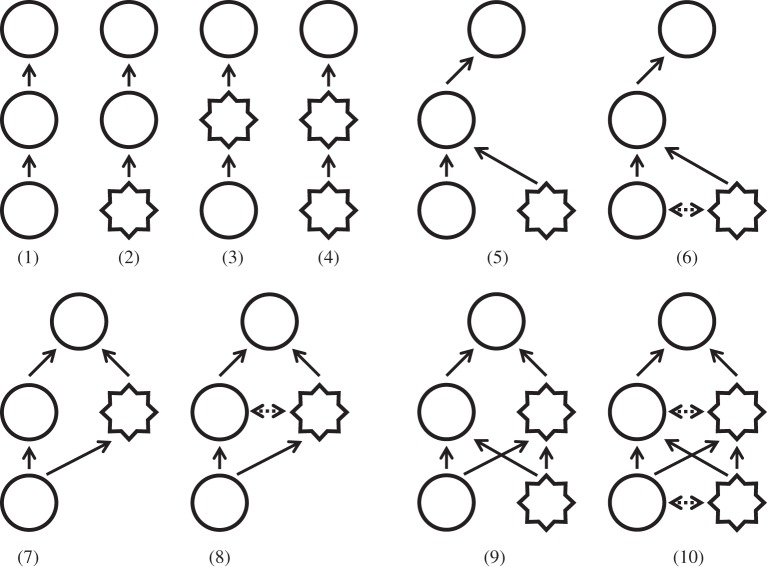
Figure 1.

The 10 tri-trophic model food webs used in the analysis of the effects of the source and trophic location of variation. Each individual circle represents a population expressing a single phenotype. Autotroph populations are at the bottom level of each food web, herbivores at the intermediate level and the carnivore at the top. The autotrophs' and herbivores' shape identifies the presence of defence (smooth circles are undefended, jagged circles are defended). A dashed horizontal arrow denotes the presence of plasticity. Solid lines indicate feeding links. Webs 1–4 have one genotype with fixed phenotypic expression; web 1 has no defence, web 2 has defence at the autotroph level, web 3 has defence at the herbivore level, web 4 has defence at both the autotroph and herbivore levels. Webs 5 and 6 have genetic and plastic variation, respectively, at the autotroph level. Webs 7 and 8 have genetic and plastic variation, respectively, at the herbivore level. Webs 9 and 10 have genetic and plastic variation, respectively, at both the autotroph and herbivore levels.

The results of our food web analyses did not allow us to reject our first hypothesis (i): plasticity promotes persistence and stability more than genetic diversity. However, we reject hypotheses (ii) and (iii) by showing that variation at the herbivore level is more stabilizing than variation at the autotroph level or at multiple levels. These results question the generality of previous findings which implicate variation for defence in the autotroph as the key driver of community dynamics [17,28].

2. Methods

We analysed 10 model food webs that vary in the degree, origin and trophic location of intraspecific variation for morphological defences (figure 1). These webs are based on, and parameterized for a rotifer–algal system (Scenedesmus sp., autotrophic phytoplankton; Brachionus spp., herbivorous rotifers; and Asplanchna sp., carnivorous rotifers [15,27]). This system allows for phenotypic variation at the autotroph and herbivore levels. Newly produced autotroph algae can be induced by the herbivore to form defensive colonies [27], and newly produced herbivorous rotifers can be induced by the carnivorous rotifer to grow long posterolateral spines [28,32]. In our model food webs, genetic variation covers the same trait range (undefended or fully defended) as plasticity, but phenotypes are produced by genotypes that are fixed for either trait value.

Webs 1–4 (figure 1) have no intraspecific variation and serve as controls with either no defence (web 1) or constitutive, fixed defences (webs 2–4). Webs 5 (‘autotroph genetic’) and 6 (‘autotroph plastic’) incorporate genetic diversity and plasticity, respectively, at the autotroph level. Webs 7 (‘herbivore genetic’) and 8 (‘herbivore plastic’) incorporate the same sources of variation at the herbivore level. Finally, webs 9 (‘two-levels genetic’) and 10 (‘two-levels plastic’) have variation at both herbivore and autotroph levels.

We adapted the equations for our model from Vos et al. [15]. Yamamichi et al. [31] analysed a related equation system for a flow-through chemostat scenario. Our formulation for food webs with plastic variation (‘plastic webs’) represents the effects of phenotypic plasticity by allowing plastic individuals to produce individuals in one of two discrete phenotypic populations (one population is undefended and the other is defended; both are linked by a ‘reproductive switching term’ S). Plastic webs are derived from food webs with genetic diversity (‘genetic webs’) by adding S and a term to describe the production of new individuals by the non-focal phenotype (see the electronic supplementary material, appendix A for detailed equation systems for all 10 model food webs). Genotypic diversity is modelled for asexual reproduction and is therefore mathematically equivalent to having two distinct species at each of the respective trophic levels. In contrast, phenotypic plasticity allows a phenotype to channel part of its future reproductive output into the opposite phenotype. The most complex food web model with phenotypic plasticity at the autotroph and herbivore levels (web 10) consists of five coupled differential equations:

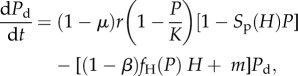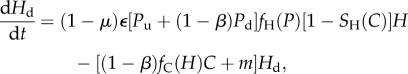with P = P_u + P_d; H = H_u + H_d with switching functions S and functional response functions f

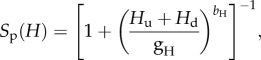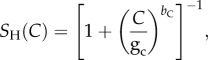P_d and P_u are the densities of the defended and undefended autotrophs, H_d and H_u are the densities of the defended and undefended herbivores and C is the carnivore density. P_d and P_u grow logistically to a joint carrying capacity K, which applies to the sum of the two phenotypes. S is a decreasing, sigmoid function that takes values between unity and greater than zero; it describes the reproductive investment towards producing undefended types (as a fraction of the whole population's growth rate r); this investment decreases with increasing densities of ‘inducers’ at the next trophic level up; conversely, the investment towards producing defended types increases with inducer densities according to (1 − S). g_H and b_H determine the shape of S_P(H); g_H is the density of herbivores that produces equal investment in defended and undefended phenotypes, and b_H describes the steepness of the function (analogously for g_C and b_C). ɛ and γ are the herbivores’ and carnivores' conversion efficiencies. β is the defence level; as β increases, (1 − β) decreases and therefore the functional response of predators on defended types is diminished. μ reflects the cost of defence, such that a high μ corresponds to high costs and a low growth rate. (See table 1 for a full list of parameters and their values.)

Table 1.

Definitions and default values of model variables and parameters (obtained from Vos et al. [16]).

parameter	value	interpretation
r	1.42 d−1	intrinsic rate of increase of autotrophs
K	0.25–19.75 mg C l−1 by [0.5]a	carrying capacity
m	0.025–0.725 d−1 by [0.025]a	mortality
vPH	0.77 l d−1 mg C−1	herbivore search rate on autotrophs
vHC	2.71 l d−1 mg C−1	carnivore search rate on herbivores
hPH	0.5 d−1	handling time of herbivores on autotrophs
hHC	0.83 d−1	handling time of carnivores on herbivores
ɛ	0.36	conversion efficiency of herbivores
γ	0.5	conversion efficiency of carnivores
β	0–0.9375 by [0.0625]a	defence level of defended phenotypes
μ	0–0.9375 by [0.0625]a	cost of defence as decrement in growth rate
S(H)	1 ≥ S(H) > 0	plastic reproductive switching function for autotrophs
S(C)	1 ≥ S(C) > 0	plastic reproductive switching function for herbivores
gH	0.06 mg C l−1	half saturation constant for plastic switching in autotroph
gC	0.02 mg C l−1	half saturation constant for plastic switching in herbivore
bH	2.05	shape of plastic switching in autotroph
bC	1.5	shape of plastic switching in herbivore

^aMarks the interval size for β, μ, m and K.

Our model formulation differs in three ways from Vos et al.'s [15]. First, we implement defence by multiplying attack rate by (1 − β) and dividing handling time by (1 − β) (note: the (1 − β) terms in the denominator cancel each other). We believe this to be the most correct way to implement defence because in our system, defences in the herbivore centre around the production of long posterolateral spines; these spines decrease the likelihood of successful attack (decrease attack efficiency) and also increase the handling time by both wasting time on unsuccessful attacks [33] and by requiring more time to manipulate the herbivore into a position where it can be consumed. Vos et al. [15] implemented defence through increasing handling time of predators on defended prey; however, handling time is present only in the denominator of the functional response equation, which is identical for both prey types; thus, defended and undefended prey obtain the same benefit under Vos et al.'s formulation (C. Kovach-Orr, M. Voss & G. Fussmann 2012, unpublished data). Additionally, defences based entirely on attack efficiency are not particularly applicable to our algal/rotifer system [15]. While it is true that decreasing attack efficiency by the same rate we increase handling time is arbitrary, it seems no less arbitrary than any other relationship between handling time and attack rate. We prefer our formulation because defended prey receive a greater benefit from defence than undefended prey, although the presence of defended prey does benefit the undefended prey through the direct interaction of the defended prey and predator [34]. Second, our mortality term represents increased environmental stress and affects all species equally, as opposed to Vos et al. [15], who manipulated mortality of the carnivore while leaving other trophic levels' mortalities static. Our analyses show that this assumption produces results that are qualitatively similar to those for a system where each species has its own mortality and only carnivore mortality is affected by environmental change (data not shown). Finally, Vos et al. used a switching function that mimics direct transfer or migration between populations of defended and undefended types. By contrast, our switching function distributes total population growth rate among types. This is a more realistic description of the mechanism of defence induction of aquatic invertebrates that cannot switch between defended and undefended states during their lifetime [31].

(a). Model analysis

We mathematically analysed the potential for community persistence in the context of varying environmental carrying capacity and natural mortality. We chose carrying capacity because it is a proxy for nutrient enrichment, a major environmental change in many aquatic ecosystems due to increased fertilizer run-off [35], and because the bottom-up effects of nutrient enrichment can destabilize predator–prey dynamics [36]. We chose to manipulate mortality, because increased natural mortality is the most general population-level effect of increased environmental stress (such as flooding, oil spills, aquatic acidification, pesticides or any other factors that increase mortality). The production of defensive traits is typically costly for the prey and incorporated into models as a trade-off between defence β and cost μ. We followed this convention but evaluated all biologically relevant trade-off combinations rather than limiting our analysis to predetermined categories of trade-off curves (concave up, linear and concave down).

We used two mathematical/computational approaches to analyse our model food webs: numerical simulations and numerical bifurcation analysis.

• — Numerical simulations. At all parameter combinations, we evaluated our models for persistence and dynamic stability. Initial population densities were: undefended and defended autotrophs each equal to half of carrying capacity, undefended and defended herbivores each equal to 0.5 mg C l⁻¹, and carnivores equal to 0.25 mg C l⁻¹. To avoid transient dynamics, we evaluated simulations from time t = 1000 until t = 21 000. For persistence versus extinction, a population was considered extinct if, at any time 1000 ≤ t ≤ 21 000 its density was below 1.6 × 10⁻⁴ mg C l⁻¹ (approx. one carnivore individual per 3000 ml [27]). We considered a community to persist if at least one population from every trophic level was always above this threshold. Note that extinction can occur either because the carnivore has a zero equilibrium (trivial equilibrium) or as a consequence of extinction through extreme oscillations [37]. For stability, we used the same numerical simulations as above, but also evaluated the maximum and minimum population density from t = 14 000 to 21 000. If the difference between the maximum and minimum was less than the equivalent of one individual carnivore per 300 ml (1.6 × 10⁻³ mg C l⁻¹), the food web was considered to be stable. Note that this operational evaluation of stability scores oscillatory dynamics with minute amplitude as factually stable.

  We used parallel computing (Guillimin cluster at Clumeq: 160 parallel threads) for numerical simulation of food web dynamics with Matlab [38]. We quantified differences between food webs by calculating the frequency of persistence and dynamic stability over 296 960 combinations of mortality m (29 intervals), carrying capacity K (40), defence level of defended phenotype β (16) and costs for the defended phenotype μ (16) (see table 1 for ranges and interval sizes).

• — Bifurcation analysis can provide deeper insights into the mechanisms underlying the distributions of persistent and stable dynamics. For instance, bifurcation analysis can reveal why variation at a certain level increases the potential for stability more than variation at a different level. All bifurcation diagrams were produced using numerical bifurcation software [39]. While our numerical simulations were performed for K = 0.25–19.75 mg C l⁻¹, our numerical bifurcations were evaluated for K = 0–50 mg C l⁻¹.

3. Results

Table 2 shows the average frequencies of persistence and stability for all food webs (figure 1) and across all combinations of carrying capacity (K), mortality (m), cost of defence (μ) and defence value (β). We found a positive correlation between the two measures that we used to quantify the potential for community rescue (R² = 0.57, for n = 10 food web types in table 2). That is, food webs with a high frequency of persistence also tended to display higher frequencies of dynamic stability. Residual variation was almost entirely owing to the differences between food webs with genetic versus plastic variation. In ‘plastic webs’ (webs 6, 8 and 10) more than half of the food web parameterizations that persisted in our simulations did so at dynamic equilibria, whereas oscillatory dynamics dominated in persisting ‘genetic webs’ (webs 5, 7 and 9; table 2).

Table 2.

Frequencies of persistence and equilibrium dynamics across 286 720 food web simulations. Average percentages for 10 food web categories that differ in degree, trophic location and source of variability. Persistence: per cent of simulations with ≥1 population persisting at each trophic level. Equilibria: per cent of simulations with stable, non-oscillatory dynamics. Only simulations exhibiting persistence were analysed for stability but per cent values are given as the fraction of all 286 720 simulations.

web no.	trophic level of defence	trophic level of variation	source of variation	persistence (%)	equilibria (%)
1	none	none	none	24.05	4.74
2	autotroph	none	none	4.06	1.27
3	herbivore	none	none	5.02	0.91
4	both levels	none	none	2.37	0.58
5	autotroph	autotroph	genetic	19.63	3.66
6	autotroph	autotroph	plastic	14.06	8.56
7	herbivore	herbivore	genetic	25.49	5.59
8	herbivore	herbivore	plastic	37.74	23.89
9	both levels	both levels	genetic	20.13	3.58
10	both levels	both levels	plastic	20.45	16.49

In our model simulations, food webs with constitutive, fixed defences were generally less persistent and less dynamically stable than webs that did not feature defences at any trophic level (webs 2–4 versus web 1). Food webs with intraspecific variation were more persistent and stable than their specific counterparts with no variation, i.e. variable defences at the autotroph level led to increased persistence and stability over webs that had permanently fixed defences for autotrophs (webs 5 and 6 versus web 2); the same was true for defences introduced at the herbivore level (webs 7 and 8 versus web 3) or at both levels (webs 9 and 10 versus web 4). Variability did not generally increase persistence but did on average increase stability in comparison with webs that were entirely undefended (webs 5–10 versus web 1; note: webs 5 and 9 showed reduced persistence and stability when compared with web 1); both the source (genetic or plastic) and trophic location of the variation critically influenced the magnitude of stability and persistence, and therefore the potential for rescue.

(a). Effect of the source and trophic location of variation

In general, plasticity was more effective than genetic diversity at increasing the frequencies of persistence and stability in our model food webs (table 2). Plasticity yielded 1.1 times more persistence and 3.8 times more stability than genetic diversity. In genetic diversity webs (webs 5, 7, 9), almost all persistence was in the form of unstable, oscillatory dynamics; only 17.8–21.9% of persistence manifested as stability (table 2). Plastic, persistent webs tended to be much more stable with 60.9–80.6% of persistent dynamics being equilibria (table 2). Using a specific simulation example, figure 2 demonstrates how this observed effect can contribute to population and community rescue. In web 1, with no variation for defence, the community exhibits regular oscillations at low carrying capacity (figure 2a); when carrying capacity is increased, the carnivore is quickly eliminated. In web 7, the community is at equilibrium at low carrying capacity, demonstrating an effect of diversity (figure 2b); when carrying capacity is increased, the web shows damped oscillations and slowly approaches equilibrium. In web 8, increased carrying capacity causes damped oscillations that quickly reach equilibrium (figure 2c).

Figure 2.

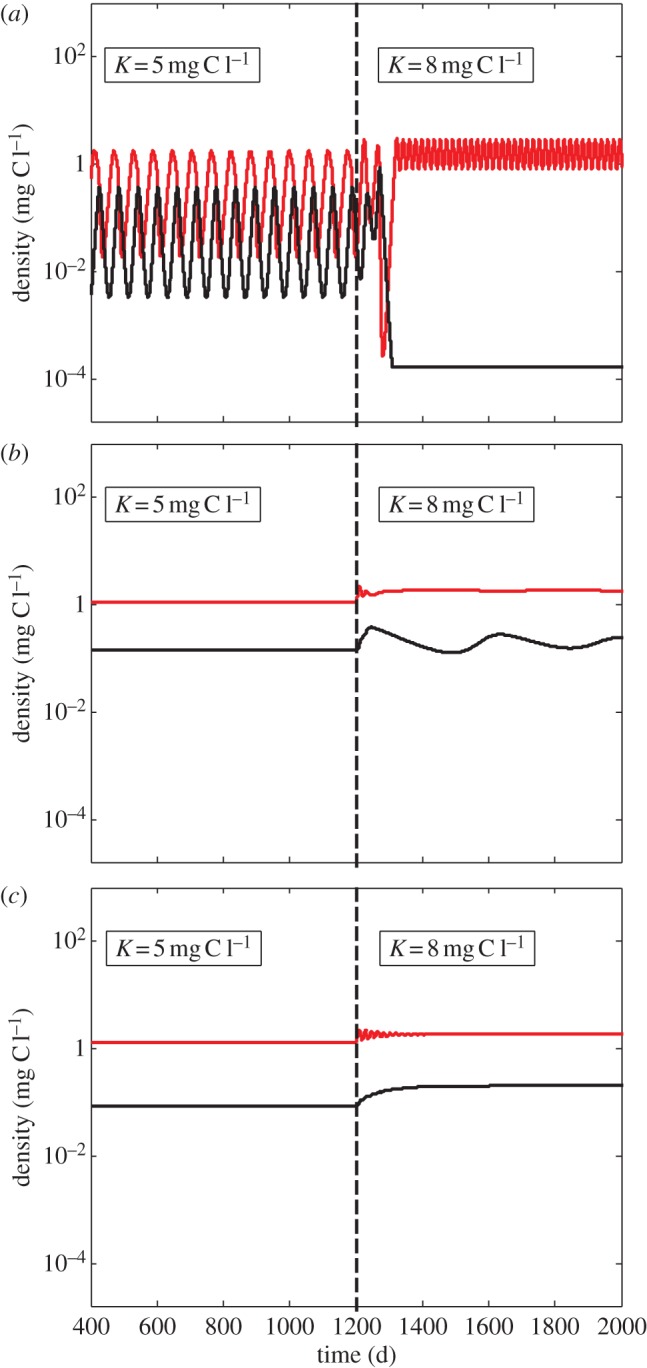
Time series of (a) web 1 with no variation and no defence (b) web 7 with genetic variation and (c) web 8 with plastic variation at the herbivore level. At the vertical dashed line, carrying capacity increases during the simulation, mimicking the sudden onset of environmental change. Black line denotes carnivore; red line denotes sum density of herbivores. Web 1 displays non-equilibrium dynamics before the change, both webs with variation display stable equilibrium dynamics before the change (K = 5); the increase in carrying capacity (K = 8) causes the extinction of the carnivore in web 1 (a), slowly damped oscillations of herbivores and carnivore in web 7 that eventually return to equilibrium (not shown) (b), while web 8 quickly returns to equilibrium (c). m = 0.25, β = 0.5, μ = 0.5.

We found that variation at the herbivore level had the greatest impact on persistence and stability, regardless of the source of variation (table 2). Webs 7 and 8 are the only webs that increased in both persistence and stability when compared with web 1. This means, interestingly, that variation at the herbivore level alone is more conducive to persistence and stability than when the same variation is introduced in combination with variation at the autotroph level.

At the autotroph level, we found that plasticity was less likely to promote persistence than genetic diversity (table 2); however, plasticity was far more likely to promote stability. On the contrary, we found that plasticity at the herbivore level promoted both stability and persistence when compared with genetic diversity. Finally, we found that genetic and plastic variation at two trophic levels promoted approximately equal levels of persistence; however, plastic variation promoted stability far more than genetic variation.

(b). Bifurcation analyses and strong versus weak stabilization

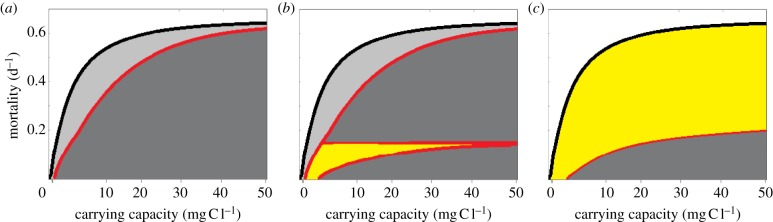
So far, we have presented the results of our numerical simulations as frequencies of persistent and stable dynamics. We now turn to bifurcation analysis, which can provide deeper insights into the mechanisms underlying the distributions of persistent and stable dynamics. Figure 3 illustrates our general framework of evaluation, using a simpler version of our model: the classic bitrophic Rosenzweig & MacArthur [40] predator–prey system (figure 3a), the bitrophic system with genetic diversity in the autotroph (figure 3b), and with plasticity (figure 3c). The carrying capacity–mortality diagram shows two bifurcation lines: a transcritical bifurcation (black line), above which persistence is not possible, because the predator cannot maintain a positive growth rate; and a Hopf bifurcation (red line), which denotes the transition from stable equilibria (above) to oscillatory dynamics (below). We analysed how plasticity and genetic diversity affect the location of these bifurcation lines. Figure 3 also demonstrates two categorically distinct patterns of stabilization (‘weak’ and ‘strong’ [34]) which we introduce because they turn out to be strongly associated with the source of variability that we apply in our model food webs. Weak stabilization occurs when the transcritical and Hopf bifurcations are moved apart, but still approach the same asymptote; thus the area of stable equilibrium is larger, but still finite (figure 2b). Strong stabilization occurs when the transcritical and Hopf bifurcations approach different asymptotes (figure 2c) [34]. Only strong stabilization allows stable dynamics at some infinite parameter values (e.g. infinite carrying capacity). In the genetic web, we were able to find only weak stabilization (through the presence of a new finite set of Hopf bifurcations). In the plastic web, we found strong stabilization.

Figure 3.

Bifurcation diagrams of a bitrophic food web. Carrying capacity (K) is shown on the x-axis, and mortality (m) on the y-axis. The higher line (black) is the transcritical bifurcation; above the transcritical bifurcation (white area), the herbivore cannot maintain positive growth. The lower line (red) is the Hopf bifurcation; below the Hopf (dark grey area), population dynamics are unstable. Between the transcritical and Hopf bifurcations (light grey area), the undefended autotroph and carnivore populations are persistent and stable. In the yellow area, both autotroph populations and the herbivore are persistent and stable. (a) The classical Rosenzweig–MacArthur [40] model. (b) Weak stabilization: a new set of Hopf bifurcations are produced, but still reach the same asymptote at high carrying capacity. (c) Strong stabilization: the transcritical and Hopf bifurcations are moved apart and approach different asymptotes, thus creating a region of stability extending to infinite carrying capacity.

We now present the results of the bifurcation analysis for the tritrophic model. Because we cannot graphically present the results for all combinations of defence level β and cost of defence μ that we analysed, figure 4 shows typical bifurcation diagrams for each of the 10 food web configurations (μ = 0.5, β = 0.5, K: x-axis, m: y-axis). While all bifurcations in figure 4 are qualitatively typical, these parameters maximize the stability of webs 6 and 10 (see the electronic supplementary material, appendix B2). The bifurcation plot for the control web without variation (web 1) shows a single finite stability band (‘weak stability’; figure 4 (1)). As carrying capacity increases, mortality must also increase in order for the community to maintain equilibrium. This continues until m = 0.533, at which point the transcritical and Hopf bifurcations converge and stability becomes nearly impossible. Bifurcation plots for food webs with fixed defences (webs 2–4) are qualitatively the same, but the transcritical bifurcation is shifted downwards (i.e. in the presence of the defended autotrophs or herbivores, the carnivore can tolerate less mortality), in agreement with results given in table 2. We were unable to find strong stabilization in any of the food webs with genetic diversity, i.e. the transcritical and Hopf bifurcations always converged at high carrying capacity resulting in finite areas of stable dynamics (figure 4 (5,7,9)). On the contrary, we found strong stabilization was possible in all of the food webs with plastic variability (figure 4 (6,8,10)).

Figure 4.

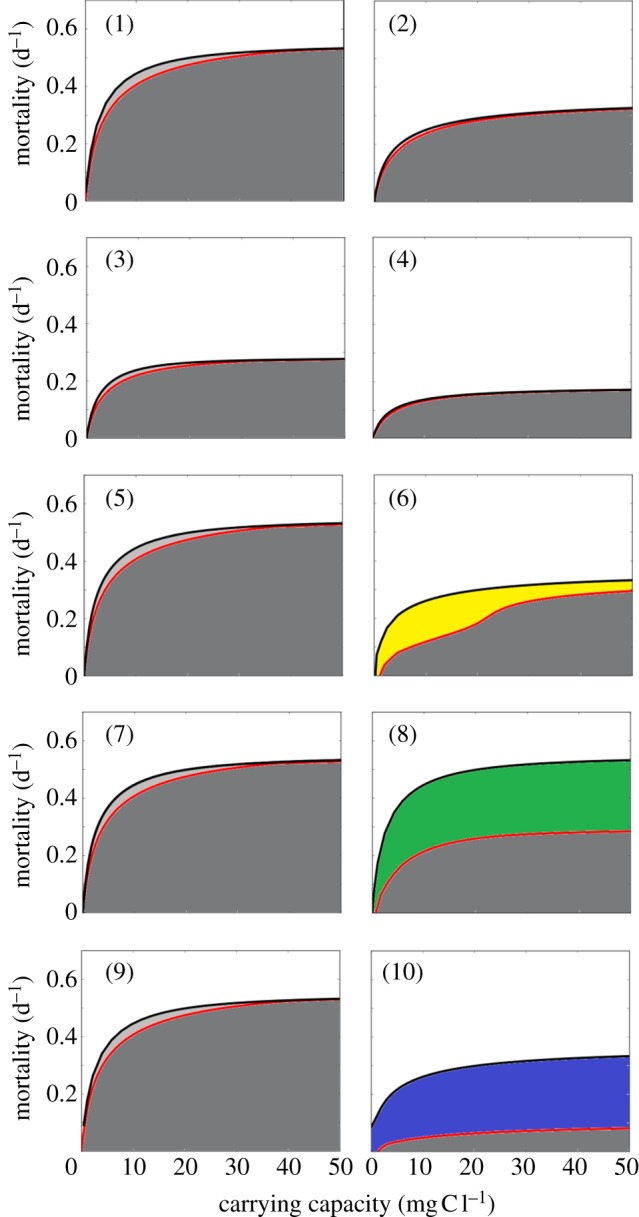
Bifurcation diagrams of all 10 food webs. Each numbered plot refers to its corresponding numbered food web in figure 1. The higher line (black) is the transcritical bifurcation; the lower line (red) is the Hopf bifurcation. In the light grey area, the carnivore persists, at equilibrium, with one herbivore population and one autotroph population; in the yellow area, both undefended and defended autotrophs exist at equilibrium with herbivores and carnivores; in the green area, both herbivore populations persist, at equilibrium, with the autotroph and carnivore; in the blue area, both herbivore populations and both autotroph populations persist, at equilibrium, with the carnivore; for description of other colours stability properties, see figure 3. Note that the transcritical and Hopf bifurcations converge at high carrying capacity for all webs except 6, 8 and 10 (the plastic webs). Note the similarity of webs 5, 7 and 9 to web 1. β = 0.5, μ = 0.5.

Specifically, genetic variation at the autotroph level (web 5) produces a single finite stability band (figure 4 (5)); its area and position are nearly identical to those in web 1 because the defended type is eliminated. Plastic variation at the autotroph level (web 6) can produce a narrow infinite stability band (indicating strong stabilization), which exists between m = 0.345 and m = 0.365 (figure 4 (6)).

Genetic variation at the herbivore level (web 7) can produce one or two finite stability bands (figure 5); the second band exists only in 14 per cent of the μ–β parameter range. Outside this parameter range, this web looks very similar to web 1 (figure 4 (7)) because the defended type is eliminated. Between the two stability bands, the community exhibits stable limit cycles; therefore, the three lower bifurcations are Hopf bifurcations (supported by numerical simulation analysis). The lower band contains both defended and undefended types and is possible because of predator-mediated coexistence. Plastic variation at the herbivore level (web 8) produces a single, broad and infinite stability band (figure 4 (8)); the transcritical bifurcation reaches its asymptote at m = 0.533 and the Hopf bifurcation reaches its asymptote at m = 0.305. When we consider variation at both the autotroph and herbivore levels, the genetic web (web 9) produces a single finite stability band (figure 4 (9)); this band is nearly identical to web 1 because the defended types are eliminated. Plastic variation (web 10) produces one infinite stability band (figure 4 (10)); this band occurs at lower mortalities than the band in web 8.

Figure 5.

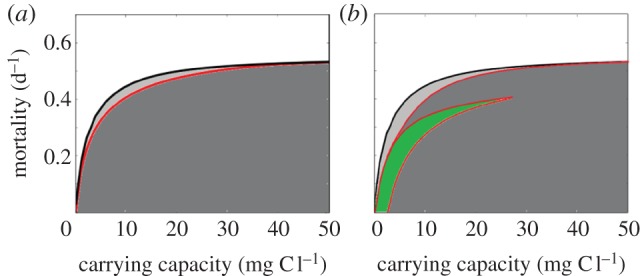
Bifurcation diagrams of web 7 (with genetic variation at the herbivore level). Description and parameter values as in figure 4, except for cost μ in figure 5b. (a) In the stable band, the defended herbivore is extinct. (b) μ = 0.15. Note the presence of a new second set of Hopf bifurcations; the upper band is identical to the band in (a); however, the lower band corresponds to an equilibrium with predator-mediated coexistence of defended and undefended herbivores. Between the upper and the new lower stability band, dynamics are characterized by oscillations.

4. Discussion

The principal concern of our study was to investigate how genetic diversity and phenotypic plasticity differentially contribute to the rescue of communities facing environmental change. ‘Evolutionary rescue’ through rapid evolution or through the use of standing adaptive genetic variation [41] is currently receiving a lot of attention [5,6,13,14,42–45], but rescue by evolution considers only one of the two potential sources of phenotypic diversity. Our ultimate goal must be to evaluate the likelihood of species survival through local adaptation in a changing environment. A realistic assessment of rescue potential will allow for a combination of genetic and plastic sources of phenotypic variation.

A few recent theoretical studies have compared how population dynamics change when either genetic or plastic variation is introduced [29–31]. In our study, we adopted a similar framework of analysing dynamic stability, but placed an emphasis on persistence versus extinction, i.e. on dynamic consequences that can be interpreted in relation to evolutionary or plastic rescue of populations and whole communities. We also paid particular attention to the trophic level at which genetic or plastic diversity is introduced into food webs and how this affects the potential for rescue.

The results support our hypothesis (i) and confirm previous findings that plasticity is significantly more likely to promote stability than genetic diversity [29–31]. There are three possible explanations for why plasticity promotes stability: (i) plasticity allows phenotypes that are maladapted to the environment to reappear when conditions are favourable, whereas in genetic webs, phenotype extinction is permanent. This would apply to our study if the abiotic environment was actively changing during simulations (it is not) or if there was a strong effect of initial conditions. We took steps to limit the impact of initial conditions and believe the reintroduction of phenotypes could only be minimally responsible for the disparity between genetic and plastic webs. (ii) Plasticity allows prey to adapt to predator density changes faster than genetic diversity [30,31]. Yamamichi et al. [31] showed that the relative abundances of prey phenotypes in plastic webs are able to change much faster than in genetic webs and that slowing the plastic response speed reduces the likelihood of stability. Although speed certainly plays a role in the observed differences between plasticity and genetic diversity, we believe there is an even greater driver for the observed differences: (iii) The reproductive switching function, S, in plastic webs creates an obligatory negative feedback loop between predator density and predator efficiency [46] that buffers predator and prey populations from extinction. If the predator becomes very abundant, prey defence increases, causing predator efficiency and ultimately, predator density to decrease (thus stabilizing the food web by moving it further from the Hopf bifurcation); on the other hand, if predators approach extinction, prey defence decreases, causing predator efficiency and ultimately, predator density to increase (thus reducing the risk of predator starvation). In plastic webs, the relative abundances of the prey phenotypes are entirely controlled by the density of the predator. At sufficiently high predator density, the switching function will cause the defended prey type to persist, even if the costs outweigh the benefits. Genetic webs also have a feedback loop, but it is not obligatorily ‘negative’, because changes in the relative abundances of prey phenotypes are driven by a combination of costs, natural mortality and predation. The defence is adaptive if the per capita growth rate of the defended type is higher than that of the undefended type; that is (for the autotroph) (1/P_d)(dP_d/dt) > (1/P_u)(dP_u/dt) which leads to β/μ > r(1 − P/K)/Hf_H(P). As a special case, we can consider the situation of a rare defended mutant invading a population containing only undefended prey (i.e. a situation with P_u = P and P_d approaches zero). Assuming the community is at a stable equilibrium (otherwise, the analysis becomes more difficult), we can set dP_u/dt = 0 from which follows H*f_H(P*) = r(1 − P*/K) − m. Plugging this into the above result yields μ < β(1−m/r(1 − P*/K)) (Here, * denotes equilibrium densities in the absence of defended prey; note that at equilibrium m/r(1 − P*/K) must be between zero and unity.) In general, whether the defence is adaptive depends not only on predator but also on prey density (because the effect of costs is reduced due to the density-dependent regulation term). Therefore, our interpretation of effects of costs is limited.

While maladaptive phenotypes persist in the plastic webs, they are eliminated from the genetic webs; thus, the parameter range where negative feedback loops are possible is much smaller for genetic webs. If genetic diversity were constrained to cost–benefit combinations that fall along continuous trade-off curves owing to adaptive evolution prior to the rescue event, such that only beneficial adaptations exist, the potential for evolutionary rescue would, on average, actually decrease for webs 5 and 9, but increase for web 7 (see the electronic supplementary material, appendix B). Webs 5 and 9 are stable only when the defended type is eliminated, adaptive evolution would allow the defended type[s] to persist, which, in turn, could cause the extinction of the carnivore. On the other hand, because both genotypes can persist in web 7, adaptive evolution can increase stability.

Furthermore, we found that plasticity, but not genetic diversity, can lead to strong stabilization and therefore, plasticity can resolve the paradox of enrichment. Strong stabilization has been shown to occur in model food webs exhibiting ecological attributes such as inducible defences, inedible prey, predator feeding thresholds or predator interference (see van Voorn et al. [47,48]). Predator interference works in a similar fashion to inducible defences; the transcritical bifurcation remains unaffected because at very low predator density there are not enough predators to induce prey to interfere with each other. As the system approaches the Hopf bifurcation, the additional predators reduce predator efficiency, either through interfering with other predators or by inducing defended prey. While these are fundamentally different processes, they both operate under the framework of creating negative feedback loops with changes in predator density.

A word of caution needs to be added when applying our results to natural communities. Genetic diversity in our study was allowed to operate only within the same confines of trait space as phenotypic plasticity, i.e. genotypes could not exceed the trait variation that was provided through plasticity. Our finding that plastic rescue is more likely than evolutionary rescue is valid within this limit of evolvability. It is, of course, conceivable that at some point, evolution will generate genetic variation that exceeds the limits of plastic response [2]. A possible scenario is that phenotypic plasticity takes the role of provisional response, rescuing populations from initial and fast environmental change of low to intermediate intensity, whereas an evolutionary, genotype-based response needs to take over if stress is severe and long lasting.

The second important result of our study is that the trophic location of variation can constrain the potential for rescue of populations and communities. Both phenotypic plasticity and genetic diversity can occur at any trophic level (from the autotroph to the top carnivore). Contrary to previous findings that variation will generally contribute to rescue [15,16,24,31], we found that variability at the herbivore is particularly likely to contribute to community rescue, and reject hypothesis (ii) that attributes the highest rescue potential to variability at the basal, autotroph level [17,28].

Variation in the herbivore is special because the presence of two herbivore phenotypes allows for two distinct relationships between carnivore dynamics and mortality/carrying capacity. In web 7 (genetic variation in the herbivore), this can create two finite bands of stability separated by an area of oscillations (figure 5b): in the upper band, only undefended herbivores are present in the population, and in the lower band, both undefended and defended herbivores are present. In web 8 (plastic variation in the herbivore), the additional herbivore phenotype allows for a wide, strongly stable band: at the upper boundary of the band, all herbivores are undefended, whereas at the lower boundary, all herbivores are defended; Vos et al. [15] obtained a similar result for a bitrophic plastic web. Variation at the herbivore level is able to create these special types of stability through a negative feedback loop that offsets changes in carnivore density with changes in herbivore defence.

Variation in the autotroph operates under the same fundamental principles; it allows the autotroph to offset changes in herbivore density with changes in autotroph defence. Why, then, doesn't variation at the autotroph level generate the same degree of rescue potential as variation at the herbivore level (compare webs 5 and 6 versus webs 7 and 8)? The reasons are different for each source of variation. In the genetic case, the increased rescue potential of web 7 (genetic variation in herbivores) derives from equilibrium coexistence of defended and undefended genotypes and carnivore (the lower stability band in figure 5b), which is possible owing to the diamond configuration of the food web [49]. At the autotroph level, equilibrium coexistence of the two genotypes, herbivore and carnivore, is impossible because of apparent competition [50], so that the stability properties of web 5 are essentially the same as those of the tri-trophic food chain (web 1). In the case of plasticity, trophic cascade dynamics prevent autotrophic plasticity from having the same impact as herbivore plasticity. Plasticity in the autotroph lowers the transcritical and Hopf bifurcations, whereas plasticity in the herbivore lowers only the Hopf bifurcation. The transcritical bifurcation defines the minimal productivity of a system, at a given mortality, that is necessary to support the carnivore. However, productivity must be transferred ‘up’ the food web, and so one can think of the transcritical bifurcation defining the minimal herbivore density of a system, at a given mortality, that is necessary to support the carnivore. When we consider plasticity only in the herbivore, as the food web approaches the transcritical bifurcation, carnivore density goes to zero, so all herbivores become undefended, carnivore efficiency increases, thus decelerating carnivore extinction. When we consider plasticity in the autotroph, as carnivore density goes to zero, herbivore density increases, which causes increased defences in the autotroph, which decreases herbivore density and accelerates extinction of the carnivore. Furthermore, the Hopf bifurcation for web 6 occurs at higher mortality values, and is therefore closer to the transcritical bifurcation, than the Hopf bifurcation for webs 8 or 10. The Hopf bifurcation for web 6 is so high because web 6 is less effective at countering increases in carnivore density. This being said, plasticity in the autotroph still enhances stability compared with the undefended tri-trophic chain (web 1) because it makes herbivore density more robust to changes in carnivore density.

Contrary to our expectations in hypothesis (iii), variation at the herbivore level alone produces more stability and persistence than variation at two levels (table 2). For the case of genetic variation, the defence and cost values that allow predator-mediated herbivore coexistence in web 7 cause the extinction of the defended herbivore when they are also present in the autotroph (web 9). Therefore, stability for web 9 is possible only when web 9 simplifies to the tri-trophic food chain (webs 1 or 2; figure 4); furthermore, this implies that stability in web 9 is possible only under the same carrying capacities and mortalities where webs 1 and/or 2 are stable. For the case of plastic variation, the addition of plasticity at the autotroph level affects web 10 through the same mechanisms described for web 6: plasticity in the autotroph effectively lowers the transcritical and Hopf bifurcations of web 8 to produce web 10.

The effect of two-level plasticity is sensitive to the concrete parameterization of the food web model. Table 2 shows the two-level plastic web has less stability than the herbivore-plasticity-only web. Nevertheless, for 75 per cent of the parameter combinations, plasticity at two levels was nearly as stable as plasticity at the herbivore level alone (figure 4 (8) and (10); electronic supplementary material, appendix B); however, for the remaining 25 per cent of parameter combinations, observed at moderate and high defence levels, web 8 is far more stable than web 10 (see the electronic supplementary material, appendix B). In this range, the Hopf bifurcation of web 10 approaches the x-axis; however, there is little stability because the transcritical bifurcation is also very close to the x-axis (data not shown). Similarly, the Hopf bifurcation of web 8 approaches the x-axis; however, there is greater stability because the transcritical bifurcation is not affected by plasticity at the herbivore level (data not shown).

Furthermore, our assumption that μ and β are identical for both trophic levels probably restricts the range of outcomes; however, the authors feel that testing different trade-offs at different levels was outside the scope of this study.

In summary, we found that variation did not generally promote rescue; rather, rescue potential depended on the trophic location and source of variation. While plasticity increased stability regardless of trophic location, genetic diversity had this effect only when present exclusively at the herbivore level. Our results suggest that variation for defence at the second highest trophic level should have a greater impact on rescue than variation at lower levels. Variation for defence traits creates negative feedback loops with changes in predator density: when defence is present at the second highest level, the negative feedback loop works to maintain the top level. When defence is present two levels below the top, it can create a positive feedback loop with changes in top-level density. Defence could also, potentially, create a negative feedback loop for changes in top-level density, if present three or five levels below the top; however, we suspect that this effect would diminish with trophic distance.

We acknowledge that some of our interpretations and conclusions are specific to introducing variation in the form of an inducible defence trait; this is particularly true for arguments involving indirect top-down and bottom-up effects in food webs. However, only a small fraction of populations' variability will typically be pre-adaptive to novel stress [2] and environmental change may produce more than one novel stressor. Defence is a general, variable trait, occurs at multiple trophic levels and may or may not serve as a pre-adaptation that helps populations persist following a change [15,16]. Overall, we feel that by modelling defensive traits we were able to provide a more general treatment of evolutionary and plastic rescue of communities than by concentrating on traits that are directly adaptive to environmental change or stress.