Predicting demographically sustainable rates of adaptation: can great tit breeding time keep pace with climate change?

Abstract

Populations need to adapt to sustained climate change, which requires micro-evolutionary change in the long term. A key question is how the rate of this micro-evolutionary change compares with the rate of environmental change, given that theoretically there is a ‘critical rate of environmental change’ beyond which increased maladaptation leads to population extinction. Here, we parametrize two closely related models to predict this critical rate using data from a long-term study of great tits (Parus major). We used stochastic dynamic programming to predict changes in optimal breeding time under three different climate scenarios. Using these results we parametrized two theoretical models to predict critical rates. Results from both models agreed qualitatively in that even ‘mild’ rates of climate change would be close to these critical rates with respect to great tit breeding time, while for scenarios close to the upper limit of IPCC climate projections the calculated critical rates would be clearly exceeded with possible consequences for population persistence. We therefore tentatively conclude that micro-evolution, together with plasticity, would rescue only the population from mild rates of climate change, although the models make many simplifying assumptions that remain to be tested.

1. Introduction

Human activities have dramatically altered the biotic and abiotic environments of many species. Species can respond to these environmental changes by evading to more suitable habitats or by adapting in situ through phenotypic plasticity and/or a micro-evolutionary response to the altered selection pressures [1]. The relative importance of these coping mechanisms for a given species or population depends on a number of ecological and evolutionary factors, for example dispersal opportunities and abilities, the limits and costs of plasticity, standing genetic variation for traits affecting fitness and generation time [1–4].

While all three mechanisms (dispersal, plasticity, micro-evolution) can enable species or populations to withstand environmental change, in the long term, evolutionary adaptation will be necessary for persistence. Evading environmental change by dispersing to more suitable areas obviously requires that such areas still exist and can be colonized rapidly enough. For species inhabiting tropical mountain habitats, for example, climate change might eliminate suitable habitat altogether and in situ adaptation might be the only option [5,6]. Range shifts in response to recent and past climate change are well documented [7,8]. However, it is highly unlikely that populations colonizing novel areas will encounter an identical suite of biotic conditions (e.g. the same set of interacting species; [9,10]) and abiotic conditions (e.g. the same relationship between temperatures and photoperiod; [11]) as in ancestral areas and hence micro-evolution is needed to adapt to these novel conditions.

Phenotypic plasticity enables individual organisms to match their phenotypes to varying conditions and thus allows species to cope with a certain amount of environmental change [12,13]. However, phenotypic plasticity is limited [14,15] and unlikely to be remain optimal if the new environmental conditions lie outside the range of previously encountered conditions under which it has evolved [16]. For example, in our long-term study population of great tits, an increasing mismatch has developed between observed breeding time and optimal breeding time because current plasticity has become suboptimal, which has intensified selection for earlier breeding [17]. While phenotypic plasticity alone is therefore unlikely to facilitate long-term population persistence, adaptive plastic responses (i.e. in the same direction as that of a moving optimum, even if not perfect) will substantially reduce extinction risk [18]. Failure to account for adaptive plasticity could thus lead to overly pessimistic assessments of extinction risk.

Evolutionary rescue (ER) refers to the phenomenon whereby micro-evolution saves a population experiencing environmental change from otherwise inevitable extinction [19–21]. For example, rabbits have evolved resistance to myxomatosis that was deliberately introduced to Australia to control rabbit over-population, and initially large reductions in rabbit numbers were soon followed by renewed population growth [22]. Another example is the well-documented and problematic evolution of pesticide and drug resistance in pest species and pathogenic organisms [23]. The majority of examples of ER, and even evolutionary responses to selection pressures in general, stem from cases of abrupt stepwise changes in the environment [23,24] (but see [25] which raises the question of whether ER is also likely under persistent directional environmental change, such as climate change).

Theoretical models [3,26,27] have assessed the conditions under which populations can adapt to continuing environmental change and demonstrated a ‘critical rate of environmental change’, defined as the maximal rate of environmental change a population can track by micro-evolution without elevated extinction risk. This rate of ‘sustainable evolution’ depends on several ecological and evolutionary parameters, e.g. maximum population growth rate, genetic variance and the strength of stabilizing selection. To the best of our knowledge, no study to date has attempted to parametrize these models of sustainable evolution with empirical data from a wild population (but see Willi & Hoffmann [28] for a laboratory setting) in order to predict the critical rate of environmental change, for example under climate change. Here, we attempt just this: we calculated the theoretical rate of sustainable evolution of breeding time in great tits, based on long-term data from a great tit study population, and the predicted rate of change in the optimal breeding time, i.e. the predicted rate of environmental change, based on climate change scenarios.

Reproductive success in great tits depends to a large extent on matching the time when food demands of the chicks are high with the period of most abundant food [29–31]. Caterpillars constitute an important food source for great tit chicks and show a pronounced peak in their abundance in spring [31]. Consequently, there is a comparably short time window when conditions are optimal for breeding. As development and growth of caterpillars are strongly temperature dependent, climate change has advanced the period of highest caterpillar abundance which, in our Dutch population of great tits, has led to a mismatch in breeding time and increasing directional selection for earlier laying dates [32]. The question now is whether this population is likely to keep pace with this ongoing environmental change caused by climate change.

To predict changes in the optimal breeding time we used a stochastic dynamic programming model. Depending on temperatures from the climate change scenario, this model predicted the optimal breeding time as a function of the timing of the food peak but also other factors, e.g. temperature-dependent costs of egg production and incubation. Taking these additional factors into account is important because elevated costs of egg production (and incubation) under cold temperatures can lead to an optimal breeding time later than that predicted by only the food supply, i.e. an adaptive mismatch [33,34].

Breeding time in great tits is phenotypically plastic in response to spring temperatures [35,36]. This plasticity will lead to an advancement of breeding time in response to warming temperatures due to climate change, but not enough to perfectly track sustained changes in the optimum. The resulting difference between the optimal phenotype and the phenotype resulting from plasticity will therefore need to be overcome by micro-evolution. Consequently, we had to incorporate plastic changes in breeding time into our calculation of the critical rate of environmental change. We accounted for phenotypic plasticity in two ways. First, we predicted phenotypically plastic changes in egg-laying dates under the same temperatures as used to predict optimal breeding time and defined the difference between these predicted egg-laying dates and the optimal breeding time as the ‘mistiming’ [33,34]. This mistiming is the ‘environmental change’ the birds have to track since it equals exactly the difference between population mean phenotype and optimal phenotype. Second, we calculated the critical rate of environmental change using the model of Chevin et al. [27], which directly incorporates phenotypic plasticity, using a linear reaction norms approach.

By using the extensive data from our long-term study population of great tits, we were hence able to obtain the genetic, ecological and demographic information necessary to parametrize these models. While this allowed us to assess the potential for ER based on adaptation of breeding time under a continuously changing environment, it also highlighted some limitations of the theoretical models.

2. Methods

(a). Study system

The data analysed come from a long-term population study of great tits (Parus major) at the Hoge Veluwe National Park in the Netherlands (52°02′ N 5°51′ E). Timing of breeding, reproductive success, juvenile and adult survival have been systematically monitored since 1955. Dates of the peak in caterpillar biomass were estimated for 1985–2010 from frass fall samples in the Hoge Veluwe [31]. While the peak date in caterpillar biomass advanced by 0.58 days per year, the birds’ breeding time advanced by only 0.25 days per year. Spring temperature from March 16 to April 20, the predictive period for the birds’ breeding time, increased by 0.07°C per year. See electronic supplementary material, §S1 for more details on study area, species and fieldwork procedures.

(b). Overview and rationale behind the models

The theoretical models of Bürger & Lynch [26] and Chevin et al. [27] provide complementary frameworks to explore critical rates of sustained environmental change. Although closely related, the two modelling frameworks differ in several fundamental respects. The model of Chevin et al. (hereafter C&al.) explicitly incorporates phenotypic plasticity but ignores stochasticity in the environment. Another important difference is that the model of Bürger & Lynch (hereafter B&L) characterizes ‘environmental change’ in terms of the rate at which the optimal phenotype changes per generation, whereas the C&al. model expresses environmental change by focusing on changes in the relevant environmental variable (e.g. rate of change in temperatures per year). When plasticity and stochasticity in the environment are ignored, the models converge and it becomes possible to directly translate from one to the other, provided that changes in the optimum can be meaningfully mapped onto changes in the environmental variable of interest.

We used a multi-step process to predict expected and critical rates of environmental change for our great tit study population. Briefly, we first predicted changes in optimal laying dates (our phenotypic trait of interest) under projected changes in regional temperatures across the period 1951–2100 according to three climate change scenarios (mild, medium and extreme). Next, we calculated the expected plastic responses in laying dates for each of these warming scenarios. This was necessary to incorporate changes in breeding time due to plasticity into the B&L model. Finally, we calculated critical rates of environmental change according to the B&L and C&al. frameworks by plugging in the relevant parameters. These were either estimated directly from our empirical data or calculated using output from our optimality model.

(c). Predicting the optimal phenotype

To model future changes in optimal trait values, we predicted optimal breeding time of great tits using a stochastic dynamic programming optimality model. This model predicts optimal egg-laying dates, depending on the stage of the breeding cycle the bird is currently in, e.g. pre-laying period or incubation, and the state of its environment. The model incorporates various ecological and physiological processes known to affect great tit laying dates and fitness, while also taking into account the stochasticity of the environment and trade-offs between fitness components. Great tits use temperatures in early spring to predict the seasonal timing of the food peak. However, because of stochasticity in temperatures around an expected seasonal profile and further development of the caterpillars after the birds have initiated breeding, this prediction of the food peak is not perfect. For more details, see electronic supplemental material, §§S2 and S3 [33].

(d). Predicting egg-laying dates

We used a proportional hazards model [37] to predict future egg-laying dates as a function of daily temperatures, as predicted from the climate scenarios. Breeding time can be viewed as ‘time to event’ and hence modelled using survival model statistical techniques such as the proportional hazards model. This approach has already been used to model breeding time in great tits and migration time in pink-footed geese [11,38,39]. We here modelled egg-laying dates dependent on current and previous temperatures and their interaction with day length. Our results were in general agreement with a previous analysis of the same population [39]. For more details, see electronic supplementary material, §S1 and Gienapp et al. [39].

(e). Parametrizing the theoretical models

(i). Bürger and Lynch model

As already mentioned earlier, the B&L model in its original formulation does not incorporate plastic changes in the phenotype directly. We hence first predicted plastic changes in egg-laying dates caused by the climate scenario temperatures using a proportional hazards model [39] (see electronic supplementary material, §S1). We then used the difference between these egg-laying dates and the predicted optimal egg-laying dates as the ‘environmental change’ that the birds need to ‘catch up’ with by micro-evolution. Thus, we effectively accounted for phenotypic plasticity ourselves first, before parameterizing the B&L model.

The ‘critical rate of environmental change’ (k_c) in the model of B&L depends on the genetic variance 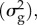the strength of stabilizing selection (V_S) around the optimum θ, and the expected per capita offspring production under environmental change (B_O).

2.1

V_S depends on the width of the fitness function (ω), with smaller values corresponding to stronger stabilizing selection and the environmental (or residual) variance in the trait :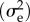

2.2

The expected per capita offspring production (B_O) depends on the maximal offspring production B for females exhibiting the optimal trait value, the width of the fitness function (ω) and the variance in population growth rate (V_λ).

2.3

The variance in population growth rate (V_λ) is obtained as follows:

2.4

where V[g_t] is the expected variation in population mean phenotype and σ_θ² is the stochastic variation in the environment around the (linear) trend.

V[g_t] depends on V_S, the effective population size (N_e), 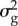and :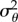

2.5

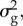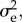To fully parametrize the B&L model, we hence need values for ω, B, 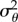and N_e.

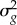and 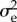were taken from a quantitative genetic analysis of egg-laying dates in our study population [40]. 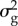estimated by this model must be halved because breeding time is a sex-limited trait in great tits [41]. The values for 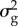and 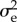were 4.3 and 23.05, respectively. The values for 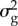explored in the sensitivity analysis correspond to a range of heritabilities from 0.09 to 0.43, which covers a range from somewhat below to somewhat above published heritability estimates of breeding time in great tits [36,40,42,43].

The width of the function (ω) was estimated from the recruitment probability of an egg in relation to egg-laying date based on observed data from our study population (3472 records of 2599 females breeding in a period of 37 years). See electronic supplemental material, §S1. In the sensitivity analysis, values of ω from 5 to 25 were explored. This range represents 33–167% of the value estimated for our population which was 14.7 and should hence cover a sufficient variation in the strength of stabilizing selection.

The parameter B in the B&L framework is the number of offspring produced per individual whose phenotype is optimal in the absence of density regulation. Because we have no direct estimate for this parameter for great tits, we used the maximum population growth rate of pied flycatchers at our study site (r₁ = 0.474; [40]) and converted this to B which gave an estimate of 1.6 offspring per individual. For the sensitivity analysis, we explored values from 1 to 2, which covers a biologically plausible range [44].

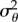was calculated using output from the stochastic dynamic programming model as the variance of the predicted optimal breeding time after correcting for the linear advancement and was 0.46.

We have no good estimate of the N_e of our study population, as the population is not closed. We arbitrarily took a value of 50, which is roughly a quarter of the breeding population. N_e has, however, virtually no effect on the estimated k_c (see electronic supplementary material, §S1 and figure S2), so uncertainties in this parameter will not affect our conclusion.

(ii). Chevin et al. model

In the C&al. framework, one must define an environmental variable believed to causally drive both selection and phenotypic plasticity in the trait of interest. In our case, this is clearly temperature, but less clear is the time period across which temperatures are important, given that actual laying dates and optimal laying dates of great tits in our study population are affected by temperatures during different periods [17]. This caveat aside, we chose mean temperatures across the period March 16–April 20 (the period across which temperatures best correlate with observed laying dates) [31] as the relevant environmental variable.

The critical rate of environmental change (η_c) in the model of C&al. depends on the maximum intrinsic rate of population increase (r_max), the strength of stabilizing selection (γ), the generation time (T), the trait heritability (h²) and genetic variance 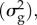the environmental sensitivity of selection (B) and the slope of the (linear) reaction norm (b):

2.6

For r_max, we used the value 0.474 (the same value as used for r when calculating the maximal offspring production parameter in the B&L framework). For the sensitivity analysis, we explored a range roughly corresponding to the range of B used for the B&L model.

To calculate γ, we made use of the following equation provided in Estes & Arnold [45]:

2.7

where ω is the width of the fitness function, as in the B&L framework, σ² is the phenotypic variance, and β is the directional selection gradient. If we assume that the population is initially well-adapted prior to the environmental change (as assumed by the B&L framework), then it experiences only stabilizing selection and β is zero. Using equation (2.7) and plugging in our values for ω² and 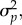we therefore estimated γ = −0.00417. Note that the negative value indicates stabilizing selection, but the absolute value must be used in equation (2.6) to calculate η_c. Again, for the sensitivity analysis, a range of values for γ was used that roughly corresponded to the value for ω used for the B&L model.

We estimated generation time T to be 2 years for our study population using a life tables approach (results not shown; a value close to Kvist et al. [46] and Garant et al. [47], who estimated T in great tits at 1.92 and 1.85 years, respectively).

The ‘environmental sensitivity of selection’ B measures how changes in the environment influence the optimum phenotype; we estimated B for each climate change scenario (see §2f) by regressing optimal egg-laying dates, as calculated by the stochastic dynamic programming model, against average temperatures during the chosen time window. Note that B need not be the same for each climate change scenario, because optimal laying dates shift at different rates but the temperature window remains fixed.

The reaction norm slope b was calculated by regressing annual laying dates, calculated from observational data across the period 1973–2010, against mean temperatures during the chosen time window. Temperature here refers to measured temperatures, the data being obtained from ‘De Bilt’ weather station of the Royal Dutch Meteorological Institute (KNMI), see (http://www.knmi.nl/klimatologie/daggegevens/download.cgi?language=eng). Accordingly, we obtained an estimate for b of −3.06 days per degree Celsius. For more details on how the models were parametrized, see electronic supplemental material, §§S2 and S3.

(f). Climate change scenarios

We used three climate scenarios: a mild, a medium and an extreme temperature increase. For the mild climate scenario, we used the IPCC climate scenario SRES A1B [48]. We obtained 17 simulated time-series of average daily temperatures for 150 years, starting 1 January 1951 to 31 December 2100, calculated by Essence simulations for a grid point centred on the southeast of the Netherlands (5.625′ E, 51.294′ N) from the Royal Netherlands Meteorological Institute (KNMI).

The recently observed (1981–2011) rate of temperature increase is higher than in the SRES A1B scenario, and therefore we used the original ‘mild’ scenario to compute the ‘medium’ and ‘extreme’ climate scenarios by doubling and tripling the temperature increase relative to the baseline period 1951–1980. See electronic supplementary material, §S1 for details.

3. Results

Predicted optimal breeding time and predicted egg-laying dates both advanced in response to the increasing temperatures obtained from the climate change scenarios (figure 1). Predicted egg-laying dates refer here to those predicted using our proportional hazards model, which takes phenotypic plasticity but not evolution into account. Optimal breeding time advanced, however, at a faster rate than predicted egg-laying dates, which led to increased mistiming, i.e. a magnifying difference between the optimal breeding time and predicted egg-laying dates (compare open and filled markers in figure 1). Mistiming increased from about 1 to 8 days over the period 1971–2100 for the mild scenario, from about 2 to 11 days for the medium scenario and from about 2 to 13 days for the extreme climate scenarios.

Figure 1.

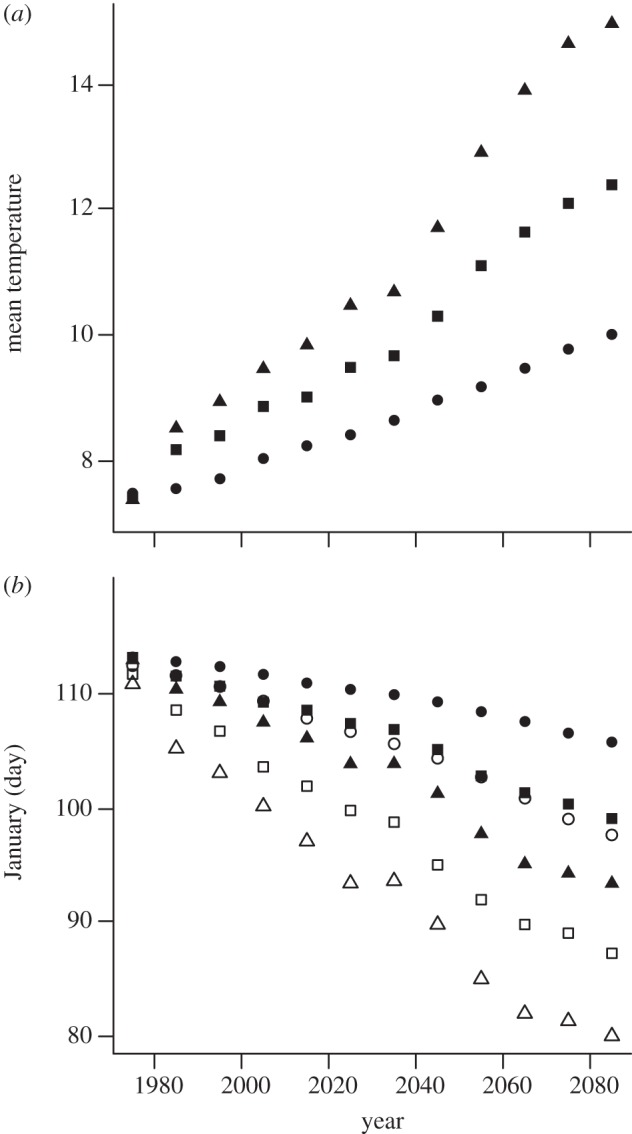
Predicted changes in spring temperature, optimal breeding time and egg-laying dates over time. In (a), mean temperature (16 March–20 April) for a mild (circles), medium (squares) and extreme (triangles) climate scenario is plotted against year. In (b), optimal breeding time (open symbols), as predicted from the optimality model, and egg-laying dates (filled symbols), as predicted from the proportional hazards model, are plotted against year. Climate scenarios are indicated as in (a).

We defined environmental change as mistiming, the difference between optimal breeding time and egg-laying date, because this is the change in the birds’ relevant environment that they cannot cope with by phenotypic plasticity in egg-laying dates. Hence, the predicted rates of environmental change for the B&L model were 0.07 days per year for the mild scenario, 0.12 days per year for the medium scenario and 0.18 days per year for the extreme scenario (figure 2). The critical rate of environmental change (k_c) calculated following the model of B&L was 0.128 days per generation. Assuming, as we did, a generation time of 2 years, this means that an increase in mistiming of 0.064 days per year would be evolutionarily sustainable, i.e. would not substantially increase extinction risk.

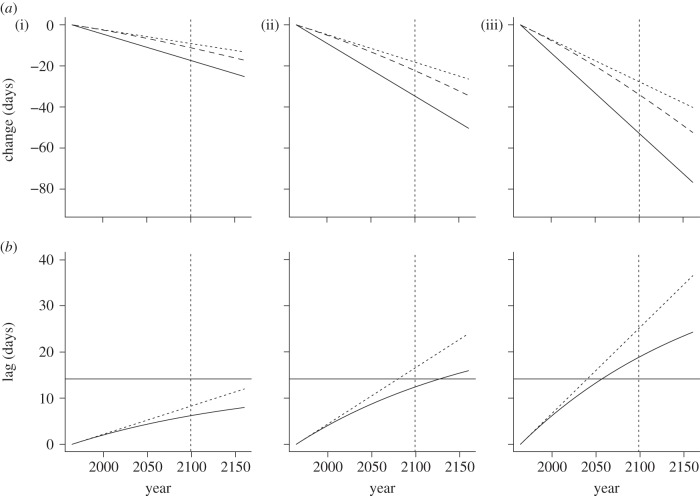
Figure 2.

(a) Predicted changes in optimal breeding time (solid line) under the mild (i), the moderate (ii) and the extreme scenario (iii); dotted lines show the predicted changes in laying dates owing to phenotypic plasticity only, whereas the dashed lines show the total change in mean phenotype (i.e. due to plasticity and micro-evolution of the reaction norm elevation, according to the B&L framework, see equation (3.2)). (b) Dotted lines show the lag (i.e. difference between the optimum phenotype and predicted phenotype) that results under the mild (i), moderate (ii) and extreme climate scenario (iii) when there is phenotypic plasticity, but no micro-evolution. Solid lines show the lag that results when there is micro-evolution in addition to the plasticity. The horizontal black lines show the critical lag, calculated according to the B&L model, beyond which extinction risk increases substantially. The vertical dotted lines are included to indicate that the optimization model was only run as far as 2100, but here we extrapolate the trends as far as 2160 to illustrate that it takes a long time for the rate of micro-evolution and the resulting lag to reach their asymptotic values. Under the mild climate scenario (i), the phenotype (dashed lines) eventually tracks the optimum in parallel, but this takes a long time. If the curves are extended out far enough, the predicted lag starts to approach the critical lag by the year 3000. So we can safely say that, over the next century, mild climate change should not substantially increase extinction risk for our great tit population. However, under the medium scenario the critical lag is reached by the year ca. 2130 and under the extreme scenario even earlier.

The critical lag (i.e. the maximum difference between the mean phenotype and the optimal phenotype, beyond which extinction risk increases substantially) can be calculated as [26]:

3.1

In our case, this gives a critical lag of 14.15 days. The expected change in mean phenotype incorporating evolutionary change and plasticity can also be calculated as

3.2

where 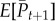is the expected mean phenotype in generation t+1, 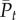is the mean phenotype in generation t, θ_t is the optimum phenotype in generation t, s is the strength of selection (see equation (3.1)) and ΔP is the change in phenotype from generation t to t+1 due to plasticity (modification of eqn 4 in Bürger & Lynch [26]). As can be seen from figure 2, the rate of change in the mean phenotype is initially slower than that of the optimum, but the mean phenotype eventually reaches an asymptotic lag. In the mild climate scenario, this asymptotic lag is 13.37 days, which is very close to the critical lag of 14.15 days. However, it takes a long time to reach this lag, and hence the predicted lag is much less than the critical lag by the year 2100 (figure 2b(i)). By contrast, the critical lag is exceeded by the year 2130, approximately, under the medium climate scenario, even though the rate of evolution is faster. Under the extreme climate scenario, the critical lag is reached by the year 2050 approximately.

The corresponding predicted environmental changes following the C&al. framework were 0.022°C per year, i.e. an increase in mean temperature from 16 March to 20 April from 1971 to 2100 for the mild, 0.044°C per year for the medium and 0.067°C per year for the extreme climate change scenario.

The critical rate of environmental change (η_c) for the model of C&al. is 0.034°C per year for the mild climate scenario, 0.051°C per year for the medium scenario and 0.102°C per year for the extreme scenario. The critical rates differ between the scenarios because the ‘environmental sensitivity of selection’ was calculated from the predicted optimal breeding time versus mean temperature from 16 March to 20 April and these relationships differ across scenarios: while for the mild scenario optimal breeding time advanced by 5.83 days per degree Celsius, it advanced by only 4.94 days per degree Celsius in the medium scenario and 3.99 days per degree Celsius in the extreme scenario.

To qualitatively assess the contributions of phenotypic plasticity versus micro-evolution to ‘ER’, we calculated the predicted rate of environmental change without taking plasticity into account for the B&L framework and the critical rates for the C&al. framework with b = 0. The predicted rates of environmental change without plasticity were 0.13 days per year, 0.22 days per year and 0.28 days per year for the mild, the medium and the extreme scenario, respectively. The critical rates (η_c) for the C&al. model were 0.016, 0.019 and 0.024°C per year for the three scenarios. Without plasticity, the critical rates would always be lower than the predicted rates of environmental change for both model frameworks and all climate scenarios.

The sensitivity of the critical rates to variation in 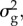, ω, 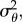B, γ, r_max, h² and B - b is shown in figures 3 and 4. There will always be some error in parameter estimation, and we could not obtain specific estimates for our population for all parameters. However, as can be seen from these figures, our general conclusions do not strongly depend on the exact value of certain parameters and are hence reasonably robust.

Figure 3.

Dependence of k_c (Bürger & Lynch) on genetic variance, width of the fitness function (a), stochastic variation in the environment and reproductive rate (b). The dot indicates the k_c calculated for our population and the lines the combination of parameter values that give the observed rate of environmental change for the mild (dotted), medium (dashed) and extreme climate scenario (solid). Note that for (b) the expected rate of environmental change for the medium scenario already lies outside the plotted parameter space.

Figure 4.

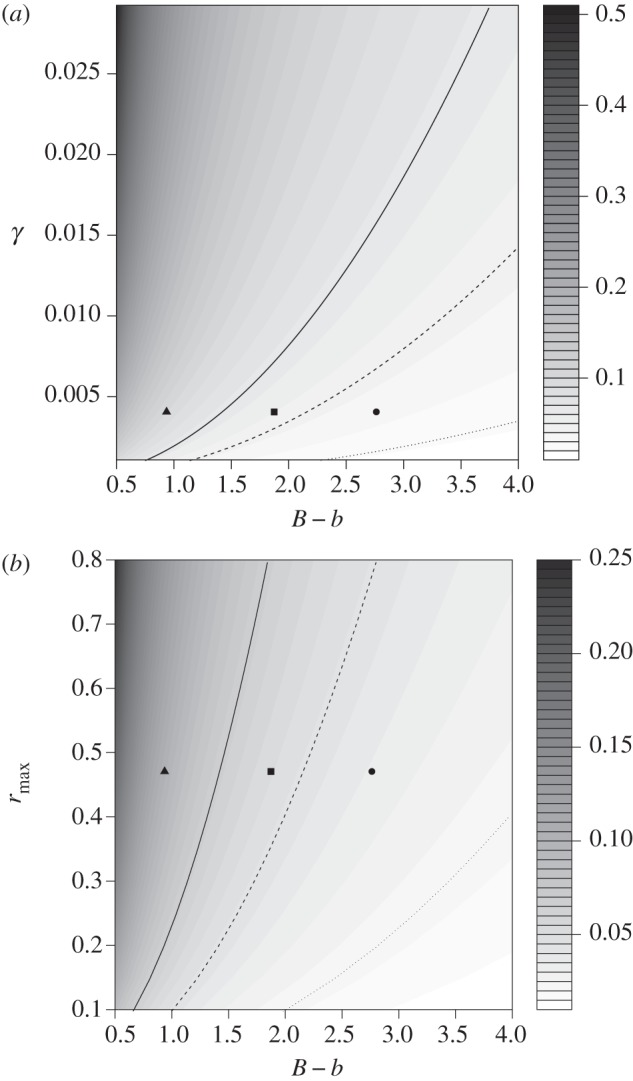
Dependence of η_c (Chevin et al.) on the difference between ‘environmental sensitivity’ and reaction norm (|B−b|), the strength of stabilizing selection (measured by γ) (a) and r_max (b). Predicted rates of environmental change (lines) and η_c (symbols) are plotted for the mild (dotted line, circle), medium (dashed line, square) and extreme climate scenario (solid line, triangle).

4. Discussion

According to our climate change scenarios, predicted egg-laying dates and optimal breeding time advanced because of increasing spring temperatures (figure 1). Optimal breeding time advanced at a faster rate than egg-laying dates under all climate scenarios, which would lead to selection for earlier egg-laying as already observed in our study population [32]. The predicted rates of environmental change under the mild climate scenario were similar to the critical rates calculated from the models. This means that the ‘evolutionary load’ imposed by the predicted advancement in optimal breeding time under this climate scenario would be sufficiently small not to substantially increase population extinction risk, at least given the various assumptions of the models, although extinction risk might be increased somewhat given that the predicted rates approached the critical rates.

While the predictions from the two models agreed for the mild scenario, they differed considerably for the medium and extreme scenarios. The predicted rates of environmental change clearly exceeded the critical rate from the B&L model. The critical rates from the C&al model, however, increased with the ‘severity’ of the climate scenario. This increase with ‘severity’ of the climate scenarios was even stronger than the increase in the predicted rates of environmental change. Consequently, our great tit population would be ‘safest’ from extinction under the strongest environmental change, which seems counterintuitive.

An important parameter determining the critical rate of environmental change η_c in the C&al model is the difference between the ‘environmental sensitivity of selection’ B, which can be viewed as the optimal reaction norm, and the trait reaction norm slope b. The closer the slopes of these two reaction norms resemble each other the larger η_c becomes (figure 4), and this can explain why we calculated a larger η_c for the more extreme scenario. We calculated B as the regression slope of optimal breeding time against the temperature most closely correlated (historically) with egg-laying dates (i.e. mean temperature from 16 April to 20 May). B was weaker under the more extreme climate scenario than under the milder ones simply because optimal breeding time advanced more strongly, and therefore correlated less well with temperatures during the fixed ‘sensitivity’ window. The parameter b was the same for all scenarios, however, so the difference between B and b was smaller under the more extreme scenario, and hence η_c was larger.

This finding highlights a general problem of describing phenological reaction norms by a (linear) regression of phenotypes against mean temperature averaged over a fixed period. This mean temperature is obviously a proxy only for the true causal variable, as it is biologically implausible that temperatures just outside the ‘predictive’ period are not relevant any more. Such a proxy probably works reasonably well under variable, but non-directionally changing, environmental conditions because the correlation between the proxy and the true causal cue does not change over time. However, this does not hold true when the environment shows a temporal trend, because then optimal phenotypes will shift relative to the ‘historically predictive’ period, such that temperatures during that period no longer predict the optimum as well (i.e. B becomes smaller). It hence seems that assuming a fixed sensitivity window for trait expression and optimal trait values might be unrealistic, as the critical window itself might change. We therefore interpret the predictions from the C&al framework with some caution, given their sensitivity to the B and b parameters (figure 4). In the following, we will hence discuss only the results from the B&L model.

In our medium climate scenario, which forecasts an increase in spring temperatures of about 4°C in 100 years, the predicted rates of environmental change are already larger than the critical rate, whereas in the extreme scenario with a temperature increase of about 6°C in 100 years the predicted rate of environmental change clearly exceed the critical rate. In the medium scenario, the critical lag is exceeded by the year 2130, approximately, while under the extreme scenario it is exceed by 2050. Consequently, climate change of these rates is expected to lead to an elevated extinction risk.

Our extreme scenario matches the so-called ‘worst-case’ A1FI scenario of the IPCC [48], which predicts an increase in global mean temperatures of circa 6°C by 2100. Soberingly, the rate of growth in carbon emissions since 2000 has already outstripped this scenario [49], suggesting that 6°C of warming is perhaps not as unlikely as previously thought, although regional predictions will of course vary hugely. Mean temperatures experienced by our study population during our reference window (March 16–April 20) increased by 2.7°C from 1973 to 2011, a rate of change of 0.07°C per year. If this temperature trend were to be sustained into the future, then according to our parametrization of the theoretical models, the risk of long-term extinction for our great tit population would be very high.

All theoretical models necessarily have to make simplifying assumptions, and the question is whether the assumptions in the models applied here have implications for our results and conclusions. In great tits approximately 50 per cent of the breeding population survives until the next season [50], but the theoretical models assume non-overlapping generation. On the one hand, adult survival will increase generation time and thereby reduce the annual rate of evolutionary change, which we accounted for in our calculations. On the other hand, the surviving adults may demographically ‘buffer’ the population against stochastic environmental variation and thereby allow population persistence under a faster rate of environmental change. Another simplification which could possibly affect the rate of sustainable evolution is the way in which selection was modelled. Fitness (offspring survival until recruitment) depended solely on the deviation of the phenotype from the optimal phenotype. However, density dependence and other processes may modify the relationship between the extent of maladaptation and mean absolute fitness. In our study population, the fitness effects of being mismatched relative to the food peak are very strong at the individual level, yet the relationship between mean mismatch and mean vital rates is relatively weak across years [51]. Moreover, there was no relationship between annual population growth and the annual strength of directional selection across the period 1973–2011, despite substantial spring warming having occurred (T. E. Reed 2012, unpublished data), suggesting that considerable maladaptation might be demographically tolerable in reality. It is also known that genetic variance is not necessarily constant over environments and that potential environmentally induced covariation between genetic variance and the strength of directional selection could affect rates of evolutionary response [52,53]. Incorporating such dynamic variation of the model parameters was unfortunately not possible, however, within the frameworks applied here. Furthermore, we would need to extrapolate the relationship of genetic variance and environmental conditions beyond the current range, which might introduce a larger error than assuming genetic variance as constant.

Besides necessary simplifying assumptions, theoretical models are sensitive to uncertainties in the input parameters. As can be seen in figure 3 for the B&L model, whether k_c is already exceeded under the mild scenario depends somewhat on the exact parameter values. However, even under substantial variation in the parameter values, (much) larger than the estimation error in our parameters, k_c is clearly exceeded by the predicted change under the medium and extreme scenario. For the C&al model, the pattern looks different with k_c closer to the predicted rate of environmental change under all scenarios. We interpreted the results of the C&al model with some caution, however, given the issues described above regarding potential shifts in the temperature-sensitivity time windows, which affected calculated values for the reaction norm slope (i.e. b parameter) and environmental sensitivity of selection (i.e. B parameter). Critical rates of environmental change are highly sensitive to |B−b| under the C&al framework; hence, uncertainty in these parameters is probably much more important than uncertainties in the other parameter estimates.

We here considered only breeding time, but genetic correlations with other traits could obviously affect and even constrain the evolution of breeding time under climate change [54,55] which would need to be taken into account when assessing the possibility of ER. Breeding time is generally correlated with clutch size in birds. While this is also the case in our population, there is no evidence that this correlation is genetic [36,40]. Consequently, we do not think that ignoring genetic correlations, a limitation imposed by the used model frameworks, would strongly affect our general conclusions, although there may of course be genetic correlations with other traits under selection, but not actually measured.

The change in phenotype is to a large extent due to plasticity (figure 2), which was incorporated directly in the C&al. model and indirectly in the B&L model. Plasticity is obviously very important to track the predicted environmental change, because when the models were re-parametrized setting phenotypic plasticity of breeding time to zero, the calculated rates of environmental change would have exceeded the calculated critical rates, even under the mild climate scenario. In this sense, ‘ER’ would not appear very likely for our great tit population in the absence of adaptive plasticity, albeit suboptimal. However, as plasticity alone is not able to shift the phenotypes sufficiently to track climate change, micro-evolution is also needed for an additional shift in phenotype over time. In a UK great tit population, adaptive plasticity still seems to be optimal and birds shift their phenology such that no mistiming occurs [12] and hence, in theory, this population could withstand limitless on-going climate change (as long as plasticity remains fully optimal). In reality, of course, plasticity is unlikely to remain perfect forever, for example if limits to plasticity are reached or if environmental change proceeds nonlinearly. In principle, there can also be micro-evolution in the plasticity itself [56] and if evolution of plasticity were to occur such that laying dates become more temperature sensitive, this would have a major effect on the critical rate. However, the C&al. model does not allow for selection to alter the plasticity (but see [57] and [58] for models that allow for plasticity evolution in other contexts), and an extension of this model in this direction would be very interesting.

The models of sustainable evolution we attempted to parametrize here [26,27] allowed us a first insight into the potential of great tits to cope with climate change by evolutionary adaptation and phenotypic plasticity. While the birds might just be able to cope with ‘mild’ climate change, the predicted rate of environmental change exceeds the ‘critical rate’ of environmental change for more extreme scenarios. Given that the observed rate of temperature change of 0.07°C per year from 1973 to 2011 already exceeds the calculated critical rates, our ‘extreme’ scenario is perhaps not so unrealistic. Consequently, ER via changes in breeding time seems unlikely for our great tit study population under moderate to extreme rates of climate change. However, the effects of maladaptation on population numbers might not be as acute as those assumed by the theoretical models applied here [51]. This caveat notwithstanding, the conclusions based on our parametrization of these models are somewhat sobering, given the fact that great tits have a comparably ‘fast’ life history with short generation time and high reproductive rate. We may hence fear that species on the ‘slower’ end of the ‘fast–slow’ life-history continuum might be very unlikely to adapt to rapid rates of continuous directional environmental change, such as might be induced by climate change.