Abstract
We present a thermodynamical approach to identify changes in macromolecular structure and dynamics in response to perturbations such as mutations or ligand binding, using an expansion of the Kullback-Leibler Divergence that connects local population shifts in torsion angles to changes in the free energy landscape of the protein. While the Kullback-Leibler Divergence is a known formula from information theory, the novelty and power of our implementation lies in its formal developments, connection to thermodynamics, statistical filtering, ease of visualization of results, and extendability by adding higher-order terms. We present a formal derivation of the Kullback-Leibler Divergence expansion and then apply our method at a first-order approximation to molecular dynamics simulations of four protein systems where ligand binding or pH titration is known to cause an effect at a distant site. Our results qualitatively agree with experimental measurements of local changes in structure or dynamics, such as NMR chemical shift perturbations and hydrogen-deuterium exchange mass spectrometry. The approach produces easy-to-analyze results with low background, and as such has the potential to become a routine analysis when molecular dynamics simulations in two or more conditions are available. Our method is implemented in the MutInf code package and is available on the SimTK website at https://simtk.org/home/mutinf.
1 Introduction
It is by now well understood that macromolecules, under biologically relevant conditions, do not adopt single conformations but display varying degrees of conformational dynamics. Equilibrium properties are thus characterized by an ensemble of conformations. Any perturbation to the system can change the energy landscape and the associated conformational ensembles; that is, both the ‘average’ or dominant conformation and the dynamics can change. These perturbations can include environmental conditions such as the solvent or temperature, ligand binding, mutations, or post-translational modifications, and can have functional consequences. For example, mutations can modulate ligand binding in this way, leading to drug resistance, and ligand binding or post-translational modification can regulate enzyme activity. Changes in conformation and dynamics need not be confined locally but can extend across the macromolecule, leading to allostery (in the broad, modern use of the word). Molecular dynamics simulations and related computational methods provide practical ways to generate macromolecular ensembles, although all such methods are limited by incomplete sampling. Many analysis methods are commonly employed to characterize the resulting ensembles, and to compare ensembles. Although routine, such analyses are fundamentally challenging because of the large number of degrees of freedom and the complexity of the conformational ensembles, which are not always well approximated by fluctuations around an ‘average’ structure. Approaches to compare molecular conformational ensembles can focus on global phenomena or localized phenomena. Approaches for capturing global differences between conformational ensembles typically reduce the dimensionality by discretizing conformational space over a subset of degrees of freedom (i.e. Cα atoms) into rapidly-converting “microstates” and slowly-converting “macrostates”1, by changing basis into a subset of the most significant collective coordinates by performing some variant of principal coordinates analysis2,3,4. Approaches for capturing localized differences between conformational ensembles typically focus on average structural changes, average flexibility changes, contact maps5, or correlated motions6,7. In this work, we describe a computational approach for comparing conformational ensembles, based on the Kullback-Leibler Divergence from information theory, that captures both conformational changes and changes in entropy/dynamics. The results are thermodynamically meaningful, easy-to-visualize, and filtered for statistical significance so that significant perturbations are easy to identify. The approach is well suited to such tasks as identifying, in an unbiased way, whether perturbations such as ligand or protein binding or post-translational modification alter conformational ensembles at distant sites, and whether two different ligands binding to the same site cause similar or different effects.
2 Overview of Method
We analyze residues’ conformational distributions in torsion space, as torsions provide an apt local description of biologically-relevant functional motions and do not have frame-fitting issues inherent to Cartesian analysis3. Especially for protein side chains, the concept of “average” positions is of limited use, as their distributions are often multimodal in torsional or Cartesian space. To quantify “population shifts” in residues’ conformational distributions, we use the Kullback-Leibler Divergence, a measure of the free energy difference between two equilibrium ensembles, where one ensemble is the “reference” ensemble and the other is the “perturbed” ensemble8,9. The Kullback-Leibler Divergence or relative entropy is a fundamental quantity in information theory, and its differential version is given by:
| (1) |
where ρ* is the probability density function (p.d.f.) of the reference ensemble, and ρ is the p.d.f. of the perturbed ensemble, and J indicates the Jacobian determinant. Torsion angles (with fixed bond lengths and angles) or orthogonal Cartesian basis sets have a Jacobian of unity, facilitating analysis. The Kullback-Leibler Divergence was previously derived to second order for a harmonic Hamiltonian and applied to normal-modes models of proteins10. It was applied to trypsinogen to not only refine a normal-mode model against atomistic simulation data, but also to quantify coupling between trypsinogen’s active and regulatory sites. To our knowledge, this study was the first to appy the Kullback-Leibler Divergence to studying allostery. In a different study, this measure was applied to identify functional sites in a large test set of proteins11. This approach to identify functional sites was based on the observation that functional sites tended to co-localize with surface sites where artificial perturbations caused a large change in the total Kullback-Leibler Divergence for the protein. The Kullback-Leibler Divergence was also applied at second order in a perturbational formulation of principal components analysis (PCA) to identify effective perturbations that contribute to differences between conformational ensembles3. In PCA of Cα atoms, a common practice in molecular dynamics simulations, these perturbation functions are identity operators on the Cartesian coordinates. The eigenvalues of the perturbation functions’ covariance matrix (or that of the Cα coordinates in typical applications of PCA) are related to the Kullback-Leibler Divergence between ensembles. To calculate the Kullback-Leibler Divergence for macromolecular conformational ensembles containing many degrees of freedom, we propose an expansion over increasing numbers of degrees of freedom. We derive a novel expansion of the K-L divergence over single degrees of freedom, pairs of degrees of freedom, etc, utilizing the Generalized Kirkwood Superposition Approximation (GKSA), which has been previously used by Matsuda12 and by Killian et al. for a configurational entropy expansion13. The most immediate application is the use of first-order terms to calculate the Kullback-Leibler Divergence for protein residues from sums of the Kullback-Leibler Divergences of their constituent torsions, which could be readily refined by use of second-order terms within residues. We expect that second- and higher-order terms will also be useful in future applications. Importantly, our expansion connects such “local” Kullback-Leibler Divergences to the global Kullback-Leibler Divergence for the conformational ensemble, which has connections to the free energy; other measures of comparison such as r.m.s. deviation or chi-squared analysis lack this strong connection to thermodynamics. Our method scales linearly with the number of residues in the protein (neglecting inter-residue second-order and higher-order terms) and is thus applicable to large macromolecules and complexes. The novelty of our work lies in: (1) providing a thermodynamics-based comparison between conformational ensembles that accounts for both changes in structure and in flexibilities, in contrast with commonly-used methods such as root-mean-squared deviation (RMSD) or root-mean-squared fluctuation (RMSF or B-factor analysis); (2) deriving an expansion that prescribes a way to compare distributions of multiple degrees of freedom (e.g., the multiple torsions of a protein residue or those of a group of residues), and a systematic way to improve the accuracy of such comparisons; and (3) the introduction of a useful quantity, which we call the “mutual divergence”—analogous to mutual information except that it uses relative entropy instead of entropy—and its higher-order analog. In the numerical implementation, we also provide a discretization correction to the Kullback-Leibler Divergence, and use bootstrap resampling on the Kullback-Leibler Divergence for statistical filtering and correction of sampling bias.
2.1 Marginal probability distributions and the Generalized Kirkwood Superposition Approximation
A protein’s geometry is most commonly described in Cartesian coordinates or in internal bond-angle-torsion (BAT) coordinates. We use BAT coordinates, and focus our analysis on φ, ψ, and χ torsion angles, as these are the most important to describe motions of biophysical relevance. The distribution of the m torsion angles (x1,…,xm) of a protein’s “perturbed” equilibrium conformational ensemble (perturbed by mutation, ligand binding, post-translational modification, etc.) give rise to a probability distribution ρ(x1,…,xm) over m degrees of freedom; these are compared with a “reference” conformational ensemble having probability distribution ρ*. The number of snapshots of a protein’s geometry required to adequately approximate this m-dimensional probability distribution function (p.d.f.) grows exponentially with increasing m. For this reason, we wish to approximate the m-dimensional p.d.f. using marginal distributions of ρ(x1,…,xm) involving only one and two variables. Such marginal distributions of order n are defined as follows:
| (2) |
| (3) |
| (4) |
where s denotes a set of degrees of freedom. In what follows, the subscript of probability densities ρn,k will either have one index indicating the number of degrees of freedom and an argument list, or be expressed in shortened notation using two indices: the first, n, indicating the number of degrees of freedom in the probability density function, and the second, {k}, indicating a set of indices of degrees of freedom comprising the p.d.f. The Generalized Kirkwood Superposition Approximation (GKSA) is of key importance for the foundation of the present work. The GKSA at order m − 1 approximates a probability distribution with m degrees of freedom using lower-order probability density functions consisting of a subset of the degrees of freedom, up to m − 1 degrees of freedom for an order m − 1 GKSA, and is perhaps easiest to express in log form:
| (5) |
where indicates all combinations of nth-order marginal probability density functions of ρ, and indicates the order m − 1 GKSA approximation of ρ. As it has been noted that the terms in this superposition are not appropriately-normalized p.d.f.’s except for the first-order terms14, it is not clear whether a GKSA-based expansion of the total Kullback-Leibler Divergence would be expected to give quantitative measures of the total free energy cost of remodeling the conformational distribution or free energy landscape of a macromolecule. Nonetheless, the successes of the configurational entropy expansion and its variants in computing configurational entropies suggests that the total Kullback-Leibler Divergence under this approximation may still be of use beyond the relative values of its terms applied in the Results section below.
3 Methods
3.1 Kullback-Leibler Divergence Expansion for three variables
To motivate the expansion of the Kullback-Leibler Divergence, consider a probability distribution ρ(x1,…,xm) = ρ(φ,Ψ,χ) that is a function of a set τ of three variables,τ = {φ,ψ,χ}. Suppose for example that these three variables denote the backbone and first sidechain torsion angles of an amino acid in a peptide or protein. The Kirkwood expansion for ρ is then:
| (6) |
where the notation denotes all q-choose-p combinations of order-p marginal distributions, and g and k denote two-member and one-member sets of degrees of freedom comprising a particular combination of these order-p marginals. Consider probability distributions ρ and ρ* over m degrees of freedom. Continuing with our example, inserting the Kirkwood expansion for ρ and ρ* into the equation above yields:
| (7) |
Converting the log of a product into a sum of logs:
| (8) |
Due to linearity,
| (9) |
For each of these sums of combinations of log terms, we can integrate out the m−n degrees of freedom that are not part of each log term, and define dτn as the differential volume element over the remaining n variables in each term.
| (10) |
Expanding, we see that this is merely the sum of Kullback-Leibler Divergences of pairwise p.d.f.’s (with respect to their equilibrium values) minus the Kullback-Leibler Divergences of individual p.d.f.’s:
| (11) |
3.2 General derivation of Kullback-Leibler Divergence Expansion
Now that we have illustrated the Kullback-Leibler Divergence Expansion for three degrees of freedom, we next provide a general derivation of the expansion to m degrees of freedom, following similar procedures used in the entropy expansion in Killian et. al. 13 and in Matsuda 12. Applying the GKSA approximation to ρ and ρ* inside the logarithm of 1,
| (12) |
The superscript above KL denotes the order of the approximation to the Kullback-Leibler Divergence. Again, indicates all combinations of nth-order marginal probability density functions of ρ, and indicates the order m-1 GKSA approximation of ρ. As before, k denotes n-member sets of degrees of freedom comprising a particular combination of these order-n marginals. Converting the log of the product into a sum over logs and taking the sum outside the integral,
| (13) |
We then integrate over the m - n dimensions that are independent of the log terms; these each integrate to unity. Next, define dτn as the differential element of volume corresponding to the n dimensions that remain (including the remaining portions of the Jacobian determinant):
| (14) |
As the term in braces in just an n-th order joint K-L divergence associated with each subset k of n degrees of freedom chosen from (x1,…,xm), which we denote as KLn,k, this simplifies to:
| (15) |
To calculate the requisite integrals, we can partition m-dimensional continuous torsional space into a discrete space of histogram bins. Each degree of freedom’s marginal p.d.f. is discretized into histogram bin probabilities pi (with reference counts ), and joint histograms for marginal p.d.f.’s involving pairs of degrees of freedom are given by bin probabilities pij (with reference counts ). These probabilities each must sum to unity: Σipi = 1, Σijpij = 1. This partitioning leads to the following expansion over contributions from single degrees of freedom, pairs, triples, etc. for m degrees of freedom:
| (16) |
Note that the signs of the terms depend on the number of terms: this is not ideal for an expansion. Thus, we need to introduce a term for the Kullback-Leibler Divergence that will play the same role as the mutual information in the entropy expansion of Matsuda 12. We call this the Mutual Divergence, M, between two degrees of freedom, with marginal p.d.f.’s specified by pi and pj and joint histogram pij in one ensemble (the “target” ensemble), and with marginal p.d.f.’s specified by pi and pj and joint histogram pij in another ensemble (the “reference” ensemble):
| (17) |
This can be equivalently expressed by combining terms into a single argument in the logarithm:
| (18) |
Here, the sums over i, j, and i j refer to one- and two-dimensional p.d.f.’s from a given pair of degrees of freedom. Alternatively, we can view this mutual divergence M2 as a cross-information minus the mutual information of the target state:
| (19) |
where indicates the mutual information between these p.d.f.’s. Mutual divergence can be generalized to higher order to provide a mutual divergence between n degrees of freedom:
| (20) |
Moreover, the mutual divergence satisfies a recursion relation analogous to Matsuda’s recursion relation for higher-order mutual information 12:
| (21) |
Here, xn-1xn indicates the joint distribution of these n degrees of freedom, as in the third term of Eq. 17. In terms of probability densities, the higher-order mutual divergence between n degrees of freedom is given by:
| (22) |
where pn is the target distribution for these n degrees of freedom, is the reference distribution, and and are their Generalized Kirkwood Superposition Approximations, which consist of up to order m − 1 probability densities. It is worth noting that the argument of the log is inverted with respect to an analogous expression for the mutual information since there is a sign change that comes from the fact that entropies are based on − pln p terms while Kullback-Leibler Divergences are based on pln(p/p*) terms. Applying this relation to the Kullback-Leibler Divergence, we obtain the desired expansion over m degrees of freedom:
| (23) |
Though this expansion and the previous expansion, Eq.16, agree when all terms are present, in practice this expansion in Eq. 23 is far more useful as it provides a well-defined way to truncate the expansion at a given complexity.
3.3 Local Kullback-Leibler Divergence
We are interested in population shifts caused by perturbations that reflect subtle changes in structure and/or dynamics in particular protein residues. We can visualize these most readily using the first-order terms from our expansion. Consider the terms in the Kullback-Leibler Divergence arising from a particular degree of freedom. These we will denote the “local” Kullback-Leibler Divergence and provide an information-theoretic, quantitative measure of the extent to which the p.d.f. for a given degree of freedom deviates from the equilibrium p.d.f. This quantifies changes in probability density with fewer assumptions and a better connection to thermodynamics than the more familiar chi-squared statistic.
| (24) |
To calculate the local Kullback-Leibler Divergence for a single protein residue, we simply sum the Kullback-Leibler Divergences between the reference and target ensemble for each of the residue’s φ, ψ, and χ torsion angles:
| (25) |
While this expression is very similar to the well-known pln p expression for entropy, with the non-uniform reference state making this the relative entropy, it is thermodynamically distinct—it is a measure of dissimilarity of two probability density functions, rather than the disorder of a particular probability density function. While presently we focus on applications of this first-order term, which has been used to compare Markov models of conformational ensembles 1 from molecular dynamics simulations but has not been widely applied on a per-residue level, the full derivation presented here establishes a systematic approach to improve our method. At the per-residue level or at the groups-of-residues level, we could improve our method by considering pairs of torsions within a residue or set of residues, etc. Furthermore, application of our method at the pairs-of-residues level or at higher order could identify changes in correlated motions, though these require substantially more sampling than first-order terms 15. This could be a promising direction for future research, but is beyond the scope of the present work. Here, however, we focus on first-order terms, as these are most readily, rapidly, and robustly calculated, and the computational cost scales linearly with system size.
3.4 Statistical corrections to the Kullback-Leibler Divergence
If the “target” ensemble is the same as the equilibrium ensemble, the Kullback-Leibler Divergence will be zero. However, in practice, when applied to ensembles generated by methods such as molecular dynamics, this is not often the case due to sample variability. In order to improve the signal-to-noise ratio in our calculation of the Kullback-Leibler Divergence, and thereby distinguish meaningful differences between conformational ensembles from artefactual population shifts due to sample variability, we calculate the K-L divergence expected from sample variability in the “reference” ensemble and use it for a significance test and to correct the calculated values. To generate a realistic measure of sample variability, we use a statistical bootstrapping approach. We split the full reference ensembles into nsims blocks (usually corresponding to clones of the same system with different random number seeds, or large continuous blocks from long simulations), and take half of the blocks at a time as a surrogate target ensemble and the complementary half as a surrogate reference ensemble. We aggregate the counts for the torsions to construct probability distributions and calculate the K-L divergence between all combinations of surrogate distributions. Any non-zero average K-L divergence between these distributions is a measure of average bias that we can later subtract from the total K-L divergence between the full “reference” ensemble and the full “target” ensemble, when it is significant. The K-L divergence under the null hypothesis that the average K-L divergence is no greater than that expected from sample variability in the reference ensemble is then given by:
| (26) |
where S denotes subsamples and SC are their complements. To test for statistical significance of the obseved Kullback-Leibler Divergence, we use the distribution of these surrogate Kullback-Leibler Divergence values to obtain a p-value for the null hypothesis that the average Kullback-Leibler Divergence is no greater than that expected from sample variability in the reference ensemble. If this p-value for a particular torsion is less than the significance level (in this case, set at a permissive α = 0.1), then the Kullback-Leibler Divergence is set to zero; if not, then the average Kullback-Leibler Divergence between the surrogate distributions described above is subtracted from the total, in a manner similar to corrections to mutual information 16, 7:
| (27) |
3.5 Truncation of Kullback-Leibler Divergence
Given the expansion in Eq. 23, one may wonder why truncation at a particular order might be appropriate, especially as the number of terms at each order increases combinatorially before contracting towards the tail of the expansion. In the analogous configurational entropy expansion 13, small molecule systems achieved remarkable agreement with entropies from rigorous free energy calculations by only including first and second-order terms in the expansion, with the highly-correlated cyclohexane requiring up to third-order terms. We note that the pairwise mutual divergence between two degrees of freedom is less than or equal to the sum of the corresponding first-order Kullback-Leibler Divergence terms. Thus, for the mutual divergence to be significantly greater than zero, at least one of the constituent degrees of freedom must be statistically significant. It is important to note that higher-order terms in Eq. 23 capture only changes in distributions missed by lower-order terms. For example, the mutual divergence captures population shifts in pairs of degrees of freedom that are missed by the first-order Kullback-Leibler Divergence. The key parameter governing the maximal order needed for convergence of the expansion is the maximum number of coupled independent components or modes (i.e. effective dimensionality) in the system. A recent study used a novel approach to partition molecular dynamics trajectories into independent subspaces of coupled modes17, and found a block-like pattern where groups of pairwise correlated modes had minimal couplings with other blocks of correlated modes in a 100 ns simulation of lysozyme. Specifically, there was a maximum of 6 modes per block, with most blocks only containing a few modes. Thus, the maximum number of coupled independent components in this study was six, so the Kullback-Leibler Divgence expansion should only require terms up to sixth order. Even though the number of terms at each order might increase, the sparsity of the matrix of mode couplings at second order suggests that a lower fraction of higher-order terms would have significant values. Other studies have also taken advantage of the sparsity of second-order couplings to more efficiently diagonalize the Hamiltonian for the protein 18, 19. To obtain better convergence of the Kullback-Leibler Divergence expansion, we could take a subset of the terms along a minimal spanning tree (treating terms as nodes), as in the MIST approach 20. Importantly, MIST avoids the combinatorial explosion in number of terms at higher orders. Practically, higher-order mutual divergences will require exponentially more data points sampled to give a robust estimate, as the volume of space increases exponentially with the number of degrees of freedom. Currently, only calculations up to third order might be practical with microseconds of simulation data 15. Neglecting high-order terms shouldn’t affect our qualitative interpretation of the pattern of local, per-residue Kullback-Leibler Divergences since there are only a small number of torsions per residue.
3.6 Jensen-Shannon Divergence
The Jensen-Shannon Divergence is a slight variation of the Kullback-Leibler Divergence, and has the added benefit of treating both “reference” and “target” ensembles symmetrically, albeit at a cost of possibly providing lower signal-to-noise due to averaging (see Eq. 28). Furthermore, the Jensen-Shannon Divergence is related to thermodynamic length, an asymptotic bound on energy dissipated in a finite-time transformation from one state to another 21. Since the Kullback-Leibler Divergence expansion is general for any “reference” distribution, we can take the new reference distribution to be merely the superposition of the former “reference” distributions, and calculate the Jensen-Shannon divergence as the mean of the Kullback-Leibler Divergences between either ensemble and this new reference distribution:
| (28) |
To apply the same statistical test and filtering as above, we take the distribution of the Jensen-Shannon Divergence under the null hypothesis as the average of the null hypothesis distributions of the Jensen-Shannon Divergences within the separate “reference” and “target” ensembles. We construct the null hypothesis distribution in this way because we want the null hypothesis to only be a function of variation within the “reference” and “target” ensembles, and not depend on their superposition, which comes into play in computing the observed Jensen-Shannon Divergence between the ensembles in Eq. 28.
3.7 Molecular dynamics simulations
We illustrate the K-L method using examples of previously-published molecular dynamics studies on human interleukin-27 and talin22 and new molecular dynamics trajectories on a kinase, PDK1. These examples highlight the role of dynamics in protein function, particularly allostery. For the new molecular dynamics simulations of PDK1, we prepared the protein and ligand with Maestro’s Protein Preparation Wizard (Schrodinger, 2009), with protonation states of histidine and Asn/Gln flips assigned by ProtAssign (Schrodinger, 2009) in the preparation wizard. Each model was solvated in SPC water23 in a cubic simulation box, and Na+ and Cl− ions were added to neutralize the system and then an additional 0.1 M NaCl was added. The full simulation system was energy-minimized using Desmond24 in two stages: (1) all protein and ligand atoms restrained with a force constant of 50.0 kcal/mol/Å−2, (2) no restraints. Minimizations were performed with no less than 10 steps of Steepest Descent minimization followed by L-BFGS optimization after a gradient of 50.0 kcal mol−1 Å−1 is reached up to a total of 2,000 steps or a gradient of 50.0 kcal mol−1 Å−1 in step 1 or 5.0 kcal mol−1 Å−1 in step 2. After full minimization of the system, an equilibration was performed. First, the systems were run at constant temperature and volume at a temperature of 10 K for 12 ps using the Berendsen thermostat25 with a relaxation time of 0.1 ps, half-sized timesteps (see below), and all protein and ligand atoms restrained with a force constant of 50.0 kcal/mol/Å−2, and velocities randomized every 1.0 ps. Subsequently, molecular dynamics at constant temperature and pressure at 10K was performed using the Berendsen thermostat and barostat 25, with all protein and ligand atoms restrained, time constants of 0.1 ps and 50.0 ps for the thermostat and barostat respectively, and velocities randomized every 1.0 ps. Then, molecular dynamics at the target temperature and pressure of 300 K and 1 atm were performed using the Berendsen thermostat and barostat with all protein and ligand atoms restrained for 12 ps using time constants of 0.1 ps and 50.0 ps for the thermostat and barostat respectively, randomizing velocities every 1.0 ps, and finally for another 24 ps without restraints and with time constants of 0.1 ps and 2.0 ps for the thermostat and barostat respectively. Production runs of 10 ns were performed on each system using the Martyna-Tobias-Klein integrator26 with a reference temperature of 300 K and a reference pressure of 1 atm. Snapshots were output every 1.002 ps. The thermostat used an equilibrium temperature of 300 K, a relaxation time of 1 ps, chain length of 2, and update frequency of 2 steps for the system and for the barostat. The barostat featured a relaxation time of 2 ps, a reference pressure of 1 atm, isotropic coupling, and a compressibility of 4.5×10−5 bar−1. Both the equilibration and production molecular dynamics simulations were performed with all bonds involving hydrogens constrained, a 2 fs time step for the bonded and short-range nonbonded interactions, and updating of long-range nonbonded interactions every 6 fs using the RESPA multiple time step approach27. For the first NVT equilibration step, 1 fs and 3 fs timesteps were used, respectively. Short-range Coulombic and van der Waals nonbonded interactions were cutoff at 9.0, and long-range electrostatics were computed using the smooth particle mesh Ewald method. Pairlists were constructed using a distance of 10.0 Å and a migration interval of 12 fs.
4 Results
4.1 An allosteric small molecule activator of PDK1
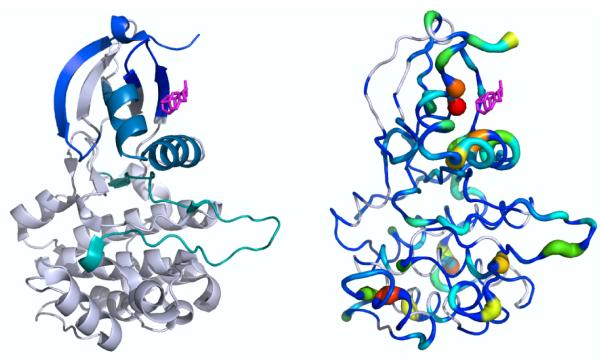
PDK1 is a member of the AGC family of kinases, which includes protein kinases A (PKA), B (AKT), and C (multiple isozymes). In recent years, small molecules have been discovered that bind outside the active site and promote or inhibit activity. Precisely how these small moleules alter PDK1’s activity is not known. The mechanism of one previously-reported noncovalent small molecule activator, PS48, was studied using hydrogen-deuterium exchange mass spectrometry experiments to determine which peptide regions of the kinase have amide protons that are protected from exchange with solvent deuterons28. In these experiments, amide protons both near the binding site and distant from the binding site (Fig. 1) showed protection from solvent exchange, indicating more stable backbone hydrogen bonds and hence reduced flexibility. Interestingly, some of these protected regions include the DFG-loop (cyan) and activation loop (teal), whose proper positioning is essential for activity. Mutation of Thr226, adjacent to the DFG sequence, to alanine abolishes the ability of PS48 to activate the kinase. We used our Kullback-Leibler Divergence method to investigate the allosteric activation mechanism. We performed a series of 10 ns molecular dynamics simulations on PDK1 with and without PS48 bound (PDB: 3HRF), saving the conformations every 1 ps. We then calculated the first-order Kullback-Leibler Divergence between apo and PS48-bound conformational ensembles from the MD simulations. The results indicate that PS48 binding caused significant population shifts in the torsion angles of residues around the compound’s binding site: the αC-helix, the beta strands 145–149 and 154–159, and the αB-helix. Furthermore, there were significant population shifts in torsion angle populations distant from the PS48 binding site, for example in the activation loop, the F-helix, and the “G” in the DFG-loop,. Though the timescale of the simulations is short relative to the timescale probed by the hydrogen-deuterium exchange experiments, the local Kullback-Leibler Divergence values and hydrogen-deuterium exchange results show compound-induced changes in the regions protected from H/D exchange. The major discrepancy is that the experiments did not show substantial protection for C-lobe residues outsdide of the DFG motif and activation loop (possibly since backbone amides here are largely protected within stable alpha-helices), whereas in the simulations a number of these residues experienced significant population shifts upon ligand binding. Nonetheless, these results serve as a powerful demonstration of how our method can identify potential allosteric effects of ligand binding or mutation.
Figure 1. Kullback-Leibler Divergence highlights PDK1 regions that show protection in hydrogen-deuterium exchange experiments upon addition of an allosteric small molecule activator.
(Left) A small molecule activator of PDK1 was previously shown to protect various peptide regions (each shown in a different color) from hydrogen-deuterium exchange. Note that the resolution of the HDX experiments is at the peptide-level, and reflect both fast and slow motions, up to the minute time-scale. (Right) Local Kullback-Leibler Divergence values between the apo and allosteric activator-bound ensembles are mapped onto the structure using PyMOL’s “β-factor putty” preset. White indicates statistically insignificant divergence, and significant divergence values increase from blue to red. Most of the regions showing protection upon ligand binding also show statistically significant K-L divergence values.
4.2 Allosteric inhibition by lysine acetylation in mitochondrial 3-hydroxy-3-methylglutaryl CoA synthase 2
Mitochondrial 3-hydroxy-3-methylglutaryl CoA synthase 2 (HMGCS2) is the rate-limiting enzyme in the synthesis of β-hydroxybutyrate and is normally acetylated at Lys310, Lys447, and Lys473, which inhibit its activity29. Both Lys447 and Lys473 are distant from the acetyl-CoA bound at the active site (Fig. 2, gray spheres). Thus, the effects of these acetylations at Lys447 and Lys443 are allosteric in nature since they inhibit activity over a distance. For each construct, wildtype and mutant, we used five molecular simulations of 11–20 ns each (started with different random number seeds) on HMGCS2 in the deacetylated (activated) form and with acetylations at various lysine residues. These MD simulations showed that acetylation of specific lysines produced significant conformational and dynamical changes in HMGCS230. As negative controls, two lysine residues whose acetylations do not inhibit activity were studied. In contrast to the other lysines, these did not show similar marked changes in structure and dynamics at the active site. The local Kullback-Leibler Divergence results showed a marked difference between the control lysine acetylations and those that inhibited enzyme activity (acetylations at Lys447 and Lys473) (Fig. 2). The control lysine acetylations did not show the pronounced divergences seen with the natural inhibitory lysine acetylations at positions 447 and 473. Importantly, acetylation at Lys447 or Lys443 causes significant population shifts in the catalytic residues: in the loop containing the active site cysteine (Cys166), and in His301. Furthermore, these acetylations both cause substantial population shifts in a turn (239–241) near the acetyl-CoA tail, in Lys83 at the other end of the acetyl-CoA near the nucleotide ring, and in a helix-turn containing residues 380–385, which buttress the loop containing the active site cysteine (residues 163–168). In summary, the local Kullback-Leibler Divergence highlighted residues showing significant perturbations upon acetylation at Lys residues distant from the active site.
Figure 2. Kullback-Leibler Divergences show position-specific effects of lysine acetylation in HMGCS2.
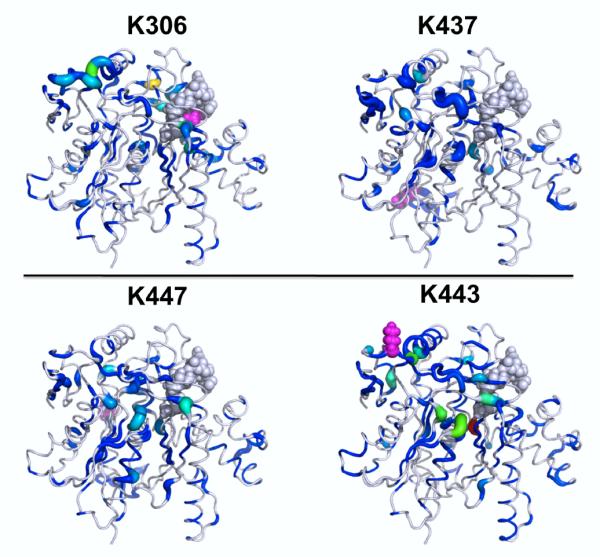
Local Kullback-Leibler Divergences between deacetylated and acetylated HMGCS2 conformational ensembles are given for different lysine acetylations (all are on the same scale). The lysine acetylated in each case is shown in purple spheres. (Top) Acetylation of Lys306 or Lys437 does not yield significant changes in structure and dynamics near the acetyl-CoA binding site (gray spheres) as assessed by the local Kullback-Leibler Divergence. (Bottom) In contrast to these negative controls, acetylation at lysine 447 or 443 causes substantial divergences proximal to the active site and the tail of the acetyl-CoA, and some background of divergences across the whole protein.
4.3 Communication between small molecule binding sites in in interleukin-2
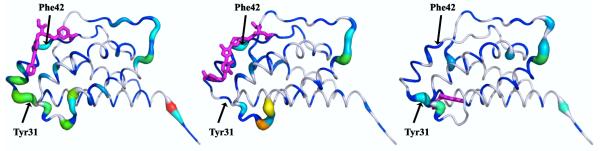
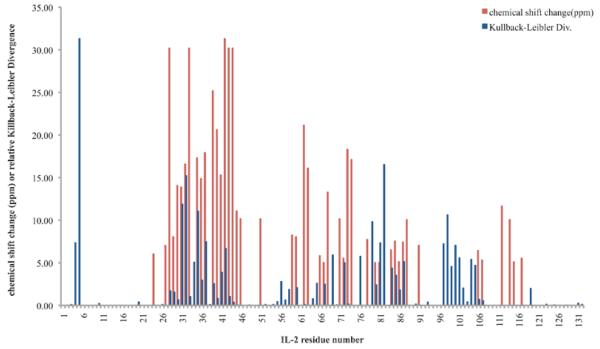
Interleukin-2 (IL-2) is a small cytokine that has been studied extensively as a model system for small molecules inhibiting protein-protein interactions. Binding of ligand to one site in IL-2 facilitates binding of a small molecule fragment to a cryptic, transient pocket, which is gated by a loop on the opposite face from the four-helix bundle32. X-ray structures were unable to show how binding to one side affected binding at the other side, making it an interesting model system for studying small-molecule cooperativity; in prior work, we identified a putative allosteric network of residues coupling the binding sites using our MutInf method7. This putative allosteric network consisted of residues from the “bottom” of IL-2 in the orientation shown to the top (where IL-2Rα binds) along a “greasy core” consisting of Leu85, Phe78, Leu80, Tyr31, Met39, and Phe42, and a “polar network” consisting of Arg81, Gln74, Lys35, and Arg38 (which is then proximal to Met39 and Phe42 in the “greasy core”). We hypothesized that the Kullback-Leibler Divergence analysis would show significant population shifts in torsion angle distributions of residues implicated in the allosteric network by our previous mutual information analysis. We calculated the local, residue by-residue Kullback-Leibler Divergence between apo (PDB: 1M47) and ligand-bound conformational ensembles from five 10-ns molecular dynamics simulations (Fig. 3). Ligand-bound conformational ensembles analyzed here include a micromolar IL-2Rα-competitive inhibitor (PDB: 1M48), a nanomolar IL-2Rα-competitive inhibitor (PDB: 1PY2), and a weak fragment that only would bind in the presence of the micromolar inhibitor at the IL-2Rα-competitive site; cooperative binding of this fragment with the nanomolar inhibitor was not tested. The smaller inhibitor (left) but not the larger one (center) shows a substantial population shift on the helix-turn-helix at the fragment’s binding site. Furthermore, the allosteric fragment (right) gives population shifts not only at its binding site but also in the helix containing hotspot residue Phe42 behind the IL-2Rα site ligands, as would be expected from thermodynamic linkage—indicating that the sampling was sufficient to observe an allosteric effect. As can be seen in Fig. 3, population shifts are seen along this structurally-contiguous network of residues upon binding of ligand at either site. In particular, Tyr31 seems to be an important mediator of allostery, as it is highlighted in both the left and right panels, whose respective ligands bind with positive cooperativity. Although this tyrosine does not directly contact the IL-2Rα-competitive inhibitor, the methionine in cyan located above it does contact the IL-2Rα-competitive inhibitor, and also contacts the allosteric fragment in the simulations. There are a number of polar residues proximal to Tyr31 that also show population shifts upon binding of allosteric fragment but that do contact the competitive inhibitor. Comparing these results to our previous study7, we find that all but two of the residues (all but Gln74 and Phe78) that were thought to be implicated in the putative allosteric network linking compound binding sites in our previous study showed statistically significant population shifts upon binding either an IL-2Rα-competitive inhibitor or an allosteric small-molecule fragment, and more specifically 5/6 “greasy core” residues and 3/5 “polar core” residues had Kullback-Leibler Divergence values in the top 25% of all residues’ divergence values. We also wondered whether our Kullback-Leibler Divergence values would highlight regions showing significant perturbations in experiments. In the case of IL-2, NMR chemical shift perturbations were available for the micromolar IL-2Rα-competitive inhibitor33, so we wondered whether regions of IL-2 showing chemical shift perturbations would also show significant Kullback-Leibler Divergence values. Such a comparison is complicated by the fact that the ligand itself, and especially its aromatic end that digs into a small pocket near a hotspot residue Phe42, will cause chemical shift perturbations in the protein residues apart from causing any shift in the protein dihedral distributions due to electronic effects and ring current effects involving aromatic residues. Nonetheless, we found in Fig. 4 that most of the regions highlighted by the NMR chemical shift perturbations also showed significant Kullback-Leibler Divergences, with the notable exceptions being large Kullback-Leibler Divergence values in residues 4-5 and 97-102 where no significant NMR chemical shift perturbations were observed, and in residues 97-116 where the two signals do not overlap well. While we do not expect Kullback-Leibler Divergences to correlate with NMR chemical shift perturbations, it is interesting that these different and complementary measures seem to be picking up on regions distant from the active site that show perturbation upon ligand binding.
Figure 3. Kullback-Leibler Divergences between apo and ligand-bound IL-2 ensembles show differential allosteric effects.
The local Kullback-Leibler Divergence between the apo IL-2 ensemble and various ligand-bound ensembles was calculated and mapped onto the apo structure. All panels are on the same scale, and ligands are superimposed for reference. These two binding sites were previously shown to be coupled through significant correlated torsional motions. 7 (Left) IL-2 with a micromolar ligand at the IL-2Rα site. (Center) IL-2 with an optimized nanomolar inhibitor at the IL-2Rα site featuring receptor-mimicking electrostatics31. (Right) IL-2 with an allosteric small molecule fragment at a cryptic site.
Figure 4. Kullback-Leibler Divergences highlight most regions showing NMR chemical shift perturbations in IL-2.
Kullback-Leibler Divergences (blue) and NMR chemical shift perturbations over 5ppm (red) are shown for each IL-2 residue for binding of the micromolar IL-2Rα-competitive inhibitor. Though quantitatively there is no significant residue-by-residue correlation between the magnitudes of these different measures of perturbation to the protein, we note that the two signals often highlight similar regions.
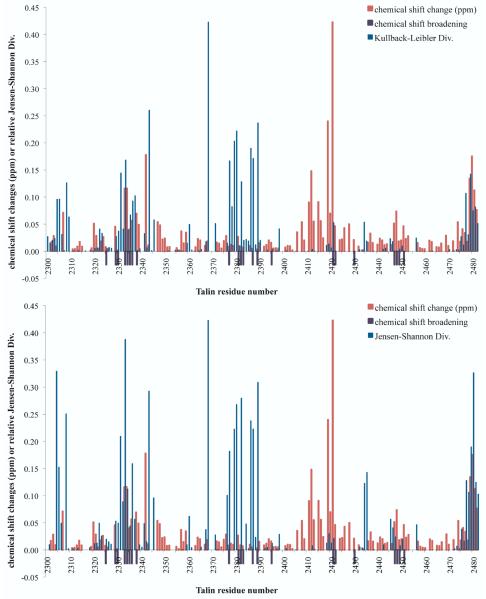
4.4 pH Regulation of Talin
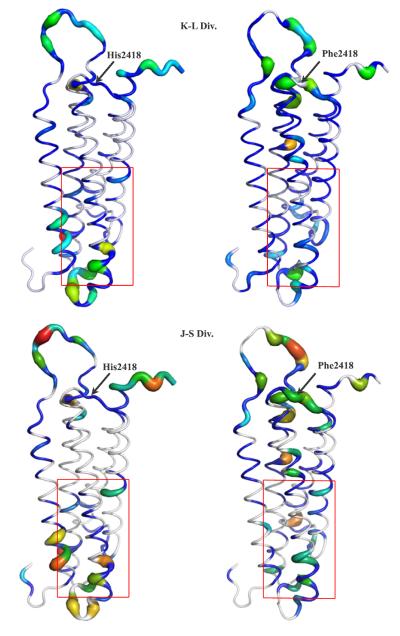
Talin is an integrin-associated focal adhesion protein that binds actin with lower affinity at high pH and higher affinity at low pH. To investigate the mechanism by which pH change alters talin’s structure, dynamics, and actin-binding ability, constant-pH molecular dynamics simulations of the I/LWEQ domain of talin1 without the C-terminal dimerization domain (PDB 2JSW) were performed at pH 8.0 and pH 6.0 for 10 ns22. A histidine and nearby acidic residues with upshifted predicted pKa values were hypothesized to constitute the pH sensor, and their protonation states were sampled during the constant-pH simulation. To test the importance of His2418, it was mutated to Phe. In NMR pH titrations, this mutant showed altered chemical shift perturbations, relative to wild type, and showed decreased F-actin binding in vitro and altered focal adhesion turnover in migrating cells. In this work, we apply the local Kullback-Leibler Divergence method to compare the conformational ensembles at these two different pH values for both wildtype and H2418F talin, using the pH 8.0 as the reference ensemble. We also wanted to compare the Kullback-Leibler Divergence and Jensen-Shannon Divergence values for this case, since our choice of reference state is somewhat arbitrary, and since the Jensen-Shannon Divergence is more robust to non-overlap of the dihedral distributions, at a cost of being less sensitive due to the reference state being an average of the two ensembles. Since the H2418F mutant showed decreased F-actin binding at lower pH, we wondered whether this mutant would show less substantial population shifts at the actin binding site relative to wildtype talin. We found (Fig. 5) that pH change caused substantial population shifts distant from the pH sensor in both cases, but that wildtype and H2418F talin in fact showed different patterns of population shifts in these actin binding site residues. The wildtype typically showed larger population shifts than the mutant in residues in the actin-binding site (boxed in red). The bottom of helices 1 and 3 in the wildtype show substantial local Kullback-Leibler Divergences; in the NMR titration experiments22, both these regions showed either chemical shift changes or line broadening. Given the population shifts in the putative pH sensor and actin binding site upon pH change in wildtype and H2418F talin, we wondered how protonation state changes in the pH sensor are propagated to the actin binding site. We suspect that a combination of correlated motions of charged residues and subtle rigid-body motions of the helices are responsible for coupling the pH sensor to the actin binding site. We observed subtle yet significant population shifts in the helices connecting the sites, which are qualitatively consistent with NMR chemical shift perturbations (Fig. 6), which generally did not show large chemical shift perturbations in these residues, except in amides proximal to the pH sensor. Both the Kullback-Leibler Divergence and Jensen-Shannon Divergence highlighted regions showing either chemical shift perturbations or line broadening in the titration, except proximal to the titrating His2418, where chemical shift perturbations would manifest direct electrostatic effects and not necessarily reflect substantial changes in the dihedral distributions.
Figure 5. Wildtype and pH-sensor mutant talin show different population shifts upon pH change.
Kullback-Leibler Divergences (top) and Jensen-Shannon Divergences (bottom) between the pH 8.0 ensemble and the pH 6.0 ensemble for Talin are shown for wildtype (left) and H2148F Talin (right). The actin-binding site region22 is shown with a red box. These divergences highlight the region proximal to the pH sensor (at the top of the structure, with His2418 labeled) and the actin-binding site.
Figure 6. Kullback-Leibler Divergences and Jensen-Shannon Divergences between the pH 8.0 ensemble and the pH 6.0 ensemble highlight regions distant from the protonation sensor that show substantial NMR chemical shift perturbations or lineshape broadening.
(Top) Kullback-Leibler Divergence values and (Bottom) Jensen-Shannon Divergence values for Talin are compared to NMR chemical shift perturbations and line broadening in a pH titration. Amides whose normalized peak intensity ratio IpH8/IpH6 were less than 51% are indicated with a purple bar below the x-axis. Chemical shift perturbations in ppm are given as abs(δω15N + 0.2δω 1 H). Generally, both divergence measures highlight regions showing substantial chemical shift pertrubations or line broadening, with the notable exception of the region proximal to the titrating His2418.
5 Discussion
We have developed a novel approach to comparing conformational ensembles that is grounded in thermodynamics, information theory, and statistics. We use the Kullback-Leibler Divergence to quantify changes in torsion angle probability distributions, which reflect biologically-relevant processes such as side chain rotamer flips, changes in local secondary structure, etc. Inspired by previous work, we developed the Kullback-Leibler Divergence expansion, which provides an approximation the Kullback-Leibler Divergence of whole molecules (proteins in this work) in terms of marginal probability density functions involving far fewer degrees of freedom. In this work, we have found that even the first-order terms can give considerable qualitative insight into which residues are most affected by perturbations such as ligand binding or pH change (i.e. proton binding). The expansion presented here to approximate the Kullback-Leibler Divergence for a macro-molecule can include couplings beyond the pairwise level. In contrast, an exact expression for the Kullback-Leibler Divergence at second order for a harmonic system was previously presented by Ming and Wall10. While Ming and Wall’s exact second-order method was based on a normal mode model, the present approach leverages data from molecular dynamics simulations that sample the free energy landscape and then account for anharmonicities in the analysis through a distribution-free measure of changes to probability densities. While the method presented here is approximate rather than exact, the use of molecular dynamics simulations provides more realistic dynamics that might reveal linkages between sites separated by long distances and through mechanisms other than vibrational couplings through semi-rigid elements, which normal mode models can often detect. In the initial applications considered here, we see evidence for allosteric communication propagating through helices, acting as semi-rigid elements. In these cases, the conformational ensembles of residues on opposite ends of the helix (or sheet) are perturbed by the same ligand or mutation, but the residues in the semi-rigid element can be minimally perturbed. We also observe many significant divergences in surface polar residues; this suggests that these residues may play a role in coupling binding at one site to a change in structure and/or dynamics at another site. As these surface polar side-chains are often not part of evolutionarily-conserved networks 34, their ability to propagate these kinds of perturbations may lie in the sum effects of multiple residues working in a parallel fashion. We speculate that, in such cases, the specific amino acid identity is less important than their physical properties, such as holding a charge or strong dipole that can reorient with the help of a flexible linker. A similar role for correlated protein side chain motions in mediating long-range couplings was suggested by DuBay and Geissler 35. There are several algorithmic improvements that could be made to our approach. Multiple calculations at different histogram bin sizes could be used, and an optimal histogram size chosen for each degree of freedom; such an approach has been shown to lead to more accurate entropy calculations 36. A k-Nearest Neighbor (KNN) approach could also be used to calculate the Kullback-Leibler Divergence37. Our residue-level analysis of the local Kullback-Leibler Divergence could be augmented by including second-order terms (i.e., the mutual divergence) within residues, which could benefit from adaptive partitioning, as in our previous work on mutual information 7.
Acknowledgement
We would like to thank Ken Dill for inspiring this work, and Steve Presse, Michael Gilson, and Andrew Fenley for helpful advice and comments on the manuscript. This work was supported by NSF Teragrid Allocation TG-MCB090109 and the Texas Advanced Computing Center (TACC). C.L.M. was supported by a PhRMA Foundation Informatics Fellowship and is currently supported by NIH grant F32 GM099197-01. This project was supported by the HARC center, NIH grant P50-GM082250. In the course of this work, analyses were performed with PyMOL (Schödinger, LLC) and the UCSF Chimera package.(39) Chimera is developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, with support from the National Institutes of Health (National Center for Research Resources grant 2P41RR001081, National Institute of General Medical Sciences grant 9P41GM103311). M.P.J. is a consultant to Schrodinger, LLC and Pfizer, Inc.
6 Appendix
6.1 Robust Histogram Estimate of Kullback-Leibler Divergence using Renyi Generalized divergence
To obtain a finite-sample size correction to the Kullback-Leibler Divergence, we adapt the derivation presented by Grassberger38. Though this was not used in the applications shown here, it is provided as an option in the program, and is provided here for completeness and for possible inclusion in other code packages. We consider the Kullback-Leibler Divergence as a limit of the Renyi Generalized Divergence,
| (29) |
where
| (30) |
For finite sample sizes there will be some uncertainty in the pi. Considering the actual histogram counts, we write:
| (31) |
To obtain < n >α, we assume a Poisson distribution for ni in successive realizations (i.e. assuming we are using a fine enough discretization such that pi ⪡ 1). For a positive integer α, we would then have
| (32) |
However, in the limit as α approaches 1, we need a continuous analog using Γ functions. Grass-berger found an asymptotic expansion for < ni >α and showed that two terms gave numerically robust results for Shannon entropies.
| (33) |
This same approximation is used in our previously-published MutInf method7. Then, we use this expression for < n > and evaluate the Renyi Generalized divergence in the α→ 1limit to give us the Kullback-Leibler Divergence. Invoking L’Hopital’s Rule, we obtain:
| (34) |
| (35) |
However, this expression is not numerically robust in practice, so we truncate the expression for < n >α at the first term:
| (36) |
which then provides a more robust estimate for Dα (P||Q):
| (37) |
Using a series approximation of the digamma function, , it can be readily seen that the Kullback-Leibler Divergence in Eq. 23 is recovered along with a correction term that decreases in size as histogram counts increase.
Footnotes
current address: Skaggs School of Pharmacy and Pharmaceutical Sciences, University of California San Diego
current address: Pfizer Global Research and Development, Groton, CT
References
- (1).Morcos F, Chatterjee S, McClendon CL, Brenner PR, López-Rendón R, Zintsmaster J, Ercsey-Ravasz M, Sweet CR, Jacobson MP, Peng JW, Izaguirre JA. PLoS Comput. Biol. 2010;6:e1001015. doi: 10.1371/journal.pcbi.1001015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Ramanathan A, Savol AJ, Langmead CJ, Agarwal PK, Chennubhotla CS. PLoS ONE. 2010;6:e15827. doi: 10.1371/journal.pone.0015827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Koyama YM, Kobayashi TJ, Tomoda S, Ueda HR. Phys. Rev. E. 2008;78:046702. doi: 10.1103/PhysRevE.78.046702. [DOI] [PubMed] [Google Scholar]
- (4).Lange OF, Grubmüller H. Proteins: Struct., Funct., Bioinf. 2008;70:1294–1312. doi: 10.1002/prot.21618. [DOI] [PubMed] [Google Scholar]
- (5).Bradley MJ, Chivers PT, Baker NA. J. Mol. Biol. 2008;378:1155–1173. doi: 10.1016/j.jmb.2008.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Lange OF, Grubmüller H. Proteins: Struct., Funct., Bioinf. 2006;62:1053–1061. doi: 10.1002/prot.20784. [DOI] [PubMed] [Google Scholar]
- (7).McClendon CL, Friedland G, Mobley DL, Amirkhani H, Jacobson MP. J. Chem. Theory Comput. 2009;5:2486–2502. doi: 10.1021/ct9001812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Qian H. Phys. Rev. E. 2001;63:042103. doi: 10.1103/PhysRevE.63.042103. [DOI] [PubMed] [Google Scholar]
- (9).Wall ME. AIP Conference Proceedings. 2006;851:16–33. [Google Scholar]
- (10).Ming D, Wall ME. Proteins: Struct., Funct., Bioinf. 2005;59:697–707. doi: 10.1002/prot.20440. [DOI] [PubMed] [Google Scholar]
- (11).Ming D, Cohn J, Wall M. BMC Structural Biology. 2008;8:5. doi: 10.1186/1472-6807-8-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Matsuda H. Phys. Rev. E. 2000;62:3096. doi: 10.1103/physreve.62.3096. [DOI] [PubMed] [Google Scholar]
- (13).Killian BJ, Kravitz JY, Gilson MK. J. Chem. Phys. 2007;127:024107–16. doi: 10.1063/1.2746329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Somani S, Killian BJ, Gilson MK. J. Chem. Phys. 2009;130:134102. doi: 10.1063/1.3088434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Killian BJ, Kravitz JY, Somani S, Dasgupta P, Pang Y-P, Gilson MK. J. Mol. Biol. 2009;389:315–335. doi: 10.1016/j.jmb.2009.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Karchin R, Kelly L, Sali A. Pac Symp Biocomput. 2005:397–408. doi: 10.1142/9789812702456_0038. [DOI] [PubMed] [Google Scholar]
- (17).Sakuraba S, Joti Y, Kitao A. J. Chem. Phys. 2010;133:185102. doi: 10.1063/1.3498745. [DOI] [PubMed] [Google Scholar]
- (18).Sweet CR, Petrone P, Pande VS, Izaguirre JA. J. Chem. Phys. 2008;128:145101. doi: 10.1063/1.2883966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Izaguirre JA, Sweet CR, Pande VS. Pac. Symp. Biocomput. 2010:240–251. doi: 10.1142/9789814295291_0026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).King BM, Tidor B. Bioinformatics. 2009;25:1165–1172. doi: 10.1093/bioinformatics/btp109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Crooks GE. Phys. Rev. Lett. 2007;99:100602. doi: 10.1103/PhysRevLett.99.100602. [DOI] [PubMed] [Google Scholar]
- (22).Srivastava J, Barreiro G, Groscurth S, Gingras AR, Goult BT, Critchley DR, Kelly MJS, Jacobson MP, Barber DL. PNAS. 2008;105:14436–14441. doi: 10.1073/pnas.0805163105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Berendsen HJC, Postma JPM, van Gunsteren WF, Hermans J. Intermolecular Forces. D. Reidel Publishing Company; Dordrecht: 1981. pp. 331–342. [Google Scholar]
- (24).Bowers KJ, Chow E, Huafeng X, Dror RO, Eastwood MP, Gregersen BA, Klepeis JL, Kolossvary I, Moraes MA, Sacerdoti FD, Salmon JK, Yibing S, Shaw DE. Proceedings of the ACM/IEEE Conference on Supercomputing (SC06); 2006.pp. 43–43. [Google Scholar]
- (25).Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- (26).Martyna GJ, Tobias DJ, Klein ML. J. Chem. Phys. 1994;101:4177–4189. [Google Scholar]
- (27).Tuckerman M, Berne BJ, Martyna GJ. J. Chem. Phys. 1992;97:1990–2001. [Google Scholar]
- (28).Hindie V, Stroba A, Zhang H, López-Garcia LA, Idrissova L, Zeuzem S, Hirschberg D, Schaeffer F, Jørgensen TJD, Engel M, Alzari PM, Biondi RM. Nat. Chem. Biol. 2009;5:758–764. doi: 10.1038/nchembio.208. [DOI] [PubMed] [Google Scholar]
- (29).McGarry JD, Foster DW. Annu. Rev. Biochem. 1980;49:395–420. doi: 10.1146/annurev.bi.49.070180.002143. [DOI] [PubMed] [Google Scholar]
- (30).Shimazu T, Hirschey MD, Hua L, Dittenhafer-Reed KE, Schwer B, Lombard DB, Li Y, Bunkenborg J, Alt FW, Denu JM, Jacobson MP, Verdin E. Cell Metab. 2010;12:654–661. doi: 10.1016/j.cmet.2010.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Thanos CD, DeLano WL, Wells JA. PNAS. 2006;103:15422–15427. doi: 10.1073/pnas.0607058103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Hyde J, Braisted AC, Randal M, Arkin MR. Biochemistry. 2003;42:6475–83. doi: 10.1021/bi034138g. [DOI] [PubMed] [Google Scholar]
- (33).Emerson SD, Palermo R, Liu C-M, Tilley JW, Chen L, Danho W, Madison VS, Greeley DN, Ju G, Fry DC. Protein Sci. 2003;12:811–822. doi: 10.1110/ps.0232803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Halabi N, Rivoire O, Leibler S, Ranganathan R. Cell. 2009;138:774–86. doi: 10.1016/j.cell.2009.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).DuBay KH, Geissler PL. J. Mol. Biol. 2009;391:484–497. doi: 10.1016/j.jmb.2009.05.068. [DOI] [PubMed] [Google Scholar]
- (36).Baron R, Hünenberger PH, McCammon JA. J. Chem. Theory Comput. 2009;5:3150–3160. doi: 10.1021/ct900373z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Piro P, Anthoine S, Debreuve E, Barlaud M. International Workshop on Content-Based Multimedia Indexing, 2008 (CBMI); 2008.pp. 230–235. [Google Scholar]
- (38).Grassberger P. Phys. Lett. A. 1988;128:369–373. [Google Scholar]
- (39).Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. J. Comput. Chem. 2004;25(13):1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]