Incorporation of evolutionary information into Rosetta comparative modeling

Abstract

Prediction of protein structures from sequences is a fundamental problem in computational biology. Algorithms that attempt to predict a structure from sequence primarily use two sources of information. The first source is physical in nature: proteins fold into their lowest energy state. Given an energy function that describes the interactions governing folding, a method for constructing models of protein structures, and the amino acid sequence of a protein of interest, the structure prediction problem becomes a search for the lowest energy structure. Evolution provides an orthogonal source of information: proteins of similar sequences have similar structure, and therefore proteins of known structure can guide modeling. The relatively successful Rosetta approach takes advantage of the first, but not the second source of information during model optimization. Following the classic work by Andrej Sali and colleagues, we develop a probabilistic approach to derive spatial restraints from proteins of known structure using advances in alignment technology and the growth in the number of structures in the Protein Data Bank. These restraints define a region of conformational space that is high-probability, given the template information, and we incorporate them into Rosetta’s comparative modeling protocol. The combined approach performs considerably better on a benchmark based on previous CASP experiments. Incorporating evolutionary information into Rosetta is analogous to incorporating sparse experimental data: in both cases, the additional information eliminates large regions of conformational space and increases the probability that energy-based refinement will hone in on the deep energy minimum at the native state.

Introduction

There are two sources of information available for prediction of protein structure in the absence of direct experimental data. The first source is based on physical chemistry, in particular, our understanding of the energetics of interactions within macromolecules. Folded protein structures are likely to be at global-free energy minimum, and, given a sufficiently accurate description of the energetics, structures can be accurately predicted by searching for very low energy conformations of the polypeptide chain. The second source is evolutionary: evolutionarily related proteins nearly always have similar structures,¹ and, with the very large number of protein structures already solved, there is likely to be information from structures of homologous proteins that can be used to predict the structure of a protein of interest.² The Rosetta program developed in our group primarily uses the first source of information, and structure prediction is essentially a search for the lowest energy structure in a physically realistic all-atom force field. In contrast, the Modeller program, developed by Andrej Sali and coworkers, uses primarily the second source of information; structure prediction with Modeller focuses on the satisfaction of spatial restraints derived from homologous protein structures.³ In this work, we combine the strengths of the two approaches by incorporating spatial restraints derived from homologues into the Rosetta high-resolution modeling protocol.

Methods

Structural databases

A nonredundant database of 7786 proteins solved by X-ray crystallography was selected using the PISCES server.⁴ Alignments between all pairs of proteins were created using HHSearch,⁵ and alignments with statistically insignificant similarities (HHSearch e-value >1) were discarded. HHSearch was configured to compare predicted secondary structure of the query sequence against a database of sequences with DSSP-assigned secondary structure. All alignment pairs with significant e-values were considered, independent of structural similarity between pairs in order to simulate a situation in which structural templates are found for a protein of unknown structure. We used these sequence-based alignments between proteins of known structure to estimate parameters for inferring spatial restraints. A set of 250 proteins was excluded in order to benchmark different probabilistic models for generating restraints (see Fig. 2 and Model Calibration on an Independent Test Set). Any proteins involved in the CASP7 experiment⁶ were discarded from both the training and testing sets, so that these proteins could be used to benchmark structural prediction using the spatial restraints.

Figure 2.

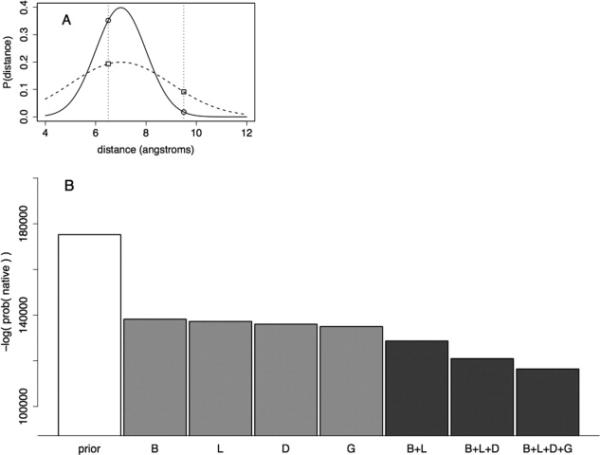
Model evaluation based on likelihood of independent test set. A: Illustration of model evaluation with distance predictions based on two Gaussians. Both Gaussians have a mean of 7.0 Å and a standard deviation of 1.0 (solid line) or 2.0 Å (dashed line). If the native distance occurs at 6.5 Å, the sharper Gaussian (solid line) is a better model. If the native distance occurs at 9.5 Å, the wider Gaussian (dashed line) is a better model. B: Different models were assessed based on the likelihood of distances from an independent set of aligned proteins. Each bar shows the likelihood of sampling a set of atom-pair distances using a fixed set of alignments and different variables to construct the models. The letters below each bar list the input features used to construct the model (B—burial in template structure, L—local sequence similarity, D— distance from a gap, and G—global sequence similarity). The prior model is a Gaussian model based only on sequence separation of the residues in the linear sequence (see Methods section) and is shown here as a negative control. The middle four bars show the performance of models based on single features, while the final three bars represent models based on two, three, and four features. All four single-variable models out-perform the prior model. Adding predictors to each model improve the likelihood of sampling the native atom-pair distance, which supports the use of all four variables in estimating deviations from template structures.

Distance restraints from a single template

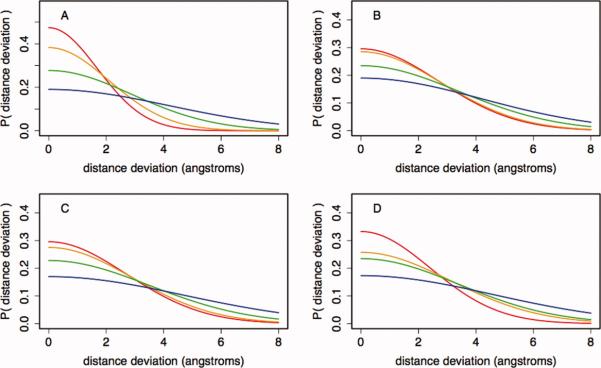
For deriving distance restraints, pairs of amino acids aligned by HHSearch⁵ were examined. HHSearch aligns protein sequences with protein structures; therefore, the alignments of pairs of proteins are not symmetric. Following standard procedure, we refer to the protein used to search the database as the query and the structures found in the database search as templates. We computed statistics over all pairs of aligned residues with Cα atoms less than 10 Å apart in the template structure that was separated by more than 10 residues along the query sequence. For each of these pairs, the magnitude of the difference in distances between the C atoms at the two positions in the aligned structures was computed (|R1_ij – R2_i’j’| where R1_ij is the distance between atoms i and j in structure 1, and R2_i’j’ is the distance between the equivalent atoms i’ and j’ in structure 2). These distance deviations were placed in a bin based on the sequence similarity and structural context of the two residues. The bins are defined by the global alignment quality (G—the negative log of the HHSearch e-value), the residue-pair alignment quality (L—the BLOSUM62⁷ score for aligned residue pair), the average distance to an alignment gap (D—the distance in number of residues from the aligned pair to the nearest gap in the sequence alignment), and the burial in the template structure (B—number of Cβ atoms within 8 Å of the template residue Cβ). The value for G is a constant for all residues from a given alignment, and values for L, D, and B are averaged over the pairs of aligned residues, as there are two residues involved in each distance calculation. These features are similar to the features used in the original Modeller paper,³ which were sequence identity, average per-residue solvent accessibility, local sequence similarity, and distance from an alignment gap. In our approach, we have replaced solvent accessibility with burial and sequence identity with HHSearch e-value, in addition to drastically increasing the database size. The dependence of the distance deviations on each variable is shown in Figure 1.

Figure 1.

Dependence of distance deviations on individual features. Conditional probability distributions were calculated using the features and approach outlined in Methods section, which follows the Modeller approach for deriving distance restraints.³ Each panel shows the distribution of distance deviations conditioned on a single feature (A—global sequence similarity, B—local sequence similarity, C—burial in the template structure, and D—distance from an alignment gap). Lines represent the distribution of deviations for quantiles of the feature (red, 0–25%; orange, 26–50%; green, 51–75%; blue, 76–100%). Boundaries that define quantiles for each variable are listed in Supporting Information Table SI.

Following the tabulation of the distance deviations, pseudocounts were added to each bin in order to reduce artifacts arising from small counts:

$$P(\Delta r\mid G,L,B,D)=\frac{N_{\mathrm{obs}}(\Delta r\mid G,L,B,D)+CF\left(\Delta r\right)}{N_{\mathrm{obs}}(G,L,B,D)+C}$$ (1)

P(Δr | G, L, B, D) is the distribution of deviations between template and native Cα–Cα distances given particular values of G, L, B, and D. F(Δr) is the observed distribution of distance deviations across all values of G, L, B, and D. N is the total number of observations in the bin, N_obs(Δr | G, L, B, D) is the number of observations with distance deviation Δr, N(G, L, B, D) is the total number of observations with the given values of G, L, B, and D, and C is the number of pseudocounts. Zero-mean Gaussians were fitted to the smoothed distributions in each bin. The 10,000 fitted standard deviations, one for each bin, are the parameters of our model.

Given this model, the prediction of restraints from a single alignment to a single input template is straightforward:

1. Iterate over all pairs of query residues that are separated by more than 10 residues along the linear sequence.

2. If a residue pair is unaligned to the template structure, or the distance between the equivalent atoms in the template structure is >10 Å, assign to these atoms a restraint given by the expected distance distribution given only sequence separation in the linear chain.

3. Otherwise, calculate the values of four predictor variables based on the alignment and the template structure. Assign a Gaussian restraint to these residues with mean given by the distance between the equivalent atoms in the template structure and standard deviation from the table based on the values of G, L, B, and D.

Combining predictions from multiple templates

More accurate distance predictions can potentially be obtained if the sequence of interest can be aligned to more than one template. The procedure for deriving distance restraints can be extended to incorporate predictions for multiple templates by combining predictions on the same pair of atoms using a weighted mixture of Gaussians. The most straightforward approach would be to weight the contributions equally. Alternatively, predictions can be weighted based on the probability that the alignment is locally correct:

$$P\left(d\right)=\sum _{i}P\left({\text{alignment}}_i\right)P(d\mid {\text{alignment}}_i)$$ (2)

The second term is the single sequence model from the previous section. The first term is the confidence in the alignment i compared to all other alignments. As in the Modeller approach, we estimate the first term in (2) using:

$$P\left({\text{alignment}}_i\right)=\frac{{\sigma }_i^{-k}}{\sum _j{\sigma }_j^{-k}}$$ (3)

where r_i is the distance between the equivalent atoms in template i, and σ_i is the standard deviation associated with that distance. The parameter k determines the extent to which predictions with lower standard deviations dominate over those with higher standard deviations, with a value of k = 0 giving all predictions equal weight. Experiments were performed on an independent set of data to find a value of k that maximized the probability of observing the data (see Model Calibration on an Independent Test Set). This approach to combining information from multiple templates is similar to the Modeller approach,³ but the weights here are based on all predictor variables rather than just the local sequence similarity, and the parameter k can be set using the independent data.

The restraint potential for a pair of positions, given a set of aligned templates, is then a mixture of Gaussians with weights dependent on the standard deviation:

$$P\left(r\right)=\sum _i\frac{{\sigma }_i^{-k}}{\sum _j{\sigma }_j^{-k}}\frac{e^{-\left(\frac{{(r-ri)}^2}{2{\sigma }_i^2}\right)}}{\sqrt[]{2\pi {\sigma }_i^2}}$$ (4)

In the equation above, r_i is the distance between the equivalent atoms in template i, and sd_i is the standard deviation associated with that distance. As the denominator of the Gaussian term is constant with respect to r_i, it can be ignored or precomputed to speed up computation.

Model calibration on an independent test set

The models as currently defined have several free parameters, including the choice of which predictor variables to use in deriving restraint potentials and how to combine predictions from multiple templates. Before populating the histograms with data from the training set, a random subset of 250 proteins was set aside. Alignments of the proteins in this independent set to all proteins in the training set were generated. A random subset of 50,000 residue pairs for which at least one template made a distance prediction was examined. Models were evaluated using the log-likelihood of observing the independent data given each model (Figures 2 and 3). This quantity avoids rounding error associated with multiplying many small numbers, and will approach 0 as the predictions approach perfection.

Figure 3.

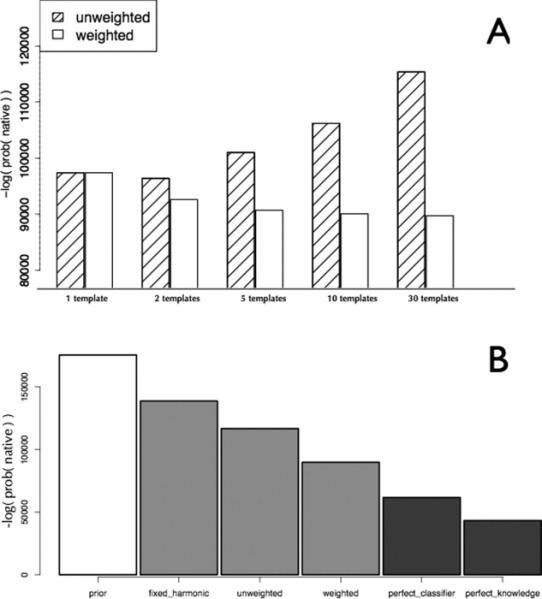
Likelihood increases using weighted predictions from multiple templates. Each bar represents the likelihood (negative log-probability) of sampling the native distance between two Cα atoms under different Gaussian mixture models. A: Gaussians were derived using the approach outlined in Methods section and evaluated using the likelihood test outlined in Figure 2, and Gaussians restraining the same pair of atoms were combined to produce a Gaussian mixture model. The probability of sampling the native distance was calculated from the resulting probability distribution. Each bar plots the negative log-likelihood of sampling the native distance, which decreases as predictions become more accurate. Shaded bars represent a model in which all predictions are given equal weight, and open bars represent a model in which predictions are given a weight proportional to sd^–10. B: Probabilistic models are compared using the likelihood test outlined in Figure 2. Prior is a Gaussian model that models query distances based solely on the sequence separation between residues in the query sequence, fixed_harmonic is a Gaussian mixture model that assigns a fixed-width standard deviation to each template’s prediction and an equal weight for each prediction, unweighted represents a model with standard deviations given by the predictor described in Methods section and an equal weight for each prediction, and weighted is a model with standard deviations estimated by the same predictor and weights estimated as a function of that standard deviation. The perfect_classifier model represents a model that adjusts weights for each prediction in order to maximize the probability of observing the native distance, and perfect_knowledge represents a model in which the query distances are modeled using a Gaussian model with a standard deviation of 1.0 Å.

Comparative modeling with spatial restraints

In previous work,⁸ our group previously described an approach to homology modeling that uses an input protein sequence, a template protein structure, and an alignment relating the two. This approach has the following steps:

1. Generation of incomplete models by copying coordinates over aligned regions.

2. Completion of the models by building unaligned regions using the Rosetta fragment-based loop-modeling protocol.⁹ This step uses a centroid representation of the protein side chains and explicit backbone atoms, a low-resolution energy function, fragments from known protein structures, and kinematics that allow rebuilding of the unaligned regions without perturbing coordinates in the aligned regions.

3. Refinement of the Rosetta full-atom energy function using discrete optimization of side-chain rotamers, small perturbations to the local backbone followed by gradient-based minimization, and a ramping repulsive function to allow atomic clashes to be resolved smoothly.¹⁰

4. Iterative rebuilds of randomly selected sections of the chain, followed by refinement. Model selection at each stage alternates between diversification and intensification.

Here, a single iteration (steps 1–3) is carried out for computational efficiency. The restraints are combined with the Rosetta energy function during optimization by adding to the calculated energy:

$$-\ln \left(P\right(\text{structure}\mid \text{restraints}\left)\right)=\sum _{i,j}-\ln \left(P\right(d_{i,j}\mid r_{i,j}\left)\right)$$ (5)

The subscript pair i,j denotes a pair of residues i and j, d_i,j is the distance between the Cα atoms of residues i and j, and r_i,j is the restraint operating on those atoms. The probability of this distance given the restraint is estimated using the Gaussian mixture from Eq. (4). A weight on the restraint term of 0.1 gives the restraints approximately half the contribution of the Rosetta full-atom energy. Restraints with mean distance > 10 Å were discarded in order to speed up evaluation of the restraint score. The restraint potential was also shifted downward by subtracting the value of the potential at 10 Å in order to make the scores negative for structures that agree well with the restraints.

To test the modified version of the Rosetta rebuild and refine protocol that incorporates restraints, a set of 20 proteins from the CASP7 experiment was used as a test set; these were excluded from both the original training set and the independent test set. Alignments were generated to template structures using HHSearch, considering a maximum of 10 alignments with e-values less than 1 and used the approach outlined above to derive distance restraints. We tested protocols that incorporated restraints into the rebuilding and model refinement portions of the protocol, and, as a control, performed the same procedure without restraints. An ensemble of 10,000 models was generated for each protocol.

Results

Modeller-style distance restraints were derived using the procedure outlined earlier, which takes advantage of several developments since the approach was first described.³ Two modifications to the original approach take advantage of the large increase in the number of known structures, which results in a massive increase in the number of residue pairs in homologous proteins that can be structurally aligned.^{2, 11} First, a fraction of the aligned pairs was held out as an independent test set. This data was used to make choices on model structure and parameters based on the log-probability of observing the independent test data. Second, data-intensive nearest neighbor methods were used to obtain the residue distance probability distributions, given a set of observables rather than parametric models, which assume a specific functional form unlikely to hold exactly throughout the range of possible observable values. Finally, the powerful HHSearch remote homologue detection software was used to generate alignments between proteins with more distant evolutionary relationships compared to the alignments used in the original Modeller paper.^{3, 5, 6}

As described in Methods, the differences in distances for over 150 million pairs of aligned residues were classified into one of 10⁴ bins based on the global sequence similarity, burial, local sequence similarity, and sequence distance to the nearest gap, and standard deviations were computed for each bin. The original Modeller approach used a parametric fit to such a table to extract relationships from sparse training data, while we use a nonparametric approach to estimating deviations that should in general fit the data better. The model with 10⁴ bins is difficult to visualize; instead the influence of each variable on the expected deviation from the template structure is illustrated in Figure 1, which shows the expected deviation from templates, given the value of a single predictor feature. The lines within each panel show the extent to which knowledge of individual variables influences the expected divergence between query and template structures. For example, the most confident predictions were from those with very low e-values (Fig. 1, panel A).

To measure the effectiveness of the different statistical models for estimating restraints, given the input alignment data, the likelihood of an independent test set of data was calculated. In this work, likelihood denotes the probability of observing a set of data under a given statistical model. To avoid rounding error associated with multiplying many small numbers, the sum of the negative log-probabilities for each distance was tabulated. A schematic of this approach is shown in Figure 2(A)—the likelihood is maximized when sharply peaked distributions are assigned to predictions with small distance deviations, and wide distributions are assigned to predictions with large distance deviations. The log-likelihood of the independent dataset for models conditioned on different features is shown in Figure 2(B). The leftmost bar shows the likelihood of the native distances under a Gaussian model conditioned only on sequence separation in the polypeptide chain. The next four bars show the log-likelihood associated with the single-variable predictors (shown in Fig. 1). Each single variable predictor improves on the first model by a wide margin, with the HHSearch e-value being the most informative feature and burial being the least informative. The next three panels show the performance of predictors conditioned on two, three, and four features, each of which improves the probability of sampling the independent test set. The likelihood test suggests that the variables are all informative individually, and the most effective model uses all four variables.

Next, we investigated different ways of combining information from multiple templates. Different models for combining information from multiple templates were compared using the likelihood of the independent test data under each model. One free parameter in the construction of these models is the weight on the Gaussian mixture term (Methods section), and different approaches for setting this parameter were investigated (Fig. 2, Methods). A model in which predictions were weighted equally was compared to models in which the weight was a function of the standard deviation. The number of templates used in prediction was varied along with the degree to which high-confidence (low-standard deviation) predictions dominated over low-confidence (high-standard deviation) predictions. The importance of preferentially up-weighting high-confidence predictions from different templates is illustrated in Figure 3 (panel A). For each aligned residue pair in the test set, the aligned templates were sorted based on their HHSearch e-values, and the top scoring alignments (x-axis) were selected for restraint derivation. If all alignments are considered as independent and equally likely (hatched bars), the joint probability of observing the test set becomes worse with increasing numbers of templates as poorer alignments contribute more and more noise. However, if the feature-dependent weighting described in Methods section is used to weight the contributions from different alignments (open bars), the likelihood of the test data improves as the number of alignments is increased. Beyond 10 alignments, there is little further improvement as the relative contribution from the poorer templates becomes very small.

Use of the same set of features to determine both the weighting of the component Gaussians and their variances may appear to count these features twice. However, the two contributions are distinct: the weighting reflects the probability that a particular alignment is correct at the aligned pair of positions, while the variance reflects the breadth of the distributions expected for the residue pair if that alignment is correct. On the other hand, the mutual exclusivity assumption is obviously false, and weighting methods that take into account relatedness between template structures could perhaps yield improved predictions.

The importance of basing both the shape of the individual distributions and their overall weights on the available indicators of local alignment accuracy is further demonstrated in Figure 3 (panel B). The likelihood of a model with fixed-width Gaussians and no weighting of the component Gaussians is clearly worse than a model with variable-width Gaussians, which is in turn worse than a model with both variable-width Gaussians and weighting. For comparison, Figure 3 (panel B) also shows the results with a perfect classifier model that re-weights the template-inferred Gaussians and the prior Gaussian in order to maximize the probability of sampling the native. The perfect knowledge model describes the query distance using a Gaussian with mean set to the query distance and a standard deviation of 1.0. The perfect knowledge and perfect classifier models give upper bounds for the performance of any inferential method in the benchmark. The two models are distinct, because some parts of proteins are never aligned to any templates, and the difference in likelihood for two models illustrates the dependence of our models on the completeness and accuracy of the input alignments to template structures.

Rosetta modeling and refinement using distance restraints

The incorporation of the restraint potential into Rosetta is straightforward and outlined in Methods. A set of 20 proteins from the CASP7 experiment was selected, and alignments to templates were made to pre-CASP7 databases using HHSearch.^{5, 6} Restraints were derived from these alignments using the multitemplate Gaussian mixture model outlined in Methods section. For each protein, 10,000 models were made using the Rosetta rebuild and refine protocol^{8, 9} both with and without restraints. The GDTMM distribution of models constructed with restraints improved in most cases, and the lowest energy models were more accurate in the restrained runs compared to the unrestrained runs (Table I, Supporting Information Text 4).

Table I. Results on CASP7 Structures.

1. Proteins were selected from the CASP7 experiment⁶ that had between 60 and 250 residues and at least one template identified from the PDB with >15% sequence identify. Three protocols were run—spatial restraints incorporated during loop-building, spatial restraints incorporated during full-atom relax, and a control with no restraints. Adding restraints to the refinement portion of the Rosetta comparative modeling protocol improved results significantly. Following refinement, we clustered the lowest 1000 models by Rosetta full-atom energy and calculated GDTMM statistics on the five biggest cluster centers. For each protocol we also examined the number of times that the cluster center with the best GDTMM also had the lowest energy of the five cluster centers.

Target Length %(ID) Method				GDTMM of low-energy models from each protocol
				No restraints	Restrained rebuild	Restrained relax	Restrained rebuild and relax
T0293	250	16.8	X-ray	34.8	45.0	49.8	47.1
T0324	208	21.7	X-ray	71.3	70.0	79.1	73.2
T0297	211	21.74	X-ray	73.8	72.1	72.1	72.5
T0348	68	21.8	X-ray	47.4	46.8	50.3	46.2
T0329	239	22.13	X-ray	69.3	79.7	77.8	76.6
T0373	147	22.52	X-ray	61.8	60.8	66.1	66.6
T0303	224	22.77	X-ray	77.0	76.9	78.5	79.4
T0374	160	23.22	X-ray	76.9	71.8	75.3	78.0
T0380	145	24.66	X-ray	82.3	83.9	83.7	83.3
T0332	159	27.67	X-ray	85.9	84.9	87.5	79.8
T0288	93	29.59	X-ray	85.2	84.9	84.5	84.1
T0317	163	30.54	X-ray	87.2	85.0	89.9	86.1
T0366	106	36.45	X-ray	80.6	80.2	84.0	83.0
T0308	165	41.82	X-ray	89.7	89.6	87.5	89.5
T0359	97	52.51	X-ray	77.3	79.0	79.0	76.9
T0340	90	57.61	X-ray	88.4	94.3	91.6	91.1
T0346	172	59.88	X-ray	93.7	95.7	98.8	97.3
T0290	173	61.27	X-ray	92.9	94.3	97.1	97.7
T0345	185	66.83	X-ray	93.0	95.8	95.6	94.8
T0302	132	97.73	NMR	79.2	81.2	81.5	80.0
Average GDTMM				77.4	78.6	80.5	79.2
P(first model best).				45%	50%	65%	40%

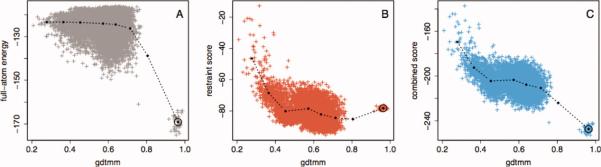
Although the restraints improved sampling, they provide poor discrimination near the native state as the native structure generally violates a number of restraints due to structural differences within the various templates. To investigate the contribution of the spatial restraints more thoroughly, blind predictions were made for target T0569 in the CASP9 structure prediction experiment. Figure 4 shows the average values of the Rosetta full-atom energy and the restraints described in this work as a function of the GDTMM, which varies from 0 to 1 as model quality increases (Supporting Information Text 4). Panel A shows that the Rosetta full-atom energy is very flat until the GDTMM values are in the 0.6–0.7 range, and hence the Rosetta full-atom energy function has difficulty distinguishing between medium (GDTMM between 0.5 and 0.3) and low-quality (GDTMM between 0.3 and 0.1) models. However, the average energy of models with GDTMM > 0.7 drops sharply, and if samples are generated close enough to the native structure, the Rosetta energy is very effective at selecting these high-quality models. The spatial restraints are qualitatively different in behavior—they are very effective at discriminating between low-quality and medium-quality models, but they are quite poor at discriminating high-quality from medium-quality models. These scores solve different model discrimination problems; and, a combination of the scores decreases almost monotonically as models become more nativelike (Panel C). Thus, the joint optimization of the Rosetta energy and the spatial restraints should be effective across the conformational landscape, even though the native structure violates some restraints, and the Rosetta energy has little ability to discriminate conformations that are far from native.

Figure 4.

Full-atom energy and homology-derived spatial restraints distinguish between models in different accuracy regimes. We constructed models for a protein of unknown structure during the CASP9 experiment (CASP9 target T0569). Models were made using the Rosetta rebuild and refine protocol supplemented with the evolutionary restraints as described in Methods section. After obtaining the experimentally determined structure of T0569, we calculated the GDTMM of each model, which approaches 1.0 as a model become more similar to the native (Supporting Information Text 4). The same statistics were calculated for an ensemble of Rosetta refined native structures. Models were assigned to GDTMM bins, which ranged from 0.1 to 1.0 in. increments of 0.1. In each plot, the points connected by lines represent the statistics calculated on each bin, and the gray, red, and blue points represent individual structures. A: Median GDTMM versus median Rosetta full-atom score, with a circle surrounding the bin containing the refined native structures. B: Median GDTMM versus median spatial restraint score. The Rosetta full-atom energy is very effective at discriminating the high-quality from medium-quality models, while less effective at discriminating medium-quality from low-quality models. Conversely, the restraints discriminate medium-quality from low-quality models very well, but are not effective at discriminating high-quality models from natives and can even provide a barrier to sampling the native conformation. C: A combination of the two scores is effective at discrimination independent of model quality.

Discussion

Derivation of probabilistic restraint models

This work describes incorporation of homologous structure-derived restraints into the Rosetta structural modeling methodology. The restraint derivation follows the approach taken by Modeller,³ with modifications to take advantage of more recent advances in database growth and sequence alignment software. A similar set of features was used, but probability estimates used a non-parametric estimation method. This method should in general fit the data more closely as it makes no underlying assumptions about dependencies between the features. This is possible because of the recent growth of the protein structural databases—thousands of proteins of known structures were used here, while Modeller used less than 100 structures due to the size of the database at the time.³ Also, the sensitive HHSearch method used to generate alignments for this work will allow structural models to be constructed based on more distant evolutionary relationships.^{5, 6}

A probabilistic benchmark was used to assess alternate formulations of the comparative modeling restraints. This benchmark shows that the features used in the models are useful both individually and jointly, and the best models investigated are parameterized on a combination of these features (Fig. 2, panel B). The same benchmark demonstrates that improved performance can be achieved by combining predictions from multiple templates using weights dependent on the confidence of each prediction (Fig. 3). This treatment of the problem formulates restraint derivation as an exercise in statistical inference and decouples restraint derivation from computationally expensive structure prediction benchmarks. Progress in this area is thus not restricted to those with access and expertise in structural modeling tools.

Our approach models each restraint as the mixture of two Gaussians, one short-range with mean given by the template distance and a long-range Gaussian with mean dependent only on the sequence separation between the two restrained atoms. The weight on the first component represents our confidence that the alignment is locally correct. Explicitly accounting for the case represented by the long-range Gaussian in which the template-based distance predictions are incorrect allows the optimization process to become more robust to alignment errors. The quadratic penalty associated with a short-range Gaussian becomes extremely large at high distances (Supporting Information Fig. 1, panel B) and would present an inappropriately strong force during model optimization. Incorporating the long-range Gaussian into the mixture model prevents this penalty from dominating structure optimization and refinement (Supporting Information Fig. 1, panel D), allowing Rosetta to disregard inaccurate restraints if they disagree strongly with the current low-energy model.

Joint optimization of energy and evolutionary information

The restraints as outlined earlier were incorporated into the refinement portion of the Rosetta rebuild and refine protocol. The restraint potential for the entire protein was formulated as the negative log-probability of the structure given the restraints. As this term is differentiable with respect to the backbone torsion angles, it can be combined with the Rosetta all-atom energy function and used during full-atom refinement. On a benchmark set of 20 proteins from the CASP7 experiment, inclusion of the restraints led to a clear improvement in model quality (Table I). This is a stringent benchmark for success, as the standard Rosetta rebuild and refine protocol copies coordinates from the same alignments from which restraints are derived. Hence the improvement upon adding restraints to the standard Rosetta comparative modeling protocol must result from confining the optimization to a smaller region of conformation-space that is closer to the native structure (Fig. 4). We also experimented with the incorporation of restraints into the rebuilding portion of the protocol. In general, the results were worse than using the restraints only during refinement (Table I). This may be because rebuilding protocol only moves a part of the protein structure, and satisfaction of the restraints can require moving parts of the protein fixed by this protocol. Also, many of the residues that are flexible during rebuilding are not aligned to any protein, and so there is no restraint information available to guide sampling during this stage of the protocol (Fig. 3, panel B).

Comparative modeling restraints and conformational sampling

There is clear analogy between the results using comparative modeling restraints and previous work incorporating sparse experimental restraints into Rosetta. Protein structures can be determined using datasets too sparse for conventional methods by using the sparse data to increase sampling near the native conformation.¹² The experimental data does not completely determine the native conformation due to experimental noise and a lack of data for some parts of the protein chain, but is sufficient in many cases to guide sampling to the native protein conformation. Similarly, comparative modeling restraints generally do not cover the entire length of the protein and will be inaccurate where the native structure differs from the homologous templates. In both cases, the restraints can be used to focus optimization on the most likely region of conformation-space, and the Rosetta full-atom optimization method can be used to find the lowest energy structure within that region. Comparative modeling restraints are expected to have more systematic errors than those from experimental data, as comparative modeling derives restraints based on statistically inferred relationships between proteins, while experiment can directly query properties of the protein structure. On the other hand, comparative modeling restraints can be derived at essentially no cost for arbitrary protein sequences, and structure determination could in principle begin with structures built by comparative modeling followed by sampling guided by experimental data. If incorporated properly, a combination of evolutionary, experimental, and physical sources of information could significantly decrease the amount of experimental data and computation necessary to determine protein structures.

Software availability

Results for this manuscript were produced using Rosetta 3.2 (SVN version r37323), which is available from http://www.rosettacommons.org/software/. Structural models and input files are available upon request from the authors. Flags for running each protocol are listed in Supporting Information Text S1 and Table SII.