In-vivo Vascular Wall Shear Rate and Circumferential Strain of Renal Disease Patients

Abstract

This study measures the vascular wall shear rate at the vessel edge using decorrelation based ultrasound speckle tracking. Results for nine healthy and eight renal disease subjects are presented. Additionally, the vascular wall shear rate and circumferential strain during physiologic pressure, pressure equalization and hyperemia are compared for five healthy and three renal disease subjects. The mean and maximum wall shear rates were measured during the cardiac cycle at the top and bottom wall edges. The healthy subjects had significantly higher mean and maximum vascular wall shear rate than the renal disease subjects. The key findings of this research were that the mean vascular wall shear rates and circumferential strain changes between physiologic pressure and hyperemia that was significantly different between healthy and renal disease subjects.

INTRODUCTION

Vascular wall shear rate measurement

Patients with chronic kidney disease (CKD) and end-stage renal disease (ESRD) are at high risk of cardiovascular disease associated with vascular calcification (Schiffrin et al. 2007) and accelerated atherosclerosis, caused at least in part by abnormal endothelial function (Schiffrin et al. 2007; Galil et al. 2009; Angelantonio et al. 2010). The vascular wall shear rate (WSR) is associated with impaired endothelial function, and evidence is mounting that WSR is an important indicator of cardiovascular disease (Toborek et al. 1999; Neunteufl et al. 2000; Perticone et al. 2001; Kuvin et al. 2001; Gocke et al. 2002; Modena et al. 2002). The WSR may also help in the diagnosis of the atherosclerosis, which has been associated with low and oscillating mean WSR (Zhao 2002; Irace 2004).

Currently, WSR estimation is usually based on the measurement of peak blood velocity in the vessel center and the assumption that the blood velocity profile is parabolic (Lou et al. 1993; Gnasso et al. 1996; Wu et al. 2004; Stroev et al. 2007). However, in areas of vascular tortuosity, branching and the presence of vascular plaque, the blood velocity profile is non-parabolic (Ku 1997). Therefore, direct measurements of blood velocity near the vascular wall edge may provide a useful tool for determining accurate WSR and reducing measurement dependence on modeling assumptions that may not be universally applicable.

Ultrasound techniques can provide direct, noninvasive measurements of the WSR. Multi-gate ultrasound Doppler measurements have adequate spatial resolution for determining the flow velocity profile at vascular wall edges (Gill et al. 1985); this has been applied to measure the WSR from longitudinal views of blood vessels based on 1D velocity measurements (Brands et al. 1995; Samijo et al. 1998; Levenson et al. 2001; Bambi et al. 2004; Tortoli et al. 2006; Tortoli et al. 2011). Doppler acquisition requires the ultrasound beam to intersect the blood flow at a non-perpendicular angle, and measures the component of the flow projected along the ultrasound beam. In some settings, the WSR may be over or underestimated if the flow direction cannot be determined, when the flow is not parallel to the wall in the presence of vascular tortuosity, branching or atherosclerosis (Gill et al. 1985).

Fortunately, decorrelation based flow velocity measurement is a method that may overcome some of the assumptions associated with WSR measurements. This method has been applied to measure the flow velocity in the transverse view of the vessel (Bamber et al. 1988; Li et al. 1998; Rubin 1999; Rubin 2001; Lupotti et al. 2003). This method is expanded by investigators in this study to identify vascular wall edges, measure WSR directly at the vessel-blood interface, and shows potential advantages for in-vivo patient study.

Arterial stiffness measurement

Arterial compliance has been shown to be a strong indicator of vascular disease, cardiovascular disease and renal failure. Arterial stiffening is caused by a change in the ratio of collagen to elastin in the extracellular matrix of the arterial media (Faury 2001; Bilato and Crow 1996; Bruel and Oxlund 1996). Both arterial compliance and WSR reflect the mechanical function of the vessel, which is indicative of disease condition.

Ultrasound speckle-tracking algorithms (Lubinski et al. 1999) have been applied to measure vascular compliance. The normal arterial wall is a highly nonlinear elastic medium (Bischoff et al. 2002; Humphrey 2003; Humphrey and Na 2002; Vito and Dixon 2003; Kim et al. 2004). The nonlinear characteristics of the arterial wall have been measured using flow mediated dilation (FMD) (Mahmoud et al. 2009). In this study, the vascular wall strains were measured during post-occlusion reactive hyperemia using ultrasound. Other groups have measured the nonlinear elasticity of the arterial wall by lowering transmural pressure with external compression coupled with ultrasound speckle-tracking (Kim et al. 2004; Weitzel et al. 2005; Park et al. 2010). High arterial wall strains can be obtained using FMD, but five minutes of blood flow occlusion is necessary to generate post-occlusion reactive hyperemia (Corretti et al. 2002). In this study, we utilized external pressure to generate high arterial wall strains while limiting the occlusion time; simplifying data collection and minimizing patient discomfort.

The research presented here utilizes ultrasound radiofrequency (RF)-signals acquired from the brachial artery in upper arm for nine healthy, six CKD and two ESRD subjects. The blood velocity profile is measured from transverse views, perpendicular to the blood flow direction in the brachial artery. The WSR is calculated as a function of time throughout the cardiac cycle using three pixels from the vascular wall edge to lumen interior of the blood velocity profile. The mean and maximum WSR are determined during sequential cardiac cycles and compared between healthy and renal disease (CKD and ESRD) subjects. The WSR and vascular circumferential strain are determined for physiologic pressure, pressure equalization and hyperemia. The change in WSR and vascular circumferential strain between the healthy and the renal disease (CKD and ESRD) subjects is compared

MATERIALS AND METHODS

Subjects

A total of 11 healthy, 10 CKD and two ESRD subjects were enrolled for our study after providing informed consent, under a study protocol approved by our Investigational Review Board. Nine healthy, six CKD and two ESRD subjects were selected because their RF-signals showed sufficiently accurate and reliable vascular wall edge tracking to be used for subsequent WSR and strain analysis. The clinical information for the healthy subjects, denoted N1 to N9, the CKD patients, denoted D1 to D6, and ESRD patients, denoted D7 and D8, are summarized in Table 1. Table 2 summarizes the disease states of the subjects.

Table 1.

The healthy and renal disease (chronic kidney disease (CKD) and end-stage renal disease (ESRD)) subjects’ general information (N: healthy subject, D: diseased subject, M: male, F: female, SBP: systole blood pressure, DBP: diastole blood pressure, eGFR: estimated glomerular filtration rate)

	Subject Number	Age	Gender	SBP	DBP	eGFR (ml/min)
Healthy Subjects	N1	53	M	106	58
	N2	60	M	145	85
	N3	41	M	140	80
	N4	66	M	154	70
	N5	24	M	122	64
	N6	60	M	132	84
	N7	55	F	139	76
	N8	46	F	134	80
	N9	37	F	124	70
Diseased Subjects	D1	73	F	142	84	21
	D2	62	F	158	60	16
	D3	62	M	130	60	39
	D4	48	F	142	88	6
	D5	42	F	180	76	10
	D6	66	M	114	64	4
	D7	49	M	160	84	5
	D8	30	M	150	74	*

^*No value due to transplant kidney

Table 2.

The disease state of subjects.

		CKD						ESRD
		D1	D2	D3	D4	D5	D6	D7	D8
Disease	Coronary artery disease
	Diabetes
	Hyperlipidemia
	Arthritis
	Congenital renal disease
	Hypertension
	Myeloma
	Thrombocytopenia

●: Denote the subject has the disease

Measurement instrumentation

The ultrasound scanner (model Epsilon DCI 6000 scanner, Epsilon Imaging, Ann Arbor, Michigan, USA) with a 9-MHz linear array acquired the 19.5 mm × 24.9 mm B-mode images from the transverse view of the brachial artery. The software EchoInsight^™ (Epsilon Imaging, Ann Arbor, Michigan, USA) performed correlation-based, 2D speckle tracking to detect vascular wall edges (Park et al. 2010) using a 5 by 3-pixel kernel and a 9 by 5-pixel filter as well as to measure blood velocity in the vessel lumen.

Measurement protocol

The subjects were examined in the sitting position and their arm was located at the level of the heart. The ultrasound transducer was placed on the anterior surface of the upper arm. The RF-signals were acquired from the transverse views of the brachial artery. The artery remained in the center of the B-mode image by applying continuous freehand positioning over the arterial region of interest during scan data acquisition.

For the physiologic pressure, the dilation of the subject’s brachial artery was observed in response to the transmitted transmural pulse pressure within the artery induced by physiologic cardiac pulsations under normal atmospheric pressure. For the pressure equalization, the artery pulsates maximally when the applied external pressure using the pressure cuff equals the diastolic pressure and the vessel collapses completely when the applied pressure is greater than the systolic pressure. Hyperemia was generated by inflating the pressure cuff for one minute, which is sufficient blood flow restriction to generate reactive hyperemia (Pyke et al. 2005). Figure 1(a) shows the transducer orientation and methods used for the physiologic pressure and the hyperemia measurements and Figure 1(b) shows the pressure equalization measurement method.

Fig. 1.

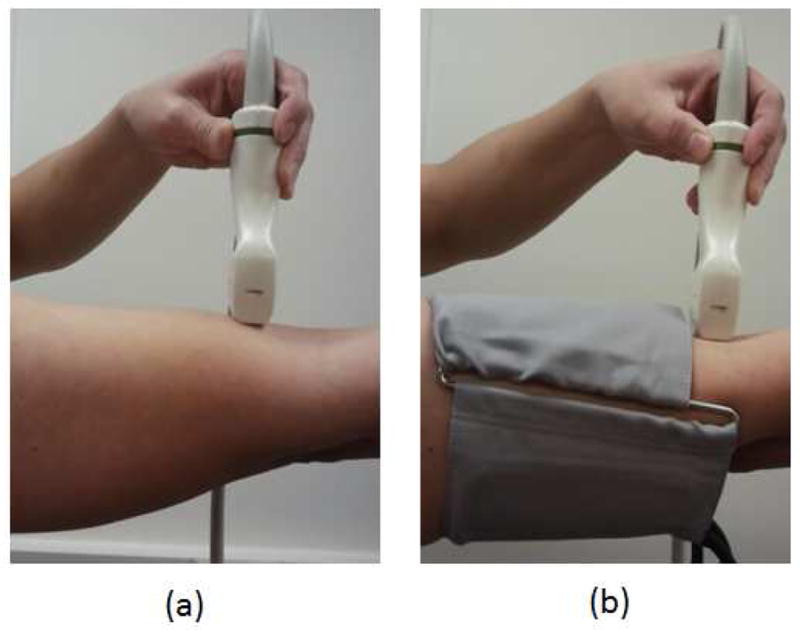
(a) Transverse blood velocity measurement in the brachial artery, (b) transverse blood velocity measurement in the brachial artery with pressure cuff.

Measurement algorithm

Post-processing of RF signals was used to measure the WSR and vascular circumferential strain from the transverse view of the brachial artery for physiologic pressure, pressure equalization and hyperemia. Speckle decorrelation was used to obtain the blood velocity profile from the transverse view of brachial artery. 2D speckle motion tracking was performed over 1000 RF-frames with a 348 Hz frame rate to obtain 999 correlation maps of the artery (2.9 s recording time). A line was visually selected through the vessel center.. Median temporal filtering with a 20 frame moving window was applied to the detected correlation coefficient along the selected line of all 999 frames using MATLAB (version 2009a, Mathworks, Natwick, MA, USA) to reduce the noise from tissue motion by removing large transient signals. A spatial filter was not applied to the correlation coefficient profile because spatial filtering could reduce the accuracy of edge detection by reducing flow signals at edges. The relationship between speckle decorrelation and speckle displacement was obtained through a calibration procedure as described in Rubin et al. (1999). The tissue (blood) velocity profile for each of the 999 selection lines was calculated by integrating the speckle displacement over the time interval between two consecutive frames.

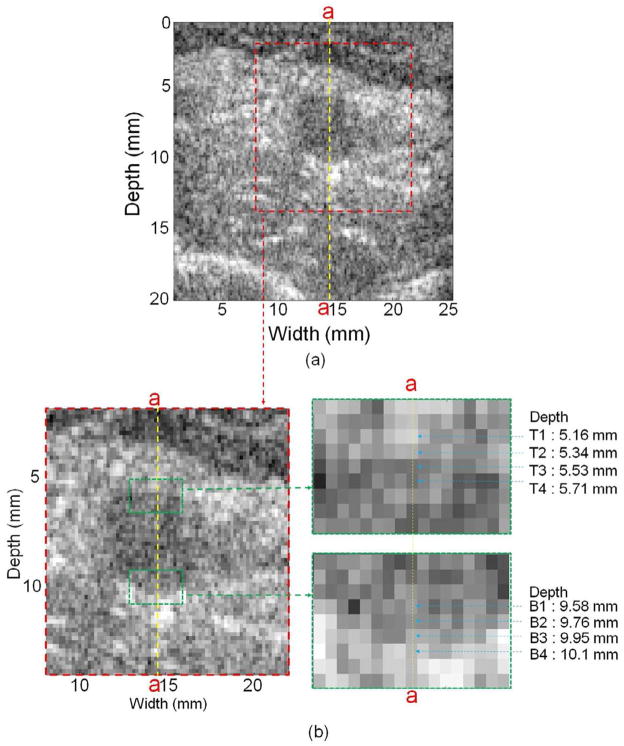
The vascular wall edges were determined from the B-mode image and the 2^nd order gradient of the blood velocity profile. Figure 2 shows an example of a healthy subject (N1) B-mode image of the transverse view of the brachial artery without cuff displaying a close-up view of pixels in the artery near the top and bottom edges as well as the center vessel section line (a-a). Four pixels near the top edge, denoted as T1, T2, T3 and T4, were identified based on the transition of grey scale at depth of 5.16, 5.34, 5.53 and 5.71 mm, respectively. Similarly, four pixels, denoted B1, B2, B3 and B4 in Figure 2(b), were selected near the bottom edge in depth from 9.58 to 10.1 mm. The 2^nd order gradient of blood velocity at T1, T2, T3, T4, B1, B2, B3 and B4 and adjacent pixels along the a-a line was calculated to determine each vascular wall edge. The WSR was calculated over 2.9 s using three pixels from the wall edge to the lumen interior of the blood velocity profile in the transverse view. A moving average filter with 40 frames using MATLAB (version 2009a, Mathworks, Natwick, MA, USA) was applied to remove the noise for WSR vs. time.

Fig. 2.

(a) B-mode image of the transverse view of the brachial artery and (b) close-up views of pixels in the artery and near the top and bottom edges as well as the center vessel section line (a-a). (N1, without cuff)

In each cardiac cycle, the mean WSR, denoted WSR_mean, and the maximum WSR, denoted WSR_max, were calculated and compared between healthy and renal disease (CKD and ESRD) subjects. The average WSR_mean, marked as ${\overline{\text{WSR}}}_{\text{mean}}$, and the WSR_max, marked as ${\overline{\text{WSR}}}_{\text{max}}$, of the two or three cardiac cycles were determined for each subject. For the ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{\text{max}}$, the Shapiro-Wilk test was performed to evaluate whether the measurements were obtained from a normally distributed population. A t-test was performed for the ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{\text{max}}$ to compare the healthy and renal disease (CKD and ESRD) subjects.

Pressure equalization using a pressure cuff was performed on healthy (N1–N9), CKD (D1–D6) and ESRD (D7 and D8) subjects. The ${\overline{\text{WSR}}}_{\text{mean}}$ was determined for the physiologic pressure, pressure equalization and hyperemia and denoted ${\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}},{\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}}$ and ${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}$, respectively. The ${\overline{\text{WSR}}}_{\text{max}}$ was also determined for the physiologic pressure, pressure equalization and hyperemia and denoted ${\overline{\text{WSR}}}_{max}^{\text{PH}},{\overline{\text{WSR}}}_{max}^{\text{PE}}$ and ${\overline{\text{WSR}}}_{max}^{\text{Hyper}}$, respectively. The change of ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{\text{max}}$ was calculated between conditions, physiologic pressure, pressure equalization and hyperemia, and compared between the healthy and renal disease (CKD and ESRD) subjects. The t-test was performed to compare ${\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}},{\overline{\text{WSR}}}_{max}^{\text{PH}}-{\overline{\text{WSR}}}_{max}^{\text{PE}},{\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}},{\overline{\text{WSR}}}_{max}^{\text{Hyper}}-{\overline{\text{WSR}}}_{max}^{\text{PE}},{\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}}$ and ${\overline{\text{WSR}}}_{max}^{\text{Hyper}}-{\overline{\text{WSR}}}_{max}^{\text{PH}}$ for the healthy and diseased subjects. We used the Bonferroni adjustment to account for multiple comparisons of changes in WSR values between the three experimental conditions.

Similarly, in each cardiac cycle, the circumferential strain, denoted ε, was calculated from eqn (1) and compared between healthy and renal disease (CKD and ESRD) subjects.

$$\%\epsilon =\frac{(D_f-D_i)}{D_i}\times 100$$ (1)

where D_f is the vascular diameter at systole, D_i is the minimum diameter at diastole.

The average of circumferential strains ε, marked as ε̄, of the two or three cardiac cycles was determined for the physiologic pressure, pressure equalization and hyperemia and denoted as ε̄^PH, ε̄^PE and ε̄^Hyper, respectively. These strains were compared between the healthy and renal disease (CKD and ESRD) subjects. For ε̄, the Shapiro-Wilk test was performed to evaluate normal distribution of healthy and disease subjects. A t-test was performed for ε̄^PH to compare the healthy and renal disease (CKD and ESRD) subjects. The change of ε̄ was calculated between conditions, physiologic pressure, pressure equalization and hyperemia, and compared between the healthy and renal disease (CKD and ESRD) subjects. The t-test was performed to compare ε̄^PE – ε̄^PH, ε̄^PE – ε̄^Hyper and ε̄^PH – ε̄^Hyper for the healthy and diseased subjects. We again used the Bonferroni adjustment to account for multiple comparisons of changes in ε̄ between the three experimental conditions.

An estimate of the elastic modulus of arterial wall (E) was calculated by compensating the intramural strain for the pulse pressure ( $E=\frac{\mathrm{\Delta }p}{\mathrm{\Delta }\epsilon }$) based on an assumption that surrounding tissue effect on the arterial elasticity is small (Kim et al. 2004; Weitzel et al. 2005).

RESULTS

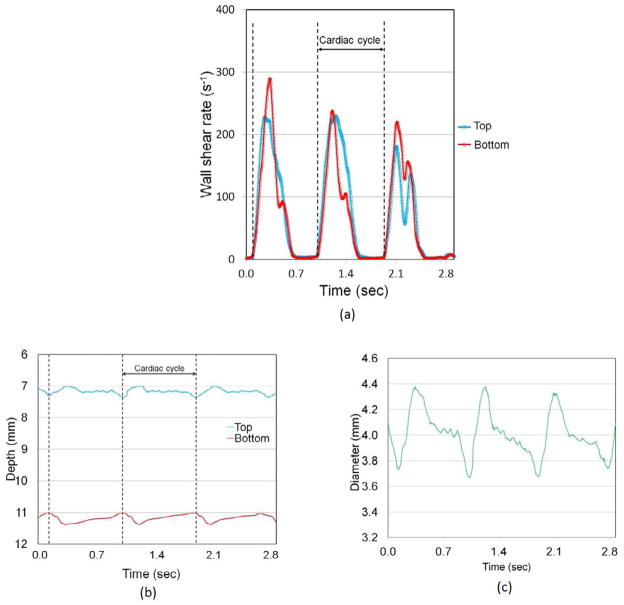
Figure 3(a) shows an example of the top and bottom vessel edge WSR vs. time for a healthy subject (N1) during the 2.9 s recording time which has three cardiac cycles using the decorrelation flow velocity measurement method. The cardiac cycle was determined from the time interval between the sharp gradient changes of the WSR. Figure 3(b) shows the depth of the top and bottom wall edge position vs. time during the recording time. A median filter with 20 frames and moving average filter with 40 frames were applied to the top and bottom wall edge position vs. time for noise reduction. The arterial diameter, as shown in Figure 3(c), was determined by subtracting from the bottom to top wall edges. The arterial diameter changed from 3.7 to 4.4 mm during the cardiac cycle.

Fig. 3.

(a) Time vs. vascular wall shear rate during recording time (in 2.9 s), (b) time vs. top and bottom vascular wall edges during recording time (in 2.9 s) and (c) time vs. arterial diameter during recording time (in 2.9 s). (N1, without cuff)

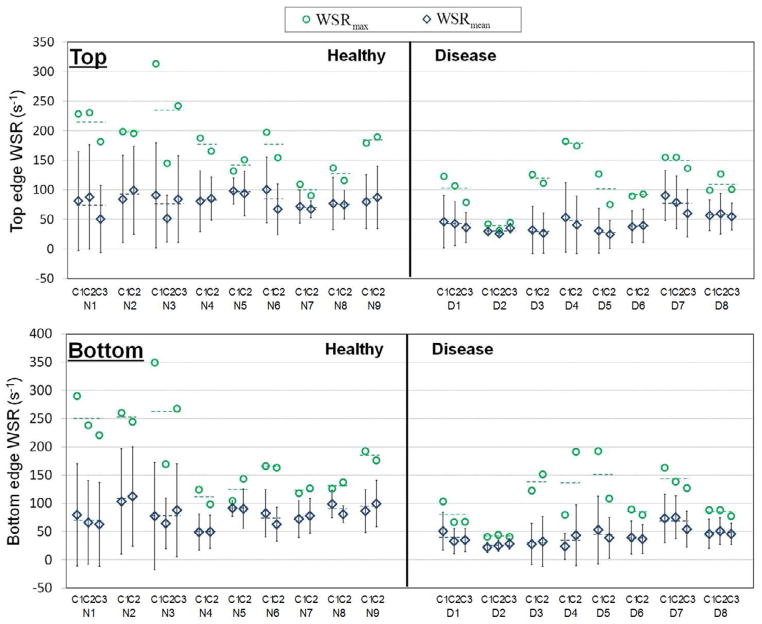
Figure 4 shows the WSR_mean and WSR_max in each cardiac cycle for nine healthy and eight renal disease (six CKD and two ESRD) subjects at the top and bottom wall edges. The WSR_mean and WSR_max are represented as open green diamond and blue circle symbols, respectively. The dashed line represents the ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{\text{max}}$ of the two or three cardiac cycles for each subject.

Fig. 4.

Mean vascular wall shear rate (WSR_mean) and maximum vascular wall shear rate (WSR_max) in each cardiac cycle during physiologic pressure for nine healthy and eight renal disease (six CKD and two ESRD) subjects from top and bottom vascular wall edges. (N1 to N9 representing healthy subjects, D1 to D6 representing CKD subjects, D7 and D8 representing ESRD subjects and C1, C2 and C3 representing cardiac cycles and dotted line representing mean values)

The ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{\text{max}}$ for nine healthy and eight renal disease (six CKD and two ESRD) subjects are shown in Figure 5 at top and bottom wall edges. The dashed line represents the average ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{max}$ for the nine healthy and eight renal disease subject groups. Both the ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{\text{max}}$ had normal distribution for healthy and renal disease subjects with p > 0.05. The average ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{\text{max}}$ were significantly different (p < 0.05)at top and bottom wall edges, as summarized in Table 3, for the healthy vs. renal disease subjects.

Fig. 5.

Mean vascular wall shear rate ( ${\overline{\text{WSR}}}_{\text{mean}}$) and maximum vascular wall shear rate ( ${\overline{\text{WSR}}}_{max}$) averaged over cardiac cycles during physiologic pressure for nine healthy and eight renal disease (six CKD and two ESRD) subjects from top and bottom vascular wall edges. (N1 to N9 representing healthy subjects, D1 to D6 representing CKD subjects, D7 and D8 representing ESRD subjects and dotted line representing mean values)

Table 3.

The average and standard error of the mean (SEM) of average mean vascular wall shear rate ( ${\overline{\text{WSR}}}_{\text{mean}}$) and maximum vascular wall shear rate ( ${\overline{\text{WSR}}}_{max}$) for nine healthy and eight renal disease (six CKD and two ESRD) subjects.

		Healthy (s−1)	Disease (s−1)	p
${\overline{\text{WSR}}}_{\text{mean}}$	Top	80.96±3.03	43.51±5.89	0.00003*
	Bottom	81.54±5.48	40.87±4.66	0.0001*
${\overline{\text{WSR}}}_{max}$	Top	168.8±13.4	111.1±14.5	0.01*
	Bottom	173.7±19.2	107.0±14.0	0.01*

^*p < 0.05

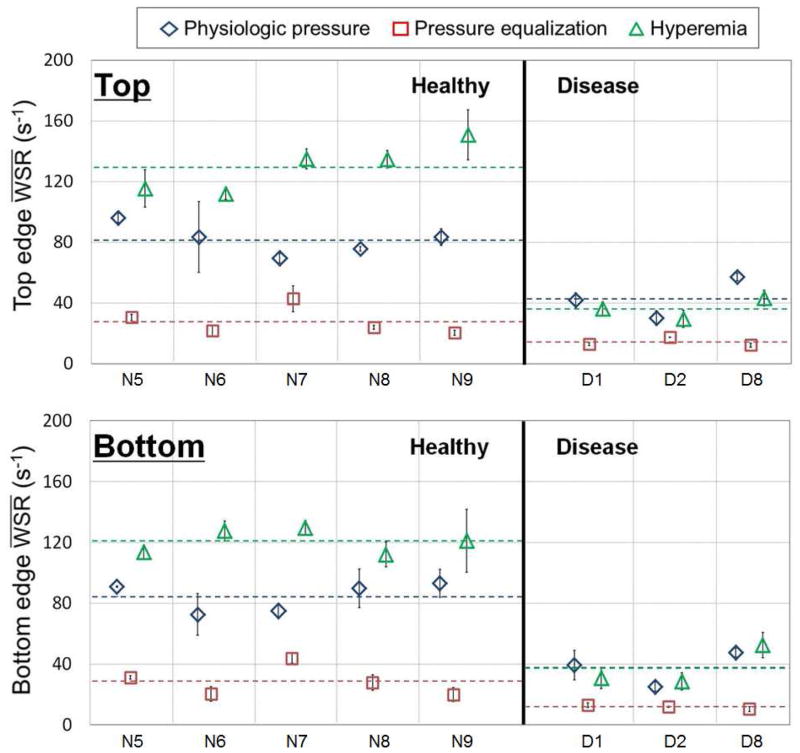
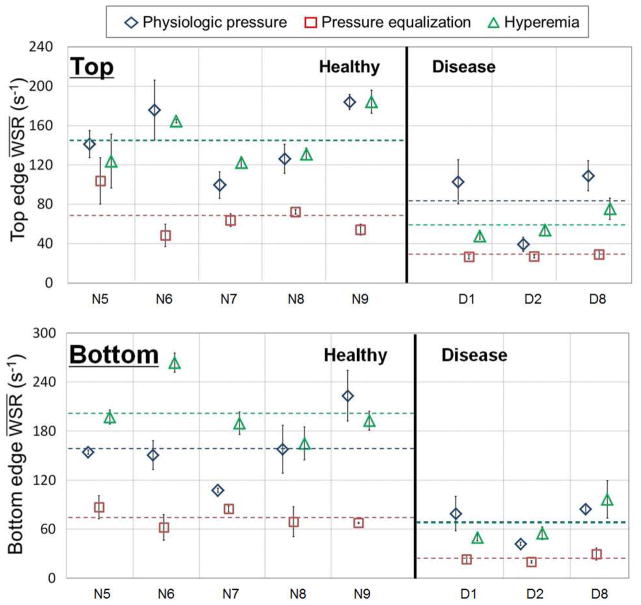
For five healthy and three renal disease (two CKD and one ESRD) subjects, the ${\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}},{\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}}$ and ${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}$ are shown in Figure 6 and the ${\overline{\text{WSR}}}_{max}^{\text{PH}},{\overline{\text{WSR}}}_{max}^{\text{PE}}$ and ${\overline{\text{WSR}}}_{max}^{\text{Hyper}}$ are shown in Figure 7 at the top and bottom wall edges. Changes from the average ${\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}}$ to the average ${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}$ and from the average ${\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}}$ to the average ${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}$ were distinctly different for the healthy and renal disease subjects as shown in Figure 7. As summarized in the t-test results in Table 4, the average ${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}}$ and average ${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}}$ were significant (p < 0.05) at the top and bottom edges for the healthy vs. renal disease subjects. On the contrary, the average ${\overline{\text{WSR}}}_{\text{max}}^{\text{PH}}-{\overline{\text{WSR}}}_{\text{max}}^{\text{PE}}$ and ${\overline{\text{WSR}}}_{\text{max}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{max}}^{\text{PH}}$ were not significantly different for the healthy and renal disease subjects at top and bottom, as summarized in Table 5.

Fig. 6.

Mean physiologic pressure ( ${\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}}$), mean pressure equalization ( ${\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}}$) and mean hyperemia vascular wall shear rate ( ${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}$) averaged over cardiac cycles for five healthy and three renal disease (two CKD and one ESRD) subjects from top and bottom vascular wall edges. (N5 to N9 representing healthy subjects, D1 and D2 representing CKD subjects, D8 representing ESRD subjects and dotted line representing mean values)

Fig. 7.

Max physiologic pressure ( ${\overline{\text{WSR}}}_{\text{max}}^{\text{PH}}$), max pressure equalization ( ${\overline{\text{WSR}}}_{\text{max}}^{\text{PE}}$) and max hyperemia vascular wall shear rate ( ${\overline{\text{WSR}}}_{\text{max}}^{\text{Hyper}}$) averaged over cardiac cycles for five healthy and three renal disease (two CKD and one ESRD) subjects from top and bottom vascular wall edges. (N5 to N9 representing healthy subjects, D1 and D2 representing CKD subjects, D8 representing ESRD subjects and dotted line representing mean values)

Table 4.

The average and standard error of the mean (SEM) of average mean vascular wall shear rate ( ${\overline{\text{WSR}}}_{\text{mean}}$) change under physiologic pressure, pressure equalization and hyperemia for five healthy and three renal disease (two CKD and one ESRD) subjects.

		Healthy (s−1)	Disease (s−1)	p
${\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}}$	Top	53.80±7.19	28.88±9.26	0.08
	Bottom	55.63±6.95	25.58±6.88	0.03
${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PE}}$	Top	101.8±8.40	22.20±5.44	0.001*
	Bottom	92.15±5.00	25.53±8.27	0.0003*
${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}}$	Top	48.00±10.0	−6.68±3.90	0.004*
	Bottom	36.52±7.50	−0.06±4.30	0.006*

^*p < 0.05/3≈0.02

Table 5.

The average and standard error of the mean (SEM) of average max vascular wall shear rate ( ${\overline{\text{WSR}}}_{max}$) change under physiologic pressure, pressure equalization and hyperemia for five healthy and three renal disease (two CKD and one ESRD) subjects.

		Healthy WSR (s−1)	Disease WSR (s−1)	p
${\overline{\text{WSR}}}_{\text{max}}^{\text{PH}}-{\overline{\text{WSR}}}_{\text{max}}^{\text{PE}}$	Top	76.88±21.4	56.23±22.0	0.551
	Bottom	84.57±21.4	44.49±11.1	0.226
${\overline{\text{WSR}}}_{\text{max}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{max}}^{\text{PE}}$	Top	76.74±20.3	31.58±7.71	0.154
	Bottom	127.6±19.1	43.02±12.3	0.02
${\overline{\text{WSR}}}_{\text{max}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{max}}^{\text{PH}}$	Top	−0.14±6.99	−24.7±20.6	0.215
	Bottom	42.97±25.6	−1.47±14.0	0.259

^*p < 0.05/3≈0.02

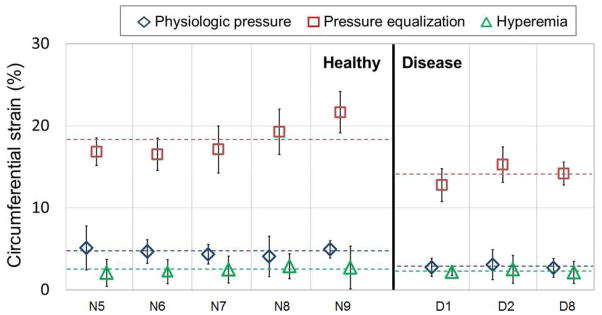
The vascular circumferential strains for physiologic pressure, pressure equalization and hyperemia were measured during the 2.9 s recording time for five healthy and three renal disease (two CKD and one ESRD) subjects. Figure 8 shows the ε̄^PH, ε̄^PE and ε̄^Hyper. The dashed line represents the average ε̄^PH, ε̄^PE and ε̄^Hyper. The ε̄^PH, ε̄^PE and ε̄^Hyper had normal distributions for healthy and renal disease subjects with p > 0.05. The average ε̄^PH and ε̄^PE were significantly different (p < 0.05), as summarized in Table 6, for the healthy vs. renal disease subjects. Changes from the average ε̄^PE to the average ε̄^Hyper and from the average ε̄^PH to the average ε̄^Hyper were distinctly different for the healthy and renal disease subjects as shown in Figure 8. Table 7 shows that the average ε̄^PE –ε̄^Hyper was moderately insignificant and average ε̄^PH –ε̄^Hyper was significant (p<0.05) at the top and bottom edges for the healthy vs. renal disease subjects as shown by t-test performed using the Bonferroni adjustment.

Fig. 8.

Physiologic pressure (ε^PH), pressure equalization (ε^PE) and hyperemia vascular circumferential strain (ε^Hyper) averaged over cardiac cycles for five healthy and three renal disease (two CKD and one ESRD) subjects. (N5 to N9 representing healthy subjects, D1 and D2 representing CKD subjects, D8 representing ESRD subjects and dotted line representing mean values)

Table 6.

The average and standard error of the mean (SEM) of average vascular circumferential strain (ε̄) under physiologic pressure, pressure equalization and hyperemia for five healthy and three renal disease (two CKD and one ESRD) subjects.

	Healthy ε	Disease ε	p
ε̄PH	4.63±0.19	2.83±0.12	0.001*
ε̄PE	18.28±0.97	14.08±0.73	0.02*
ε̄Hyper	2.48±0.15	2.17±0.02	0.17

^*p < 0.05

Table 7.

The average and standard error of the mean (SEM) of average vascular circumferential strain (ε̄) change under physiologic pressure, pressure equalization and hyperemia for five healthy and three renal disease (two CKD and one ESRD) subjects.

	Healthy ε	Disease ε	p
εPE –εPH	13.64±0.99	11.24±0.64	0.14
εPE –εHyper	15.80±0.86	11.91±0.73	0.02
εPH –εHyper	2.16±0.31	0.67±0.11	0.01*

^*p < 0.05/3≈0.02

The average blood pressure for the renal disease and healthy subjects was 160/73 mmHg and 135/75 mmHg, respectively. The pulse pressure (Δp = 73±20 mmHg) of the renal disease subjects was higher than that of the healthy subject (Δp = 59±11mmHg). The arterial wall elasticity changed from 0.7 to 3.5 kPa and from 0.4 to 1.7 kPa from physiologic pressure to pressure equalization for the renal disease and healthy subjects, respectively. This arterial wall elasticity change was significantly different (p < 0.05) for the renal disease and healthy subjects. Thus, the differences in elastic properties between the renal disease and healthy subjects became more pronounced when measured in the low-preload region using pressure equalization as shown in Figure 8.

DISCUSSIONS AND CONCLUSIONS

This study demonstrated that healthy subjects have significantly higher ${\overline{\text{WSR}}}_{\text{mean}}$ and ${\overline{\text{WSR}}}_{max}$ than renal disease (CKD and ESRD) subjects. The findings were substantiated by using analysis from both top and bottom vascular wall edges. The average ${\overline{\text{WSR}}}_{\text{mean}}^{\text{Hyper}}-{\overline{\text{WSR}}}_{\text{mean}}^{\text{PH}}$ was also significantly higher for healthy subjects compared with renal disease subjects, again at both the top and bottom wall edges (p= 0.004 and 0.006, respectively). The healthy subjects had significantly higher ε̄^PH and ε̄^PE than renal disease (CKD and ESRD) subjects. The ε̄^PE –ε̄^Hyper and ε̄^PH –ε̄^Hyper was also distinctively different between the healthy subjects and renal disease (CKD and ESRD) subjects (p= 0.02 and 0.01, respectively). Although this is a small clinical study, an interesting observation is that the WSR and vascular circumferential strain were both found to be significantly different between the study groups. Since the WSR is thought to be an important underlying physical stimulus for vascular dilation it may represent an important indicator for disease, worthy of further study. Since the vascular wall elasticity plays a crucial role in vascular dilation, the vascular wall elasticity measurements may strengthen the assessment of vascular disease in addition to the WSR measurements. Furthermore, these results suggest that using the appropriate measurement and analysis vehicle, WSR and circumferential strain may be practical and robust measurements to determine the vascular sequelae of renal disease or vascular disease in association with renal disease. Important also in interpreting the results of this study, is to recognize that our renal disease group had a high prevalence of vascular disease, which is common for these patients. Knowing this, these results suggest that this measurement method should be tested in future studies in other patient populations with known vascular disease to see if these results are reproducible in other settings. Should these findings be reproducible, this method could potentially provide cardiovascular disease risk stratification.

An additional observation is that a real-time scanner that provides WSR and velocity profiles would be an improvement for future clinical studies to further test the benefits of speckle decorrelation in comparison with Doppler methods. This would allow assessment of velocity information obtained perpendicular to flow, including flow measurements at vessel wall edge, compared directly with Doppler measurements that may be less accurate in detecting small frequency shifts at low flow rates near the vessel edge.

One significant limitation of this study is in our assumption for calculation purposes that the artery is circular in cross section so that the circumferential strain can be computed from two vascular wall edges. Since the artery is not perfectly circular over the entire pressure equalization cycle, this assumption is not completely correct. However, this circumferential strain calculation is an appropriate first order component of strain and not likely to introduce significant error with small deformation under physiologic pressure. These effects will require additional study in the future.

One limitation of the speckle decorrelation method in measuring flow velocity is that the maximum measurable flow velocity is restricted by the maximal frame rate and the beam correlation width. When the speckle movement during the time interval between two consecutive firings of the transducer exceeds the beam correlation width, complete loss of correlation occurs (Rubin et al. 2001). In this study, the limit for accurate decorrelation measurement of flow velocity was about 100 mm/s, which was determined by the beam correlation width (about 0.3 mm) and the acoustic frame rate (348 Hz). Since we were measuring the flow velocity close to the wall, where the velocity is much lower than in the middle of the vessel, and using relatively high frame rates (348Hz), we did not experience this limitation in measuring the WSR. However, this will need to be considered for translation of this method into clinical practice.

In addition to these limitations, we also encountered wall edge detection problems using our automated 2^nd order gradient algorithm due to the well documented echogenicity problem during slow or stagnant flow caused by aggregation of red blood cells (Cloutier et al. 1996; Qin et al. 1998). However, since we were able to sample at a very high frame rate, statistical methods, such as standard error and interpolation, were manually used to minimize this measurement error. We are currently working on methods to automate this measurement noise reduction method.

In summary, this report describes a potentially robust method for vascular assessment based on the WSR and vascular circumferential strain. This method was tested in a clinical pilot study showing significant differences in measurements between disease and control study subjects. Further clinical study is necessary to evaluate the application of these measurements for diagnosis of vascular disease, cardiovascular disease and chronic kidney disease.